2016年南开大学光学(电子信息与光学工程学院)考研考试科目-考研参考书

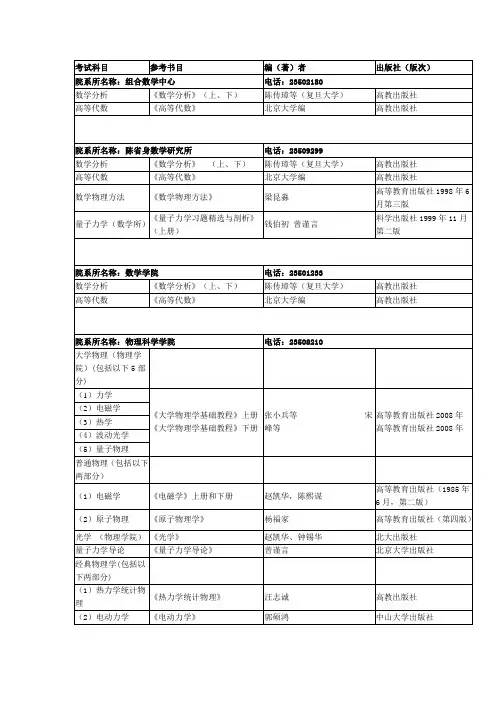
《光学》考试大纲一、考试目的本考试是全日制光学硕士专业学位研究生及全日制光子学与光子技术硕士专业学位研究生的入学资格考试之专业基础课。

各语种考生统一用汉语答题。

各招生院校根据考生参加本考试的成绩和其他三门考试的成绩总分来选择参加第二轮，即复试的考生。

二、考试的性质与范围本考试是测试考生光学知识的尺度参照性水平考试。

考试范围包括本大纲规定的简答、证明、设计和计算水平。

三、考试基本要求1.具备一定光学基础知识。

对光学的基本概念，基本原理，基本计算等内容的掌握程度较高。

2.能够应用光学基础知识解决实际问题。

运用光学等相关物理知识，分析、计算光学问题。

四、考试形式试题采用单项技能测试与综合技能测试相结合的方法，强调考生的基本概念、基本知识的掌握，以及运用知识进行分析、计算、设计等方面的能力。

试题分类参见“考试内容一览表”。

五、考试内容本考试包括三个部分：简答题、证明题、设计题、计算题。

总分150分。

I.简答题1.考试要求考察考生对光学基本概念、原理的掌握程度。

要求考生利用基本概念、基本原理对光学现象进行定性或定量解释。

2.题型要求考生对5个问题进行简要回答。

必要时需要用相关公式、图表等形式进行回答。

每个问题6分，总分30分。

考试时间为约40分钟。

II.证明题1.考试要求根据所需光学知识，对一个特定命题进行证明。

要求学生能够通过公式，图表，语言等手段的综合应用，对该特定命题给出逻辑清晰、公式合理、论述详细的证明。

2.题型试卷提供一个光学命题，要求证明该命题成立、不成立等情形。

共1个小题，共计20分。

考试时间约为20分钟。

【育明教育】中国考研考博专业课辅导第一品牌育明教育官方网站：1III.设计题1.考试要求综合运用光学知识，通过定量分析等方法，设计相关光学实验，实现特定光学应用。

要求借助公式推导，画光路图，列相关图表等手段，对设计方案进行清晰的描述。

2.题型共1小题，共计20分。

考试时间约为30分钟。

Ⅳ.计算题1.考试要求对光学相关问题进行定量计算，并对结论进行分析。

南开大学光学考研真题资料（含参考书信息）南开大学自2013年开始不再指定考研参考书目，官方仅提供考研大纲，这对于备考的研友来讲提出了更高要求。

天津考研网签约硕博团队结合近年考研大纲及考试实际变动总结得出，往年考研参考书对于考研必考仍旧具有重要参考价值。

以下是天津考研网小编为研友汇总的南开大学光学（物理学院）科目详细考研参考书目：①赵凯华《光学》本书是根据作者在北京大学物理系讲授光学课程的讲义修改补充而成。

本书内容丰富，以波动光学为重点，并以“波前”这一概念为纽带联接现代变换光学与传统光学，反映了本学科的现代面貌。

书中附有较多的思考题和习题。

全书分上、下两册。

上册主要内容：几何光学、波动光学基本原理、干涉装置和光场的时空相干性。

下册主要内容：衍射光栅、傅里叶变换光学、全息照相、光在晶体中的传播、光的吸收、色散和散射、光的量子性和激光。

本书可作为高等院校物理专业光学课程教材，也可供其他专业有关师生及工程技术人员参考。

与本书全书习题思考题相应的配套教材《光学习题思考题解答》，已由北京大学出版社出版，可供读者参考。

②《南开大学物理学院光学专业（光学+量子力学导论）考研红宝书》本资料由天津考研网签约的南开大学光学专业高分研究生团队倾力所作，该团队考生在考研中取得了优异成绩并在复试中更胜一筹，该资料包含考研经验、考研试题解题思路分析、复试流程经验介绍以及针对官方指定参考书的重难要点并根据南开大学本科授课重点整理等，从漫漫初试长路到紧张复试亮剑为各位研友提供全程考研指导攻关。

该资料适合于考取南开大学物理学院、泰达应用物理学院光学专业的考生复习使用，也即初试考光学、量子力学导论课程的考生使用。

本资料格式为A4纸打印版+手写版，总量达到了近400页，清晰易复习，已于编写者签订资料保真转让协议，各位研友可放心使用参考！特别提示：本站尽力保证资料的有用性，但由于个人复习态度进度不同，故请酌情参考本资料！南开大学光学考研真题信息本资料部分内容摘自《南开大学物理学院光学专业（光学+量子力学导论）考研红宝书》，更多考研资料请登录网站进行下载！。

天津考研网()天津考研网，考研快乐主义倡导者！天津地区考研门户网站！ 第 1 页 共 1 页 南开大学光学工程硕士考研资料和辅导经验南开大学电光学院的光学工程硕士考研资料其实并不少，而且复习不到位的话要再重新耗费很长时间。

光是指定复习教材有《光学》上下册。

两本书要用四个月的时间学通、学透不是一件容易的事情，对于跨考的同学来说更是难上加难，而且在这期间同学们还要准备复习数学，英语及政治，所以花在光学工程上的时间就更加有限，而这专业课成绩的好坏会直接影响考研录取，因此如何利用有限的时间高效的准备专业课的复习，如何合理安排时间在两门课程间的权重才能达到事半功倍很的效果呢？我必须向考研的朋友们推荐我使过的天津考研网主编的这套《南开大学电光学院光学考研红宝书》，因为我是跨考的，自身对这个专业不了解，甚至说完全陌生。

又没有认识的学长学姐，我能怎么办，我也很无奈啊！但是我在交流群里认识一些考其他专业的朋友，他们都用的天津考研网的资料，我就买这套试试看，到手发现材料特别厚，内容量也很大，不单包含复习指导、总体复习步骤、历年专业课试卷答案及简要分析、还有南开大学光学2013、2015真题答案和解析，如果你们2018考研的孩子需要的话，2017年考研真题会在10月份开售吧。

资料中2013年为原版考研试卷，2015、2017年都是由考生回忆版的。

这套材料中的政治、英语、数学辅导材料、新东方在线考研体验课程都属于赠送的。

关于南开大学光学工程硕士考研辅导的问题，我个人是没有经验的，我想分享给大家一些更有价值的内容所以问来了参加考研辅导同学的经验。

首先他偏文科，政治英语是没问题的，但是光学工程对他来说太难了，自己复习了两个月都发愁的挠头皮叫苦。

无奈，只好选择找辅导班，最先咨询的就是天津考研网，就决定了他家，因为我朋友就是需要本专业的研究生学长一对一的带他，帮着他依据自身情况指定复习计划，平时不是每天都做辅导的，是和研究生学长定好时间，在自己复习几天攒下来一些难题去找学长辅导。

研途宝考研/
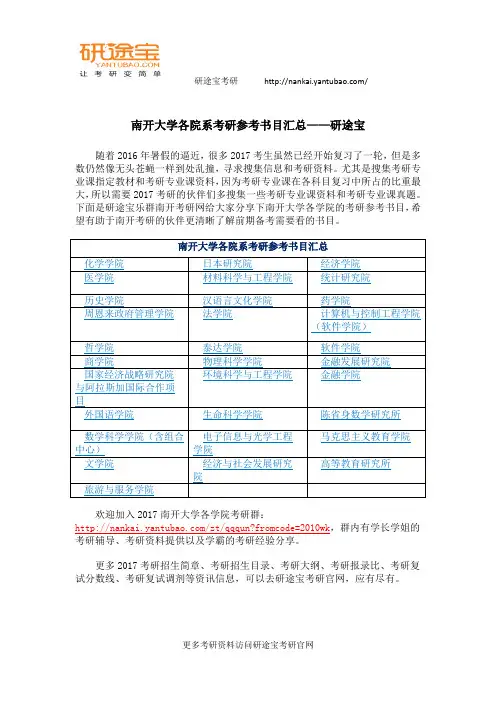
南开大学各院系考研参考书目汇总——研途宝
随着2016年暑假的逼近，很多2017考生虽然已经开始复习了一轮，但是多数仍然像无头苍蝇一样到处乱撞，寻求搜集信息和考研资料。

尤其是搜集考研专业课指定教材和考研专业课资料，因为考研专业课在各科目复习中所占的比重最大，所以需要2017考研的伙伴们多搜集一些考研专业课资料和考研专业课真题。

下面是研途宝乐群南开考研网给大家分享下南开大学各学院的考研参考书目，希望有助于南开考研的伙伴更清晰了解前期备考需要看的书目。

欢迎加入2017南开大学各学院考研群：
/zt/qqqun?fromcode=2010wk，群内有学长学姐的考研辅导、考研资料提供以及学霸的考研经验分享。

更多2017考研招生简章、考研招生目录、考研大纲、考研报录比、考研复试分数线、考研复试调剂等资讯信息，可以去研途宝考研官网，应有尽有。

更多考研资料访问研途宝考研官网。

南开大学考研全面解析南开大学本科科研创新百项工程和国家大学生创新性实验计划的实施，一些同学作为第一作者在国内外顶级刊物上发表高水平论文。

物理学院本科生张英杰等同学的研究论文“Fluorescence enhancement of quantum emitters with different energy systems near a single spherical metal nanoparticle”在光学顶级期刊《Optics Express》刊发。

该论文是张英杰、张若洋、张志帅、朱海波4名同学2008年起承担的本科生创新科研“百项工程”项目“表面等离子体激元对稀土材料发光的影响”的研究成果之一。

该项目的另一研究成果“Surface polariton generation and fluorescence enhancement using a superlens”被同样是光学领域前沿期刊的《Journal of Optical Society of America B》刊登。

化学学院化学专业2007级本科生张时远，在4年期间发表了14篇高水平论文。

其中10篇被SCI收录，影响因子大于4.0的文章有5篇，最高的一篇发表在世界顶级化学刊物Chemical Communications上，为5.504。

他的科技作品“以钴(II)离子作为功能基元的配合物性质研究”在天津市第十一届“挑战杯”中脱颖而出，并获得2011年第十二届“挑战杯”全国课外学术科技作品竞赛一等奖。

2012年11月16日，国际顶级刊物《科学》杂志发表了由南开大学化学学院陈永胜教授组博士生李娜和美国德州达拉斯大学雷·鲍曼教授组博士后马修·立玛共同担任第一作者的研究成果。

研究组发明了由石蜡填充的碳纳米管纤维制造的人工肌肉，这种“肌肉”可以驱动超过自身体重10万倍的重物，并提供超过天然骨骼肌85倍以上的机械功率。

第一章 几何光学例题1.1 人眼前一小物体，距人眼2５厘米，今在人眼和小物体之间放置一块平行平面玻璃板，玻璃板的折射率为1.5 ，厚度为5毫米 ．试问此时看小物体相对它原来的位置移动多远？解：已知玻璃板的折射率5.1=n ，板厚.5mm d =物体S 经玻璃板两次折射成像， 第一次以O 1为原点, 向右为正, 物距s ＝－a ，曲率半径r ＝∞，代入成像公式得00.11=--'as n ，解得第二次成像,以O 2为原点，向右为正，物距为 ,12d na d s s --=-'= 代入成像公式得,01=---'dna n s解得).(nd a s +-='小物体的像向着玻璃板移动了).(35)5.111(5)11()(mm nd d s a s =-⨯=-=-'-=∆1.2 如习题1.2图所示，空气中的尖劈棱镜顶角α很小，折射率为n ，点光源S 到尖 劈棱镜的距离为a ，求S 通过棱镜成的像在何处？并讨论像的虚实．解：点光源S 通过尖劈的两个界面，两次折射成像．第一次折射成像，以原点Ｏ为顶点， 物距为－a ，物方折射率为1.0，像方折射率为n ，曲率半径为无穷大，代入单球面成像 公式，得,0.10.11∞-=--'n as n.1na s -=' 如计算题1.2解图所示建立坐标，像点Ｓ１' 的坐标为（－na ，０），第二次折射成像，以O ' 为顶点，物距为－na ，像距为s '，物方折射率为n ，像方折射率为1.0，曲率半径无穷大，代入成像公式，得 ,0.10.1∞-=--'n na ns,a s -='α ·Sa 计算题1.2图.1na s -=' adS S 'S '1 O 1O 2计算题1.1解图最后像点在点光源上方，由几何关系可求出.)1(a n S S α-='因此，最后像点Ｓ'的坐标为（－a ，a n α)1(-），是虚象．1.3 在报纸上放一个平凸透镜，眼睛通过透镜看报纸，当平面在上时，报纸的虚像在平面下13.３毫米处，当凸面在上时，报纸的虚像在凸面下14.6毫米处．若透镜的中央厚度为20毫米，求透镜的折射率和凸球面的曲率半径．解：人眼看到的是字透过透镜成的像．第一种情况，字在球面的顶点，此次成像物、像重合．字再经过平面折射成像，物距为－20毫米，像距为-13.3毫米，由成像公式，得,0203.130.1=---n（１）第二种情况，字仅通过折射成像，物距为－20毫米，像距为－14.6毫米，成像公式为.0.1206.140.1rn n -=---（２）解（１）（２）两方程，得5.1=n ， 84.76-=r 毫米．1.4 物与像相距为1米，如果物高4倍于像高，求凹面镜的曲率半径，并作出光路图． .解 题中给出凹面镜，0<r ，又知物高４倍于像高，即4/1=β，所以应有两种情况．（１）4/1+=β，则41='-=''=s s s n s n β，即s s '-=4．这说明物像分居于凹面镜的两侧．由于物像之间距离为1000毫米，故可得出像距200='s 毫米．凹面镜成像公式为rs s 211=+'，若以200='s 毫米，800-=s 毫米代入，则得0>r ，不合题意．若用200-='s 毫米，800=s 毫米代入，可求得凹面镜的曲率半径为3.533-=r 毫米．这种成像情况画在计算题1.4解图（a ）中，为虚物实象． （２）若41-=β，则41-='-ss ，即s s '=4．此种情况物像居于凹面镜的同侧．题中报纸 计算题1.3解图Ｘ Ｏ α a 计算题1.2解图 ∙ ∙Ｓ１'S S ' Ｙ Ｏ'给出物与像距离1000毫米，则像距数值为3.333='s 毫米．若选3.333='s 毫米，则得0>r 的结果，不合题意．选3.333-='s 毫米，解得3.533-=r 毫米．此种情况实物成实像，光路图画于计算题1.4解图(b)中．两种情况所得曲率半径一样．1.5 如计算题1.5图 所示的系统，C 为凹面镜的曲率中心，物点S 经薄透镜和凹面镜成像，最后像点S '与物点S 重合，求薄透镜的焦距．解法一：如计算题1.5解图所示，物点S 与像点S ' 重合有两种情况. 第一种情况是：第一次经薄透镜成像,像在凹面镜的曲率中心, 此次是实物成虚象, 物距为-10厘米,像距为-20厘米,代入薄透镜成像公式 ,111f S S '=-'解得cm f 20='．第二种情况是：第一次成像在透镜的２倍焦距处，即凹面镜的顶点，因此有cm f 102='， cm f 5='．计算题1.5图 · · 10cm 10cm 10cm C S S ' 计算题1.5解图· · 10cm10cm10cmCSS 'Ｏ１Ｏ２· ·Ｃ Ｆ 法线 虚物 实像计算题1.4解图(a) Ｆ 法线 实物 实象计算题1.4解图(b)解法二：物点 Ｓ经过透镜和凹面镜三次成像，第一次经透镜折射成像，以Ｏ１为顶点，向右为正，物距cm s 10-=，像距为1s '，焦距为f '．根据薄透镜成像公式得方程：,110111f s '=--'（１）第二次经凹面镜反射成像，以Ｏ２为顶点，向右为正，物距为),10(1cm s -'像距为2s '，曲率半径r=-30cm 由反射镜成像公式得方程：,302)10(1112-=-'+'s s （２）第三次经透镜折射成像，以Ｏ１为顶点，向左为正，物距为cm s )10(2+'-，像距为s '，代入成像公式，得：,1)10(112f s s '=+'--'（３）联立方程（１）、（２）、（３），得两解.5,2021cm f cm f ='='1.6 一个新月形状的薄凸透镜，由折射率 n=1.5的玻璃制成．半径为15厘米的后表面镀铝，半径为20厘米的前表面正前方40厘米处的光轴上，有一高1厘米的实物．试求最后像的位置、大小和虚实．解：薄透镜厚度不计，如计算题1.6解图所示，O 1 O 2距离可视为零．物经系统三次成像． 第一次折射成像，以O 1为原点，向右为正，物距为－40cm ，物方折射率为１.0，像方折射率为１.5，r 1=-－20cm ，代入单球面折射成像公式，得.200.15.1400.15.11--=--'S解得第一次成像的像距为cm s 301-='．垂轴放大率21)40(5.1)30(0.111=-⨯-⨯='=nss n β．第二次反射成像，以Ｏ2为原点，向右为正．物距为－30cm ，像距2s '，曲率半径r ２=－15cm ，代入球面反射成像公式，得.15230112-=-+'s解得,102cm s -='第二次成像的垂轴放大率为313010122-=---=''-=s s β．第三次折射成像，以Ｏ1为顶点，向左为正．物距为10cm ，像距为s '．物方折射率为1.5，像方折射率为1.0，曲率半径为20cm ．代入成像公式，得205.10.1105.10.1-=-'s .解得cm s 8='，最后像的位置在镜前８cm 处．第三次成像垂轴放大率为2.1100.185.13=⨯⨯=β系统的总放大率为：.2.02.1)31(21321-=⨯-⨯=⋅⋅=ββββ因此，系统最后成像高为.2.012.0cm y y -=⨯-=⋅='β 系统最后成一缩小的、倒立的实象.1.7 如计算题1.7图所示，薄透镜是一透明容器，两侧呈曲率半径相同的凹球面的，器壁甚薄，可不计厚度．左侧为空气，右侧为n ＝4/3的水．试问在容器中到入液体的折射率xn 为多大时，才能对左侧轴上10厘米远的实物产生一正立、同大的虚象？解产生正立同大的虚象，为无焦系统，系统的光焦度0=φ．又因系统的光焦度为两个折射球面的和，即0121=-+--=+=rn n r n xx φφφ，且∞≠r ，故有 0237=-x n ，67=x n ．1.8 正透镜将某物成像于屏幕上，已知实象高50毫米，物至幕的距离150毫米．在物至幕的距离不变的情况下，如何移动透镜才能在幕上得高度为20毫米的实像？解 现将两种成像情况表示在计算题1.8解图中．第一种情况，实物成实象．物与像距离Ｄ＝150毫米，设物距为s 1，则像距为11s D s +=', (1)设第二种情况透镜移动距离为d ，则第一种情况下物距可表示为2/)(1d D s --=． (2)第二种情况物距为12s s -='，像距为d s s -=12．设物高h ，则有 h s s 5011-='， (3)hds s 2011-=--.(4)1 O 240cm 计算题1.6解图 Ｓ S ' 0.1=n3/4='n10cmx n计算题1.7图将已知量代入，解上面四个方程，得第二次成像透镜移动的距离d=33.75毫米．1.9 计算题1.9图中四面直角体，其顶角A 到斜面的距离为d ，四面直角体由折射率为n 的玻璃制成，试证明由斜面进入四面体的光线，依次经过三个相互垂直的平面反后，出射光线与入射光线反向，并求出光在四面直角体中的光程．（四面直角体的折射率为n ）解：如计算题1.9解图(a)建立坐标系．设xz 面、yz 面和xy 面分别为1面、2面和3面．光线MP 以 i 角入射于斜面上P 点，折射后方向为(cos α,cos β,cos γ)．α、β、γ 分别为光线PO 1与三个坐标轴的夹角.光线PO 1经1面反射后,方向变为(cos α, -cos β, cos γ) 再 依 次经2面3面反射后, 方向变为 (-cos α, -cos β, -cos γ)．因此, PO 1与O 3P '平行反向, MP 与P 'M '平行反向.光线在四面体走过的光程为光程[L]可以用镜像法求出．将四面体依次对1面，2面，3面成像，三次像的位置分别在第4，第3和第7挂限．斜面在第7挂限的位置与在第1 挂限的位置严格平行，相距2d ．延长光线PO １，延长线依次通过第4，第3和7挂限，且必过P '点在第7挂限的像点P "，PP "等于光在四面直角体中走过的路程，由计算题１.9解图(b)，其光程为)(][332211P O O O O O PO n nL L '+++==计算题1.9图A Ｐ Ａ 屏幕150mm d 计算题1.8解图 －s 120 50 S '1S '2 计算题1.9解图 y Ｍ' x1o2o 3o１２ ３ Ｍ（a ） P P ' z i 'i ２d Ｐ" (b ) Ｐi nd P P n L '=''=cos /2)(][其中22/)(sin 1cos n i i -='．1.10 一开普勒天文望远镜，物镜的焦距为40厘米，相对孔径为f/5.0．今测得出瞳孔直径为２厘米，试求望远镜的放大率和目镜的焦距．解 已知开普勒望远镜相对孔径为0.5/f ，焦距40='f 厘米，所以它的直径为80.5/401==D 厘米．出瞳直径为21='D 厘米，所以放大率4/1-='-=D D M .由于放大率21/f f M ''-=＝－４，可求出102='f 厘米．1.11 一架显微镜，物镜焦距为４毫米，中间像成在物镜第二焦点后160毫米处．如果目镜是20⨯，问显微镜总的放大率是多少？ 解 显微镜的物镜成像公式为111111f s s '=-'，现已知41='f 毫米，1641='s 毫米，代入上式求得物距为1.41644164411111-=-⨯='-'''=s f s f s （毫米）．被观察物恰在物镜物方焦点外一点点的地方，物镜的垂轴放大率401.4164111-≈-='=s s β．乘以目镜的放大率，得显微镜的总放大率80020)40(-=⨯-=M ．得放大的倒像．1.12 开普勒望远镜的物镜焦距为25厘米，直径为５厘米，而目镜焦距为５厘米，调节望远镜的远点置向无限远处，如果在目镜外放置一毛玻璃，改变毛玻璃的位置时，在毛玻璃上可以看到一个尺寸最小，但边界清晰的圆形光圈．试求: （1） 此时毛玻璃与目镜相距多远？ （2） 毛玻璃上的圆圈直径有多大？解 （１）物镜的孔径Ｄ＝５厘米，焦距为25厘米，目镜的焦距为5厘米. 物镜到目镜的距离为3021='+'f f 厘米．在开普勒望远镜系统中，物镜为孔径光阑，其相对于目镜的像为出射光瞳．由薄透镜成像公式，可求出出射光瞳的位置和大小．5130112=--'s ，解得62='s 厘米． 将开普勒望远镜的光路作在计算题1.12解图中，由图中可以看出，成像光束都通过出瞳，光束在出瞳处孔径最小，因此毛玻璃应该放在出瞳处，距目镜６厘米．（２）毛玻璃上光斑直径就是出瞳直径，为15306=⨯=='D D β（厘米）．ＤＤ'物镜目镜计算题1.12解图毛玻璃作图题1.1 已知作图题1.1图中1和1'是一对共轭光线，作图求2的共轭光线.．解 已知共轴球面系统的节点、主点、共轭光线1和1'及光线2，求２的共轭光线的步骤是（见作图题1.1解图）： （1) 过节点N 、N '作平行于１的共轭辅助光线３和3'，3'必定和1'交于系统像方焦平面上一点，过此交点作光轴的垂线，得到像方焦点． （2) 过节点N 、N '作平行于２的共轭辅助光线４和4'，4'交于系统像方焦平面上一点． （3) 延长光线２，交于物方主平面上一点，其共轭光线2'必定由像方主平面上的等高点出发，过4'与像方焦平面的交点出射．1.2 如作图题1.２图所示，已知共轴球面系统的主点焦点，作图求光线1的共轭光线１'．解：已知光线１、共轴球面系统的焦点和主点，且两焦距不同，因此主点与系统的节点不重合．作图步骤为(见作图题1.2解图)：（１） 过物方焦点Ｆ作光线１的平行线２，光线２到达物方主平面，其共轭光线2'由像方主平面的等高点出发平行光轴出射．（２） 延长光线１到系统的物方主平面，其共轭光线1'由像方主平面上的等高点出发,过2'与像方焦平面的交点出射.H ' N 'H N 11'2作图题1.1图 H H ' · F· F ' 作图题1.2图１ Ｎ Ｈ Ｎ'Ｈ' １ 1'F ' 2 2' 3 3' 44'作图题1.1解图 Ｆ'⋅⋅1 1'F F ' 2 2' 焦平面作图题1.2解图 H H '１.3 惠更斯目镜由两片平凸薄透镜组成（作图题1.3图），场镜L 1的焦距为a 3，接目镜L 2的焦距为a ，两透镜间距为a 2．试用作图法求惠更斯目镜的焦距和焦点、主点的位置．解 惠更斯目镜系统子系统的基点已知，作图法求系统的基点的步骤是： （１） 作一条平行于光轴的入射光线１，该光线过场镜Ｌ1后，拐向L 1的焦点F '1．1'为光线1在场镜L 1和接目镜L 2之间的共轭光线．（２） 过透镜Ｌ２的光心（Ｌ２的主点和节点）作一条平行于光线２'的辅助线（图中用虚线），该辅助线交接目镜Ｌ２的焦平面于Ｐ点．（３） 1'在L 2后的共轭光线1"必经过P 点．（４） 1"与光轴的交点就是系统的像方焦点Ｆ'．反向延长1"，该延长线与光线１的延长线交点必在系统的像方主平面上．过两延长线交点作光轴的垂线，交光轴于像方主点（平行于光轴的入射光线，到达像方主平面上开始拐折，并拐向系统的像方焦点）．由作图题1.3解图可以看出，系统的像方焦距为1.5a ，为正值，是会聚系统．可以作一条平行光轴的出射光线用同样的方法求系统的物方主点和物方焦点，问答题1.1 平面镜反射成像时，像和物左右互易，为什么像和物并不上下颠倒？答：平面反射镜是一个理想的光学系统，其物、像对于镜面是对称的，人照镜子感到左右互换，上下不颠倒，不过是照镜子人的主观看法．设想人要是躺在床边上照镜子，他会得出镜子成像上下颠倒左右不颠倒．实际上平面镜是镜面对称成像．这种像加上人们平时观察物体的习惯，就产生了上面的混乱的观点．1.2 为什么金刚石比切割成相同形状的玻璃仿制品看起来更加闪耀夺目？答：作为透明介质的金刚石，其折射率比一般玻璃要大．根据菲涅耳反射公式可知，对于相同形状的金刚石和仿制品，金刚石的反射光强要比纺仿制品的大，所以显得更亮．而题中所说闪耀的含义是有些表面看起来特别亮，而另一些表面看起来则不甚亮．即不同倾斜程度的表面，其反射光强差别很大．或同一表面的不同方向观察，其反射光强变化剧烈，因此形成闪耀的印象．作图题1.3解图 ２a a３a Ｌ１ Ｌ２F 1'F '2 F ' H '１ 1'Ｐ1" 焦平面主平面作图题1.3图２aa３a Ｌ１ Ｌ２ F 2 F 1' F 2'由于金刚石折射率高，其能发生全内反射的临界角小，具有各种不同倾斜度内表面的金刚石较之相同形状的玻璃制品更易发生全内反射，所以显得更加闪耀夺目．1.3调节显微镜是改变载物台与镜筒间相对距离而不改变物镜和目镜的相对距离．但调节望远镜却采用调节物镜和目镜相对位置的办法，何以解释？答：显微镜的焦距是确定的，为了把它的β标定在物镜上，则必须固定它的物距和像距．我+∆）为定值，即筒长固定，而在实用中调节物距，使它正是β所要求们使像距（即f '物的物距值，这样做既可能，又方便．望远镜的物距几乎是无限大，实用中调节物距是无效的．故我们可以调节物镜和目镜的间距，使物镜的像正好落在目镜的焦平面上．1.4正常人眼使用开普勒望远镜看星星时，将使物镜焦距与目镜焦距重合，若对近视眼和远视眼，应如何调节？答：正常人眼，远点在无穷远．近视眼的眼球过长，当睫状肌完全松弛时，无限远的物体成像在视网膜的前方，它的远点在有限远的位置．因此对于近视眼，开普勒望远镜的目镜应当向靠近物镜的方向移动一点，以便使光学间隔∆为负值，保证向近视眼投以发散光束．远视眼的眼球过长，无穷远的物成像在视网膜的后方，因此开普勒望远镜的目镜应该向着远离物镜的方向移动一点，使光学间隔∆为正，以保证向远视眼投以会聚光束．1.5若在惠更斯目镜、冉斯登目镜中放叉丝，应放在什么地方？目镜本质上是放大镜，为什么惠更斯目镜不能当放大镜使？答：惠更斯目镜的物方焦点位于场镜和接目镜之间，即故不能观察实物，不能做放大镜使用．叉丝应放置在接目镜的物方焦平面上，此处为虚物平面．冉斯登目镜的物方焦点在场镜表面上或场镜前一点的地方，叉丝和物镜的像都应放置在这一位置上．填空题1.1人眼是__ ；望远镜是；显微镜是_ ；惠更斯目镜是_ _．（变焦系统，无焦系统，发散系统，会聚系统）1.2一台开普勒望远镜，其孔径光阑位置在，视场光阑位置在_ ．1.3人眼作为一个观察系统，当物在的位置时人眼最放松．1.4正常人眼，远点在无穷远，近点约在眼前1０厘米处．与正常人眼相比，近视眼远点变得更加___，近点变得更加_ ____；远视眼远点变得更加_ __，近点变得更加_ ____．1.5共轴球面系统光轴上有一点，当整个系统绕这一点转动一小角度时，焦平面屏幕上的像点不移动，这点是_ _____．1.6一个实际的光学系统一般都有孔径光阑和视场光阑，这两种光阑中最有效控制成像光束光能量者是_，最有效限制成像物空间范围者是___．1.7在讨论几何光学成像问题时，用笛卡儿坐标规定物距和像距符号．可以根据物距和像距的正负来判定物、像的虚实．对于薄透镜，物距大于零为____物，物距小于零为__ ___物，像距大于零为_ 像，像距小于零为__像；对于反射球面镜，物距大于零为_ ____物，物距小于零为____物，像距大于零为___像，像距小于零为_____像．选择题1.1下列四种说法正确的是：（1）游泳池的实际水深比站在池边的人所感觉到的水深要深；（2）二氧化碳（n=1.63）中的凸透镜(n=1.50)将具有会聚性质；（3）空气中的凸薄透镜对一切实物构成一倒立实象；（4）空气中的凹薄透镜对实物均得一正立的虚象．1.2两个薄凸透镜，焦距分别为f1和f2，将它们叠在一起组成一个系统，则其总的焦距应是：（1）f = f1+f2；（2）f= - f1f2/(f1+f2)；（3）f = f1f2/（f1+f2）；（4）f = （f1+f2）/f1f2．1.3 图中，光学元件的折射率小于它周围介质的折射率，下面的光路图对的是1.4 下面的说法正确的是（1） 球面折射系统的焦距与系统所在介质的折射率有关，而光焦度与系统所在介质的折射率无关；（2） 球面反射系统的焦距与系统所在介质的折射率无关，光焦度与系统所在介质的折射率有关；（3） 光焦度大于零的系统为会聚系统，光焦度小于零的系统为发散系统；（4） |φ|大的系统对平行光的拐折本领大，|φ|小的系统对平行光的拐折本领小．1.5 玻璃三棱镜对白光分光的作用，是由于：（1） 在棱镜中不同色的光反射不同；（2） 在棱镜中不同色的光传播速度不同；（3） 在进入棱镜后的折射不同；（4） 某一色的光进入棱镜后改变了其频率．1.6 对于一个光学系统，物方折射率是：（1） 实物和虚物所在的几何空间的折射率；（2） 未经系统变换的光束所在的几何空间的折射率；（3） 入射光瞳、入射窗所在几何空间的折射率．1.7 一束平行单色光从左则进入光学元件箱，已知自元件箱出射的光束有下面选择题１.7图(一)中有四种情况，每一种情况对应的装置分别是选择题１.7图(二)中的哪一种？(a) （d） （c ） （b ） 选择题1.3图（二）（１） （２） （３） （４）选择题１.7图（一） （b ） （c ） （a ）（d ）1.8空气中的薄负透镜可以使：（1）虚物成放大的虚象；（2）实物成缩小的实象；（3）虚物成放大的实象；（4）虚物成缩小的实象；（5）实物成放大的实象．1.9凹面镜可以有（1）虚物成虚象的情况；（2）实物成放大的虚象的情况；（3）实物成缩小的虚象的情况；（4）实物成正立的实象的情况．。

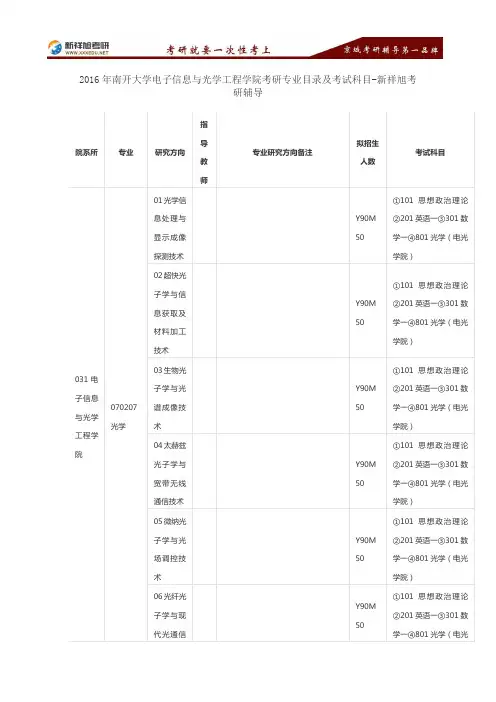
2016年南开大学电子信息与光学工程学院考研专业目录及考试科目-新祥旭考研辅导院系所专业研究方向指导教师专业研究方向备注拟招生人数考试科目031电子信息与光学工程学院070207光学01光学信息处理与显示成像探测技术Y90M50①101思想政治理论②201英语一③301数学一④801光学（电光学院）02超快光子学与信息获取及材料加工技术Y90M50①101思想政治理论②201英语一③301数学一④801光学（电光学院）03生物光子学与光谱成像技术Y90M50①101思想政治理论②201英语一③301数学一④801光学（电光学院）04太赫兹光子学与宽带无线通信技术Y90M50①101思想政治理论②201英语一③301数学一④801光学（电光学院）05微纳光子学与光场调控技术Y90M50①101思想政治理论②201英语一③301数学一④801光学（电光学院）06光纤光子学与现代光通信Y90M50①101思想政治理论②201英语一③301数学一④801光学（电光传感技术学院）080300光学工程01光学信息处理与显示成像探测技术Y90M50①101思想政治理论②201英语一③301数学一④801光学（电光学院）02超快光子学与信息获取及材料加工技术Y90M50①101思想政治理论②201英语一③301数学一④801光学（电光学院）03生物光子学与光谱成像技术Y90M50①101思想政治理论②201英语一③301数学一④801光学（电光学院）04太赫兹光子学与宽带无线通信技术Y90M50①101思想政治理论②201英语一③301数学一④801光学（电光学院）05微纳光子学与光场调控技术Y90M50①101思想政治理论②201英语一③301数学一④801光学（电光学院）06光纤光子学与现代光通信传感技术Y90M50①101思想政治理论②201英语一③301数学一④801光学（电光学院）080900电子科学与技术01光伏材料、器件与应用电子综合基础含：数字电路、模拟电路各1/2；大学物理（电光学院）含：电磁学、光学各1/2。

第三章 光的干涉例题３.1 菲涅耳双面镜干涉装置．双面镜M 1和M 2的夹角是20角分，准单色缝光源S 对M 1和M 2成两个虚的相干光源S 1和S 2， S 到双面镜交线的距离L 1=10厘米，接收屏幕与双面镜交线的距离L 2=100厘米，光源所发光的波长λ=600纳米．试问屏幕上干涉条纹间距是多少？解:由菲涅耳双面镜干涉装置条纹间距公式ϕλ1212)(L L L x +=∆，式中 弧度0058.01803,1000,10010,60021=⨯=====πϕλmm L mm cm L nm 代入上式,得 mm x 57.0=∆.３.2 将焦距为 50厘米的薄正透镜从正中切去宽度为a 的部分,再将剩下的两半粘接在一起, 形成一块比累对切透镜,如计算题 3.2图所示. 在透镜一侧的对称轴上放置一个波长为600纳米的单色点光源,另一侧远方的垂轴屏幕上出现干涉直条纹 ,测得条纹间距为5.0毫米,且沿轴向移动屏幕时条纹间距不变,求a .解：在比累对切装置中，若将屏幕前后移动干涉条纹间距不变，则干涉区是有一定夹角的两平行光波干涉场，干涉条纹间距公式)2/sin(2/θλ=∆x ，θ为两相干光束夹角． 点光源Ｓ位于比累对切透镜的焦平面上．比累对切透镜中心不是透镜的节点．对于下半透镜，节点在Ｏ1点,对于上半透镜，节点在O 2点（计算题３.2解图），Ｏ1Ｏ2的距离即为切去部分的长度a ．由几何光学作图法，可以画出光束经比累透镜上下两部分折射后的平行光束．根据图中的几何关系有,sin f a '=θ).(6.05.010600500sin 6mm x f f a =⨯⨯=∆'='=-λθ计算题3.2图３.3 将杨氏双缝干涉装置照明光源波长为λ，S 2缝覆盖以厚度为h ，折射率为n 的透明介质薄膜（计算题3.3图），使零级干涉条纹移至原来的第Ｋ级明条纹处，试问介质薄膜的厚度h 是多少？解：如计算题 3.3图所示，Ｓ2缝盖以透明介质片，介质片产生附加光程差为h n )1(-=∆因为零级明条纹移至原来第Ｋ级明条纹处，在原K 级明条纹处,)1(21h n r r -=-λk r r =-12,因此有1--=n k h λ. 介质片厚度应为正值，因此Ｋ为负值，零级条纹应在屏幕的下方．３.4 如计算题３.4图所示的杨氏干涉装置．双孔屏S 1S 2右侧10厘米远处放置一枚焦距为10厘米的薄凸透镜L ，L 的光轴与干涉装置的对称轴重合．在L 的右侧10厘米远处又放置一垂轴屏幕．已知双孔间距d=0.02毫米，且用λ=500纳米的光照明．试计算题3.4图计算题3.3图解：杨氏双孔恰在透镜Ｌ的焦平面上，自双孔发出的相干光，经过透镜拐折后，变为夹角为α的两束平行光（计算题３.4解图a ）．两束平行光的夹角为f d '=/α．今将两束平行光波场表示在计算题3.4图(b)中．两相干光波为平面波，Ｋ1、Ｋ2分别表示两波的传播方向，在干涉场中，两平面波波峰与波峰相重和波谷与波谷相重的点为相干加强的点．在三维空间中，这些点形成一组等间距、平行于两相干光束夹角平分面的平面．计算题3.4解图（b ）中，屏幕上Ａ和Ｂ点就是相干加强的点，是干涉明条纹的中心，显然，ＡＢ两倍于条纹间距．由图中的几何关系，得条纹间距)(5.210002.0105002/sin 26mm f d x =⨯⨯='=≈=∆-λαλαλ．３.5 在计算题3.4中，将透镜L 向左移近双孔２厘米，则屏幕上的条纹间距是多少？解法一：如计算题3.5解图（a ）所示，若无透镜Ｌ，屏幕上Ｐ点光强由r １和r ２的光程差来决定．加透镜后，r １和r ２拐折了，不在Ｐ点会聚了．双孔屏和屏幕被透镜隔开在两个不同的光学空间．Ｐ点的光强由另外两光线Ｒ1和R 2的光程差决定．Ｒ1和R 2应分别发自Ｓ１和Ｓ２．怎样确定Ｒ1和R 2？Ｒ1和R 2会聚于Ｐ点，必来自Ｐ的共轭点Ｐ'．用薄透镜成象公式求出Ｐ'点的位置．这里物距12-=s 厘米，焦距10='f 厘米，代入成象公式计算题3.4解图（a ）计算题３.4解图(b),1011211=--'s 解得60='s 厘米， 垂轴放大率1260-='=s s β．设Ｐ和Ｐ'点到光轴的距离分别为h 和h '，则,5h h h -=='β因此，Ｐ'在Ｌ左60厘米、光轴下－５h 处（计算题3.5解图a ）．相干光束必从Ｐ'出发，分别过Ｓ１和Ｓ２，经Ｌ拐折后会聚到Ｐ点．双孔前面光程分别为［Ｒ'１］和［Ｒ'２］，双孔后光程分别为［Ｒ１］和［Ｒ２］．Ｒ１和Ｒ２是实际的光线，［Ｒ１］和［Ｒ２］称为实光程，［Ｒ'１］和［Ｒ'２］为虚光线的光程，称为虚光程．在近轴情况下，共轭点Ｐ、Ｐ'之间的光线等光程，因此有 ],[][][][2211R R R R +'=+'][][][][1212R R R R -='-'． 即双孔右实光线光程差正好等于左边虚光线的光程差的负值．我们可以把对实光程差的讨论，用对虚光程差的讨论来代替．或者说，我们把屏幕成象在双孔屏所在的光学空间，在屏幕的像面形成虚干涉．虚干涉条纹间距为3.12.0520105006=⨯⨯=''='∆-d L x λ（毫米）．屏幕上实干涉与其像面上的虚干涉条纹共轭．因此，干涉条纹间距为26.053.15=='∆=∆x x （毫米）．解法二将双孔变换到屏幕所在的光学空间，由透镜成象公式求出双孔屏的位置．,101811=--'s40-='s 厘米，计算题3.5解图a5840=--=β． 双孔的像Ｓ'1和Ｓ'2（计算题 3.5解图b ）间距为12.055=⨯=='d d 毫米，524012=+='L 厘米，虚光源在屏幕上产生实干涉．屏幕上条纹间距为26.01520105006=⨯⨯=''=∆-d L x λ（毫米）．３.6 菲涅耳双面镜的夹角为20角分，缝光源离双面镜交线10厘米，接收屏幕与光源的双像连线平行，屏幕距离双镜交线210厘米，光波波长600纳米，试求 （1） 屏幕上干涉条纹的间距；（2） 屏幕上可以看到几个干涉条纹？（3） 如果光源到两镜交线的距离增大一倍，干涉条纹有什么变化？ （4） 如果光源与两镜交线距离不变，只是在横向有一小的位移δx ，干涉条纹有什么变化？（5） 如果使屏幕上干涉条纹可见度不为零，缝光源的最大宽度为多少？※※※解：（１）双面镜夹角20=α角分18031π⨯=弧度，1001=L 毫米，21002=L 毫米，屏幕上条纹间距为100)1803/(2)2100100(106002)(6121⨯⨯⨯+⨯⨯=+=∆-παλL L L x 13.1≈（毫米）（２）屏幕上干涉区宽度为222L L l αθ=≈∆，屏幕上的干涉条纹条数为22≈∆∆≈∆xlN 条． （３）由于21L L <<，当1L 增加一倍时，条纹间距计算题3.5解图Ｌ'＝52cm12122)(L L L x ⋅+=∆αλ，分子中21212L L L L +≈+，条纹间距将减少为原来的一半，干涉区干涉条纹数 增加一倍．44≈∆N 条．（４）如计算题3.6图所示，当光源Ｓ移动δs 时，双像也作相应地移动，双像S 1、S 2连线的垂直平分线与屏幕交点O （原点，零级干涉条纹处）在屏幕上移动δx ．由几何关系，21L xL sδδ=，由于光源的移动是横向的，移动时L 1、L 2和α都不变，因此条纹间距不变，屏幕上干涉图样只作平移，移动的距离为12L L sx δδ=． （５）设光源宽度为b ，边缘光源点在屏幕上的干涉图样彼此错开δx ，当δx 与干涉条纹的宽度∆x 一样大时，干涉条纹会因非相干叠加而消失，干涉也就消失．就是说，当x x ∆=δ时，干涉消失．此时有112122)(L L L b L L αλ+=，αλαλ22)(221≈⋅+=L L L b ．S d 计算题3.6解图αλ2=b 是光源的极限宽度，αλ2<b 干涉可见度不为零． ３.7 透镜表面通常覆盖一层氟化镁（MgF 2）（n=1.38）透明薄膜，为的是利用干涉来降低玻璃表面的反射．为使波长为632.8纳米的激光毫不反射地透过，这覆盖层至少有多厚？解 从实际出发,可以认为光垂直入射于透镜表面．当某种波长的光在氟化镁薄 膜上下表面的反射相干相消时，我们认为该波长的光毫不反射地透过．薄膜干 涉光程差公式2/cos 222λ±=∆i d n ，相干相消满足λλ)2/1(2/cos 222+=±k i d n ，式中02=i ，1cos 2=i ，由于氟化镁膜上表面是折射率为１.0的空气，下表面是玻璃，玻璃折射率大于氟化镁的折射率，所以光程差公式中无2/λ±一项，上式可简化为λ)2/1(22+=k d n ，计算膜最小厚度，取k=0，得膜最小厚度46210146.138.14108.6324--⨯=⨯⨯==n d λ（毫米）．３.8 焦距为30厘米的薄透镜沿一条直径切成L 1和L 2两半，将这两半彼此移开8.0厘米的距离（如计算题3.7图）．位于光轴上的光源S 波长为500纳米，到L 1的距离是 60厘米，S '1和S '2 为光源形成的两个像． （1） 在图上标出相干光束的交叠区，（2） 在干涉区垂轴放置一屏幕，屏幕上干涉条纹的形状怎样？ （3） 在两像连线中点垂轴放置屏幕，屏幕上条纹间距为多少？解 (1) 题中的干涉装置称为梅斯林干涉装置．光源点Ｓ经梅斯林透镜形成两个实象点Ｓ'1和S '2．干涉区如计算题3.8解图（a ）所示，是像空间成像光束的交计算题3.8图n ＝计算题3.7解图叠区．(2) 将干涉区放大，如计算题3.8解图（b ）建立坐标系．光源S 的像Ｓ'1(0,0,-a)和S '2(0,0,a)相距2a ，屏幕垂轴放置，Ｐ为干涉场中屏幕上任意一点，它是光线1'和2'的交点．以S '2为圆心，以２a 为半径作圆弧，交光线1'于Ｓ'1，交光线2'于Ｑ，可认为光源Ｓ到Ｓ'1和Ｑ点等光程，因此，1'和2'两光线到达Ｐ点，在Ｐ点的光程差为 ][2211S P S Q P S QP P S '-'-'=-'=∆2/12222/1222])[(2])[(y x z a a y x z a ++-+-+++=不同的Ｐ点将有不同的光程差，光程差为常数的点的轨迹方程为2/12222/1222])[(])[(y x z a y x z a ++++++-=+∆=a 2常数．这是一个以Ｓ'1和S '2为焦点的椭球方程，因此等光程差的轨迹是以Ｓ'1和S '2为焦点的旋转椭球面族．以垂直于光轴放置的屏幕截这些椭球面族，则得到以光轴为圆心、半圆形的、不定域的干涉条纹．（x,y ）计算题3.8解图c计算题3.8解图b（3）以焦距30厘米，物距分别为60-厘米和)860(+-厘米，代入薄透镜成像公式，计算出两像距分别为60厘米和53.68厘米．两像点相距２a=1.68厘米，故干涉区在光轴的下方．若屏幕在两像点连线中垂面上，如计算题3.8解图c 所示，P 为屏幕上任意一点，相干光1' 和2' 在P 点的光程差为a r r a r QP P S 22)2(1211-=--=-'=∆, 因2/1222/12221)1()(ay x a a y x r ++=++=，在透镜孔径1s D '<<，222y x a +>>时，ay x a a y x a r 2)211(222221++≈+++= ，故1'和2'在P 点的相位差为]2)2(2[2222a ay x a -++=∆=λπλπδay x 222+=λπ．当λk ay x =+22时（ ,2,1=k ），πδk 2=，该点是相干加强的点，为明条纹的中心．因此明条纹满足λka y x =+22，（ ,2,1=k ）令λρka =2，则222ρ=+y x ．上式为标准的圆方程，k ∝ρ．由中心向外，条纹的半径分别为λρa =1，λρa 22=，……条纹间距为λρρρa k k k k ⋅-+=-=∆+)1(1．３.9 用钠光灯做杨氏干涉实验，光源宽度被限制为2毫米，双缝屏到光源的距离D=2.5米．为了使屏幕上获得可见度较好的干涉条纹，双缝间距选多少合适？ 解 取钠光波长3.589=λ纳米．已知光源的宽度b ＝２毫米，相干孔径角被λθ≤b 式限制．即bλθ≤．由计算题3.9解图所示，要想得到可见度不为零的干涉条纹，双孔间距必需在上式孔径角所限制的范围内，即bD d λ<， 因此，双缝间距为736.02105.2103.58936=⨯⨯=<-b D d λ（毫米）． 若想得到可见度较好的干涉条纹，光源上边缘光源点在屏幕上的光程差的差要小于或等于四分之一光源波长．即4λθ≤b ，或184.04=⋅≤bDd λ（毫米）． 此种情况下，屏幕上干涉条纹可见度可达0.9以上．３.10 观察肥皂水薄膜（n=1.33）的反射光呈绿色（λ=500纳米），且这时法线和视线间角度为0145=i ，问膜最薄的厚度是多少？若垂直注视，将呈现何色？ 解 入射到肥皂水薄膜表面光线的入射角为450，可求出光在膜内的折射角2i ．由折射定律，20sin 33.145sin 0.1i ⨯=⨯，解出0212.32=i ，8470.0cos 2=i ． 由于光在空气中的肥皂水膜上表面反射时有π的相位变化，在其下表面反射时无π的相位变化，因此光程差中要计入半波突变．对于相干加强的500纳米的绿光，应满足λλk i d n =-2/cos 222．题意求最薄厚度，应取0=k ，以各值代入上式，得8470.033.121210500cos 212622⨯⨯⋅⨯=⋅=-i n d λ41011.1-⨯=（毫米）．同一厚度的肥皂水膜，若眼改微微垂直注视，则1cos 2=i ，此时看到的相干加计算题3.9解图强的波长λ'应满足λλ''='-k d n 2/22，将 2,1,0='k 代入上式发现，仅当0='k 时λ'才落在可见光范围内，以0='k 代入，求得3.590='λ纳米，为深黄色的光．可见，从不同方向观看，可以呈现不同颜色，这一现象也表现在一些鸟的羽毛薄膜上．有时从不同方向观看羽毛，颜色不同，这是一种薄膜干涉现象．３.11 如计算题3.11图所示，两平板玻璃在一边相连接，在与此边距离20厘米处夹一直径为0.05毫米的细丝，以构成空气楔．若用波长为589纳米的钠黄光垂直照射，相邻暗条纹间隔为多宽？这一实验有何意义？解 两玻璃板之间形成一尖劈空气隙，劈角4105.220005.0-⨯=÷=α弧度．经空气隙上下表面反射的光形成等厚干涉，由条纹间距公式18.1105.2210589246=⨯⨯⨯==∆--αλx （毫米）．从上式可以看出，劈角愈小，条纹间距越大，越容易数出干涉条纹的条数．因为每相临两个等厚干涉条纹对应的厚度差等于半个波长，数出条纹数可以计算出细丝的直径．干涉条纹数越少，丝越细．因此，此实验可以做精密测量用．３.12 在牛顿环实验中，平凸透镜的凸面曲率半径为5米，透镜直径为20毫米，在钠光的垂直照射下（λ=589纳米），能产生多少个干涉条纹？要是把整个装置浸入n=1.33的水中，又会看见多少条纹？解 牛顿环实验装置产生等厚圆条纹．条纹半径公式为λkR r k =．式中k 是干涉圆条纹的序数．透镜的直径为20毫米，对应的干涉条纹序数为3410589105106322≈⨯⨯⨯==-λR r k k 条. 若装置放入水中，波长应为n /λλ='，看到的条纹数为452≈=''λR n r k k 条．计算题3.11图３.13 光学冷加工抛光过程中，经常用“看光圈”的办法检查工件的质量是否符合设计要求．如计算题3.13图所示，将标准件平凸透镜的球面放在工件平凹透镜的凹面之上，用来检验凹面的曲率．此时，凸面和凹面之间形成一空气层．在光线照射下，可以看到环状干涉条纹．试证明由中央外数第k 个明环的半径k r 和凸面半径R 1、凹面半径R ２以及波长λ之间的关系为12212)21(R R R R k r k --=λ．解 如计算题3.13解图所示，平凸透镜和平凹透镜之间形成空气隙，设Ａ点处形成 k 级明条纹，明条纹半径为r k ，该处对应的空气膜厚度为d k ．由图中几何关系得211221)(d R r R k -+=，将上式展开，并消去无穷小量21d ，得1212R r d k =， 同理可得2222R r d k =． K 级明条纹对应的膜厚为)11(221221R R r d d d k k -⋅=-=，k 级明条纹满足光程差公式λλk d k =+2/2．将k d 代入，整理得计算题3.13图 计算题3.13解图d12212)21(R R R R k r k --=λ．３.14 机加工中常常要用块规来校对长度．计算题3.14图中，块规G 1的长度是标准的，G 2是要校准的块规，两块块规的两个端面经过磨平抛光．G 1 和G 2的长度不等，在它们的上面盖以透明的平板玻璃G ，G 与G 1、 G 2之间形成空气隙，当用单色光照明G 的表面时，可产生干涉条纹．（1） 设所用光波波长为500纳米，图中，间距l ＝５厘米，观察到等间距的干涉条纹，条纹间距为0.5毫米．试求块规的高度差．怎样判断它们之中哪个长？（2） 如果G 和 G 1间干涉条纹间距是0.5毫米，Ｇ和G 2间干涉条纹间距是0.3毫米，则说明什么问题？解 （１）在玻璃平板Ｇ与块规之间形成尖劈形状的空气隙（计算题3.14解图a ），劈角α与产生的干涉条纹间距之间的关系为αλ2=∆x ， 因此块规G 1、G 2之间的高度差为26105.25.021*******--⨯=⨯⨯⨯=∆==∆x l l h λα（毫米）．轻轻压玻璃板Ｇ，Ｇ1和Ｇ2中短者与G 之间夹角变小，干涉条纹变疏；长者与Ｇ之间夹角变大，条纹变密(计算题3.14解图b)．（２）在不加压力于Ｇ的情况下，若与Ｇ1、Ｇ2间干涉条纹间距不同，说明Ｇ1Ｇ2的上表面不严格平行，两表面空气劈角不等劈角差为2)11(1212λαααx x ∆-∆=-=∆计算题3.14图计算题3.14解图（a ）（b ）46103.3210500)5.013.01(--⨯=⨯⨯-=（弧度）３.15 若用钠光灯（λ1=589.0纳米，λ2=589.6纳米）照明迈克尔孙干涉仪，首先调整干涉仪，得最清晰的干涉条纹，然后移动M 1，干涉图样为什么逐渐变得模糊？问第一次干涉条纹消失时，M 1由原来位置移动了多少距离？解 迈可耳孙干涉仪双光束干涉,可以等效为空气中的空气膜的干涉．空气膜折射率为1.0．取视场中心，则0.10cos cos 2==i ．今以λ1=589.0纳米和λ2=589.6纳米钠双线照明．设在空气膜厚度为d 1时，对λ1和λ2，干涉条纹中心都为明条纹，前者级次为1k ，后者级次为m k -1．视场中心同时满足 1112λk d =,（１）211)m k (d 2λ-=．（２）由于两谱线波长相差很小，所以它们干涉条纹宽度分布规律基本上一样．即在两者干涉图样中心都是亮条纹时，其他亮条纹也重合得很好．使得视场中干涉条纹看起来很清晰． 今逐渐移动Ｍ1，增加等效空气膜厚度d ，视场中心两种波长的干涉条纹各自以不同的速度外冒，由于两套干涉条纹非相干叠加的结果，使得视场中条纹可见度越来越坏，直至条纹完全消失．此时两套干涉图样恰好是一个的极大与另一个的极小相重合．因此有 1222λk d =，（３）222)21(2λ--=m k d ．（４）代入已知量解上面四个方程，求得M 1移动的距离1447.012=-=∆d d d (毫米).３.16 用水银蓝光(λ =435.8纳米)扩展光源照明迈克耳孙干涉仪，在视场中获得整20个干涉圆条纹．现在使Ｍ１远离Ｍ'２，使d 逐渐加大，由视场中心冒出500个条 纹后，视场内等倾圆条纹变为40个．试求此干涉装置的视场角、开始时的间距d 1和最后的间距d 2．解 计算题3.16解图中，Ｍ1是圆形反射镜, Ｍ'2是圆形反射镜Ｍ2的像，二者等效为空气 膜面．它们对观察透镜中心的张角22i 是视场角．当Ｍ1和Ｍ'2的起始间距为d １时，对于视场中心 和边缘，分别有λ中k d =12，1 '2计算题3.16解图λ)20(cos 221-=中k i d ．间距由d １增加到d ２的过程中，冒出500个条纹，则此时对中心和边缘有 λ)500(22+=中k d ，λ)40500(cos 222-+=中k i d ．已知λ＝435.8纳米,解上面四方程，可得0226.16=i ，500=中k ， 109.01=d 毫米，218.02=d 毫米．３.17 用迈克耳孙干涉仪作精密测长，光源为632.8纳米的氦氖激光，其谱线宽度为10-4纳米，光电转换接收系统的灵敏度可达到1/10个条纹，求这台仪器的测长精度和测长量程．解 迈克耳孙干涉仪的测长精度由接收系统的灵敏度来决定．由于干涉条纹每变化一个，长度就变化半个波长．接收系统灵敏度可达到1/10个条纹，因此测长精度为64.312101=⋅=λδl （纳米）． 一次测长量程m l 由相干长度0l 来决定．2212120≈∆⋅==λλl l m （米）．３.18 我们大致知道某谱线的能量分布在600～600.018纳米范围内，并且其中包含很多细结构，最细结构的波长间隔为6×10-4纳米．试设计一标准具，用它可以研究这一谱线的全部结构．解 由于要分析的谱线能量在600~600.018纳米范围内，要求所设计的标准具（即d 固定的法布里－珀罗干涉仪）自由光谱范围应为018.022==∆dλλ自（纳米）．由此计算出标准具反射面之间距离最大应为10018.02600222=⨯=≤自λλd （毫米）． 所得最大的干涉级次为λdk m 2=．因最细结构的波长间隔为6×10-4纳米，此为要求的最小可分辨波长间隔．由此求出对标准具分辨本领的要求．即64101106600⨯=⨯=∆=-辨λλR ．又因21r rk R m-=π，将k m 代入可求得反射面的振幅反射比为r ≥0.95．因此，要分析能量分布在600～600.018纳米范围内，最细结构的波长间隔为6×10-4纳米的谱线，标准具d 最大为10 毫米，反射面 r ≥0.95.３.19 设法－珀腔腔长5厘米，照明的扩展光源波长为600纳米，试求（１） 所得到的等倾干涉圆条纹中心的级次是多少？（２） 设光强反射率为0.98，在倾角10附近干涉环的半角宽度是多少？ （３） 如果用这个法－珀腔分辨谱线，其色分辨本领有多高：（４） 如果用这个法－珀腔对白光进行选频，透射最强的谱线有几条？每条谱线的宽度为多少？（５） 由于热胀冷缩，引起腔长的改变量为510-（相对值），则谱线的漂移量为多少？解 （１）法布里－珀罗干涉仪透射光相干加强的件是 λk i nd =cos 2，对于干涉圆条纹中心，0.1cos =i ，上式为 λk nd =2，其中0.1=n ，5=d 厘米，600=λ纳米，代入上式，得干涉条纹中心级次56107.1106005022⨯≈⨯⨯==-λdk ． （２）k 级亮环的半角宽度公式98.098.011sin 502106001sin 20622/0ππλ∆-⋅⨯⨯⨯=-⋅=-r r d i k I6102.2-⨯=（弧度）54.0''≈．可见亮环非常细锐． （３）分辨本领72106.21⨯=-=r rk R π，可分辨的最小波长间隔：57103.2106.2600-⨯=⨯==Rλδλ（纳米） （４）用白光做光源进行选频，相邻两极大的波长间隔32110025.32-=∆⨯==∆dk λλ（纳米）。

南开大学电子科学与技术专业最新考研专业目录信息 考研作为鲤鱼跳龙门、屌丝逆袭、改变命运的重要渠道之一，热度持续升温。

作为已经确定目标院校的考生来说，考研专业目录能够帮助考生清晰知道自己所报考院校目标专业的具体研究方向以及相关考试科目，同时还可以关注学校的特殊招生政策要求。

天津考研网教研部以今年最新招生专业目录为蓝本，为考生整理最新的考研专业课信息，供考生备考参考！南开大学电子科学与技术最新考研专业目录专业代码、名称及研究方向 考试科目 备注0900电子科学与技术_ 01光电子学与信息显示技术_ 02功能薄膜材料与器件_ 03电子技术及应用_ 04可编程逻辑与信号处理_ 05嵌入式系统与DSP技术_ 06电路系统分析与设计_ 07传感器技术与智能系统_ 08微电子技术与应用_ 09大规模集成电路设计①101思想政治理论②201英语一③301数学一④816电子综合基础或817大学物理（电光学院）或818物理化学（电光学院）电子综合基础含：数字电路、模拟电路各1/2；大学物理（电光学院）含：电磁学、光学各1/2。

_ 10光电子技术与应用_ 11薄膜光电子器件与应用_ 12信息显示技术与应用_ 13光电子与信息电子系统设计与应用_ 14电磁场理论与技术_ 15微波与毫米波理论与技术_ 16激光理论与技术_ 17电子系统应用专业课很重要，要花了很多时间很多精力都耗在专业课上了。

首先要准备好报考学校的考试用书，最好找到考试科目的笔记和真题，对他们本校老师出的教材,一定要多加注意.因为一般学校指定的教材不是自己的老师自己出的就是自己的老师参与其中的几个章节的编写.对这部分,一定要认真复习的.出卷的老师一般就喜欢出自己的研究成果。

还有一个重要的环节就是要拿到历年的试卷,然后对试卷要进行认真研究,尽量找出他们的命题规律,就算是考过的,不要以为不会再出现.也要认真的把握.至于连续几年都出现的题目也有可能是今年的重点.我自己专业课就是按照上面两个方法来复习的.我觉得这样子的复习方法还是挺有用处的。

南开大学805《光学基础》考研大纲_考试大纲题型资料_光学工程专业南开大学805《光学基础》考研大纲的作用就是明确考研内容试题题型知识点，备考南开大学，首先要了解到的便是考研大纲，决定着自己复习的方向是否正确。

天津考研网建议在复习南开大学805《光学基础》考研过程中增强自己的实力，调整自己的心态，增强成功信心。

祝大家考研复习顺利！一、考试目的本考试是全日制“085202光学工程”硕士专业学位研究生入学资格考试的专业基础课。

根据考生参加本考试的成绩和其他三门考试的成绩总分来选择参加第二轮，即复试的考生。

二、考试的性质与范围本考试是测试考生对光学基础知识掌握程度的水平考试。

考试范围包括本大纲考试内容中规定的几何光学、波动光学及激光方面的基础知识。

三、考试基本要求1.熟悉光学的基本概念，对光学的基础知识有较全面的了解。

2.理解并掌握光学的基础理论和重要定理。

3.具备一定的解决光学相关的理论和应用问题的能力。

四、考试形式本考试为闭卷笔试，试卷包括填空、选择、作图、计算中的全部或部分题型，总分150分。

五、考试内容本考试包括如下内容：（一）几何光学1．几何光学的基本概念和基本定律2.折射率与光程3．光在单球面上的折射、反射及近轴成像4．共轴球面组傍轴成像5．薄透镜成像6．几何光学仪器（二）波动光学的基本概念1．光波的复振幅描述2．单色平面波和球面波3．光的横波性与五种偏振态4.光在电介质表面的反射和折射，菲涅耳公式（三）光的干涉1．光波的叠加原理2．光的干涉现象、相干条件、时间相干性和空间相干性3．分波阵面法产生的光的干涉4．分振幅法产生的光的干涉5．薄膜干涉6．迈克尔逊干涉仪7．多光束干涉与法布里-珀罗干涉仪（四）光的衍射1．光的衍射现象与惠更斯-菲涅耳原理2．圆孔、圆屏、直边、单狭缝的菲涅耳衍射3.单狭缝、矩孔、圆孔的夫琅和费衍射4.多缝夫琅和费衍射及衍射光栅5．光学仪器的像分辨本领（五）光在各向异性介质中传播1．双折射现象和基本规律2.单轴晶体中的波面及惠更斯作图法3.晶体光学器件：偏振器、波片4.圆偏振光和椭圆偏振光的获得与检验5.偏振光的干涉（六）光的吸收、色散1．光吸收的线性规律2.正常色散和反常色散的概念3.群速度和相速度参考书:1.新概念物理教程-光学，赵凯华，高等教育出版社，2.光学(上下册),赵凯华，钟锡华，-北京大学出版社;3.光学,母国光等，-高等教育出版社;。

第五章 光在介质界面上的反射和折射例题5.1 试计算如计算题5.1图 所示的全反射棱镜（n=1.6），在实现光路转折过程中的光能损失百分之多少？假定介质是无吸收.解 光经过棱镜过程中，三次发生反射，其中第二次全反射，无能量损失，仅在玻璃和空气界面上通过时有反射能量损失，每次因反射损失的百分数为%3.5)0.16.10.16.1()(221212=+-=+-=n n n n R ，故总的能量损失为%37.10053.0)053.01(053.0=⨯-+．5.2 由于一般光学玻璃在红外线波段不透光，所以在此波段要用锗板（n=4）作为红外线仪器的窗口。

试问光经过由锗板作的窗片时，光能损失多少？ 解 光在锗板表面的能流反射率为36.0).10.40.10.4().10.1(22=--=--=n n R ，两次总能流的反射损失为%5959.036.0)36.01(36.0==-+．5.3 一复合物镜由两个透镜组成，其中一个的折射率52.11=n ，另一个的折射率60.12=n ，将这两个透镜用54.10=n 的树胶粘在一起．设光在透镜上的入射角都很小，试求光在透过此物镜时由于反射而造成的损失．将此损失与两透镜不粘在一起而使其间留一空气薄隙时的损失相比较． 解 （１）用54.1=n 的加拿大树胶粘合时，共有４次反射损失，各次能流反射率为 %26.4)152.1152.1(21=+-=R ，522103.4)52.154.152.154.1(-⨯=+-=R ，423106.3)54.160.154.160.1(-⨯=+-=R ，%33.5).160.10.160.1(24=+-=R ．总的透过能流为%64.90)1)(1)(1)(1(4321=----R R R R ．n 计算题5.1图（２）未用树胶粘合时，可求出%26.421==R R ，%33.543==R R ，总能流透过率为82.2％.5.4 如计算题5.5图所示，已知一束自然光光入射到 3/4=n 的水面上时，反射光是完全偏振的．一块折射率0n 2/3=的平面玻璃浸没在水面下，欲使玻璃表面的反射光p 也是完全偏振的，问玻璃表面与水平面的夹角θ应该是多少？解 如计算题5.４解图所示，光束入射到水面上Ａ点，反射光是完全偏振光，入射角必然是布儒斯特角．015333.1==-tg i p ，折射角为0002375390=-=i ．又因光线p 是线偏振光，所以在水中玻璃表面的Ｂ点，光线的入射角也为布儒斯特角，14.48)4323(=⨯='-tgi p ．由图中的几何关系可计算得玻璃表面与水面的夹角004.11)4.4890(3790180=----=θ5.5 已知红宝石的折射率为1.76，线偏振态的激光通过红宝石棒，光束在棒内沿棒轴线方向传播,欲使光在棒的端面上没有反射损失．试问光束的入射角i 应为多大？棒端面对棒轴倾角应取何值？入射光的振动方向如何？解欲使入射线偏振光在红宝石棒的端面无反射损失，光线应以布儒斯特角入射，且线偏振光的振动面要平行与入射面．因此011.6076.1==-tg i ，由几何关系，棒端面与棒轴线的夹角应为09.291.6090=-．5.6 已知5.11=n ，0.12=n ，015.54=i ，入射的是8.6320=λ纳米的氦氖激光，计算题5.5图计算题 5.４图计算题5.４解图试求穿透深度．解 氦氖激光由光密媒质进入光疏媒质，临界角0142)5.1/1(sin ==-c i ，入射角大于临界角，发生全内反射．穿透深度为（毫米）．3226212010173.242sin 5.54sin 12108.632sinsin12--⨯=-⨯=-=ππλci i d问答题5.1 试举一透射光强大于入射光强的具体例子．答：当内反射时，折射光束横截面比入射光束横截面小，因此在透射光能流小于入射光流时，可能有透射光光强大于入射光光强的情况．例如，5.11=n ，0.12=n ，0130=i ，026.48=i ，代入菲涅耳公式，得325.1=s t ，398.1=p t ，171.1=s T ，303.1=p T ．光强透射比大于１．5.2 在平静水面湖边洗脸时，我们很难看到自己对水面的反射像．但是站在平静水面的湖边看湖对岸的山、树以及建筑物的水中倒影却十分明亮，试解释之．答：因为在湖边洗脸时，观察的是垂直入射、外反射的光，在空气与水界面上，由菲耳公式可知，这种情况下反射光能量很小，因此看不到自己的像．而观察湖对岸的山、树以及建筑物，是观察外反射、掠入射的光，此时光能量几乎全部反射到人眼中来，看到的景物清晰明亮．5.3 如何测量一块形状不规则的，外表面毛糙的固体光学介质对于某种准单色可见光的折射率？答：将待测光学介质放入某种折射率可调的液体中，用单色光光源照明.若光学介质的折射率与透明液体的折率相同，则界面没有光能量反射，因此我们无法看到介质的存在．设法调透明液体的折射率，直至界面消失为止，用Ａbbe 折射仪测得液体的折射率，即为固体光学介质的折射率．假如用白光照射会看到什么情景呢？首先要说明的是世界上不存在对可见光有相同色散曲线（即折射率n 随波长λ变化的曲线）的不同介质，所以固体和液体对某一波长可以有相同的折射率，但对其他波长却不可能再有相同的折射率．这样对白光中的其他波长能流就会有些反射，使人们见到与某一波长互补颜色的固体块．5.4 光束由空气射向玻璃，什么情况下光能全部透射？什么情况下光能全部反射？ 答：当入射光束是线偏振光，振动面与入射面平行，并且以布儒斯特角入射时，光能全部透过；当入射光以接近900的角入射，即掠入射时，光能量全部反射． 5.5 在实验室里，偏振片的透振方向常常没有标出，用什么简单方法可以将它鉴别出来？答：在实验室中，选择一光亮的桌子面（或玻璃板），拿来偏振片放在眼前，迎着入射光观看桌子表面的反射光，并不断地改变反射角，同时不停地旋转偏振片，直至看到＂两明两零＂（即旋转偏振片一周，看到两次最大光强，两次零光强）的现象为止．此时，偏振片的透振方向恰于入射面垂直，此时光线的入射角恰为布儒斯特角．5.6 入射的线偏光通过外反射入能否变为椭圆偏振光？通过内反射能不能？通过全反射能不能？答：入射的线偏振光通过外反射及小于临界角内反射时，相移非零即π，故反射光不会是椭圆偏振光．但通过全内反射则可以成为椭圆偏振光．5.7 入射的椭圆偏振光通过外反射能否变为线偏振光？通过内反射能不能？通过全反射能不能？答：以布儒斯特角入射的椭圆偏振光外反射和内反射都可以得到振动面垂直于入射面的线偏振光．在大于临界角入射的全反射情况下，若（s pδδ-）值恰能将入射椭圆偏振光已有的δ补偿为零或π，则反射的是线偏振光． 5.8 入射的线偏振光通过单次全内反射后能否成为圆偏振光？答：不能．因为要成为圆偏振光应有两个条件，一是分解的s 分量和p 分量振幅相等，这容易作到．第二个条件是分解的s 分量和p 分量应有π/2的相位差,这在单次全内反射的情况下，不能实现．5.9 虚波矢的物理意义是什么？振幅反射比为复数代表什么物理意义？答：虚透射波矢说明光疏介质中有倏逝波存在．r 为复数说明反射光振动与入射光振动不是同时达到最大值．5.10 光强反射率R=(R s + R p )/2公式对于怎样偏振态的入射光才能成立．答：当入射光的s 分量和p 分量相等时，例如自然光，圆偏振光，总的光强反射率才有)(21])2()2[(120200p s p s R R r I r I I R +=+=．5.11 一束右旋圆偏振光由空气中垂直入射到玻璃上，试分析反射光的偏振态． 答：如问答题5.11图(a)建立坐标系．由于观察者对于入射光是顺着光传播方向＂看＂，所以入射右旋圆偏振光在所建立的xy 平面内（图b ），电矢量的端点是随时间左旋的．光振动方程可以表示为)2sin(πω+=t A E x ，)sin(t A E y ω=．根据菲涅耳公式，光在空气玻璃界面上反射时应分解为s 分量和p 分量，在本题中就是振动面沿x 方向和y 方向的线偏振光．这两个方向的振动在垂直入射外反射情况下，入射光相对于反射光有π的相位变化，且两线偏振光振幅等比例地减小，因此反射光光振动方程为)2sin(ππω++'=t A E x ，)sin(πω+'=t A E y． 这显然是一左旋圆偏振光的方程．反射光仍然是圆偏振光，不过右旋变为左旋（图c ），同时能量变小．因此，对于观察者来说，一个电矢量向左旋转入射于｛｛玻璃表面的圆偏振光，反射光电矢量仍然向左旋转着反射回来．就是说，右旋填空题5.1 折射率为4/3的水和折射率为3/2的玻璃界面,水中的偏化角为____，玻璃中的偏化角片偏化角为______．5.2 自然光仅在______的情况下，反射的光才是自然光．5.3 一束光由空气中以600的入射角进入各向同性透明介质，此时光光能量没有反射损失．这种介质的折射率为 ，入射光的偏振态为___________．5.4 线偏振光通过外反射______（能，不能）变为椭圆偏振光；圆偏振光通过外反射__ __（能，不能）变为线偏振光．5.5 一束自然光以布儒斯特角通过折射率为1.5的玻璃片堆，当玻璃片的数目为___________时，透射光的偏振度为90%(忽略玻璃的吸收).5.6 布儒斯特定律提供了一种测定不透明电解质折射率的方法，今测得某一电解质的起偏振角为580，则这种电解质的折射率为_ _ ___.选择题：5.1 指出下列各种说法的正误： （1） 偏化角i p 可能比临界角c i 大，（2） 同一个介质中偏化角i p 总比临界角i c 小，（3） 临界角只能在光密介质中存在，偏化角只能在光疏介质中存在，（4） 只要存在两种介质的界面，则两种介质都有自己的偏化角值，且二者之和等于900. 5.2 下列各种说法正确的是：（1） 除全内反射情况外，线偏振光单次经介质表面反射，永远得不到椭圆偏振光， （2） 光波在不同介质界面上反射可能存在光能量毫不反射的情况，（3） 光波在不同介质界面上反射，有可能存在入射能流全部反射的情况，（4） 对于入射角固定的外反射情况下，两种介质折射率差别越大，则界面反射出更多的光能量．5.3 光在两各向同性介质界面上反射，下面哪一种说法是对的： （1） 自然光入射，能得到部分偏振光的反射， （2） 自然光入射，得不到反射的自然光， （3） 自然光入射，不可能反射出线偏振光，（a ）（b ）（c ）反射光在xy 平面内也左旋问答题5.12图（4）线偏振光入射，反射出的不可能是自然光．5.4下列各种说法，哪种是对的？（1）光波从空气入射到透明介质表面，透入介质的能流总比返回空气的能流要强，（2）外反射和内反射情况下，对于自然光来说，反射的S能流一般总比P能流大，（3）在外反射情况下，随着入射角的增大，反射能流也越来越大，（4）光波入射到透明介质截面上，入射光能流与反射光、透射光能流符合能量守恒定律．。

南开大学光学工程专业考研真题南开大学光学工程专业考研复习都是有依据可循的,考研学子关注事项流程为：考研报录比-大纲-参考书-资料-真题-复习经验-辅导-复试-导师，缺一不可。

不知道报考南开大学光学工程专业的小伙伴们是否找到心仪的真题资料了呢？如果没有的话，那么恭喜你，下面的干货可以为你提供一个不错的选项，快来看看吧。

南开大学光学工程专业的初试科目有：①思想政治理论；②英语一；③数学一；④光学（电光学院）。

光学作为唯一的一门专业课，分量不言而喻，大家一定要好好复习。

而关于这门专业的课真题资料，我本人用的是天津考研网主编的《南开大学电光学院光学考研红宝书》。

资料中包含了：南开大学光学2002-2013、2015年考研真题；南开大学光学2002-2010年考研试题参考答案；南开大学光学考研题库（无答案），打印版，包括各种题型共计600余道题。

下面是我摘抄的部分2016年的试题以及2010年的答案，以供小伙伴们参考：南开大学2016年硕士研究生入学考试试题注意：请将所有答案写在专用答题纸上，答在此试题上无效。

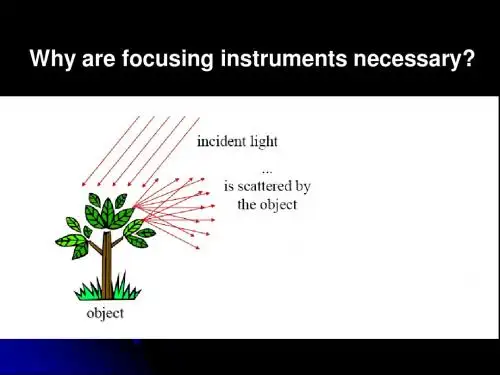
一、简答题（每题6分，共30分）1.一束单色光射到单晶体上，能否从出射光中只观察到一束光？为什么？2.请用光的散射解释生活中的现象？并简单说明其原理。

3.请说明增益介质的作用。

南开大学光学2010年考研试题参考答案及点评一、简答题1.在薄片前后放置一对正交的偏振片，如果没有光透过，则是玻璃片。

如果有光透过，则是晶体薄片。

2.迈克尔逊干涉仪的两臂没有严格垂直，造成各点之间光程差不同。

3.旋转角度0度和180度时，亮条纹变为暗条纹，暗条纹变为亮条纹；旋转角度为90度和270度时，干涉条纹消失。

4.不是，因为圆盘直径越大，挡住的半波带越多，干涉光越弱。

5.入射光经物平面发生夫琅和费衍射，在透镜焦面上形成一系列衍射光斑，各衍射光……考研路漫漫，坚持到最后一刻你就是胜利者。

最后，祝福大家考试顺利，金榜题名，可以成功成为南开大学光学工程专业的一名研究生学子。