树的结构定义和基本术语
- 格式:ppt
- 大小:1.46 MB
- 文档页数:15

树状结构知识点简介树状结构是一种非常重要的数据结构,它以分层的方式来组织数据。
在计算机科学中,树状结构被广泛应用于各种领域,如文件系统、数据库、编译器等。
本文将介绍树状结构的基本概念、特性和常见的应用。
1. 树状结构的定义和特点树状结构是一种由节点和边组成的层次化数据结构。
它具有以下特点:•树状结构中只有一个根节点,它是整个树的起始点。
•每个节点可以有零个或多个子节点,子节点又可以有自己的子节点,形成层次结构。
•除了根节点外,每个节点都有且只有一个父节点,即除了根节点外,每个节点都有唯一的直接上级。
•节点之间通过边连接,表示节点之间的关系。
2. 树状结构的基本术语在研究树状结构时,有几个基本的术语需要了解:•根节点(Root):整个树的起始点,它没有父节点。
•叶节点(Leaf):没有子节点的节点。
•父节点(Parent):有子节点的节点,一个父节点可以有多个子节点。
•子节点(Child):一个节点的直接下级节点。
•兄弟节点(Sibling):有相同父节点的节点。
•子树(Subtree):以某个节点为根节点的树,也是一个树状结构。
•深度(Depth):从根节点到某个节点的路径的长度。
3. 常见的树状结构树状结构有很多种类,其中一些常见的包括:•二叉树(Binary Tree):每个节点最多有两个子节点,分别为左子节点和右子节点。
•二叉搜索树(Binary Search Tree):二叉树的一种特殊类型,左子节点的值小于根节点的值,右子节点的值大于根节点的值。
•AVL树:一种自平衡的二叉搜索树,用于提高搜索和插入的效率。
•B树(B-Tree):一种自平衡的树状结构,通常用于文件系统和数据库中的索引结构。
•字典树(Trie):用于高效存储和检索字符串的树状结构。
4. 树状结构的应用树状结构在计算机科学中有广泛的应用,以下是一些常见的应用场景:•文件系统:计算机的文件系统通常使用树状结构来组织文件和文件夹。



数据结构的树的概念和基本术语作业嘿,朋友!咱们今天来聊聊数据结构里那神奇的树。
你知道吗?数据结构中的树,就像是一棵真实的大树。
它有根,有枝干,还有叶子。
只不过这里的根、枝干和叶子可不是真的植物部分,而是一些数据和它们之间的关系。
咱们先来说说根节点。
这根节点啊,就像是大树的树根,是整个树的起始点。
所有其他的节点都从它这儿延伸出去,你能想象到那种感觉吗?就好像树根给整棵树提供了支撑和养分,根节点也是整个树结构的基础和核心。
再说说子树,这子树就像是大树上分出的小树枝。
一棵大树可以有好多小树枝,每个小树枝又能自成一个小小的树的模样。
这是不是很神奇?还有父节点和子节点,这关系就像爸爸和孩子。
父节点有它的子节点,子节点依靠着父节点存在。
就像咱们生活中,孩子依赖着父母,而父母也为孩子遮风挡雨。
那兄弟节点呢?这就好比是兄弟姐妹呀,它们有着共同的父节点,相互之间有着类似的地位和关系。
度这个概念也很有趣。
节点的度,就好比一个人有多少只手。
有的节点“手多”,能连接的节点就多;有的节点“手少”,连接的就少。
层次呢,就像是大树的不同高度。
越往上层次越高,越往下层次越低。
叶子节点就像是大树最末梢的小叶子,它们没有孩子节点,孤孤单单但又有着自己独特的作用。
朋友,你想想,如果没有根节点,这树还能立得住吗?如果没有子节点,这树还能枝繁叶茂吗?所以啊,理解了这些基本术语,咱们就能更好地掌握树这个数据结构啦。
就像了解了大树的各个部分,咱们就能更清楚大树的整体模样一样。
咱们在处理数据的时候,树结构能帮咱们更高效、更有条理地组织和管理信息。
怎么样,是不是觉得很有意思?总之,数据结构中的树虽然看起来复杂,但只要咱们用心去理解,就会发现它就像咱们身边熟悉的事物一样,有着自己的规律和逻辑。
加油吧,朋友,相信你能把这树的概念和基本术语搞得明明白白!。
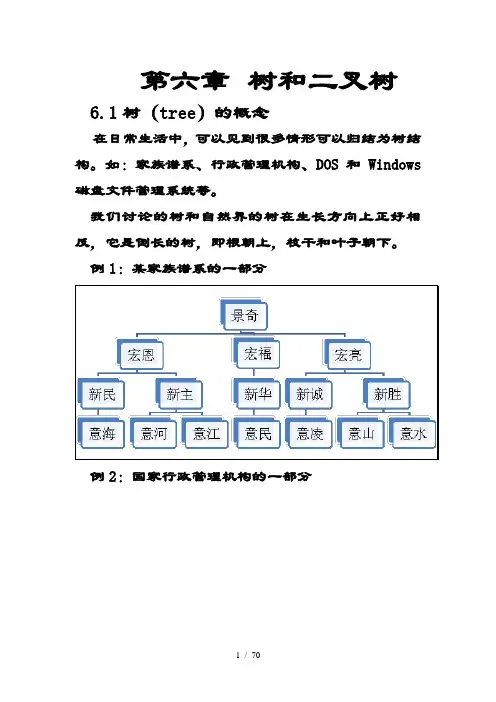
第六章树和二叉树 6.1树(tree)的概念在日常生活中,可以见到很多情形可以归结为树结构。
如:家族谱系、行政管理机构、DOS和Windows 磁盘文件管理系统等。
我们讨论的树和自然界的树在生长方向上正好相反,它是倒长的树,即根朝上,枝干和叶子朝下。
例1:某家族谱系的一部分例2:国家行政管理机构的一部分例3:DOS和Windows磁盘文件的一部分C:\TC20VC6.0数据结构课件数据结构讲稿第一章第二章……MyTc程序Tc1Tc2……MyVc程序Vc1Vc2……树是一种层次结构,属于非线性结构。
我们学过的线性表可以灵活组织数据,但它受到线性结构的限制,表达层次结构不太方便。
6.1.1树的定义·树T是n(n≥0)个结点的有限集合。
它满足:(1)仅有一个特定的结点,称为根(root)结点;(2)其余结点分为m(m≥0)个互不相交的非空有限集合T,1,T2,……,T m,其中每个集合自身又是一棵树,称为根的子树(subtree)。
·为了表述方便,把没有结点的树称为空树。
·树的定义具有递归性:即一棵树是由根及若干棵子树构成的,而子树又是由根及若干棵子树构成的,……。
表达树的方法通常有4种:树形、凹入、集合和广义表(1) 树形表示法AB C DE F G H(2)凹入表示法ABCEFDGH(3)集合嵌套表示法A○E C○F○G D○H B(4)广义表表示法T(A(B,C(E,F),D(G,H)))6.1.3 树的基本术语为了对树的形态表述清楚和形象,通常引用树和人的特征及术语来描述。
(1)结点和树的度(degree)结点所拥有的子树的个数称为该结点的度,而树中各结点的度的最大值称为该树的度。
AB C DE F G H如:·结点B、E、F、G和H的度数是0·结点C和D的度数都是2·结点A的度数是3;显然3也是树的度数(2)叶子(leaf)结点和分支结点度为0的结点称为叶子结点(终端结点);度不为0的结点称为分支结点(非终端结点)。


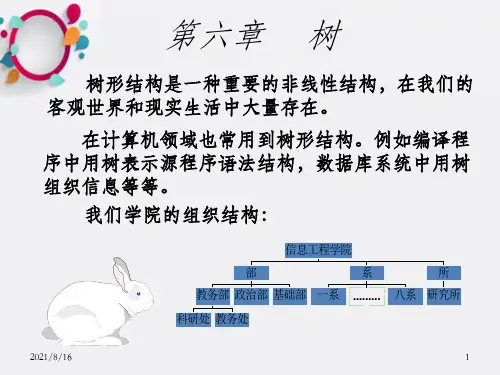
树的基本构造1. 什么是树树是一种非线性的数据结构,它由一组以边连接的节点组成。
树的基本构造包括根节点、子节点和父节点。
树的结构具有层次性,每个节点除了根节点外,都有一个父节点,可以有零个或多个子节点。
树是一种重要的数据结构,在计算机科学中广泛应用。
例如,文件系统就是一种树的结构,目录可以看作是树的节点,文件可以看作是树的叶子节点。
2. 树的基本术语在学习树的基本构造之前,我们首先需要了解一些树的基本术语。
•根节点(Root):树的顶端节点,没有父节点。
•子节点(Child):一个节点可以有零个或多个子节点。
•父节点(Parent):一个节点的直接上级节点。
•叶子节点(Leaf):没有子节点的节点。
•兄弟节点(Sibling):具有相同父节点的节点。
•子树(Subtree):节点及其所有后代节点构成的树。
•深度(Depth):节点到根节点的边数。
•高度(Height):树中节点的最大深度。
3. 树的表示方法树的结构可以通过不同的方式进行表示,常见的表示方法有以下几种:3.1. 嵌套列表表示法嵌套列表表示法是一种简单直观的表示方法。
每个节点用一个列表表示,列表的第一个元素表示节点的值,后续元素表示子节点。
例如,以下是一个用嵌套列表表示的树:[1, [2, [4], [5]], [3, [6], [7]]]3.2. 链表表示法链表表示法是一种常用的表示方法。
每个节点用一个对象表示,对象中包含节点的值和指向子节点的指针。
例如,以下是一个用链表表示的树:class TreeNode:def __init__(self, value):self.value = valueself.children = []3.3. 数组表示法数组表示法是一种紧凑的表示方法。
将树的节点按照层次遍历的顺序存储在一个数组中,数组中每个元素保存节点的值。
例如,以下是一个用数组表示的树:[1, 2, 3, 4, 5, 6, 7]4. 树的基本操作树的基本操作包括创建、插入、删除、查找和遍历等。

树和二叉树知识考点整理●树的基本概念●树的定义●n个结点的有限集●n=0代表空树●满足条件●只有一个根的结点●其余结点是互不相交的有限集,每个集合本身是一棵树,是根的子树●树是一种递归的数据结构●树的根结点没有前驱,其余结点只有一个前驱●树中所有结点可以有零个或多个后驱●基本术语●双亲、兄弟、孩子、祖先●度:孩子个数●分支结点:度大于0●叶子结点:度为0●深度:从下往上;●高度:从上往下;●有序树:从左到右是有次序的●路径和路径长度:路径是从上往下的●森林:m棵互不相交的树的集合。
●树的基本性质●结点数=所有结点度数之和+1●度为m的树中第i层上至多有m的i-1次分个结点●高度为h的m叉树至多有(m^h-1)/(m-1)个结点●具有n个结点的m叉树的最小高度为「logm(n(m-1)+1)]●二叉树的概念●定义●一种树形结构,特点是每个结点至多只有两棵子树(即二叉树中不存在度大于2的结点)并且二叉树的子树有左右之分,次序不可颠倒●二叉树与度为2的有序树区别●度为2的可以有三个结点,二叉树可以是空树●度为2的有序树的孩子左右之分是根据另一个孩子而言的;二叉树无论有没有,都要确定左右●特殊的二叉树●满二叉树●树中每一层都含有最多的结点●完全二叉树●高度为h,有n个结点的二叉树,当且仅当,每个结点都与高度为h的满二叉树中的编号一一对应●二叉排序树●用途:可用于元素的排序、搜索●左子树上所有结点的关键字均小于根结点的关键字;右子树上所有结点的关键字均大于根结点的关键字;左子树和右子树又是一棵二叉排序树●二叉树的性质●非空二叉树上的叶子结点数等于度为2的结点树加1,即n0=n2+1●非空二叉树上第k层至多有2^(k-1)个结点●高度为h的二叉树至多有2^h-1个结点●具有n个结点的完全二叉树的高度为log2(n+1)取顶或者log2n取底+1●二叉树的存储结构●顺序存储结构●只适合存储完全二叉树,数组从0开始●链式存储结构●顺序存储的空间利用率太低●至少三个指针域:数据域、左指针域、右指针域●增加了指向父结点后,变为三叉链表的存储结构●在含有n个结点的二叉链表中,含有n+1个空链域●二叉树的遍历和线索二叉树●二叉树的遍历●先序遍历●根左右●应用:求树的深度●中序遍历●左根右●后序遍历●左右根●应用:求根到某结点的路径、求两个结点的最近公共祖先等●三个遍历时间复杂度都是O(n)●递归算法和非递归算法的转换●层次遍历●需要借助队列●步骤●二叉树根结点入队,然后出队,访问出队结点,若有左子树,左子树根结点入队●遍历右子树,有右子树,右子树根结点入队。


树的基本术语一、树的定义树(Tree)是一种非线性的数据结构,它由n(n>=1)个节点组成的有限集合。
其中,有且只有一个节点被称为根节点,其余节点被分为若干互不相交的、且看作一个整体(子树)来处理的、有限集合。
二、树的基本术语为了更好地理解树的概念,我们需要了解一些树的基本术语:1. 节点(Node)节点是树的基本构成单元,每个节点包含数据和指向其他节点的指针或引用。
节点可以有零个或多个子节点。
2. 根节点(Root)根节点是树的顶端节点,它是树中唯一一个没有父节点的节点。
根节点用于标识树的起点。
3. 父节点(Parent)一个节点的直接上层节点称为其父节点。
一个节点可以有零个或一个父节点。
4. 子节点(Child)一个节点的直接下层节点称为其子节点。
一个节点可以有零个或多个子节点。
5. 兄弟节点(Sibling)拥有共同父节点的节点称为兄弟节点。
兄弟节点之间的关系是平等的。
6. 叶节点(Leaf)没有子节点的节点称为叶节点,也可以叫做终端节点。
7. 子树(Subtree)子树是由一个节点及其所有子孙节点组成的树。
每个子节点可以看作是该子树的根节点。
8. 深度(Depth)节点的深度是指从根节点到该节点的唯一路径上的边的数量。
根节点的深度为0。
9. 高度(Height)节点的高度是指从该节点到最深叶节点的路径上的边的数量。
叶节点的高度为0。
整棵树的高度是指根节点的高度。
10. 祖先节点(Ancestor)一个节点的祖先节点是从根节点到该节点的路径上的所有节点。
11. 后代节点(Descendant)一个节点的后代节点是从该节点到叶节点的所有节点。
三、树的分类树可以分为多种不同的类型,常见的树包括二叉树、二叉搜索树、平衡二叉树等。
1. 二叉树(Binary Tree)二叉树是一种特殊的树结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。
二叉树可以是空树,也可以是非空树。
2. 二叉搜索树(Binary Search Tree)二叉搜索树是一种特殊的二叉树,其中任意节点的左子树中的值都小于该节点的值,任意节点的右子树中的值都大于该节点的值。
树(⼀)树的基本知识树结构1) 了解树的定义、表⽰形式和基本术语2) 了解⼆叉树的概念和性质3) 掌握⼆叉树的⼏种遍历⽅法4) 理解⼆叉树的遍历⽅法的C语⾔代码实现5) 了解树的存储结构6)了解哈夫曼树和哈夫曼编码的基本概念树的定义树(Tree),是n(n≥0)个结点的有限集。
若n=0时称为空树;若n>0时为⾮空树。
在⼀个⾮空树中,有且仅有⼀个称为根的结点。
除根以外的其他结点划分为m(m>0)个互不相交的有限集T1,T2,. . .,Tm,其中每⼀个集合本⾝⼜是⼀棵树,并且称为根的⼦树(SubTree)。
例如下图是只有⼀个结点的树,这个唯⼀的结点也是这棵树的根节点:再⽐如下⾯这棵树:这棵树有9个结点,其中A是根,其余结点组成2个互不相交的⼦集:T1={B, D, E, I},T2={C, F, G, H},T1和T2都是A的⼦树,其本⾝也是⼀棵树:在树T1中,B是根节点,其余结点⼜分为两个互不相交的⼦树:T11={D, I},T12={E}。
在树T11中D是根,其包含由结点I组成的⼦树。
从这个概念上我们可以看出树的定义是⼀个递归的定义,即在树的定义中⼜⽤到了树的定义,⽽递归也将是实现树的相关操作的⼀个重要⼿段。
树的表⽰⽅法树形表⽰法⽬录结构表⽰韦恩图表⽰法⼴义表表⽰法凹⼊表⽰法树的基本概念(※有关术语※重点※)以下图为例⼦:结点:数据元素以及指向⼦树的分⽀。
图中的A,B,C等都是结点。
根结点:⾮空树中⽆前驱结点的结点。
图中的A结点。
结点的度(Degree):结点拥有的⼦树数量。
图中度为3的有:A、D,度为2的有:B、E、H,度为1的有:C、H。
:树内各结点的度的最⼤值。
上图中树的度为3。
叶⼦结点(终端结点)(Leaf):树没有⼦结点,即度为0的结点。
图中的F,G,I,J,K,L,M 都是叶⼦结点。
分⽀结点(分⽀点或⾮终端结点):不属于叶⼦结点的结点,即度不为0的结点。
A,B,C,D等都是分⽀结点。