机电传动控制机电传动系统动力学基础
- 格式:pptx
- 大小:690.70 KB
- 文档页数:17




机电传动系统的动力学基础基本要求:①掌握机电传动系统的运行方程式,学会用它来分析与判别机电传动系统的运行状态;②了解在多轴拖动系统中,为了列出系统的运动方程式,必须将转矩等进行折算,掌握其折算的基本原则和方法;③了解几种典型生产机械的机械特性n =f (TL);④掌握机电传动系统稳定运行的条件,并学会用它来分析与判别系统的稳定平衡点。
难点:根据机电传动系统中TM 、TL、n的方向,确定TM 、TL是拖动转矩还是制动转矩,从而判别出系统的运行状态,是处于加速、减速还是匀速;在机械特性上判别系统稳定工作点时,如何找出TM 、TL。
2.1 机电传动系统的运动方程式机电传动系统是一个由电动机拖动,并通过传动机构带动生产机械运转的机电运动的动力学整体。
2.1 机电传动系统的运动方程式机电传动系统的运动方程式是描述机电系统机械运动规律的最基本方程式,它决定着系统的运行状态。
dn动态转矩T d =T M -T L ;加速度 a =dt=0时,a=0 ,表示系统处于稳态,系统为匀速运动。
当Td≠0时,a≠0 ,表示系统处于动态,当TdT>0时,拖动转矩>制动转矩,a为正,系统加速运动;dT<0时,拖动转矩<制动转矩,a为负,系统减速运动。
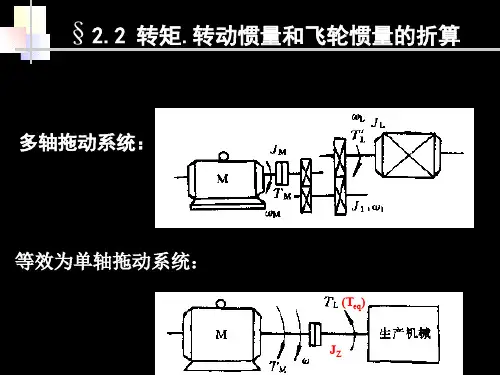
d2.2 转矩、转动惯量和飞轮转矩的折算机电传动系统运动方程式中的转矩、转动惯量及飞轮转矩等,均分别为同一轴上的数值。
若运动系统为多轴系统,则必须将上述各量折算到同一转轴上才能列出整个系统的运动方程式。
由于一般均以传动系统的电动机轴为研究对象,因此,一般都是将它们折算到电动机轴上。
转矩折算应依据系统传递功率不变的原则。
转动惯量和飞轮转矩折算应依据系统贮存的动能 不变的原则。
2.2.1 负载转矩的折算依据系统传递功率不变的原则 实际负载功率=折算后的负载功率)7.2(cL L LM L L L M L L L j T T j T T T T T ηωωωω'='='=='多轴旋转拖动系统⋯=⋯=321321 传动效率)(/ 速比ηηηηωωc LM j j j j多轴直线运动系统(下放重物))8.2(55.9602Mc L Mc L M L n FvT n Fv T T Fv ηπωωηω====)9.2(55.9c ML n FvT η'=c c cc ηηηη<'-='122.2.2转动惯量和飞轮转矩的折算(旋转型)依据动能守恒原则,折算到电机轴上的总转动惯量为数。






机电传动控制复习提纲第二章 机电传动系统的动力学基础2.1 知识要点2.1.1 基本内容1.机电传动系统的运动方程式机电传动系统是一个由电动机拖动,并通过传动机构带动生产机械运转的机电运动的动力学整体[如图2.1(a)所示]尽管电动机种类繁多、特性各异,生产机械的负载性质也可以各种各样,但从动力学的角度来分析时,则都应服从动力学的统一规律,即在同一传动轴上电动机转矩T M 、负载转矩T L 、转轴角速度ω三者之间符合下面的关系: T M -T L =Jdt d (2.1) 或用转速n 代替角速度ω,则为 T M -T L =dt dn GD 3752 (2.2)式(2.1)和式(2.2)称为机电传动系统的运动方程式。
机电传动系统的运动方程式是描述机电系统机械运动规律的最基本方程式,它决定着系统的运行状态,当动态转矩T d =T M -T L =0时,加速度a =dt dn =0 ,表示没有动态转矩,系统恒(匀)速运转,即系统处于稳态;当T d ≠0时,a =dt dn ≠0 ,表示系统处于动态,T d >0时,a =dt dn 为正,传动系统为加速运动;T d <0时,a =dt dn为负,系统为减速运动。
因式(2.1)和式(2.2)中的T M 、T L 既有大小还有方向(正负),故确定传动系统的运行状态不仅取决于T M 和T L 的大小,还要取决于T M 和T L 的正负(方向)。
因此,列机电传动系统的运动方程式和电路平衡方程时,必须规定各电量的正方向,也必须规定各机械量的正方向。
对机电传动系统中各机械量的正方向约定[见图2.1(b)]如下:在确定了转速n 的正方向后,电动机转矩T M 取与n 相同的方向为正向,负载转矩T L 取与n 相反的方向为正向,因此,若T M 与n 符号相同,则表示T M 与n 的方向一致;若T L 与n 符号相同,则表示T L 与n 方向相反。
也可以由T M 、T L 的方向来确定T M 、T L 的正负。
第二章机电传动系统的动力学基础1. 引言在机械工程中,机电传动系统是指将电力或者其他形式的动力转化为机械运动的系统。
机电传动系统的设计与分析依赖于对动力学基础的理解。
本章将介绍机电传动系统的动力学基础,并探讨其在机械工程中的应用。
2. 动力学基础的概念2.1 动力学的基本概念动力学是研究物体在受力作用下运动规律的科学。
在机电传动系统中,动力学研究的重点是描述和分析物体受到力后的运动状态和运动规律。
2.2 机电传动系统的动力学模型机电传动系统可以用动力学模型来描述其运动规律。
动力学模型由四个基本要素组成:质点、力、力矩和功。
•质点:质点是物体的理想模型,具有质量但没有尺寸。
在机电传动系统中,质点被用来描述物体的运动状态。
•力:力是导致物体产生加速度的原因。
在机电传动系统中,力可以分为正向力和反向力,正向力使物体加速,而反向力使物体减速。
•力矩:力矩是力围绕某个轴产生转动的效果。
在机电传动系统中,力矩用来描述力对物体产生的转动效果。
•功:功是通过力对物体施加力学作用而产生的能量转移。
在机电传动系统中,功可以用来描述能量的转化和传递过程。
2.3 动力学基础的方程机电传动系统的动力学基础可以用一系列方程来描述。
其中,最基本的方程是牛顿第二定律和动能定理。
•牛顿第二定律:牛顿第二定律描述了力对物体产生加速度的关系。
其公式为 F = ma,其中 F 表示力,m 表示物体的质量,a 表示物体的加速度。
•动能定理:动能定理描述了物体的动能与力对其做功之间的关系。
其公式为 K = 1/2 * mv^2,其中 K 表示物体的动能,m 表示物体的质量,v 表示物体的速度。
3. 机电传动系统的应用机电传动系统的动力学基础在机械工程中有着广泛的应用。
下面列举了几个常见的应用场景:3.1 机械设计在机械设计中,动力学基础被用来分析和优化机械系统的运动性能。
通过对力、力矩和功的计算和分析,设计工程师可以确定合适的传动比例和功率需求,以实现理想的机械运动效果。