minitab做柏拉图(经典)

22.03.2018 Fußzeile
8
选择数据数列
设置需要突出重点的 百分比
22.03.2018 Fußzeile
5
1分钟让你搞定柏拉图——MINITAB操作步骤4
进入选项设置
添加轴标签 及图表标题
22.03.2018 Fußzeile
6
1分钟让你搞定柏拉图——完成柏拉图
柏拉图做好啦
22.03.2018 Fußzeile
7
1分钟让你搞定柏拉图
1分钟让你搞定柏拉图
1分钟让你搞定柏拉图——学习目的
经常需要使用柏拉图进行数据分析？ 用Excel制作，需要 —— 整理数据、排序；设置坐标轴；调整图 表格式…….繁琐、低效、麻烦？
通过4个步骤的学习，让你使用 Minitab软件快速制作柏拉图。
添加数据
选择图表பைடு நூலகம்
选择数列、设置突出百分比
添加坐标轴标签，图标题
22.03.2018 Fußzeile
2
1分钟让你搞定柏拉图——MINITAB操作步骤1
添加数据在工作表区域， （注意数据排放方式为数列）
22.03.2018 Fußzeile
3
1分钟让你搞定柏拉图——MINITAB操作步骤2
选择柏拉图工具
22.03.2018 Fußzeile
4
1分钟让你搞定柏拉图——MINITAB操作步骤3

第一步:将数据输入Minita表
第二步:选择“Stat>Quality Tools>cause-and Effect……”
第三步:在出现的对话框输入下图所示信息
选择包含因果图相应分枝 的原因列表栏
改变缺陷分枝标识的缺 省设置,缺陷设置为人、 机、料、法、环、测量
使用Minitab制作步骤如下:
第一步:将数据输入Minitab工作表
输入不良项目
相对应的输入 不良数
第二步:选择“Stat>Quality Tools>Pareto Chart”
第三步:在出现的对话框输入下图所示信息 -1
选择包含原始数 据的栏
第三步:在出现的对话框输入下图所示信息 -2
如数据输入格式为缺陷名和 缺陷频率时选择该项
Machines
柏
拉
定义:
图
根据所搜集之数据,按不良原因、不良状况、不良 发生位置等不同区分标准,以寻求占最大比率之原因、 状况或位置的一种图形. 1897年,意大利学者柏拉撬分析社会经济结构,发 现绝大多数财富掌握在极少数人手里,称为“柏拉法 则”. 美国质量专家朱兰博士将其应用到品管上,创出了 “Vital Few, Trivial Many”(重要的少数,琐细的多 数)的名词,称为“柏拉图原理”.
如何使用Minitab 制作鱼骨图、 柏拉图、散布图和直方图
鱼骨图
定义:
对于结果与原因间或所期望之效果与对策间的关系, 以箭头连结,详细分析原因或对策的一种图形称为特性 要因图,工程鱼骨图或因果图. 它为1952年日本品管权威学者石川馨博士所发明, 又称“石川图”.
使用Minitab制作步骤如下:
第三步:在出现的对话框输入下图所示信息 -3

28
第一步:将数据输入Minitab工作表
第二步:选择
29
选择包含因果 图相应分枝的 原因列表栏
输入因果图对 应的问题。
改变缺陷分枝标识的缺省设置, 缺陷设置为人、机、料、法、 环、测量
输入图形标题
30
31
量具重复性和再现性
１、量具重复性和再现性研究的目的是确定观察到的过程变异中测量系统变异所占的
37
测量系统能力 说明 P/TV或P/V≤10% 测量系统能力很好 10%<P/TV或P/V≤30% 测量系统能力处于临界状态 P/TV或P/V>30% 测量系统能力是不满意的，必须改进
小于20%良好
大于4良好
38
样品间的差异为主要原因
测量值随样品的变动，主 要变动为样品
所有点在管理界限内为佳
测量值随作业员的变动， 相差不大
大部分点落在管理界限外， 部品差异为主因
显示作业员测量有差异的 样品 39
能力分析---CPK
一旦一个过程处于统计控制状态,既可以连续生产,这时可能要确定其 否有能力生产出满足规格的产品,能力计算是将规格宽度和过程变异宽度 进行比较。
40
影响工序能力的因素
• • • • • • 人: 操作者的技术水平及责任心 机: 生产设备功能和精度 料: 材料的性能(包括直接材料如拉料,附助料如切削油) 法: 工艺方法的特点(机床程序,夹具,刀具及加工参数) 环: 环境变化(温度,湿度,振动,噪音,光线等) 测量: 测量仪器的误差和工装误差 每个方面都存在一些偶然性因素,这些因素都可能使质量特 性发生差异或波动,形成自已的频率分布,这些频率分布通常都具 有正态分布或近似分布的性质,若我们用σ表示各方面的标准 差,6σ则表示工序能力,而这个工序能力只能表示我们目前的工 序能力能够达到某种水平,但不能衡量该工序能力是否满足该工 序的质量要求.这个要求一般表现为图纸公差(T),为了体现工序 能力是否满足工序的质量要求,引进CP工序能力指数,并规定 CP=T/6σ,当公差中心M与分布中心U重合时,CP、T与6σ存在以下 关系：

结果输出
• The end! • TKS
怎样制作柏拉图
定义
• 柏拉图是指根据所收集的数据以不良原因, 不良状况,不良发生的位置,客户抱怨的种类 或安全事故等等的项目别进行分类,并计算 出分类项目所占比例,然后按照比例的大小 顺序排列,加上累积值的一种图形
• 建立柏柆图须先以层别建立, 故在制作此图 前,对统计的另一方法层别法要有一定的认 识. • 层别即将很多的数据按照其所持有的特性 进行层次划分 • 层别法-----即将多种多样的数据,因目的而分 类成数个项目,并以个别特征加以归类与统 计
找出关键的Y特性
练习
项次
1 2 3 4 5
缺陷项
虚焊 漏焊 强度不够 外观受损 其它
数量
500 300 200 150 160
输入数据
• Select: Chart Stat > Quality tools> Pareto
填好各项参数
输入缺陷列 输入频数列 其他项所占的比率
可以对柏拉图进行命名
一、使用Excel制作柏拉图
柏拉图制作步骤
• 确定数据的分类项目. • 依项目别统计数据并记录于图表中. • 绘制坐标:横轴用以表示项目.纵轴有2条,左边一条表示不 良数等,右边一条用于表示累计值.关于刻度最大值则一般 用累计数与100%. • 将所统计的数值用柱状排列于坐标上.(从大到小,其它项则 排在最后即最右端). • 将所占比率用曲线表示(累计曲线),各项的累计数据在相应 的上方打点,然后用折线连接,绘累积比率线. • 记下数据及图表的条件(时间,期限,制成者,核准或改善目 标,分析方案)
修改两Y轴-2
• 1、双击次数值Y轴，选择刻度项，对最大 值进行更改，最大值一般为１.0；同时对主 要刻度值进行更改，数值更改为合适比例 后，点击确定。

S R-Sq R-Sq(adj) 0.0728539 87.7% 86.1%
smartscope
10.4 10.3 10.2 10.1 10.0 10.1 10.2 10.3 10.4 cmm 10.5 10.6 10.7
注意：相关结果 分析在90%以上 说明两者之间存 在关系！！
直
方
图
定义：
直方图是将所收集的测定值或数据之全距分为几个 相等的区间作为横轴,并将各区间内之测定值所出现次 数累积而成的面积,用柱子排起来的图形.用来对品质现 状了解，找出比较深入的问题。
第一步:将数据输入Minitab工作表
根据5M1E分析原因依次输入工作表
第二步:选择“Stat>Quality Tools>cause-and Effect……”
第三步:在出现的对话框输入下图所示信息
选择包含因果图相应分枝 的原因列表栏
改变缺陷分枝标识的缺 省设置,缺陷设置为人、 机、料、法、环、测量
使用Minitab制作步骤如下:
第一步:将数据输入Minitab工作表
输入不良项目
相对应的输入 不良数
第二步:选择“Stat>Quality Tools>Pareto Chart”
第三步:在出现的对话框输入下图所示信息 -1
选择包含原始数 据的栏
第三步:在出现的对话框输入下图所示信息 -2
如数据输入格式为缺陷名和 缺陷频率时选择该项
使用Minitab制作步骤如下:
第一步:将数据输入Minitab工作表
将收集数据输入
第二步:选择“Graph>Histogram”
第三步:在出现的对话框输入下图所示信息-1
选择所需直方图 的图样

1、双击Minitab运行程序图标‘
’打开Minitab软件；
2、在Excel电子文档中输入的‘钢板厚度的数据列表’然后将表
格复制到Minitab的工作表中。
3、在主菜单栏，选择选择‘统计/质量工具/能力分析/正太’ ，打
开
‘能力分析（正太分布）’对话框；
4、勾选对话框中的‘单列’选项，包含回归’ 将光标放置在其
1、Minitab作图（柏拉图）的一般步骤
１、双击Minitab运行程序图标‘
’打开Minitab软件；
２、在电子文档的Ｃ1与Ｃ2列中输入各种不良原因与不良数
３、在主菜单栏，选择‘Stat（统计）/Quality Tools（质
量工具）/Pareto （柏拉图）’打开柏拉图 对话框；
4、 勾选‘已整理成表格的数据缺陷’栏，将光标置‘标签位
右边的空白栏，选择对话框左上角的‘C12 其它’行，再点击 ‘选
择’，选择分支‘其它’； 11 .在‘因果图’对话框的‘效应’右边的空白栏输入‘假焊’；在 ‘标题’右
边的空白栏输入‘假焊不良原因的因果图’； 12. 点击‘确定’，完成作图。
详细步骤参见下页截图：
5
2、Minitab作图（因果图）的一般步骤
Cpm CL 下限
2100.. 08
1 9
Minitab作图有何优点？ 最关键是什么？
Minitab作图的优点：简单、高效，图形直观、 一目了然；无与伦比的易学性。
最关键是：分类整理好数据列； 选择所要做图的类别； 逐步勾选进行运算。
21 2024/4/3
复制到Minitab的工作表中。
３、在主菜单栏，选择‘统计/控制图/单值的变量控制图/单值’
，打开‘控制图’对话框；

170以下占比 0.04% 0.11% 0.18% 0.05% 0.04% 0.06%
205以上占比 0.00% 0.11% 0.35% 0.05% 0.00% 0.00%
主轮时间 0 40 90 130 200 248
备注：散布图中两组变量的对应数至少在30个以上，最好50个，100个最佳。 此为示例。
常用工具栏和菜单栏
根据输入的格式丌同会显 示丌同的数列类型
柏拉图的使用
柏拉图主要用于分析，发现主要问题。
收集各项质量特性缺陷 列成表 输入到MINITAB中
MINITAB绘出图形
找出关键的Y特性
1. 数据录入表格内（手动输入或者粘貼的方式）
2. 选择柏拉图选项，并在弹出的对话框进行选择。
C2-T列 C3列
更深入的分析可以考虑制程能力分析。
正态分布图的使用
正态分布图的主要用于判定数组的集中性、均匀性，并综合评价其的能力水平。 我们一般用CPK值来评价过程的制程能力。 Cpk的评级标准：（可据此标准对计算出之制程能力指数做相应对策） A++级 Cpk≥2.0 特优 可考虑成本的降低
A+ 级 2.0 ＞ Cpk ≥ 1.67 优 应当保持之
3. 生成图形并进行分析。
前三项不良为D级+破片、边缘、线痕，提供改善方向。
因果图的使用
因果图主要头脑风暴法找出可能的原因，进行改善。 例：以切片的掉片、掉棒为例。 数据组： 人
胶水配比出错
机
设备抖动严重
料
砂切割力弱，切 割深度丌均匀
法
切割深度过深
环
粘晶房温湿度超 标
胶层偏厚
晶棒、玻璃板表 面没有擦拭干净
砂浆冷却水异常， 胶水里存在异物 冷却效果差，切 割温度过高

柏拉图的制作及步骤
一、数据整理与输入
注意输入格式
柏拉图的制作及步骤
二、选择图形及设置
柏拉图的制作及步骤
二、选择图形及设置
柏拉图的制作及步骤
三、Minitab柏拉图制作完成，对数据进行分析
练习一、某工厂把影响××产品质量的缺陷项进行 统计，列出下表，试用柏拉图进行分析。
项次 1 2 3 4 5 缺陷项 虚焊 漏焊 强度不够 外观受损 其它 数量 500 300 200 150 160
柏拉图的应用范围： 如：时间管理、安全、士气、不良率、成本、营业额等。
柏拉图的注意事项
柏拉图的使用时机： • 1.把握重点问题.
• 2.调查问题原因. • 3.预计改善效果.
柏拉图的注意事项：
• • • • 1.横轴按项目类别,依大小顺序由高而低排列下来,“其他”项排末位. 2.次数少的项目太多时,可归纳成“其他”项. 3.前2～3项累计影响度在70%以上. 4.纵轴除不良数外,也可表示其他項目.
次数 比例
72
练习二、2014年上半年电工成品检验统计出来的质 量问题数据，试绘制柏拉图分析。
2014年上半年质量问题统计（成品） 产品错 漏装 15 20.83% 产品错漏 包 22 30.56% 产品结构 缺陷 8 11.11% 产品外观问 题 16 22.22% 装配不到 位 11 15.28%
质量问题
合计
柏拉图的制作及步骤
一、数据整理与输入
1.对数据进行整理计算，做统计表。一般为不良项目、不良数（不良率、累计 不良率、影响度、累计影响度）。 2.项目排列要按照数值从大到小排列，其它项排最后。 例如： 项次 1 2 缺陷项 虚焊 漏焊 数量 500 300

NO.2:选择柏拉图
单击“统计”—“质量工具”—Pareto图
数据后台 排序
柏拉图制作步骤
NO.3：界面设定
选择此处
选择C1
选择C2
选项处可以编辑标题 点击确定
柏拉图制作步骤
NO.4：柏拉图图形
发生数量 百分比
不良项目 的 Pareto 图
单击可以编辑标题，修改字体等
20
100
80 15
60 10
柏拉图注意事项 柏拉图注意事项
1.minitab制作柏拉图会自动后 台排序，列出其他选项，数据搜 集只需要列出项目、数量即可。
2.点击已经处理成表格的缺陷数， 否则不能制作柏拉图
3.一般将最后的5%合并为其他， 也可选择不合并
柏拉图制作步骤
NO.1：数据搜集
打开minitab；将项目、发生数 量统计成两列
定义
定义:根据所搜集之数据,按不良原因、 不良状况、不良发生位置等不同区分 标准,以寻求占最大比率之原因, 状况 或位置的一种图形.
柏拉图的用途及应用范围
决定改善的攻击目标.
作为降低不良的依据.
用于发掘现场的重要问 点
柏拉图的用 途及应用范 围
确认改善效果
用于整理报告或记 录
可作不同条件的评价.
柏拉图的应用范围：时间管理、安全、士气、不良率、成本、营业额、客诉等
培训教程
minitab制作柏拉图
培训：王利江
目录
1.柏拉图由来 2.柏拉图用途和使用范围 3.柏拉图使用注意事项 4.柏拉图制作步骤 5.柏拉图制作练习
柏拉图的由来
由来 1897年,意大利学者柏拉撬分析社会经济结构, 发现绝大多数财富掌握在极少数人手里,称为 “柏拉法则”.

Minitab 操作1、柏拉图：找主要因子，大于或等于80%为主要因子。

路径：统计----质量工具----柏拉图（选已整理成表格的缺陷数据）2、正态分布：正态检验三种方法①概率图：图形---概率图（看P值，P大于0.05说明服从正态分布）;②图形化汇总: 统计---基本统计量----图形化汇总(看P值，P大于0.05说明服从正态分布）;③正态性检验: 统计---基本统计量----正态性检验3、产生随机数据：计算----随机数据（然后再选所需要产生何种数据）4、数据堆叠：数据---堆叠5、计算中行统计量、列统计量分别于计算所在行或列的均值、和、标准偏差等6、文本、数字转换：数据---更改数据类型7、概率计算：计算---概率分布----正态----累积概率8、分位数的计算：计算---概率分布----正态----逆累积概率9、稳定性：统计---控制图---单值的变量控制图----单值（单值控制图选项中S限制）10、测量系统分析①量具研究：统计—质量工具---量具研究---量具R&R研究(交叉)注:非破坏性测试用交叉,破坏性测试用嵌套.②属性一致性分析(合格与不合格)统计---质量工具---属性一致性分析③量具线性与偏倚研究:统计——质量工具——量具研究——量具线性与偏倚研究（看所有的P值，所有P值小于0.05时）11、非正态数据与正态数据转换①正态性检验，②如非正态，转换成正态分布：统计—控制图---BOX-COX12、过程能力分析统计---质量工具---能力分析13、置信区间的算法：①正态总体均值的置信区间（σ已知）用1Z单样本：统计—基本统计量—1Z单样本输入的标准差为已知的总体标准差；样本数量为所取的样本量；均值为样本的均值；请注意选取置信水平②正态总体均值的置信区间（σ未知）用1t单样本：统计—基本统计量—1t单样本请注意汇总数据中的样本数量为所取的样本量；均值为样本的均值；标准差为样本的标准差；请注意选取置信水平④比率P的置信区间用1P单样本：统计—基本统计量—1P单样本（试验数为样本量，事件数为要计算的概率的数）⑤正态总体方差和标准差的置信区间用单方差：统计—基本统计量—σ2单方差（请注意用汇总数据，及置信水平）14、假设检验第一步：首先建立原假设及备择假设；第二步：进行检验；①正态总体均值检验（σ已知）用1Z单样本：统计—基本统计量—1Z单样本输入的标准差为已知的总体标准差；样本数量为所取的样本量；均值为样本的均值；请注意选取置信水平及假设检验，并输入假设的均值及选取相应的备择假设。

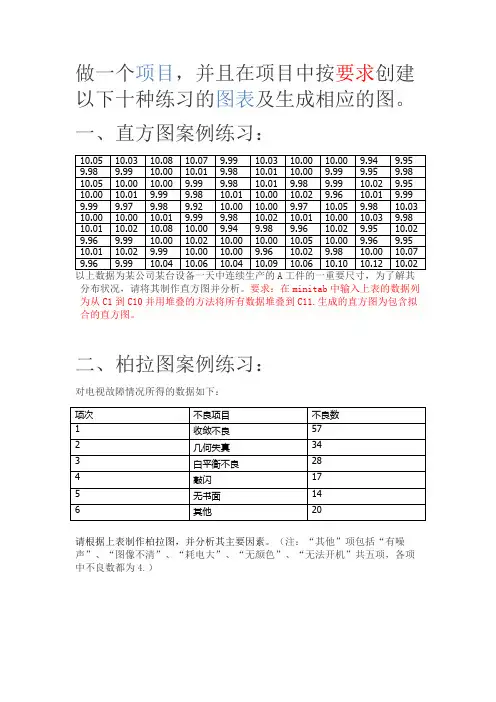
做一个项目，并且在项目中按要求创建以下十种练习的图表及生成相应的图。

一、直方图案例练习：分布状况，请将其制作直方图并分析。

要求：在minitab中输入上表的数据列为从C1到C10并用堆叠的方法将所有数据堆叠到C11.生成的直方图为包含拟合的直方图。

二、柏拉图案例练习：对电视故障情况所得的数据如下：请根据上表制作柏拉图，并分析其主要因素。

（注：“其他”项包括“有噪声”、“图像不清”、“耗电大”、“无颜色”、“无法开机”共五项，各项中不良数都为4.）三、特性要因图（因果图）的练习：请用minitab软件生成如上图的因果图。

四、饼图的练习：请用minitab软件生成如上图的饼图。

要求：1.饼图中只显示类别名称及百分比，而且有从标签到扇形区的连线。

2.扇形区按递增排列，起始角度30。

3.输出四个地区的缺陷饼图。

五、散布图的练习。

根据以上数据请用minitab软件生成散布图。

要求：将序号为1到15分为一组，16到30分为一组，生成出包含回归和组的散点图。

六、Xbar-R Chart练习：加工某产品的计量数据如下表：请依据上表数据用minitab绘制出Xbar-R Chart，判断该过程是否处于稳定状态。

如果不处于，指出异常点样本号并计算其均值与标准差。

要求：控制图的上下控制线为黑色虚线。

七、Xbar-S Chart的练习。

请依据上表用minitab绘制出Xbar-S Chart。

并判断该过程是否处于稳定状态。

八、P Chart的练习。

某汽车配件厂的曲轴整形加工工段，通过检查曲轴的擦伤情况如下表：试根据上表的数据用minitab为该工段绘制P Chart图。

并判断是否处于控制状态。

九、NP Chart的练习。

某晶体管厂对所生产的晶体管实行质量管理，检查每批样本晶体管，检查结果如下表：用minitab生成出NP Chart图。

十、过程能力分析以下数据为某加工过程中杂质含量与批次情况，请用minitab对该过程能力分析。

Minitab做柏拉图分析
1.将C1 定义为不良项目， C2 定义为数量频次
2.将资料输入相应的栏位中。
3、打开统计菜单，点选质量工具>pareto图
4.这是弹出的柏拉图定义界面。
5.在“标签位于”处填入C1，在“频率位于”处填入C2，在“超过此百分比 后将乘余缺陷合并为一个类别” 处填入适当的数字，一般默认为95，这表示 95%以后的少数不良项目将会合并在一起。你也可以根据自己的需要选择其，点选Options 按钮，这是弹出的界面。
7. 在弹出的界面上填入相应的内容，然后按下所有的OK。
8.这是输出的柏拉图。
自动线不良项目柏拉图分析
50000 100 40000 80
数量频次
60 20000 40
10000
20
0 不良项目 数量频次 百分比 累积 %
0 粘丝 17913 40.4 40.4 脏污 13896 31.4 71.8 异物 8536 19.3 91.1 针孔 1561 3.5 94.6 导线粘粉 514 1.2 95.8 其他 1878 4.2 100.0

!
o
.c
散点图（scatter diagram/ Scatter plot）:数据点 在直角坐标系平面上的分布图，查看X，Y变量 之间关系或者点的分别。
散点图可以提供三类关键信息： 1、变量之间是否存在数量关联趋势 2、如果存在关联趋势，是线性还是曲线的 3、如果有某一个点或者某几个点偏离大多数点，也就是离群 值，通过散点图可以一目了然。从而可以进一步分析这些离群 值是否可能在建模分析中对总体产生很大影响。 通过散点图也可以查分布
PD
PD
F-
XC
h a n g e Vi e
w
F-
XC
h a n g e Vi e
w
er
er
!
O W
N
w
.d o
c u -tr a c k
.c
025 Minitab 图形操作 直方图
y
bu
to
k
lic
C
m
C
lic
k
to
bu
y
N
w
.d o
c u -tr a c k
O W
!
o
.c
QC七大手法
• • • • • • •
o
m
w
w
w
w
o
m
w
w
w
w
PD
PD
F-
XC
h a n g e Vi e
w
F-
XC
h a n g e Vi e
w
er
er
!
O W
N
w
.d o
c u -tr a c k
.c
028 Minitab 图形操作 散点图

防焊 磨板不潔
防焊不良
印 偏 (粘 漆 )
文字
滲墨
文字脫落
保 護 膜 印 偏 (粘 漆 ) 保護膜脫落
斷短路 10
15
步驟三：列出過程作 業步驟列出左列
步驟四：針對每個輸 出變量，在每個作業 步驟確認該輸出有影 響的輸入變量
因果矩陣步驟
流程
客戶關鍵品 質
刮傷
輸入變數
10
滲墨
0
線
印偏
0
路 蝕刻不良
3
柏拉圖步驟
步驟1：決定數據的分類項目 步驟2：決定效果數據的期間；並按分類項目，在
期間內收集數據 步驟3：依分類項目別，做數據整理，並作出統計
表。 步驟4：記入圖表紙並依數據大小排列畫出柱狀圖。 步驟5：繪累計曲線。 步驟6：繪累計比率。 步驟7：記入必要的事項。
4
柏拉圖范例
對產品進行品質檢驗，對其中的不合格品進行原因分 析，共檢查了七批，將每個不合格品原因分析如下：
1~10等級區分重要度。 輸入變數X視為投入此流程的可能變因。 避免做出完美的解決對策，只需要概略統計。 執行後，專案可以重新修正、評估。
12
因果矩陣(C-E Matrix)
對顧客的重要性 Y
過程作業的 步驟
過程 步驟
過程 輸入
X
第3步
X1
X2
第4步
X3
在每個作業
X4
步驟確認該
輸出有影響
的輸入變量
Y1 Y2 Y3
X n-1
13
Xn
第2步
主要輸出變量對顧客的
重要性:可將最重要的項
合 目給9分，最低分
計
第1步
Y n-1 Y n

QC七大工具之柏拉图（Pareto）分析示例2
分析路径：统计-质量工具-pareto图
以下是minitab数据堆叠格式与参数设 置界面
不良频数
瑕疵数（按 期间 分组）的 Pareto 图
期间 = 日期
钳杆
草稿 其他 期间 = 傍晚
污迹
ห้องสมุดไป่ตู้
20
瑕疵数
钳杆
15
草稿
其他
10
污迹
5
期间 = 夜间 20
0 期间 = 周末
15
10
5
0 钳杆 草稿 其他 污迹
瑕疵项
解释
总体来说，夜班生产的缺陷数量更多。大多数问题是因划痕和掉漆所致。如果您检查夜班过程 中的那部分，就会了解到问题所在。
原始数据
瑕疵 数 期间
草稿 日期 草稿 日期 钳杆 日期 钳杆 日期 污迹 日期 草稿 日期 其他 日期 其他 傍晚 钳杆 傍晚 钳杆 傍晚 钳杆 傍晚 钳杆 傍晚 草稿 傍晚 草稿 傍晚 钳杆 夜间 草稿 夜间 污迹 夜间 草稿 夜间 钳杆 夜间 钳杆 夜间 钳杆 夜间 钳杆 夜间 其他 夜间 其他 夜间 草稿 夜间 草稿 夜间 钳杆 夜间 草稿 夜间 污迹 夜间 草稿 夜间 其他 夜间 草稿 夜间 草稿 夜间 钳杆 周末 钳杆 周末 钳杆 周末 污迹 周末 污迹 周末 污迹 周末 其他 周末

7
统计基础
范围和四分位数
范围（Range）：数据集合中的最大值和最小值之差。 Range＝最大值－最小值
四分位数（Quartile）：对数据集合按四等份进行排列。
Q1：第一四分位数（First Quartile）＝25％对应值。 Q2：第二四分位数（Second Quartile：组中值）＝50％对应值。 Q3：第三四分位数（Third Quartile）＝75％对应值。 四分位范围（IQR：Inter quartile Range）：Q3－Q1
19
Minitab 图表分析
箱图（Box plot）
是对多个图表间数据分布的差异点，中心位置和散步 大小的比较。
Boxplot of C1
2.06 2.04 2.02 2.00 1.98 1.96
C1
Lishen battery Confidential Proprietary
20
Minitab 图表分析
Histogram of C1, C2
30
25
20
15
10
5
0 1.97 1.98 1.99 2.00 2.01 2.02 2.03 Data
Variable C1 C2
Lishen battery Confidential Proprietary
18
Lishen battery Confidential Proprietary
饼图（pie chart）
Lishen battery Confidential Proprietary
24
Minitab 图表分析
饼图（pie chart）
Pie Chart of C2 vs C1
2.20%.7% 6.6% 8.8%

Minitab全面经典教程
-------Minitab统计分析
Session Window:
•分析结果输出窗口Data Window:
•输入数据的窗口
•每一列的名字可以写在最前面的列
•每一列的数据性质是一致的
不同的要求选择不同的保存命令
•Select: Data > Change Data Type > Numeric to Text
需要转换的列
转换后数据存放列，
可以是原来的数据列
•Select: Data > Stack > columns
原始数据
顺序进行输入
输入堆栈后存
放列的位置
注解可以用来区
分数据的来源
原始数据
在对话框中输入2~5
列数据，注解列在前面
输入新工作表
和注解的位置
输入需要转置的列输入新工作表的位置可以输入注解列
输入需要连
接的数据列输入新数据
列的位置
•Select: Data > code>Numeric to Text 原始数据被编码的
变量
存储编码值的栏
编码
规则
注意输入格式
输入缺陷列
输入频数列在此指定“95%”将使
余下的图示为“Others”。

设置X轴,Y轴标签
可以对柏拉图进行命名
可以选择不同的输出表现形式
•可以用直接方式判定，有正相关的倾向。

•更详细的说明可以参见回归分析
可以选择不同的输出表现形式变量作直方图点击此选项
输入上下规格界限。