电磁学第4章

电磁学第四章恒定电流和电路前三章讨论了静电场，场源电荷相对于观察者是静止不动的。

从本章起讨论电荷运动时引起的有关现象。

若电荷作有规则的定向运动就会形成电流，要维持电流的存在，必须要有相应的电场，所以本章主要讨论恒定电流和电场，并引入许多重要的物理概念。

§ 4.1恒定电流一、电流、电流强度、电流密度导体放在静电场中时，导体中的自由电子在外电场作用下发生定向运动，当导体内部场强为零时，定向运动停止。

若能使内部场强不为零，定向运动就会持续下去，这时，在导体中就有电流产生。

1、电流（1）定义：带电粒子（在外电场作用下）作宏观的定向运动便形成电流（叫做电流）本章只讨论：导体内部的电流。

（2）载流子：导体中的能在电场力作用下发生定向运动的带电粒子叫做该导体的载流子，它们是形成电流的内在因素。

不同性质的导体有不同的载流子：金属导体的载流子是自由电子，酸、碱、盐的水溶液中的载流子：是正负离子等。

（3）电流的方向正电荷运动的方向为电流的方向。

结论:A :导体中电流的方向总是沿着电场方向，从高电势处指向低电势处；B :导体中的载流子为负电荷（自由电子），此时可以把电流等效为等量的正电荷沿负电荷的反方向运动形成。

2、电流强度描述，电流的大小（1）定义：单位时间内通过导体任一横截面的电荷量，叫做该截面的电流强度。

（这里的截面可以推广到任意曲面）Aq表示为：I 二lim t >0-△t（2）电流强度I是反映导体中某一截面整体特征的标量。

A qI就某S面：1=三：平均地反映了S面的电流特征。

3、电流密度J（1）定义：导体中每一点的J的方向是该点正电荷运动方向（电场方向），J的大小等于过该点并与电流方向（正电荷运动方向）垂直的单位面积上的电流强度，写为：(2) J与I有不同：I是一个标量，描写导体中的一个面;J是矢量点函数，描写导体中的一个点。

(3) J与I的普遍关系只反映了J与I的特殊关系（要求面元与J垂直），下面推dS_导J与I的一般关系nJ在导体中某点处取一任意面元dS （dS与J并非垂直），面元dS的法线方向n?与该点的J夹角为二，则dS在与J垂直的平面上的投影为：dS〕二dScos^而dl 二JdS = JdScos^ （标量）二J r?d^ = J dS（二矢量点乘仍为标量）所以通过导体中任意曲面S的电流强度I与J的关系为：I 二J dSS此式说明：一曲面上的I是J对该曲面的通量（J通量）。

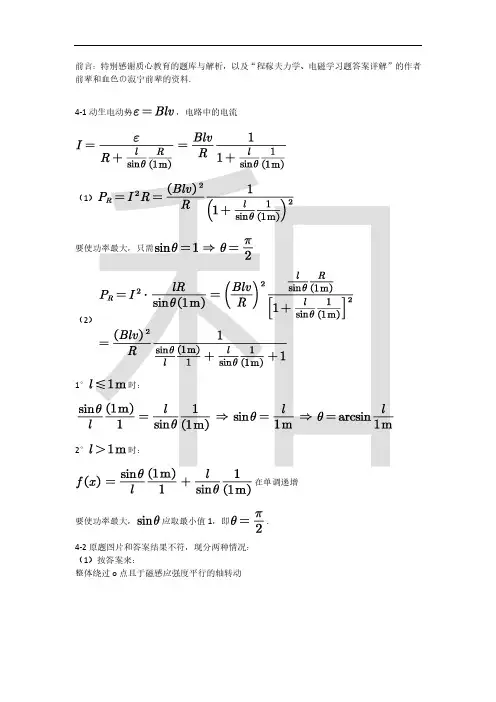
前言：特别感谢质心教育的题库与解析，以及“程稼夫力学、电磁学习题答案详解”的作者前辈和血色の寂宁前辈的资料.4-1动生电动势，电路中的电流要使功率最大，应取最小值1，即.4-2原题图片和答案结果不符，现分两种情况：（1）按答案来：整体绕过o点且于磁感应强度平行的轴转动将运动分解为绕c的平动和转动，转动对电势差无贡献4-3（1）OP电势相等时，OP速度沿磁场方向，显然当OP位于YOZ平面时，OP电势相等（2）当OP在YOZ平面右侧即X＞0时，电势差（3）当OP在XOZ平面第一象限时，电势差最大4-4在任意时刻t，线圈中的电流为，则由电磁感应定律和欧姆定律得，该式也可以由能量得到4-5其中后一项式中与直杆平行，当与直杆方向垂直时，电动势绝对值最大故有.4-6对于回路有，故有力矩平衡故有.4-7（1）当转轮在磁场中旋转时，每一根轮辐上的感应电动势为四根辐条作为电源是并联的，轮子产生的感应电动势不变（2）根据戴维宁定理，将轮子作为电源，此时将外电路断路计算等效电动势. 4-8式中当转轮1和转轮2分别以ω1和ω2旋转并达到稳定时，闭合回路中感应电流为注意，因转轮1的四根轮辐并联，总电阻为；转轮2类似，其余连接导线、电刷、轮边缘的电阻均忽略不计.又，因转轮1和转轮2同方向旋转，ε1和ε2同方向，但在电路中的作用是彼此减弱的稳定转动时，转轮2所受磁力矩应与阻力矩抵消.磁力矩是四轮辐所受安培力产生的力矩，为式中是转轮2每根轮辐中的电流.阻力矩是阻力闸提供的力矩，因阻力恒为F，故有稳定将要向下滑动时安培力加滑动摩擦力等于重力分力解得可变电阻最大值匀速向上滑动时，电路中同时杆受力平衡，有联立解得.4-11注意题文描述中磁场竖直向上而所给图垂直于轨道平面，此处以文字为正.（1）下滑时，动生电动势与电源同向，故当加速下滑时，电流增大，V2读数增大，V1减小.（2）由牛顿第二定律及欧姆定律得：4-4-4-内电阻阻值负载电阻与内阻相等时，负载上功率最大.4-15平板的宽度d切割磁感线产生感应电动势，积累电荷产生电场，使自由电荷磁场力和4-16由受力平衡，；由力矩平衡，解得.4-17由于圆盘有厚度D，故当圆盘在磁场区域内竖直下落的速度为v时，在圆盘的厚度方向分离变量：两边积分：又初态，代入得：最大焦耳热：4-23（1）如图所示，当小球在管中任意位置x时，设该处的涡旋电场为E，则故式中r是小球在x位置时与O′的距离，式中的负号表示E的方向如图所示，即E与B的变化构成左手螺旋.因此，E的x分量为其中用到几何关系表示沿y轴正方向.小球所受洛仑兹力沿y方向，无x分量，为可见，即洛仑兹力沿y轴负方向小球在y方向还受管的支持力，因三力平衡，故管对小球的支持力为，于是，小球对管的作用力为.4-24法一：cd法二：记圆心为O，连接，.封闭回路中，与段无感生电动势，则.4-25由图中磁场方向及均匀减小，可知圆周上感应电动势方向为顺时针，大小为已知，联立解出故A、B两点电势差.4-26磁场变化产生感应电动势（负号代表逆时针方向）圆环电阻阻值，感应电流电功率.4-27回路以逆时针指向纸外为正，则磁通ab上解得做功.4-29K反向时，励磁电流反向，磁场反向，磁通量变化量大小为原来的两倍，方向相反.4-32根据自感定义，单匝线圈磁通为.4-36设原线圈电路电流为，副线圈电路电流为，由理想变压器性质由题整理得要求灯正常发光，所以算出额定电流，然后能得到每个回路上的电流.4-38（1）如图，由输入等效电路原理（2）原线圈上的电压；副线圈上的电压（3）变压比为.4-39（1）由题，安培力等于阻力（2）代入，（3）单位时间克服阻力做功单位时间电路中消耗代入得（2）当C2断路时，没有感应电流，C1中无互感电动势此时C2中只有互感电动势，a′、b′两端的电压为.。

第四章 习题一(磁场)1、一根载有电流I 的无限长直导线，在A 处弯成半径为R 的圆形，由于导线外有绝缘层，在A 处两导线并不短路，则在圆心处磁感应强度B的大小为( C )(A) I (μ0＋1)／(2πR) (B) μ0πI ／(2πR) (C) μ0I(1＋π)／(2πR) (D) μ0I(1＋π)／(4πR)2、载有电流为I 的无限长导线，弯成如图形状，其中一段是半径为a 的半圆，则圆心处的磁感应强度B的大小为( D )(A) μ0I ／(4a ) + μ0I ／(4πa )(B))8/(2)4/()4/(a I a I a I o o o πμπμμ++(C) ∞(D))4/(2)4/()4/(a I a I a I o o o πμπμμ+-3、如图，电流I 均匀地自下而上通过宽度为a 的 无限长导体薄平板，求薄平板所在平面上距板的一 边为d 的P 点的磁感应强度。

解：该薄板可以看成是由许多无限长的细直载流 导线组成的，每一条载流线的电流为dI =Idx /a ， 根据无限长直载流线磁场公式，它们在P 点产 生的磁感应强度的大小为xdxa πI μx πdI μdB 2200==，B d 的方向⊗ ∴ dad a πI μx dx a πI μdB B a d d ad d+===⎰⎰++ln 2200，B 的方向⊗PB4、电流均匀地自下而上通过宽为2a 的无限长导体薄平板，电流为I ，通过板的中线并与板面垂直的平面上有一点P ，P 到板的垂直距离为x ，设板厚可略去不计，求P 点磁感应强度B 。

解：面电流线密度a I j 2/=在离轴线y 处取一宽为dy 的窄条，其电流为dy a Ijdy dI 2==, 22y x r +=P 点B d的方向如图所示。

r πdI μdB 20=220044yx dy a πI μr dy a πI μ+== 22cos sin yx x rx φθ+===，22sin cos yx y ry φθ+===2204cos y x ydya πI μθdB dB x +==，2204sin y x xdy a πI μθdB dB y+== 04220=+==⎰⎰--a a aa x x yx ydya πI μdB Bxaa πI μx y a πI μy x dy aπIx μdB B aa aa aa y y arctan 2arctan 4400220==+==---⎰⎰ y y y x x e x a aπIμe B e B B ⎪⎭⎫ ⎝⎛=+=arctan 205、求上题当a →∞，但维持aIj 2=(单位宽度上的电流，叫做电流线密度)为一常量时P 点的磁感应强度。

《中学物理》第3册电磁学第4章电磁感应知识重点在“第4章电磁感应”主要是研究感生电流、感生电动势的大小、方向、自感现象、自感电动势等物理基础知识。

电场、磁场只是局限于静态场。

而楞次定律则是涉及到了变化的磁场、变化的感应电流磁场之间的相互关系，属于是动态场。

由“静”到“动”，这是1个飞跃过程。

所以说，楞次定律是学习物理学的又1个难点问题。

一、感生电流⒈产生闭合导体放在变化磁通量（Ф原）的磁场（B新）中，产生感应电动势（ε）。

而感应电动势（ε）则驱使导体中的自由电子移动，而形成了感生电流（I ）（感应电流）。

⒉作用在闭合回路的原有磁场（B原）中，产生了新的磁场（B新），来阻碍原有磁场（B 的磁通量（Ф原）发生变化。

原）分析：①当闭合回路中的1部分导体，在磁场中做切割磁感线运动时，闭合回路中的磁通量一定会发生变化。

②在这1部分导体两端，就会产生了感应电动势。

于是，在闭合回路中，就会产生了感应电流。

⒊描述描述产生感生电流（I ）的2种方法。

①线圈内的磁通量：通过线圈的磁通量（Ф）发生变化时，线圈里就产生感生电动势（ε）。

如果电路是闭合的，电路中就会产生感生电流（I ）。

②导体切割磁力线：导体在磁场里，切割磁力线时，导体内部就产生感生电动势（ε）。

如果导体是闭合电路的一部分，就会产生感生电流（I ）。

⒋因素影响感生电流（I ）大小的因素：①导体（L）切割的速度（v）大小。

②导体（L）切割的运动（α）方向。

③永磁体的磁力强度（B）。

④切割导体（L）的条数（n）。

⑤切割导体的有效长度（L）。

二、感生电动势的大小⒈切割磁力线导体做切割磁力线运动时，感生电动势（ε）：ε= B L v sinα其中：ε：感生电动势。

单位：伏特（v）。

B：磁感应强度。

单位：特斯拉（T）。

L：导线的长度。

单位：米（m）。

v：运动速度。

单位：米/秒（m / s）。

α：磁场方向（B）与运动速度（v）方向之间的夹角。

单位：度（°）。

第四章 习题2、平行板电容器（面积为S,间距为d ）中间两层的厚度各为d 1和d 2（d 1+d 2=d ），介电常数各为1ε和2ε的电介质。

试求：（1）电容C ；（2）当金属板上带电密度为0σ±时，两层介质的分界面上的极化电荷密度'σ；（3）极板间电势差U;（4）两层介质中的电位移D ； 解：（1）这个电容器可看成是厚度为d 1和d 2的两个电容器的串联：12210212121d d SC C C C C εεεεε+=+=（2）分界处第一层介质的极化电荷面密度（设与d 1接触的金属板带正电）1111011111εσεεεσ)(E )(P n P '-=-=-=⋅=分界处第二层介质的极化电荷面密度：21222022211εσεεεσ)(E )(P n P '--=--=-=⋅=所以， 21021211εεσεεσσσ+-=+=)('''若与d 1接触的金属板带负电，则21021211εεσεεσσσ+--=+=)('''（3）2101221202010102211εεσεεεεσεεσ)d d (d d d E d E U +=+=+= （4）01101σεε==E D ，02202σεε==E D4、平行板电容器两极板相距3.Ocm ，其间放有一层02.=ε的介电质，位置与厚度如图所示，已知极板上面电荷密度为21101098m /c .-⨯=σ，略去边缘效应，求: (1)极板间各处的P 、E 和D 的值; (2)极板间各处的电势(设正极板处00=U );(3)画出E-x ，D-x ，U-x 曲线;解：（1）由高斯定理利用对称性，可给出二极板内：2111098m /c .D e -⨯==σ（各区域均相同），在0与1之间01==P ,r ε，m /V DE 20101⨯==ε在1与2之间210000010454112m /c .D)(E )(P ,r r r -⨯=-=-==εεεεεεε，m /V D E r500==εε 在2与3之间，01==P ,r ε，m /V DE 20101⨯==ε（2）0=A V ：0-1区：,x dx E V xD 100=⋅=⎰1-2区：),x x (dx E V xx 1501-=⋅=⎰)x x x ,.x x )x x (V 2111505010050≤≤+=+-=2-3区：),x x (dx E V xx 2100021-=⋅=⎰∆)x x x (,.x ).x (,x x x x x )x x (V 3212221501000050100505010010010050≤≤-=-=+-=-++=题4图6、一平行板电容器两极板相距为d,其间充满了两种介质，介电常数为1ε的介质所占的面积为S 1, 介电常数为2ε的介质所占的面积为S 2。

1.如图所示，一根细长的永磁棒沿轴向均匀磁化，磁化强度为。

试求图中表示的1、2、3、4、5、6、7各点的磁感应强度和磁场强度。

解永磁体被磁化，可以认为表面出现磁化电流，由磁化电流与磁化强度的关系，可知。

并且磁化电流产生的磁感应强度可与一细长螺线管产生的磁场等效，所以由细长螺线管磁场分布可知，在细长螺线管轴线上，其端部的磁感应强度恰为其中部的一半，故表明磁感应线连续。

因为沿方向的投影式为所以表明磁场不连续。

2有一圆柱形无限长载流导体，其相对磁导率为，半径为，今有电流沿轴线方向均匀分布，试求： 导体内任一点的 ； （2）导体外任一点的 ； （3）通过长为的圆柱体的纵截面的一半的磁通量。

解 （1）在导体内过距轴线为 的任一点作一个与轴垂直，圆心在轴线上，半径为 的圆周作为积分线路，如图所示。

此圆周与磁场线重合，而且沿圆周 是常数。

故得根据含介质的安培环路定理因导体内电流均匀分布，所以电流密度为在半径为 的截面中所以 ,则（2）在导体外任一点 ，以过这一点而圆心在轴线上的圆周作为积分线路，同样得因 ，故 ，所以 ,(3)如图所示，通过长为的圆柱体纵截面的一半的磁通量为3同轴电缆由两同心导体组成，内层是半径为的导体圆柱，外层是半径分别为、的导体圆筒，如图所示。

两导体内电流等量而反向，均匀分布在横截面上，导体的相对磁导率为,两导体间充满相对磁导率为的不导电的均匀磁介质。

试求在各区域中的分布。

解:对称性分析可知，在半径相等处的磁场强度大小相等，方向与电流方向成右手螺旋关系。

可用含介质时的安培环路定理求得，再由、之间的关系求得分布。

在中，,所以在中所以在中所以在中,, 各区域的方向与内层导体圆柱中的电流方向成右手螺旋关系。

4 一铁环外均匀绕有绝缘导线，导线中通有恒定电流，今若在环上开一条狭缝。

试求：（1）开狭缝前后，铁环中的，和如何变化；（2）铁环与缝隙中的，和。

解由高斯定理可知，磁场中磁感应强度总是闭合曲线，而磁场强度线却不一定连续；的环流是由回路中的传导电流决定的，而的环流是由回路中的传导电流和磁化电流（也称束缚电流）共同决定的。

第四章 静电场电磁运动是物质的又一种基本运动形式。

电磁学就是研究物质电磁运动规律及其应用的学科。

历史上，人们在电磁学方面的研究成就，曾经促进了电气工程技术的高速发展，加深了人们对物质世界的认识。

当今，电磁学理论不仅普遍应用于科技生产各个部门，而且也越来越成为新科学、新技术发展的理论基础。

一般说来，运动电荷将同时激发电场和磁场，电场和磁场是相互关联的。

当我们研究的电荷相对某个参考系静止时，电荷在此静止参考系中只激发电场，而无磁场，这个电场就是静电场。

本章我们研究真空中静电场的基本特性，引入描述电场的两个重要物理量—电场强度和电势，并讨论它们的叠加原理及两者之间的积分关系，同时介绍反映静电场基本性质的高斯定理和静电场环路定理，最后讨论了静电场的能量。

电荷起源及电荷守恒定律4.1.1 电荷电荷有两种——正电荷和负电荷，同种电荷相斥，异种电荷相吸。

实验证实，原子中的电子带负电，质子带正电，中子不带电。

在组成物质的原子里，电子的电荷集中在半径小于m 1018-的小体积内。

因此，电子被看成是一个具有有限质量和电荷的“点”，由质子、中子组成的原子核集中在m 1015-的小体积内，整个原子集中在m 1010-的小体积内。

在正常情况下，每个原子中的电子数与质子数相等，故物体显示电中性。

如果把两个物体，例如丝绢和玻璃棒放在一起摩擦，则有少量电荷从一个物体迁移到另一个物体上去，因而破坏了每个物体原来的电中性状态，玻璃棒显正电，丝绢显负电。

物体能够产生电磁现象，都归因于物体带上了电荷以及这些电荷的运动。

一个物体带电称作带电体，带电体所带电荷的多少叫电量，用Q 或q 表示。

在国际单位制(SI )中，电荷的单位为库仑，简记为C 。

0>q 表示正电荷，0<q 表示负电荷。

一个带电体所带总电量为其所带正负电量的代数和。

实验证明，在自然界中，电荷总是以一个基本单元的整数倍出现，电荷的这一特性叫做电荷的量子性。

电荷的基本单元就是一个电子所带电量的绝对值，常以e 来表示。

§5 温差电及电子发射一、能量转换的可逆与不可逆现象不可逆：焦耳热——电阻媒质导电产生热量Q 、散发，与I 流向无关，一去不返； 热扩散——12T T 低温从高温→热扩散（传导），单向过程； 浓度扩散——粒子从小大n n →扩散，单向进行。

可 逆：电池——充电，电能转化为化学能；放电，化学能转化为电能。

温差电——实现：热能电能⇔，下面即述： 二、ThomSon effect温差引起，发生于体内。

1、汤姆孙效应及解释两端不等温的金属棒，当在其中通过电流时，除产生与R 有关的焦耳热外，还要吸收或放出一定的热量，且是吸收还是放出热量与I 的流向有关，此即Thomson ’s effect.结合图4-29解释：设12T T >，则电子从高温向低温扩散，非静电力——热扩散作用，形成 force ive electromot son T hom ：⎰⋅=21),(21T T l d K T Tε图4-29外加电流：两种情况。

只看图4-30中A 、B 点之上的部分,可以理解为(1) 当I 的流向在金属棒内方向时顺沿K T T,21→，相当于电源放电，金属棒吸热；(2) 当I 的流向在金属棒内方向时反K T T,12→，相当于电源充电，金属棒放热。

2T 1T KK12T T >－图4-302、汤姆孙电动势的计算 实验表明：dl dTT K )(σ=，其中⎩⎨⎧—绝对温度。

—；—金属材料汤姆孙系数—T T )(σ ⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧≠==→→⋅==⋅=∑⎰⎰⎰—珀耳帖效应出现。

—但有另一种效应。

不同，形成闭路可伴因不同金属不等温接触，温而形成闭路，有一种金属多处接触不等闭路汤姆孙电动势：同向顺积分限说明：：一段金属汤姆孙电动势总汤总汤0)(0),(),0()()(),(2121210021εσεεσσεT T T K l T T dT T dl dl dT T l d K T T i i i i l T T l三、Peltier effect数密度差引起，发生于面上。