电磁学赵凯华陈熙谋第三版习题及解答
- 格式:pdf
- 大小:4.77 MB
- 文档页数:69

例析妙用动量定理解决电磁学中问题摘要:自从2017年高考改革增加选修3-5模块为必考内容,众所周知动量是3-5的主要内容,而动量观点、能量观点与力学观点是解决动力学问题的三种途径。
如今动量变成必考模块,使学生的知识架构更加完善,在解题思维方面视野将更加开阔,总体来说对于学生解决物理问题还是有帮助的。
但通过平时教学发现大部分学生在运用动量定理解决有关电磁学问题是较薄弱的。
本文通过典例分析加深学生对动量定理在电磁学中运用的认识。
关键词:动量定理电磁感应冲量安培力洛伦兹力电容器1.动量定理解决叠加场中恒力(电场力、重力)与洛伦兹力作用下的运动问题在解决这类问题之前,先分析下运动电荷所受洛伦兹力的冲量,假设在xoy平面存在一垂直该平面的匀强磁场,磁感应强度为B,有一带电量为q的带电粒子,以速度v在磁场中做匀速圆周运动。
某时刻速度方向如图1所示。
分别将v、f正交分解,可知:在时间t内f沿x轴方向的冲量为:同理,f在y轴方向的冲量为:【例1】如图所示,某空间同时存在场强为E、方向竖直向下的匀强电场以及磁感应强度为B、方向垂直纸面向里的匀强磁场。
从该叠加场中某点P由静止释放一个带电粒子,质量为m,电量为+q(粒子受到的重力忽略不计),其运动轨迹如图中虚线所示。
求带电粒子在电、磁场中下落的最大高度H?解答:设小球运动到最低位置时速度最大为v,方向水平任意时刻v沿x轴正向、y轴负向的分速度分别为vx ,vy.。
与vy.对应的洛仑兹力水平分力方向沿x轴正向,小球由静止释放到最低点的过程中,在水平方向上,应用动量定理得:······①小球由静止释放到最低点的过程中,由动能定理得:······②联立①②可得:如果上例1中,重力不可忽略不计(已知重力加速度为g),实际上水平方向上动量定理①式不变,全程由动能定理得:·····③联立①③同样可得:1.动量定理解决电磁感应中电荷量相关问题根据电流的定义式,式中q是时间t内通过导体截面的电量;又欧姆定律,R是回路中的总电阻;结合电磁感应中可以得到安培力的冲量公式,此公式的特殊性决定了它在解题过程中的特殊应用。

电磁学第三版(梁灿彬)思考题与习题解答第一章 静电场的基本规律思考题1.1答案: (1) ×,正的试探电荷; (2) √ ;(3)× 在无外场是,球面上E⃗ 大小相等。
1.2 答案: 利用对称性分析,垂直轴的分量相互抵消。
1.3答案:(1)× 没有净电荷 ;(2)×; (3)×;(4)√;(5)×;(6)×;(7)×。
1.4答案:无外场时,对球外而言是正确的。
1.5答案:(1)无关 (2) 有关 (3)不能(导体球)、可以(介质球)。
场强叠加原理应用到有导体的问题时,要注意,带电导体单独存在时,有一种电荷分布,它们会产生一种电场;n 个带电导体放在一起时,由于静电感应,导体上的电荷分布发生变化,这时,应用叠加原理应将各个导体发生变化的电荷分布“冻结”起来,然后以“冻结”的电荷分布单独存在时产生的电场进行叠加。
1.6答案:(a 图) 能 ,叠加法(补偿法); (b 图) 不能 。
1.7答案:222121q q φφφφεε-==+,;113131+ -q q φφφφεε==,;134410+0 -q φφφφε==,。
1.8答案:(1)× ;(2)×; (3)×;(4)×;(5)√;(6)×。
1.9答案:n VE en∂=-∂ ,例如匀强电场;E 大,电势的变化率就大,并非一定121122010101.+.=4424R q E dl E dl rR R R πεπεπεπε∞⎝⎰⎰.0E dl =,0n VE e n∂=-=∂。
1.14证明:设s 面上有场强平行于分量,补上另一半球后球内各点的总场强应为零,可见s 面上不能有场强的平行分量,s 面上只有场强垂直分量,故s 面上应为等势面。
习题1.2.1解:(1)设一个电量为q 1,则q 2=4q 1,由公式12204q q F r πε=可以得到: ()2122041.64 5.010q πε-=⨯解之得: q 1=±3.3×10−7(C), q 2=1.33× 10−6(C) (2)当r=0.1时,所受排斥力为:12204q q F r πε==0.4(N ) 1.2.2解:设其中一个电荷电量为q ,则另一个电荷电量为Q -q ,由库仑力 ()2q Q q F k r -= 可知,当()220dF k Q q dq r =-=,即:2Qq = 时两电荷间的斥力最大,所以两者电量均为2Q。

电磁学赵凯华陈熙谋1. 引言电磁学是物理学中的一个重要分支,研究电荷与电荷、电荷与磁场之间的相互作用。
电磁学的理论基础是麦克斯韦方程组,这些方程描述了电场和磁场的变化过程以及它们之间的相互关系。
电磁学的研究对于现代科学和技术的发展具有重要意义。
在本文中,我们将介绍一些电磁学的基本概念和原理,以及一些常见的应用。
2. 麦克斯韦方程组麦克斯韦方程组是电磁学的核心理论,由麦克斯韦根据他的实验结果和电磁学的基本原理推导得出。
麦克斯韦方程组包括四个方程:高斯定律、法拉第电磁感应定律、安培环路定律和高斯安培定律。
这些方程描述了电场和磁场的分布、变化以及它们之间的相互作用。
4.1 高斯定律高斯定律描述了电场的分布和电荷之间的关系。
它的数学表达式为:$$\ abla \\cdot\\mathbf{E}=\\frac{\\rho}{\\varepsilon_0}$$其中,$\ abla \\cdot \\mathbf{E}$表示电场$\\mathbf{E}$的散度,$\\rho$是电荷密度,$\\varepsilon_0$是真空介电常数。
4.2 法拉第电磁感应定律法拉第电磁感应定律描述了磁场随时间的变化引起的电场感应。
它的数学表达式为:$$\ abla \\times \\mathbf{E}=-\\frac{\\partial\\mathbf{B}}{\\partial t}$$其中,$\ abla \\times \\mathbf{E}$表示电场$\\mathbf{E}$的旋度,$\\mathbf{B}$是磁场的矢量,t是时间。
4.3 安培环路定律安培环路定律描述了磁场沿闭合回路的磁场积分与通过这个回路的电流之间的关系。
它的数学表达式为:$$\ abla \\cdot \\mathbf{B}=0$$4.4 高斯安培定律高斯安培定律描述了磁场的分布和电流之间的关系。
它的数学表达式为:$$\ abla \\times \\mathbf{B}=\\mu_0 \\mathbf{J}$$其中,$\ abla \\times \\mathbf{B}$表示磁场$\\mathbf{B}$的旋度,$\\mu_0$是真空磁导率,$\\mathbf{J}$是电流密度。
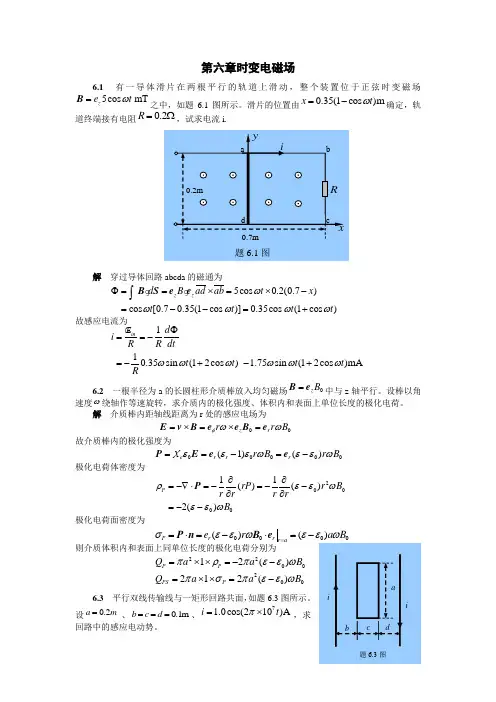
第六章时变电磁场6.1 有一导体滑片在两根平行的轨道上滑动,整个装置位于正弦时变磁场5cos mT z e t ω=B 之中,如题6.1图所示。
滑片的位置由0.35(1cos )m x t ω=-确定,轨道终端接有电阻0.2R =Ω,试求电流i.解 穿过导体回路abcda 的磁通为5cos 0.2(0.7)cos [0.70.35(1cos )]0.35cos (1cos )z z d B ad ab t x t t t t ωωωωωΦ==⨯=⨯-=--=+⎰ B S e e故感应电流为110.35sin (12cos ) 1.75sin (12cos )mAin d i R R dt t t t t R ωωωωωωΦ==-=-+-+E6.2 一根半径为a 的长圆柱形介质棒放入均匀磁场0z B =B e 中与z 轴平行。
设棒以角速度ω绕轴作等速旋转,求介质内的极化强度、体积内和表面上单位长度的极化电荷。
解 介质棒内距轴线距离为r 处的感应电场为 00z r r r B φωω=⨯=⨯=E v B e e B e故介质棒内的极化强度为 00000(1)()e r r r r B r B εεεωεεω==-=-P E e e X极化电荷体密度为2000011()()2()P rP r B r r r rB ρεεωεεω∂∂=-∇⋅=-=--∂∂=--P极化电荷面密度为00()()P r r r a e r a B σεεωεεω==⋅=-⋅=-P n B e 则介质体积内和表面上同单位长度的极化电荷分别为220020012()212()P P PS P Q a a B Q a a B πρπεεωπσπεεω=⨯⨯=--=⨯⨯=-6.3 平行双线传输线与一矩形回路共面,如题6.3图所示。
设0.2a m =、0.1m b c d ===、71.0cos(210)A i t π=⨯,求回路中的感应电动势。

电磁场与电磁波第三版课后答案本文是对《电磁场与电磁波》第三版的课后习题答案的整理与解答。
本书是电磁场与电磁波领域的经典教材,其中的习题对于巩固和加深对电磁场与电磁波知识的理解非常重要。
以下是本文对第三版的习题答案的详细解析。
第一章电磁场基本概念1.1 电磁场基本概念习题答案:1.电磁场的基本概念是指在空间中存在着电场和磁场,它们相互作用产生相互关联的现象;它们是由带电粒子的运动而产生的,是物理学的基本概念之一。
2.宏观电荷位移是指电荷在物体内部的移动;它的存在使得物体表面或其周围的电场产生变化,从而产生an内部电磁场。
3.电磁场的基本方程是麦克斯韦方程组,由四个方程组成:高斯定律、法拉第电磁感应定律、法拉第电磁感应定律的积分形式和安培环路定律。
1.2 矢量分析习题答案:1.根据题目所给的向量,求两个向量的点乘积:$\\vec{A}\\cdot\\vec{B}=A_{x}B_{x}+A_{y}B_{y}+A_{z}B_{ z}$2.根据题目所给的向量,求两个向量的叉乘积:$\\vec{A}\\times\\vec{B}=(A_{y}B_{z}-A_{z}B_{y})\\hat{i}+(A_{z}B_{x}-A_{x}B_{z})\\hat{j}+(A_{x}B_{y}-A_{y}B_{x})\\hat{k}$3.定义标量和矢量场,然后利用高斯定理得出结论。
1.3 电场与静电场习题答案:1.静电场是指电场的源是静止电荷,不会随时间变化,不产生磁场。
2.在静电场中,高斯定律表示为:$\ abla \\cdot\\vec{E} = \\frac{1}{\\varepsilon_0}\\rho$,其中$\ abla\\cdot \\vec{E}$表示电场的散度,$\\varepsilon_0$表示真空介电常数,$\\rho$表示电荷密度。
3.电场的位移矢量$\\vec{D}$定义为$\\vec{D} =\\varepsilon_0 \\vec{E} + \\vec{P}$,其中$\\varepsilon_0$表示真空介电常数,$\\vec{E}$表示电场强度,$\\vec{P}$表示极化强度。



电磁场第三版思考题目答案Revised final draft November 26, 2020一:1.7什么是矢量场的通量通量的值为正,负或0分别表示什么意义矢量场F穿岀闭合曲面S的通量为:当大于0时,表示穿出闭合曲面S的通量多于进入的通量,此时闭合曲面S 内必有发出矢量线的源,称为正通量源。
当小于0时,小于有汇集矢量线的源,称为负通量源。
当等于0时等于、闭合曲面内正通量源和负通量源的代数和为0,或闭合面内无通量源。
1. 8什么是散度定理它的意义是什么矢量分析中的一个重要定理:称为散度定理。
意义:矢量场F的散度在体积V上的体积分等于矢量场F在限定该体积的闭合积分,是矢量的散度的体积与该矢量的闭合曲面积分之间的一个变换关系。
1.9什么是矢量场的环流环流的值为正,负,或0分别表示什么意义矢量场F沿场中的一条闭合回路C的曲线积分,称为矢量场F沿的环流。
大于0或小于0,表示场中产生该矢量的源,常称为旋涡源。
等于0,表示场中没有产生该矢量场的源。
1.10什么是斯托克斯定理它的意义是什么该定理能用于闭合曲面吗在矢量场F所在的空间中,对于任一以曲面C为周界的曲面S,存在如下重要关系这就是是斯托克斯定理矢量场的旋度在曲面S上的面积分等于矢量场F在限定曲面的闭合曲面积分,是矢量旋度的曲面积分与该矢量沿闭合曲面积分之间的一个变换关系。
能用于闭合曲面.1,11如果矢量场F能够表示为一个矢量函数的旋度,这个矢量场具有什么特性=0,即F 为无散场。
1.12如果矢量场F能够表示为一个标量函数的旋度,这个矢量场具有什么特性=0即为无旋场1.13只有直矢量线的矢量场一定是无旋场,这种说法对吗为什么不对。
电力线可弯,但无旋。
1.14无旋场与无散场的区别是什么无旋场F的旋度处处为0,即,它是有散度源所产生的,它总可以表示矢量场的梯度,即=0无散场的散度处处为0,即,它是有旋涡源所产生的,它总可以表示为某一个旋涡,即2.4简述—-ate.早:2.1点电荷的严格定义是什么点电荷是电荷分布的一种极限悄况,可将它看做一个体积很小而电荷密度很的带电小球的极限。



第三章3.1 解:因螺绕环内的磁感应强度I n B 0μ=,所以副线圈中的感应电动势为VdtdI S dtd Sdtd 30103.1nN B N N --⨯===Φ=με副副副感应电流为A103.6RI 4-⨯==ε3.2 解:(1)设线圈发现→n 与→B 的夹角为零度时作为计时的起点,则t 时刻线圈中的感应电动势为tNBS dt t B d dt d ωωωεsin )cos S (-N-N==Φ=由此可以看出,当2t πω=或23t πω=时,即线圈法线与地磁场→B 的夹角为2π或23π时,感应电动势的值最大,此时ωεNBS m=(2)97N==ωεBS m 匝3.3 解:因距直导线为r 处的ri πμ2B 0=,所以(1)穿过回路ABCD 的磁通量t I a b l ldr riS d B basωπμπμsin ln 22000⎪⎭⎫⎝⎛==⋅=Φ⎰⎰⎰→→(2)回路ABCD 中的感应电动势 tI ab l dtωπωμεcos )(ln2d 00-=Φ-=3-5解:设t=0时,线圈与直导线处于同一平面内。
t 时刻俯视线圈与导线的相对位置如图3-19所示。
此时,线圈的有效面积是宽为AB 长为2a 的与长直导线共面的矩形面积。
穿过此有效面积的磁通量t t ab b a t ab b a b Ia tt ωωωπωμsin cos 21cos 21d )(d ε222220⎪⎭⎫⎝⎛-++++=Φ-=3-10解:设l 正方向如图3-23所示,则ac 段产生的感应电动势Vbc vB l d B l d B cbba30109.160cos 0)()(-→→→→→→⨯=+=⋅⨯+⋅⨯=⎰⎰ννε故感应电动势的方向为c a →,即c 点的电位高。
所以 V3oc 109.1U -⨯-=3-13解:(1)a,b 间的感应电动势22222121)(NBRR N B R B ldl B l d B d RLbaππωωυεε=⋅⋅===⋅⨯==⎰⎰⎰→→→(2)因ε的方向从轮心指向边缘,故在外电路上,I 的方向为b 指向a 。