第二节 工作机构转矩、力、飞轮力矩和质量的折算
- 格式:ppt
- 大小:1.49 MB
- 文档页数:3


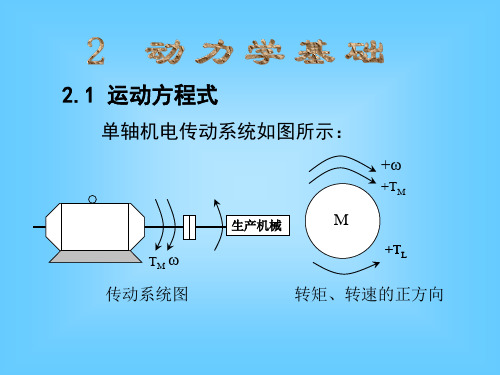
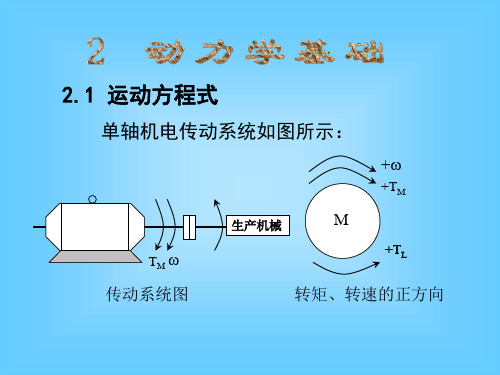
转矩、转动懊量和飞轮转矩的折算上节所介绍的是单轴拖动系统的运动方程式,但实际的拖动系统一般是多轴拖动系统,如图2-20所示。
在这种情况下,为了列出这个系统的运动方程,必须先将各转动部分的转矩和转动惯量或直线运动部分的质量都折算到某一根轴上,一般折算到电动机轴上,即折算成图2-18所示的最简单的典型单轴系统,折箅时的基本原则是折算前的多轴系统同折算后的单轴系统,在能量关系上或功率关系上保持不变。
下面介绍折算方法。
负载转矩是静态转矩,可根据静态时功率守恒原则进行折算。
对于旋转运动,如图2-20(0所示,当系统勾速运动时,生产机械的负载功率为』式中,71和"^生产机械的负载转矩和旋转角速度。
图2-20多轴抱动系统率的过程中有损耗,—输出功莾1=11^11 (?―的),0^ 1^3式中,》为电动机拖动产生机械运动时的传动效率,)^"^/^为传动机构的速比。
对于直线运动,如图2-20(10所示的卷扬机构就是一例。
若生产机械直线运动部件的负载力为尸,运动速度为^则所需的机械功率为它反映在电动机轴上的机械功率为如果是电动机拖动生产机械旋转或移动,则传动机构中的损耗应由电动机承担,根据功率平銜关系就有丁,^^0〜。
将^》^,^!^""/^代人上式可得(^!^^-?. 551 "丄)』―"〉'―〉、1-11、式中,〜为电动机轴的转速。
如果是生产机械拖动电动机旋转,例如,卷扬机构下放重物时,本文章由轴承网站整理发布,转载请注明出处第2章机电传动分析的基础知识式中,八为生产机械拖动电动机运动时的传动效率。
1.转动惯最和飞轮转矩的折算由于转动惯量和飞轮转矩与运动系统的动能有关,因此,可根据动能守恒原则进行折箅。
对于旋转运动,如图2-20(10所示的拖动系统,折算到电动机轴上的总转动惯量为式中,^丄、入为电动机轴、中间传动轴、生产机械轴上的转动惯量;为电动机轴与中间传动轴之间的速比&^^/^为电动机轴与生产机械轴之间的速比;咖、的、^分别为电动机轴,中间传动轴、生产机械轴上的角速度。


常用机构的转动惯量与扭矩的计算引言:在机械工程中,常常需要计算机构的转动惯量和扭矩,这些参数是设计和分析机械系统的重要指标。
本文将介绍一些常用机构的转动惯量和扭矩的计算方法,以帮助读者更好地理解机械系统的运动行为。
一、刚性转动连杆机构刚性转动连杆机构是一种常见的机构,在此之前,我们需要对转动惯量和扭矩有所认识。
1.转动惯量的计算转动惯量是描述物体绕一些轴线转动的惯性大小。
对于刚性连杆机构而言,其转动惯量可以通过以下公式计算:I=m*r^2其中,I表示转动惯量,m表示物体的质量,r表示质点与轴线距离。
扭矩是描述物体受力作用下产生的转动效果的物理量。
对于刚性连杆机构而言,其扭矩可以通过以下公式计算:T=r*F其中,T表示扭矩,r表示力矩臂,F表示力的大小。
二、常见机构的转动惯量和扭矩计算1.单摆机构单摆机构由一个固定轴和一个摆动物体组成,其转动惯量和扭矩的计算公式如下:I=m*L^2T = m * g * L * sinθ其中,I表示摆动物体的转动惯量,m表示摆动物体的质量,L表示摆长,g表示重力加速度,θ表示摆动物体相对垂直方向的偏角。
2.齿轮传动机构齿轮传动机构由驱动轮和从动轮组成,其转动惯量和扭矩的计算公式如下:I=m*r^2T=F*r其中,I表示轮的转动惯量,m表示轮的质量,r表示轮的半径,F表示作用在轮上的力。
3.曲柄摇杆机构曲柄摇杆机构由曲柄和摇杆组成,其转动惯量和扭矩的计算公式如下:I=m*r^2T=F*r其中,I表示摇杆的转动惯量,m表示摇杆的质量,r表示摇杆的长度,F表示作用在摇杆上的力。
4.平行四边形机构平行四边形机构由两个平行的连杆和两个交叉连杆组成,其转动惯量和扭矩的计算公式如下:I = m * a^2 * (sinδ)^2 + 1/12 * m * b^2T = F * a * sinδ其中,I表示交叉连杆的转动惯量,m表示交叉连杆的质量,a表示平行连杆的长度,δ表示平行连杆与交叉连杆之间的夹角,b表示交叉连杆的长度,F表示作用在交叉连杆上的力。
转动力矩计算公式转动力矩又称为转矩,是使物体发生转动的一种特殊的力矩。
在物理学和工程学中,转动力矩可是个相当重要的概念。
咱们先来说说转动力矩的基本定义。
简单来讲,转动力矩就是力和力臂的乘积。
这就好比你用扳手拧螺丝,你施加在扳手上的力,乘以从螺丝到你施力点的距离,得到的就是转动力矩。
那转动力矩的计算公式是啥呢?一般来说,转动力矩 T 等于力 F 乘以力臂 L ,用公式表示就是 T = F × L 。
这里的力 F 单位通常是牛顿(N),力臂 L 的单位通常是米(m),所以转动力矩 T 的单位就是牛顿米(N·m)。
给您讲个我之前遇到的事儿吧。
有一次我去朋友的汽修厂玩,正好看到他们在修一辆车的发动机。
师傅们需要拆卸一个大螺丝,可是怎么都拧不动。
我就好奇地凑过去看,发现他们用的扳手不太合适,力臂太短了。
后来找了一个更长力臂的扳手,施加差不多的力,一下子就把螺丝拧下来了。
这其实就是转动力矩在实际生活中的应用。
力没变,增加了力臂,转动力矩就增大了,也就更容易完成工作。
在机械设计中,转动力矩的计算那可是至关重要。
比如说设计一个齿轮传动系统,如果不精确计算各个齿轮所受到的转动力矩,那整个系统可能就运转不顺畅,甚至会出故障。
再比如在电机的选择上,得根据负载所需要的转动力矩来挑选合适功率的电机。
如果电机提供的转动力矩不够,设备就没法正常工作;要是选的电机转动力矩太大,又会造成浪费,增加成本。
在物理学的实验中,我们也经常会用到转动力矩的知识。
比如研究杠杆平衡的时候,通过改变力和力臂的大小,来观察转动力矩对杠杆平衡的影响。
总之,转动力矩虽然听起来有点抽象,但在我们的生活和工作中可是无处不在。
无论是简单的日常修理,还是复杂的机械工程,都离不开对转动力矩的准确计算和合理应用。
只要我们掌握了转动力矩的计算公式,并且能够灵活运用,就能解决好多实际问题,让我们的生活变得更加便捷,工作更加高效。
希望您通过我的这番讲解,对转动力矩计算公式有了更清晰的认识和理解!。