理论力学讲讲义义第十四讲

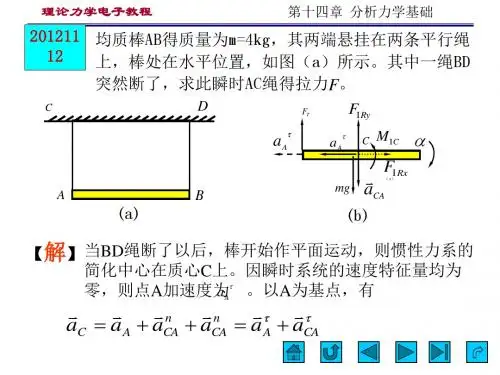
20121112 均质棒AB 得质量为m=4kg ，其两端悬挂在两条平行绳 上，棒处在水平位置，如图（a ）所示。

其中一绳BD突然断了，求此瞬时AC 绳得拉力F 。

ABCD(a)I CM )(τCAa mgτAa TF τAa CI RxF I RyF (b)α【解】 当BD 绳断了以后，棒开始作平面运动，则惯性力系的简化中心在质心C 上。

因瞬时系统的速度特征量均为零，则点A 加速度为 。

以A 为基点，有τA a ττCAA n CA n CA A C a a a a a a +=++=ττCAA n CA n CA A C a a a a a a +=++=其中,l 为棒长。

ατ2la CA =虚加惯性力系，如图（b ）所示，有I I I 2C C Rx A RymlM J F ma F ταα===，，02220)(=-⋅-=∑ααC A J lml l mg F m ， 则 因，得 2121ml J C =lg 23=α020=-+=∑mg ml F F T y α，又 Nmg F 8.91==得质量为m1和m2的两均质重物，分别挂在两条绳子上，绳又分别绕在半径为r1和r2并装在同一轴的两鼓轮上，已知两鼓轮对于转轴O的转动惯量为J，系统在重力作用下发生运动，求鼓轮的角加速度（轴O处摩擦不计，绳与轮无相对滑动）。

, 111I a m F =由动静法：, 0)(=∑F MO列补充方程： αα2211 , r a r a ==g Jr m r m r m r m ++-=2222112211α取系统为研究对象，虚加惯性力和惯性力偶：解： 方法1 用达朗伯原理求解, 222I a m F =ααJ J M O O ==I 0I 22I 11I 2211=----O M r F r F gr m gr m 02221112211=----⇒αJ r a m r a m gr m gr m 代入上式方法2 用动量矩定理求解 ωω)( 222211222111J r m r m J r v m r v m L O ++=++=g Jr m r m r m r m ++-=2222112211 α所以根据动量矩定理：2211222211])[(d d gr m gr m J r m r m t-=++ω取系统为研究对象2211)e ()(gr m gr m F M O -=1212，得由∑=-W T T )(2212121222211222222112J r m r m J v m v m T ++=++=ωω取系统为研究对象，任一瞬时系统的g r -m r m r g m r g m s g m s g m W ϕϕϕ⋅=⋅-⋅=⋅-⋅=)( 22112211221112r m r m d -2211ωα两边对时间t 求导数，得 方法3 用动能定理求解)(1某确定值C T =ϕω⋅-=-++g r m r m C J r m r m )()(222112222112 dtd )g r m r (m J)r m r (m dt d ωωϕ⋅-=++2211222211 任意假定一个初始值第十四章分析力学基础§14－1 质点系的自由度§14－2 虚位移原理§14－3 保守系统平衡的稳定性§14－4 达朗贝尔原理与动力学普遍方程§14－5 第二类拉格朗日方程网上作业系统1、告知作业网站的网址：222.18.54.19\homework。

M IO
解 :
FI ma
FA
FB
M I0
J
J
a R
FI
M B 0 mgl2 FIl2 Pl3 M IO FA l1 l2 0
Fy 0 FA FB mg P FI 0
解得 :
FA
l1
1 l2
mgl2
Pl3
a
ml2
Fx 0, Fx FI sin 0
Fy 0, Fy (m1 m2 )g FI cos 0
M A 0, M m2ge sin FI h sin 0
因 t, 得
Fx m2e2 sin t
Fy m1 m2 g m2e 2 cost
M
m2
ge
sin
t
m e h 第15页/共28页2 2
sin
t
第17页/共29页
例14-6 已知：如图所示,电动绞车安装在梁上,梁的两端搁在支座上,
绞车与梁共重为P.绞盘半径为R,与电机转子固结在一 起,转动惯量为J ,质心位于O 处.绞车以加速度a提升 质 求：量支为座mA的，重B受物到,其的它附尺加寸约如束图力..
第16页/共28页 第18页/共29页
如果刚体有质量对称面且该面与转动轴垂直,简化中心取 此平面与转轴的交点,则
J xz mi xi zi 0, J yz mi yi zi 0
M IO M Iz J z
３ 刚体 作平面 运动 （平行 于质量 对称面 ）
向质心简化
M Ic JC
FI第R 11页/共m28页aC
第13页/共29页
例144 已知：如图所示均质杆的质量为m,长为l,绕定轴O转动的角
速度为 ,角加速度为 .
求：惯性力系向点Ｏ简化的结果(方向在图上画出).

得到
δxB tan δyA
图14-6
第三节
虚功与理想约束
虚功与理想约束
设某质点上作用有力 F，并给该质点一个虚位移 δr ，如图 14-7 所示。 则力 F 在虚位移 δr 上做的功称为虚功，即
δW F δr
或
δW F cos(F ，δr) | δr |
（14-4）
显然，虚功也是假设的，并且与虚位移是同阶无穷小量。
第十四章
虚位移原理
目录
01约束及其分类
02虚位移及其计算
03虚功与理想约束
04虚位移原理
05质点系的自由度与 广义坐标
06以广义坐标表示的 质点系平衡条件
第一节
约束及其分类
几何约束与运动约束
限制质点或质点系在空间的几何位置的条件称为几何约束。
单摆上一质点M，可绕固定点O在平面Oxy内摆动，摆 杆长l。此时摆杆对质点M的限制条件是：质点M必须在 以点O为圆心，以l为半径的圆周上运动。若用x，y表示 质点的坐标，则约束条件可写成
用点的合成运动来分析A点的虚位移，如图14-10所示，应 有
δrA sin δre
摇杆上A，B两点的虚位移关系为
δre sin δrB
h
l
δrB

l h
δre
sin

l h
sin
2

δrA
（4）列虚功方程（14-6），求解。
由
F2δrB F1δrA 0
得
F1 δrB
F2 δrA
将式（14-6）写成解析形式
δWF (Fixδxi Fiyδyi Fizδzi ) 0
（14-7）

d(1 2mivi2)Wi
dTWi
质点系动能的增量，等于作用于质点系全部力所作的元功的
和
微分形式。
T2T1 Wi
质点系在某一段运动过程中动能的改变量，等于作用于质点
系全部力所作功的和
积分形式。
第十四章 动能定理
3. 理想约束
dr
F′ O
F
B A
W F d r F d r 0
第14章 动能定理
※ 力的功 ※ 质点和质点系的动能 ※ 动能定理 ※ 势力场·势能·机械能守恒定律 ※ 功率·功率方程·机械效率 ※ 质点系普遍定理的综合应用 ※ 结论与讨论
第十四章 动能定理
§14-1 力的功
a. 常力的功
WFcoss
F
M
M1

M2
S
功是代数量，其国际单位制为 J（焦耳）。
d1
dt
1,
d1
dt
1
Ⅱ M2
1(M1M i122) (J1iJ1222)
主动力的功：
W 12M 11M 2 2(M 1M i122)1
由动能定理得： 1 2(J1iJ1 222) 1 20(M 1M i12 2) 1
第十四章 动能定理
Ⅰ M1
driC
d
Mi
C
§14-2 质点和质点系的动能
质点的动能
T 1 mv 2 2
动能和动量都是表征机械运动的量，前者与质点速度的平 方成正比，是一个标量；后者与质点速度的一次方成正比，是 一个矢量，它们是机械运动的两种度量。动能与功的量纲相同 ，也为 J 。
质点系的动能
第十四章 动能定理
T
b. 变力的功

FT1＝FT1
cos m1 m2 g m1l 2
§14-2 质点系的动静法
F1
Fg1
m1
a1
FN1 FNi
mi
Fg2
FN2
Fgi
m2
ai Fi
F2
a2
质点系的主动力系
F1 ,F2 ,,Fi ,,Fn 质点系的约束力系 FN1 , FN2 ,,FNi ,, FNn 质点系的惯性力系
Fg1, Fg2 ,, Fgi ,, Fgn
刚体的惯性力为面积力，组成平面力系。
对于一般问题，刚体的惯性力为体积力， 组成空间一般力系。
§14-3 刚体惯性力系的简化 刚体惯性力系简化结果－ 主矢与主矩 惯性力系的主矢
FgR ＝ Fgi＝ (－mi ai )＝－m aC
i
i
惯性力系的主矢等于刚体的质量与刚体质心 加速度的乘积，方向与质心加速度方向相反。 这一简化结果与运动形式无关。
i
i
i
§14-3 刚体惯性力系的简化
刚体惯性力系特点 刚体惯性力系简化结果
—— 主矢与主矩 刚体惯性力系主矢与主矩与动量
和动量矩之间的关系
§14-3 刚体惯性力系的简化 刚体惯性力系特点
刚体惯性力的分布与刚体的质量分布以及 刚体上各点的绝对加速度有关。
Fgi＝－ 对于平面问题m(或ia者i 可以简化为平面问题)，
§14-3 刚体惯性力系的力系的主矩 —— 惯性力系的主矩与刚体的 运动形式有关。
3、平面运动
具有质量对称平面的刚体作平面运动，并且运动平 面与质量对称平面互相平行。对于这种情形，先将刚 体的空间惯性力系向质量对称平面内简化，得到这一 平面内的平面惯性力系，然后再对平面惯性力系作进 一步简化。

由于 ，于是得 0
P 2 Qtg
例2 图示机构中，当曲柄OC绕轴摆动时，滑块A沿曲柄自 由滑动，从而带动杆AB在铅垂导槽K内移动。已知OC=a， OK=l，在C点垂直于曲柄作用一力Q，而在B点沿BA作用一力 P。求机构平衡时，力P与Q的关系。
rC
y
rA re a rr A
y A ltg
C
a
A
O
Q
y A
l cos
2
x C a cos
y C a sin
xC
a sin


l
K
B
x
y C a cos
主动力在坐标方向上的投影为
P
YA P
X C Q sin
Y C Q sin
y
r
O
l
x
2 2
xA yA r
2 2
B (xB , yB )
2 2
(xB xA ) ( yB y A ) l yB 0
几何约束方程的一般形式为
f r ( x1 , y 1 , z 1 , , x n , y n , z n ) 0
不仅能限制质点系的位置，而且能限制质点系中各质点的 速度的约束称为运动约束。
C
Q
O

l
K
B
x
P
解1：（几何法）以系统为 研究对象，受的主动力有P、 Q 。给系统一组虚位移如图。
r A re rr 由虚位移原理 F i ri 0 ，得
y
rA re a rr A
rC

4、平移与转动的合成(1) 平移速度矢与转动角速度矢垂直xO'x'刚体以角速度ω绕轴O'z'转动，转轴和动坐标系一起以速度v O'在垂直于ω的方向平移。

ωv O'刚体在平行于O'x 'y '的平面上做平面运动。

CC C 点是平面图形的瞬心，则与O'z'平行的轴CC 为瞬轴。

O'C 与速度v O'垂直，且：O v O C w¢¢=v e =v O'ωa =-v e 当平移速度矢与转动角速度矢垂直时，刚体的平移与转动可以合成为绕平行于原转轴的瞬轴的转动，瞬轴到原转轴之间的距离为v O'/ω。

(2) 平移速度矢与转动角速度矢平行xO'x'ωvO'刚体以角速度ω绕轴O'z'转动，转轴和动坐标系一起度v O'沿着O'z'方向运动。

称为螺旋运动。

平移速度与转动角速度方向相同时称为右螺旋，方向相反时称为左螺旋。

平移速度与转动角速度的比值O v pw¢=—螺旋率4、平移与转动的合成若以s 表示刚体沿O'z'轴的轴向位移，φ为刚体绕O'z'轴的转角，则：d d d d O s v t tj w ¢==，螺旋率可写成：jd d sp =表示绕轴转过单位角度时沿轴前进的距离。

一般情况下，螺旋率为恒定值，则有：jp s =令：2jp=2s pj=—螺距当平移速度矢与转动角速度矢平行时，刚体的平移与转动可以合成为绕原转轴的螺旋运动，平移速度与转动角速度的比值为螺旋率，螺旋率乘以2π为螺距。

(3) 平移速度矢与转动角速度矢成任意角xO'x'ωv O '刚体以角速度ω绕轴O'z'转动，同时又以速度v O'平移，ω与v O'之间的夹角为θ。

解： 选杆AB为研究对象， 虚加惯性力系：
FgR

ml
2
FgnR man 0
M gA

J A

ml 2
3
根据动静法，有
F 0 , FA mg cos0 FgR 0 (1)
Fn 0 , FAn mg sin 0 FgnR 0 (2)
M A (F ) 0 , mg cos0 l / 2 M gA 0 (3)
C
解：以杆AB为研究对象, 受力如图。

杆AB匀速转动, 杆上距A点x 的微元段dx
的加速度的大小为
A
an (x sin ) 2
an
dFg
微 元 段 的 质 量 dm ＝ Pdx/gl 。 在 该 微 元 段
虚加惯性力dFg ,它的大小为
dFg

d m an

P 2
gl
sin
x
Z (e) i

FI iz 0 ,
mz (Fi(e) ) mz (FI i ) 0
实际应用时, 同静力学一样任意选取研究对象, 列平衡方 程求解。
11
[例3] 重P长l的等截面均质细杆AB, 其A端铰接于铅直轴AC上, 并
以匀角速度 绕该轴转动, 如图。求角速度 与角 的y 关系。
6
[例1] 列车在水平轨道上行驶，车厢内悬挂一单摆，当车厢向
右作匀加速运动时，单摆左偏角度 ，相对于车厢静止。求车
厢的加速度 a 。
7
解： 选单摆的摆锤为研究对象 虚加惯性力
FI ma ( FI ma ) FI
由动静法, 有
X 0 , mg sin FI cos 0

2、运动分析：
虚位移（按虚
速度对应法分析）；
rrBA
BP AP
3、建立动力学关系：虚位移原理；
F A δrAF B δrB0
4、求解：
FAFBtan
2020/12/12
13
例14-2
已知：如图所示曲柄压榨机构中，M=50Nm，
OA=r，
BD=DC=ED=l， ； A
若杆重均不计、
B
忽略各处摩擦， E
W F r
（2）集中力偶的虚功： W M
2）约束力：
（1）光滑面、光滑铰链、固定端等约束力的功：
2020/12/12
s
F
做功均为零；
8
（2）滑动摩擦力的功： A、静滑动摩擦力的功：为零； 如：只滚不滑；
Fs
B、动滑动摩擦力的功：不为零； 4、理想约束：
1）做功为零的约束称为理想约束：光滑面、光滑铰 链、静滑动摩擦力等；
且机构在图示 求位：置求平压衡榨.力 P。
o M
D C
P
2020/12/12
14
PPT教学课件
谢谢观看
Thank You For Watching
15
第十四章 虚位移原理
虚位移原理 一种用动力学的原理求解静 力学问题的方法；
§14-1 约束 · 虚位移 · 虚功
一、几个基本概念：
1、自由度：空间物体在三维空间内自由运 动的程度；
2、完全自由的物体在三维空间内的自由度：
2020/12/12
1
完全自由的物体在空间可以沿三根独立的坐标
轴做移动运动、同时还可以绕三根坐标轴做转动运
故，非完全自由的物体的自由度为：6-约 束方程的个数。

对于任一质点系：（ vi ' 为第i个质点相对质心的速度）
13
三．刚体的动能 1．平动刚体
1 1 1 2 2 1 T mi vi (mi )v 2 Mv 2 MvC 2 2 2 2
2．定轴转动刚体
1 1 1 2 2 2 T mi vi ( mi ri ) J z 2 2 2 2
F dr
FX dx FY dy FZ dz
( F FX i FY j FZ k , dr dxi dyj dzk
F dr FX dx FY dy FZ dz)
2 总功 力 F 在曲线路程 M1M 2 中作功为
W F cosds F ds （自然形式表达式）
授课教师：薛齐文 土木与安全工程学院力学教研室
1
第十四章
§14–1 §14–2 §14–3
动能定理
力的功 质点和质点系的动能 动能定理
§14–4＊ 功率 ·功率方程
§14–5＊ 势力场 ·势能 ·机械能守恒定理
§14–6 动力学普遍定理及综合应用
2
引 言
与动量定理和动量矩定理用矢量法研究不同，动能定理用
W F dr k ( r l0 )r0 dr
M2 M1 m2
r0 r /r 矢量单位
k—弹簧的刚度系数，表示使弹簧发生单位变形时所需的力。
M1
r 1 1 r0 dr dr d (r r ) d (r 2 ) dr r 2r 2r
W k ( r l0 )dr
10
五．质点系内力的功
W F drA F 'drB
F drA F drB
F d (rA rB )

C M
v2
vr2
a2
D

B
v1 + vr1 = v2 + vr2
上式沿⊥CD方向投影得 v1 cos + vr1 sin = v2 vr1 = (v2 － v1 cos )/ sin v1
A
+
v2
a2
D
vr2
vr1

M
B
C
vM v v
2 1 2 r1
2 2 v1 v2 2v1v2cos sin
aen AO r2 aC CA 2r2
va aA art vr
A
aC
大小
ve
art 方向 ⊥AC 大小 ?
arn
C D
aen
O
根据牵连运动为定轴转 动的加速度合成定理得
B
+
aA = aet+aen+art+arn+aC
式中
aA art
A
aC
aen
O
aet = 0, aen = r2,

aC
vr
3. 在定理的应用中常用解析法。在平面问题中， 将公式投影到两个坐标轴上, 可得两个独立 的标量方程, 解两个未知数。注意投影时应 保持公式的原有形式不变。
1. 正弦平动机构如图示,已知OM = R ,当 = 45º 时，滑道的速度和加速度分别为 u和a0 , 求此时 刻OM的角速度和角加速度。
理论力学
第16讲
理论力学
点的合成运动(三)
加速度合成定理的应用
1. 加速度合成定理的基本公式
牵连运动为平动
牵连运动为定轴转动
aa = ar + ae

3、绕相交轴转动的合成AO(1) 绕两个相交轴转动的合成绕相交轴转动的合成运动是定点运动，两轴的交点为定点。

刚体绕Oz '的转动为相对运动，相对角速度ωr =ω2;动坐标系绕Oz 的转动为牵连运动，牵连角速度ωe =ω1;刚体绕O 点的定点运动为绝对运动。

C i 以ω1和ω2为邻边，做平行四边形OACB ，连接OC ，OC 即为刚体绕O 做定点运动的瞬轴。

（证明略）ii 平行四边形OACB 的对角线即为刚体绕瞬轴转动的绝对角速度ωa 动轴Oz '上点A 的速度为：1A v ADw =×AEw =×a 1a w w AEAD =1OACB S AD OC AE w =×=×Y 由：OCw =a 三个角速度的关系可写成：12=+a ωωω指向由点A 的速度方向确定。

当刚体同时绕两相交轴转动时，合成运动为绕瞬轴的转动，绕瞬轴转动的角速度等于绕两轴转动的角速度的矢量和。

3、绕相交轴转动的合成如果刚体绕相交于一点的3个轴或者更多轴转动时，绕瞬轴转动的角速度为：121na n ii ==++×××+=åωωωωω当刚体同时绕相交于一点的多轴转动时，合成运动为绕瞬轴的转动。

绕瞬轴转动的角速度等于绕各轴转动的角速度的矢量和，而瞬轴则沿此合矢量方向。

(2) 绕多个相交轴转动的合成3、绕相交轴转动的合成例2 行星锥齿轮II 与固定齿轮I 相啮合，可绕动轴OO 2转动，而动轴OO 2以角速度ωe 绕定轴OO 1转动。

设在点C 处，轮I 的半径为r 1，轮II 的半径为r 2。

求：锥齿轮II 相对于动轴的角速度ωr 。

例3 已知陀螺绕定点运动时，3个欧拉角表示的运动方程为：2π23246t t t y q j =+==，，式中t 以s 计，ψ，θ，φ以rad 计。

求：当t =1s 时陀螺绕瞬轴转动的角速度。

解：属于绕多个相交轴转动的合成问题。

i1
2
R2 R1
1 2
Ⅱ
M2
Ⅰ
M1
T2 12(J1 iJ1222)12
主动力的功：
W 12M 11M 2 2(M 1M i122)1
由动能定理得： 1 2(J1iJ1222) 120(M 1M i12 2) 1
第十四章 动能定理
将上式对时间求导，并注意:
3 mR22
4
P
O

B
FT
C
主动力的功： W 12Ps2mgfs
由动能定理得： 3mR 220Ps2mgfs F
4
mg P
O B
2 (Pmg)f
FN
3mR
第十四章 动能定理
关于摩擦力的作功
M F
O
FN
0
功是力与其作用点位移的点乘。这里“位移”并不是 力作用点在空间中的位移，而是指受力物体上受力作用那 一点的位移。
R2)
v W
第十四章 动能定理
例 题3
已知： m ，R, f ， 。 求： 纯滚时盘心的加速度。
解：取系统为研究对象
T1 0
T2

1 2
mvC2

1 2
JC2
vC R
T2

3 4
mvC2

s
C
vC
F
mg

FN
主动力的功： W 12mgsis n
由动能定理得：
43mC 2v0mgssin
求：重物下落的加速度
O
第十四章 动能定理
P W
解：取系统为研究对象
T1 0
T2

1W 2g

F1 , F2 ,, Fi ,, Fn
质点系的约束力系
Fi
FN1
mi
FNi
ai
FN1 , FN 2 , , FNi , , FNn
质点系的惯性力系
a2
Fg1 , Fg 2 ,, Fgi ,, Fgn
对质点系应用达朗伯原理，得到
Fi FNi Fgi 0 M O ( Fi ) M O ( FNi ) M O ( Fgi ) 0
非自由质点达朗贝尔原理的投影形式
Fx FNx Fgx 0 Fy FNy Fgy 0 Fz FNz Fgz 0
飞球调速器的主轴O1y1以匀角 速度w转动。试求调速器两臂的张角a。 设重锤C的质量为m1，飞球A，B的质量 各为m2，各杆长均为l，杆重可以忽略 不计。
取上式在自然轴上的投影式，有：
F
b
0,
F cos q mg 0
F sin q Fg 0
mg F 19.6 N cos q
Fl sin 2 q u 2.1 m s m
F
n
0,
§14.2 质点系达朗伯原理
F1
Fg1
质点系的主动力系
m1 a1
FN2 Fg2 F2 m2 Fgi
n Fx 0 FAx ( FgR FgR ) cos 45 0
MA
FAy
A
FAx

C
mg
B
Fy 0 FAy mg ( F F ) cos 45 0
n gR
gR
M O 0 M A FAx r mgr M gO 0
O
n gR
F

ve
C
A
θ
O’ O
2)选动系(与动点不在同一构件上) 凸轮
3)运动分析系(Va、Ve、Vr) x’ ?
v v v x
a
e
r
退出
vr θ v ve a
vavect gvc3t0 g3v
§9－3 点的速度合成定理
12 12
例9-3： 刨床急回机构如图
所示；曲柄 OA的一端与滑快 A 用铰链联接。当曲柄 OA以匀 角速度ω绕定轴O转动时，滑块 在 摇 杆 O1B 的 槽 中 滑 动 ， 并 带 动 摇 杆 O1B 绕 固 定 轴 O1 转 动 。 设 曲 柄 长 OA=r ， 两 轴 间 距 离 OO1=L ， 求 曲 柄 在 水 平 位 置 的 瞬时，摇杆O1B绕Ol轴转动的角 速度ωl及滑块A对于摇杆O1B的 相对速度。
1)选动点（研究对象：联接点） A(OA上) 2)选动系(与动点不在同一构件上) 摇杆O1B
ωO
va
r
vr
A
3)运动分析系(Va、Ve、Vr)
? ? ve va sin
v v v s 1 a i O n v 1eA e c lro r2s irvs r2 n v va al 2 c orr s2 r2
牵连速度 vr0vave
ve0vavr
§9－3
8 8
点的速度合成定理
点的速度合成定理
动点的绝对速度等于它的牵连速度与相对速度的矢量
和。
vavevr
z
C1
证明：
牵连位移、相对位移、绝
C’
对位移的矢量关系知：
B
CC1CC'C'C1
z’ x’A1 y’

实位移: dr , dx, d 等
实位移与虚位移的区别
虚位移是假想的，实位移是实际发生的。 虚位移是瞬时的，实位移是有时间经历的。 虚位移可朝约束允许的任意方向运动，实位移只 朝某一方向运动。 质点系静止时，可有虚位移，而无实位移。 虚位移与运动的初始条件无关，而实位移与运动 的初始条件有关。 定常约束中，实位移是所有虚位移中的一个，对 于非定常约束，某瞬时的虚位移是指将时间固定， 约束所允许的无限小位移，而实位移是不能固定时 间的，所以虚位移不是实位移中的一个。
光滑固定面约束、光滑铰链、无重刚杆，不 可伸长的柔索、固定端等约束为理想约束.
§ 14-2 虚位移原理
设 质点 系处于平衡,有:
Fi FNi 0 Fi δri FNi δri 0
Fi δr i FN0i δri 0
即 F iδri 0 或: δWFi 0
对于具有理想约束的质点系,其平衡的充分必要 条件是:作用于质点系的所有主动力在任何虚位移中 所作的虚功的和等于零
约束方程中不包含坐标对时间的导数，或者约 束方程中的积分项可以积分为有限形式的约束为 完整约束.
例如：车轮沿直线轨道作纯滚动时
xA r 0 微分形式
积分 xA r C
完整约束
约束方程是等式的，称双侧约束（或称固执约束）. 约束方程为不等式的，称单侧约束（或称非固执单 侧约束）
本章只讨论定常的双侧、完整、几何约束.
例如：车轮沿直线轨道作纯滚动时 几何约束：yA r
运动约束：vA r 0
或 xA r 0
（2）定常约束和非定常约束 不随时间变化的约束称定常约束 约束条件随时间变化的称非定常约束
x2 y2 l0 vt 2
约束方程中显含时间t
（3） 其它分类

2、绕两个平行轴转动
的合成
绕两个平行轴转动的合成
O 1
O I
II
ωe
x'
O 1
ωr
M
O 1
O 2
ωe 与ωr 同向时，瞬轴在O 1O 2之间
ωe 与ωr 反向时，瞬轴在O 1O 2之外
齿轮绕瞬轴转动的角速度ωa 的大小和方向。

i 当ωe 与ωr 同向时2
12O v O O w =×e 2O C w =×a 因此：2
1222O v O O O C O C
w w =
=a e 当ωe 与ωr 同向时，O 1O 2= O 1C+ O 2C
1r
O C O C w w =并且：a e r w w w =+方向与ωe 、ωr 相同e r 122112r
e
O C O C w w =并且：a e r w w w =-方向与ωe 、ωr 中较大的一个相同※当刚体同时绕两平行轴反向转动时，刚体的合成运动为绕瞬轴的转动，绝对角速度等于牵连角速度与相对角速度之差，转向与较大的角速度的转向相同；瞬轴的位置外分两轴间的距离，在较大的角速度的轴外侧，外内分比与两个角速度成反比。

当两角速度大小相同时，刚体合成运动为平移—转动偶。

2、绕两个平行轴转动的合成
例1系杆O 1O 2以角速度ωe 绕轴O 1转动，半径为r 2的行星齿轮活动地套在与系杆一端固结的轴O 2上，并与半径为r 1的固定齿轮相啮合。

求：行星齿轮的绝对角速度ω2，以及它相对于系杆的角速度ωr 。

O 1
O ωe。