当前位置：文档之家 › 14.10量子物理之氢原子的电子云图和概率密度等值面图

14.10量子物理之氢原子的电子云图和概率密度等值面图

  • 格式：pdf
  • 大小：7.81 MB
  • 文档页数：34

下载文档原格式

  / 34

合集下载

原子的结构--氢原子PPT课件

原子的结构--氢原子PPT课件


原子轨道(波函数)的空间图示与径向分布
1s 3s
0
2s
0.2
0.1
3d
r
0
-0.1
3p
r
3s
2s
2p
3p
3d
4d
节面数（n-l-1）
空间图示与径向分布图的比较
3p概率密度（电子云）图示
2pz
3pz
氢原子轨道的zx等值线图
氢原子轨道的zx等值线图
最概然半径
电子出现概率最大的球壳半径
dD 0 dr
Yl,m(θ,φ)较 Y2l,m(θ,φ)： ➢无正、负号。 ➢更瘦小。
原 子 轨 道 电 子 云 界 面 p轨道 图 l=1
角度节面数目为l
s轨道
l=0
d轨道
l=2
空间分布图
电子云图：以黑点的疏密表示空间各点概率密
度ψ2的大小。
1s
2s
3s
1s、2s、3s电子云的剖面示意
f z3 3 zr2 5
(
E
Ze2 ) R(r) Y ( , ) 4 0r
0
r2
两边同乘以
，整理得：
R(r) Y ( , )
1
Rr
r
r2
r
Rr
2mr 2
2
E
2m Ze 2
4 0 2
r
Y
1
,
1
sin
sin
1
sin2
2
2
Y
,
只含r
1 R(r)
r
(r2
R(r) ) r
mZe 2
2 02
r
2m 2
D
l相同
氢原子中电子云的概率分布

氢原子中电子云的概率分布

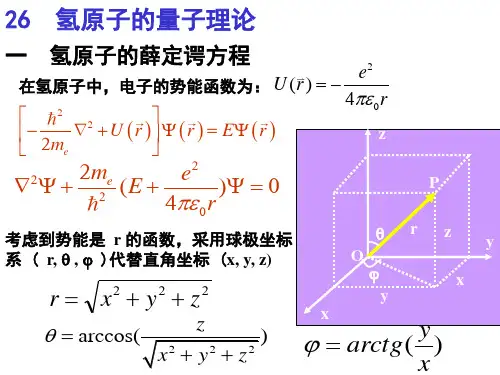
计算物理期中作业题目： 氢原子中电子云的概率分布摘要：通过氢原子的波函数(,,)r ψθϕ求解氢原子中电子在(),θϕ方向立体角 d Ω 中的概率密度，然后编程进行计算并画图给出氢原子角向电子云分布图，通过对比可以看出不同(,)l m 给出的角向电子云分布图呈现一定规律。

关键词：氢原子，概率密度，连带勒让德多项式氢原子中电子在(),θϕ方向立体角 d Ω 中的概率为22(,,)nlm d r r drψθϕΩ⎰2220(,)()lm nl d Y R r r drθϕ+∞=Ω⎰2(,)lm Y d θϕ=Ω则立体角d Ω内的电子云角向概率密度为222(,)(cos )(cos )mim mlm l l Y P eP ϕθϕθθ==连带勒让德多项式为2/2()()(1)()m m m l l P x x P x =-则对勒让德多项式求m 次导数易得()()()mm l l md P x P x dx=[]/220(1)(22)!2!()!(2)!l mk l kmlk d l k x dxk l k l k -=--=--∑[]()/220(1)(22)!2!()!(2)!l m k l k ml k l k xk l k l k m ---=--=---∑得连带的勒让德多项式[]()/22/220(1)(22)!()(1)2!()!(2)!l m k m m l k ml l k l k P x x xk l k l k m ---=--=----∑为求解氢原子角向电子云概率密度2(cos )ml P θ编程如下程序OPEN( 1, FILE='STAR.TXT')WRITE(*,*)'请输入角量子数L和磁量子数M' READ(*,*)ZL,ZMPI=3.141DO T=0,PI,0.01R=PPP(ZL,ZM,COS(T))**2WRITE(1,*)R*COS(T),R*SIN(T)ENDDOENDFUNCTION PPP(ZL,ZM,X)PPP=PP(ZL,ZM,X)*(1.0-X*X)**(ZM/2.0)RETURNENDFUNCTION PP(ZL,ZM,X)IF(MOD((ZL-ZM),2).EQ.0) THENZLL=ZL-ZMELSEZLL=ZL-ZM-1ENDIFPP=0DO ZK=0,ZLL/2.0PP=PP+P(ZL,ZM,ZK,X)ENDDORETURNENDFUNCTION P(ZL,ZM,ZK,X)P=(-1)**ZK*F(2*ZL-2*ZK)/2**ZL/F(ZK)! /F(ZL-ZK)/F(ZL-2*ZK-ZM)*X**(ZL-2*ZK-ZM) RETURNENDFUNCTION F(ZN)F=1.0DO ZK=1.0,ZNF=F*ZKENDDORETURNEND图形结果m变化的关系（图a）电子云的1/2剖面图随角量子数l和磁量子数m234角量数l（图b ）图a各图沿y轴的旋转立体图图b的放大图Y10Y20Y21Y31Y32Y40Y41Y428642Y43结论定义m l -≡δ称之为差量子数。

氢原子光谱

氢原子光谱


N l ,m
(l m )! ( 2l 1) 4 (l m )!
Y0,0 ( , )
1 4
3 Y1,1 ( , ) sin e i 8 Y1, 0 ( , ) 3 cos 4
3 i Y1, 1 ( , ) sin e 8
3. 对应一个能量本征值 E n 有 g
(2l 1) n 2 个本征函数，
l 0
n 1
g n 2 称为简并度。
§3-4
核外电子的几率分布
一. 空间概率分布－－电子云：
粒子出现在体积元 d 中的概率
dP n,l ,m (r , , ) d Yl ,m ( , ) Rn,l (r ) d
（3） （4）
1. 求 ( )
d 2 0 2 d ( ) Ae i
( ) ( 2k )
m （ m 0, 1, 2, ）
( ) m ( ) Ae im
或
( ) m ( ) Ae im （ m 0, 1, 2, ）
2. 求 ( )
1 d d m2 (sin ) ( 2 ) 0 sin d d sin
令 则
cos ， ( ) P( )
d 2P dP m2 (1 2 ) 2 2 ( )P 0 2 d d 1
――缔合勒让德（Legendre）方程。
Rn ,l ( r ) r 2 dr
2
dPn,l (r ) dr
Rn ,l (r ) r dr
2
2
(r, , ) R(r )Y ( , )
1 2 d 2R dR 2 r 2 r dr 2 2r dr 2 [ E U (r )] R 1 1 Y 1 2Y (sin ) 2 2 sin Y sin d 2 R 2 dR 2 2 [ E U (r )] 2 R 0 2 r dr dr r
原子轨道空间分布图的描绘

原子轨道空间分布图的描绘

固定中的一或多个参数中的一或多个参数原子轨道等值线图界面图轮廓图网格线图电子云分布图原子轨道等值线图界面图轮廓图网格线图电子云分布图2pz2pz作为作为r的单位取的单位取式作为式作为的单位上式可简化为
结构化分布图的描绘
氢原子和类氢离子的Schrödinger方程： 方程： 氢原子和类氢离子的 方程
原子轨道等值线图、界面图、轮廓图、网格线图， 原子轨道等值线图、界面图、轮廓图、网格线图，电子云分布图
氢原子ψ 轨道数学表达式： 氢原子ψ2pz 轨道数学表达式：
取 作为 r 的单位，取 的单位， 上式可简化为： 位，上式可简化为：
式作为ψ的单
氢原子 ψ2pz 轨道等值线图--- 坐标单位不同 轨道等值线图---
h Ze 2 − 2 ∇ − ψ = Eψ 4πε0r 8π µ
2 2
原子轨道的波函数形式复杂，将它们用图形表示出 原子轨道的波函数形式复杂， 来，有利于了解原子结构、性质及成键等信息。 有利于了解原子结构、性质及成键等信息。 原子轨道和电子云有多种图形, 原子轨道和电子云有多种图形, 应了解这些图形是 怎么画出来的, 相互之间是什么关系？ 怎么画出来的, 相互之间是什么关系？ 原子轨道和电子云都是三元函数，无法在三维空间 原子轨道和电子云都是三元函数， 中作图，为解决这一难题，须对函数作处理： 中作图，为解决这一难题，须对函数作处理： 1、径向分布图、角度分布图 径向分布图、 2、简化：固定 Ψ (r,θ,φ) 中的一或多个参数 简化：
步骤一： 步骤一： 作Ψ-r 图
0 0° 15° 15° 30° 30° 45° 45° 60° 60° 75° 75° 0 0 0 0 0 0 0.5 0.389 0.376 0.337 0.275 0.195 0.101 1.0 0.607 0.586 0.526 0.429 0.304 0.157 1.5 0.709 0.685 0.614 0.501 0.355 0.184 2 0.736 0.711 0.637 0.520 0.368 0.190 3 0.669 0.646 0.579 0.473 0.335 0.173 4 0.541 0.523 0.469 0.383 0.271 0.140 5 0.410 0.396 0.355 0.290 0.205 0.106 6 0.299 0.289 0.259 0.211 0.150 0.077 7 0.211 0.204 0.183 0.149 0.106 0.055 8 0.147 0.142 0.127 0.104 0.074 0.038 9 0.100 0.097 0.087 0.071 0.050 0.026
氢原子的量子理论

氢原子的量子理论


1)
R
0
(1) (2)
(3)
其中 m 和 l 是引入的常数。
解此三个方程，并考虑到波函数应满足的
标准化条件，即可得到波函数 (r, , )
并且可得到： 能量量子化 角动量量子化 角动量空间量子化
三个量子数
1.能量量子化和主量子数
求解方程(3) ，并使 R ( r ) 满足标准化条件，求得 E必等于
32 2022
1 n2
L l(l 1)
Lz m
对于给定的 n ，l 可以有n 个值
对于给定的 l ，m 可以有 2l+1 个值
对于给定的 n ，可能的波函数(状态)数量
n1
N (2l 1) n2 简并度
l 0
n 1, 2 , 3 ,
K, L, M, N, …… 壳层
l 0,1, 2 , , n 1
26.5.2.原子的壳层结构
原子中的电子 n , l , m , ms
壳层 n 1, 2,3, K, L, M, N, …… 壳层
次壳层 l 0, 1, 2 , , n 1 s, p, d, f, g, …… 次壳层
如：n = 3, l = 0, 1, 2 分别称为3s态,3p态,3d态
电子在原子内的分布 多电子原子系统中，核外电子在不同的壳层上
r 2 r r r 2 sin
r 2 (sin )2 2
同乘 r 2/RY,并且移项
1 R
d dr
(r 2
dR ) dr
K 2r2
Y
1 sin
(sin
Y
)
Y
1 (sin
)2
2Y
2
1 R
d dr
(r 2
2-2-2 原子轨道和电子云的图形

2-2-2 原子轨道和电子云的图形


4. 等值线、轨道界面
电子云的等值线图形
例1. 讨论氦离子He+2s态波函数的节面位置和 形状.
1
2s
1 4
Z3
2a03
2 2
Zr a0
e
Zr a0
2s
A 2
Zr a0
e
Zr a0
要使2s=0
应有:
2 2rБайду номын сангаас 0 a0
氢原子3pz电子云界面图
原子轨道界面与电子云界面是同一界面, 原子轨道界 面值的绝对值等于电子云界面值的平方根, 原子轨道界面 图的不同部分可能有正负之分, 由波函数决定.
轨道节面分为两种: 角度节面(平面或锥面)有l个;
径向节面(球面)有n-l -1个. 共有n-1个节面.
通常所说的原子轨道图形，应当是轨道界面图.
规律：
① 在r=0处（核处） s型函数在核处有最大值 p型函数在核处为0
② 节面 (n-l-1)个 ns 有n-1个节面 np 有n-2个节面 Rn, l，有n-l-1个节面
③ 最大值分布 ns n，最大值离核越近 np n，最大值离核越近
R(r)与R2(r)的最大值离核越近 意味着电子主要出现在核附近
这说明r=a0处在单位球壳厚度内找到电子的几率 比任何其它地方单位球壳内电子出现的几率要大
② 极大值个数：
0.6
0.3
1s
0
径向分布函数有n-l个极大值，00..2146
有n-l-1个节面
0.08 0
2s
0.24
③ 主峰-最大值出现的位置
0.16 0.08
2p
ns n，主峰离核越远
0 0.16
ns n，主峰离核越远
氢原子结构PPT课件

氢原子结构PPT课件

I
第19页 共23页
V
0 4.9 9.8 14.7 19.6
第19页/共24页
缺陷
1) 不能预言光谱线的强度。 2) 不能解释谱线的非周期性。 3) 无法解释光谱线的精细结构。
4) 无法解释比氢光谱线更复杂的光谱。
原因：带有经典的残余
玻尔理论是半经典、半量子化的理论
第20页 共23页
第20页/共24页
第21页 共23页
精品课件！
第21页/共24页
第22页 共23页
精品课件！
第22页/共24页
经典物理在解释热辐射上的困难—
普朗克能量子论 1900年
经典物理在解释光电效应上的困难—
旧
爱因斯坦光量子论 1905年
量 子
经典物理在解释氢光谱上的困难—
论
年 玻尔氢原子理论
玻尔氢原子理论1913
•在物理学史上曾起重要作用。 •半经典、半量子过渡性理论，已被量子力学所取代。
L mvr n n 1,2,3, 主量子数
能级:
En
m e4
802h2n2
E1 n2
n 1, 2, 3,
第14页 共23页
E1
m e4
8 02 h 2
13.6 eV
第14页/共24页
3) 频率假设—原子从一个定态 E2 跃迁到另一定态E1 时，将辐射电磁波，电磁波的频率由下式决定
h E2 E1
人类对物质结构的认识
古代中国“五行说”：金、木、水、火、土 古希腊“四根说”：火、水、土、气 古希腊德谟克利特：“原子论”
1661年英国波意耳提出元素的概念 英国化学家道尔顿：原子是元素的最小单元 1869年俄国的门捷列夫发现了元素周期律
MATLAB可视化大学物理学

MATLAB可视化大学物理学


5．玻尔的氢原子理论
(1)定态假设：原子系统只能处于一系列不连 续的稳定状态(简称定态)，在这些稳定状态上 具有能量E1，E2，E3，…，原子不辐射能量。
(2)量子跃迁假设：当原子从一个稳定 态En跃迁到另一稳定态Em时才发射或 吸收辐射，发射和吸收光子的频率为
En Em
h
(3)轨道角动量量子化假设：电子 轨道的角动量L是h/2π的整数倍 L
(1)能量 量子化
En
E0
1 n2
(n
=
1，2，3，…)n1称3.6为eV主称量为子基数态，能E量n =。-
(2)角动量量子化 L l(l 1)h (l = 0，1，2，…，n - 1)
其中，l称为角量子数或副量子数。
(3)角动量空间量子化Lz = mlħ (ml = 0，±1， ±2，…， ±l) 其中，ml称为磁量子数。 氢原子中的电子还有自旋 S s(s 1)h 3 h
{范例14.8} 角动量空间量子化矢量模型
*{范例14.9} 氢原子的角向概率密度和径向概率密度
*{范例14.10} 氢原子的电子云图和概率密度等值面图
基本内容
1．黑体辐射的规律 (1)辐射能量
M(λ,T)的单
1)单色辐射本领(能力)：物体表面在单位时间 位是W/m3。
内在单位面积上所发射的波长在λ到λ + dλ范围 内的辐射能量dP(λ,T)与波长间隔dλ之比
n
h 2π
n称为量子数，角动量是量子化的。
(n = 1，2，3，…)
6．德布罗意波
德布罗意认为：微观粒子除了粒子性之外也同样具有波动性。
一个具有能量E和动量p运动 粒子的频率和波长分别为
E h
,
h
概率密度和电子云

概率密度和电子云

继续
（一）概率密度和电子云
(a)
(b)
图 基态氢原子的电子云
电子的概率密度经常用它的几何图形来直观 地表现。图（a）是基态氢原子的的立体图形， 图（b）是它的剖面图。 从图上看出，离核越近，电子云越密集，即 电子出现的概率密度愈大；离核愈远，电子云愈 稀疏，电子出现的概率密度愈小。 继续
Байду номын сангаас一）概率密度和电子云
（一）概率密度和电子云 氢原子核外只有一个电子， 电子的位置虽不确定，但它具有 统计规律性。 ∣ψ1s∣2 表示氢原子1s电子在 核外空间某点(r,θ， )出现的概率 密度，离核越近概率密度越大。 为了形象地表示基态氢原子核外空间各处电 子出现的概率密度大小的分布情况，将空间各处 的∣ψ1s∣2值的大小用疏密程度不同的小黑点表 示出来。这种在单位体积内黑点数与∣ψ1s∣2成 正比的图形称为电子云(electron cloud)。
(a)
(b)
图 基态氢原子的电子云
应注意两点: 1.不要把电子云中的一个个小黑点看成一个 个电子，因为氢原子核外只有一个电子。 2.这里讲的是概率密度，不是概率。
返回
用MATLAB画出氢原子的电子概率密度图

用MATLAB画出氢原子的电子概率密度图

原子物理课后问题——用MATLAB画出氢原子的电子概率密度图1、蒙特卡罗方法的基本思想对某一个待解决的物理问题（当这个物理问题可以抽象为数学问题时）建立一个概率模型，即确定某个随机事件X，使得待求问题的解等于随机事件X出现的概率或随机变量的数学期望值。

然后进行模拟实验，重复多次地模拟随机事件X。

最后对随机实验结果进行统计平均，求出X出现的频数作为问题的近似解。

这就是蒙特卡罗方法的基本思想。

具体来说：假设所要求的量x是随机变量ζ的数学期望E(ζ) ，那么近似确定x的方法是对ζ进行N 次重复抽样，产生相互独立的ζ值的序列、……、，并计算其算术平均值：根据大数定理有因此，当N充分大时，下式成立的概率为1,亦即可以用作为所求量x的估计值。

2、求解氢原子核外电子概率密度函数氢原子的薛定谔方程其解，则氢原子核外电子的概率密度函数：N为主量子数，决定轨道的能量，既能层，n=0、1、2、…，L为角量子数，决定轨道角动量大小，即能级，l=0、1、2、…、n-1，M为磁量子数，决定轨道角动量在磁场上方向的分量，即轨道在空间分布上的方向，m=0、±1,、±2、 (1)由课本《原子物理学》P130某些球谐函数的表达式和P134径向波函数的表达式可推出以下各能级核外电子的概率密度函数：2S能级2Px能级最大概率密度…,(即第一玻尔轨道半径)数据生成1计算机在一定的范围内随机地选取坐标点（），并计算概率密度函数ρ（r）在点（）的值，是概率密度函数ρ（r）的最大值，并计算。

2.计算机产生一个0至1之间均匀分布的随机数M。

3.将Y与M进行比较若Y≥M，则选取该点（）若YM，则舍去该点（）。

重复1至3重新选取坐标点，即可得到一个按ρ（r）分布的随机函数序列。

3、具体代码及结果2Px能级所需计算公式>> a0=5.29e-11;>> plot(0,0,'.r','marKerSize',32) % 显示原子核位置，’.r’为红色的点，marker是图上画上点的地方表上符号后面的size就是符号的大小>> axis([-5e-10 5e-10 -5e-10 5e-10 ]) %设置坐标轴的范围>> grid on %设置网格>> hold on>> xlabel('x');ylabel('y'); %标注xy轴>> i=1;>> while i<=3000 %设置循环PHI=2*pi*rand; %产生0到2π的随机数赋值给PHIR=9*a0*rand; %产生0到9a0的随机数赋值给RY=0.5*(1/a0).^2*R.^2*exp(2-(R/a0))*(cos(PHI)).^2; %计算Y[x,y]=pol2cart(PHI,R); %将极坐标转化为直角坐标M=rand;if Y>=M %设置判断hold onpoint=plot(x,y,'.g','EraseMode','none','marKerSize',5); %画出绿色的点，点不会被擦除’none’方式不做任何擦除，直接在原来图形上绘制。

氢原子电子云空间分布的可视化

氢原子电子云空间分布的可视化

氢原子电子云空间分布的可视化1 技术指标1）设计一个用户界面，从不同角度直观揭示氢原子电子云空间几率分布的规律。

要求：有用户任意输入量子数的界面；2）根据量子力学中对氢原子的求解，设计出各个模块的参数（例如径向分布概率，角向分布概率等）；3）用Matlab来进行模拟；4）通过给定量子数，可以弹出绘图窗口，给出该量子态下，三维空间中氢原子中电子在空间各点的几率分布。

2 基本原理2.1 电子云模型及其量子力学实质电子云是电子在原子核外空间概率密度分布的形象描述，电子在原子核外空间的某区域内出现，好像带负电荷的云笼罩在原子核的周围，人们形象地称它为“电子云”。

用现代量子力学的观点来看，电子有波粒二象性，它不像宏观物体的运动那样有确定的轨道，因此画不出它的运动轨迹。

我们不能预言它在某一时刻究竟出现在核外空间的哪个地方，只能知道它在某处出现的机会有多少。

为此，就以单位体积内电子出现几率，即几率密度大小，用小黑点的疏密来表示。

小黑点密处表示电子出现的几率密度大，小黑点疏处几率密度小，看上去好像一片带负电的云状物笼罩在原子核周围，因此叫电子云。

用一个波函数Ψ（x，y，z）表征电子的运动状态，并且用它的模的平方|Ψ|^2的值表示单位体积内电子在核外空间某处出现的几率，即几率密度，所以电子云实际上就是几率密度|Ψ|^2在空间的分布。

研究电子云的空间分布主要包括它的径向几率分布和角度几率分布两个方面。

径向分布探求电子出现的几率大小和离核远近的关系，被看作在半径为r，厚度为dr的薄球壳内电子出现的几率。

角度分布探究电子出现的几率和角度的关系。

2.2 用matlab软件编程实现电子云模型根据氢原子束缚态电子的波函数表达式Ψnlm=Rnl*Ylm，其中Rnl 和Ylm分别是径向波函数和球谐波函数，n是波函数的主量子数，l是角量子数，m是磁量子数。

径向波函数和球谐波函数均可以根据薛定谔方程求解出具体表达式，从而确定了其波函数表达式，利用matlab软件超强的函数编程功能和作图功能，可以作出在给定n、l、m条件下，电子的径向概率函数、角向概率分布函数和在整个空间分布的概率函数图。

氢原子电子云初步探究


一. 测不准原理(uncertainty principle)
Heisenberg指出，无法同时确定微观粒子 的位置和动量： △x· △px≥h/4π △x为粒子在x方向的位置误差，△px为动量 在x方向的误差。由于h是极小的量，所以 △x越小，△px越大，反之亦然。测不准原理 是粒子波动性的结果，意味着微观粒子运动 不存在既确定位置又有确定速度的运动轨迹。
能级符号 l s p d f · · ·
0
1
2
3
· · ·
3. •
•
•
磁量子数（magnetic quantum number） 符号 m ，可以取 –l 到 +l 的 2l+1个值， 即 m = 0、±1、±2，…，±l 它决定原子轨道的空间取向。L 亚层共有 2l+1个不同空间伸展方向的原子轨道。 例如 l =1时，m = 0、±1，p轨道有三种 取向，或 l 亚层有3个p轨道。 相同能级的轨道能量相等，称为简并轨 道或等价轨道（equivalent orbital）。
2、ψ的意义 ψ本身物理意义并不明确，但ψ2却有明确的物 理意义。表示在原子核外空间某点处电子出现的概 率密度（probability density），即在该点处单位体 积中电子出现的概率。
波函数及其意义
波函数与电子云
电子云（electron cloud） 图形a是基态氢原子ψ2（概率密度）的立体 图，b是剖面图。黑色深的地方概率密度大， 浅的地方概率密度小。概率密度的几何图形 俗称电子云。
总结
电子云对应的是原子电子轨道，是解薛定 谔方程的结果。 薛定谔方程的解称为“波 函数”，又称“轨道”，表示的是电子在 该空间范围出现的概率，而不应该理解为 电子在空间中的运动轨迹。 其中有四个量子数： 主量子数n（能层）， 角量子数l（能级）， 磁量子数m （电子云伸展方向），自旋量 子数s

2.9 氢原子s态的ψ—r图和ψ2—r图


2.9 氢原子s态的ψ—r图和|ψ|2—r图
⑤ 径向分布函数(D)表示
几率：电子出现在半径为r，厚度为dr的球壳内的几率 dw = 4π r2 ψ 1s 2 dr

ψ
1s=2
dd=wτ 几率4π密drw2度dr：
径向分布函数(D) ：半径为r的单位厚度球壳内发现电子的几率。=D
d=w dr
结构 化学
2.9 氢原子s态的ψ—r图和|ψ|2—r图
ψ n,l,m (r,θ ,φ ) = Rn,l (r) ⋅Yl,m (θ ,φ )
波函数，原子轨道
径向波函数
角度波函数
径向分布 电子云： |ψ|2在空间的分布
角度分布
若单电子原子的波函数只是 r 的函数，与角度部分的函数 Y 无关，
这样的波函数所描述的状态称为 s 态，记为ψ s ，即 ψ s =ψ s (r)
4π r 2 ψ 1s 2
(注意与几率密度概念上的差别)
曲线有一极大值。当 dD = 0 时， dr
求出D为极大时的半径 r = a0 Z
r = a0 Z
氢原子或类氢离子1s态电子云径向分布图：D ~ r 作图 4
结构 化学
2.9 氢原子s态的ψ—r图和|ψ|2—r图
2.9.3 氢原子的其它s态
ψ2s——第一激= 发态 ψ 2s
3
4
1
2π
Z a0

2

2
−
Zr a0

−
e
Zr a0
3
ψ3s——第二激发态= ψ 3s
8
1
3π
Z a0

2

27
−
18Zr a0

氢原子电子云的计算和可视化分析（ＰＤＦ）


-
Zr na0
2Z na0
r
L l 2l+ 1 n+ l
2Z na0
r
( 2)
其中, Z 为原子序数 ( 氢原子的 Z = 1) , a0 是第一玻 尔半径; N n l是归一化常数,
Nnl = -
2Z 3 ( n - l- 1)! na0 2n [ ( n + l) ! ] 3
( 3)
L2l+ 1 n+ l
52
大学物 理
第 28卷
概率密度 W n lm是 r 和 的函数 , 某点的 r 和 是一定的, 概率密度也是一定的. 应用递推算法 可计算缔 合 拉 盖尔 多 项 式和 缔 合 勒让 德 函 数的 值, 因此, 根据上述公式就能计算任何一点的概 率密度.
2 蒙特卡罗方法
假设用 1 000个均匀分布在 0和 1之间的随机 数表示电子, 那么 0. 2以下的随机数就表示出现在 该点的电 子. 对于任意一个 随机数来说, 如果它 小 于 0. 2, 就表 示一个 电子出现 在该点. 用计 算机 模 拟时, 如果某随机数小于 (很难等于 )该点的概率 密度, 就在该点画一个点. 这种用随机数模拟电子 概率密度的方法称为蒙特卡罗方法. 假设某点的概 率密度为 0. 2, 如果 1 000个电子 都有相同的机 会 先后出现在该 点, 就会 有 200 个电子出现在 该点, 只是无法断定哪些电子出现在该点. 或者说, 如果 一个电子先后有 1 000次机会出现在该点, 那么 就 有 200次出现在该点, 只是无法预测哪一次出现在 该点.
其中
M lm =
( 2l + 1) ( l - |m | ) ! 4∀( l + |m | ) !

电子云与原子课件 -高二化学人教版(2019)选择性必修2

2、原子轨道：电子在原子核外的一种空间运动状态称为一个原子轨道。
常用电子云轮廓图的形状和取向来表示原子轨道的形状和取向。
=
s电子
p电子
d电子
s能级的原子轨道呈_球___形, p能级的原子轨道呈_哑__铃_ 形。
(1) s能级的电子云轮廓图(原子轨道)
【思考】同一原子的能层越高， s电子云半径越大，则2s电子一 定在比1s电子离核更远的地方运 动吗？ 不一定，只是概率更大
1. 不同能层的s能级原子轨道形状 相同 ，均为 球形 ； 2. s能级有 1 个原子轨道 3. 能层越高，s能级的原子轨道半径 越大 。 原因？
(2) p能级的原子轨道
p能级的原子轨道形状：__哑__铃__形_ 在同一能级中px、py、pz的能量 相同 。
p能级有__3__个原子轨道， 分别为 px、py、pz 。
B.电子云表示处于一定空间运动状态的电子在核外空间出现的概率 密度分布
C.电子云图中的小点越密,表示核概外率空越间大的电子越多 D.钠原子的1s、2s、3s电子云完形全状相相同同，半径不同
哑铃型
B
× × √
√
N
课本第17页
√
3
(1) 同一能层上各原子轨道能量的高低： E(ns)＜E(np)＜E(nd)＜E(nf)
【思考】原子核外电子的运动状态是怎样的呢？
玻尔模型
电子云模型
一定空间运动状态的电子在核外空间
各处都可能出现，但出现的 概率不同
四、电子云与原子轨道
1、电子云 ——核外电子的概率密度分布（看起来像一片云雾）
【思考】图中许许多多的小点表示氢原子的电子吗？
概率密度 ρ = P V
电子在某处 出现的概率

浙江省温州市2024高三冲刺(高考物理)人教版质量检测(预测卷)完整试卷

浙江省温州市2024高三冲刺（高考物理）人教版质量检测(预测卷)完整试卷一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题如图，三个固定的带电小球a、b和c，相互间的距离分别为ab=5cm，bc=3cm，ca=4cm．小球c所受库仑力的合力的方向平行于a、b的连线．设小球a、b所带电荷量的比值的绝对值为k，则（）A．a、b的电荷同号，B．a、b的电荷异号，C．a、b的电荷同号，D．a、b的电荷异号，第(2)题为了粗略测量月球的直径，小月同学在满月的夜晚取来一枚硬币并放置在合适的位置，使之恰好垂直于视线且刚刚遮住整个月亮，然后测得此时硬币到眼睛的距离为x，硬币的直径为d，若已知月球的公转周期为T，地表的重力加速度g和地球半径R，以这种方法测得的月球直径为（）A．B．C．D．第(3)题玻尔原子理论描述的氢原子的电子轨道示意图如图所示，E1、E2、E3分别表示电子处于轨道1、2、3时原子具有的能量，E k1、E k2、E k3分别表示电子处于轨道1、2、3时具有的动能，则（ ）A．E1>E2>E3B．E k3>E k2>E k1C．D．第(4)题一矩形线框置于匀强磁场中，线框平面与磁场方向垂直．先保持线框的面积不变，将磁感应强度在1 s时间内均匀地增大到原来的两倍．接着保持增大后的磁感应强度不变，在1 s时间内，再将线框的面积均匀地减小到原来的一半．先后两个过程中，线框中感应电动势的比值为( )A．B．1C．2D．4第(5)题关于万有引力定律，下列说法正确的是（ ）A．万有引力定律是爱因斯坦发现的B．引力常量G的单位是C．引力常量G是比例系数，没有单位D．万有引力定律只适用于天体之间的相互作用第(6)题将一轻弹簧水平放在光滑水平桌面上，一端固定，另一端与一质量为m的小物体相连，将小物体拉至O点由静止释放，小物体的加速度a与离开O点的距离的关系如图所示。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

对于4d态电子，当m = 0时， 概率密度分为上下双峰，上下 还有两包，左右还有四双包。 彩色电子云图分上下左右八片， 上下的中间两片比较鲜艳。 概率密度的等值面是六个曲面，上下 四个是封闭曲面，中间两个是环面。
对于4d态电子，当m = ±1时，概 率密度分为对称的四峰和四包。 彩色电子云图分为四角对称的八片。 概率密度的等值面是 上下四个分立的环面。
对于4f态电子，当m =±2时，概率 密度分为上下左右四峰和左右两包。 彩色电子云图分上下左右 六片，上下四片比较鲜艳。 概率密度的等值面是三个曲面，上下 两个是封闭曲面，中间一个是环面。
对于4f态电子，当m = ±2时， 概率密度分为对称的四峰，与m = ±1的3d态电子类似。 彩色电子云图分为四角对称的四片。 概率密度的等值面是上下两个分 立的环面，其形状与3d态(m = ±1)电子的概率密度形状相似。
MATLAB可视化 大学物理学
第十四章结束 湖南大学物电院 子，当磁量子数m = 0时，概 率密度曲面形成上下双峰，峰顶比较圆。 上下两片电子云是双峰的投影， 等值线分别围绕着两个峰。 概率密度的等值面是两个分立的闭合曲 面，由此可知：上下两片电子云是分立。
对于2p态电子，当m = ±1时，概 率密度曲面分为左右双峰。 在彩色电子云图中，左右 两片电子云是双峰的投影。 概率密度的等值面是中间空心的环面， 左右两片电子云是绕z轴联成一体的。
对于4p态电子，当m = 0时，概率密度 除了上下双峰之外，还有四个波包， 比m = 0的3p态电子多两个波包。 彩色电子云图分为上下六片，相 邻的波峰和波包是分开的，等值 线分别围绕着各自的波峰和波包。 概率密度的等值面是上 下六个分立的闭合曲面。
对于4p态电子，当m = ±1时，概 率密度分为左右双峰和四个波包， 比m = ±1的4p态电子多一对波包。 彩色电子云图分为左右对称的六片。 概率密度的等值面是三个 空心的环面，环面层层相 套，三个环面是相似的。
对于4d态电子，当m = ±2时，概 率密度分为左右双峰和双包，与m = ±1的3p态电子的概率密度类似。 彩色电子云图分为左右对称的四片。 概率密度的等值面是两个空 心的环面，并且外环面套着 内环面，两个环面是相似的。
对于4f态电子，当m = 0时，概率 密度分为上下双峰和左右四包。 彩色电子云图分上下左右 六片，上下两片比较鲜艳。 概率密度的等值面是四个曲面，上下 两个是封闭曲面，中间两个是环面。
对于2p态电子，当m = ±1时，概率密度分为左右两片，每一 片都有一个中心，随着到中心距离的增加，点数不断减小。
*{范例14.10} 氢原子的电子云图和概率密度等值面图
根据氢原子的薛定谔方程的解，求概率密度。 (1)为什么说用点的疏密表示的概率密度称为电子云图？ (2)氢原子的概率密度曲面是什么形状？彩色电子云图是 如何分布的？通过氢原子最大概率密度的百分之一的等 值曲面，说明概率密度的三维形状。 [解析](2)由于概率密度是轴对称的，可取一个 截面，例如O-xz截面，求出每一点概率密度。 在概率密度的O-xz截面上取一条等值曲线，例如 最大值的1%，由于概率密度是轴对称的，将曲 线绕z轴旋转，就形成概率密度的三维曲面。 三维概率密度曲面反映了概率密度的空间分布形状。
对于3d态电子，当m = ±2时， 概率密度分为左右双峰。 彩色电子云图分为左右两片。 概率密度的等值面是一个环 面，其形状与2p态(m = ±1) 电子的概率密度形状相似。
4s态电子的概率密度曲面与3s 态电子的概率密度曲面类似。 尖峰外面的峰环太低无法用不同颜色显示。 彩色电子云图除了中间彩色部分 外，只能显示一个淡蓝色的环。 取最大概率密度的1%，4s态电子 的概率密度的等值面是三个球面。 如果取最大概率密度的0.1%，4s态电子 的概率密度还可显示多个等值球面。
2s态电子的概率密度曲面关于中心轴对称，尖峰的概率密度 最大，但是只有1s态的最大概率密度的1/8；随着距离的增加， 概率密度先减小再增加，达到次级最大值之后再减小。 次级最大值相对中心峰值是很小的，所以次级峰附近圆环呈浅蓝色。 2s态电子的彩色电子云图的概率密度等值线也是圆，最 外面三条等值线的值是相等的，都只有最大值的1%。 取最大概率密度的1%，2s态电子的概率密度的 等值面是三个球面。如果概率密度取大一些， 只能显示一个球面。因此，最大概率密度的1% 的等值曲面可基本反映概率密度的立体形状。
对于3d态电子，当m = 0时，概率 密度分为上下双峰和左右双包。 彩色电子云图分上下左右 四片，上下两片比较鲜艳。 概率密度的等值面是三个曲面，上下 两个是封闭曲面，中间一个是环面。
对于3d态电子，当m = ±1时， 概率密度分为对称的四峰。 彩色电子云图分为四角对称的四片。 概率密度的等值面是 上下两个分立的环面。
*{范例14.10} 氢原子的电子云图和概率密度等值面图
根据氢原子的薛定谔方程的解，求概率密度。 (1)为什么说用点的疏密表示的概率密度称为电子云图？ (2)氢原子的概率密度曲面是什么形状？彩色电子云图是 如何分布的？通过氢原子最大概率密度的百分之一的等 值曲面，说明概率密度的三维形状。 氢原子中的电子在体积元dV之中出现的概率为 wnlmdV = |ψnlm|2dV = |Rnl|2|Θlm|2|Φm|2dV， 由于|Φm(φ)|2 = 1/2π，所以电子出 现在原子核周围的概率密度为 1 1 | Θlm (θ ) |2 wnlm (r ,θ , ϕ ) | Rnl (r ) |2 = 2 wnl (r ) wlm (θ ) 2π r wlm(θ) = |Θlm(θ)|2/2π是角向概率密度， wnl = |Rnl(r)r|2是径向概率密度。 当主量子数和角量子数确定之后，径向概率密度就 确定了，磁量子数不同，概率密度的分布就不同。
对于4f态电子，当m = ±3时， 概率密度分为左右双峰。 彩色电子云图分为左右两片。 概率密度的等值面是一个环 面，其形状与2p态(m = ±1) 电子的概率密度形状相似。
当主量子数大于4的时候，对于不同的轨道量子 数和磁量子数，概率密度可呈现更多的波峰和 波包；概率密度的等值面可呈现更多的形式， 而基本形状是闭合面(包括球面)和环面 。
*{范例14.10} 氢原子的电子云图和概率密度等值面图
根据氢原子的薛定谔方程的解，求概率密度。 (1)为什么说用点的疏密表示的概率密度称为电子云图？ (2)氢原子的概率密度曲面是什么形状？彩色电子云图是 如何分布的？通过氢原子最大概率密度的百分之一的等 值曲面，说明概率密度的三维形状。 [解析](1)玻尔理论认为电子具有确定的轨道。 量子力学中得出电子出现在某处的概率。 为了形象地表示电子的空间分布规律，通常将概率大 的区域用较多的点，将概率小的区域用较少的点表示 出来，如同天空中的星云一样，称为电子云图。 注意：电子云并不表示电子真的像一团云雾罩在原子 核周围，而是电子概率密度分布的一种形象化的描述。
对于3p态电子，当m = 0时，概率密度 除了上下双峰之外，还有两个波包。 由于波包的概率密度相对于 波峰较小，所以颜色较暗。 彩色电子云图分为上下四片，相 邻的波峰和波包是分开的，等值 线分别围绕着各自的波峰和波包。 概率密度的等值面是上下四个分立的闭合曲面。
对于3p态电子，当m = ±1时， 概率密度分为左右双峰和双包。 彩色电子云图分为左右对称的四片。 概率密度的等值面是两个空 心的环面，并且外环面套着 内环面，两个环面是相似的。
1s态电子的概率密度曲面关于中心轴 对称，尖峰是概率密度最大处；随 着距离的增加，概率密度单调减小。 曲面的投影就是用颜色表示的概率密度，不妨 称为彩色电子云图，概率密度等值线是圆。 取最大概率密度的1%，1s态电 子的概率密度的等值面是球面。 其实，不论取多大的概率密 度，其等值面都是单一球面。
1s态电子云是球对称分布的，点数表示 概率密度。中间点数多，周围点数少。
2s态电子云 也是球对称 分布的，中 间点数最多， 随着距离的 增加，点数 先减小再增 加，达到最 大值之后再 减小。
对于l = 0的s态电子，电子云转动的角动量为零，表 示电子云不转动，所以电子云的分布具有球对称性。
对于2p态电 子，当m = 0 时，电子云 分为上下两 片，每一片 都有一个中 心，点数最 多，随着到 中心距离的 增加，点数 不断减小。
3s态电子的概率密度曲面关于中心轴对称，尖峰 的概率密度最大，但是比2s态的最大概率密度小。 尖峰外面有两个峰环，但是外面峰环 的高度太小，无法用不同颜色显示。 彩色电子云图除了中间彩色部分 外，只能显示一个淡蓝色的环。 取最大概率密度的1%，3s态电子的 概率密度的等值面是三个球面。 如果取最大概率密度的0.1%，3s态电 子的概率密度的等值面是五个球面。