1994年东方航空杯——上海市初中数学竞赛

专题13三角形的基本知识阅读与思考三角形是最基本的几何图形，是研究复杂几何图形的基础，许多几何问题都可转化为三角形的问题来解.三角形基本知识主要包括三角形基本概念、三角形三边关系定理及推论、三角形内角和定理及推论等，它们在线段和角度的计算、图形的计数等方面有广泛的应用.解与三角形的基本知识相关的问题时，常用到数形结合及分类讨论法，即用代数方法解几何计算题及简单的证明题，对三角形按边或按角进行恰当分类.应熟悉以下基本图形：例题与求解【例1】在△ABC中，∠A=50°，高BE，CF交于O，则∠BOC=________.（“东方航空杯”——上海市竞赛试题）解题思路：因三角形的高不一定在三角形内部，故应注意符合题设条件的图形多样性.【例2】等腰三角形一腰上的中线把这个三角形的周长分成12cm和21cm两部分，则这个等腰三角形底边的长为（）A.17cmB.5cmC.5cm或17cmD.无法确定（北京市竞赛试题）解题思路：中线所分两部分不等的原因在于等腰三角形的腰与底的不等，应分情况讨论.【例3】如图，BE 是∠ABD 的平分线，CF 是∠ACD 的平分线，BE 与CF 交于G ，若∠BDC =140°，∠BGC =110°，求∠A 的大小.（“希望杯”邀请赛试题）解题思路：运用凹四边形的性质计算.【例4】在△ABC 中，三个内角的度数均为正数，且∠A ＜∠B ＜∠C ，4∠C ＝7∠A ，求∠B 的度数.（北京市竞赛试题）解题思路：把∠A ，∠C 用∠B 的代数式表示，建立关于∠B 的不等式组，这是解本题的突破口.【例5】（1）周长为30，各边长互不相等且都是整数的三角形共有多少个？（2）现有长为150cm 的铁丝，要截成)2(>n n 小段，每段的长不小于1cm 的整数，如果其中任意3小段都不能拼成三角形，试求n 的最大值.此时有几种方法将该铁丝截成满足条件的n 段.（江苏省竞赛试题）解题思路：对于（1），不妨设三角形三边为a ，b ，c ，且c b a <<，由条件及三角形三边关系定理可确定c 的取值范围，从而可以确定整数c 的值.对于（2），因n 段之和为定值150cm ，故欲使n 尽可能的大，必须使每段的长度尽可能的小.这样依题意可构造一个数列.【例6】在三角形纸片内有2008个点，连同三角形纸片的3个顶点，共有2011个点，在这些点中，没有三点在一条直线上.问：以这2011个点为顶点能把三角形纸片分割成多少个没有重叠部分的小三角形？（天津市竞赛试题）解题思路：本题的解题关键是找到规律：三角形内角每增加1个内点，就增加了2个三角形和3条边.能力训练A 级1.设a ，b ，c 是△ABC 的三边，化简c b a c b a --+++=____________.2.三角形的三边分别为3，a 21-，8，则a 的取值范围是__________.3.已知一个三角形三个外角度数比为2:3:4，这个三角形是_______（按角分类)三角形.4.如图，∠A +∠B +∠C +∠D +∠E 的度数为____________.（“缙云杯“试题）（第4题）（第5题）（第6题）5.如图，已知AB ∥CD ，GM ，HM 分别是∠AGH ，∠CHG 的角平分线，那么∠GMH =_________.（第7题）（第9题）6.如图，△ABC 中，两外角平分线交于点E ，则∠BEC 等于（）A .)90(21A ∠-︒B .A ∠+︒2190C .)180(21A ∠-︒D .A ∠-︒211807.如图，在△ABC 中，BD ，BE 分别是高和角平分线，点F 在CA 的延长线上，FH ⊥BE 交BD 于G ，交BC 于H .下列结论：①∠DBE =∠F ；②2∠BEF =∠BAF +∠C ；③∠F =21（∠BAC -∠C ）；④∠BGH =∠ABE +∠C .其中正确的是（）A .①②③B .①③④C .①②③D .①②③④8.已知三角形的每条边长的数值都是2001的质因数，那么这样的不同的三角形共有（）A .6个B .7个C .8个D .9个9.如图，将纸片△ABC 沿着DE 折叠压平，则（）A .∠A =∠1+∠2B .∠A =21（∠1+∠2）C .∠A =31（∠1+∠2）D .∠A =41（∠1+∠2）（北京市竞赛试题）10.一个三角形的周长是偶数，其中的两条边分别是4和1997，则满足上述条件的三角形的个数是（）A .1个B .3个C .5个D .7个（北京市竞赛试题）11.如图，已知∠3=∠1+∠2，求证：∠A +∠B +∠C +∠D =180°.（河南省竞赛试题）12.平面内，四条线段AB ，BC ，CD ，DA 首尾顺次连接，∠ABC =24°，∠ADC =42°.（1）∠BAD 和∠BCD 的角平分线交于点M （如图1），求∠AMC 的大小.（2）点E 在BA 的延长线上，∠DAE 的平分线和∠BCD 平分线交于点N （如图2），求∠ANC .图1图213.三角形不等式是指一个三角形的两边长度之和大于第三边的长度.在下图中，E 位于线段CA 上，D 位于线段BE 上.（1）证明：AB +AE ＞DB +DE ；（2）证明：AB +AC ＞DB +DC ；（3）AB +BC +CA 与2（DA +DB +DC ）哪一个更大？证明你的结论；（4）AB +BC +CA 与DA +DB +DC 哪一个更大？证明你的结论.（加拿大埃蒙德顿市竞赛试题）B 级1.已知三角形的三条边长均为整数，其中有一条边长是4，但不是最短边，这样的三角形的个数有_______个.（“祖冲之杯”邀请赛试题）2.以三角形的3个顶点和它内部的9个点共12个点为顶点能把原三角形分割成______个没有公共部分的小三角形.3.△ABC 中，∠A 是最小角，∠B 是最大角，且有2∠B =5∠A ，若∠B 的最大值是 m ，最小值是 n ，则=+n m ___________.（上海市竞赛试题）4.如图，若∠CGE =α，则∠A +∠B +∠C +∠D +∠E +∠F =_______.（山东省竞赛试题）（第4题）（第5题）5.如图，在△ABC 中，∠A =96°，延长BC 到D ，∠ABC 与∠ACD 的平分线相交于1A 点，BC A 1∠与CD A 1∠的平分线相交于2A 点，依此类推，BC A 4∠与CD A 4∠的平分线相交于5A 点，则5A ∠的大小是（）A .3°B .5°C .8°D .19.2°6.四边形ABCD 两组对边AD ，BC 与AB ，DC 延长线分别交于点E ，F ，∠AEB ，∠AFD 的平分线交于点P .∠A =64°，∠BCD =136°，则下列结论中正确的是（）①∠EPF =100°；②∠ADC +∠ABC =160°；③∠PEB +∠PFC +∠EPF =136°；④∠PEB +∠PFC =136°.A .①②③B .②③④C .①③④D .①②③④7.三角形的三角内角分别为α，β，γ，且γβα≥≥，βα2=，则β的取值范围是（）A . 4536≤≤βB . 6045≤≤βC . 9060≤≤βD .3245≤≤β（重庆市竞赛试题）8.已知周长小于15的三角形三边的长都是质数，且其中一边的长为3，这样的三角形有（）A .4个B .5个C .6个D .7个（山东省竞赛试题）9.不等边△ABC 的两条高的长度分别为4和12，若第三条高的长也是整数，试求它的长.（第三十二届美国邀请赛试题）10.设m ，n ，p 均为自然数，满足p n m ≤≤且15=++p n m ，试问以m ，n ，p 为三边长的三角形有多少个？11.锐角三角形用度数来表示时，所有角的度数为正整数，最小角的度数是最大角的度数的41，求满足此条件的所有锐角三角形的度数.（汉城国际数学邀请赛试题）12.如图1，A 为x 轴负半轴上一点，B 为x 轴正半轴上一点，C （0，-2），D （-2，-2）.（1）求△BCD 的面积；（2）如图2，若∠BCO =∠BAC ，作AQ 平分∠BAC 交y 轴于P ，交BC 于Q .求证：∠CPQ =∠CQP ；（3）如图3，若∠ADC =∠DAC ，点B 在x 轴正半轴上运动，∠ACB 的平分线交直线AD 于E ，DF ∥AC交y 轴于F ，FM 平分∠DFC 交DE 于M ，EDMF BCF ∠∠-∠2的值是否发生变化？证明你的结论.图1图2图313.如图1，),0(m A ，)0,(n B .且m ，n 满足0)42(32≤-+-n m .图1图2（1）求A ，B 的坐标；（2）C 为y 轴正半轴上一动点，D 为△BCO 中∠BCO 的外角平分线与∠COB 的平分线的交点，问是否存在点C ，使∠D =41∠COB .若存在，求C 点坐标；（3）如图2，C 为y 轴正半轴上A 的上方一动点，P 为线段AB 上一动点，连CP 延长交x 轴于E ，∠CAB 和∠CEB 平分线交于F ，点C 在运动过程中FECO ABO ∠∠+∠的值是否发生变化？若不变求其值；若变化，求其范围.专题13三角形的基本知识例1130°或50°例2B例380°提示：∠A＝2∠BGC－∠BDC例4设∠C＝x°，则∠A＝(47 x)°，∠B＝180°－∠C－∠A＝180°－117 x°由∠A＜∠B＜∠C，得47x＜180－117x＜x．解得70＜x＜84．∵47x是整数，∴x＝77．故∠C＝77°，则∠A＝44°，∠B＝180°－77°－44°＝59°．例5（1）不妨设a＜b＜c，则由30a b ca b c+=-⎧⎨+>⎩，得10＜c＜15．∵c是整数，∴c＝11，12，13，14．当c＝11时，b＝10，a＝9．当c＝12时，b＝11，a＝7；b＝10，a＝8．当c＝13时，b＝12，a＝5；b＝11，a＝6；b＝10，a＝7；b＝19，a＝8．当c＝14时，b＝13，a＝3；b＝12，a＝4；b＝11，a＝5；b＝10，a＝6；b＝9，a＝7．（2）这些小段的长度只可能分别是1，1，2，3，5，8，13，21，34，55，89…但1＋1＋2＋5＋8＋13＋21＋34＋55＝143＜150，1＋1＋2＋3＋5＋8＋13＋21＋34＋55＋89＞150，故n的最大值为10.共有以下7种方式：（1，1，2，3，5，8，13，21，34，62）；（1，1，2，3，5，8，13，21，35，61）；（1，1，2，3，5，8，13，21，36，60）；（1，1，2，3，5，8，13，21，37，59）；（1，1，2，3，5，8，13，22，35，60）；（1，1，2，3，5，8，13，22，36，59）；（1，1，2，3，5，8，14，22，36，58）.例6解法1我们不妨先考察三角形内有1个点、2个点、3个点…的简单情况，有下表所示的关系：三角形内点数1234…连线得到的小三角形个数3579…不难发现，三角形内有一个点时，连线可得到3个小三角形，以后每增加一个点，这个点必落在某一个小三角形内，它与该三角形的三个顶点可得到三个小三角形，从而增加了两个小三角形，于是可以推出，当三角形内有2008个点是，连线可得到小三角形的个数为：3＋2×（2008－1）＝4017（个）.解法2整体核算法设连线后把原三角形分割成n个小三角形，则它们的内角和为180°·n，又因为原三角形内每一个点为小三角形顶点时，能为小三角形提供360°的内角，2008个点共提供内角2008×360°，于是得方程180n ＝360×2008＋180，解得n ＝4017，即这2008个点能将原三角形纸片分割成4017个小三角形.A 级1.2（b ＋c ）2.－5＜a ＜－23.钝角4.180°5.90°6.C7.D8.B9.B 10.B11.提示：过G 作GH ∥EB ，可推得BE ∥CF .12.（1）∠AMC ＝12（∠ABC ＋∠ADC ）＝12×（24°＋42°）＝33°（2）∵AN 、CN 分别平分∠DAE ，∠BCD ，∴可设∠EAN ＝∠DAB ＝x ，∠BCN ＝∠DCN ＝y ，∴∠BAN ＝180°－x ，设BC 与AN 交于S ，∴∠BSA ＝∠CSN ，∴180°－x ＋∠B ＝y ＋∠ANC ，①同理：180°－2x ＋∠B ＝2y ＋∠D ，②由①×2－②得：2∠ANC ＝180°＋∠B ＋∠D .∴∠ANC ＝12（180°＋24°＋42°）＝123°.13.（1）（2）略提示：（3）DA ＋DB ＞AB ，DB ＋DC ＞DC ，DC ＋DA ＞CA ，将三个不等式相加，得2（DA ＋DB ＋DC ）＞AB ＋CB ＋CA .（4）由（2）知AB ＋AC ＞DB ＋DC ，同理BC ＋BA ＞DC ＋DA ，CA ＋CB ＞DA ＋DB ，故AB ＋BC ＋CA ＞DA ＋DB ＋DCB 级1.82.193.175提示：设∠A ＝（2x ）°，∠B ＝（5x ）°，则∠C ＝180°－（7x ）°，由∠A ≤∠C ≤∠B 得15≤x ≤204.2a5.A6.D7.D8.B9.提示：设长度为4和12的高分别是边a ，b 上的，边c 上的高为h ，△ABC 的面积为S ，则24S a =，212S b =，2S c h =，由22222412412S S S S S h -<<+得36h <<，故5h =.10.711.设锐角三角形最小角的度数为x ，最大角的度数为4x ，另一角为y ，则41804490x x y x y x x ++=︒⎧⎪⎨⎪<︒⎩，解得20≤x ≤22.5，故x ＝20或21或22.所有锐角三角形的度数为：(20°，80°，80°)，(21°，75°，84°)，(22°，70°，88°).12.（1）S △BCD ＝2（2）略（3）设∠ABC ＝x ，则∠BCF ＝90°＋x ，可证：∠E ＝12x ，∠DMF ＝45°.∴2(90)245212BCF DMF x E x ∠-∠︒+-⨯︒==∠。

上海市首届“金桥杯”中学生数学知识应用竞赛(1991～1992)首届“金桥杯”中学生数学知识应用竞赛初赛于1991年10月举行．决赛于1992年3月举行．【初赛试题】初赛试题共有十五题，其中一～十题，每题满分为10分；十一～十五题，每题满分为16分．满分为180分．一、小明家前面造了一幢高层楼房，小明在自己楼房的A层测得高层楼房CD的仰角为α，俯角为β；小明又在自己楼房的B层测得高层高层楼房与小明楼房之间的距离d．二、筹建中的天然气管道网设计如图3—2所示，A，B，…，L表示压缩机站，流动主向用箭头表示，每个管道旁的数字表示管段长度．现需要求该网络从起点A到终点L的最短通道，并确定沿最优路径相应的压缩机站所处的节点．三、某厂1989年生产产值是1979年生产产值的8倍(即翻三番)，那么从1979年到1989年产值平均年增长率为多少？按这样速度发展，到了2000年的产值是1989年产值的几倍？(取整数)四、相距40公里的两个城镇A、B之间有一个圆形湖泊，它的圆心落在AB连线的中点O，半径为10公里，如图3—3所示．现要修建一条连结两城镇的公路，问应如何选择公路的路线，使公路最短，并给出证明．五、有一批1米长的合金钢材，现要截成长为23厘米和13厘米两种规格，用怎样方案截取使材料利用率为最高？并求出材料最高利用率．六、四种小商品A、B、C、D的价格分别为0.13元、0.17元、0.22元、0.35元，现在用2元钱恰好买了10件小商品，问买得小商品A、B、C、D各为多少？七、某工厂生产甲、乙两种产品，生产每一吨产品需要电力、煤、劳动力及相应产值如下表所示：该厂的劳动力满员是200人，根据限额每天用电不得超过160千度，用煤不得超过150吨．问每天生产这两种产品各几吨时，才能创造最大的经济价值？八、用两根绳子牵引重为F1＝100kg物体，两根绳子拉力分别为F2、F3，保持平衡，如图3—4所示．如果F2＝80kg，F2与F3夹角α＝135°，求F3的大小和F3与F1的夹角β值．九、在一边长为9m，一边长为16m的长方形的土地内，任意种植49颗树，试证明其中总有两颗树之间的距离不大于2.5m．十、仓库有一种堆垛方式，如图3—5所示，最高一层2盒，第二层6盒，第三层12盒，第四层20盒，第五层30盒……，当堆垛到第n层时，求出总的盒数．十一、数学竞赛给出了A、B、C三道题目，有30个学生参加，每人至少解出一道题．只解出A题的人数比其余解出A题的人数多3人；在没有解出A题的人中，解出B题人数是解出C题人数的3倍；在只解出一题的人中，解出A题的人数是没有解出A题的人数的一半，求至少解出两题的学生人数．十二、根据下列三视图(如图3—6)，画出这个立体的直观图与展开图，并求出它的体积．十三、A、B、C三个工厂，它们之间的距离为AB＝13公里、BC＝14公里、CA＝15公里，要求寻找一个供应站点H，使得它到三个工厂的距离和HA＋HB＋HC为最短，并且求出这最短距离．十四、某矿石基地A和冶炼厂B在铁路MN的两侧，A距铁路m公里，B距铁路n公里，在铁路上要建造两火车站C、D，A地矿石先用汽车由公路运到火车站C，然后用火车运输到火车站D，再用汽车运到B地，如图3—7所示，且A、B在铁路MN上投影A＇B＇距离长l公里，若汽车速度每小时u公里，火车速度每小时v公里，这里v＞u，要使运输矿石的时间最短，火车站C，D应该建立在什么地方？十五、将一个母线为2a，底面半径为a的圆锥(有底)的铁皮模型，沿着母线剪开摊平作材料做一个圆柱形罐子(有底无盖)，试问材料如何剪裁，使做出的圆柱形罐子的体积为最大？(这里圆柱侧面不能用两块材料拼接，且不考虑裁剪损耗．)【决赛试题】决赛试题共五题，其中一～三题，每题满分为32分，四、五题，每题满分为42分，总共满分为180分．一、如图3—8，有一块半径为a的圆铁皮，剪去一个圆心角α，将它卷成一个圆锥(无底)，试问：(2)求出这个圆锥的体积最大值．二、A、B、C三厂联营生产同一种产品，产品是哪个厂生产就在产品上盖上那个厂的厂名，如果产品是两个厂或三个厂联合生产，那么产品上就盖上两个厂或三个厂的厂名．今有一批产品，发现盖过A厂、B厂、C厂的厂名的产品分别为18件、24件、30件，同时盖过A、B厂，B、C厂，C、A厂的产品，分别有12件、14件，16件，问这批产品的总数最多有几件？三、某项科学实验显示：实验结果y与实验时的温度t，呈现y＝at2＋bt(a≠0)关系，由实验条件限制，温度t取值范围为｜t｜≤c(c＞0)．试问：当温度t取什么值时，实验结果y达到最小值，并求出其最小值．四、已知某工程中的重点部位计划完工期为14天，预算总费用为63000元(包括每天的管理费1000元)．若对某些工序增加一些费用的投入(如加班或技术改造等费用)，则它的完工时间可以缩短．一个工序的最短完工时间，我们称为该工序的“极限时间”．另外，如该重点部位的完工期能缩短，则相应的管理费可以节省，有关工序流程图与数据如图3—9所示．注：赶工费用率为工序每提前一天耗用的加班或技术改造等费用．试回答下列两个问题：(1)求这个重点部位工程的最低完工费用，并制定相应的施工方案(包括完工期)．(2)求这个重点部位最短完工期，并制定相应的施工方案(包括费用)．五、要对几种药品进行试验，每次选择3种药品作试验，要求这样来安排试验方案，使得任意两种药品都至少有一次被安排在同一次试验中，同时为了节省时间与费用，还要求试验次数尽可能少．我们以C(n)表示对n种药品所作符合上述要求的最少试验次数．例如：当n＝4，记所要作试验的药品为a1，a2，a3，a4，下面的分组试验方案(a1，a2，a3)，(a1，a2，a4)，(a2，a3，a4)，是符合要求的．这个方案共进行了三次试验，因此，C(4)≤3．问题：(1)证明C(4)＜3是不可能的．(2)试确定C(6)的值，并给出证明．(3)试给出C(n)的一个下界．【初赛试题解答要点与参考答案】二、最短通道：A→D→E→G→J→L．4＋3＋2＋1＋4＝14．三、(1＋x)10＝8，x＝23.11％(平均年增长率)．(1＋0.2311)21÷8＝9.48≈10．(2000年产值是1989年产值的10倍)四、过A、B在AB同侧分别作⊙O的切线AA＇、BB＇，则AA＇2)，则4×13＋2×23＝98，即截4段13厘米，2段23厘米，材料利用率为98％．六、设购买A、B、C、D商品数分别为x、y、z、w，则w只可能取0、1、2、3，相应找出z、y、x非负整数值，得到解答列表如下：七、设甲、乙产品分别生产x、y吨，则由题意得：满足上述约束条件的点在下列五条直线2x＋8y＝160，3x＋5y＝150，5x＋2y＝200，x＝0，y＝0所围成的五边形内(包括边界九、将长方形土地平分成48块相等的小长方形，每块长为2m、宽为1.5m，总有一块小长方形土地有两颗树，它的距离不大于对角线：十一、画出集合图如图3—10，只解出A题x人，只解出B题y人，只解出C题z人，解出A、B题w＋t人，解出B题、C题u＋t人，解出A 题、C题v＋t人，解出A题、B题、C题t人．根据题意可列出方程：所以 u＝5，y＝13，x＝7，z＝1．即u＋v＋w＋t＝30－x－y－z＝9(人)十二、直观图，展开图分别如图3—11，3—12．V＝(2a)3÷2＝4a3．十三、H点应取∠AHB＝∠BHC＝∠CHA＝120°时，AH＋BH＋CH为最小，由Fermat-steiner最短线定理可证得(证略)．十五、将圆锥侧面展开为半圆，半圆内裁出圆柱侧面，圆锥底改成圆柱底就可以(如图3—13所示)．【决赛试题解答要点与参考答案】二、由题意得：m(A)＝18，m(B)＝24，m(C)＝30，m(A∩B)＝12，m(B ∩C)＝14，m(C∩A)＝16．当m(A∩B∩C)≤9或m(A∩B∩C)≥13时，与题意有矛盾，所以10≤m(A∩B∩C)≤12．m(A∪B∪C)＝m(A)＋m(B)＋m(C)－m(A∩B)－m(B∩C)－m(C∩A)＋m(A∩B∩C)＝30＋m(A∩B∩C)．当m(A∩B∩C)＝12时，m(A∪B∪C)＝42(件)，故这批产品总数最多为42件．四、从工程网络列表如下：△C1＝2400－3000＝－600，△C2＝2400＋500＋1000＋2800－6000＝700．(1)最优费用方案：工序(1，3)减少3天，赶工费增加 2400，间接费用减少3000，总工期减少3天为11天完成．总费用 C＝63000＋(2400－3000)＝62400(元)．(2)最优时间方案：工序(1，3)减少3天，(3，6)，(5，6)各减少1天，(6，7)减少2天，总工期减少6天共为8天完成．总费用C＝63000＋(2400＋500 ＋ 1000＋ 2800－ 6000)＝63700(元)五、(1)设这4种药品为a1，a2，a3，a4由于每个组包含三种药品，而a1至少与a2，a3，a4相遇一次，因此至少有两个组包含a1，不妨设为｛a1a2a3｝，｛a1a2a4｝，但这里a3、a4没有相遇，因此，至少还应有一组，所以C(4)≥3．(2)设这6种药品为a1，a2，a3，a4，a5，a6，对每一个1≤i≤6，固定i，则包含a i的每次试验，正好还包含两种不同于a i的药品，而每次试验包含3种药品，因此试验总次数不小于6×3÷3＝6，即C(6)≥ 6．我们构造一个用6次试验的方案满足条件：｛a1a2a3｝，｛a1a4a5｝，｛a1a4a6｝，｛a2a3a4｝，｛a2a5a6｝，｛a3a5a6｝因此，C(6)≤6，综合之即得C(6)＝6．(3)设n种药品为a1，a2，…，a n，对任意取定a i(1≤i≤n)，则i≠j 时，a i与a j至少相遇一次，而每一个包含a i的组正好包含两个不3．2 上海市第二届“金桥杯”中学生数学知识应用竞赛(1993)上海市第二届“金桥杯”中学生数学知识应用竞赛初赛于1993年3月举行，决赛在9月举行．【初赛试题】初赛试题共有十五题，其中一～十题，每题满分为10分；十一～十五题，每题满分为16分．满分为180分．一、为测量建造中的上海东方明珠电视塔已达到的高度．小明在学校操场某一直线上选择三点A、B、C，且AB＝BC＝60米，分别在A、B、C三点观察塔的最高点，测得仰角为45°，54.2°，60°，小明身高为1.5米，试问建造中的电视塔现在已达到的高度．(结果保留一位小数)二、已知边长为a的正三角形铁皮材料，剪去三个全等的四边形，如图3—14所示，可制成无盖的正三棱柱的盒子．试问如何剪裁才能使正三棱柱的体积最大？并求出体积最大值和此时材料利用率．三、某布店的一页帐簿上沾了墨水，如下图所示：所卖呢料米数看不清楚了，但记得是卖了整数米；金额项目只看到后面三个数码7.28，但前面的三个数码看不清楚了，请您帮助查清这笔帐．四、某出口加工区总公司与下属各子公司进行信息联网，已测得各子公司A、B、C、D、E、F、G、H、J之间与总公司S联网费用如图3—15所示(单位：千元)．现拟设计一个联网优化方案，既要求各子公司之间与总公司都能连通，又要使联网费用最省，试问如何联网？费用是多少？五、在下乡劳动中，30个学生，每人拾了一篮稻穗放在田埂旁，每隔5米排成一列，不妨依次叫第1号、第2号、…、第30号，每人将篮中稻穗集中到第n号处(1≤n≤30)，放在一起，然后带着空篮走回原处，试求使大家所走路程总和最小的n值．六、一半径R＝150mm球形工件，打一斜孔如图3—16(a)所示，为了准确测量斜孔两端半径r1和r2，用两精密量球(半径R2＝100mm和R2＝80mm)以如图3—16(b)所示方式测量，测得两球外端水平距离L1＝651.40mm；再将右端量球换为半径R3＝80mm，左端量球不变仍为R2＝80mm，又测得L2＝610.17mm．(1)求r1和r2(结果保留两位小数)；(2)求小孔的斜角α的值(结果保留分)．七、A、B两个产地分别生产同一规格产品12千吨、8千吨，而D、E、F三地分别需要8千吨、6千吨、6千吨，每千吨的运价表如下：怎样确定调运方案，使总的运费为最小？八、在机械设计中，已知AB＝AC＝a，CD⊥BD，∠CAD＝θ(图3—17)，当θ为何值时，△BDC面积最大，并求出最大值．九、某一信托投资公司，考虑投资1600万元建造一座涉外宾馆，经预测，该宾馆建成后，每年底可获利600万元，试问三年内能否把全部投资收回？假设银行每年复利计息，利率为10％，若需要在三年内收回全部投资，每年至少应收益多少万元？(结果保留一位小数)十、在正方形铁皮上任意划9条直线，如果每一条直线都将正方形分成两部分面积之比为m∶n(m， n∈N)，那么这样9条直线中至少有3条直线交于一点，对吗，为什么？十一、五种商品价格如下：现在用60元恰好选购10件商品，试问有哪几种选购方式？十二、根据图3—18所示零件的视图，画出它的直观图、展开图(并要留出做成模型的粘贴处)，并求出这个零件的表面积与体积．一个供应站H的位置，使它到四个工厂距离和HA＋HB＋HC＋HD为最小，说明道理，并求出最小值．十四、一个零件模具的底面由甲、乙、丙三个边长均为a的正方形按如下要求叠合而成：甲的一个顶点落在乙的中心上，乙的一个顶点落在丙的中心上，丙的一个顶点落在甲的中心上．求这个模具底面的面积．十五、一煤粉炉球磨机衬板为圆台的侧面，上底半径R1＝270 mm，下底半径R2＝1147 mm，轴截面母线夹角为154°，这圆台侧面是由18块相同的扇环形钢板焊接而成。

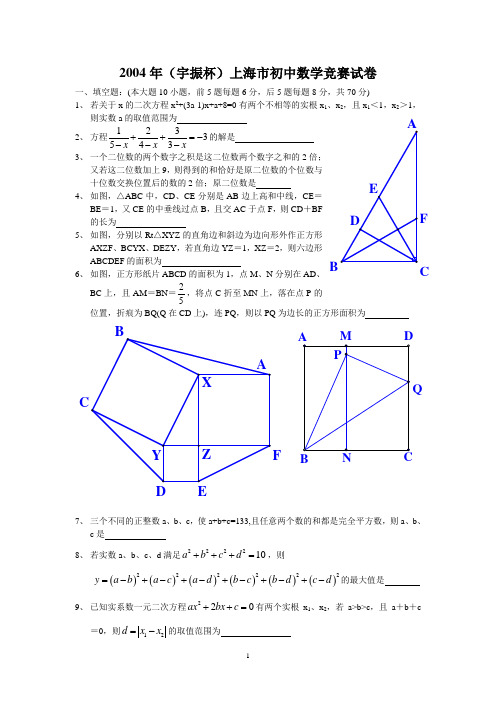
12004年（宇振杯）上海市初中数学竞赛试卷一、填空题：(本大题10小题，前5题每题6分，后5题每题8分，共70分)1、 若关于x 的二次方程x 2+(3a-1)x+a+8=0有两个不相等的实根x 1、x 2，且x 1＜1，x 2＞1，则实数a 的取值范围为2、 方程1233543x x x++=----的解是3、 一个二位数的两个数字之积是这二位数两个数字之和的2倍；又若这二位数加上9，则得到的和恰好是原二位数的个位数与十位数交换位置后的数的2倍；原二位数是4、 如图，△ABC 中，CD 、CE 分别是AB 边上高和中线，CE ＝BE ＝1，又CE 的中垂线过点B ，且交AC 于点F ，则CD ＋BF 的长为5、 如图，分别以Rt △XYZ 的直角边和斜边为边向形外作正方形AXZF 、BCYX 、DEZY ，若直角边YZ ＝1，XZ ＝2，则六边形ABCDEF 的面积为6、 如图，正方形纸片ABCD 的面积为1，点M 、N 分别在AD 、BC 上，且AM ＝BN ＝25，将点C 折至MN 上，落在点P 的位置，折痕为BQ(Q 在CD 上)，连PQ ，则以PQ 为边长的正方形面积为Q7、 三个不同的正整数a 、b 、c ，使a+b+c=133,且任意两个数的和都是完全平方数，则a 、b 、c 是 8、 若实数a 、b 、c 、d 满足222210a b c d +++=，则()()()()()()222222y a b a c a d b c b d c d =-+-+-+-+-+-的最大值是9、 已知实系数一元二次方程220ax bx c ++=有两个实根x 1、x 2，若a>b>c ，且a ＋b ＋c＝0，则12d x x =-的取值范围为FBCCF210、 如图，△ABC 中，AB ＝CD ，点P 、Q 分别在AC 、AB 上，且AP ＝PQ ＝QB ＝BC ，则∠A 的大小是二、(本题16分)如图PQMN 是平行四边形ABCD 的内接四边形 (1) 若MP ∥BC 或NQ ∥AB ，求证：12PQMN ABCD S S =Y ； (2) 若12PQMN ABCD S S =Y ，问是否能推出MP ∥BC 或NQ ∥AB ？证明你的结论.三、(本题16分)设n 是正整数，1234d d d d <<<是n 的四个最小的正整数约数，若n=22221234d d d d +++，求n 的值.四、(本题18分)如图，已知△ABC ，且S △ABC ＝1，D 、E 分别是AB 、AC 上的动点，BD 与CE 相交于点P ，使S BCDE ＝169S △BPC ，求S △DEP 的最大值.BCBCN。

八年级数学竞赛专题训练13 三角形的基本知识阅读与思考三角形是最基本的几何图形，是研究复杂几何图形的基础，许多几何问题都可转化为三角形的问题来解.三角形基本知识主要包括三角形基本概念、三角形三边关系定理及推论、三角形内角和定理及推论等，它们在线段和角度的计算、图形的计数等方面有广泛的应用.解与三角形的基本知识相关的问题时，常用到数形结合及分类讨论法，即用代数方法解几何计算题及简单的证明题，对三角形按边或按角进行恰当分类.应熟悉以下基本图形：图4图3图2图1CDBAD CBADCBA DCOBA例题与求解【例1】 在△ABC 中，∠A =50°，高BE ，CF 交于O ，则∠BOC =________.（“东方航空杯”——上海市竞赛试题）解题思路：因三角形的高不一定在三角形内部，故应注意符合题设条件的图形多样性.【例2】 等腰三角形一腰上的中线把这个三角形的周长分成12cm 和21cm 两部分，则这个等腰三角形底边的长为（ ）A .17cmB .5cmC .5cm 或17cmD .无法确定（北京市竞赛试题）解题思路：中线所分两部分不等的原因在于等腰三角形的腰与底的不等，应分情况讨论.【例3】 如图，BE 是∠ABD 的平分线，CF 是∠ACD 的平分线，BE 与CF 交于G ，若∠BDC =140°，∠BGC =110°，求∠A 的大小.（“希望杯”邀请赛试题）解题思路：运用凹四边形的性质计算.GC DBEF A【例4】 在△ABC 中，三个内角的度数均为正数，且∠A ＜∠B ＜∠C ，4∠C ＝7∠A ，求∠B 的度数.（北京市竞赛试题）解题思路：把∠A ，∠C 用∠B 的代数式表示，建立关于∠B 的不等式组，这是解本题的突破口.【例5】 （1）周长为30，各边长互不相等且都是整数的三角形共有多少个？（2）现有长为150cm 的铁丝，要截成)2(>n n 小段，每段的长不小于1cm 的整数，如果其中任意3小段都不能拼成三角形，试求n 的最大值.此时有几种方法将该铁丝截成满足条件的n 段.（江苏省竞赛试题）解题思路：对于（1），不妨设三角形三边为a ，b ，c ，且c b a <<，由条件及三角形三边关系定理可确定c 的取值范围，从而可以确定整数c 的值. 对于（2），因n 段之和为定值150cm ，故欲使n 尽可能的大，必须使每段的长度尽可能的小.这样依题意可构造一个数列.【例6】 在三角形纸片内有2 008个点，连同三角形纸片的3个顶点，共有2 011个点，在这些点中，没有三点在一条直线上.问：以这2 011个点为顶点能把三角形纸片分割成多少个没有重叠部分的小三角形？（天津市竞赛试题）解题思路：本题的解题关键是找到规律：三角形内角每增加1个内点，就增加了2个三角形和3条边.能力训练A 级1.设a ，b ，c 是△ABC 的三边，化简c b a c b a --+++=____________.2.三角形的三边分别为3，a 21-，8，则a 的取值范围是__________.3.已知一个三角形三个外角度数比为2:3:4，这个三角形是_______（按角分类)三角形.4.如图，∠A +∠B +∠C +∠D +∠E 的度数为____________. （“缙云杯“试题）EDCBAHDCMG BAEC BA（第4题） （第5题） （第6题）5.如图，已知AB ∥CD ，GM ，HM 分别是∠AGH ，∠CHG 的角平分线，那么∠GMH =_________.T ED GHCBA F21AC EDB（第7题） （第9题） 6.如图，△ABC 中，两外角平分线交于点E ，则∠BEC 等于（ ）A .)90(21A ∠-︒ B .A ∠+︒2190 C .)180(21A ∠-︒ D .A ∠-︒21180 7.如图，在△ABC 中，BD ，BE 分别是高和角平分线，点F 在CA 的延长线上，FH ⊥BE 交BD 于G ，交BC 于H .下列结论：①∠DBE =∠F ；②2∠BEF =∠BAF +∠C ；③∠F =21（∠BAC -∠C ）；④∠BGH =∠ABE +∠C . 其中正确的是（ ）A .①②③B .①③④C .①②③D .①②③④8.已知三角形的每条边长的数值都是2 001的质因数，那么这样的不同的三角形共有（ ） A .6个 B .7个 C .8个 D .9个 9.如图，将纸片△ABC 沿着DE 折叠压平，则（ ） A .∠A =∠1+∠2 B .∠A =21（∠1+∠2）C .∠A =31（∠1+∠2） D .∠A =41（∠1+∠2）（北京市竞赛试题）10.一个三角形的周长是偶数，其中的两条边分别是4和1 997，则满足上述条件的三角形的个数是（ ） A .1个 B .3个 C .5个 D .7个（北京市竞赛试题）11.如图，已知∠3=∠1+∠2，求证：∠A +∠B +∠C +∠D =180°.（河南省竞赛试题）321EG FDCBA12.平面内，四条线段AB ，BC ，CD ，DA 首尾顺次连接，∠ABC =24°，∠ADC =42°. （1）∠BAD 和∠BCD 的角平分线交于点M （如图1），求∠AMC 的大小.（2）点E 在BA 的延长线上，∠DAE 的平分线和∠BCD 平分线交于点N （如图2），求∠ANC .CDBAEND CBA图1 图213.三角形不等式是指一个三角形的两边长度之和大于第三边的长度.在下图中，E 位于线段CA 上，D 位于线段BE 上.（1）证明：AB +AE ＞DB +DE ； （2）证明：AB +AC ＞DB +DC ；（3）AB +BC +CA 与2（DA +DB +DC ）哪一个更大？证明你的结论； （4）AB +BC +CA 与DA +DB +DC 哪一个更大？证明你的结论.（加拿大埃蒙德顿市竞赛试题）E DCBAB 级1.已知三角形的三条边长均为整数，其中有一条边长是4，但不是最短边，这样的三角形的 个数有_______个.（“祖冲之杯”邀请赛试题）2.以三角形的3个顶点和它内部的9个点共12个点为顶点能把原三角形分割成______个没有公共部分的小三角形.3.△ABC 中，∠A 是最小角，∠B 是最大角，且有2∠B =5∠A ，若∠B 的最大值是m ，最小值是n ，则=+n m ___________.（上海市竞赛试题）4.如图，若∠CGE =α，则∠A +∠B +∠C +∠D +∠E +∠F =_______.（山东省竞赛试题）αGFEDCBADA 2A 1CBA（第4题） （第5题）5.如图，在△ABC 中，∠A =96°，延长BC 到D ，∠ABC 与∠ACD 的平分线相交于1A 点，BC A 1∠与CD A 1∠的平分线相交于2A 点，依此类推，BC A 4∠与CD A 4∠的平分线相交于5A 点，则5A ∠的大小是（ ）A .3°B .5°C .8°D .19.2°6.四边形ABCD 两组对边AD ，BC 与AB ，DC 延长线分别交于点E ，F ，∠AEB ，∠AFD 的平分线交于点P .∠A =64°，∠BCD =136°，则下列结论中正确的是（ ）①∠EPF =100°； ②∠ADC +∠ABC =160°； ③∠PEB +∠PFC +∠EPF =136°； ④∠PEB +∠PFC =136°.A .①②③B .②③④C .①③④D .①②③④FEDPCBA7.三角形的三角内角分别为α，β，γ，且γβα≥≥，βα2=，则β的取值范围是（ ） A .4536≤≤β B .6045≤≤β C .9060≤≤β D .3245≤≤β（重庆市竞赛试题）8.已知周长小于15的三角形三边的长都是质数，且其中一边的长为3，这样的三角形有（ ） A .4个 B .5个 C .6个 D .7个（山东省竞赛试题）9.不等边△ABC 的两条高的长度分别为4和12，若第三条高的长也是整数，试求它的长.（第三十二届美国邀请赛试题）10.设m ，n ，p 均为自然数，满足p n m ≤≤且15=++p n m ，试问以m ，n ，p 为三边长的三角形有多少个？11.锐角三角形用度数来表示时，所有角的度数为正整数，最小角的度数是最大角的度数的41，求满足此条件的所有锐角三角形的度数.（汉城国际数学邀请赛试题）12.如图1，A 为x 轴负半轴上一点，B 为x 轴正半轴上一点，C （0，-2），D （-2，-2）. （1）求△BCD 的面积；（2）如图2，若∠BCO =∠BAC ，作AQ 平分∠BAC 交y 轴于P ，交BC 于Q .求证：∠CPQ =∠CQP ；（3）如图3，若∠ADC =∠DAC ，点B 在x 轴正半轴上运动，∠ACB 的平分线交直线AD 于E ，DF ∥AC交y 轴于F ，FM 平分∠DFC 交DE 于M ，EDMFBCF ∠∠-∠2的值是否发生变化？证明你的结论.x图313.如图1，),0(m A ，)0,(n B .且m ，n 满足0)42(32≤-+-n m.图1 图2（1）求A ，B 的坐标；（2）C 为y 轴正半轴上一动点，D 为△BCO 中∠BCO 的外角平分线与∠COB 的平分线的交点，问是否存在点C ，使∠D =41∠COB .若存在，求C 点坐标； （3）如图2，C 为y 轴正半轴上A 的上方一动点，P 为线段AB 上一动点，连CP 延长交x 轴于E ，∠CAB 和∠CEB 平分线交于F ，点C 在运动过程中FECOABO ∠∠+∠的值是否发生变化？若不变求其值；若变化，求其范围.专题13 三角形的基本知识例1130°或50°例2 B 例380°提示：∠A＝2∠BGC－∠BDC例4设∠C＝x°，则∠A＝(47 x)°，∠B＝180°－∠C－∠A＝180°－117x°由∠A＜∠B＜∠C，得47x＜180－117x＜x．解得70＜x＜84．∵47x是整数，∴x＝77．故∠C＝77°，则∠A＝44°，∠B＝180°－77°－44°＝59°．例5（1）不妨设a＜b＜c，则由30a b ca b c+=-⎧⎨+>⎩，得10＜c＜15．∵c是整数，∴c＝11，12，13，14．当c＝11时，b＝10，a＝9．当c＝12时，b＝11，a＝7；b＝10，a＝8．当c＝13时，b＝12，a＝5；b＝11，a＝6；b＝10，a＝7；b＝19，a＝8．当c＝14时，b＝13，a＝3；b＝12，a＝4；b＝11，a＝5；b＝10，a＝6；b＝9，a＝7．（2）这些小段的长度只可能分别是1，1，2，3，5，8，13，21，34，55，89…但1＋1＋2＋5＋8＋13＋21＋34＋55＝143＜150，1＋1＋2＋3＋5＋8＋13＋21＋34＋55＋89＞150，故n的最大值为10.共有以下7种方式：（1，1，2，3，5，8，13，21，34，62）；（1，1，2，3，5，8，13，21，35，61）；（1，1，2，3，5，8，13，21，36，60）；（1，1，2，3，5，8，13，21，37，59）；（1，1，2，3，5，8，13，22，35，60）；（1，1，2，3，5，8，13，22，36，59）；（1，1，2，3，5，8，14，22，36，58）.例6 解法1一个小三角形内，它与该三角形的三个顶点可得到三个小三角形，从而增加了两个小三角形，于是可以推出，当三角形内有2008个点是，连线可得到小三角形的个数为：3＋2×（2008－1）＝4017（个）.解法2 整体核算法设连线后把原三角形分割成n个小三角形，则它们的内角和为180°·n，又因为原三角形内每一个点为小三角形顶点时，能为小三角形提供360°的内角，2008个点共提供内角2008×360°，于是得方程180n＝360×2008＋180，解得n＝4017，即这2008个点能将原三角形纸片分割成4017个小三角形.A 级1. 2（b ＋c ）2. －5＜a ＜－23. 钝角4. 180°5. 90°6. C7. D8. B9. B 10. B 11. 提示：过G 作GH ∥EB ，可推得BE ∥CF . 12. （1）∠AMC ＝12（∠ABC ＋∠ADC ）＝12×（24°＋42°）＝33° （2）∵AN 、CN 分别平分∠DAE ，∠BCD ，∴可设∠EAN ＝∠DAB ＝x ，∠BCN ＝∠DCN ＝y ，∴∠BAN ＝180°－x ，设BC 与AN 交于S ，∴∠BSA ＝∠CSN ，∴180°－x ＋∠B ＝y ＋∠ANC ，① 同理：180°－2x ＋∠B ＝2y ＋∠D ，②由①×2－②得：2∠ANC ＝180°＋∠B ＋∠D . ∴∠ANC ＝12（180°＋24°＋42°）＝123°. 13. （1）（2）略 提示：（3）DA ＋DB ＞AB ，DB ＋DC ＞DC ，DC ＋DA ＞CA ，将三个不等式相加，得2（DA ＋DB ＋DC ）＞AB ＋CB ＋CA .（4）由（2）知AB ＋AC ＞DB ＋DC ，同理BC ＋BA ＞DC ＋DA ，CA ＋CB ＞DA ＋DB ， 故AB ＋BC ＋CA ＞DA ＋DB ＋DCB 级1. 82. 193. 175 提示：设∠A ＝（2x ）°，∠B ＝（5x ）°，则∠C ＝180°－（7x ）°，由∠A ≤∠C ≤∠B 得15≤x ≤204. 2a5. A6. D7. D8. B9. 提示：设长度为4和12的高分别是边a ，b 上的，边c 上的高为h ，△ABC 的面积为S ， 则24S a =，212S b =，2S c h =，由22222412412S S S S S h -<<+得36h <<，故5h =. 10. 711. 设锐角三角形最小角的度数为x ，最大角的度数为4x ，另一角为y ，则41804490x x y x y xx ++=︒⎧⎪⎨⎪<︒⎩，解得20≤x ≤22.5，故x ＝20或21或22. 所有锐角三角形的度数为：(20°，80°，80°)，(21°，75°，84°)，(22°，70°，88°). 12. （1）S △BCD ＝2 （2）略（3）设∠ABC ＝x ，则∠BCF ＝90°＋x ，可证：∠E ＝12x ，∠DMF ＝45°. ∴2(90)245212BCF DMF x E x ∠-∠︒+-⨯︒==∠。

竞赛中二次根式的配方技巧225500江苏省姜堰市励才实验学校肖维松配方法在初中数学竞赛中有着极其广泛的应用．开阔学生视野、启迪学生思维、提高分析问题和解决问题的能力，丰富学生的课外学习内容．本文主要介绍配方技巧在二次根式中的应用．1化简例1（2010年全国初中数学联赛江西省初赛题）化简槡槡槡槡3+5－13+48槡槡6+2的结果是槡A．2B．槡22C．2D．12解因为槡13+48=（槡23）2槡+1+43=（槡1+23）2，5－（槡1+23）槡=4－23=（槡3－1）2，3+（槡3－1）槡=2+3=槡4+232=（槡3+1）22=（槡槡6+22）2，所以，原式=12，故选D ．点评此题是形如A ʃ槡槡B C 形式的复合二次根式化简问题，解题关键是通过三次变形，将分子中二次根式的被开方数配成完全平方，然后化简即可．例2（2009年第20届“希望杯”初二第1试）化简（槡11+47）32+（槡11－47）32，结果等于槡槡槡A．58B．387C．247D．327解原式=（槡7+2ˑ27+22）32+（槡7－2ˑ27+22）32=（槡7+2）[]232+（槡7－2）[]232=（槡7+2）3+（槡7－2）3槡=387，故选B ．点评当问题中的被开方数出现a +槡b c 与a －槡b c 互为有理化因式时，采用配方变成完全平方形式求解较为简便．2计算例3（1996年“东方航空杯”上海市初中数学竞赛题）计算槡26槡槡槡3+2－5．解因为（槡3）2+（槡2）2－（槡5）2=0，所以原式=（槡3）2槡+26+（槡2）2－（槡5）2槡槡槡3+2－5=（槡槡3+2）2－（槡5）2槡槡槡3+2－5=（槡槡槡3+2+5）（槡槡槡3+2－5）槡槡槡3+2－5槡槡槡=3+2+5．点评本题通常利用分母有理化进行计算，但较繁，然而巧用“数0”的特征，来助添项配方的技巧，使原来较难的化简题轻松获解，一气呵成，真正是别具风格，新颖独特．例4（2007年河北省初中数学创新与知识应用竞赛题）计算1+20072+200722008槡2－12008．解原式=（1+20072+2ˑ2007）－2ˑ2007+200722008槡2－12008=（1+2007）2－2ˑ2008ˑ20072008+200722008槡2－12008=（2008－20072008）槡2－12008=2008－20072008－12008=2007．点评本题是通过添项，经过两次变形，配成完全平方数进行计算的，方法巧，过程简，有新意．3求值例5（2008年数学周报初中数学竞赛题）已知实数a ，b ，c 满足条件槡a +b 槡－1+c 槡－2=14（a +b+c +9），则abc =．解将条件变形为（12槡a －1）2+（12b 槡－1－1）243（2011年第8期·初中版）·解题研究·+（12c 槡－2－1）2=0，则由非负数性质，得槡a =2，b 槡－1=2，c 槡－2=2{，故a =4，b =5，c =6{，ʑabc =120．点评解决本题的关键在于对条件等式进行配方，配成三个完全平方式，利用平方数是非负数这一特点，求得a ，b ，c 的值即可．4证明例6（2001年绍兴地区初中数学联赛题）已知n为整数，求证1+1n 2+1（n +1）槡2=1+1n －1n +1．证明左边=（1+1n ）2－2n +1（n +1）槡2=（n +1n ）2－2ˑn +1n ˑ1n +1+（1n +1）槡2=（n +1n －1n +1）槡2=n +1n －1n +1=1+1n －1n +1=右边，ʑ结论成立．点评解决本题的关键是通过两次配方，使命题获证．例7（2001年大连市第八届“育英杯”数学竞赛题）已知a ，b ，c 为△ABC 的三边长，且有（槡a +槡b +槡c ）2=3（槡ab +槡ac +槡bc ），求证△ABC 是等边三角形．证明ȵ（槡a +槡b +槡c ）2=3（槡ab +槡ac +槡bc ），ʑ（槡a ）2+（槡b ）2+（槡c ）2+2槡ab +2槡ac +2槡bc =3槡ab +3槡ac +3槡bc ，ʑ（槡a ）2+（槡b ）2+（槡c ）2－槡ab －槡ac －槡bc =0，ʑ2［（槡a ）2+（槡b ）2+（槡c ）2－槡ab －槡ac －槡bc ］=0，ʑ［（槡a ）2－2槡ab +（槡b ）2］+［（槡a ）2－2槡ac+（槡c ）2］+［（槡b ）2－2槡bc +（槡c ）2］=0，ʑ（槡a －槡b ）2+（槡a －槡c ）2+（槡b －槡c ）2=0，ʑ槡a －槡b =0，槡a －槡c =0，槡b －槡c =0{，ʑa =b =c ，故△ABC 是等边三角形．点评本题通过整理配方转化成三个完全平方式的和为零，再利用非负数的性质，导出了a ，b ，c 相等的关系而得证．5纠错例8阅读下列材料，回答问题．对于题目“化简并求值：1a+1a2+a 2槡－2，其中a =15”，甲、乙两人的解答不同．甲的解答：原式=1a+（1a －a ）槡2=1a +1a－a =2a －a =495．乙的解答：原式=1a+（a －1a ）槡2=1a +a －1a=a =15，谁的解答是错误的，为什么？解乙的解答是错误的．ȵ当a =15时，1a =5，a －1a＜0，故（a －1a ）槡2≠a －1a，而是（a －1a ）槡2=1a－a．点评利用配方技巧将平方式变形为完全平方式，以便于求其算术平方根，这是化简二次根式的一种通法，甲、乙两人都是这么做的．分歧在于a =15，（1a －a ）槡2是等于a －1a ，还是等于1a－a ？因此理解和运用a 槡2=a =a ，（a ≥0）－a．（a ＜0{）是一个难点，应引起重视．（收稿日期：20110501）53·解题研究·（2011年第8期·初中版）。

八年级数学竞赛专题训练21 梯形阅读与思考梯形是一类具有一组对边平行而另一组对边不平行的特殊四边形，梯形的主要内容是等腰梯形、直角梯形等相关概念及性质.解决梯形问题的基本思路是：通过适当添加辅助线，把梯形转化为三角形或平行四边形，常见的辅助线的方法有：（1）过一个顶点作一腰的平行线（平移腰）；（2）过一个顶点作一条对角线的平行线（平移对角线）；（3）过较短底的一个顶点作另一底的垂线；（4）延长两腰，使它们的延长线交于一点，将梯形还原为三角形．如图所示：例题与求解【例1】如图，在四边形ABCD中，AB//CD，∠D＝2∠B，AD和CD的长度分别为a，b，那么AB的长是___________. （荆州市竞赛试题）解题思路：平移一腰，构造平行四边形、特殊三角形．AB【例2】如图1，四边形ABCD是等腰梯形，AB//CD．由四个这样的等腰梯形可以拼出图2所示的平行四边形．（1）求四边形ABCD四个内角的度数；（2）试探究四边形ABCD 四条边之间存在的等量关系，并说明理由；（3）现有图1中的等腰梯形若干个，利用它们你能拼出一个菱形吗？若能，请你画出大致的示意图． （山东省中考试题） 解题思路：对于（1）、（2），在观察的基础上易得出结论，探寻上、下底和腰及上、下底之间的关系，从作出梯形的常见辅助线入手；对于（3），在（2）的基础上，展开想象的翅膀，就可设计出若干种图形．图2图1A【例3】如图，在等腰梯形ABCD 中，AD//BC ，AB ＝DC ，且AC ⊥BD ，AF 是梯形的高，梯形的面积是49cm 2，求梯形的高.（内蒙古自治区东四盟中考试题） 解题思路：由于题目条件中涉及对角线位置关系，不妨从平移对角线入手．B【例4】 如图，在等腰梯形ABCD 中，AB//DC ，AB ＝998，DC ＝1001，AD ＝1999，点P 在线段AD 上，问：满足条件∠BPC ＝900的点P 有多少个？（全国初中数学联赛试题） 解题思路：根据AB ＋DC ＝AD 这一关系，可以在AD 上取点构造等腰三角形．D【例5】如图，在等腰梯形ABCD中，CD//AB，对角线AC，BD相交于O，∠ACD＝600，点S，P，Q分别为OD，OA，BC的中点．（1）求证：△PQS是等边三角形；（2）若AB＝5，CD＝3，求△PQS的面积；（3）若△PQS的面积与△AOD的面积的比是7：8，求梯形上、下两底的比CD：AB．（“希望杯”邀请赛试题）解题思路：多个中点给人以广泛的联想：等腰三角形性质、直角三角形斜边中线、三角形中位线等.A【例6】如图，分别以△ABC的边AC和BC为一边，在△ABC外作正方形ACDE和CBFG，点P是EF的中点，求证：点P到边AB的距离是AB的一半．（山东省竞赛试题）解题思路：本题考查了梯形中位线定理、全等三角形的判定与性质．关键是要构造能运用条件EP＝PF的图形．EF能力训练A级1. 等腰梯形中，上底：腰：下底＝1：2：3，则下底角的度数是__________.（天津市中考试题）2. 如图，直角梯形ABCD中，AB⊥BC，AD＝3，BC＝5，将腰DC绕点D逆时针方向旋转900至DE，连接AE，则△ADE的面积为______________. （宁波市中考试题）3．如图，在等腰梯形ABCD 中，AB//CD ，∠A ＝060，∠1＝∠2，且梯形的周长为30cm ，则这个等腰梯形的腰长为______________.第3题图第4题图第2题图ABAB4.如图，梯形ABCD 中，AD//BC ，EF 是中位线，G 是BC 边上任一点，如果222cm S GEF =∆，那么梯形ABCD 的面积为__________. （成都市中考试题）5.等腰梯形的两条对角线互相垂直，则梯形的高h 和中位线的长m 之间的关系是 ( )A ．m ＞hB ．m ＝hC ．m ＜hD ．无法确定6. 梯形ABCD 中，AB//DC ，AB ＝5，BC ＝23，∠BCD ＝045，∠CDA ＝060，则DC 的长度是( )A .3327+B ．8 C.219 D.38+ E. 338+（美国高中考试题）7．如图，在等腰梯形ABCD 中，AC ＝BC ＋AD ，则∠DBC 的度数是 ( )A.300B.450C.600D.900（陕西省中考试第7题图第8题图BBAC第9题图B8．如图，在直角梯形ABCD 中，AD//BC ，AB ⊥BC ，AD ＝2，BC ＝DC ＝5，点P 在BC 上移动，则当P A ＋PD 取最小值时，△APD 中边AP 上的高为( )A ．17172 B ．17174 C ．17178 D ．3 （鄂州市中考试题）9．如图，在等腰梯形ABCD 中，AD //BC ，AB ＝CD ，点P 为BC 边上一点，PE ⊥AB ，PF ⊥CD ，BG ⊥CD ，垂足分别为E ，F ，G ．求证 ：PE ＋PF ＝BG ．（哈尔滨市中考试题）10. 如图，在梯形ABCD 中，AD//BC ，E ，F 分别为AB ，AC 中点，BD 与EF 相交于G ．求证：)(21AD BC GF -=．BC11.如图，等腰三角形ABC 中，AB ＝AC ，点E 、F 分别是AB 、AC 的中点，CE ⊥BF 于点O ． 求证：（1）四边形EBCF 是等腰梯形；（2）2222BE BC EF =+． （深圳市中考试题）B12.如图1，在等腰梯形ABCD 中，AD//BC ，E 是AB 的中点，过点E 作EF//BC 交CD 于点F ，AB ＝4，BC ＝6，∠B ＝060．（1）求点E 到BC 的距离；（2）点P 为线段EF 上的一个动点，过P 作PM ⊥EF 交BC 于点M ，过M 作MN//AB 交折线ADC 于点N ，连接PN ，设EP ＝x ．①当点N 在线段AD 上时（如图2），△PMN 的形状是否发生改变？若不变，求出△PMN 的周长；若改变，请说明理由．②当点N 在线段DC 上时（如图3），是否存在点P ，使△PMN 为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由． （江西省中考试题)图5(备用图)图4(备用图)图2图1图3B B BC B BB 级1. 如图，在梯形ABCD 中，AB//DC ，AD ＝BC ，AB ＝10，CD ＝4，延长BD 到E ，使DE ＝DB ，作 EF ⊥AB 交BA 的延长线于点F ，则AF ＝__________.（山东省竞赛试题）第2题图第1题图EBF2.如图，在梯形ABCD 中，AD//BC ，AB ＝DC ＝10cm ，AC 与BD 相交于G ，且∠AGD ＝060，设E 为CG 中点，F 是AB 中点，则EF 长为_________.（“希望杯”邀请赛试题）3.用四条线段：7,9,13,14====d c b a 作为四条边，构成一个梯形，则在所构成的梯形中，中位线的长的最大值为_________. （湖北赛区选拔赛试题）4.如图，梯形ABCD 的两条对角线AC ，BD 相交于O 点，且AO ：CO ＝3：2，则两条对角线将梯形分成的四个小三角形面积之比为=∆∆∆∆AOB COB DOC AOD S S S S :::_________. （安徽省中考试题）MABBC第4题图 第5题图 第6题图5.如图，在四边形ABCD 中，AD//BC ，E 是AB 的中点，若△DEC 的面积为S ，则四边形ABCD 的面积为 ( )A ．S 25 B ．2S C ．S 47 D ．S 49（重庆市竞赛试题）6.如图，在梯形ABCD 中，AD//BC ，∠B ＝020，∠C ＝070，E ，M ，F ，N 分别为AB ，BC ，CD ， DA 的中点，已知BC ＝7，MN ＝3，则EF 的值为 ( )A ．4B ．214C ．5D ．6 （全国初中数学联赛试题）7.如图，梯形ABCD 中，AB//DC ，E 是AD 的中点，有以下四个命题：①若AB ＋DC ＝BC ，则∠BEC ＝090；②若∠BEC ＝090，则AB ＋DC ＝BC ；③若BE 是∠ABC 的平分线，则∠BEC ＝090； ④若AB ＋DC ＝BC ，则CE 是∠DCB 的平分线.其中真命题的个数是 ( )A ．1个B ．2个C ．3个D ．4个（重庆市竞赛试题）第8题图第7题图NDAC B8.如图，四边形ABCD 是一梯形，AB//CD ，∠ABC ＝090，AB ＝9cm ，BC ＝8cm ，CD ＝7cm ，M 是AD 的中点，从M 作AD 的垂线交BC 于N ，则BN 的长等于 ( )A ．1cmB ．1.5cmC ．2cmD ．2.5cm（“希望杯”邀请赛试题）9.如图，在梯形ABCD 中，AB//DC ，M 是腰BC 的中点，MN ⊥AD .求证：AD MN S ABCD ⋅=四边形（山东省竞赛试题）AB10.如图，在梯形ABCD 中，AD//BC ，分别以两腰AB ，CD 为边向两边作正方形ABGE 和正方形DCHF ，设线段AD 的垂直平分线l 交线段EF 于点M.求证：点M 为EF 的中点.（全国初中数学联赛试题）GH11.已知一个直角梯形的上底是3，下底是7，且两条对角线的长都是整数，求此直角梯形的面积.（“东方航空杯”上海市竞赛试题）12.如图1，平面直角坐标系中，反比例函数)0,0(>>=x k xky 的图象经过矩形OABD 的边BD 的三等分点（BD DF 31=）交AB 于E ，AB ＝12，四边形OEBF 的面积为16. （1）求k 值.（2）已知)0,13(C ，点P 从A 出发以0.5cm/s 速度沿AB 、BD 向D 运动，点Q 从C 同时出发，以1.5cm/s 的速度沿CO ，OA ，AB 向B 运动，其中一个动点到达端点时，另一个动点也随之停止运动.从运动开始，经过多少时间，四边形PQCB 为等腰梯形（如图2）.（3）在（2）条件下，在梯形PQCB 内是否有一点M ，使过M 且与PB ，CQ 分别交于S ，T 的直线把PQCB 的面积分成相等的两部分，若存在，请写出点M 的坐标及CM 的长度；若不存在，请说明理由.图2图1专题21梯形例1 a ＋b例2⑴上底角为120°，下底角为60°；⑵梯形的上底等于下底的一半，且等于腰长； ⑶能拼出菱形，以下图形供参考：例3 7cm 提示：过A 作AE ∥BD 交CB 延长线于E ，则S △AEC ＝S 梯形ABCD . 例4(1）如图a ，若E 为AD 中点，则∠BEC ＝90°且CE,BE 分别平分∠BCD ，∠ABC ； ⑵如图b ，在BC 上取一点M ，使AB ＝MB ，连结AM,DM ，则∠AMD ＝90°； ⑶如图c ，将a ，b 组合，则四边形GEHM 为矩形.图a 图b 图c ∴当P 为AD 中点时，可以证明∠BPC ＝90°；在AD 上截取AP ＝AB ，可以证明∠BPC ＝90°，故满足条件∠BPC ＝90°的点P 有2个.例5⑴连结SC,PB .∴△OCD,△OAB 均为等边三角形，S ，P ，Q 分别为OD,OA,BC 中点， ∴SQ ＝12BC ＝12AD ＝SP ＝PQ .故△SPQ 为等边三角形.⑵∵SB ＝12DO ＋OB ＝132,CS ＝323,BC ＝7.∴△SPQ 的边长SQ ＝12BC ＝72.∴S △SPQ ＝34×(72)2＝49316.(3）设CD ＝a ，AB ＝b (a <b ),BC 2＝SC 2＋BS 2＝(32a )2＋(b ＋a2)2＝a 2＋b 2＋ab . ∴S △SPQ ＝316(a 2＋ab ＋b 2).又S △AOD S △COD ＝b a ，则S △AOD ＝34ab . 又S △AOD S △COD ＝b a ,则S △AOD ＝34ab .∵S △PQS S △AOD ＝78,∴8×316 (a 2＋ab ＋b 2)＝7×34ab . 即2a 2－5ab ＋2b 2＝0，化简得a b ＝12. 故CD ：AB ＝1:2.例6如图，分别过E,F ,C,P 作AB 的垂线，垂足依次为R ，S ，T ，Q ，则PQ 就是点P 到AB 的距离，且有ER ∥PQ ∥CT ∥FS ，故四边形ERSF 为直角梯形，PQ ＝12(ER ＋FS ).易证Rt △AER ≌Rt △CAT ，Rt △BFS ≌Rt △CBT ，∴ER ＝AT ，FS ＝BT ，又AT ＋BT ＝AB ＝ER ＋FS ， 故PQ ＝12AB .A 级1.60°2.33.6cm4.82cm 25.B6.D7.C8.C 提示:如图，作点D 关于直线BC 的对称点D '，连结DD '交BC 于E ，连结AD '交BC 于P ，过D 作DF ⊥AP 于F ,故P A ＋PD 此时最小.由BE ＝AD ＝2，EC ＝3，则可得：DE ＝4，∴DD '＝8,则AD '＝217. 又∵AD '·DF ＝AD ·DD ',则DF ＝81717.9.提示：过P 点作PQ ⊥BG 于Q ，证明PE ＝BQ .10.提示：连结DF 并延长交于BC 于H ，则GF ＝12BH ，AD ＝CH . 11.略12.⑴ 3⑵①当点N 在线段AD 上运动时，△PMN 形状不发生改变，其周长为3＋7＋4.②当点在线段DC 上运动时，△PMN 的形状发生改变，但MNC 恒为等边三角形，过E 作EG BC 于G 。

3．3 上海市第三届“浦东金桥杯”中学生数学知识应用竞赛(1994)上海市第三届“浦东金桥杯”中学生数学知识应用竞赛初赛于1994年5月举行，决赛于1994年9月举行．【初赛试题】初赛试题共有十五题，其中一～十题，每题满分为10分；十一～十五题，每题满分为16分，总共为180分．一、某露天仓库有水泥电线杆100根，用卡车运往公路旁安装．第一根电线杆距仓库3公里，以后每间距50米安装一根，一辆卡车每次限运三根．试求：(1)若用一辆卡车从仓库出发，直到运完回库，共行了多少公里？(2)若有甲、乙两辆卡车从仓库出发，依次轮流运送直到运完回库，两车各行了多少公里？的圆心为BC的中点O，半径为2m，AB、CD均垂直于BC，且AB＝CD＝1m．现要截一块矩形板，若不计损耗，求材料的最大利用率(精确到0.001)．三、如图3－36所示，表示某区域的交通网络，各条边旁所注的数字表示通过该公路所估计行驶的时间(单位：小时)，试问从S到T估计至少要行驶多少小时？并写出最短路径．四、已知汽车从刹车到停车所滑行的距离与时速平方及汽车的总重量成正比．某辆卡车不装货物，以时速50公里行驶时，从刹车到停车滑行20米。

如果这辆卡车装着等于车重1.5倍重的货物行驶时，发现前面大约20米处有人(假设卡车从发现人到刹车需经过0.8秒钟)，为了行驶安全，车必须在离人5米处停住，试问这时最大限制时速应是多少？(答案只要保留一位小数)五、某仓库如图3－37所示堆放一批零件：第一层4盒，第二层10盒，第三层18盒，第四层28盒，…，能否求出堆了n层零件总盒数的公式？然后算出第38层的盒数与堆了38层零件总盒数．六、某工厂生产A、B两种产品，分别需要原材料每件2千克、3千克；消耗能源每件1百元、6百元；劳动力每件需要4个人工、2个人工；获利每件5千元、6千元。

但库存原材料有1750千克；能源消耗总额不超过2405百元；全厂满员2500人．试问怎样安排生产任务使获得利润最大？并求出最大利润额．七、如图3－38所示，窗架上部分为半圆，下部分是宽为x，长为相应的最大值与最小值．2r，接头长边为b、短边为a(a＜b)．(1)画出弯管接头的展开图；(2)选择适当坐标系，推导出接缝展开曲线的方程．九、如图3－40所示的一块均匀薄片，由于工艺设计要求，试确定薄片的重心位置．十、设甲、乙两地相距2千公里，计划将甲地的电视节目用微波传送到乙地．由于微波是沿直线传播的，因而必须在甲、乙间设立若干个微波接力站，将信号从上一站传送到下一站．假设每个站的天线高度都是100米，且暂不考虑信号强度在空中传播时的衰减因素，问甲、乙两地之间至少需要设立几个微波接力站？十一、有一批136cm长的合金材料，需要截出13cm、18cm、25cm的三种规格，每种规格都要有，试找出所有使材料利用率在97％以上的落料方案．十二、有两块长和宽分别为a、b的矩形(a＜b)，四块上、下底分别为a、b，底角为60°的等腰梯形厚纸板，拼接成一个封闭的几何体模型．(1)画出这个模型的直观图、三视图、展开图；(2)求出这个模型的体积．十三、某宾馆大楼现有三种可行的空调安装方案，每种方案的初期投资K与每年初投入的经营费用C，如下页表所示．若三种方案的使用寿命n均为10年，年利率R为10％(复利)，问哪一种方案最优？(写出具体计算步骤，答案保留一位小数)十四、某公交车队停车场内有15辆车，从上午7时正开始发车，每一辆车出发后，每隔6分钟再开出一辆车。