最新版精编2019高考数学《导数及其应用》专题完整考试题(含参考答案)

2019年高中数学单元测试卷导数及其应用学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．22(1cos )x dx ππ-+⎰等于（ ）A ．πB . 2C . π-2D . π+2(2009福建理)2．函数y=12x 2-㏑x 的单调递减区间为 （ ）A ．(-1,1]B ．(0,1]C ．[1,+∞)D ．(0,+∞) （2012辽宁文）3．设球的半径为时间t 的函数()R t 。

若球的体积以均匀速度c 增长，则球的表面积的增长速度与球半径A.成正比，比例系数为CB. 成正比，比例系数为2CC.成反比，比例系数为CD. 成反比，比例系数为2C 9.4．（2009天津卷理）设函数1()ln (0),3f x x x x =->则()y f x = A 在区间1(,1),(1,)e e 内均有零点。

B 在区间1(,1),(1,)e e 内均无零点。

C 在区间1(,1)e 内有零点，在区间(1,)e 内无零点。

D 在区间1(,1)e内无零点，在区间(1,)e 内有零点。

【考点定位】本小考查导数的应用，基础题。

二、填空题5．若3()3f x ax x =-在R 上是单调函数，则a 的取值范围为______.6．在实数集R 上定义运算：()().(),xx y x a y a f x e ⊗=-=为实常数若(),xg x ex -=+令()()().F x f x g x =⊗若函数))0(,0()(F P x F 在点处的切线斜率为1，则此切线方程为________________.7．已知(0)1,()(1)()f f n nf n n N +==-∈，则(4)f = ▲ . 8．函数2|32|y x x =-+的极大值为 ．9．已知曲线y=ax 2在x=1处切线的斜率是﹣4，则实数a 的值为10．（文科、艺体学生做）曲线2x y =的一条切线的斜率是4-，则切点坐标是 __ ___.（理科学生做）已知直线l ：y=－1及圆C ：x 2+(y －2)2=1，若动圆M 与l 相切且与圆C 外切，则动圆圆心M 的轨迹方程是 .11．(文)设()f x 是定义在(,0)(0,)ππ-⋃上的奇函数，其导函数为'()f x .当0x π<<时，0)(sin cos )(>⋅-⋅'x f x x x f , 则不等式0cos )(>⋅x x f 的解集为 12．若直线2+=kx y 与曲线3y x mx n =++相切于点)4,1(，则n = ▲ ．三、解答题13．已知函数()()2ln ,f x x a x x a R =+-∈ (1)若1,a =-求证()f x 有且仅有一个零点；(2）若对于[]1,2x ∈函数()f x 图像上任意一点处的切线的倾斜角都不大于4π，求实数a 的取值范围；(3）若()f x 存在单调递减区间，求实数a 的取值范围。

2019年高中数学单元测试卷导数及其应用学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．设P 为曲线2:23C y x x =++上的点,且曲线C 在点P 处切线倾斜角的取值范围是[0,]4π,则点P 横坐标的取值范围是( )A.1[1,]2--B.[1,0]-C.[0,1]D.1[,1]2(2008辽宁理)2．若()ln f x x x x 2=-2-4，则'()f x >0的解集为A. (,)0+∞B. -+10⋃2∞（，）（，）C. (,)2+∞D. (,)-103．如下图，已知()32()0,f x ax bx cx d a =+++≠记()243,b ac ∆=-则当00()a f x ∆≤>且时，的大致图象为（ ）.答案 C二、填空题 4．已知x=12是()2ln bf x x x x=-+的一个极值点 (1)求b 的值；(2)求函数()f x 的单调增区间； (3)设1()()g x f x x=-，试问过点（2，5）可作多少条曲线y=g(x )的切线？为什么？ 5．若()22x x f =，则()1f '-等于 ▲ .xyO(2,0)P()y f x =()y f x '=1 （第10题6． 已知函数()y f x =的图象在点(1,(1))f 处的切线方程为32y x =-，则函数2()()g x x f x =+的图象在点(1,(1))g 处的切线方程为 ▲ .7．设函数21()ln .2f x x ax bx =--若x =1是()f x 的极大值点，则实数a 的取值范围是 ．8．设曲线(1)xy ax e =-在点A 01(,)x y 的切线为1l ，曲线1x xy e-=在点B 02(,)x y 的切线为2l ，若存在013[,]22x ∈-，使得12l l ⊥，则实数a 的取值范围是_______9．已知可导函数)(x f )(R x ∈的导函数)(x f '满足)(x f '＞)(x f ，则不等式()(1)x e f x f e >的解集是 ▲ ．10．已知函数()322f x x ax bx a =+++在1x =处有极值10，则a b += ．11．设曲线1*()n y xn N +=∈在点（1，1）处的切线与x 轴的交点的横坐标为n x ,则12n x x x ⋅⋅⋅的值为(A) 1n (B) 11n + (C) 1n n + (D) 1（2009陕西卷文）12．设0()cos f x x =，10()()f x f x '=，21()()f x f x '=，…，1()()n n f x f x +'=，n *∈N ，则函数20082009|4()()1|y f x f x =⋅-的最小正周期为13．已知函数()y f x =及其导函数()y f x '=的图象如图所示，则曲线()y f x =在点P 处的切线方程是 ▲ ．14．已知函数)(ln )(R a ax x x f ∈-=（1）若1=a ，求函数)(x f 的单调区间（2）当0>a 时，求函数)(x f 在]2,1[上的最大值15．曲线12++=x xe y x在点（0,1）处的切线方程为 ．三、解答题16．（本题16分）已知函数2()ln ,af x x a R x=+∈． （1）若函数()f x 在[2,)+∞上是增函数，求实数a 的取值范围； （2）若函数()f x 在[1,]e 上的最小值为3，求实数a 的值．17．若函数()f x 在0x x =处的导数为0，则称点00(,())x f x 为函数()f x 的驻点，若点(1,1)为函数f (x )的驻点，则称f (x )具有“1—1驻点性”.（1）设函数f (x )=ln x a x -+，其中0a <.①求证：函数f (x )不具有“1—1驻点性”；②求函数f (x )的单调区间.（2）已知函数g (x )=bx 3+3x 2+cx +2具有“1—1驻点性”，给定x 1，x 2∈R ，x 1＜x 2，设λ为实数，且λ≠1-，α=x 1+λx 21+λ，β=x 2+λx 11+λ，若|g (α)-g (β)|＞|g (x 1)-g (x 2)|，求λ的取值范围.18．已知a∈R,函数f(x)=2x 3-3(a+1)x 2+6ax(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;(Ⅱ)若|a|>1,求f(x)在闭区间[0,|2a|]上的最小值. （2013年高考浙江卷（文））19．已知函数．（a ∈R ）（1）当a=1时，求f （x ）在区间[1，e]上的最大值和最小值；（2）若在区间（1，+∞）上，函数f （x ）的图象恒在直线y=2ax 下方，求a 的取值范围． 关键字：对数；求最值；求导；恒成立问题；不能参变分离；求参数的取值范围20．已知函数4()1xx e f x e =+（e 为自然对数的底数）设方程()f x x =的一个根为t ，且a >t ，()f ab =。

2019年高中数学单元测试卷导数及其应用学校：__________ 姓名：__________ 班级：__________ 考号：__________一、填空题1．曲线32242y x x x =--+在点(13)-，处的切线方程是 ． 答案 520x y +-=2．若函数f (x )＝ax 4＋bx 2＋c 满足(1) 2f '=，则(1)f '-= ． 3．函数f (x )＝12x －sin x 在区间[0，π]上的最小值为 ．4．已知A 、B 、C 是直线l 上的三点，向量,,OA OB OC u u u r u u u r u u u r满足()[2'(1)]ln OA f x f x OB x OC =+-⋅u u u r u u u r u u u r，则函数()y f x =的表达式为 ▲ ．5．设函数()2ln f x x x =+，若曲线()y f x =在点()()1,1f 处的切线方程为y ax b =+，则a b += ．6．给出下列命题：①函数)(x f y =的图象与函数3)2(+-=x f y 的图象一定不会重合； ②函数)32(log 221++-=x x y 的单调区间为),1(∞+；③ππ---=+⎰edx e x x 1)(cos 0；④双曲线的渐近线方程是x y 43±=，则该双曲线的离心率是45．其中正确命题的序号是 （把你认为正确命题的序号都填上）． 答案 ③7．已知函数f(x)= ()2f π'sinx+cosx ，则()4f π= .8．函数()sin ln f x x x =+的导函数()f x '= ▲ .二、解答题9．已知函数()f x 的导函数()f x '是二次函数，且()0f x '=的两根为1±．若()f x 的极大值与极小值之和为0，(2)2f -=． （1）求函数()f x 的解析式；（2）若函数在开区间(99)m m --, 上存在最大值与最小值，求实数m 的取值范围． （3）设函数()()f x x g x =⋅，正实数a ，b ，c 满足()()()0ag b bg c cg a ==>，证明：a b c ==．10．已知函数21()2,()log 2a f x x x g x x ==－（a ＞0，且a ≠1），其中为常数．如果()()()h x f x g x =+ 是增函数，且()h x '存在零点（()h x '为()h x 的导函数）．(Ⅰ）求a 的值；(Ⅱ）设A （x 1，y 1）、B （x 2，y 2）（x 1<x 2）是函数y ＝g （x ）的图象上两点，21021()y y g x x x -'=-（()g'x 为()g x 的导函数），证明：102x x x <<．11．过点A （2，1）作曲线()f x =l ． (Ⅰ）求切线l 的方程；(Ⅱ）求切线l ，x 轴及曲线所围成的封闭图形的面积S ．12．设函数()32221f x x mx m x m =---+-（其中2m >-）的图象在2x =处的切线与直线512y x =-+平行。

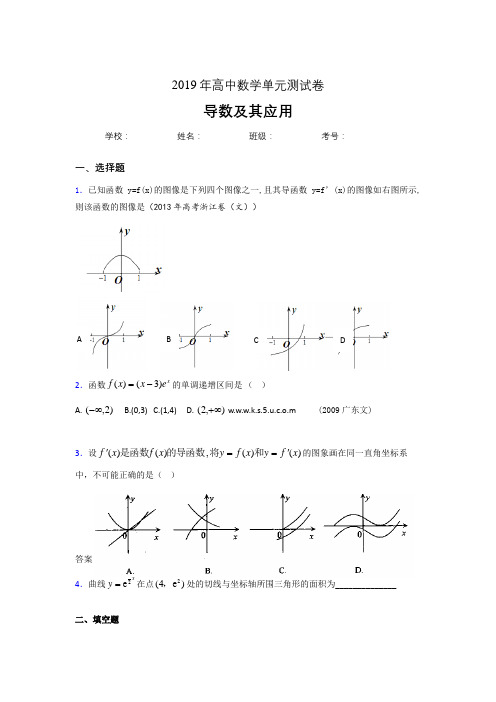
2019年高中数学单元测试卷导数及其应用学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．已知函数y=f(x)的图像是下列四个图像之一,且其导函数y=f’(x)的图像如右图所示,则该函数的图像是（2013年高考浙江卷（文））2．函数x exxf)3()(-=的单调递增区间是（）A. )2,(-∞ B.(0,3) C.(1,4) D. ),2(+∞ w.w.w.k.s.5.u.c.o.m (2009广东文) 3．设)()(,)()(xfyxfyxfxf'=='和将的导函数是函数的图象画在同一直角坐标系中，不可能正确的是（）答案 D4．曲线12e xy=在点2(4e)，处的切线与坐标轴所围三角形的面积为______________ 二、填空题5．函数f（x）=e x（sinx+cosx）的导数为f(x)=2 e x.cosx 。

D6．函数2()l n 1f x a x x=++在[,)e +∞上是减函数，则实数a 的取值范围是 ．7．函数e x y =的图象在点()e k a k a , 处的切线与x 轴的交点的横坐标为1k a +，其中*k ∈N ，10a =，则135a a a ++= ．8．设函数e x y =的图象在点(e )k a k a ,处的切线与x 轴的交点的横坐标为1k a +，其中*k ∈N ，10a =，则135a a a ++= ▲ .9．已知函数432()2f x x ax x b =+++（x R ∈），其中R b a ∈,．若函数()f x 仅在0x =处有极值，则a 的取值范围为10．定积分⎰dx x |sin |230π的值是 .答案 311．在平面直角坐标系xoy 中，点P 在曲线3:103C y x x =-+上，且在第二象限内，已知曲线C 在点P 处的切线的斜率为2，则点P 的坐标为 . 解析 考查导数的几何意义和计算能力。

2019年高中数学单元测试卷导数及其应用学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．曲线311y x =+在点P(1，12)处的切线与y 轴交点的纵坐标是( ) （A ）-9 （B ）-3 （C ）9 （D ）15（2011山东文4） 二、填空题2．函数()ln f x x =的图象在点()e ,(e)f 处的切线方程是3． 若对任意的x D ∈,均有()()()12f x f x f x ≤≤成立，则称函数()f x 为函数()1f x 到函数()2f x 在区间D 上的“折中函数”．已知函数()()()11,0,f x k x g x =--= ()()1ln h x x x =+，且()f x 是()g x 到()h x 在区间[]1,2e 上的“折中函数”，则实数k 的取值范围为 ．4．若对任意的x D ∈,均有()()()12f x f x f x ≤≤成立，则称函数()f x 为函数()1f x 到函数()2f x 在区间D 上的“折中函数”．已知函数()()()11,0,f x k x g x =--= ()()1ln h x x x =+，且()f x 是()g x 到()h x 在区间[]1,2e 上的“折中函数”，则实数k 的取值为 ▲5．，则曲线过点)4,2(P 的切线方程为6．函数xe x a xf 32sin )(+=,若7)0('=f , 则a 的值是 ▲7．在实数集R 上定义运算：()().(),x x y x a y a f x e ⊗=-=为实常数若(),xg x ex -=+令()()().F x f x g x =⊗若函数))0(,0()(F P x F 在点处的切线斜率为1，则此切线方程为________________.8．已知函数()cos(2)(0)f x x θθπ=+<<，若'()()y f x f x =的图象关于6x π=对称，则θ= ．9． 如果函数y ＝f (x )的导函数的图象如图所示，给出下列判断：①函数y ＝f (x )在区间⎝⎛⎭⎫－3，－12内单调递增； ②函数y ＝f (x )在区间⎝⎛⎭⎫－12，3内单调递减； ③函数y ＝f (x )在区间(4,5)内单调递增； ④当x ＝2时，函数y ＝f (x )有极小值； ⑤当x ＝－12时，函数y ＝f (x )有极大值．则上述判断中正确的是__________． 三、解答题10．设函数f (x )＝ax 3＋bx 2＋cx ，在x ＝1和x ＝－1处有极值，且f (1)＝－1，求a 、b 、c 的值，并求出相应的极值． [解析] f ′(x )＝3ax 2＋2bx ＋c .∵x ＝±1是函数的极值点，∴－1、1是方程f ′(x )＝0的根，即有又f (1)＝－1，则有a ＋b ＋c ＝－1，此时函数的表达式为f (x )＝12x 3－32x .∴f ′(x )＝32x 2－32.令f ′(x )＝0，得x ＝±1.当x 变化时，f ′(x )，f (x )变化情况如下表：由上表可以看出，当x ＝－1时，函数有极大值1；当x ＝1时，函数有极小值－111．若函数1)1(2131)(23+-+-=x a ax x x f 在区间（1,4）内为减函数，在区间（6，＋∞）上为增函数。

2019年高中数学单元测试卷导数及其应用学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．函数f （x ）的定义域为R ，f （-1）=2，对任意x ∈R ，2)(>'x f ，则f （x ）＞2x+4的解集为（ ）（A ）（-1，1） （B ）（-1，+∞） （C ）（-∞，-1） （D ）（-∞，+∞）（2011辽宁理11）2．将边长为1m 正三角形薄片，沿一条平行于底边的直线剪成两块，其中一块是梯形，记2(S =梯形的周长）梯形的面积,则S 的最小值是____ ____。

3．已知()f x 与()g x 是定义在R 上的连续函数，如果()f x 与()g x 仅当0x =时的函数值为0，且()()f x g x ≥，那么下列情形不可能．．．出现的是 （ ）A ．0是()f x 的极大值，也是()g x 的极大值B ．0是()f x 的极小值，也是()g x 的极小值C ．0是()f x 的极大值，但不是()g x 的极值D ．0是()f x 的极小值，但不是()g x 的极值 答案 C 二、填空题4．已知32()26(f x x x m m =-+为常数）在[2,2]-上有最大值3，那么此函数在[2,2]-上的最小值为____________5．已知函数f (x )＝e x －ax 在区间(0，1)上有极值，则实数a 的取值范围是 ▲ ．6．已知函数y ＝f (x )在定义域⎝⎛⎭⎫－32，3上可导，其图象如图，记y ＝f (x )的导函数y ＝f ′(x )，则不等式xf ′(x )≤0的解集是______ __．xyO(2,0)P()y f x =()y f x '=1 （第10题7．直线y ＝a 与函数f (x )＝x 3－3x 的图象有相异的三个公共点，则实数a 的取值范围是 ．8．设函数f (x )在其定义域D 上的导函数为f ′(x )．如果存在实数a 和函数h (x )，其中h (x )对任意的x ∈D 都有h (x )＞0，使得f ′(x )＝h (x )(x 2－ax ＋1)，则称函数f (x )具有性质P (a )．给出下列四个函数：①f (x )＝13x 3－x 2＋x ＋1；②f (x )＝ln x ＋4x ＋1；③f (x )＝(x 2－4x ＋5)e x ；④f (x )＝x 2＋x2x ＋1，其中具有性质P (2)的函数是 ．(写出所有满足条件的函数的序号) 9．设函数ln ,0()21,0x x f x x x >⎧=⎨--≤⎩，D 是由x 轴和曲线()y f x =及该曲线在点(1,0)处的切线所围成的封闭区域，则2z x y =-在D 上的最大值为 .10．函数y ＝2xx 2＋1的极大值为______，极小值为______．[答案] 1 －1[解析] y ′＝2(1＋x )(1－x )(x 2＋1)2，令y ′>0得－1<x <1，令y ′<0得x >1或x <－1， ∴当x ＝－1时，取极小值－1，当x ＝1时，取极大值1.11．已知函数()y f x =及其导函数()y f x '=的图象如图所示，则曲线()y f x =在点P 处的切线方程是 ▲ ．12．已知函数)(x f 是定义在R 上的奇函数，0)1(=f ，)()(2>-'x x f x f x ）（0>x ，则不等式0)(2>x f x 的解集是 ．13．如图为函数32()f x ax bx cx d =+++的图象，'()f x 为函数()f x 的导函数，则不等式'()0x f x ⋅<的解集为______ ______．答案 (,-∞⋃14．已知函数f (x )的定义域为[－2，+∞)，部分对应值如下表,)(x f '为f (x )的导函数，函数)(x f y '=的图象如右图所示，若两正数a ，b 满足1)2(<+b a f ，则33++a b 的取值范围是 ． 答案 ⎪⎭⎫⎝⎛37,53 15．已知一辆轿车在公路上作加速直线运动，设ts 时的速度为3)(2+=t t v )/(s m ，则s t 3=时轿车的瞬时加速度为______________________．16． 函数5()sin 2sin cos2cos66f x x x ππ=⋅-⋅在[,]22ππ-上的单调递增区间为 ．三、解答题17．已知函数()ln f x x x a x =--.(1)若a =1，求函数()f x 在区间[1,]e 的最大值; (2)求函数()f x 的单调区间；(3)若()0f x >恒成立，求a 的取值范围．18．已知函数2()21()f x x ax a R =++∈，'()f x 是()f x 的导函数 （1）若[2,1]x ∈--，不等式()'()f x f x ≤恒成立，求a 的取值范围； （2）解关于x 的方程()'()f x f x =；（3）设函数'(),()'()()(),()'()f x f x f xg x f x f x f x ≥⎧=⎨<⎩，求()g x 在[]2,4x ∈时的最小值.19．设L 为曲线C:ln xy x=在点(1,0)处的切线. (I)求L 的方程;(II)证明:除切点(1,0)之外,曲线C 在直线L 的下方. （2013年高考北京卷（理））20．设a ∈R ，函数233)(x ax x f -=，2=x 是函数)(x f y =的极值点． （Ⅰ）求a 的值；（Ⅱ）求函数233)(x ax x f -=在区间[]1,5-上的最值．21．已知函数()ln 3f x a x ax =--(a R ∈). （１）求函数()f x 的单调区间；（２）若函数()y f x =的图象在点(2,(2))f 处的切线的倾斜角为4π，对于任意[]1,2t ∈，函数32()()2m g x x x f x ⎡⎤'=++⎢⎥⎣⎦在区间(t ,3)总不是单调函数,求m 的取值范围．22．已知函数()ln f x x x a x =--.（1）若a =1，求函数()f x 在区间[1,]e 的最大值; （2）求函数()f x 的单调区间；（3）若()0f x >恒成立，求a 的取值范围．（本小题满分16分）23．已知函数()||x f x e bx =-，其中e 为自然对数的底. （1）当1b =时，求曲线()y f x =在x=1处的切线方程； （2）若函数()y f x =有且只有一个零点，求实数b 的取值范围；（3）当0b >时，判断函数()y f x =在区间（0，2）上是否存在极大值，若存在，求出极大值及相应实数b 的取值范围.24．已知a ，b 是实数，函数,)(,)(23bx x x g ax x x f +=+= )(x f '和)(x g '是)(),(x g x f 的导函数，若0)()(≥''x g x f 在区间I 上恒成立，则称)(x f 和)(x g 在区间I上单调性一致（1）设0>a ，若函数)(x f 和)(x g 在区间),1[+∞-上单调性一致,求实数b 的取值范围；（2）设,0<a 且b a ≠，若函数)(x f 和)(x g 在以a ，b 为端点的开区间上单调性一致，求|a -b |的最大值。

2019年高中数学单元测试卷导数及其应用学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．设函数()xf x xe =，则（ ）A. 1x =为()f x 的极大值点B.1x =为()f x 的极小值点C. 1x =-为()f x 的极大值点D. 1x =-为()f x 的极小值点[学2．如图，一个正五角星薄片（其对称轴与水面垂直）匀速地升出水面，记t 时刻五角星露出水面部分的图形面积为()()()00S t S =，则导函数()'y S t =的图像大致为二、填空题3．已知函数210()0x x f x a x ⎧+>⎪=≤ 在点（1,2）处的切线与()f x 的图像有三个公共点，则a 的取值范围是 ；4．已知f (x )＝x 3，g (x )＝－x 2＋x －29a ，若存在x 0∈[－1，a3](a ＞0)，使得f (x 0)＜g (x 0)，则实数a 的取值范围是 ▲ ．(0，－3＋212)5．曲线32242y x x x =--+在点(13)-，处的切线方程是 ． 答案 520x y +-=6．（文）已知函数13)(23++-=ax ax x x f 在区间),(+∞-∞内既有极大值，又有极小值，则实数a 的取值范围是7．函数2(0)y x x =>的图像在点2(,)k k a a 处的切线与x 轴交点的横坐标为1k a + ,k 为正整数，116a =，则135a a a ++= .8．函数x x x f sin )(3+=的导函数是 ☆ ；9．已知可导函数)(x f )(R x ∈的导函数)(x f '满足)(x f '＞)(x f ，则不等式()(1)x e f x f e >的解集是 ▲ ．10．过点(1 0)P -，作曲线C ：e x y =的切线，切点为1T ，设1T 在x 轴上的投影是点1H ，过点1H 再作曲线C 的切线，切点为2T ，设2T 在x 轴上的投影是点2H ，…，依次下去，得到第1n +()n ∈N 个切点1n T +．则点1n T +的坐标为 ▲ ．11．计算：︒-︒+︒80cos 110sin 310cos ＝ .12．已知32()33f x x bx cx =++有两个极值点12,x x ，且[][]121,0,1,2x x ∈-∈，则(1)f 的取值范围 ．13．已知函数32()f x x ax bx c =+++（其中,,a b c 为常数），若()y f x =在1x =-和13x =-时分别取得极大值和极小值，则a = ▲ ．14．已知函数32()(6)1f x x ax a x =++++有三个单调区间，则实数a 的取值范围是______________15．曲线42x y =上一点到直线1--=x y 的距离的最小值为 .答案 162516．已知函数qx px x x f --=23)(的图象与x 轴切于点)0,1(，则)(x f 的极大值和极小值分别为 和 。

2019年高中数学单元测试卷导数及其应用学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．函数31y ax =+的图象与直线y x =相切，则a =（ ）A ．18B ．14C ．12D ．1(2005浙江文)2．曲线y ＝x 3－3x 2＋1在点(1，－1)处的切线方程为（ ） （A ）y ＝3x －4 （B ）y ＝－3x ＋2（C ）y ＝－4x ＋3 （D ）y ＝4x －5（2004全国2文）（3） 3．函数1222131)(23++-+=a ax ax ax x f 的图象经过四个象限，则实数a 的取值范围是 A ．16356<<-a B ．16358-<<-a C ．16158-<<-a D ．16356-<<-a答案 D 二、填空题4．已知函数32()39f x x x x m =-+++在区间[22]-，上的最大值是20，则实数m 的值等于 ．5．曲线xy e =（其中 2.71828e =）在1x =处的切线方程为 。

6．设()2sin f x x x =-,若0()0f x '=且0(0,)x π∈,则0x =____▲____.7． 函数y ＝x 2(x >0)的图象在点(a k ，a k 2)处的切线与x 轴的交点的横坐标为a k ＋1，其中k ∈N *.若a 1＝16，则a 1＋a 3＋a 5的值是________．8．已知函数f (x )=3231x ax ax -++在区间(,)-∞+∞内既有极大值,又有极小值,则实数a 的取值范围是___________9． 若直线y x b =-+为函数1y x =的一条切线，则实数b = ▲ ．10．已知f (x )是定义在(0，＋∞)上的单调函数，且对任意的x ∈(0，＋∞)，都有f [f (x )－x 3]＝2，则过点(1，2)且与曲线y ＝f (x )相切的直线方程是________．11．省环保研究所对市中心每天环境放射性污染情况进行调查研究后，发现一天中环境综合放射性污染指数f (x )与时刻x （时）的关系为f (x )＝|x x 2＋1－a |＋2a ＋23，x ∈[0，24]，其中a 是与气象有关的参数，且a ∈[0，12]，若用每天f (x )的最大值为当天的综合放射性污染指数，并记作M (a )．（1）令t ＝xx 2＋1，x ∈[0，24]，求t 的取值范围；（2）省政府规定，每天的综合放射性污染指数不得超过2，试问目前市中心的综合放射性污染指数是否超标？12．已知函数()x x mx x f 2ln 2-+=在定义域内是增函数，则实数m 的取值范围为_________．13．设曲线1*()n y xn N +=∈在点（1，1）处的切线与x 轴的交点的横坐标为n x ,令lg n n a x =，则1299a a a +++的值为 . (2009陕西卷理)三、解答题14．已知函数()1ax x ϕ=+，a 为正常数. （1）若()ln ()f x x x ϕ=+，且92a =，求函数()f x 的单调增区间；（2）若()|l n |g x x x ϕ=+，且对任意12,(0,2]x x ∈，12x x ≠，都有2121()()1g x g x x x -<--，求a 的的取值范围.15．已知函数32()22f x x bx cx =++-的图象在与x 轴交点处的切线方程是510y x =-。

2019年高中数学单元测试卷导数及其应用学校：__________ 姓名：__________ 班级：__________ 考号：__________一、选择题1．设函数()f x 在R 上可导,其导函数()f x ',且函数()f x 在2x =-处取得极小值,则函数()y xf x '=的图象可能是（2012重庆文）二、填空题2．函数()ln (1),(0)f x x a x a =-->的单调增区间是 ．3．如果曲线y ＝x 4－x 在点P 处的切线垂直于直线y ＝－13x ，那么点P 的坐标为_________4．设0a >.若曲线y =,0x a y ==所围成封闭图形的面积为2a ，则a =______.5．函数y=x 3+lnx 在x=1处的导数为 .6．已知函数()c x x x x f +--=22123，若对任意[]2,1-∈x 都有()2c x f <，则c 的取值范围是 ．[来7．若曲线 y=lnx+1的一条切线方程为 y=x+b,则b= .8．在平面直角坐标系xOy 中，点P 是第一象限内曲线31y x =-+上的一个动点，点P 处的切线与两个坐标轴交于,A B 两点,则AOB △的面积的最小值为 ▲ .9．已知函数⎩⎨⎧<≥-=0,0,)(2x x x x x f ，则=-))3((f f _____________________．10．函数cos sin y x x x =-在3,22ππ⎡⎤⎢⎥⎣⎦的最小值为 .11．已知函数()x x mx x f 2ln 2-+=在定义域内是增函数，则实数m 的取值范围为_________．12．如图，质点P 在半径为10cm 的圆上逆时针作匀速圆周运动，角速度为1/rad s ，设(10,0)A 为起始点，则时刻2t =时，点P 在x 轴上的射影点M13．设()sin (,)44f x x x x ππ⎡⎤=+∈-⎢⎥⎣⎦， ()f x 的最大值为 。