第三章 微专题6 晶体结构的分析与计算
- 格式:docx
- 大小:691.28 KB
- 文档页数:5

晶体结构分析与计算湖南省浏阳市第一中学潘丹张水强410300在2005年高考考纲中,在思维能力中增加了“对原子、分子、化学键等微观结构有一定的三维想象能力”的要求。
三维想象能力可能通过“晶体结构”试题来体现,而“晶体结构”这一知识点前几年是高考的热点之一(如92年的金刚石、96年的SiO2 、97年的C60、98年的GBO、99年的NiO等等)。
间隔了几年,笔者认为有必要引起广大考生足够的重视。
本文从最常见的几种晶体结构题型入手,分析晶体结构有关的问题,帮助同学们更好地掌握晶体结构的内容,培养空间想象能力和形象思维能力。
一、常见的几种晶体结构分析(一)、氯化钠晶体1、NaCl晶体是一种简单立方结构——Na+和Cl-交替占据立方体的顶点而向空间延伸。
2、在每个Na+周围最近且等距离(设边长为a)的Cl-有6个,在每个Cl-周围最近且等距离的Na+有6个。
3、在每个Na+周围最近且等距离(平面对角线为2a)的Na+有12个,在每个Cl-周围且最近等距离(平面对角线为2a)的Cl-有12个。
(二)、氯化铯晶体1、CsCl晶体是一种立方体心结构——每8个Cs+、8个Cl-各自构成立方体。
在每个立方体的中心有一个异种离子(Cl-或Cs+)。
2、在每个Cs+周围最近且等距离的Cl-(设为3a/2)有8个。
在每个Cl-周围最近且等距离的Cs+有8个。
3、在每个Cs+周围最近且等距离(必为a)的Cs+有6个,在每个Cl-周围最近且等距离的Cl-有6个。
(三)、金刚石晶体1、金刚石晶体是一种空间网状结构——每个C原子与另4个C原子以共价键结合,前者位于正四面体中心,后者位于正四面体顶点。
2、晶体中所有C—C键键长相等(1.55×10-10m),键角相等(均为109028'),晶体中最小碳环由6个C组成且六者不在同一平面内。
3、晶体中每个C原子参与了4条C—C键的形成,而在每条键中的贡献只有一半,故C原子个数与C—C键数之比为1:4×21=1:2。
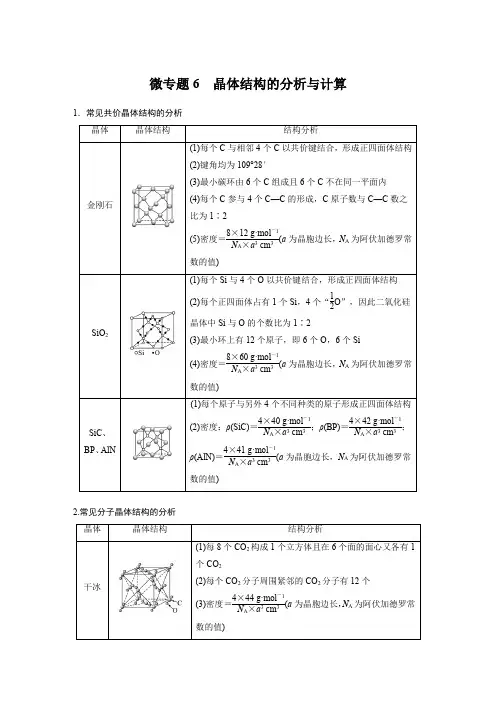
微专题6晶体结构的分析与计算1.常见共价晶体结构的分析晶体晶体结构结构分析金刚石(1)每个C与相邻4个C以共价键结合,形成正四面体结构(2)键角均为109°28′(3)最小碳环由6个C组成且6个C不在同一平面内(4)每个C参与4个C—C的形成,C原子数与C—C数之比为1∶2(5)密度=8×12 g·mol-1N A×a3 cm3(a为晶胞边长,N A为阿伏加德罗常数的值)SiO2(1)每个Si与4个O以共价键结合,形成正四面体结构(2)每个正四面体占有1个Si,4个“12O”,因此二氧化硅晶体中Si与O的个数比为1∶2(3)最小环上有12个原子,即6个O,6个Si(4)密度=8×60 g·mol-1N A×a3 cm3(a为晶胞边长,N A为阿伏加德罗常数的值)SiC、BP、AlN (1)每个原子与另外4个不同种类的原子形成正四面体结构(2)密度:ρ(SiC)=4×40 g·mol-1N A×a3 cm3;ρ(BP)=4×42 g·mol-1N A×a3 cm3;ρ(AlN)=4×41 g·mol-1N A×a3 cm3(a为晶胞边长,N A为阿伏加德罗常数的值)2.常见分子晶体结构的分析晶体晶体结构结构分析干冰(1)每8个CO2构成1个立方体且在6个面的面心又各有1个CO2(2)每个CO2分子周围紧邻的CO2分子有12个(3)密度=4×44 g·mol-1N A×a3 cm3(a为晶胞边长,N A为阿伏加德罗常数的值)白磷密度=4×124 g·mol-1N A×a 3 cm 3(a为晶胞边长,N A为阿伏加德罗常数的值)3.常见离子晶体结构的分析NaCl型CsCl型ZnS型CaF2型晶胞配位数684F-:8;Ca2+:4密度的计算(a为晶胞边长,N A为阿伏加德罗常数的值)4×58.5 g·mol-1N A×a3 cm3168.5 g·mol-1N A×a3 cm34×97 g·mol-1N A×a3 cm34×78 g·mol-1N A×a3 cm31.AB型化合物形成的晶体结构多种多样。


浅谈有关晶体结构的分析和计算 摘要:晶体结构的分析和计算是历年全国高考化学试卷中三个选做题之一,本文从晶体结构的粒子数和化学式的确定,晶体中化学键数的确定和晶体的空间结构的计算等方面,探讨有关晶体结构的分析和计算的必要性。
关键词:晶体、结构、计算、晶胞在全国统一高考化学试卷中,有三个题目是现行中学化学教材中选学内容,它们分别《化学与生活》、《有机化学基础》和《物质结构与性质》。
虽然三个题目在高考时只需选做一题,由于是选学内容,学生对选学内容往往重视不够,所以在高考时学生对这部分题目得分不够理想。
笔者对有关晶体结构的分析和计算进行简单的归纳总结,或许对学生学习有关晶体结构分析和计算有所帮助,若有不妥这处,敬请同仁批评指正。
一、有关晶体结构的粒子数和化学式确定(一)、常见晶体结构的类型1、原子晶体(1)金刚石晶体中微粒分布:①、每个碳原子与4个碳原子以共价键结合,形成正四面体结构。
②、键角均为109°28′。
③、最小碳环由6个碳组成并且六个碳原子不在同一平面内。
④、每个碳原子参与4条C-C 键的形成,碳原子与C-C 键之比为1:2。
(2)二氧化硅晶体中微粒分布①、每个硅原子与4个氧原子以共价键结合,形成正四面体结构。
②、每个正四面体占有1个Si ,4个“21氧”,n(Si):n(O)=1:2。
③、最小环上有12个原子,即:6个氧原子和6个硅原子.2、分子晶体:干冰(CO 2)晶体中微粒分布①、8个CO 2分子构成立方体并且在6个面心又各占据1个CO 2分子。
②、每个CO 2分子周围等距离紧邻的CO 2分子有12个。
3、离子晶体(1)、NaCl 型晶体中微粒分布①、每个Na +(Cl -)周围等距离且紧邻的Cl -(Na +)有6个。
每个Na +周围等距离紧邻的Na +有12个。
②、每个晶胞中含4个Na +和4个Cl -。
(2)、CsCl 型晶体中微粒分布①、每个Cs +周围等距离且紧邻的Cl -有8个,每个Cs +(Cl -)周围等距离且紧邻的Cs +(Cl -)有6个。

浅谈有关晶体结构的分析和计算浅谈有关晶体结构的分析和计算摘要:晶体结构的分析和计算是历年全国高考化学试卷中三个选做题之一,本文从晶体结构的粒子数和化学式的确定,晶体中化学键数的确定和晶体的空间结构的计算等方面,探讨有关晶体结构的分析和计算的必要性。
关键词:晶体、结构、计算、晶胞在全国统一高考化学试卷中,有三个题目是现行中学化学教材中选学内容,它们分别《化学与生活》、《有机化学基础》和《物质结构与性质》。
虽然三个题目在高考时只需选做一题,由于是选学内容,学生对选学内容往往重视不够,所以在高考时学生对这部分题目得分不够理想。
笔者对有关晶体结构的分析和计算进行简单的归纳总结,或许对学生学习有关晶体结构分析和计算有所帮助,若有不妥这处,敬请同仁批评指正。
一、有关晶体结构的粒子数和化学式确定(一)、常见晶体结构的类型1、原子晶体(1)金刚石晶体中微粒分布:①、每个碳原子与4个碳原子以共价键结合,形成正四面体结构。
②、键角均为109°28′。
③、最小碳环由6个碳组成并且六个碳原子不在同一平面内。
④、每个碳原子参与4条C-C键的形成,碳原子与C-C键之比为1:2。
(2)二氧化硅晶体中微粒分布①、每个硅原子与4个氧原子以共价键结合,形成正四面体结构。
②、每个正四面体占有1个Si ,4个“21氧”,n(Si):n(O)=1:2。
③、最小环上有12个原子,即:6个氧原子和6个硅原子.2、分子晶体:干冰(CO 2)晶体中微粒分布①、8个CO 2分子构成立方体并且在6个面心又各占据1个CO 2分子。
②、每个CO 2分子周围等距离紧邻的CO 2分子有12个。
3、离子晶体(1)、NaCl 型晶体中微粒分布①、每个Na +(Cl -)周围等距离且紧邻的Cl -(Na +)有6个。
每个Na +周围等距离紧邻的Na +有12个。
②、每个晶胞中含4个Na +和 4个Cl -。
(2)、CsCl 型晶体中微粒分布①、每个Cs +周围等距离且紧邻的Cl -有 8个,每个Cs +(Cl -)周围等距离且紧邻的Cs +(Cl -)有6个。



【考点概括】1.晶胞化学式的计算晶体中微粒的摆列拥有周期性,晶体中最小的构造重复单元称为晶胞,利用“均派法” 能够计算一个晶胞中的粒子数,进而确立晶体的化学式。
“均派法”的基本思想是晶胞中随意地点上的一个粒子被 n 个晶胞共用,那么每个晶胞对这个原子分得份额就是里波及的晶胞有立方晶胞、六方晶胞、三棱晶胞,以立方晶胞最为常有。
常有考题( 1)立方晶胞:每个极点上的粒子被8 个晶胞共用,每个粒子只有属于该晶胞;每条棱上的粒子被 4 个晶胞共用,每个粒子只有属于该晶胞;每个面心上的粒子被 2 个晶胞共用,每个粒子只有属于该晶胞;晶胞内的粒子完整属于该晶胞。
( 2)六方晶胞:每个极点上的粒子被 6 个晶胞共用;每条横棱上的粒子被 4 个晶胞共用;每条纵棱上的粒子被 3 个晶胞共用;每个面心上的粒子被 2 个晶胞共用;晶胞内的粒子完整属于该晶胞。
( 3)三棱晶胞:每个极点上的粒子被12 个晶胞共用;每条横棱上的粒子被 4 个晶胞共用;每条纵棱上的粒子被 6 个晶胞共用;每个面心上的粒子被 2 个晶胞共用;晶胞内的粒子完整属于该晶胞。
2.晶体密度及微粒间距离的计算(1) 晶体微粒与M、ρ之间的关系:若 1 个晶胞中含有 x 个微粒,则 1mol晶胞中含有 xmol33为晶胞的体积,微粒,其质量为 xM g(M 为微粒的相对“分子”质量 );1 个晶胞的质量为ρag(a33ρ为晶胞的密度 ),则 1mol 晶胞的质量为ρa N A g,所以有xM =ρa N A。
( 2)金属晶体中体心立方聚积、面心立方聚积中的几组公式(设棱长为 a):面对角线长=2 a;体对角线长=3a;体心立方聚积4r= 3a(r 为原子半径 );面心立方聚积4r= 2a(r为原子半径 )。
( 3)空间利用率的计算:空间利用率=晶胞据有的微粒体积晶胞体积。
【过关练习】1.下列图是甲、乙、丙三种晶体的晶胞,则甲晶体中x 与 y 的个数比是 ______,乙中 a 与 b 的个数比是 ______,丙中一个晶胞中有________个 c 离子和 ________个 d 离子。

晶体结构相关计算晶体结构是指晶体中原子、离子或分子排列的方式和有序性。
理解并计算晶体结构对于研究材料的性质和应用至关重要。
在本文中,我们将讨论晶体结构相关的计算方法和技术,包括晶体结构描述、晶胞参数的测定、晶体中原子位置的确定以及晶体结构的表征等。
晶体结构描述是对晶体中原子、离子或分子排列方式的表达和描述。
最常用的方法是借助晶胞和晶胞参数来描述晶体的周期性结构。
晶胞是晶体中具有完整结构的最小重复单元,晶胞参数包括晶体的晶胞底面积、晶胞的夹角以及晶胞的长度。
根据晶体的对称性和周期性,可以确定晶体的晶胞参数。
晶胞参数的测定可以通过多种方法实现。
最常用的方法是X射线衍射技术,该技术通过探测晶格中的衍射峰位置和强度,可以确定晶胞参数。
其他常用的方法包括中子衍射、电子衍射以及粉末衍射等。
这些技术具有高分辨率和非破坏性的特点,可以广泛应用于晶体结构的测定。
确定晶体中原子位置是理解晶体结构的关键步骤之一、常用的方法包括X射线衍射法和电子显微镜技术。
X射线衍射法中常使用的方法是最小二乘法,通过对比实验观测到的衍射图案和理论计算的衍射图案,可以确定原子的位置和晶体结构。
除此之外,还常使用的方法有中子衍射、红外光谱等。
晶体结构的表征是对晶体结构及其特征进行总结和描述。
常用的表征方法包括晶体结构的空间群、点群和晶体系统的表示。
空间群是指描述晶体中原子、离子或分子排列的对称性元素,其中包括旋转、镜面反射、滑移等操作。
点群描述晶体中原子、离子或分子排列方式的旋转对称性。
晶体系统是指晶胞参数中所包含的对称操作的种类和数量。
综合以上的内容,我们可以实现晶体结构的相关计算。
首先,通过X 射线衍射或其他方法测定晶体的晶胞参数。
然后利用最小二乘法等方法确定晶体中原子的位置。
最后通过对称性分析,确定晶体的空间群、点群和晶体系统。
这些计算方法和技术在材料科学和凝聚态物理的研究中得到了广泛应用。

晶体结构相关计算晶体结构是晶体学研究的核心内容之一、晶体结构计算指的是通过实验数据和理论推演来确定晶体的原子排列和晶胞参数的过程。
晶体结构计算的目的是为了揭示晶体的物理和化学性质,为材料设计和性能优化提供理论依据。
晶体结构计算的方法主要分为实验方法和理论方法两大类。
实验方法主要包括X射线衍射、中子衍射和电子衍射等,通过测量晶体衍射图样的强度和角度,可以确定晶体的空间对称群和晶胞参数。
而理论方法则是基于量子力学原理,通过计算和模拟来预测晶体的结构。
实验方法中,X射线衍射是最常用的手段。
X射线衍射仪可以通过测量样品对入射X射线的衍射角度和强度来获得晶体结构信息。
X射线衍射法的基本原理是根据布拉格定律,通过入射射线与晶面的散射计算出晶面的间距和晶胞参数。
而中子衍射则是利用中子和晶体原子之间的散射实现晶体结构的测定。
相比于X射线,中子衍射具有更好的穿透性,可以探测出晶体中更重的原子和氢原子。
电子衍射则主要用于研究纳米晶体的结构,通过电子束的散射来确定晶体的晶胞参数和原子排列。
理论方法中,最常见的是密度泛函理论(DFT)。
DFT是一种基于量子力学的计算方法,通过求解电子的运动方程来计算晶体的结构、能带、电子密度等性质。
DFT计算是一种数值计算方法,可以处理包括周期性、缺陷等多种晶体性质,非常适合用来研究晶体的结构和性质。
DFT计算的精度和计算效率都取决于所采用的泛函和基组。
近年来,随着超级计算机的发展和计算技术的进步,DFT计算已经成为了研究晶体结构的重要手段。
在晶体结构计算中,还需考虑一些可能的误差和限制。
例如,衍射实验中,晶体的位相问题会导致相位不确定性,即无法直接观测到晶体的原子位置。
此外,晶胞参数的确定也有一定的误差范围,需要通过多个衍射实验或理论计算来进一步确定。
在理论计算中,计算效率和计算误差是一个权衡的问题。
选择合适的泛函和基组可以提高计算的准确性,但会带来更高的计算成本。
晶体结构计算在材料科学和凝聚态物理研究中具有重要意义。
晶体结构解读与晶体计算一、晶体常识1、晶体与非晶体的比较2、晶体获得的途径①熔融态物质凝固②气态物质冷却不经过液态直接凝固(凝华)③溶质从溶液中析出3、晶胞:晶胞是描述晶体结构的基本单元,数量巨大的晶胞无隙并置就构成晶体。
4、晶胞中粒子数目的计算方法:均摊法①原则:晶胞任意位置上的一个原子如果被n 个晶胞所共有,那么,每个晶胞对这个原子分得的份额就是1n。
②对于长方体或立方体,位于顶点的粒子为8个晶胞所共有,位于棱上的粒子位为4个晶胞所共有,位于面上的粒子为2个晶胞所共有,位于内部的粒子不为其他晶胞所共有。
③对于六棱柱晶胞,位于顶点的粒子为6个晶胞所共有,位于底面棱上的粒子位为4个晶胞所共有,位于侧面棱面上的粒子为3个晶胞所共有,位于面心的粒子为2个晶胞所共有,位于内部的粒子不为其他晶胞所共有。
④对于其他晶胞中的粒子视具体情况而定。
比如,石墨,每一个C 原子为三个六边形所共有。
⑤根据晶胞粒子数的计算,结合晶胞体积的计算,可以计算晶体的密度。
5、注意:具有规则几何外形的固体不一定是晶体,比如玻璃;晶胞不是从晶体中截取出来具有代表性的最小部分,而不一定是最小的平行四边形。
二、各类典型晶体的晶体模型解读1、金刚石:(1)每一个C 原子与相邻4个C 原子以共价键结合,形成正四面体构型。
(2)键角为109°28'(3)最小环由6个C 原子组成,并且不在同一个平面上。
(4)C 原子和C —C 键的比值为1:2(5)金刚石属于面心立方晶胞,即C 原子处在立方体的8个顶点、6个面心,4个体心,每个晶胞含8个C 原子。
2、二氧化硅(1)每一个Si 原子与4个O 原子以共价键相连,形成正四面体,每一个O 原子与2个Si 原子以共价键相连;(2)O —Si —O 键角为109°28'。
(3)最小环含12个原子,其中6个Si ,6个O ;(4)Si 与Si —O 键的比值为1:4;(5)晶胞属于面心立方,含8个Si,16个O;3、干冰:(1)晶胞属于面心立方,含4个CO2;(2)每个CO2分子与等距离紧邻的CO2有12个。
晶体结构的计算方法晶体结构的计算方法是通过计算机模拟和各种实验技术来确定晶体的原子排列方式和结构特征。
通过计算方法可以预测晶体的力学性质、电学性质、光学性质和热学性质等。
这些预测以及对晶体结构的理解有助于设计新材料、优化材料性能和解释实验结果。
下面将介绍常见的晶体结构计算方法。
1. 密度泛函理论(Density Functional Theory,DFT)密度泛函理论是现代材料计算中最常用的方法之一、该理论基于电子结构的泛函理论,通过求解系统的电子密度函数来计算晶体的能量、结构和性质。
DFT的基本思想是将体系的总能量表示为电子的密度的函数。
通过求解Kohn-Sham方程,可以得到体系中的电荷密度分布和电子能级结构。
DFT方法可以模拟大多数晶体和材料的结构和性质,并且具有较高的计算效率。
2. 分子动力学模拟(Molecular Dynamics,MD)分子动力学模拟是一种基于牛顿运动定律的方法,它模拟原子或分子在经典力场作用下的运动轨迹,从而获得晶体的结构和动力学性质。
通过冷却、加热、压缩、拉伸等操作,可以模拟实验中无法实现的条件,并研究晶体的变形、相变、热膨胀和热导等特性。
MD方法可以提供分子尺度上晶体的变形和热运动信息,并揭示材料的物理机制。
3. 第一性原理计算方法(First-Principles Calculation)4. 蒙特卡罗模拟(Monte Carlo Simulation)蒙特卡罗模拟是一种统计模拟方法,通过随机抽样和概率统计的方法模拟系统的行为。
在晶体结构计算中,蒙特卡罗模拟可以模拟晶体的随机行为、相变和热力学等过程。
通过引入不同的物理模型和相互作用势能,可以模拟不同条件下的晶体结构和性质。
蒙特卡罗模拟方法可以有效地研究相变、精细结构和相互作用动力学等问题。
除了这些方法,还有许多其他的计算方法被应用于晶体结构计算,例如微扰理论、格林函数方法、电子迁移路径分析等。
不同的计算方法具有不同的适用范围和计算复杂度,根据具体问题的需求选择不同的方法进行晶体结构的计算和模拟。
新教材适用高中化学学案新人教版选择性必修2:微专题5 常见晶体结构的比较与分析晶体结构的计算一、常见晶体结构的比较与分析1.常见共价晶体结构的分析晶体晶胞结构结构分析金刚石(1)每个C与相邻_4__个C以共价键结合,形成正四面体结构。
每个晶胞中含_8__个C原子(2)键角均为_109°_28′__(3)最小碳环由_6__个C组成且6个C不在同一平面内,每个C原子被12个六元环共用(4)每个C参与_4__个C—C的形成,C原子数与C—C数之比为_12__(5)ρ=8×12N A·a3g·cm-3键长=34a(a为晶胞边长,N A 为阿伏加德罗常数的值)SiO2(1)每个Si与_4__个O以共价键结合,形成正四面体结构(2)每个正四面体占有1个Si,4个“12O”,因此二氧化硅晶体中Si与O的个数比为_12__(3)最小环上有_12__个原子,即_6__个O,_6__个Si(4)ρ=8×60N A·a3g·cm-3(a为晶胞边长,N A为阿伏加德罗常数的值)SiC、BP、AlN (1)每个原子与另外_4__个不同种类的原子形成_正四面体__结构(2)密度:ρ(SiC)=4×40N A·a3g·cm-3;ρ(BP)=4×42N A·a3g·cm-3;ρ(AlN)=4×41N A·a3g·cm-3(a为晶胞边长,N A为阿伏加德罗常数的值)2.常见分子晶体结构的分析晶体晶胞结构结构分析干冰(1)_8__个CO2分子占据立方体顶角且在_6__个面的面心又各有1个CO2分子(2)每个CO2分子周围紧邻的CO2分子有_12__个(3)ρ=4×44N A·a3g·cm-3(a为晶胞边长,N A为阿伏加德罗常数的值)白磷ρ=4×124N A·a3g·cm-3(a为晶胞边长,N A为阿伏加德罗常数的值)3.常见离子晶体结构的分析晶体晶胞结构结构分析(a为晶胞边长)NaCl (1)在晶体中,每个Na+同时吸引_6__个Cl-,每个Cl-同时吸引_6__个Na+,配位数为6。
晶体结构的分析与计算
晶体结构是研究物质结构的重要工具,且晶体结构的理解和计算是研究晶体物理性质的重要环节。
一般情况下,研究晶体结构可以采用实验测量,或者从理论角度进行计算和分析。
本文将主要介绍晶体结构的理论计算和分析方法。
晶体结构计算主要是通过对原子数据或经典力场模型的理论模拟进行计算,给出单位晶体的几何结构,从而得出晶体结构的基本描述。
其中,原子数据计算是指以原子原子半径和原子间相对位置及其他参数为基本参数,使用编程计算机模拟晶体结构的方法。
其中,一般而言,原子间之间的位置及其数量以初始结构尔定义,根据这些原子的位置和量,求出晶体的空间坐标和原子的位错等参数,从而构建晶体的格子,以确定晶体的空间结构。
而经典力场模型计算虽然也可以得出晶体结构,但与原子数据计算相比,其精度和准确性就会受到极大程度的影响。
因此,经典力场模型计算的主要应用,主要是用于拟合实验数据,以获取晶体结构参数,改善晶体结构的准确性。
晶体结构分析主要是通过晶体拓扑结构、晶体相位结构、晶体近似和位错结构等方法进行的。
微专题6晶体结构的分析与计算
1.常见共价晶体结构的分析
晶体晶体结构结构分析
金刚石(1)每个C与相邻4个C以共价键结合,形成正四面体结构
(2)键角均为109°28′
(3)最小碳环由6个C组成且6个C不在同一平面内
(4)每个C参与4个C—C的形成,C原子数与C—C数之比为1∶2
(5)密度=
8×12 g·mol-1
N A×a3 cm3
(a为晶胞边长,N A为阿伏加德罗常数的值)
SiO2(1)每个Si与4个O以共价键结合,形成正四面体结构
(2)每个正四面体占有1个Si,4个“
1
2O”,因此二氧化硅晶体中Si与O的个数比为1∶2
(3)最小环上有12个原子,即6个O,6个Si
(4)密度=
8×60 g·mol-1
N A×a3 cm3
(a为晶胞边长,N A为阿伏加德罗常数的值)
SiC、BP、AlN (1)每个原子与另外4个不同种类的原子形成正四面体结构
(2)密度:ρ(SiC)=
4×40 g·mol-1
N A×a3 cm3
;ρ(BP)=
4×42 g·mol-1
N A×a3 cm3
;ρ(AlN)=
4×41 g·mol-1
N A×a3 cm3
(a为晶胞边长,N A为阿伏加德罗常数的值)
2.常见分子晶体结构的分析
晶体晶体结构结构分析
干冰(1)每8个CO2构成1个立方体且在6个面的面心又各有1个CO2
(2)每个CO2分子周围紧邻的CO2分子有12个
(3)密度=
4×44 g·mol-1
N A×a3 cm3
(a为晶胞边长,N A为阿伏加德罗常数的值)。