指数函数的概念

指数与指数函数知识点数学中的指数与指数函数是非常重要且常见的概念。

在我们的日常生活中，指数和指数函数可以用来描述各种自然现象、科学问题以及经济趋势等。

本文将详细介绍指数与指数函数的定义、性质以及一些常见应用，以加深读者对这一概念的理解。

一、指数的定义和性质在数学中，指数是一种表示幂次方的数学运算。

指数是由两个数构成，其中一个为底数，另一个为指数。

底数表示要进行幂运算的数字，指数表示底数要乘以自身多少次。

例如，2的3次方即为2的指数为3的结果，即2x2x2=8。

指数函数是指数的一种特殊形式，即以常数为底数的幂函数。

指数函数的一般形式为y=a^x，其中a是底数，x是指数，y是指数函数的值。

指数函数的图像通常具有特定的特征，例如，当底数大于1时，指数函数呈现递增趋势；当底数在0和1之间时，指数函数呈现递减趋势。

指数有一些基本的性质。

首先，任何数的0次方都等于1，即a^0=1。

其次，任何非零数的负指数都是倒数，即a^(-n)=1/(a^n)。

此外，指数相乘等于底数不变指数相加，即a^m * a^n = a^(m+n)。

二、指数函数的应用指数函数在各个领域都有广泛的应用。

以下是指数函数在生活和科学中的一些常见应用：1. 经济增长：经济学家常常使用指数函数来描述一个国家或地区的经济增长趋势。

经济增长往往呈现指数增长的形式，即以固定的增长率逐渐增加。

指数函数可以帮助经济学家预测未来的经济趋势和制定相应的政策。

2. 生物衰变：在生物学的研究中，指数函数可以用来描述物种的衰变过程。

例如，放射性物质的衰变速度可以用指数函数进行建模。

指数函数的形式可以提供准确地描述和计算物种在特定时间内的衰减情况。

3. 自然增长：人口学家使用指数函数来研究人口的自然增长过程。

指数函数可以帮助人口学家了解一个地区的人口趋势和人口变化的因素，为政府提供人口规划和政策制定方面的参考。

4. 电子电路：在电子学中，指数函数可以用来描述电路中的电流和电压变化。

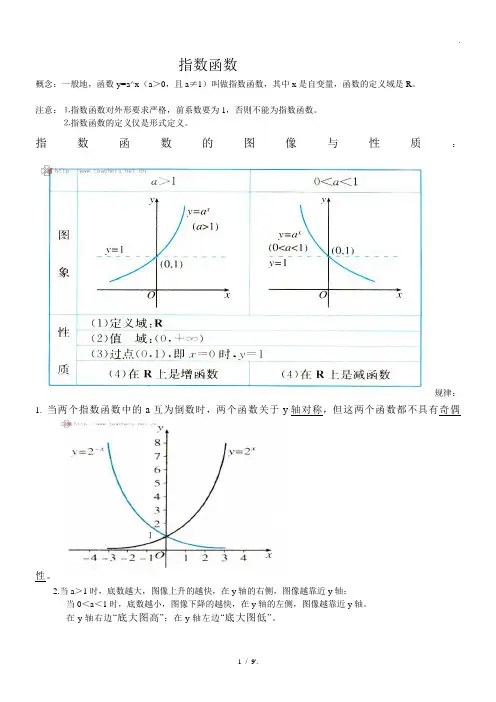
指数函数概念：一般地，函数y=a^x（a＞0，且a≠1）叫做指数函数，其中x是自变量，函数的定义域是R。

注意：⒈指数函数对外形要求严格，前系数要为1，否则不能为指数函数。

⒉指数函数的定义仅是形式定义。

指数函数的图像与性质：规律：1. 当两个指数函数中的a互为倒数时，两个函数关于y轴对称，但这两个函数都不具有奇偶性。

2.当a＞1时，底数越大，图像上升的越快，在y轴的右侧，图像越靠近y轴；当0＜a＜1时，底数越小，图像下降的越快，在y轴的左侧，图像越靠近y轴。

在y轴右边“底大图高”；在y轴左边“底大图低”。

3.四字口诀：“大增小减”。

即：当a ＞1时，图像在R 上是增函数；当0＜a ＜1时，图像在R 上是减函数。

4. 指数函数既不是奇函数也不是偶函数。

比较幂式大小的方法：1. 当底数相同时，则利用指数函数的单调性进行比较；2. 当底数中含有字母时要注意分类讨论；3. 当底数不同，指数也不同时，则需要引入中间量进行比较；4.对多个数进行比较，可用0或1作为中间量进行比较底数的平移：在指数上加上一个数，图像会向左平移；减去一个数，图像会向右平移。

在f(X)后加上一个数，图像会向上平移；减去一个数，图像会向下平移。

对数函数1.对数函数的概念由于指数函数y=a x 在定义域(-∞，+∞)上是单调函数，所以它存在反函数，我们把指数函数y=a x (a ＞0，a ≠1)的反函数称为对数函数，并记为y=log a x(a ＞0，a ≠1).因为指数函数y=a x 的定义域为(-∞，+∞)，值域为(0，+∞)，所以对数函数y=log a x 的定义域为(0，+∞)，值域为(-∞，+∞).2.对数函数的图像与性质对数函数与指数函数互为反函数，因此它们的图像对称于直线y=x . 据此即可以画出对数函数的图像，并推知它的性质.为了研究对数函数y=log a x(a ＞0，a ≠1)的性质，我们在同一直角坐标系中作出函数y=log 2x ，y=log 10x ，y=log 10x,y=log 21x,y=log 101x 的草图由草图，再结合指数函数的图像和性质，可以归纳、分析出对数函数y=log a x(a＞0，a≠1)的图像的特征和性质.见下表.图象a＞1 a＜1性质(1)x＞0(2)当x=1时，y=0(3)当x＞1时，y＞00＜x＜1时，y＜0(3)当x＞1时，y＜00＜x＜1时，y＞0 (4)在(0，+∞)上是增函数(4)在(0，+∞)上是减函数补充性质设y1=log a x y2=log b x其中a＞1，b＞1(或0＜a＜1 0＜b＜1) 当x＞1时“底大图低”即若a＞b则y1＞y2当0＜x＜1时“底大图高”即若a＞b，则y1＞y2比较对数大小的常用方法有：(1)若底数为同一常数，则可由对数函数的单调性直接进行判断.(2)若底数为同一字母，则按对数函数的单调性对底数进行分类讨论.(3)若底数不同、真数相同，则可用换底公式化为同底再进行比较.(4)若底数、真数都不相同，则常借助1、0、-1等中间量进行比较.3.指数函数与对数函数对比幂函数幂函数的图像与性质幂函数ny x =随着n 的不同，定义域、值域都会发生变化，可以采取按性质和图像分类记忆的方法．熟练掌握n y x =，当112,1,,,323n =±±±的图像和性质，列表如下． 从中可以归纳出以下结论：① 它们都过点()1,1，除原点外，任何幂函数图像与坐标轴都不相交，任何幂函数图像都不过第四象限．② 11,,1,2,332a =时，幂函数图像过原点且在[)0,+∞上是增函数．③ 1,1,22a =---时，幂函数图像不过原点且在()0,+∞上是减函数．④ 何两个幂函数最多有三个公共点．.定义域R R R奇偶性奇奇奇非奇非偶奇在第Ⅰ象限的增减性在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递减ny x=奇函数偶函数非奇非偶函数1n>01n<<0 n<O xyO xyO xyO xyO xyO xyO xyO xyO xy幂函数y x α=（x ∈R ，α是常数）的图像在第一象限的分布规律是：①所有幂函数y x α=（x ∈R ，α是常数）的图像都过点)1,1(；②当21,3,2,1=α时函数y x α=的图像都过原点)0,0(；③当1=α时，y x α=的的图像在第一象限是第一象限的平分线（如2c ）；④当3,2=α时，y x α=的的图像在第一象限是“凹型”曲线（如1c ）⑤当21=α时，y x α=的的图像在第一象限是“凸型”曲线（如3c ）⑥当1-=α时，y x α=的的图像不过原点)0,0(，且在第一象限是“下滑”曲线（如4c ）当0>α时，幂函数y x α=有下列性质：（1）图象都通过点)1,1(),0,0(；（2）在第一象限内都是增函数；（3）在第一象限内，1>α时，图象是向下凸的；10<<α时，图象是向上凸的； （4）（在第一象限内，过点)1,1(后，图象向右上方无限伸展。

指数函数的三个特征指数函数是高中数学中的重要概念，它具有以下三个特征：增长速度快、函数值始终大于零、具有对称轴。

在本文中，我们将深入探讨这三个特征，并分别进行详细解释。

指数函数的增长速度非常快。

指数函数的定义是f(x) = a^x，其中a为底数，x为指数。

当底数a大于1时，指数函数呈现出递增趋势，随着x的增大，函数值以指数级别增长。

例如，当a=2时，f(x) = 2^x的函数值随着x的增大呈现出指数增长的趋势，增长速度迅猛。

这种增长速度快的特点使得指数函数在描述许多现实世界中的增长和衰减过程时非常有用。

指数函数的函数值始终大于零。

由于底数a的任何正数次幂都大于0，所以指数函数的函数值始终大于零，即f(x)>0。

这使得指数函数在描述比例关系时非常有用。

例如，当a=0.5时，f(x) = 0.5^x 的函数值随着x的增大逐渐接近于0，但始终大于0。

这种特性使得指数函数在概率、百分比、利润等方面的计算中得到广泛应用。

指数函数具有对称轴。

指数函数的对称轴是y轴，即当x取任意值时，f(x) = a^x的函数值与f(-x)的函数值相等。

这是因为指数函数的定义中指数x可以是任意实数，正数和负数的函数值是相等的。

例如，当a=3时，f(x) = 3^x的函数值与f(-x)的函数值相等，这意味着函数图像关于y轴对称。

这种对称性使得指数函数在研究对称性质时非常方便。

指数函数具有增长速度快、函数值始终大于零、具有对称轴等三个特征。

这些特征使得指数函数在数学、科学和工程等领域中得到广泛应用。

我们在实际问题中，可以利用指数函数的快速增长特性来描述人口增长、物质衰变等现象；可以利用函数值始终大于零的特性来计算概率、百分比、利润等；可以利用对称轴的特性来研究对称性质。

因此，深入理解和掌握指数函数的三个特征对于数学学习和实际应用具有重要意义。

指数函数概念指数函数是一种重要的数学函数，可以用来描述某种特定情况下量级增长的情况。

它由变量x和常数a共同决定，表达式可以写作f(x)=a^x 。

指数函数中a叫做指数，x叫做底数，当x为负值时，指数函数会产生一定的不同，变成f(x)=a^(-x) 。

指数函数的含义是指底数x的次方乘以指数a，因此指数函数又可以描述为：f(n)=a^n 。

在这里，n为正整数，表示底数的次方，a 为正实数，表示指数。

当n=0时，f(n)=a^0 一定是1，这是因为任何次方除0以外的任何正整数都可以写成乘方来求出，所以当n为0时，应该乘以1来结果f(n)为1。

从另一个角度来看，指数函数体现了一种指数与实际情况相关的增长速度，也就是如果每次乘以同一个值，则产生的增长速度越来越快。

另一方面，指数函数也可以用来表示某物的指数衰减，比如衰减的音量可以用f(x)=a^(-x)表示，其中a表示初始音量，而x为衰减次数，当x越大，衰减量就越大。

指数函数的应用广泛，它可以广泛应用于经济学，物理学，生物学等领域，可以更好地描述某一种以指数形式增长或者衰减的规律，比如对物体衰减的热量，物质散失指数衰减等情况。

指数函数也可以用来表示在某一种增长速率下，物质量的变化情况，以及在科学研究中与指数概念相关的情况，例如詹姆斯-库克公式也是通过指数函数表达的。

求解指数函数也是一个非常重要的数学技能。

首先，当指数和底数都是实数时，可以用求导的方法来求解，即求f(x)=ln(a)*a^x 。

同时，还可以采用求和的方法来解决求解指数函数，即用π函数求和的方式来求解。

总之，指数函数是一种重要的数学函数，可以用来描述特定情况下量级增长或衰减的情况，它有着广泛的应用，而且能够更好地描述某一种以指数形式增长或者衰减的规律，作为一门必修课程，认真学习指数函数的基础知识，并如实理解和掌握指数函数概念是非常有必要的。