BP网络用于催化剂配方建模--MATLAB实例

bp神经网络及matlab实现分类：算法学习2012-06-20 20:56 66399人阅读评论(28) 收藏举报网络matlab算法functionnetworkinput本文主要内容包括： (1) 介绍神经网络基本原理，(2) 实现前向神经网络的方法，(3) Matlab实现前向神经网络的方法。

第0节、引例本文以Fisher的Iris数据集作为神经网络程序的测试数据集。

Iris数据集可以在找到。

这里简要介绍一下Iris数据集：有一批Iris花，已知这批Iris花可分为3个品种，现需要对其进行分类。

不同品种的Iris花的花萼长度、花萼宽度、花瓣长度、花瓣宽度会有差异。

我们现有一批已知品种的Iris花的花萼长度、花萼宽度、花瓣长度、花瓣宽度的数据。

一种解决方法是用已有的数据训练一个神经网络用作分类器。

如果你只想用C#或Matlab快速实现神经网络来解决你手头上的问题，或者已经了解神经网络基本原理，请直接跳到第二节——神经网络实现。

第一节、神经网络基本原理1. 人工神经元( Artificial Neuron )模型人工神经元是神经网络的基本元素，其原理可以用下图表示：图1. 人工神经元模型图中x1~xn是从其他神经元传来的输入信号，wij表示表示从神经元j到神经元i的连接权值，θ表示一个阈值 ( threshold )，或称为偏置( bias )。

则神经元i的输出与输入的关系表示为：图中 yi表示神经元i的输出，函数f称为激活函数 ( Activation Function )或转移函数 ( Transfer Function ) ，net称为净激活(net activation)。

若将阈值看成是神经元i的一个输入x0的权重wi0，则上面的式子可以简化为：若用X表示输入向量，用W表示权重向量，即：X = [ x0 , x1 , x2 , ....... , xn ]则神经元的输出可以表示为向量相乘的形式：若神经元的净激活net为正，称该神经元处于激活状态或兴奋状态(fire)，若净激活net为负，则称神经元处于抑制状态。

化工进展Chemical Industry and Engineering Progress2024 年第 43 卷第 3 期基于BP 神经网络模型优化Fe 1-x O 基氨合成催化剂张书铭，刘化章（浙江工业大学工业催化研究所，浙江 杭州 310014）摘要：运用BP 神经网络建立了助催化剂含量与催化剂活性之间的预测模型，对Fe 1-x O 基氨合成催化剂的助催化剂进行优化。

首先将前期实验数据整理归纳为含有3、4、5、6和7个助催化剂等5类催化剂，以助催化剂含量（体积分数）为输入变量，以425℃反应器出口氨浓度（活性）为输出变量，对助催化剂进行优化。

结果表明，BP 神经网络预测模型拟合值均方误差最高为0.2784，预测值均方误差最高为0.1592，构建的BP 神经网络模型准确度较高。

在该模型的基础上，运用多种群遗传算法进行极值寻优，求解最优的催化剂配方，并进行实验验证。

结果表明，根据优化结果制备5个样品的实验测定值与预测值的相对误差最高为2.88%，优化结果较为准确；含有7个助催化剂的催化剂活性最高为18.83%，比原样本的统计平均活性值（17.52%）高1.31%，相对提高7.48%，助催化剂含量优化取得满意的结果。

关键词：Fe 1-x O ；催化剂；助催化剂；神经网络；遗传算法；优化中图分类号：O643.36 文献标志码：A 文章编号：1000-6613（2024）03-1302-07Optimization of Fe 1-x O ammonia synthesis catalyst by BP neural networkmodelZHANG Shuming ，LIU Huazhang(Institute of Industrial Catalysis, Zhejiang University of Technology, Hangzhou 310014, Zhejiang, China)Abstract: A prediction model between the content of promoter and the activity of catalyst was established by BP neural network, with which the promoter of Fe 1-x O ammonia synthesis catalyst was optimized. Firstly, the preliminary experimental data were summarized into five types of catalysts including three, four, five, six and seven promoters. With the content of the promoters (volume fraction) as the input model variable and the ammonia concentration (reactivity) at the outlet of the reactor at 425℃ as the output one, the formula of the promoter was optimized. The results showed that maximum mean square error of fitting values of BP neural network prediction model was 0.2784, while that of the predicted values was 0.1592, indicating the accuracy of the BP neural network model was high. On the basis of this model, multiple population genetic algorithm was used to search the extreme value, and the optimal catalyst formula was obtained and verified by experiments. The maximum relative error between the measured values of 5 samples prepared according to the optimized formula and the predicted ones was 2.88%. The highest activity was 18.83% for the catalyst containing seven promoters, 1.31% higher than the average reactivity value of the original sample (17.52%), and a relative increase of 7.48%.Keywords: Fe 1-x O; catalyst; promoters; neural networks; genetic algorithm; optimization研究开发DOI ：10.16085/j.issn.1000-6613.2023-0433收稿日期：2023-03-22；修改稿日期：2023-05-30。

MATLAB 程序代码--BP 神经网络的设计实例例 1 采用动量梯度下降算法训练BP 网络。

训练样本定义如下：输入矢量为p =[-1 -2 3 1-1 1 5 -3]目标矢量为t = [-1 -1 1 1]解：本例的MA TLAB 程序如下：close allclearecho on clc% NEWFF ——生成一个新的前向神经网络% TRAIN ——对BP 神经网络进行训练% SIM ——对BP 神经网络进行仿真pause% 敲任意键开始clc% 定义训练样本% P 为输入矢量P=[-1, -2, 3, 1; -1, 1, 5,-3];% T 为目标矢量T=[-1, -1, 1, 1];pause; clc% 创建一个新的前向神经网络net=newff(minmax(P),[3,1],{'tansig','purelin'},'traingdm')% 当前输入层权值和阈值inputWeights=net.IW{1,1} inputbias=net.b{1}% 当前网络层权值和阈值layerWeights=net.LW{2,1} layerbias=net.b{2} pause clc% 设置训练参数net.trainParam.show = 50; net.trainParam.lr = 0.05; net.trainParam.mc = 0.9;n et.tra in Param.epochs = 1000;n et.tra in Param.goal = 1e-3;pauseclc% 调用TRAINGDM 算法训练BP网络[n et,tr]=trai n(n et,P,T);pauseclc% 对BP网络进行仿真A = sim( net,P)% 计算仿真误差E = T - AMSE=mse(E) pause clc echo off例2采用贝叶斯正则化算法提高BP网络的推广能力。

神经网络的设计实例(MATLAB编程)例1 采用动量梯度下降算法训练BP 网络。

训练样本定义如下：输入矢量为p =[-1 -2 3 1-1 1 5 -3]目标矢量为t = [-1 -1 1 1]解：本例的MATLAB 程序如下：close allclearecho onclc% NEWFF——生成一个新的前向神经网络% TRAIN——对BP 神经网络进行训练% SIM——对BP 神经网络进行仿真pause% 敲任意键开始clc% 定义训练样本P=[-1, -2, 3, 1; -1, 1, 5, -3]; % P 为输入矢量T=[-1, -1, 1, 1]; % T 为目标矢量pause;clc% 创建一个新的前向神经网络net=newff(minmax(P),[3,1],{'tansig','purelin'},'traingdm') % 当前输入层权值和阈值inputWeights=net.IW{1,1}inputbias=net.b{1}% 当前网络层权值和阈值layerWeights=net.LW{2,1}layerbias=net.b{2}pauseclc% 设置训练参数net.trainParam.show = 50;net.trainParam.lr = 0.05;net.trainParam.mc = 0.9;net.trainParam.epochs = 1000;net.trainParam.goal = 1e-3;pauseclc% 调用TRAINGDM 算法训练BP 网络[net,tr]=train(net,P,T);pauseclc% 对BP 网络进行仿真A = sim(net,P)% 计算仿真误差E = T - AMSE=mse(E)pauseclcecho off例2 采用贝叶斯正则化算法提高BP 网络的推广能力。

在本例中，我们采用两种训练方法，即L-M 优化算法（trainlm）和贝叶斯正则化算法（trainbr），用以训练BP 网络，使其能够拟合某一附加有白噪声的正弦样本数据。

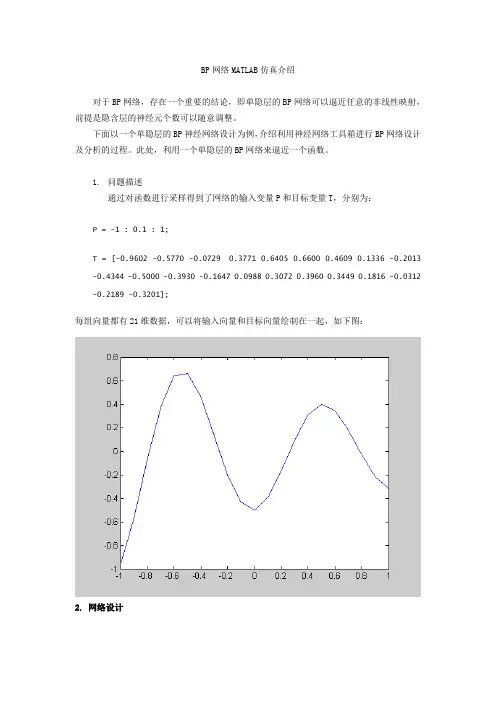
BP网络MATLAB仿真介绍对于BP网络，存在一个重要的结论，即单隐层的BP网络可以逼近任意的非线性映射，前提是隐含层的神经元个数可以随意调整。

下面以一个单隐层的BP神经网络设计为例，介绍利用神经网络工具箱进行BP网络设计及分析的过程。

此处，利用一个单隐层的BP网络来逼近一个函数。

1.问题描述通过对函数进行采样得到了网络的输入变量P和目标变量T，分别为：P = -1 : 0.1 : 1;T = [-0.9602 -0.5770 -0.0729 0.3771 0.6405 0.6600 0.4609 0.1336 -0.2013 -0.4344 -0.5000 -0.3930 -0.1647 0.0988 0.3072 0.3960 0.3449 0.1816 -0.0312 -0.2189 -0.3201];每组向量都有21维数据，可以将输入向量和目标向量绘制在一起，如下图：2. 网络设计网络的输入层和输出层的神经元个数均为1，根据隐含层设计经验，解决该问题的网络的隐层神经元个数应该在3~8之间。

下面设计一个隐含层神经元数目可变的BP网络，通过误差对比，确定最佳的隐含层神经元个数，并检查隐含层神经元个数对网络性能的影响。

网络设计及训练代码如下：P = -1 : 0.1 : 1;T = [-0.9602 -0.5770 -0.0729 0.3771 0.6405 0.6600 0.4609 0.1336 -0.2013 -0.4344 -0.5000 -0.3930 -0.1647 0.0988 0.3072 0.3960 0.3449 0.1816 -0.0312 -0.2189 -0.3201];s = 3 : 8; % S表示隐层数目的可选项res = 1 : 6;for i = 1 : 6% 隐含层神经元的传递函数为tansig，输出层神经元的传递函数为logsig% 目标函数在[-1, 1]间，刚好满足tansig的输出要求。

MATLAB下BP神经网络的设计开发BP网络在神经网络工具箱中的仿真本文利用Matlab6.5神经网络工具箱，以一组动态冲击实验数据为例建立网络模型。

实验数据共有13组，将其中对曲线形状有关键性影响的10组数据作为网络的训练数据，另外3组作为测试数据用以验证网络的预测性能。

①BP网络的建立在建立BP神经网络时，首先要根据应用的问题确定网络结构，即选择网络的层数和隐层节点数。

由于本例中实验数据较少，采用最基本的两层网络就可以很好地逼近未知函数了。

隐层节点数的选择在神经网络的应用中一直是一个复杂的问题：隐层节点数过多，将导致网络的预测能力不够，并容易导致网络陷入局部极小值难以跳出；隐层节点数过少，网络训练不出来，或不能识别以前没有的样本，且容错性差。

在设计中，比较实际的做法是通过对不同神经元数的网络进行训练、对比，找出网络效果最好时的隐层节点数。

在本例中，经大量的训练、对比，最终取中间隐层节点数为10。

另一方面，BP隐层传递函数采用正切Sigmoid 函数tansig，可以逼近任意非线性函数；输出层神经元则采用线性函数purelin，可以把输出值释放到任意值。

至此，一个1-10-1的神经网络模型建立完毕。

②BP网络的训练Matlab神经网络工具箱为用户提供了三种可用于BP网络的训练函数，它们是：trainbp、trainbpx和trainlm。

它们用法类似，采用不同的学习规则。

trainlm训练函数使用Levenberg-Marquardt算法，是三种规则中迭代次数最少、训练速度最快的一个，缺点是该算法在每次迭代时的计算量比其他算法大，故需要大量的存储空间，对于参数很大的应用是不实用的，考虑到待处理问题的参数较小，因此采用trainlm训练函数。

目标误差设为0.01，最大训练步数设为10 000。

设定好参数之后开始训练网络，训练结果显示：网络在训练了32次之后达到目标误差0.01，训练停止。

③BP网络的测试由于初始值取随机值，每次训练得到的结果都不相同，经多次训练得到最好的结果，并记录下此时的权值和阈值。

神经⽹络建模及Matlab中重要的BP⽹络函数神经⽹络建模及Matlab中重要的BP⽹络函数⼀、神经组织的基本特征1．细胞体是⼀个基本的初等信号处理器，轴突是信号的输出通路，树突是信号的输⼊通路。

信号从⼀个神经细胞经过突触传递到另⼀个细胞。

2．不同的神经元之间有不同的作⽤强度，称为联接强度。

当某细胞收到信号时，它的电位发⽣变化，如果电位超过某⼀阈值时，该细胞处于激发态，否则处于抑制状态。

3．两神经元之间的联接强度随其激发与抑制⾏为相关性的时间平均值正⽐变化，也就是说神经元之间的联接强度不是⼀成不变的。

这就是⽣物学上的Hebb律。

∑t j ij t S w )(⼆、⼈⼯神经元的M-P 模型（McCulloch 、Pitts,1943）1．构造⼀个模拟⽣物神经组织的⼈⼯神经⽹络的三要素：（1）．对单个神经元给出定义；（2）．定义⽹络结构：决定神经元数量及连接⽅式；（3）．给出⼀种⽅法，决定神经元之间的联接强度。

2．M-P 模型其中，t 表⽰时间S i (t)表⽰第i 个神经元在t 时刻的状态，S i (t)=1表⽰处于激发态，S i (t)=0表⽰处于抑制态w ij 表⽰第j 个神经元到第i 个神经元的联接强度，称之为权，可正可负表⽰第i 个神经元在t 时刻所接收到的所有信号的线性迭加。

µi 表⽰神经元i 的阈值, 可以在模型中增加⼀个S k (t)=1神经元k ，并且w ik =-µi ,则阈值可归并到和号中去。

注：1．M-P 神经元虽然简单，但可以完成任何计算。

2．神经元的状态可以取[0，1]中的连续值，如⽤以下函数代替θ(x):<≥=-=+∑00011x x x t S w t S i jj ij i )())(()(θµθ∑=>+=-j j ij h t S w h eh g )()(0 11 2ββ三、多层前传⽹络1.特点：相邻层全互连同层没有连接输出与输⼊没有直接联系2．各层神经元个数的确定输⼊层、输出层的神经元个数由研究对象的输⼊、输出信息来确定。