格雷码、二进制转换及译码电路

在精确定位控制系统中，为了提高控制精度，准确测量控制对象的位置是十分重要的。

目前，检测位置的办法有两种：其一是使用位置传感器，测量到的位移量由变送器经A/D转换成数字量送至系统进行进一步处理。

此方法精度高，但在多路、长距离位置监控系统中，由于其成本昂贵，安装困难，因此并不实用；其二是采用光电轴角编码器进行精确位置控制。

光电轴角编码器根据其刻度方法及信号输出形式，可分为增量式、绝对式以及混合式三种。

而绝对式编码器是直接输出数字量的传感器，它是利用自然二进制或循环二进制（格雷码）方式进行光电转换的，编码的设计一般是采用自然二进制码、循环二进制码、二进制补码等。

特点是不要计数器，在转轴的任意位置都可读出一个固定的与位置相对应的数字码；抗干扰能力强，没用累积误差；电源切断后位置信息不会丢失，但分辨率是由二进制的位数决定的，根据不同的精度要求，可以选择不同的分辨率即位数。

目前有10位、11位、12位、13位、14位或更高位等多种。

其中采用循环二进制编码的绝对式编码器，其输出信号是一种数字排序,不是权重码，每一位没有确定的大小，不能直接进行比较大小和算术运算，也不能直接转换成其他信号，要经过一次码变换，变成自然二进制码，在由上位机读取以实现相应的控制。

而在码制变换中有不同的处理方式，本文着重介绍二进制格雷码与自然二进制码的互换。

一、格雷码（又叫循环二进制码或反射二进制码）介绍在数字系统中只能识别0和1，各种数据要转换为二进制代码才能进行处理，格雷码是一种无权码，采用绝对编码方式，典型格雷码是一种具有反射特性和循环特性的单步自补码，它的循环、单步特性消除了随机取数时出现重大误差的可能，它的反射、自补特性使得求反非常方便。

格雷码属于可靠性编码，是一种错误最小化的编码方式，因为，自然二进制码可以直接由数/模转换器转换成模拟信号，但某些情况，例如从十进制的3转换成4时二进制码的每一位都要变，使数字电路产生很大的尖峰电流脉冲。

二进制数和格雷码的转换二进制数和格雷码是数字电路中常用的编码方式，它们在数据传输、存储等方面都有广泛的应用。

下面我们来介绍一下二进制数和格雷码的转换方法。

一、二进制数转换为格雷码1.将二进制数的最高位复制到格雷码的最高位上。

2.从左到右扫描二进制数的每一位，如果该位与前一位相同，则在格雷码中该位上写入0，否则写入1。

例如，将二进制数101101转换为格雷码：第一步：将最高位1复制到格雷码的最高位上，得到10xxxx。

第二步：从左到右扫描剩余部分，第2位与第1位不同，故在格雷码中该位上写入1；第3、4、5位与前一位相同，故在格雷码中这三个位置上均写入0；第6位与前一位不同，故在格雷码中该位置上写入1。

最终得到的格雷码为111001。

二、格雷码转换为二进制数1.将格雷码的最高位复制到二进制数的最高位上。

2.从左到右扫描剩余部分，在每个位置上依次执行以下操作：若该位置上的数字为0，则在对应位置上写入前一个数字的值；若该位置上的数字为1，则在对应位置上写入前一个数字的值的补数。

例如，将格雷码111001转换为二进制数：第一步：将最高位1复制到二进制数的最高位上，得到1xxxxx。

第二步：从左到右扫描剩余部分，第2位是1，则在二进制数中该位置上写入前一个数字0的补数1；第3、4、5位均为1，则在二进制数中这三个位置上写入前一个数字0的补数1；第6位为0，则在二进制数中该位置上写入前一个数字1的值0。

最终得到的二进制数为101101。

总结：以上就是二进制数和格雷码之间转换的方法，需要注意的是，在实际应用中要根据具体情况选择合适的编码方式，并且要注意编码转换过程中可能出现的错误。

EDA技术与应用实验报告实验名称：格雷码、二进制转换及译码电路姓名：陈丹学号：2班级：电信（2）班时间：南京理工大学紫金学院电光系一、实验目的1）学习用VHDL代码描述组合逻辑电路的方法。

2) 掌握when….else….，generate和case并行语句的使用。

二、实验原理1）学习VHDL的when….else….，generate和case并行语句。

2）利用when….else….并行语句描述4位二进制码/格雷码转换电路。

3）利用generate并行语句描述n位格雷码/二进制码转换电路。

4）利用case并行语句实现译码电路。

5）利用实验箱验证所设计的电路的正确性，要求将输入输出的数据用数码管显示。

三、实验内容1、二进制转换为格雷码4位二进制格雷码转换的真值表如图所示：建立工程，输入代码先建立工程，工程命名为“btog”,顶层文件名为“btog”。

选择“file→new”，在弹出的窗口中选择“VHDL File”建立“VHDL”文件。

在新建的VHDL文件中输入二进制格雷码转换的VHDL代码，将文件保存。

二进制转换为格雷码的代码：编译仿真对当前文件进行编译，编译通过以后建立仿真波形，保存为“”.为波形文件添加节点，将“end time”设置为100μs ，将输入输出编组，并为输入信号赋值，其中“start value”为“0000”，“count every”设置为5μs.其波形如下：仿真结果2、generate语句实现格雷码转换为二进制对于n位二进制转换为格雷码的码转换电路，转换表达式如下：Bn=GnBi=Gi⊕B(i+1)建立工程，输入代码先建立工程，工程命名为“gtob”,顶层文件名为“g_to_b2”。

选择“file→new”，在弹出的窗口中选择“VHDL File”建立“VHDL”文件。

在新建的VHDL文件中输入格雷码二进制转换的VHDL代码，将文件保存。

转换代码：编译仿真对当前文件进行编译，编译通过以后建立仿真波形，保存为“”.为波形文件添加节点，将“end time”设置为100μs ，将输入输出编组，并为输入信号赋值，其中“start value”为“0000”，“count every”设置为5μs.其波形如下：3、case语句实现译码电路代码描述：仿真波形：4、管脚配置利用实验箱的模式6来验证设计电路的正确性。

EDA技术与应用实验报告实验名称：格雷码、二进制转换电路一、实验目的1、学习使用VHDL代码组合逻辑电路的方法。

2、掌握when...else...和generate并行语句的使用。

二、实验内容1、学习VHDL代码修改。

2、利用case语句描述4位格雷码/二进制码转换电路，要求将输入输出的数据用数码管显示。

3、利用generate并行语句描述n位格雷码/二进制码转换电路（n=4）。

4、利用实验箱验证所设计电路的正确性，要求将输入输出的数据用七段数码管显示。

三、实验原理1、4位格雷码转换为二进制表达式为：四、 实验代码library ieee ;use ieee.std_logic_1164.all; use ieee.std_logic_arith.all;use ieee.std_logic_unsigned.all;entity gtob isport(g:in std_logic_vector(3 downto 0);b:buffer std_logic_vector(3 downto 0));end gtob;architecture rhg of gtob isbeginb<="0000"when g="0000"else"0001"when g="0001"else"0011"when g="0010"else"0010"when g="0011"else"0111"when g="0100"else"0110"when g="0101"else"0100"when g="0110"else"0101"when g="0111"else"1111"when g="1000"else"1110"when g="1001"else"1100"when g="1010"else"1101"when g="1011"else"1000"when g="1100"else"1001"when g="1101"else"0011"when g="1110"else"1010";end rhg;33232121010B G B B G B B G B B G ==⊕=⊕=⊕五、电路仿真结果六、管脚配制。

格雷码二进制码转换电路格雷码（Gray code），又称格雷码二进制码转换电路，是一种特殊的二进制编码方式。

它的特点是相邻的两个数值仅有一位二进制数发生变化，适用于数字和模拟电路中的编码和传输。

格雷码的起源可以追溯到19世纪，由法国数学家弗兰索瓦·格雷（François Gray）发明。

他的目的是设计一种编码方式，可以减少在数字传输过程中由于噪声、抖动等原因引起的误差。

在传统的二进制编码方式中，相邻的两个数值之间可能会发生多个二进制位的变化，这样在数字传输中就容易引起误差。

而格雷码通过仅改变一位二进制数来表示相邻的数值，可以有效地降低传输误差的风险。

格雷码的转换电路由多个逻辑门组成，常见的实现方式有反馈式和非反馈式两种。

反馈式格雷码转换电路使用触发器和逻辑门组成，适用于需要连续转换的应用场景。

非反馈式格雷码转换电路则使用逻辑门组成，适用于只需要单次转换的应用场景。

格雷码转换电路的核心是通过逻辑门的组合实现码字之间的变换。

逻辑门的输入信号由当前码字和目标码字决定，通过逻辑运算得到输出信号。

常见的逻辑门有与门、或门、非门等，它们可以实现不同的逻辑运算。

格雷码转换电路的功能包括格雷码到二进制码的转换和二进制码到格雷码的转换。

格雷码到二进制码的转换可以通过逻辑门的组合实现，将格雷码逐位进行异或运算，并与之前的结果进行与运算。

而二进制码到格雷码的转换则可以通过逻辑门的组合实现，将二进制码逐位进行异或运算，得到格雷码。

在数字电路中，格雷码转换电路广泛应用于各种编码器和解码器中。

编码器可以将多个输入信号转换为相应的格雷码输出，解码器则可以将格雷码输入转换为相应的输出信号。

格雷码转换电路还可以用于数字计数器、旋转编码器等应用中。

总结起来，格雷码二进制码转换电路是一种特殊的二进制编码方式，通过逻辑门的组合实现码字之间的变换。

它的应用范围广泛，可以用于数字电路中的编码和传输。

格雷码的特点是相邻的两个数值仅有一位二进制数发生变化，可以减少传输误差的风险。

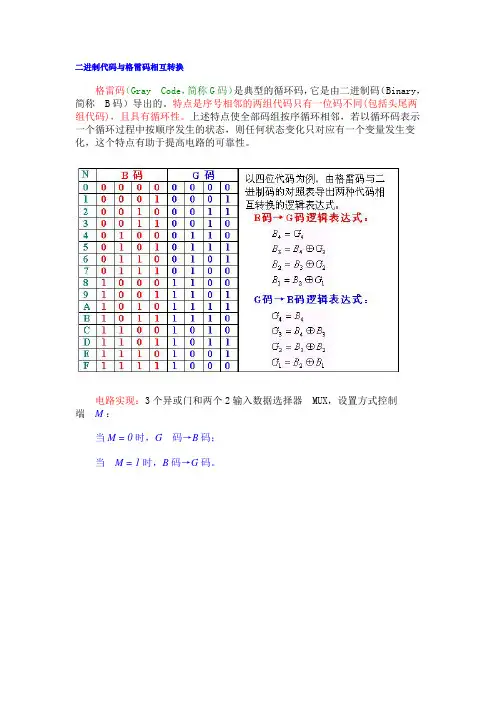
二进制代码与格雷码相互转换格雷码（Gray Code，简称G码）是典型的循环码，它是由二进制码（Binary，简称B码）导出的。

特点是序号相邻的两组代码只有一位码不同(包括头尾两组代码)，且具有循环性。

上述特点使全部码组按序循环相邻，若以循环码表示一个循环过程中按顺序发生的状态，则任何状态变化只对应有一个变量发生变化，这个特点有助于提高电路的可靠性。

电路实现：3个异或门和两个2输入数据选择器MUX，设置方式控制端M：当M = 0 时，G码→B码；当M = 1时，B码→G码。

十进制数的二进制编码在人机交互过程中，为了既满足系统中使用二进制数的要求，又适应人们使用十进制数的习惯，通常用4位二进制代码对十进制数字符号进行编码，简称为二-十进制代码，或称BCD(Binary Coded Decimal)码。

它既有二进制的形式，又有十进制的特点。

常用的BCD码有8421码、2421码和余3码3种，它们与十进制数字符号对应的编码如表1.4所示。

表1.4 常用的3种BCD码进制字符8421码2421码余3码0 0000 0000 00111 0001 0001 01002 0010 0010 01013 0011 0011 01104 0100 0100 01115 0101 1011 10006 0110 1100 10017 0111 1101 10108 1000 1110 10119 1001 1111 1100一、8421码8421码是最常用的一种有权码，其4位二进制码从高位至低位的权依次为23、22、21、20，即为8、4、2、1,故称为8421码。

按8421码编码的0～9与用4位二进制数表示的0～9完全一样，所以，8421码是一种人机联系时广泛使用的中间形式。

注意：※ 8421码中不允许出现1010～1111四种组合，因为没有十进制数字符号与其对应。

※ 十进制数字符号的8421码与相应ASCII码的低四位相同，这一特点有利于简化输入输出过程中BCD码与字符代码的转换。

格雷码简介及格雷码与二进制的转换程序格雷码简介及格雷码与二进制的转换程序格雷码简介格雷码（英文：GrayCode,GreyCode,又称作葛莱码，二进制循环码）是1880年由法国工程师Jean-Maurice-EmlleBaudot发明的一种编码[1]，因FrankGray于1953年申请专利“PulseCodeCommunication”得名。

当初是为了机械应用，后来在电报上取得了巨大发展[2]，现在则常用于模拟－数字转换[3]和转角－数字转换中[4]。

典型格雷码是一种具有反射特性和循环特性的单步自补码，它的循环、单步特格雷码简介及格雷码与二进制的转换程序格雷码简介格雷码（英文：Gray Code, Grey Code,又称作葛莱码，二进制循环码）是1880年由法国工程师Jean-Maurice-EmlleBaudot发明的一种编码[1] ，因Frank Gray于1953年申请专利“Pulse Code Communication”得名。

当初是为了机械应用，后来在电报上取得了巨大发展[2]，现在则常用于模拟－数字转换[3]和转角－数字转换中[4] 。

典型格雷码是一种具有反射特性和循环特性的单步自补码，它的循环、单步特性消除了随机取数时出现重大误差的可能，它的反射、自补特性使得求反非常方便[5] 。

格雷码属于可靠性编码，是一种错误最小化的编码，因为它大大地减少了由一个状态到下一个状态时电路中的混淆。

由于这种编码相邻的两个码组之间只有一位不同，因而在用于模－数转换中，当模拟量发生微小变化而可能引起数字量发生变化时，格雷码仅改变一位，这样与其它码同时改变两位或多位的情况相比更为可靠，即可减少出错的可能性．这就允许代码电路能以较少的错误在较高的速度下工作。

格雷码在现代科学上获得了广泛的应用，人们还发现智力玩具九连环的状态变化符合格雷码的编码规律，汉诺塔的解法也与格雷码有关。

除了已知的特点，格雷码还有一些鲜为人知的性质。

二进制数转化为格雷码1. 二进制数和格雷码的介绍在计算机科学中，二进制数和格雷码是两种常见的数字编码方式。

二进制数是一种由 0 和 1 组成的计数系统，而格雷码则是一种不同于二进制的编码方式。

在二进制数中，每个数字位都表示了相应的权值，而在格雷码中，两个相邻数值之间仅有一位数字不同。

2. 二进制数和格雷码的转换原理将二进制数转换为格雷码，我们需要对其进行逐位求异或操作。

具体来说，对于一个二进制数，我们需要将其最高数位保留，然后将其余位依次进行异或操作，得到相邻数值之间仅有一位数字不同的格雷码。

而将格雷码转换为二进制数，则需要进行逐位求异或操作，但由于格雷码的特殊性，它的最高位和最低位不需要特殊处理，而只需要将其余位进行异或操作即可得到原始的二进制数。

3. 示范转换下面我们来举一个例子，以便更好地理解二进制数和格雷码的转换过程。

我们以四位二进制数 1101 为例，将其转换为对应的格雷码：- 首先将最高位保留，即 1。

- 对于其余的三位数字，我们需要将其依次进行异或操作，得到对应的格雷码：1011。

现在我们将这个格雷码转换回二进制数：- 由于格雷码的最高位为 1，我们可以保留它。

- 对于其余的三位数字，我们需要将其依次进行异或操作，得到对应的二进制数：1110。

通过这个例子，我们可以看到，二进制数和格雷码之间的转换并不复杂，只需要逐位进行异或操作即可得到相应的结果。

4. 适用范围在实际应用中，二进制数和格雷码的转换经常出现在数字电路设计和硬件逻辑控制中。

由于格雷码的特殊性，它在数字电路中能够降低电路的延迟和功耗，提高电路的可靠性和稳定性。

因此，掌握二进制数和格雷码的转换技巧对于数字电路设计和硬件逻辑控制非常重要。

5. 结语二进制数和格雷码是数字编码中的两种重要方式，它们在计算机科学和数字电路设计中发挥着重要的作用。

通过学习二进制数和格雷码的转换原理和技巧，我们可以更好地理解它们的应用和优势，为实际工作提供帮助。

格雷码简介及格雷码与二进制的转换程序一、格雷码简介格雷码（英文：Gray Code, Grey Code,又称作葛莱码，二进制循环码）是1880年由法国工程师Jean-Maurice-EmlleBaudot发明的一种编码[1] ，因Frank Gray于1953年申请专利“Pulse Code Communication”得名。

当初是为了机械应用，后来在电报上取得了巨大发展[2]，现在则常用于模拟－数字转换[3]和转角－数字转换中[4] 。

典型格雷码是一种具有反射特性和循环特性的单步自补码，它的循环、单步特性消除了随机取数时出现重大误差的可能，它的反射、自补特性使得求反非常方便[5] 。

格雷码属于可靠性编码，是一种错误最小化的编码，因为它大大地减少了由一个状态到下一个状态时电路中的混淆。

由于这种编码相邻的两个码组之间只有一位不同，因而在用于模－数转换中，当模拟量发生微小变化而可能引起数字量发生变化时，格雷码仅改变一位，这样与其它码同时改变两位或多位的情况相比更为可靠，即可减少出错的可能性．这就允许代码电路能以较少的错误在较高的速度下工作。

格雷码在现代科学上获得了广泛的应用，人们还发现智力玩具九连环的状态变化符合格雷码的编码规律，汉诺塔的解法也与格雷码有关。

除了已知的特点，格雷码还有一些鲜为人知的性质。

多数数字电子技术和计算机技术的文献认为格雷码是无权码，只有J.F.A.Thompson认为可以从格雷码直接转换成十进制数[6]。

如果将格雷码的“权”及格雷码的奇偶性等性质在数学上给予证明，将有助于格雷码研究与应用的发展，有助于自动化技术的发展，还可有助于计算机科学的发展。

二、格雷码与二进制的转换程序* 本程序采用递推的方法进行推导,可以转换0~2147483647之间的数(1~31位)* 推导方式如下(以三位格雷码为例):* 序号格雷码格雷码实值二进制码二进制实值* 0 000 0 000 0* 1 001 1 001 1* 2 011 3 010 2* 3 010 2 011 3* 4 110 6 100 4* 5 111 7 101 5* 6 101 5 110 6* 7 100 4 111 7* 由上面的数据可看出.如果,按照序号01327645的方式遍历格雷码.其编* 码实值是按自然数顺序排列.反之,如果按此顺序遍历其二进制实值.则会发* 现遍历过的数据的个数减一即为二进制码所对应格雷码的实值.再观察序号* 顺序,我们会发现: 如果把二进制码分半,前半部分从前向后遍历,后半部分* 从后向前遍历.如果分半部分可再分,则再将其分半.并按照前半部分从前向* 后遍历(分解),后半部分从后向前遍历的方式遍历(分解).直到不可分.即可* 实现按序号所描述顺序遍历二进制码.如果,按此顺序遍历二进制码,我们可* 以很方便地在序列中找到所要的二进制码与其对应的格雷码.本思想可以很* 方便地用递归实现.这样就实现了二进制到格雷码的转换.同样,格雷码到二* 进制的转换,也可以用相同的方法推出.为了加快运算,我们跳过不必要的遍* 历将递归改为递推.这样就实现了格雷码与二进制之间的快速转换.* 此算法的时间复杂度约为O(n),n为要转换数据的BIT数.* ****************************************************************** 补充说明：* 其它的转换方法还有* 1、查表法（建立一个二进制与格雷码的对应表）* 2、公式法（根据卡诺图建立一个二进制到格雷码的每一位的公式）*///#define test＃i nclude <stdio.h>#ifdef test＃i nclude <time.h>#endif/*** 二进制转换成格雷码* @param lStart lValue所在区间下界* @param lEnd lValue所在区间上界* @param lValue 要转换的二进制数的实值* @return 返回格雷码对应的二进制数的实值* @see g2b() g2b 格雷码转换二进制* @see BtoG() BtoG 二进制转换格雷码* @see GtoB() BtoG 格雷码转换二进制* @author 黄毅* @useage a=b2g(0,15,4); //取得4所对应格雷码的二进制值结果a等于6* @memo lValue的值必须在区间[lStart,lEnd]里,否则无法求得所求结果.相应地,如果区间越小,求得结* 果所用的时间就越少.而且lStart,lEnd的值必须为2的N次方减1. 通常lStart为0.为了方便求得* 其值,建议使用BtoG()函数来进行操作.不过这样会使计算时间加长到原来的120%~180%.*/unsigned long b2g(unsigned long lStart,unsigned long lEnd,unsignedlong lValue){unsigned long Start=lStart,End=lEnd,Temp=0,Counter=0;bool Type=true;while(Start<End){Temp=(End+Start-1)>>1;if (lValue<=Temp){if(!Type)Counter+=((End-Start+1)>>1);End=Temp;Type=true;}else{if(Type)Counter+=((End-Start+1)>>1);Start=++Temp;Type=false;}}return Counter;}/*** 格雷码转换成二进制* @param lStart lValue对应二进制数所在区间下界* @param lEnd lValue对应二进制数所在区间上界* @param lValue 要转换的格雷码的实值* @return 返回二进制数对应的格雷码的实值* @see b2g() b2g 二进制转换格雷码* @see BtoG() BtoG 二进制转换格雷码* @see GtoB() BtoG 格雷码转换二进制* @author 黄毅* @useage a=b2g(0,15,6); //取得6所对应二进制值的格雷码结果a等于4* @memo lValue对应二进制数的值必须在区间[lStart,lEnd]里,否则无法求得所求结果.相应地,如果区* 间越小,求得结果所用的时间就越少.而且lStart,lEnd的值必须为2的N次方减1. 通常lStart 为0.* 为了方便求得其值,建议使用GtoB()函数来进行操作.但会使计算时间加长到原来的105%~14 0%.*/unsigned long g2b(unsigned long lStart,unsigned long lEnd,unsignedlong lValue){unsigned long Start=lStart,End=lEnd,Counter=0,Temp=0;bool Type=true;while(Start<End){Temp=Counter+((End-Start+1)>>1);if(Type^(lValue<Temp)){if(Type) Counter=Temp;Start=(Start+End+1)>>1;Type=false;}else{if(!Type) Counter=Temp;End=(Start+End-1)>>1;Type=true;}}return Start;}//b2g外壳程序,用来算lStart,lEnd;long BtoG(unsigned long lValue){register unsigned long lV=lValue,lMax=1; while (lV>0){lV>>=1;lMax<<=1;}if (lMax==0) return -1;return b2g(0,--lMax,lValue);}//g2b外壳程序long GtoB(unsigned long lValue){register unsigned long lV=lValue,lMax=1; while (lV>0){lV>>=1;lMax<<=1;}if (lMax==0) return -1;return g2b(0,--lMax,lValue);}main(){long input=0;#ifdef test//程序测试部分clock_t cStart,cEnd;unsigned long dTime;cStart=clock();for (input=0;input<9999999;input++)BtoG(32768);cEnd=clock();dTime=(cEnd-cStart);printf("BtoG: %ld / %ld\n",dTime,CLOCKS_PER_SEC);//------------------------------------------------------cStart=clock();for (input=0;input<9999999;input++)b2g(0,65535,32768);cEnd=clock();dTime=(cEnd-cStart);printf("b2g: %ld / %ld\n",dTime,CLOCKS_PER_SEC);//------------------------------------------------------cStart=clock();for (input=0;input<9999999;input++)GtoB(32768);cEnd=clock();dTime=(cEnd-cStart);printf("GtoB: %ld / %ld\n",dTime,CLOCKS_PER_SEC);//------------------------------------------------------cStart=clock();for (input=0;input<9999999;input++)g2b(0,65535,32768);cEnd=clock();dTime=(cEnd-cStart);printf("g2b: %ld / %ld\n",dTime,CLOCKS_PER_SEC);#else//程序演试部分printf("Input(HEX):");scanf("%x",&input);while (input!=-1){printf("------BtoG------\nBinary:%08Xh\nGray:%08Xh\n------GtoB------\nGray:%08Xh\nBinary:%08Xh\n----------------\n",input,BtoG(input),input,GtoB(input)); printf("Input(HEX):");scanf("%x",&input);}#endif。

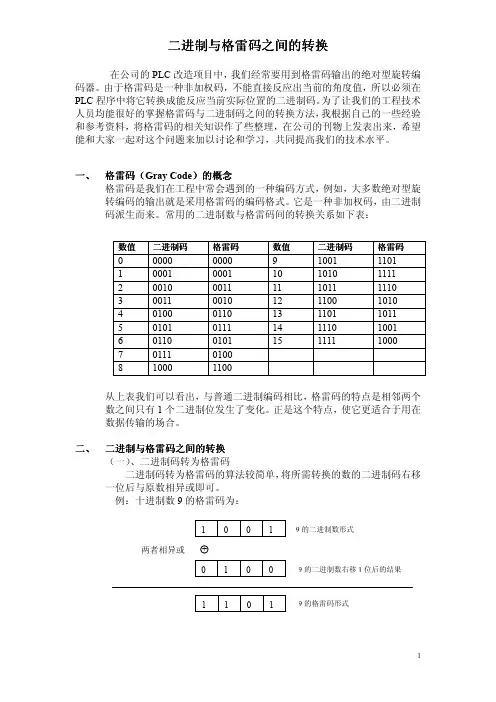
二进制与格雷码之间的转换在公司的PLC 改造项目中，我们经常要用到格雷码输出的绝对型旋转编码器。

由于格雷码是一种非加权码，不能直接反应出当前的角度值，所以必须在PLC 程序中将它转换成能反应当前实际位置的二进制码。

为了让我们的工程技术人员均能很好的掌握格雷码与二进制码之间的转换方法，我根据自己的一些经验和参考资料，将格雷码的相关知识作了些整理，在公司的刊物上发表出来，希望能和大家一起对这个问题来加以讨论和学习，共同提高我们的技术水平。

一、 格雷码格雷码（（Gray Code ）的概念格雷码是我们在工程中常会遇到的一种编码方式，例如，大多数绝对型旋转编码的输出就是采用格雷码的编码格式。

它是一种非加权码，由二进制码派生而来。

常用的二进制数与格雷码间的转换关系如下表：从上表我们可以看出，与普通二进制编码相比，格雷码的特点是相邻两个数之间只有1个二进制位发生了变化。

正是这个特点，使它更适合于用在数据传输的场合。

二、 二进制与格雷码之间的转换（一）、二进制码转为格雷码二进制码转为格雷码的算法较简单，将所需转换的数的二进制码右移一位后与原数相异或即可。

例：十进制数9的格雷码为：数值 二进制码格雷码 数值 二进制码格雷码0 0000 0000 9 1001 1101 1 0001 0001 10 1010 1111 2 0010 0011 11 1011 1110 30011 0010 12 1100 1010 40100 0110 13 1101 1011 50101 0111 14 1110 1001 60110 0101 15 1111 1000 70111 0100 81000 1100 9的二进制数形式 9的格雷码形式 9的二进制数右移1位后的结果 两者相异或（二）、格雷码转为二进制码格雷码转为二进制码的算法则较为繁琐，计算公式如下： Rn 为n 位的格雷码，Cn 为转换后的二进制码C n = R n ，C n-1 = R n R ⊕n-1，C n-2 = R n R ⊕n-1R ⊕n-2，…C 1 = R n R ⊕n-1R ⊕n-2…R ⊕⊕2R ⊕1，C 0 = R n R ⊕n-1R ⊕n-2…R ⊕⊕2R ⊕1R ⊕0例：格雷码(1001)转位二进制数C 4= R 4=1C 3= R 4⊕R 3=1⊕0=1C 2= R 4⊕R 3⊕R 2= C 3⊕R 2=1⊕0=1C1= R 4⊕R 3⊕R 2⊕R1= C 2⊕R 1=1⊕1=0三、 编程举例根据工业控制的特点，现分别给出在PLC 梯形图中和在VB 中实现格雷码转二进制码的程序。