正弦函数余弦函数的图像
- 格式：ppt
- 大小：1.08 MB
- 文档页数：14
下载文档原格式
合集下载
《正弦余弦函数图像》课件
可以使用数学软件或绘图工具绘制余 弦函数的图像。
图像具有对称性，关于y轴对称，且在 每个周期内有两个峰值和两个谷值。
图像描述
余弦函数的图像是一个周期性的波形 ，形状类似于拱门。
01
正弦与余弦函数的 对比
定义与性质对比
定义
周期性
奇偶性
振幅与相位
正弦函数是三角函数的一种， 定义为直角三角形中锐角的对 边与斜边的比值；余弦函数是 三角函数的另一种，定义为直 角三角形中锐角的邻边与斜边 的比值。
三角函数计算
在数学和物理领域，经常需要使 用正弦和余弦函数来进行三角函 数计算，解决实际问题。
01
习题与思考
基础习题
总结词
考察基础概念和图像绘制
详细描述
针对正弦和余弦函数的定义、性质和图像绘制进行基础习题练习，包括选择题、填空题和简答题等题 型，帮助学生巩固基础知识，提高解题能力。
进阶思考题
总结词
课程目标：掌握正弦 余弦函数图像的绘制 方法，理解其在生活 中的应用
学习目标
01
02
03
04
掌握正弦余弦函数的基本概念 和性质
学会使用数学软件绘制正弦余 弦函数图像
了解正弦余弦函数在生活和科 学领域中的应用实例
提高数学思维能力和分析能力
01
正弦函数图像
正弦函数的定义
总结词
周期性、波动性
详细描述
详细描述
可以使用多种工具绘制正弦函数的图像，如几何画板、Excel和手动画图。在几何画板中，可以自定义参数，观 察不同参数下图像的变化。在Excel中，可以使用其图表功能绘制正弦函数图像。手动画图则要求具备一定的绘 图技巧和理论知识。
01
余弦函数图02
正弦余弦正切函数图象
2
1-
643 34 6
y 3 1 3 3 1 3 0
3
3
o
1 -
2
-
3
2
x
2
(2) 描点
2-
(3) 连线
正切函数图像： ytanx,
y
xxR,且 xk2,kZ
思考：
2
正切函数 ytanx
1
图像是否有渐近线？
3 2
2
o
1 2
3 2
x
渐近线方程：
2
xk,(kZ)
2
二、三角函数图象的性质
上平移一个
单位得到的
.●
2
x
y=sinx
(2)按五个关键点列表
x
0
2
3 2
2
cosx 1 0 -1 0 1
-cosx
.y
1
o
-1 ●
-1 0 1 0 -y1= -cosx和
y=cosx 关
. y= cosx x [0,2 ] 于X轴对称 ●
.●
2
.
.3●
2
2
●
x
y= - cosx x [0, 2]
y=cosx
左移
2
y=cosx y=sinx
余弦曲线
返回目录
二、正弦函数的“五点画图法”
(0,0)、( , 1)、( ,0)、( 3 ,-1)、 (2 ,0)
2
2
y
1
●
●
0Hale Waihona Puke 2-1●3
2
●
●
2
x
y
●
1
●
0
2
-1
1-
643 34 6
y 3 1 3 3 1 3 0
3
3
o
1 -
2
-
3
2
x
2
(2) 描点
2-
(3) 连线
正切函数图像： ytanx,
y
xxR,且 xk2,kZ
思考：
2
正切函数 ytanx
1
图像是否有渐近线？
3 2
2
o
1 2
3 2
x
渐近线方程：
2
xk,(kZ)
2
二、三角函数图象的性质
上平移一个
单位得到的
.●
2
x
y=sinx
(2)按五个关键点列表
x
0
2
3 2
2
cosx 1 0 -1 0 1
-cosx
.y
1
o
-1 ●
-1 0 1 0 -y1= -cosx和
y=cosx 关
. y= cosx x [0,2 ] 于X轴对称 ●
.●
2
.
.3●
2
2
●
x
y= - cosx x [0, 2]
y=cosx
左移
2
y=cosx y=sinx
余弦曲线
返回目录
二、正弦函数的“五点画图法”
(0,0)、( , 1)、( ,0)、( 3 ,-1)、 (2 ,0)
2
2
y
1
●
●
0Hale Waihona Puke 2-1●3
2
●
●
2
x
y
●
1
●
0
2
-1
正弦函数、余弦函数的图像(完整)
(
3 2
,1)
(1) 列表(列出对图象形状起关键作用的五点坐标)
(2) 描点(定出五个关键点)
(3) 连y线(用光滑的曲线顺次连结五个点)
图象的最高点
1-
-
(0,1) (2 ,1)
与x轴的交点
-
-1
o
6
2
3
2 3
5
7
6
6
4 3
3 5
2
3
11 6
2
x
(
2
,0)
(
3 2
,0)
-1 -
图象的最低点 ( ,1)
三角函数
三角函数线
正弦函数 余弦函数 正切函数
sin=MP
正弦线MP cos=OM 余弦线OM tan=AT 正切线AT
y PT
-1
O
M A(1,0) x
正弦函数的图象
问题：如何作出正弦函数的图象？
途径：利用单位圆中正弦线来解决。
描图：用光滑曲线
y
B
1
将这些正弦线的 终点连结起来
A
O1
O
2
4
5
2
x
4
5 6 x
正弦、余弦函数的图象
如何由正弦函数图像得y 到余弦函数图像？
1
-4 -3
-2
- o
-1
2
3
4
5 6 x
正弦函数的图象
y=cosx=sin(x+ ), xR
2
余弦函数的图象
y
1
正弦曲 线
形状完全一样 只是位置不同
余弦曲 线
-4 -3
-2
- o
-1
正弦余弦函数的图象
陈经纶中学
高一备课组
复习
y r=1 α O M P(x,y)
y＝sinα= MP (正弦线 正弦线) 正弦线
x
y＝cosα=OM (余弦线 余弦线) 余弦线
正弦函数、 正弦函数、余弦函数
y=sinα y=sin x
一般地，我们用x表示自变量，即x表示角的大小， 表示自变量， 表示角的大小， 一般地，我们用 表示自变量 表示角的大小 表示函数值， 用y表示函数值，这样，我们就定义了任意角的 表示函数值 这样， 正弦函数y=sinx，其定义域为 正弦函数 ，其定义域为R.
上移1 上移1个单位
横坐标不变， 横坐标不变， 纵坐标伸长 为原来的2 为原来的2倍
沿x轴翻折
四、小结 小结
正弦、 正弦、余弦函数的图象
几何法 五点作图法（作图常用此法） 五点作图法（作图常用此法）
1. 正弦曲线、余弦曲线 正弦曲线、
2.注意与诱导公式、三角函数线等知识的联系 注意与诱导公式、 注意与诱导公式
●
-1 -2
3π 2
●
●
2π
x
练习（ ） 练习（2） 画y=-cosx，x∈[0, 2π]的简图 ， ∈ π 的简图 解：按五个关键点列表 π 3π π 2π x 0 2 2 cosx -cosx
y 1
1 -1
0 0
-1 1
0 0
1 -1
y=-cosx x∈ 2 ] [0, π
●
o
-1
●
π
●
2
π
y=cosx x∈ [0, 2π ]
y 1
π
2
y=cosx，x∈[0, 2π] ， ∈ π
π
2
−
o -1
高一备课组
复习
y r=1 α O M P(x,y)
y＝sinα= MP (正弦线 正弦线) 正弦线
x
y＝cosα=OM (余弦线 余弦线) 余弦线
正弦函数、 正弦函数、余弦函数
y=sinα y=sin x
一般地，我们用x表示自变量，即x表示角的大小， 表示自变量， 表示角的大小， 一般地，我们用 表示自变量 表示角的大小 表示函数值， 用y表示函数值，这样，我们就定义了任意角的 表示函数值 这样， 正弦函数y=sinx，其定义域为 正弦函数 ，其定义域为R.
上移1 上移1个单位
横坐标不变， 横坐标不变， 纵坐标伸长 为原来的2 为原来的2倍
沿x轴翻折
四、小结 小结
正弦、 正弦、余弦函数的图象
几何法 五点作图法（作图常用此法） 五点作图法（作图常用此法）
1. 正弦曲线、余弦曲线 正弦曲线、
2.注意与诱导公式、三角函数线等知识的联系 注意与诱导公式、 注意与诱导公式
●
-1 -2
3π 2
●
●
2π
x
练习（ ） 练习（2） 画y=-cosx，x∈[0, 2π]的简图 ， ∈ π 的简图 解：按五个关键点列表 π 3π π 2π x 0 2 2 cosx -cosx
y 1
1 -1
0 0
-1 1
0 0
1 -1
y=-cosx x∈ 2 ] [0, π
●
o
-1
●
π
●
2
π
y=cosx x∈ [0, 2π ]
y 1
π
2
y=cosx，x∈[0, 2π] ， ∈ π
π
2
−
o -1
正弦函数、余弦函数的图象 课件
〔跟踪练习1〕用“五点法”画出下列函数在区间[0,2π]上的简图． (1)y＝2－sinx；(2)y＝cosx－1．
[解析] (1)按五个关键点列表：
x
0
π 2
π
3π 2
2π
sinx
0
1
0
－1
0
2－sinx
2
1
2
3
2
描点并将它们用光滑的曲线连接起来(如图(1))．
(2)按五个关键点列表：
x
0
π 2
利用正、余弦函数的图象解三角不等式
典例 3 画出正弦函数 y＝sinx(x∈R)的简图，并根据图象写出 y≥12时 x 的 集合．
[思路分析] (1)作出 y＝sinx，与 y＝12的图象．(2)确定 sinx＝12的 x 值．(3)确 定 sinx>12的解集．
[解析] 用“五点法”作出 y＝sinx 的简图．
〔跟踪练习2〕关于三角函数的图象，有下列说法： ①y＝sin|x|与y＝sinx的图象关于y轴对称； ②y＝cos(－x)与y＝cos|x|的图象相同； ③y＝|sinx|与y＝sin(－x)的图象关于x轴对称； ④y＝cosx与y＝cos(－x)的图象关于y轴对称； 其中正确说法的序号是__②__④____．
〔跟踪练习 4〕函数 y＝sinx 与 y＝12x 的图象在(－π2，π2)上的交点有
A．4 个
B．3 个
C．2 个
D．1 个
( D)
π
3π 2
2π
cosx
1
0
－1
0
1
cosx－1
0
－1
－2
－1Βιβλιοθήκη 0描点并将它们用光滑的曲线连接起来(如图(2))．
正弦函数、余弦函数的图像 课件
2
6
6
为定义域.由定义域得 ≤1 sinx≤1,∴0≤ ≤2s1in,即x 值1 域
2
为{y|0≤y≤1}.
【归纳】利用正弦、余弦函数图象求解三角函数不等式的思路 以及方法步骤. 提示：(1)先作简图，然后观察在哪个区域能使不等式成立. (2)使用单位圆中的三角函数线与三角函数图象，都可求得满足 某些条件的角的范围，可先在［0,2π］的区间上找到适合不等 式的解，再根据诱导公式一写出整个定义域上的解集.
tanx
2
其图象如图所示.
②
……………………………………………………………………12分
【阅卷人点拨】通过阅卷后分析，对解答本题的失分警示和解题
启示总结如下：(注：此处的①②见规范解答过程)
在解答过程中，若忽略①处，就会在化简过程中忽视
①
该函数的定义域，造成扩大了定义域，使化简前后不 等价，画此函数图象时把不符合要求的点画出，造成
失
错误.
分
若没有考虑到该函数的定义域，则②处可能画成如图
警
所示的图象：
示 ②
把不符合要求的点都画出,导致错误.
解 题 启 示
(1)在作函数图象时，如果需要先对函数式化简，应 特别注意函数的定义域，使化简前后等价，不能使定 义域变小或扩大. (2)画出的函数图象应注意与定义域对应，不符合定 义域内的点应用虚点画出.
x
0
①
3
2π
2
2
-sinx
②
-1
0
③
0
①__________；②__________；③__________. 2.用“五点法”作出y=1+cosx(0≤x≤2π)的简图.
【解析】1.由五点作图法知①处应该填π;②处应填0;③处应填1. 答案：①π ②0 ③1 2.解题流程：
三角函数正弦函数余弦函数的图象
三角函数正弦函数余弦函数的图象xx年xx月xx日•引言•正弦函数图像•余弦函数图像目录•正弦与余弦函数图像的对比•应用•结论01引言三角函数是数学中的基础知识正弦函数和余弦函数是三角函数的重要组成部分图象是数学中重要的表达方式之一课程背景研究目的和意义理解正弦函数和余弦函数的图象及性质掌握函数图象的绘制方法理解函数图象在实际问题中的应用本文将分为以下几个部分：正弦函数和余弦函数的定义、正弦函数和余弦函数的图象及性质、函数图象的绘制方法以及实际应用案例分析我们将通过观察图象来理解正弦函数和余弦函数的性质，并通过绘制函数图象来解决实际问题本文结构02正弦函数图像正弦函数sin(x)表示直角三角形中一个锐角的对边与斜边的比值。
定义域实数集，即x∈(-∞,∞)。
值域[-1,1]，即sin(x)∈[-1,1]。
1 2 3正弦函数的图像呈现出一种波动或振荡的形状，以原点为中心，左右对称。
图像形状正弦函数是周期性的，即对于任意的x∈(-∞,∞)，都有sin(x+2kπ)=sin(x)，其中k为任意整数。
周期性正弦函数的振幅为1，即正弦函数的取值范围在-1到1之间。
振幅奇偶性正弦函数是奇函数，即对于任意的x∈(-∞,∞)，都有sin(-x)=-sin(x)。
最大值最小值正弦函数的最小正周期为2π，即在2π的时间内完成一次完整的波动。
在每个周期内，正弦函数达到最大值1和最小值-1。
导数求导得sin'(x)=cos(x)。
01020303余弦函数图像余弦定理c² = a² + b² - 2ab cos(C)余弦函数图像以y轴为对称轴，以原点为对称中心，取一段区间，可以是[0,π]或[-π/2,π/2]或[π/2,3π/2]等余弦函数cos(x) = 邻边/斜边 = (b²+c²-a²)/(2bc)余弦函数的图像是在y轴上，以原点为中心，向左右两侧同时对称延长的。
正弦,余弦函数的图像PPT教学课件
y= sinx，x[0, 2]
和
y=
cosx，x[
2
,
3 2
]的简图：
x
0 2
20
csionsx
10
01
3
3
2
2
22
-01
0-1
10
向左y平移 个单位长度 22
1
o
2
-1
3
2
2
y= cosx，x[ , 3 ]
22
y=sinx，x[0, 2]
2
x
正弦、余弦函数的图象
几何画法
小 1. 正弦曲线、余弦曲线 五点法 结
2 ,0)
( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0)
正弦、余弦函数的图象
y
1
-4 -3
-2
- o
-1
2
3
4
5 6 x
正弦函数的图象 y=cosx=sin(x+ ), xR
2
正弦曲 线
形状完全一样 只是位置不同
余弦函数的图象
y
余弦曲
-4 -3
-2
(0,11)
正弦、余弦函数的图象
X
正弦、余弦函数的图象
三角函数
三角函数线
正弦函数 余弦函数 正切函数
-1
sin=MP
正弦线MP cos=OM 余弦线OM tan=AT 正切线AT
y PT
O
M A(1,0) x
注意：三角 函数线是有 向线段！
正弦、余弦函数的图象
问题：如何作出正弦、余弦函数的图象？
途径：利用单位圆中正弦、余弦线来解决。
必修4正弦,余弦函数图像
y
y = cos x
π
x ∈ [0, 2π ]
-
1-
-
-1
o
-1 -
π
6
π
3
π
2
2π 3
5π 6
7π 6
4π 3
3π 2
5π 3
π 11 6
2π
x
在函数 y = cos x, x ∈ [0, 2π ] 的图象上，起关键作用的点有： 的图象上，起关键作用的点有： 最高点： 最高点： (0,1) (2π ,1) 最低点： 最低点：
9π −4π − 7π −3π 2 2
5π−2π 3π − 2 2
x∈R
−π
−
π 2
y
1
−
−
-1
π 2
π
3π 2π 5π 2 2
3π
7π 4π 9π 2 2
5π x
y 余弦曲线： 余弦曲线： = cos x
−
9π −4π 7π −3π 5π −2π 3π − − − 2 2 2 2
x∈R
−π
−
π 2
y
1
-1
π 2
π
3π 2π 5π 2 2
3π
7π 2
4π 9π 2
5π x
y
1-
y = sin x
x ∈ [0, 2π ]
-
-1
o
-1 -
π
6
π
3
π
2
2π 3
5π 6
π
7π 6
4π 3
3π 2
5π 3
11 π 6
2π
x
在函数 y = sin x, x ∈ [0, 2π ] 的图象上，起关键作用的点有： 的图象上，起关键作用的点有： 最高点： 最高点： (
正弦,余弦函数的图像PPT课件
途径：利用单位圆中正弦、余弦线来解决。
描图：用光滑曲线
y
B
1
将这些正弦线的 终点连结起来
A
O1
O
2
4
5
2
x
3
3
3
3
-1
y=sinx
终边相同角的三角函数值相等 即： sin(x+2k)=sinx, kZ
x[0,2]
f(x2k)f(x)利用图象平移
y=sinx xR
正弦、余弦函数的图象
y 1
o
2
2
-1
y=sinx x[0,2]
y
y=sinx xR
1
-4 -3
-2
- o
-1
3
2
x
2
正弦曲 线
2
3
4
5 6 x
正弦、余弦函数的图象
如何作出正弦函数的图象（在精确度要求不太高时）？
y
五点画图法
1
(2
,1)
( 2 ,1)
( ,0)
( 2 ,0)
五点法——
2
(
(0,0)o
(0,0)
2
(0,0)
-1
(0,0)
汇报人：XXX 汇报日期：20XX年10月10日
2 ,0) x
2 ,0)
( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0)
正弦、余弦函数的图象
y
1
-4 -3
-2
- o
-1
2
3
4
5 6 x
正弦函数的图象 y=cosx=sin(x+ ), xR
2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
练习：在同一坐标系内，用五点法分别画出函数 练习：在同一坐标系内， y= sinx，x∈[0, 2π] 和 y= cosx，x∈[ − 2 , ， ∈ π ， ∈
π
3π 2
]的简图： 的简图： 的简图
3π 22π
x
cosx sinx
−0
π
2
π
0 2
π2 0 -1
π
3π 2π
0 1 1 0 π y 向左平移 个单位长度 2 2
问题：如何作出正弦、余弦函数的图象？ 问题：如何作出正弦、余弦函数的图象？ 途径：利用单位圆中正弦、余弦线来解决。 途径：利用单位圆中正弦、余弦线来解决。
B
y 1
描图： 描图：用光滑曲线 将这些正弦线的 终点连结起来 终点连结起来
O1
A O
-1
π
3
2π 3
π
4π 3
5π 3
2π
x
y=sinx ( x ∈[0, 2π ] )
π π π 2π 5π
π
6
π
3
π
2
2π 3
5π 6
π
7π 6
4π 3
3π 2
5π 3
11 π 6
2π
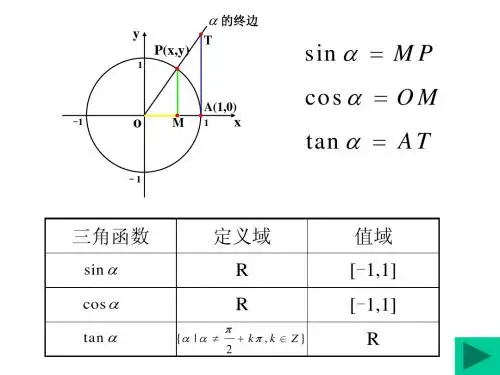
sin a ,cos a , tan a 的几何意义是什么?
y
T
1
P
A
正弦线MP sinα=MP α 余弦线OM cosα=OM α
o
M
1
x
正切线AT tanα=AT α
既然作与单位圆有关的三角函数线可得相应的角的 三角函数值,那么通过描点( x, sin x ) ,连线即可得到函数 y = sin x, x ∈[0,2π ] 的图象
描点并将它们用光滑曲线连 接起来
1
y y = sin x , x ∈ R 1
− 2π
−
3π 2
−π
−
π
2
o
π
2
-1
π
3π 2
2π
x
y=sinx，x∈[0, 2π] ， ∈ π
13
正弦、余弦函数的图象 正弦、
小 结
2.注意与诱导公式、三角函数线等知识的联系 注意与诱导公式、 注意与诱导公式
y 1
π
2
1. 正弦曲线、余弦曲线 正弦曲线、
几何画法 五点法
y=cosx，x∈[0, 2π] ， ∈ π
π
2 3π 2
−
o -1
π
2π
x
y=sinx，x∈[0, 2π] ， ∈ π
14
图象的最高点 0 ,1 ) (2π ,1) (
3π 2
,0)
9
2π 例1：（1）画出y=1+sinx , x∈[0，π ]的简图 ：（1 画出y=1+sinx x∈[0，
x
sinx
1 + sinx
0 0 1
π
2
π
0 1
3π 2
2π 0 1
1
-1 0
2 y 1. o -1
.
π 2
2
y = 1 + sinx, x ∈ [0,2π]
图象与x轴的交点( 0 , 0 ) (π , 0 ) (2π ,0) y = sin x, x ∈[0,2π ] 图象的最低点( − 1)
,1 )
3π 2,
图象的最高点 ( π 2
π y = cos x, x ∈ [0,2π ] 图象与x轴的交点( 2 , 0 ) ( 图象的最低点(π ,−1)
1
-1 0
0 1
y=sinx，x∈[0, 2π] ， ∈ π
−
π
2
o -1
π
2
π
3π ] 2 2
3π 2
2π
x
y= cosx，x∈[− π , ， ∈
12
思考：如何画出函数
解：按关键点列表
x sinx 0 π
2
π
0 0
-1 1
3π 2 1
2π
0 0
y = sin x 0
1.4.1正弦函数、余弦函数的图像
授课人：魏同花
物理中把简谐运动的图像叫做“正弦曲线” 物理中把简谐运动的图像叫做“正弦曲线”或“余弦曲 线”
沙漏单摆实验
知识探究：正弦函数y=sinx y=sinx的图象 知识探究：正弦函数y=sinx的图象
思考1 作函数图象最原始的方法是什么？ 思考1：作函数图象最原始的方法是什么？
1
π -4
π -3
π -2
-π
-1
o
π/2 π 3π/2 2 π
3 π
4 π
x
函数y=sinx, x∈R的图象 函数 ∈ 的图象
正弦曲线
正弦、 正弦、余弦函数的图象
y
1 -4π -3π -2π -π
o
-1
π
2π
3π
4π
5π
6π
x
正弦函数的图象 正弦函数的图象 y=cosx=sin(x+ ), x∈R
2
π
π
( π ,0) ( π ,0)
3π 2
( 2π ,0) ( 2π ,0)
2π
x
0 0
π
2
π 0
3π 2
1
-1
2π 0
6
y=sinx x∈[0,2π]
终边相同角的三角函数值相等 即： sin(x+2kπ)=sinx, k∈Z
f ( x + 2 kπ ) = f ( x ) 利用图象平移
y
y=sinx x∈R
−
π
五个关键点— 五个关键点
x
sinx
( ,1) ( 2π ,0) 2 (0,0) π -1 ( π ,0) (3π ,-1) ( ,1) ( 2π ,0) 3π 2 (0,0) π π3π ( π ,0)2 3,1) (2 ( 2π ,0) ( 2 ,1) ( π ,0) ( 2 ,1)π ( 3 ,1) ( 2π ,0) (0,0) π 2( 3,1) π (0,0) ( π ,0) ( 2π ,0) 2 3π π ( 2 ,1) (0,0) 3π ( 2 ,-1) ( 2π ,0) (π ,1) ( π ,0) (2 (0,0) 3π ( ,-1),-1) 2 2 ( 2π ,0) ( π ,0) ( 2 ,-1) ( 2 ,1) (0,0)
2
π
正弦曲 线
形状完全一样 只是位置不同
余弦函数的图象 余弦函数的图象
y
(0,1) 1
3π ( ,0) 2
( 2π ,1) 2π 3π 4π
余弦曲 线
5π 6π
8
-4π
-3π
-2π
-π
π (o ,0) 2 -1
π
( π ,-1)
x
像作二次函数图象那样为了快速用描点法 作出正弦曲线与余弦曲线。下面我们通过观察 函数图象寻找图象上起关键作用的点：
5
我们在作正弦函数y=sinx x∈[0,2 π]的图象时，描 的图象时， 我们在作正弦函数 ∈ 的图象时 出了12个点，但其中起关键作用的点是哪些？ 12个点 出了12个点，但其中起关键作用的点是哪些？分 别说出它们的坐标。 别说出它们的坐标。 y π 五点法
1
π
2
(0,0) o (0,0) ( ,1) 2π ( 2 ,1) π ( 2 ,1) ( π ,0)
.
π
. . 3π
2
2π π
x
y = sinx, x ∈ [0,2π]
（2）画出y=-cosx , x∈[0，2π]的简图
x 0 π 2 π 3π 2 2π
cosx
1
0
- 1
0
1
- cosx
y 1
- 1
0
1
0
- 1
y = − cosx , x ∈ [0,2π]
π 2 3π 2
O
π
2π
x
-1
y = cosx , x ∈ [0,2π]
答：列表、描点、连线 列表、描点、
7π 4π 3π 5π 11 π 让 取 , , , , , ,π, , , , , , 2π等值来列表 x 0 6 3 2 3 6 6 3 2 3 6
x sinx
0
思考2 用描点法作正弦函数y=sinx在[0， 思考2：用描点法作正弦函数y=sinx在[0， y=sinx 2π]内的图象 可取哪些点？ 内的图象， 2π]内的图象，可取哪些点？