当前位置：文档之家 › 理论力学达朗贝尔原理PPT课件

理论力学达朗贝尔原理PPT课件

  • 格式：ppt
  • 大小：5.77 MB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

《理论力学(Ⅰ)》PPT 第11章

《理论力学(Ⅰ)》PPT 第11章
第11章 达朗贝尔原理
11.1 惯性力·质点的达朗贝尔原理
设一个质量为m的质点，受到固定曲线约
束而沿此曲线运动，作用于质点的主动力为
F，约束力为N，其加速度为a。
牛顿第二定律 ma F N
F
F N ma 0
质点的惯性力：FI ma
ma N
⑴ 假想的，并不作用在质点上；
⑵ 应用时大小、方向分开；
FAy
l aC1 2 α1
ml FIC1 maC1 2 α1
M IC1
ml 2 12 α1
A
FIC1
FAx αM1
IC1
l aC2 lα1 2 α2
ml 2 M IC2 12 α2
FIC2
maC2
mlα1
ml 2
α2
Fmg C1aC1
B α FIC2
2
M IC2
mg C2aC2
Fix 0
ωα O aC ain
MO
MO JOα
Fi M O Fit α miri2 M
负号表示矩的转向与α相反
IO
x
C
FIO FIit
y
ait FIin
结论：⑴ 定轴转动刚体惯性力系向轴心简
化，结果为通过轴心的一个惯性力和一个惯
性力偶。 FIO MaC，M IO JOα ⑵ 定轴转动刚体惯性力系向质心简化，结
ae P
FIAe
ar
P sin 2φ
aB ae 2 Q P sin2 φ
B Q FIB
φ
N
例11-6 长为l、质量为m的两均质细杆AB和 BD，用光滑铰链B相连接，并自由地挂在铅 直位置。今以水平力F作用于AB杆的中点， 求此瞬时两杆的角加速度及A点的约束力。

理论力学第十四章 达朗贝尔原理与动静法 教学PPT

理论力学第十四章 达朗贝尔原理与动静法 教学PPT
Fi Ni Qi 0
mO (Fi ) mO (Ni ) mO (Qi ) 0
质点系达朗贝尔原理
Fi Ni Qi 0 mO (Fi ) mO (Ni ) mO (Qi ) 0
上式表明，在任意瞬时，作用于质点系的主动力、约束力和该点 的惯性力所构成力系的主矢等于零，该力系对任一点O的主矩也等于 零。
达朗贝尔原理一方面广泛应用于刚体动力学求解 动约束力；另一方面又普遍应用于弹性杆件求解 动应力。
工程实例
工程实例
爆破时烟囱怎样倒塌
工程实例
爆破时烟囱怎样倒塌
达郎贝尔原理
质点达朗贝尔原理
设质量为m的非自由质点M，在主动 力F和约束力N作用下沿曲线运动，
该质点的动力学基本方程为
N B
ma F N
考虑到式上式中的求和可以对质点系中任何一部分进行，而不限于 对整个质点系，因此，该式并不表示仅有6个平衡方程，而是共有3n个 独立的平衡方程。同时注意，在求和过程中所有内力都将自动消去。
达朗贝尔原理提供了按静力学平衡方程的形式给出质点系动力学 方程的方法，这种方法称为动静法。这些方程也称为动态平衡方程。
这表明，在质点系运动的任一瞬时，作用于每一质 点上的主动力、约束力和该质点的惯性力在形式上构成一 平衡力系。
这就是质点系的达朗贝尔原理。
质点系达朗贝尔原理
Fi Ni Qi 0
对于所讨论的质点系，有n个形式如上式的平衡方程， 即有n个形式上的平衡力系。将其中任何几个平衡力系合在 一起，所构成的任意力系仍然是平衡力系。根据静力学中 空间任意力系的平衡条件，有
Mac Mrc Macn Mrc 2
显然，当质心C在转轴上时，刚 体的惯性力主矢必为零。
z
RQn

第十四章达朗贝尔原理PPT课件

第十四章达朗贝尔原理PPT课件

M
* C
m L2
/ 12
29
S
F*x mg
M
* C
FA
F*y
2021/2/13 .
Fx m aCx 3m L Fy m aCy m L / 2 MC* m L2 / 12
取两约束力的交点为矩心
mS 0:
M C *F x 3 L F y L /2m/g 2 L 0
FB
3g
20 L
30
C
FN
2021/2/13 34
.
运动分析
根据运动分析加惯性力、惯性力偶
F*y
O F*x
A
acy
M
* A
acx
2mg
B
Ff
C
FN
acxao r
acyaco r
2021/2/13 35
.
MC 0
M * AF x*rFy*r2mg 0r
F*y
O
A
M
* A
B
Ff
F*x C
2mg
MO0
FN
M * AFfrFy*r2mg 0r
.
1、平移刚体
F2 *
m2 F1* m1 a2
F * m aC
Fn * mn an
F maC
a1
M 0 0
刚体平移时，惯性力系简化为 通过刚体质心的合力。
2021/2/13 12
.
2、定轴转动刚体
MO *
O
C
F
0
F 0 － m a C ＝ m (－ a τ C a C n)
M 0 ＝M O (F iτ)＝(－ m iri2) ＝JO －
2021/2/13 16

达朗贝尔定理PPT(完整版)

达朗贝尔定理PPT(完整版)
F A y0 0..7 35 5 m gF Iy 1.0 9k 6N
Theoretical Mechanics
例题
返回首页
定轴转动刚体的轴承动约束力
例题
mAy F 0,
0.75FAx 0.4FIx 0
FBx
0.40 0.75
FIx
4.0N
Fx 0, FAxFBxFIx 0
FAxFIx FBx3.0N
Theoretical Mechanics
返回首页
达朗贝尔原理
钢球随着筒壁作匀速圆周运动，只有法
向惯性力ＦI，大小F1 mr2 ，方向背离
中心 O。列出沿法线方向的平衡方程：
F n 0 i F N P co F 1 s 0
例题
FN
P
r2
g
cosa
FN 0
脱离角 1 arccosrg2
例题
由达朗贝尔原理
mF 0 ,Mm1 6 glco s0 这 解说：明设，AB在杆O 制转造至安装角转位速置比时较，高角的速转IO 度子、时角，加必速须度尽为量减、小质。心偏离转轴的距离e。
F 0 ,F F s i n F co 0 s 惯性力系向O点简化的主矢、主矩为
Theoretical Mechanics
Theoretical Mechanics 为了保证钢球在适当的角度脱离筒壁，故要求
Theoretical Mechanics
3 gcos
解：研究AB杆，画受力图
2l
飞轮作匀角速度 转动，半圆环的惯性力分布如图示，对应于微小单元体积的惯性力dFI为
设轮缘较薄，质量均匀分布，轮辐的质量忽略不计。
分离变量、积分，即 3g 在y向的静约束力和附加动约束力分别为

《达朗贝尔原理》课件

《达朗贝尔原理》课件
达朗贝尔原理的微分方程形式为：dM/dt=∫F·d(dr/dt)dr，其中dM/dt表示动量 矩对时间的变化率，dr/dt表示速度矢量，∫F·d(dr/dt)dr表示力矩对时间的积分 。
该微分方程描述了刚体在力矩作用下的动态行为，是刚体动力学中的基本方程之 一。
达朗贝尔原理的积分方程形式
达朗贝尔原理的积分方程形式为：M(t2)-M(t1)=∫t1t2F·dr， 其中M(t2)和M(t1)分别表示刚体在时刻t2和t1的动量矩， ∫t1t2F·dr表示在时间t1到t2之间力矩的积分。
船舶工程
用于分析船舶的运动特性和稳定性。
02
达朗贝尔原理的数学表达
达朗贝尔原理的公式表达
达朗贝尔原理的公式表达为： M=∫F·dr，其中M表示刚体绕固定 点O转动的动量矩，F表示刚体上任 一点的速度矢量，dr表示矢径。
该公式描述了刚体在力矩作用下的运 动规律，是刚体动力学中的基本原理 之一。
达朗贝尔原理的微分方程形式
限制条件
达朗贝尔原理在处理复杂系统时，可能无法考虑所有 相互作用力和能量转换，导致预测精度下降。
与其他物理定律的互补性
与牛顿第三定律互补
达朗贝尔原理与牛顿第三定律互补，强调了 力和运动的相互关系。
与能量守恒定律的互补性
达朗贝尔原理在处理保守系统时，与能量守 恒定律相一致，但在非保守系统中存在差异
。
详细描述
在弹性力学中，达朗贝尔原理可以用来分析 各种复杂的力学问题，如梁的弯曲、板的变 形等。通过应用该原理，我们可以建立各种 弹性力学问题的数学模型，并进一步求解其 解析解或近似解。
05
达朗贝尔原理的局限性
适用范围和限制条件
适用范围
达朗贝尔原理主要适用于线性、保守的力学系统。对 于非线性、非保守系统，达朗贝尔原理可能不适用。

理论力学课件 第十三章 达朗贝尔原理

理论力学课件 第十三章 达朗贝尔原理

MO(F) 0
FΙC
r
l 2
MΙC
MΙO
M
0
联立求解，可得
1 7.9rad / s2 2 4.44rad / s2
由ΣFx=0 解得轴承O 水平方向的约束反力
FOy
O
FOx M mg
A
FΙ C
M ΙO
C
M ΙC
m1 g
B
FOx
FC
m1( r1
l 2
2
)
8.91N
由ΣFy=0 解得轴承O 铅垂方向的约束反力
Fii
F 0 Ii
MO (Fie ) MO (Fii ) MO (F Ii ) 0
由于质点系的内力总是成对出现的，且等值反向共线，它们相互抵消，这样， 上面两式可简化为
Fie FIi 0
MO (Fie )
MO (FIi ) 0
上式表明，作用于质点系上的所有外力与虚加在每一个质点上的惯性力 在形式上组成平衡力系，这就是质点系达朗贝尔原理的又一表述形式。
解得
FI mgtan
由于
FI
man
m
v2 lsin
FN
an
v
mg FI
解得
v gl tan sin
【例13-2】 如图所示的列车在水平轨道上行驶，车厢内悬挂一单摆，摆锤的
质量为m。当车厢向右做匀加速运动时，单摆向左偏转的角度为 ，求车厢
的加速度a。
解：选摆锤为研究对象，受力分析 如图所示。由达朗贝尔原理，列x方向 的平衡方程
解得
FAx FBx 0
FAy 200kN
FBy 200kN
FAz 20kN
z
B FBx

理论力学第十四章达朗贝尔原理(动静法)课件

理论力学第十四章达朗贝尔原理(动静法)课件

动静法的物理意义
物理背景
实际应用
达朗贝尔原理反映了牛顿第二定律在 静力学中的应用，通过引入惯性力， 将动力学因素考虑到平衡问题中。
在工程实际中，达朗贝尔原理广泛应 用于分析高速旋转的机械、振动系统 以及瞬态动力学问题。
意义阐述
通过动静法，我们可以分析在某一瞬 时，运动系统由于惯性作用而产生的 力，从而更准确地描述系统的平衡条 件。
03
在应用动静法时，要确 保惯性力与主动力相平 衡，避免出现误差。
04
在求解方程时，要注意 解的物理意义和实际情 况是否相符。
04
CATALOGUE
达朗贝尔原理的应用实例
简单实例解析
总结词
通过一个简单的实例，介绍达朗 贝尔原理的基本应用。
详细描述
以一个单摆为例，运用达朗贝尔 原理分析其运动状态，通过对比 理论计算和实验结果，验证达朗 贝尔原理的正确性。
具体推导过程
在受力分析的基础上，列出系统的平 衡方程。
解出未知数，得到系统的运动状态。
将动静法应用于平衡方程，将惯性力 与主动力相平衡。具体来说，就是在 平衡方程中加入惯性力项，使得该力 与主动力相平衡。
推导过程中的注意事项
01
确定研究对象和系统时 要明确，避免出现混淆 。
02
在建立平衡方程时，要 确保所有力的方向和大 小都正确。
理论力学第十四章 达朗贝尔原理(动静 法)课件
contents
目录
• 达朗贝尔原理概述 • 达朗贝尔原理的基本概念 • 达朗贝尔原理的推导过程 • 达朗贝尔原理的应用实例 • 达朗贝尔原理的扩展与深化
01
CATALOGUE
达朗贝尔原理概述
达朗贝尔原理的定义

理论力学--达朗贝尔原理及其应用 ppt课件

理论力学--达朗贝尔原理及其应用 ppt课件
0tetftehtftegmmii2??????????????????????cossinsincoscos??????????0thftegmmi2????????????????coscos22i?emf?coscoscos22i2hgtemthftegmm??????????????????????31ppt课件?达朗贝尔原理应用示例例例题2长为l重为w的均质杆ab其a端闰接在铅垂轴z上并以匀角速绕此轴转动
FIti miait mi ri
FIni miain mi 2 ri
ppt课件
21
刚体作定轴转动时惯性力系的简化结果 再将平面惯性力系向点
O简化，得一力和一力偶。 因为所有质点的法向惯性力 都通过O点，所以所有质点 法向惯性力对O点之矩的和 等于零：
力偶的力偶矩等于惯性力系对转轴的主矩，其大小
为刚体对转轴的转动惯量与角加速度的乘积，方向与角
加速度的方向相反。
ppt课件
23
刚体作定轴转动时惯性力系的简化结果
讨论：
FIR

ma C

ma
t C

ma
n C
MI O MO ( FIti ) ( miri2 ) JO
电机所受真实力有m1g、 m2g 、 Fx 、Fy、M；惯性力如图所示。
惯性力的大小为 FI m2e 2
方向与质心加速度相反。因转子 匀速转动，只有法向加速度，故 惯性力方向沿O1O2向外。
应用动静法，由平衡方程
MA 0
M m2 g e cos t FI cos t(h e sin t) FI sin t(e cos t) 0
MIC MC (FIti ) ( miri2 ) JC

《理论力学》第十三章 达朗贝尔原理.ppt

《理论力学》第十三章 达朗贝尔原理.ppt

O
aCn C
A
Fix FOx－ma2lCn 2 mg sin 0
aCτ α
4.由动能定理计算2，T1-T2=∑Wi
1 2
J O 2

0

mg

l 2
sin

外力只有重力
例4: OB质量不计，AB长l、质量m。试求绳OA剪
HOHAI UNIVERSITY ENGINEERING MECHANICS
Fix FOx 0 （3）
4.补充方程
aC l / 2
FOx

0;
FOy

1 4
mg ;
3g
2l
HOHAI UNIVERSITY ENGINEERING MECHANICS
例3: 约束均质杆A端的绳索突然被剪断，试求杆转
到任一位置时的角加速度 、角速度及O处约束力
惯性系中：
0 FR ma FR FI
达朗贝尔原理将动力学加速度问题形 式上转换成静力学中的平衡问题，也 叫动静法
一、质点的达朗贝尔原理
ma FR F FN
FI
F
记

F N

ma

FI ma

0
称为质点的惯性力， 与加速度方向相反
则有 F FN FI 0


MIO MO (FIi ) MO FIi
MO miii miii
mi i2 JO
ω
MIO
FaOICFCρIii
i FIin
故定轴转动刚体惯性力系简化为：
作用在转轴上，且与质心加速 度方向相反的惯性力FI=maC 在对称平面内，转向与角加速度方 向相反的惯性力偶MIO=JOα

理论力学PPT课件第7章 达郎贝尔原理

理论力学PPT课件第7章 达郎贝尔原理

答：
2 aC 3 g
FT
1 3
mg
2021年11月2日
20
思考：
①匀质杆质量m,长L，接触面光滑。
求: 杆AB在图示水平位置静止释放时的角加速度。
解：杆作平面运动,此瞬时的角速度为零。
分别取A，B为基点，则有
2021年11月2日
21
acxacyaBaC B
acyacxaAaC A
aA
acx3L, acyL/2
交点上
2021年11月2日
16
§7.4 达朗贝尔原理的应用
例1 质量为m、长为L的匀质杆
AB在图示位置无初速释放。 求：释放瞬时杆AB的加速度、 柔索A、B内的拉力。
答：
agsin
FAFB
1mgcos
2
扩展性讨论
2021年11月2日
17
④已知滑轮A：m1、R1，R1=2R2，JO; 滑轮B：m2、R2，JC ；物体C：m3 求系统对O轴的动量矩。
56
FN
mg 29
2021年11月2日
27
例4 求匀质圆盘转动的角加速度和柔索的拉力。
2021年11月2日
答：
2mBg
mA 2mB
R
FT
mAmBg mA 2mB
扩展性讨论
28
例5 已知：两均质杆m, L。 求绳子剪断瞬时两杆的角加速度 1和2 ，
O
O
A
B
A
B
答： 1 0
2
3g 2L
2021年11月2日
2021年11月2日
37
思考:
如图(a)、(b)、(c)、(d)所示定轴转动情形，哪些情况 满足静平衡，哪些情况满足动平衡？

理论力学经典课件-第七章 达朗贝尔原理

理论力学经典课件-第七章 达朗贝尔原理

aD
O
研究整体，由MA=0，经化简得:
aO
mg AD
A
FAx
FN ml AD 2 3mg
图(b)
FAy
(b)
7-3 动静法的应用
7-3-2 典型问题
再研究轮与BD杆，由MD=0,并注意到式(a),得
1 3 3 FN l AD mg (c) 3 2 F (b) – (c) 得
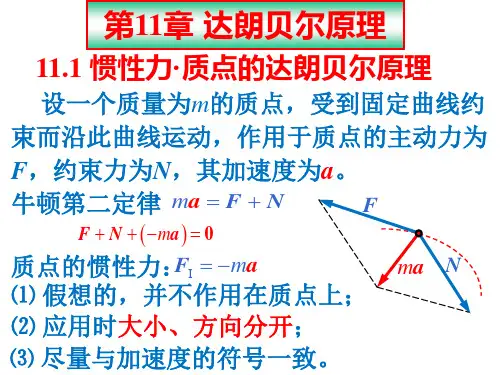
1. 质点达朗贝尔定理 由 F FN m a 即 F FN m a 0
FI ma
m
FN
引入惯性力 FI m a
F
ma
则 F FN FI 0 — 质点的达朗贝尔定理 即作用于质点的主动力，约束力与惯性力构成平衡力系。
2.关于惯性力: 1) 质点加速运动时,外部物质世界作用在质点上的
已知 G, ,求BC绳断瞬时,求AB绳张力。
A
C

FI
给小球加惯性力, 受力如图。 由 FT G FI 0
FT
B
a
FI
G
FT G cos
7-1 质点系的达朗贝尔原理
G FT
7-1-2 质点系的达朗贝尔原理 1. 一般形式 对 mi 有:
Fi e FNi FIi 0
FN
FBy
B
aD
aO
FBx
mg
图(b)
mg AD
A
FAx
FAy
图(c)
7-3-2 典型问题
运动至AEB水平时，速度如图(d)，易知BD=AD。
vB 3lωAD
由T–T0=W，有
(d)
B
B
C
E
A

理论力学PPT课件第7章达郎贝尔原理

理论力学PPT课件第7章达郎贝尔原理

动力学方程的概念
总结词
动力学方程是描述系统运动状态变化的数学方程，包括牛顿第二定律、动量守恒定律、角动量守恒定律等。
详细描述
动力学方程是描述系统运动状态变化的数学模型，包括牛顿第二定律、动量守恒定律、角动量守恒定律等。这些 方程描述了系统在不同条件下运动状态的变化规律，是理论力学中的基本方程。通过求解动力学方程，可以预测 系统在不同条件下的运动状态。
冲量
在给定的时间间隔内，力对物体 的积累效应，等于物体动量的增 量。
达郎贝尔原理的重要性
揭示了力的作用效果
达郎贝尔原理揭示了力的作用效果与 冲量之间的关系，为研究动力学问题 提供了重要的理论基础。
简化问题
通过引入冲量，可以将复杂的动力学 问题简化为更易于处理的形式，有助 于理解和分析物体的运动规律。
等效约束反力在任意虚位移上所做的虚功等于原系统在相同 虚位移上所做的内力虚功。
达郎贝尔原理的证明方法
证明方法一
利用虚功原理和牛顿第二定律推 导达郎贝尔原理。
证明方法二
利用拉格朗日方程和约束反力推导 达郎贝尔原理。
证明方法三
利用哈密顿原理和变分法推导达郎 贝尔原理。
04
CATALOGUE
达郎贝尔原理的应用实例
广义达郎贝尔原理的意义
这个原理是经典力学和量子力学中的重要原理，对于理解 物理系统的动力学行为和演化规律具有重要意义。
非惯性系中的达郎贝尔原理
非惯性系中的达郎尔原理
在非惯性系中，由于存在额外的惯性力，达郎贝尔原理的形式会有所不同。此时，系统受 到的外力等于动量的时间变化率。
非惯性系中的达郎贝尔原理推导
理论力学ppt课件第 7章达郎贝尔原理
目 录
• 达郎贝尔原理的概述 • 达郎贝尔原理的基本概念 • 达郎贝尔原理的推导过程 • 达郎贝尔原理的应用实例 • 达郎贝尔原理的扩展与深化

理论力学 第十五章 达朗伯原理.ppt

理论力学 第十五章 达朗伯原理.ppt

④虚加惯性力。在受力图上画上惯性力和惯性力偶，一定要
在 正确进行运动分析的基础上。熟记刚体惯
性力系的简化结果。 ⑤列动静方程。选取适当的矩心和投影轴。
⑥建立补充方程。运动学补充方程（运动量之间的关系）。
静平衡与动平衡的概念
§15-1 惯性力的概念
一、惯性力的概念 人用手推车 F ' F ma
力 F '是由于小车具有惯性，力图保持原来
的运动状态，对于施力物体(人手)产生的
反抗力，称为小车的惯性力。
定义：质点惯性力 FI ma 加速运动的质点，对迫使其产生加速运动的物体的惯
性反抗的总和。
惯性力的大小等于质点的质量与其加速度的乘积，方
向与加速度的方向相反，不作用于运动质点本身，而作用
于周围的施力物体。
4
惯性力在直角 坐标轴上的投影：
FIx

max

m
d2x dt2
FIy

may

m
d2y dt2
FIz

maz

m
d2z dt2
惯性力在自然 坐标轴上的投影：
FI

ma
授课教师：薛齐文 土木与安全工程学院力学教研室
本章介绍动力学的一个重要原理——达朗伯原理。应用 这一原理，就将动力学问题从形式上转化为静力学问题，从 而根据关于平衡的理论来求解。这种解答动力学问题的方法， 因而也称动静法。
2
第十五章 达朗伯原理
§15–1 惯性力的概念 §15–2 达朗伯原理 §15–3 刚体惯性力系的简化 ＊§15–4 定轴转动刚体的动约束力
则有：


FFiii e M0
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
达朗贝尔原理应用于每个质点，得到n个矢量平衡方程。
Fi FNi Fi* 0
这表明，在质点系运动的任一瞬时，作用于每一质 点上的主动力、约束力和该质点的惯性力在形式上构成一 平衡力系。
这就是质点系的达朗贝尔原理。
§ 5-2 达朗贝尔原理 质点系达朗贝尔原理
Fi FNi Fi* 0
注意
惯性力系的主矢与刚体的运动形式无关。
惯性力系的主矩与刚体的运动形式有关。
§ 5-2 惯性力系的简化
二、刚体常见运动情况下惯性力的主矢和主矩 1. 刚体作平动 刚体平移时，惯性力系向质心简化
● 主矢
F*2
m2 F*1
m1 a2
a1
F *＝ (－miai )
F* M aC F*n mn an
MO

M
* O

0
1.惯性力系的主矢
由质心运动定理有 F = maC ,得
F* maC
即,质点系惯性力的主矢恒等于质点系总质量与质心加速度的乘积，而 取相反方向。
§ 5-2 惯性力系的简化
2.惯性力系的主矩
● 对任意固定点
由对任意固定点O的动量矩定理有
MO

d LO dt
，
得
M
* O


d LO dt
对于所讨论的质点系，有n个形式如上式的平衡方程， 即有n个形式上的平衡力系。将其中任何几个平衡力系合在 一起，所构成的任意力系仍然是平衡力系。根据静力学中 空间任意力系的平衡条件，有
Fi FNi Fi* 0
MO (Fi ) MO (FNi ) MO (Fi* ) 0
● 对固定轴
代入
MO

M
* O
0
现将上式两端投影到任一固定轴Oz上，
M
* z


dLz dt
上式表明：质点系的惯性力对于任一固定点（或固定轴）的主矩，
等于质点系对于该点（或该轴）的动量矩对时间的导数，并冠以负号。
§ 5-2 惯性力系的简化
● 对质心点
惯性力系的主矩
利用相对于质心的动量矩定理，可以得到质点系的惯性力对质
设质量为m的非自由质点M，在主动
力F和约束力FN作用下沿曲线运动，
FN
该质点的动力学基本方程为
B
ma F FN
或
F* M
ma a
F FN (ma) 0
引入质点的惯性力F* =－ma 这 一概念，于是上式可改写成
AF
F FN F* 0
上式表明，在质点运动的每一瞬时，作用于质点的主动力、约束力和 质点的惯性力在形式上构成一平质点系达朗贝尔原理
Fi FNi Fi* 0 MO (Fi ) MO (FNi ) MO (Fi* ) 0
上式表明，在任意瞬时，作用于质点系的主动力、约束力和该点 的惯性力所构成力系的主矢等于零，该力系对任一点O的主矩也等于 零。
§ 5-2 达朗贝尔原理 质点达朗贝尔原理
质点达朗贝尔原理
F FN F* 0 质点达朗贝尔原理的投影形式
Fx FNx Fx* 0 Fy FNy Fy* 0 Fz FNz Fz* 0
§ 5-2 达朗贝尔原理
二、质点系达朗贝尔原理 上述质点的达朗贝尔原理可以直接推广到质点系。将
aC aCt aCn
设质心C的转动半径为rC，则 Ft* 和 Fn* 的大小可分别表示为
Fn*
aCt
O
y
C aCn
x
Ft*
F * Ft* Fn*
§ 5-2 惯性力系的简化
刚体做定轴转动
F * Ft* Fn*
z
其中 Ft* maCt ; Fn* maCn ;
动力学
达朗贝尔原理
动力学
第
§5– 1 达朗贝尔原理
五
章
§5–2 惯性力系的简化
达
§5–3 动静法应用举例
朗
贝 尔
§5–4 定轴转动刚体对轴承的动压力
原
§5–5 消除附加动压力的条件
理
·动平衡和静平衡
目录
第五章 达朗贝尔原理
引言
达朗贝尔原理为解决非自由质点系的动力学问题提供了 有别于动力学普遍定理的另外一类方法。
＝ (－miaC )＝－maC
● 主矩 M *＝0
刚体平移时，惯性力系简化为通过刚体质心的合力。
§ 5-2 惯性力系的简化
刚体做定轴转动
2. 刚体做定轴转动
具有质量对称平面的刚体绕垂直于对称平面的固定轴转动。
设刚体绕固定轴Oz转动，在任意瞬
时的角速度为ω，角加速度为α。
z
● 主矢 F *＝ (－miai ) ＝－maC
考虑到上式中的求和可以对质点系中任何一部分进行，而不限于 对整个质点系，因此，该式并不表示仅有6个平衡方程，而是共有3n个 独立的平衡方程。同时注意，在求和过程中所有内力都将自动消去。
达朗伯原理提供了按静力学平衡方程的形式给出质点系动力学方 程的方法，这种方法称为动静法。这些方程也称为动态平衡方程。
引进惯性力的概念，将动力学系统的二阶运动量表示为惯 性力，进而应用静力学方法研究动力学问题 —— 达朗贝 尔原理。
达朗贝尔原理一方面广泛应用于刚体动力学求解动约束 力；另一方面又普遍应用于弹性杆件求解动应力。
第五章 达朗贝尔原理
工程实际问题
第五章 达朗贝尔原理
工程实际问题
爆破时烟囱怎样倒塌
§ 5-2 惯性力系的简化
惯性力系的简化
刚体常见运动情况下 惯性力的主矢和主矩
§ 5-2 惯性力系的简化
一、 惯性力系的简化
对于作任意运动的质点系，把实际所受的力和虚加惯性力各自向
任意点O简化后所得的主矢、主矩分别记作F，MO 和F* ，M*O ，于是，
由力系平衡条件，可得
F F* 0
心C的主矩表达式 ● 对质心轴
M
* C

dLC dt
以及它在通过质心C的某一平动轴 Cz上的投影表达式
M
* z


dLz dt
上式表明：质点系的惯性力对质心（或通过质心的平动轴）的主 矩，等于质点系对质心（或该轴）的动量矩对时间的导数，并冠以负 号。
§ 5-2 惯性力系的简化 惯性力系的主矩
第五章 达朗贝尔原理
工程实际问题
爆破时烟囱怎样倒塌
第五章 达朗贝尔原理
车底盘距路面的高度为什么不同？
第五章 达朗贝尔原理
舰载飞机降落过程中的动力学问题
拦阻装置为什么装在飞机的后部？
§ 5-1 达朗贝尔原理
质点达朗贝尔原理 质点系达朗贝尔原理
§ 5-2 达朗贝尔原理
一、质点达朗伯原理