高中数学最全的思维导图

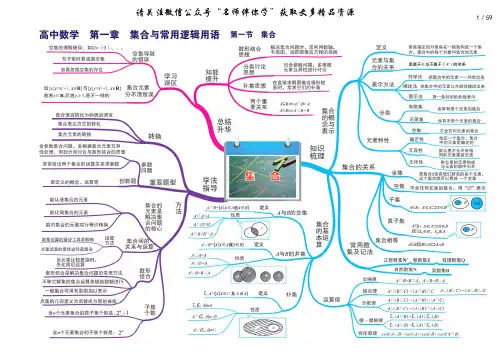
高中数学思维导图高中数学思维导图一、基础数学思维1. 数学思想的基础：公理与定义2. 数学的证明方法：归纳法、反证法、直接证明法等3. 数学符号的运用：数学符号的含义、符号的运算法则等4. 数学运算：四则运算、幂运算、根号运算等5. 基础数学工具：比例、百分数、坐标系、三角函数等二、代数思维1. 代数基础：代数式、方程、函数等2. 函数的性质：奇偶性、周期性、单调性等3. 多项式函数：求极限、图像、导数、零点等4. 三角函数：定义、性质、公式、图像等5. 指数与对数：定义、性质、公式、应用等三、几何思维1. 几何基础：点、线、面、角等基本概念2. 几何证明：直线、三角形、四边形等几何图形的证明方法3. 圆与圆周角：圆的性质、圆心角、圆周角等4. 圆锥曲线：椭圆、双曲线、抛物线等5. 空间几何：立体图形、体积、表面积等四、数据思维1. 统计学基础：数据的收集、整理、描述等2. 统计学方法：中心极限定理、样本误差、置信区间等3. 概率学基础：试验、随机事件、概率等4. 概率学应用：概率分布、期望、方差等5. 统计学计算：统计量、协方差、相关系数等五、应用思维1. 数学建模：基础模型、优化模型、决策模型等2. 实际应用：金融、物流、航空、生物等实际问题的数学分析3. 数学思维应用：思维方法的应用于科学、技术、文化、艺术等领域4. 跨学科思维：数学与其他学科的融合，如数理化、数理生等交叉学科5. 数学思维与未来：数学思维在新时代的重要性和应用前景六、总结与展望1. 数学思维的学习方法2. 数学思维的培养和提升3. 数学思维在求学与职场中的应用4. 数学思维的发展趋势和未来展望5. 数学思维对人类文明进步的贡献。

高中数学最全的思维导图—倾科角和糾率—（倾斜角加化詡率的变厂）直线的万程T徐距----- (・4 區F/i=0 ) 玄鸟,-&出产0 )直线方程的形式L垂克•（ *吐+8】民二0)—点斜式2 $-比=曲一心）———辭飲式：3=fcr+b k祈7 厂＞】一以一心两弑Exr—*擬式；-^1=1—」般式：jj+5y+C=0两宜线的交点|饪童各种形式的对牡筷麻aa J压童;故距可正 .可员〉也可为oj点到线的距断e笥第3平僚间距哥匸黑圆的方程囚的标准方程因的一般方程晝线与圈討位赛壬紊两圍的位賈关系—I 瘫（一（、＜0,或-| 相切［―（\=0,或箜尸（、＞0,或tfO ）三角函数的圉隊平面向里角的槪念弧度制任意角的三角函数的走义同角三角函数的关系诱导公式和角、差角公式二倍角公式正弦函数）=nnx—余弦因数尸0X —)=Jsm(^uc+ ~弧长公式、扇形面积公式三角函数线_（化际求值、豳（恒等变形）走义域奇偶性单调性周期性对称性|—最值值城囹象4寸称轴（正切函教廉外八经过函数图象的最高（或低）点且垂直乂轴的直线，对不中心是正余弦函敎圏象的零点，正切函數的对称中心为（V> 0）（t€Z） / V2J①囹象可由正弦曲线经过平移V伸缩得到，但要注意先平移后伸缩与先伸缩后平移不同;②图象也可以用五点作囹法；③用整体代换求单调区间（注意啪符号〉；@最小正周期丁=于；⑤对称轴J" 二对称中心为（W，小（.疋Z）•数列不等式就念表示「歹戚去—通项公式——家和公式——性履—1——J—I通项公式—I通擅公式I—I爹蚤数列h—I爭比数列卜* :怜辛数列与苓比数列的类* J(‘=ai+ (并-(ai+a丄牛十①\(1丄护)爭差册方苓比数列的类比ffi H项和s /6+ad前w I彎g>0)匚二妬乔①却］一厶=/(")③条•尸皿r卜&勞f許“转为®t谡商案就J 冃造華比数列附鬥］-(公式法：应用尊绘・爭比數列筛”项和公式j常见通推类型及方法常见求和方注T不爭式时歩T -元二次不爹式错位扌em )助二;炮戮的图象J-C三个二次的关系)-)可行域| pH -沁歐：czp卜r—简单的细中規划几何碌兀的口倍•>轴上J IM潮希丿二二、/(工-莎十()-0)：:构锻距离和10L别»大,积疋亀和最小、应用^注熱一芷三亡相手丿「I异面宜线所成的角卜「范倒：（OS 90・）空间炳 --------- 宜线与平面術成的角卜（范困：［0。

一张思维导图掌握高一数学必修1全部知识点，冲刺满分
1.3基本初等函数及其性质
1.指数函数
（1）了解指数函数模型的实际背景.（2）理解有理指数幂的含义，了解实数指数幂的意义，掌握幂的运算.（3）理解指数函数的概念，理解指数函数的单调性，掌握指数函数图像通过的特殊点.（4）知道指数函数是一类重要的函数模型.
2.对数函数
（1）理解对数的概念及其运算性质，知道用换底公式能将一般对数转化成自然对数或常用对数；了解对数在简化运算中的作用.（2）理解对数函数的概念，理解对数函数的单调性，掌握对数函数图像通过的特殊点.（3）知道对数函数是一类重要的函数模型.（4）了解指数函数与对数函数互为反函数.
3.幂函数
（1）了解幂函数的概念.（2）结合幂函数的图像，了解它们的变化情况.
表1-2基本初等函数图像及性质
1.4函数的应用
1.函数与方程
(1)结合二次函数的图像，可以了解函数零点与方程根的关系，判断一个二次方程根的存在性和个数。

(2)根据具体函数的图像，用二分法求出相应方程的近似解。

2.函数模型及其应用
（1）了解指数函数、对数函数以及幂函数的增长特征，知道直线上升、指数增长、对数增长等不同函数类型增长的含义.（2）了解函数模型（如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型）的广泛应用.
1.5函数图像变换。