【】Matlab 小波工具箱入门

• 常用的小波基函数。 • 连续小波变换及其应用。 • 离散小波变换及其应用。 • 小波包变换。 • 信号和图像的多尺度分解。 • 基于小波变换的信号去噪。 • 基于小波变换的信号压缩。
2021/7/28
常用的小波基函数：
参数表示
morl mexh meyr haar dbN symN coifN biorNr.Nd
whitnois.mat
warma.mat
wstep.mat
nearbrk.mat
scdd/7/28
……
说明
三个正弦函数的叠加 存在频率断点的组合正弦信号 均匀分布的白噪声 有色AR(3)噪声 阶梯信号 分段线性信号 具有二阶可微跳变的信号 叠加了白噪声的斜坡信号
加窗Fourie变 r 换：STFT( f ) f , gt, f ,0,0,0(t)
小波变换： WT( f )(a,t) f , gt,0,a,0,0(u)
高斯线调频小波变换 GC：T(s)(t, f ) s(u),gt, f ,log(t),0,q(u)
1 s(u)exp [1(ut)2]exp [j2( fuqu2)]du
说明： s:输入信号 scales: 需要计算的尺度范围 wname:所用的小波基 plot: 用图像方式显示小波系数
2021/7/28
例子：
•
c = cwt(s,1:32,'meyr')
•
c = cwt(s,[64 32 16:-2:2],'morl')
•
c = cwt(s,[3 18 12.9 7 1.5],'db2')
2021/7/28
• Goodman等提出多小波的概念，其基本思想是将单小 波中由单个尺度函数生成的多分辨分析空间，扩展为 由多个尺度函数生成，以此来获得更大的自由度。 1994年，Geronimo,Hardin和Massopus构造了著名的 GHM多小波。它既保持了单小波所具有的良好的时域 与频域的局部化特性，又克服了单小波的缺陷，将实 际应用中十分重要的光滑性、紧支性、对称性、正交 性完美地结合在一起。与此同时，在信号处理领域， 人们将传统的滤波器组推广至矢值滤波器组、块滤波 器组，初步形成了矢值滤波器组的理论体系，并建立 了它和多小波变换的关系。

2. 抽取近似系数和细节系数 从C中抽取3层近似系数 cA3 = appcoef(C,L,'db1',3); 从C中抽取3、2、1层细节系数 cD3 = detcoef(C,L,3); cD2 = detcoef(C,L,2); cD1 = detcoef(C,L,1); 或者 [cD1,cD2,cD3] = detcoef(C,L,[1,2,3]);
subplot(2,1,1);plot(s); title('Original')
subplot(2,1,2);plot(A3); title('Level 3 Approximation')
阈值去噪
当然，摒弃所有高频信息，我们会失去原始信号中的很多最尖锐的特 征。最佳的去噪需要通过一种更精细的叫阈值方法，它只丢弃部分超 过一定范围的细节。
一层小波分解分析 多层小波分解及粗糙去噪 阈值去噪
一层小波分解分析
我们用一个真实世界的信号----测量3天的电功耗， 这个信号很典型，因为它包含一个很明显的测量噪声，而 小波分析以有效的移除噪声。
一层小波分解分析
一维分析----使用命令行
1. 加载信号 load leleccum 截取信号 s = leleccum(1:3920); l_s = length(s); 2. 对信号执行一层小波分解 使用db1小波执行一层小波分解，执行下面的语句产生近似系数cA1、 细节系数cD1 [cA1,cD1] = dwt(s,'db1');
阈值去噪
cD1,cD2,cD3是向量，那么我们就可以通过直接操纵这些向量来达到 目的，即设置这些向量小于其峰值或平均值的一部分，然后就可以由 这些设定了阈值的系数重建新的细节信号D1、D2、D3。 实际去噪过程中，可以使用ddencmp函数来计算默认的阈值参数，然 后用wdencmp函数来执行实际的去噪过程，代码如下： [thr,sorh,keepapp] = ddencmp('den','wv',s); clean = wdencmp('gbl',C,L,'db1',3,thr,sorh,keepapp); 注意wdencmp使用了第1步中小波分解的结果C、L，另外指定了db1小 波来做分析，指定全局阈值选项gb1.

(2011-11-10 20:12:39)转载▼分类：学科知识标签：小波分析连续小波变换尺度系数信号最近想尝试一下小波的用法，就这matlab的帮助尝试了一下它的例子，顺便翻译了一下帮助的内容，发现matlab帮助做的确实不错，浅显易懂！现把翻译的文档写出来吧，想学习的共同学习吧！小波工具箱简介小波工具箱包含了图像化的工具和命令行函数，它可以实现如下功能：l 测试、探索小波和小波包的特性l 测试信号的统计特性和信号的组分l 对一维信号执行连续小波变换l 对一维、二维信号执行离散小波分析和综合l 对一维、二维信号执行小波包分解（参见帮助Using Wavelet Packets）l 对信号或图像进行压缩、去噪另外，工具箱使用户更方便的展示数据。

用户可以做如下选择：l 显示哪个信号l 放大感兴趣的区域l 配色设计来显示小波系数细节工具箱可以方便的导入、导出信息到磁盘或matlab工作空间。

具体详见File Menu Options一维连续小波分析这一部分来测试连续小波分析的特性。

连续小波分析只需要一个小波函数cwt。

在这一部分将学到如下内容：l 加载信号l 对信号执行连续小波变换l 绘制小波系数l 绘制指定尺度的小波系数l 绘制整个尺度小波系数中的最大值l 选择显示方式l 在尺度和伪频率之间切换l 细节放大l 在普通或绝对模式下显示系数l 选择执行小波分析的尺度使用命令行执行连续小波分析这个例子是一个包含噪声的正弦波1. 加载信号load noissin可以使用whos显示信号信息2. 执行连续小波变换c = cwt(noissin,1:48,'db4');函数cwt的参数分别为分析的信号、分析的尺度和使用的小波。

返回值c包含了在各尺度下的小波系数。

对于这里，c是一个48x1000的矩阵，每一行与一个尺度相关。

3. 绘制小波系数cwt函数可以接受第四个参数，来指定函数在执行结束后是否绘制连续小波变换系数的绝对值。

连续小波发换：
格式： coefs=cwt(s,scales,’wname’) coefs=cwt(s,scales,’wname’,’plot’) 说明： s:输入信号 scales: 需要计算的尺度范围 wname:所用的小波基 plot: 用图像斱式显示小波系数
例子：
c = cwt(s,1:32,'meyr') c = cwt(s,[64 32 16:-2:2],'morl') c = cwt(s,[3 18 12.9 7 1.5],'db2')
q j t 2 2 1 j t 2 p
g (t )
g (t )
发换的统一表述：
将五种变换分别用下标 表示： g t0 , f 0 ,a , p ,q (t ) 则： ˆ Fourier 变换：f f , g 0, f ,0,0, 0 (t ) 加窗Fourier 变换：STFT( f ) f , g t , f ,0, 0, 0 (t ) 小波变换：WT ( f )(a, t ) f , g t , 0,a , 0,0 (u ) 高斯线调频小波变换： GCT ( s )(t , f ) s (u ), g t , f ,log(t ),0,q (u ) 1 1 u t 2 s (u ) exp[ ( ) ] exp[ j 2 ( fu qu2 )]du 2 T t
coifwavf biowavf
计算近似对称的紧支集双正交小波滤波器系数
计算Coifmant小波尺度滤波器系数 计算双正交样条小波尺度滤波器参数
wname='bior2.2'; [rf,rd]=biorwavf(wname)
rf =

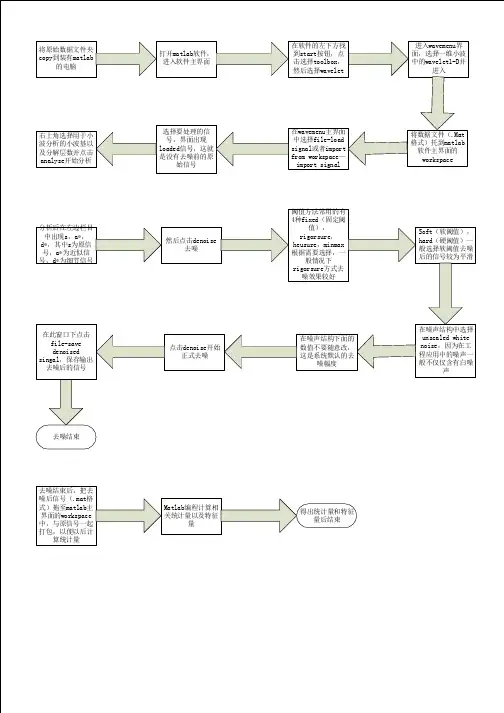
小波分析MATLAB工具箱简介MATLAB的小波分析一、小波分析用于降噪的基本过程1、分解过程：选定一种小波，对信号进行N层分解；2、作用阈值过程：对分解得到的各层系数选择一个阈值，并对细节系数进行软阈值处理；3、重建过程：降处理后的系数通过小波重建恢复原始信号；二、基本降噪模型函数一维离散小波分解命令Dwt [cA cD] = dwt(X,’wname’)使用小波’wname’对型号X 进行单层分解，求得的近似系数存放于数组cA中，细节系数存放在数组cD 中；[cA cD] = dwt(X,’wname’,’mode’,MODE) 利用MODE方式进行扩展[cA cD] = dwt(X,Lo_D,Hi_D) 利用指定滤波器进行小波分解Wanedec [C, L] = wavedec(X,N,’wname’) 使用wname的小波进行N层分解，C为层数，L为各层系数Idwt X= idwt(cA,cD,’wname’) 利用小波wname把近似系数CA和CD重建为上一层近似系数XX= idwt(cA,cD,’wname’,L) 重建至L层Waverec X= waverec（C，L，‘wname‘）重建为原始信号Wrcoef X = wrcoef(‘type’,C,L,’wname’,N) 通过分解系数重构指定的数，type为a 或者dX= wrcoef(‘type’,C,L,’wname’) 把分解系数重建至最高层Upcoef Y= upcoef（O,X,’wname’,N）用适当的滤波器作用在X上N次，求得重建系数Y，O为a表示低通滤波器，d表示高通滤波器Detcofe D= detcoef（C，L，N）从分解系数中提取第N层近似系数D= detcoef（C，L，N）提取至最后一层Appcoef A= appcoef(C,L,’wname’,N) 用小波从分解系数中提取第N层系数Wnoisest stdc = woisest（c,l,s）根据传入的小波分解系数[c,l]对s中标识的小波层数求得其标准差，作为对噪声强度的估计；Ddencmp [THR,SORH,KEEPAPP,CRIT] = ddencmp(IN1,IN2,X) 根据传入的参数IN1 和IN2所指定的方式，对输入信号X求得其降噪或压缩的各级阈值。

选择要处理的信 号，界面出现 loaded信号，这就 是没有去噪前的原 始信号
在wavemenu主界面 中选择file-load signal或者import from workspace— import signal
将数据文件（.Mat 格式）托到matlab 软件主界面的 workspace
分析后在左边栏目 中出现s，a*， d*，其中s为原信 号，a*为近似信 号，d*为细节信号
点击denoise开始 正式去噪
在噪声结构下面的 数值不要随意改， 这是系统默认的去 噪幅度
在噪声结构中选择 unscaled white noise，因为在工 程应用中的噪声一 般不仅仅含有白噪 声
去噪结束
去噪结束后，把去 噪后信号（.mat格 式）拖至matlab主 界面的workspace 中，与原信号一起 打包，以便以后计 算统计量
Matlab编程计算相 关统计量以及特征 量
得出统计量和特征 量后结束
将原始数据文件夹 copy到装有matlab 的电脑
打开matlab软件， 进入软件主界面
在软件的左下方找 到start按钮，点 击选择toolbox， 然后选择wavelet
Hale Waihona Puke 进入wavemenu界 面，选择一维小波 中的wavelet1-D并 进入
右上角选择用于小 波分析的小波基以 及分解层数并点击 analyse开始分析
然后点击denoise 去噪
阈值方法常用的有 4种fixed（固定阈 值）， rigorsure， heusure，minmax 根据需要选择，一 般情况下 rigorsure方式去 噪效果较好
Soft（软阈值）， hard（硬阈值）一 般选择软阈值去噪 后的信号较为平滑

例子：
c = cwt(s,1:32,'meyr') c = cwt(s,[64 32 16:-2:2],'morl') c = cwt(s,[3 18 12.9 7 1.5],'db2')
一维离散小波变换：
dwt [cA,cD]=dwt(X,’wname’) [cA,cD]=dwt(X,H,G) 其中：cA ：低频分量， cD：高频分量 X：输入信号。 wname：小波基名称 H：低通滤波器 G：高通滤波器
1 ≤ t < 500 ⎧sin(0.03t ) freqbrk (t ) = ⎨ ⎩ sin(0.3t ) 501 ≤ t ≤ 1000
连续小波变换：
格式： coefs=cwt(s,scales,’wname’) coefs=cwt(s,scales,’wname’,’plot’) 说明： s:输入信号 scales: 需要计算的尺度范围 wname:所用的小波基 plot: 用图像方式显示小波系数
LastWave 小波信号和图像处理软件，用C语言编写，可在 Unix和Macintosh上运行。 下载地址：
值得关注的几个发展方向：
提升小波变换（Lifting scheme wavelet transform) 多小波变换（Multiwavelet transform) 线调频小波变换(chirplet transform)。
小波基的名称 计算Morlet小波滤波器系数 计算墨西哥草帽小波滤波器系数 计算Meyer小波与尺度滤波器系数 计算Meyer小波辅助函数 计算紧支集双正交小波滤波器系数 计算紧支集双正交小波尺度滤波器系数 计算近似对称的紧支集双正交小波滤波器系数 计算Coifmant小波尺度滤波器系数 计算双正交样条小波尺度滤波器参数

Matlab小波工具箱的使用2工具箱提供了如下函数做一维信号分析：在这一部分，可以学到l 加载信号l 执行一层小波分解l 从系数重建近似和细节l 显示近似和细节l 通过逆小波变换重建信号l 执行多层小波分解l 抽取近似系数和细节系数l 重构第三层近似l 重构第1、2、3层细节l 显示多层分解的结果l 从第三层分解重构原始信号l 从信号中去除噪声l 改善分析l 压缩信号l 显示信号的统计信息和直方图一维分析---使用命令行这个例子包含一个真实世界的信号---测量3天的电功耗。

这个信号很典型，因为它包含一个明显的测量噪声，而小波分析可以有效的移除噪声。

1. 加载信号load leleccum截取信号s = leleccum(1:3920);l_s = length(s);2. 对信号执行一层小波分解使用db1小波执行一层小波分解，执行下面的语句产生近似系数cA1、细节系数cD1 [cA1,cD1] = dwt(s,'db1');3. 从系数中构建近似和细节从系数cA1和cD1中构建一层近似A1和细节D1，执行以下代码A1 = upcoef('a',cA1,'db1',1,l_s);D1 = upcoef('d',cD1,'db1',1,l_s);或A1 = idwt(cA1,[],'db1',l_s);D1 = idwt([],cD1,'db1',l_s);4. 显示近似和细节subplot(1,2,1); plot(A1); title('Approximation A1')subplot(1,2,2); plot(D1); title('Detail D1')5. 使用逆小波变换恢复信号A0 = idwt(cA1,cD1,'db1',l_s);err = max(abs(s-A0))err =2.2737e-0136. 执行多层小波分解执行3层信号分解[C,L] = wavedec(s,3,'db1');函数返回3层分解的各组分系数C（连接在一个向量里），向量L里返回的是各组分的长度。

Matlab⼩波⼯具箱的使⽤3⼀维离散平稳⼩波分析离散平稳⼩波分析所⽤到的函数有swt⼩波分解和iswt⼩波重构。

在这⼀部分可以学到如下内容：l 加载信号l 执⾏平稳⼩波分解l 从⼩波系数中构造近似和细节l 显⽰第⼀层的近似和细节l 平稳⼩波逆变换恢复原始信号l 执⾏多层平稳⼩波分解l 重构第3层近似l 重构1、2、3层细节l 重构1、2层近似l 显⽰分解的结果l 从3层分解中重构原始信号l 除噪使⽤命令⾏实现⼀维分析1. 加载信号（⼀个噪声污染的多普勒效应信号）2. 设置变量s = noisdopp;对于SWT变换，如果需要在第k层分解信号，那么原始信号需要能够平分成2^k份。

所以如果原始信号的长度不满⾜要求，需要使⽤Signal Extension GUI⼯具或使⽤wextend函数来扩展它。

3. 执⾏⼀层平稳⼩波分解[swa,swd] = swt(s,1,'db1');函数执⾏将产⽣1层近似和细节的系数，两者和信号的长度是相等的，这也是平稳⼩波和普通⼩波不同的地⽅，从⽽使它在某些领域有好的效果。

4. 显⽰近似、细节⼩波系数显⽰⼀层近似和细节的系数subplot(1,2,1), plot(swa); title('Approximation cfs')subplot(1,2,2), plot(swd); title('Detail cfs')5. 使⽤平稳⼩波逆变换恢复原始信号A0 = iswt(swa,swd,'db1');重构的误差为err = norm(s-A0)2.1450e-0146. 从系数中构建近似和细节构建⼀层近似和细节，输⼊如下代码nulcfs = zeros(size(swa));A1 = iswt(swa,nulcfs,'db1');D1 = iswt(nulcfs,swd,'db1');显⽰结果如下subplot(1,2,1), plot(A1); title('Approximation A1');subplot(1,2,2), plot(D1); title('Detail D1');7. 执⾏多层平稳⼩波分解使⽤db1⼩波做3层⼩波分解[swa,swd] = swt(s,3,'db1');产⽣的近似系数在swa中，细节系数在swd中，⽽且它们有相同的长度。

MATLAB小波分析工具箱常用函数1. wfilters 函数：用于生成小波滤波器和尺度函数，可以根据指定的小波和尺度类型生成小波滤波器系数。

2. wavedec 函数：用于将信号进行小波分解，将输入信号分解为多个尺度系数和小波系数。

3. waverec 函数：用于将小波系数和尺度系数进行重构，将小波分解后的系数重构为信号。

4. cwt 函数：用于进行连续小波变换，可以获得信号在不同尺度上的时频信息。

5. icwt 函数：用于进行连续小波反变换，可以将连续小波变换的结果重构为原始信号。

6. cmorlet 函数：用于生成复数 Morlet 小波。

Morlet 小波是一种基于高斯调制正弦波的小波函数。

7. modwt 函数：用于进行无偏快速小波变换，可以获取多个尺度下的小波系数。

8. imodwt 函数：用于进行无偏快速小波反变换，可以将无偏快速小波变换的结果重构为原始信号。

9. wdenoise 函数：用于对信号进行去噪处理，可以去除信号中的噪声。

10. wavethresh 函数：用于对小波系数进行阈值处理，可以实现信号压缩。

11. wenergy 函数：用于计算小波系数的能量，可用于分析小波系数的频谱特性。

12. wscalogram 函数：用于绘制小波系数的时频谱图，可以直观地显示信号的时频信息。

13. wpdec 函数：用于进行小波包分解，可以将输入信号分解为多个尺度系数和小波系数。

14. wprec 函数：用于将小波包系数和尺度系数进行重构，将小波包分解后的系数重构为信号。

15. wptree 函数：用于提取小波包树的信息，可以获得小波包树的结构和节点信息。

这些函数可以实现小波分析中主要的操作和功能。

通过使用这些函数，你可以进行小波分析、信号去噪、信号压缩等应用。

同时，你也可以根据具体的需求使用这些函数进行函数的扩展和自定义。

其中：cA ：低频分量， cH：水平高频分量 cV：垂直高频分量 cD：对角高频分量 X：输入信号。 wname：小波基名称 H：低通滤波器 G：高通滤波器
15
二维信号的多层小波分解：
[A,L]=wavedec2(X,N，’wname’) [A,L]=wavedec2(X,N,H,G) 其中：A ：各层分量， L：各层分量长度
Regularity
indefinitely derivable
Symmetry
yes
Reference: I. Daubechies, Ten lectures on wavelets, CBMS, SIAM, 61, 1994, 117-119, 137, 152.
5
计算小波滤波器系数的函数：
29
多小波变换还需要解决的问题：
多小波变换是和矢值滤波器组对应的。因此，需要对“好的”矢 值滤波器组和多小波给出合理的解释并提出更好的多小波及多滤 波器组设计准则。
不平衡多小波的实现中，预滤波器的设计是一个关键。针对不同 多小波的特性，采取怎样的预滤波器设计方案及怎样评价这些设 计方案是需要继续深入研究的课题。
30
线调频小波变换：
寻求Fourier变换，加窗Fourier变换和小 波变换的统一。
寻求对信号的时间－频率－尺度的完美 表达。
31
仿射时频变换的合成算子：
设g (t )是窗函数，则五种仿射变换为：
（1）时间平移算子：g(t t0 ) （2）频率平移算子：e j2f0t g(t)
（3）时频拉伸算子：ea/2 g(ea (t a))
j 1 t 2
（4）时间倾斜算子：（－jp)1/2 e p g(t)
（5）
频

Fourier变换： fˆ f , g0, f ,0,0,0 (t)
加窗 Fourier变换： STFT ( f ) f , gt, f ,0,0,0 (t)
小波变换： WT ( f )(a, t) f , gt,0,a,0,0 (u)
高斯线调频小波变换： GCT (s)(t, f ) s(u), gt, f (u) ,log(t),0,q
2020/11/23
小波基的名称
Morlet小波 墨西哥草帽小波 Meyer小波 Haar小波 紧支集正交小波 近似对称的紧支集双正交小波 Coifmant小波 双正交样条小波
怎样获取小波基的信息：
• 在Matlab窗口键入“waveinfo(‘参数名’ ）?waveinfo('meyr')
MEYRINFO Information on Meyer wavelet.
• 对变换信号的伪彩色编码：wcodemat • 反变换：idwt2,idwtper2, • 重构： upwlev2,waverec2,wrcoef2,
2020/11/23
小波包分解：
• 树操作
allnodes 列出数结构的所有节点。 isnode 判断指定位置是否存在节点。 istnode 判断一个节点是否为终端节点。 nodejoin 树的剪枝。
其中：(x)＝(1,2,,r )T
2020/11/23
双尺度方程：
( x) Pk (2 x k ) k
其中： Pk是 r r矩阵。 由于研究无穷矩阵序列 的困难，通常的双尺度 方程 为有限项。
M
( x) Pk (2 x k ) k 0
2020/11/23
• 多小波在理论上所表现出来的优势以及它在应用领域 所具有的潜力，使其受到高度重视。在它诞生的短短 几年时间内，从理论方面，多小波的构造、多小波变 换实现中，预滤波器的设计及信号的边界处理正迅速 成为新的研究热点，而对它在图像处理方面的应用， 人们正进行积极探索，并在静止图像编码、图像去噪 两方面取得了一定的成果。

2020/11/23
小波基的名称
Morlet小波 墨西哥草帽小波 Meyer小波 Haar小波 紧支集正交小波 近似对称的紧支集双正交小波 Coifmant小波 双正交样条小波
怎样获取小波基的信息：
• 在Matlab窗口键入“waveinfo(‘参数名’ ）?waveinfo('meyr')
MEYRINFO Information on Meyer wavelet.
（ 3）时频拉伸算子：
e a / 2 g ( e a (t a ))
（ 4）时间倾斜算子：（－
j 1 t 2
jp ) 1 / 2 e p g ( t )
（ 5）频率倾斜算子：
j q t 2
e 2 g (t)
2020/11/23
变换的统一表述：
将五种变换分别用下标 表示：
则：
gt0 , f0 ,a, p,q (t )
2020/11/23
多小波变换还需要解决的问题 ：
• 多小波变换是和矢值滤波器组对应的。因此，需要对“好的”矢 值滤波器组和多小波给出合理的解释并提出更好的多小波及多滤 波器组设计准则。
• 不平衡多小波的实现中，预滤波器的设计是一个关键。针对不同 多小波的特性，采取怎样的预滤波器设计方案及怎样评价这些设 计方案是需要继续深入研究的课题。
2020/11/23
二维离散小波变换：
• dwt2 [cA,cH,cV,cD]=dwt2(X,’wname’) [cA,cH,cV,cD]=dwt2(X,H,G)
其中：cA ：低频分量， cH：水平高频分量 cV：垂直高频分量 cD：对角高频分量 X：输入信号。 wname：小波基名称 H：低通滤波器 G：高通滤波器

15
二维信号的多层小波分解：
[A,L]=wavedec2(X,N，’wname’) [A,L]=wavedec2(X,N,H,G) 其中：A ：各层分量， L：各层分量长度
N：分解层数 X：输入信号。 wname：小波基名称 H：低通滤波器 G：高通滤波器
2021/3/7
CHENLI
16
其他的二维函数：
dwt2
[cA,cH,cV,cD]=dwt2(X,’wname’)
[cA,cH,cV,cD]=dwt2(X,H,G) 其中：cA ：低频分量， cH：水平高频分量
cV：垂直高频分量 cD：对角高频分量 X：输入信号。 wname：小波基名称 H：低通滤波器 G：高通滤波器
2021/3/7
CHENLI
g (t t0 ) e j2f0t g (t)
（ 3）时频拉伸算子：
e a / 2 g ( e a (t a ))
（ 4）时间倾斜算子：（－
j 1 t 2
jp ) 1 / 2 e p g ( t )
（ 5）频率倾斜算子：
j q t 2
e 2 g (t)
2021/3/7
CHENLI
32
变换的统一表述：
CHENLI
9
连续小波变换：
格式： coefs=cwt(s,scales,’wname’) coefs=cwt(s,scales,’wname’,’plot’)
说明： s:输入信号 scales: 需要计算的尺度范围 wname:所用的小波基 plot: 用图像方式显示小波系数
2021/3/7
CHENLI
小波基的名称
Morlet小波 墨西哥草帽小波 Meyer小波 Haar小波 紧支集正交小波 近似对称的紧支集双正交小波 Coifmant小波 双正交样条小波