§4.4 变化率与相关变化率
- 格式:ppt
- 大小:640.50 KB
- 文档页数:2





2.4.3相关变化率相关变化率问题是指:在某一变化过程中变量 ,,y x ,它们都与变量t 有关,且它们之间有关系式0),,(= y x F ,知道了其中一些变量对t 的变化率,要求另外一些变量对t 的变化率。
求相关变化率的步骤:(1)建立变量 ,,y x 之间的关系式0),,(= y x F ;(2)将关系式0),,(= y x F 两边对t 求导(注意到 ,,y x 都是t 的函数),从而得各变量对t 的变化率之间的关系式;(3)将已知的变化率(包括一些已知数据)代入并求出所要求的变化率。
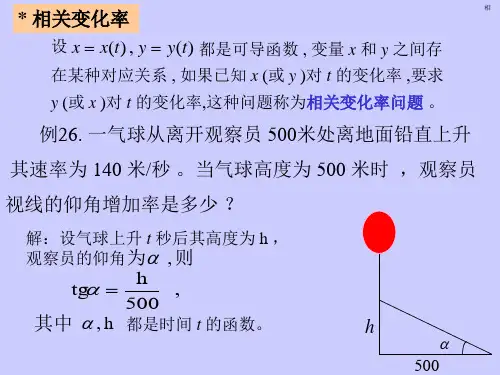
例1.一架直升飞机在m 500高空,以s m /50的均匀速度从西向东飞越观察者的头顶,观察者的视线与地面夹角θ 为。
求当3π=θ时,t 对θ的变化率。
解:以直升飞机飞过观察者头顶时算起的距离为x , 显然x ,θ均为t 的函数,已知飞机的速度50=dt dx 米/秒,求3π=θ时的dtd θ。
θ=ctg x 500,dt d dt dx θθ-=)csc (5002, dtdx dt d θ-=θ2sin 5001, 当3π=θ时,23sin =θ,50=dt dx米/秒,代入上式得075.03-=θπ=θdtd 弧度/秒,负号表示θ随时间 t 增加而减少。
例2.某人以m 2/s 的速度通过一座桥,桥面高出水面m 20,在此人的正下方有一条小船以m 34/s 的速度在与桥垂直的方向航行,求经s 5后,人与小船相分离的速度。
解:设经t 秒钟后船与人的距离为m s ,人行走距离为m x ,船航行距离为m y , 则222220)()()(++=t y t x t s ,所建立的方程并不是s 与t 的直接函数关系, 但因为所求的是dt ds v =,且已知2=dt dx,34=dt dy ,所以可借助于相关变化率来求。
dt dy ydt dx x dt ds s222+=, ∵当5=t 时,10=x ,320=y , ∴37020)320(10222=++=s , ∴)/(2126370343202105s m dt ds t =⋅+⋅==. §2.5高阶导数与高阶微分2.5.1显函数高阶导数定义 若函数)(x f y =的导数)(x f y '='在x 点可导,则称)(x f y '='在x 点的导数为)(x f y =在x 点处的二阶导数,记作)(x f '',或y '',或22dxy d ,即xx f x x f x f x ∆'-∆+'=''→∆)()(lim)(0,)(''=''y y , ])([)(''=''x f x f ,)(22dxdy dx d dx y d =。





相关变化率问题的求解方法及应用1. 引言相关变化率问题是数学中一个重要而复杂的概念,涉及到微积分和函数的导数。
在实际生活和工作中,我们经常会遇到各种各样的相关变化率问题,比如物体的速度、加速度、成本的边际变化等等。
掌握相关变化率问题的求解方法对于理解和解决实际问题至关重要。
本文将从基础概念入手,逐步展开相关变化率问题的求解方法及应用。
2. 相关变化率问题的基本概念相关变化率问题涉及到两个变量之间的关系,通常表现为一个变量随着另一个变量的变化而变化。
一个物体的位移随着时间的变化而变化,这就涉及到了速度的概念。
相关变化率的求解方法是通过求取两个变量的导数来得到它们之间的关系。
在数学中,相关变化率通常通过函数的导数来呈现,这需要我们熟练掌握导数的求解方法。
3. 相关变化率问题的求解方法相关变化率问题的求解方法主要涉及到求取函数的导数。
对于给定的函数,我们首先需要求取它关于自变量的导数,然后根据具体问题中的变量关系,进一步求取相关变化率。
常见的求导方法包括常数法则、幂函数法则、指数函数法则、对数函数法则、三角函数法则等等,我们需要根据具体的函数形式和问题需求,灵活运用这些求导法则。
另外,对于一些复杂的函数,我们还需要运用链式法则、乘积法则、商法则等高阶导数的求法则来求取相关变化率。
4. 相关变化率问题的应用相关变化率问题的应用非常广泛,涉及到物理、经济、生物、工程等各个领域。
在物理学中,我们可以用相关变化率来求取物体的速度、加速度、力的功率等等,进而解决各种运动问题。
在经济学中,相关变化率可以被用来求取成本的边际变化率、收益的边际变化率,帮助企业制定最优的生产和经营策略。
在生物学和工程学中,相关变化率可以帮助我们理解各种生物体的生长规律,以及设计各种工程结构和装置。
5. 个人观点和总结相关变化率问题是微积分中一个非常有意义和应用价值的内容,掌握相关变化率的求解方法对于理解和解决实际问题至关重要。
通过学习和熟练运用相关变化率的求解方法,我们可以更好地理解和应用微积分知识,解决我们在生活和工作中遇到的各种问题。
§4.4法拉第电磁感应定律李洋一、教材分析前面几节的内容是从感应电流的角度来认识电磁感应现象的。
本节是从感应电流进一步深入到感应电动势来理解的,即研究“决定感应电动势大小的因素”。
教科书在这个问题的处理上并没有通过实验探究,而是一陈述事实的方式,引入法拉第电磁感应定律,即教科书用“在法拉第、纽曼、韦伯等人工作的基础上,人们认识到:。
感应电动势。
成正比”的表述给出了电磁感应定律。
教科书之所以这样处理,是力图通过这一物理规律的教学,充分体现人类认识事物的一种真实图景。
也就是说,物理学中多数定律的得出,并不一定是直接归纳的结果,而是在分析了很多间接的实验事实后被“悟”出来的,并且定律的正确性往往也是有他的推论的正确性来验证的。
因此,本节教学不要求通过实验探究来建立规律。
二、学情分析通过前面几节的学习,学生已经知道:当闭合线圈里的磁通量发生变化的时候,线圈里就会产生感应电流;再结合到电路的相关知识,学生不难理解:既然在闭合回路里产生了电流,那就一定存在着电源,也就不难理解会产生感应电动势了,但对影响感应电动势大小的因素缺乏直观的认识,可能在理解上会存在一定的困难。
另外公式:tn E ∆∆Φ=和BLv E =的推导过程学生可能不能够独立完成,故需加强指导。
三、教学策略1、本节教学的设计的总体思路:首先,建立感应电动势概念;其次,通过对实验的定性分析,探索感应电动势的大小跟那些因素有关;随后,得出感应电动势大小的一般表达式tn E ∆∆Φ=;最后,再利用发来第电磁感应定律对“导线切割磁感线时的感应电动势”和“反电动势”这两种特殊情况进行分析。
2、本节教学的重点是法拉第电磁感应定律,为突出重点教师应重点强调,同时教师应该带领学生推导法拉第电磁感应定律的数学表达式tn E ∆∆Φ=等。
3、难点是磁通量的变化及磁通量的变化率的理解,为突破难点,教师可以通过以下方法来实现:(1)、利用上一节的演示实验演示磁通量的变化及磁通量的变化的快慢,以此加强学生的直观印象。
相关变化率问题的求解方法及应用赵红杰;李杨;柏继云【摘要】相关变化率问题是高等数学导数部分的一个内容.它广泛地存在于现实生活中.但目前的高等数学教材中,对这部分内容阐述得比较少,只是列举一两个例子,学生不能很好地了解相关变化率问题的应用,甚至对其求解方法感到困惑,因此极大影响了学生的学习兴趣和质量.该文旨在通过展示相关变化率问题的一些实际应用,重点介绍其求解方法,引导学生学会用数学的思维方式观察、分析、解决实际问题,以提高学生学习兴趣、学习质量.【期刊名称】《安徽农业科学》【年(卷),期】2013(041)019【总页数】3页(P8088-8089,8210)【关键词】高等数学;导数;相关变化率;教学方法【作者】赵红杰;李杨;柏继云【作者单位】东北农业大学,黑龙江哈尔滨150030;东北农业大学,黑龙江哈尔滨150030;东北农业大学,黑龙江哈尔滨150030【正文语种】中文【中图分类】S11现实生活中普遍存在着相关变化率问题。
了解它的应用,掌握相关变化率问题的解题方法,不仅可以拓宽学生的知识面,而且可以使学生理论联系实际,学以致用[1]。
所谓的相关变化率问题是这样定义的:设x=x(t)和y=y(t)都是可导函数,而变量x 与y之间存在某种关系,从而变化率dx/dt与dy/dt间也存在一定关系。
这2个相互依赖的变化率被称为相关变化率。
相关变化率问题就是研究这2个变化率之间的关系,以便从其中一个变化率求出另一个变化率[2]。
以一个例子来说明相关变化率问题,再具体举例说明求解方法。
假定我们正在对一个球形气球充气,气球的体积和半径都随时间增加。
若气球在某个时刻t的体积为V,半径为r,则利用链式法则求导数,得到相关变化率方程为: 实际上,直接测量体积增加的速率(气球充气的速率)比测量半径增加的速率更加容易。
所以,如果知道气球在给定时刻的半径(r)和体积增加的速率(dV/dt),那么就能够通过上面的方程求解dr/dt,得到半径在那个时刻增加的速率。