matlab空间曲面绘图

10
三、加密：取更二多维的点作图举例
>> x=[0:pi/20:2*pi]; >> y=sin(x); >> plot(x,y,'.')
11
三维曲线作图过程
x t
例：绘制三维螺线：
y
sin( t )
z cos(t)
( 0 < t < 20 )
先画点，后连线
1) 计算空间离散点的坐标 (x,y,z) 2) 将这些点按顺序连接即可
调用 Matlab 的绘图命令作出曲面图形
怎样得到网格矩阵 X 和 Y ？
—— 利用 Matlab 的网格生成函数 meshgrid
5
网格生成函数
网格生成函数 [X,Y] = meshgrid(x,y) x,y 是分别对 x 变化区域和 y 变化区域进行分割后
得到的向量 X, Y 即为我们所需要的网格矩阵
>> x= -8:0.5:8; >> y= -8:0.5:8; >> [X,Y]=meshgrid(x,y); >> r=sqrt(X.^2+Y.^2)+eps; >> Z=sin(r)./r; >> mesh(X,Y,Z)
＋eps？
1) x 与 y 可以取不同的步长 2) 注意这里采用的数组运算
最后一个命令能否改为 mesh(Z)？
gray cool
线性灰色系 hot 青和洋红色系 pink
黑红黄白色系 柔和色系
26
Matlab 符号作图
27
二维曲线 ezplot
二维曲线绘图命名： ezplot ezplot(f(x),[a,b])

3、Matlab绘图功能的美观性与精确性是其它软件所不能比的。但是由于自身 数学知识的缺乏，很多函数还不能深入的掌握，不能把所想到的图形图像轻松 转化成源程序绘出。说明我们应当多进行绘图练习，在绘图中感受乐趣，培养 自己对空间几何的认识。
我们是 13级软件工程（1）班
第七小组
制作人： 黄 蓉
谢谢！
用Matlab作空间曲面的切平面与法线图像
实验小组：13级软件工程（1）班第七小组
姓名 王子乐
王寿奎
小组成员（具体分工）
学号
1304091031
具体分工
画图、参写报告（实验程序） 演示PPT
1304091032
收集资料、画图
卞鹏程
1304091033
参写报告（实验目的）
孙蕊蕊
1304091034
画图、参写报告（图像方程）
最后重新输入正确源程序， 得到图像：
程序代码：
>> syms x y z; >> f='2/(x^2+y^2+1)-z'; >> u=diff(f,x); >> v=diff(f,y); >> x=1/4;y=1/2;z=32/21; >> a=eval(u);b=eval(v); >> X=-1:0.1:1; >> Y=X; >> [x,y]=meshgrid(X,Y); >> z1=2./(x.^2+y.^2+1); >> z2=a*(x-1/4)+b*(y-1/2)+32/21; >> mesh(x,y,z1); >> hold on; >> mesh(x,y,z2) >> t=-1:0.1:1; >> x3=a*t+1/4;y3=b*t+1/2;z3=-t+32/21; >> plot3(x3,y3,z3)

2、本次实践教学，我们小组的任务是“作一个空间曲面的切平面及法线”， 为了能更好的完成实验，我们选取了不同的图形进行作图，要求组内五个成员 每个人完成一个图形的源程序编写和图像绘制，这样分配不仅锻炼了我们独立 解决问题的能力，也培养了我们团结合作的精神。当实验过程中遇到解决不了 的问题，我们会积极在利完成。完全做到人人参与。 3、Matlab绘图功能的美观性与精确性是其它软件所不能比的。但是由于自身 数学知识的缺乏，很多函数还不能深入的掌握，不能把所想到的图形图像轻松 转化成源程序绘出。说明我们应当多进行绘图练习，在绘图中感受乐趣，培养 自己对空间几何的认识。
用Matl组：13级软件工程（1）班第七小组
小组成员（具体分工）
姓名 王子乐 学号 具体分工
画图、参写报告（实验程序） 演示PPT 收集资料、画图
1304091031
王寿奎
1304091032
1304091033 1304091034 1304091035
卞鹏程
我们是 13级软件工程（1）班 第七小组
制作人： 黄 蓉
实验结果
f 2 z 2 2 x y 1
2 2 2 f x y z
实验总结
1、通过本次实验，我们学习了使用Matlab作空间曲面图像的基本方法。当我 们自己成功写出程序，绘出理想中的图形图像，当源程序得以无误地实现，图 像窗口跳出的那一刻，感觉好开心、好神奇！这不仅激发了我们对高数的兴趣， 而且使我们对高数空间几何有了更清楚的认识，对我们后续课程的学习有很大 的帮助。
参写报告（实验目的）
孙蕊蕊
画图、参写报告（图像方程）
黄蓉（组长）
画图、总写报告、制作PPT
实验目的
1、掌握使用Matlab“作空间曲面及其在某点 的切平面与法线图像”基本方法； 2、通过作图，加强学生对偏导知识点的理解 和应用，同时培养学生的创新精神，锻炼学 生的实践能力。

例。
要］ 研 究 ＭＡ Ｌ Ｂ软件表现 空间曲面交线的原理和 方法 ， 出绘制 空间曲面交线及其投 影的一般步骤和 实 ＴＡ 给
【 关键词］ ＭＡ Ｌ Ｂ； Ｔ Ａ 曲面的交线； 影 投 【 中图分类号］ ０１２ ２ 【 ８． 文献标识码 ］ Ａ 【 文章编 号］ １０ ４ ５ （０７ ０ Ｏ ４ ０ ０８— ６ ７ ２ ０ ）９一 Ｏ６— ３
１ 算 法 与 实例
利用 ＭＡ Ｌ Ｂ可视 化数据 的功 能指令 （ ｐ ｔｓｒ ｍ ｓ ） 可 以容 易地 表 现 出二元 函数 的三 维 ＴＡ 如 ｌ 、ｕｆ ｅｈ等 ， ｏ 、
图像。要描绘两个 曲面的交线， 实质是寻找两个曲面上坐标相同的数据点的集合 ， 然后将坐标相同的数
据 点可视 化 。 基 于这一思想 ， 设计 算 法和步 骤如 下 ： １ ）对于两 个解析 式 已知 的曲面 （ ’
，
ｔ２＝ （ Ｙ ｚ ，）
估计 交线 上 的点 的坐标大致 变化范 围 ；
２ ）设定横 纵坐标 的 变化范 围 ， 以适 当 的步长产 生坐标 面 Ｘ Ｙ上 的格点 （ Ｙ ； Ｏ ，）
３ 计算两个曲面在格点处的竖坐标 （ ） 的值 ）使用绘图指令描绘两个 曲面图像； ，
４ ）比较同一格点 （ ，） Ｙ 处两个曲面的竖坐标 ， 记录两个数据点 的状态 ， 同则标记 为逻辑值 １ 不 相 ，
荆 门职业技 术学院学报
Ｊ ｕ ｎ ｌｏ ｉｇ ｎ Ｔ ｃ ｎ ｃ ｌＣ ｌ ｇ ｏ ｒ ａ ｆＪｎ ｍｅ ｅ ｈ ｉａ ｏｌ ｅ ｅ
２０ ０７年 ９月
Ｓ ｐ． ０ ７ ｅ ２０
利用 Ｍ Ｔ Ａ Ａ Ｌ Ｂ表现空 间曲面的交线
习长 新
（ 荆楚理工学院 计算机学 院， 湖北 荆门 ４ ８０ ） ４ ０ ０ 【 摘

Matlab绘图在数学教学中的应用摘要：数学是一门工具化的科学语言，我们用数学解决很多问题。

然而在学习数学的同时，有很多空间曲面难以用手工画出它们的图形。

例如：有一些多元函数，对于其图形却难以用人工画出。

而matlab的绘图语言正是解决这种难题的最好工具，方便并且直观。

关键词：多元函数 matlab语言绘图0 引言高职数学教学中，讲授空间曲面与曲线这个内容时，总感到“虚”，不直观、具体，利用matlab强大的绘图功能，可方便地展示空间曲面与曲线。

1 matlab绘图功能matlab绘图功能非常强大，这里只介绍几个常用函数的调用，抛砖引玉，希望对空间解析几何及多元函数部分的教学有所帮助。

1.1 产生三维数据在matlab中，利用meshgrid函数产生平面区域内的网格坐标矩阵。

其格式为：x=a：d1：b；y=c：d2：d；[x，y]=meshgrid（x，y）；语句执行后，矩阵x的每一行都是向量x，行数等于向量y的元素的个数，矩阵y的每一列都是向量y，列数等于向量x的元素的个数。

1.2 绘制三维曲面的函数 surf函数和mesh函数的调用格式为：mesh（x，y，z，c）surf（x，y，z，c）一般情况下，x，y，z是维数相同的矩阵。

x，y是网格坐标矩阵，z是网格点上的高度矩阵，c用于指定在不同高度下的颜色范围。

此外，还有带等高线的三维网格曲面函数meshc和带底座的三维网格曲面函数meshz。

其用法与mesh类似，不同的是meshc还在xy 平面上绘制曲面在z轴方向的等高线，meshz还在xy平面上绘制曲面的底座。

1.3 标准三维曲面 sphere函数的调用格式为：[x，y，z]=sphere（n）cylinder函数的调用格式为：[x，y，z]= cylinder（r，n）matlab还有一个peaks函数，称为多峰函数，常用于三维曲面的演示。

2 matlab绘图案例2.1 空间曲面的三维网线图与三维曲面图案例1、函数z=10-2x2-y2的三维网线图。

例1、已知向量x=[1 2 3],y=[4 7 9 0],生成它们对应的 格点矩阵。注意：输出的X、Y都是4*3矩阵，X的行 向量都是向量x，Y的列向量都是向量y
机动 目录 上页 下页 返回 结束
二、三维网格图命令mesh
• mesh(X,Y,Z) 生成网格曲面，X,Y,Z是同维数的矩阵 • mesh(x,y,Z) x,y是向量，而Z是矩阵。等价于
机动 目录 上页 下页 返回 结束
三、三维表面图命令surf
• surf的调用格式与mesh相同，不同之处是surf绘的是曲面 而不是网格。
• 三维表面图可以用shading命令修饰其显式形式。
Matlab还提供了waterfall(x,y,z)及contour3(x,y,z)等命 令绘制三维图形。
3
2
在[0,4π]间的图形。
解：syms t

ezplot(‘2/3*exp(-t/2)*cos(3/2*t)’,[0,4*pi])
第二节 Matlab二维特殊图形
Matlab提供了许多其他的二维绘图指令， 大大扩充了Matlab的曲线作图指令，可以满足 用户的不同需要。
注 目录 上页 下页 返回 结束
axis equal 使坐标轴在三个方向上刻度增量相同
axis square 使坐标轴在三个方向上长度相同
axis
返回表示当前图形坐标轴的范围
机动 目录 上页 下页 返回 结束
第四节 Matlab空间曲面绘图
二元函数 z f (x, y) 的图形是三维空间曲面，函
数图形在了解二元函数的特性上帮助很大。
第3章 Matlab 绘图与例题
第一节
第3章
Matlab二维曲线绘图
一、基本绘图指令plot

西安邮电大学《Matlab程序设计基础》课内实验报告题目：实验四MATLAB的绘图院系名称：计算机学院专业名称：计算机科学与技术班级：计科1502班内序号：05141107(29)学生姓名：赵阳指导教师：张老师实验四MATLAB的绘图一、实验目的：掌握基本的绘图函数plot。

二、实验内容：1、在同一坐标系下绘制下面三个函数在[0，4pi]的图象。

代码如下：t=0:pi/100:4*pi;y1=t;y2=sqrt(t);y3=4*pi*exp(-0.1*t).*sin(t);plot(t,y1,t,y2,t,y3)2、编写程序，选择合适的步距，绘制下面函数在区间[-6，6]中的图象。

代码如下：x=linspace(-6,6,100);y=[];for x0=xif x0<=0y=[y,sin(x0)];elseif x0<=3y=[y,x0];elsey=[y,-x0+6];endendplot(x,y)3、用compass函数画下面相量图ua=1;ub=cos(-2*pi/3)+sin(-2*pi/3)*i;uc=cos(2*pi/3)+sin(2*pi/3)*i;compass([ua,ub,uc,ua-ub,ub-uc,uc-ua])代码如下：ua=1;ub=cos(-2*pi/3)+sin(-2*pi/3)*i;uc=cos(2*pi/3)+sin(2*pi/3)*i;compass([ua,ub,uc,ua-ub,ub-uc,uc-ua])4、三维空间曲线绘制z=0:0.1:4*pi;x=cos(z);y=sin(z);plot3(x,y,z)代码如下：z=0:0.1:4*pi;x=cos(z);y=sin(z);plot3(x,y,z)5、用mesh或surf函数，绘制下面方程所表示的三维空间曲面，x和y的取值范围设为[-3，3]。

代码如下：[x,y]=meshgrid(-3:0.5:3);z=-x^2/10+y^2/10;mesh(x,y,z)三、思考题在同一坐标系下，用不同颜色和线型绘制以下两个函数在tÎ[-2p，2p]范围内的图象。

文章标题：深入探讨Matlab中plot3的功能和用法一、引言在Matlab中，plot3是一个非常常用且功能强大的函数，它可以在3D空间中绘制出各种图形，包括曲线、曲面和散点图等。

本文将深入探讨plot3函数的功能和用法，帮助读者更加全面、深入地了解和掌握这一重要工具。

二、plot3函数的基本用法在Matlab中，plot3函数的基本语法如下：```matlabplot3(X,Y,Z)```其中，X、Y和Z分别是要绘制的数据点的x、y、z坐标。

通过plot3函数，可以将这些数据点连接成为曲线或曲面，并在3D空间中进行可视化展示。

三、绘制3D曲线通过plot3函数，可以轻松地绘制出3D空间中的曲线。

以绘制螺旋线为例，我们可以使用以下代码：```matlabt = 0:0.1:10;x = sin(t);y = cos(t);z = t;plot3(x,y,z)```通过上述代码，即可在3D空间中绘制出一条螺旋线，令人眼前一亮。

这种绘制3D曲线的功能，为研究和展示曲线在三维空间中的特性提供了极大的便利。

四、绘制3D曲面除了绘制3D曲线，plot3函数还可以用来绘制3D曲面。

以绘制扭曲的正弦曲面为例：```matlab[X,Y] = meshgrid(-2:0.2:2, -2:0.2:2);Z = sin(sqrt(X.^2 + Y.^2));plot3(X,Y,Z)```通过上述代码，可以在3D空间中绘制出一幅扭曲的正弦曲面，展现了plot3函数在绘制3D图形方面的强大威力。

五、绘制3D散点图除了曲线和曲面，plot3函数还可以用来绘制3D散点图。

以绘制三维空间中的散点分布为例：```matlabx = rand(1,100);y = rand(1,100);z = rand(1,100);plot3(x,y,z,'o')```通过上述代码，可以在3D空间中绘制出100个随机生成的散点，并用'o'符号进行标记。

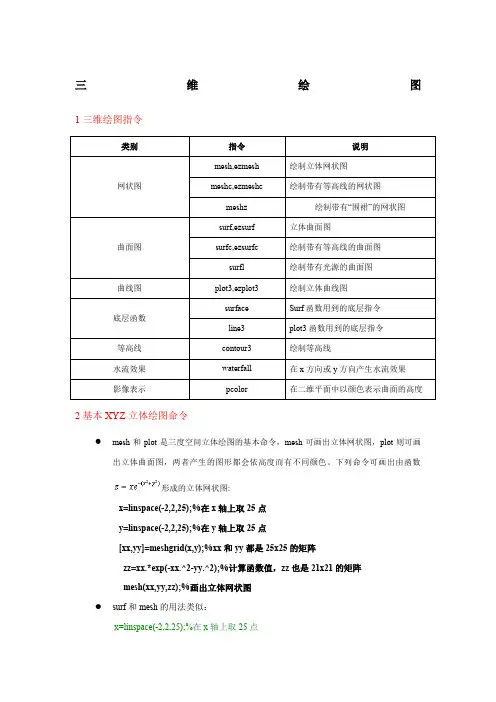
三维绘图1三维绘图指令2基本XYZ 立体绘图命令●mesh 和plot 是三度空间立体绘图的基本命令，mesh 可画出立体网状图，plot 则可画出立体曲面图，两者产生的图形都会依高度而有不同颜色。

下列命令可画出由函数形成的立体网状图:x=linspace(-2,2,25);%在x 轴上取25点 y=linspace(-2,2,25);%在y 轴上取25点[xx,yy]=meshgrid(x,y);%xx 和yy 都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2);%计算函数值，zz 也是21x21的矩阵 mesh(xx,yy,zz);%画出立体网状图● surf 和mesh 的用法类似：x=linspace(-2,2,25);%在x 轴上取25点y=linspace(-2,2,25);%在y轴上取25点[xx,yy]=meshgrid(x,y);%xx和yy都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2);%计算函数值，zz也是25x25的矩阵surf(xx,yy,zz);%画出立体曲面图●peaks为了方便测试立体绘图，MATLAB提供了一个peaks函数，可产生一个凹凸有致的曲面，包含了三个局部极大点及三个局部极小点，其方程式为：要画出此函数的最快方法即是直接键入peaks：peaksz=3*(1-x).^2.*exp(-(x.^2)-(y+1).^2)-10*(x/5-x.^3-y.^5).*exp(-x.^2-y.^2)-1/3*exp(-(x+1).^2-y.^2)●我们亦可对peaks函数取点，再以各种不同方法进行绘图。

meshz可将曲面加上围裙：[x,y,z]=peaks;meshz(x,y,z);●waterfall可在x方向或y方向产生水流效果：[x,y,z]=peaks;waterfall(x,y,z);●下列命令产生在y方向的水流效果：[x,y,z]=peaks;waterfall(x',y',z');●meshc同时画出网状图与等高线：[x,y,z]=peaks;meshc(x,y,z);●surfc同时画出曲面图与等高线：[x,y,z]=peaks;surfc(x,y,z);●contour3画出曲面在三度空间中的等高线：contour3(peaks,20);●contour画出曲面等高线在XY平面的投影：contour(peaks,20);●plot3可画出三度空间中的曲线：t=linspace(0,20*pi,501);plot3(t.*sin(t),t.*cos(t),t);亦可同时画出两条三度空间中的曲线：t=linspace(0,10*pi,501);plot3(t.*sin(t),t.*cos(t),t,t.*sin(t),t.*cos(t),-t);3三维绘图的主要功能绘制三维线图绘制等高线图绘制伪彩色图绘制三维网线图?绘制三维曲面图、柱面图和球面图?绘制三维多面体并填充颜色（一）三维线图plot3?——?基本的三维图形指令调用格式：plot3(x,y,z)?——?x,y,z是长度相同的向量plot3(X,Y,Z)?——?X,Y,Z是维数相同的矩阵plot3(x,y,z,s)?——?带开关量plot3(x1,y1,z1,’s1’,?x2,y2,z2,’s2’,?…)二维图形的所有基本特性对三维图形全都适用。

实验三 MATLAB 绘图一、实验目的1．掌握二维图形的绘制。

2．掌握图形的标注3．了解三维曲线和曲面图形的绘制。

二、实验的设备及条件计算机一台（带有以上的软件环境）。

设计提示1．Matlab 允许在一个图形中画多条曲线：plot(x1，y1，x2，y2，……)指令绘制y 1 = f 1(x 1), y 2 = f 2 (x 2 )等多条曲线。

Matlab 自动给这些曲线以不同颜色。

标注可用text 函数。

2．绘图时可以考虑极坐标和直角坐标的转换。

3．三维曲线绘图函数为plot3，注意参考帮助中的示例。

三、实验内容1．生成1×10 维的随机数向量a ，分别用红、黄、蓝、绿色绘出其连线图、杆图、阶梯图和条形图，并分别标出标题“连线图”、“杆图”、“阶梯图”、“条形图”。

2、绘制函数曲线，要求写出程序代码。

(1) 在区间[0:2π]均匀的取50个点，构成向量t(2) 在同一窗口绘制曲线y1=sin(2*; y2=3cos(t+；要求y1曲线为红色点划线，标记点为圆圈；y2为蓝色虚线，标记点为星号。

(3) 分别在靠近相应的曲线处标注其函数表达式。

3.将图形窗口分成两个绘图区域，分别绘制出函数：⎩⎨⎧+-=+=1352221x x y x y 在[0,3]区间上的曲线，并利用axis 调整轴刻度纵坐标刻度，使1y 在[0,12]区间上，2y 在[-2,]区间上。

4．用mesh 或surf 函数，绘制下面方程所表示的三维空间曲面，x 和y 的取值范围设为[-3，3]。

101022y x z +-=思考题：1. 编写一个mcircle(r)函数，调用该函数时，根据给定的半径r ，以原点为圆心,画一个如图所示的红色空心圆。

（图例半径r=5）；左图参考polar函数的用法，右图绘制圆形的参数方程为x=sin （t ），y=cos （t ）。

其中，t 的区间为0~2*pi ，步长为。

2．（1）绘一个圆柱螺旋线（形似弹簧）图。

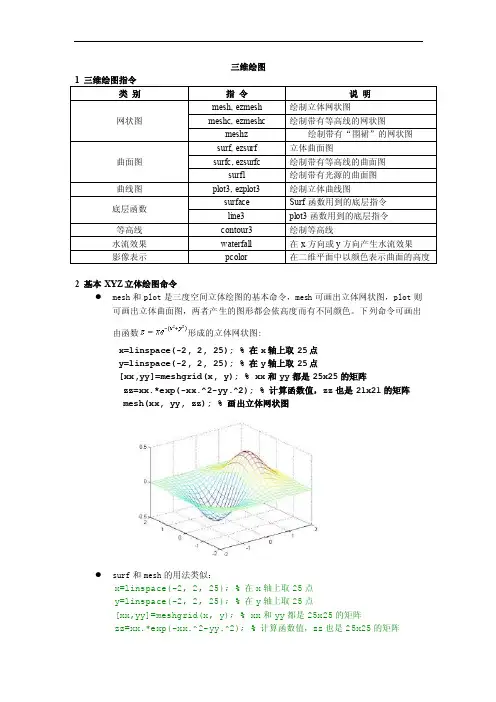
三维绘图2 基本XYZ立体绘图命令●mesh和plot是三度空间立体绘图的基本命令，mesh可画出立体网状图，plot则可画出立体曲面图，两者产生的图形都会依高度而有不同颜色。

下列命令可画出由函数形成的立体网状图:x=linspace(-2, 2, 25); % 在x轴上取25点y=linspace(-2, 2, 25); % 在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值，zz也是21x21的矩阵mesh(xx, yy, zz); % 画出立体网状图●surf和mesh的用法类似：x=linspace(-2, 2, 25); % 在x轴上取25点y=linspace(-2, 2, 25); % 在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是25x25的矩阵zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值，zz也是25x25的矩阵surf(xx, yy, zz); % 画出立体曲面图●peaks为了方便测试立体绘图，MATLAB提供了一个peaks函数，可产生一个凹凸有致的曲面，包含了三个局部极大点及三个局部极小点，其方程式为：要画出此函数的最快方法即是直接键入peaks：peaksz = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) - 1/3*exp(-(x+1).^2 - y.^2)●我们亦可对peaks函数取点，再以各种不同方法进行绘图。

meshz可将曲面加上围裙：[x,y,z]=peaks;meshz(x,y,z);●waterfall可在x方向或y方向产生水流效果：[x,y,z]=peaks;waterfall(x,y,z);●下列命令产生在y方向的水流效果：[x,y,z]=peaks;waterfall(x',y',z');●meshc同时画出网状图与等高线：[x,y,z]=peaks;meshc(x,y,z);●surfc同时画出曲面图与等高线：[x,y,z]=peaks;surfc(x,y,z);●contour3画出曲面在三度空间中的等高线：contour3(peaks, 20);●contour画出曲面等高线在XY平面的投影：contour(peaks, 20);plot3可画出三度空间中的曲线：t=linspace(0,20*pi, 501);plot3(t.*sin(t), t.*cos(t), t);亦可同时画出两条三度空间中的曲线：t=linspace(0, 10*pi, 501);plot3(t.*sin(t), t.*cos(t), t, t.*sin(t), t.*cos(t), -t);三维绘图的主要功能：绘制三维线图绘制等高线图绘制伪彩色图绘制三维网线图绘制三维曲面图、柱面图和球面图绘制三维多面体并填充颜色（一）三维线图plot3 ——基本的三维图形指令调用格式：plot3(x,y,z) —— x,y,z是长度相同的向量plot3(X,Y,Z) —— X,Y,Z是维数相同的矩阵plot3(x,y,z,s) ——带开关量plot3(x1,y1,z1,’s1’,x2,y2,z2,’s2’,…)二维图形的所有基本特性对三维图形全都适用。

一、设计目的Matlab 有两类绘图命令,一类是直接对图形句柄进行操作的低层绘图命令，另一类是在低层命令基础上建立起来的高层绘图命令。

高层绘图命令简单明了、方便高效。

利用高层绘图函数，用户不需过多考虑绘图细节，只需给出一些基本参数就能得到所需图形。

在三维曲面的绘制中，Matlab提供了meshgrid 函数、mesh waterfall、函数、surf函数、Surfl函数和patch函数。

他们的使用方法基本相同。

在Matlab中，为了表现图形的显示效果，提供了一些控制函数，有视角的控制、光度的控制、色彩的控制和透明度的控制等。

在三维图形的最佳视觉效果中，Matlab提供了两种方法：一是改变观看的角度（视角），二是旋转图形。

视角由函数view控制，旋转有两个指令：rotate和rotate3d。

光照的控制主要有camlight指令、lighting 指令、material函数、light函数、lightangle函数。

色彩控制包括颜色的向量表示、色图、三维表面图形的着色以及浓淡处理。

图形的透明值用0和1之间的值表示，常用alpha来说明。

二、设计思路绘制所代表的三维曲面图，先要在平面选定一矩形区域，假定矩形区域，然后将在方向分成份，将在方向分成份，由各划分点分别作平行于两坐标轴的直线，将区域D分成个小矩形，生成代表每一个小矩形顶点坐标的平面网格坐标矩阵，最后利用有关函数求对应网格坐标的Z矩阵。

在MATLAB中，利用meshgrid函数产生平面区域内的网格坐标矩阵。

其格式为：x=a：d1：b；y=c：d2：d；[X，Y]= meshgrid（x，y）；语句执行后，矩阵X的每一行都是向量x，行数等于向量y的元素的个数，矩阵Y的每一列都是向量y，列数等于向量x的元素的个数。

当x=y时，meshgrid 函数可写成meshgrid（x）。

当函数不能简单表示出来时，便只能用for循环或while循环来计算z的元素。

y

b

sin

sin

z c cos
0 2 0
例：取 a=3, b=3, c=1
>> ezsurf('3*sin(u)*cos(v)', ... '3*sin(u)*sin(v)','1*cos(u)', ... [0,pi,0,2*pi]);
单叶双曲面的绘制
第一自变量的取值范围 第二自变量的取值范围
按字母顺序
球面的绘制
法三、利用 sphere 函数数值作图
>> [X,Y,Z]=sphere(60); >> R=3; >> X=R*X; Y=R*Y; Z=R*Z; >> surf(X,Y,Z);
椭球面的绘制
x a sin cos
t
例：取 a=3, b=5, 0 t 50
>> ezplot3('3*cos(t)','3*sin(t)','5*t',... [0,50]);
圆锥螺线的绘制
x a t cos t

y

b

t

sin
t
z c t
0 t
例：取 a=2, b=2, c=3, 0 t 50

sin
t
z b t
( t )
圆锥螺线标准方程
x a t cos t

y

b

t

sin
t
z c t

55总结总结空间曲线plot3基本的三维图形指令由二维绘图函数plot扩展与plot函数用法相似plot3xxyz是维数相同的矩阵空间曲面三维网格绘图函数meshxyzcmeshcmeshz三维曲面绘图函数surfxyzcsurfcsurfl其他曲面spherecylinderpeaksbar3stem3pie3fill3waterfallcontour356主要内容主要内容二维图形三维图形三维图形的精细处理隐函数绘图低层绘图操作光照和材质处理图像显示与动画制作57三维图形的精细处理三维图形的精细处理视点处理从不同的视点绘制的三维图形其形状也是不同的色彩处理图形的裁剪处理58视点处理视点处理matlab提供了设置视点的函数view
第六章
MATLAB 绘图
1
MATLAB 绘图
matlab语言丰富的图形表现方法，使得数学计算结果可以
方便地、多样性地实现了可视化，这是其它语言所不能比 拟的。

–高层绘图函数
» 不需过多考虑绘图细节，只需给出一些基本参数 » 简单明了、方便高效 –低层绘图操作 » 将图形的每个元素（坐标轴、曲线、曲面或文字） 分配一个句柄，通过该句柄对该图形元素进行操作 » 控制和表现图形的能力更强
–当选项省略时，MATLAB规定，线型一律用实线，颜色将根据曲线的先后 顺序依次采用表中给出的前7种颜色。 –t=0:0.2:2*pi; –x=sin(t); –y=cos(t); –plot(t,x,'+r',t,y,'-b')
11
二维图形（续）
双纵坐标函数plotyy
– 将函数值具有不同量纲、不同数量级的两个函数绘制在同一坐标中，有 利于图形数据的对比分析。 – 调用格式为：plotyy(x1,y1,x2,y2)

MATLAB中绘图命令介绍本节将介绍MATLAB基本xy平面及xyz空间的各项绘图命令，包含一维曲线及二维曲面的绘制。

plot是绘制一维曲线的基本函数，但在使用此函数之前，我们需先定义曲线上每一点的x 及y座标。

下例可画出一条正弦曲线：close all;x=linspace(0, 2*pi, 100); % 100个点的x坐标y=sin(x); % 对应的y坐标plot(x,y);小整理：MATLAB基本绘图函数plot: x轴与y轴均为线性刻度（Linear scale）loglog: x轴与y轴均为对数刻度（Logarithmic scale）semilogx: x轴为对数刻度，y轴为线性刻度semilogy: x轴为线性刻度，y轴为对数刻度若要画出多条曲线，只需将座标对依次放入plot函数即可：hold on 保持当前图形，以便继续画图到当前坐标窗口hold off 释放当前图形窗口title（’图形名称’）（都放在单引号内）xlabel（’x轴说明’）ylabel（’y轴说明’）text（x，y，’图形说明’）legend（’图例1’，’图例2’，…）plot(x, sin(x), x, cos(x));若要改变颜色，在座标对後面加上相关字串即可：plot(x, sin(x), 'c', x, cos(x), 'g');若要同时改变颜色及图线型态，也是在座标对後面加上相关字串即可：plot(x, sin(x), 'co', x, cos(x), 'g*');小整理：plot绘图函数的叁数字元、颜色元、图线型态，y 黄色 .点k 黑色o 圆w 白色x xb 蓝色++g 绿色* *r 红色- 实线c 亮青色: 点线m锰紫色-. 点虚线-- 虚线plot3 三维曲线作图图形完成后，我们可用axis([xmin,xmax,ymin,ymax])函数来调整图轴的范围： axis([0, 6, -1.2, 1.2]);axis函数的功能丰富，其常用的用法有：axis equal ：纵横坐标轴采用等长刻度axis square：产生正方形坐标系（默认为矩形）axis auto：使用默认设置axis off：取消坐标轴axis on ：显示坐标轴此外，MATLAB也可对图形加上各种注解与处理：xlabel('Input Value'); % x轴注解ylabel('Function Value'); % y轴注解title('Two Trigonometric Functions'); % 图形标题legend('y = sin(x)','y = cos(x)'); % 图形注解grid on; % 显示格线我们可用subplot来同时画出数个小图形於同一个视窗之中：subplot(2,2,1); plot(x, sin(x));subplot(2,2,2); plot(x, cos(x));subplot(2,2,3); plot(x, sinh(x));subplot(2,2,4); plot(x, cosh(x));MATLAB还有其他各种二维绘图函数，以适合不同的应用，详见下表。

线条之间的空挡填充颜色，沿z轴按每一网
格变化
调用格式： surf(x,y,z) —— 与mesh的调用方式相同 例： [X,Y,Z]=peaks(30) ※peaks为matlab 自动生成的三维测 试图形 surf(X,Y,Z)

surfc(X,Y,Z) — 带等高线的曲面图 [X,Y,Z]=peaks(30);surfc(X,Y,Z)
mesh(X,Y,Z) mesh(Z) —— Z为n×m的矩阵， 默认x=1:n, y=1:m

meshc —— 生成网格线，在xoy面上
生成曲面的等高线图形

meshz —— 生成网格线，在曲面下面 加上一个长方形的台柱

mesh，meshc，meshz的调用方式相 同
例：
x=1:0.1:3; y=1:0.1:4; [X,Y]=meshgrid(x,y); Z=ones(size(X)); mesh(X,Y,Z)
第二讲 matlab 绘图
——matlab语言丰富的图形表 现方法，使得数学计算结果可 以方便地、多样性地实现了可 视化，这是其它语言所不能比 拟的。
一、二维绘图
plot —— 最基本的二维图形指令，绘制线 性图形（描点、连线）
plot的调用格式
plot(x) —— 缺省自变量绘图格式，x为 向量, 以x元素值为纵坐标，以相应元素 下标为横坐标绘图 plot(x,y) —— 基本格式，以y(x)的函数 关系作出直角坐标图。P36
在图形的顶端加注文字作为图名

在当前图形的x轴旁边加注文字 在当前图形的y轴旁边加注文字 在当前图形的z轴旁边加注文字

图形标注 text (x, y, ‘String’) 在(x,y)处加文字‘String’(二维图 形) text (x, y, z, ‘String’) 在(x,y,z)处…(三维图形) gtext (‘String’) 在鼠标指定位置上标注

MATLAB绘制空间曲面的命令一、介绍在科学计算和工程领域中，经常需要对空间曲面进行可视化分析。

MATLAB作为一种强大的数值计算软件，提供了丰富的绘图函数和命令，可以轻松地绘制空间曲面。

本文将介绍MATLAB中常用的绘制空间曲面的命令，并通过示例代码详细说明其使用方法和效果。

二、绘制三维曲面1. meshgrid函数在绘制空间曲面之前，我们需要先创建一个网格。

MATLAB中的meshgrid函数可以用来生成二维或三维的坐标网格，为后续的曲面绘制提供基础。

示例代码：[x, y] = meshgrid(-10:0.5:10, -10:0.5:10);2. 曲面方程在绘制空间曲面时，我们需要定义一个曲面方程。

曲面方程可以是一个显式方程，也可以是一个隐式方程。

示例代码：z = x.^2 + y.^2;3. surf函数一旦我们定义了曲面方程和坐标网格，就可以使用surf函数来绘制空间曲面了。

surf函数可以根据给定的坐标网格和曲面方程，生成一个三维曲面图。

示例代码：surf(x, y, z);4. 其他参数设置除了基本的绘图命令外，还可以通过设置其他参数来调整曲面的外观和显示效果。

例如，可以设置曲面的颜色、透明度、光照等。

示例代码：surf(x, y, z, 'FaceColor', 'interp', 'EdgeColor', 'none');light('Position', [1 1 1]);三、绘制特殊曲面1. 球面球面是一种常见的空间曲面，可以通过给定球心和半径来定义。

MATLAB中的sphere函数可以绘制球面。

示例代码：[x, y, z] = sphere;surf(x, y, z);2. 圆柱面圆柱面是由平行于一个固定直线的所有直线和平行于一个固定平面的所有直线形成的曲面。

MATLAB中的cylinder函数可以绘制圆柱面。