复摆侧重力加速度

实验名称： 复摆法侧重力加速度仪器与用具：复摆、秒表。

复摆，一块有刻度的匀质钢板，板面上从中心向两侧对称的开一些悬孔。

另有一固定刀刃架用以悬挂钢板。

调节刀刃水平螺丝，调节刀刃水平。

实验目的：①了解复摆小角摆动周期与回转轴到复摆重心距离的关系。

②测量重力加速度。

实验报告内容（原理预习、操作步骤、数据处理、误差分析、思考题解答）[实验原理]一个围绕定轴摆动的刚体就是复摆。

当复摆的摆动角θ很小时，复摆的振动可视为角谐振动。

根据转动定律有22dtd JJ mgb θβθ-=-=即022=+θθJm g b dtd可知其振动角频率 Jm g b =ω角谐振动的周期为m g b J T π2= （3.3.10）式中J 为复摆对回转轴的转动惯量；m 为复摆的质量；b 为复摆重心至回转轴的距离；g 为重力加速度。

如果用Jc 表示复摆对过质心轴的转动惯量，根据平行轴定理有2mbJc J += (3.3.11)将式（3.3.11）代入式（3.3.10）得 mgbmb Jc T 22+=π（3.3.12）以b 为横坐标，T 为纵坐标，根据实验测得b 、T 数据，绘制以质心为原点的T-b 图线，如图3.3.3所示。

左边一条曲线为复摆倒挂时的b T '-'曲线。

过T 轴上1T T =点作b 轴的平行线交两条曲线于点A 、B 、C 、D 。

则与这4点相对应的4个悬点A '、B '、C '、D '都有共同的周期T 1。

设1b A O ='，2b B O ='，1b C O '='，2b D O '='，则有 121121122b mg b m Jc mgb mb Jc T ''+=+=ππ或222222122b mg b m Jc mgbmb Jc T ''+=+=ππ消去Jc ，得gb b gb b T 2211122'+='+=ππ（3.3.13）将式（3.3.13）与单摆周期公式相比较 ，可知与复摆周期相同的单摆的摆长 11b b l '+=或 22b b l '+=，故称11b b '+（或22b b '+）为复摆的等值摆长。

分类号密级U D C 编号本科毕业论文(设计)题目测重力加速度的几种方法比较及误差分析系别专业名称物理学年级学生姓名学号指导教师二00 八年五月摘要：地球表面及附近的物体受到地球重力的作用，如果忽略空气摩擦的影响，则所有落地物体都将以同一加速度下落，这个加速度称为重力加速度。

重力加速度是一个重要的地球物理常数，准确测定它的量值，不仅在理论上，而且在生产上、科研上都有着极其重要的意义。

在实验室内测量重力加速度的方法有很多种。

本文利用实验室的仪器，通过单摆法、电磁打点计时器法、倾斜气垫导轨法以及复摆法进行测量重力加速度的实验。

通过实验原理、实验方法、实验记录数据、误差分析、最终结果等方面进行比较与研究，针对可能造成较大误差的变量，提出可实施的改进办法，提高实验测量值的可靠性。

关键词：重力加速度单摆电磁打点计时器气垫导轨复摆Abstract: On Earth, everything feels the downward force of gravity. If we neglect the friction force of the air, all the masses will be falling freely with the same downward acceleration because gravity is the only force acting. This is the acceleration of free fall. The constant acceleration, g, is very important. Measuring exactly plays a significant role in theory, production and scientific research. There are many methods for measuring g in laboratories. The major content about this thesis is doing experiments through using the simple pendulum, the electromagnetic pointing set, the sloping air track and the compound pendulum. Then compare the principle, method or result of the four experiments and analyze the error. At the end, suggest practicable and improvable measures in accordance with the larger error for raising accuracy.Key words: acceleration of gravity simple pendulum electromagnetic pointing set air track compound pendulum文献综述一、概述测量重力加速度的方法有很多种，包括用单摆测重力加速度、用电磁打点计时器测重力加速度、用自由落体法测重力加速度、用复摆测重力加速度、用凯特摆测重力加速度、倾斜气垫导轨上测重力加速度以及频闪照相法测重力加速度等。

复摆的实验报告-精品复摆的实验报告-精品2020-12-12【关键字】方案、目录、情况、方法、动力、成绩、质量、系统、有效、平衡、了解、研究、特点、位置、关键、理想、项目、资源、作用、水平、任务、反映、速度、关系、分析、调节、指导、分工、方向、中心篇一：实验报告_复摆实验【实验题目】复摆实验【实验记录】1. 复摆中心G的位置：0刻度处3. 计算重力加速度g:4?2T12?T22T12?T22g2(h1?h2)2(h1?h2)g=9.905kg/m214. 作T-h图5. 利用mgT2h?4?2IG?4?2mh2，作T2h~h2关系图，考察其线形关系，由最小二乘法计算g和复摆对重心的转动惯量IG。

IG=0.002536kg*m*m【结论与讨论】误差分析：1 在实验中，复摆的摆动不能很好的控制在同一平面摆动。

2 实验前没有很好的调节复摆对称。

3 复摆摆动可能幅度过大。

结论：利用复摆可以测量重力加速度，同时还可以由这个方法衍生开来测量不规则物体的转动惯量。

成绩（满分30分）：指导教师签名：日期：篇二：复摆实验报告【实验题目】复摆实验【实验记录】1. 复摆中心g的位置：0刻度处3. 计算重力加速度g:4?2t12?t22t12?t22g2(h1?h2)2(h1?h2)g=9.905kg/m2 14. 作t-h图5. 利用mgt2h?4?2ig?4?2mh2，作t2h~h2关系图，考察其线形关系，由最小二乘法计算g和复摆对重心的转动惯量ig。

ig=0.002536kg*m*m 【结论与讨论】误差分析：1 在实验中，复摆的摆动不能很好的控制在同一平面摆动。

2 实验前没有很好的调节复摆对称。

3 复摆摆动可能幅度过大。

结论：利用复摆可以测量重力加速度，同时还可以由这个方法衍生开来测量不规则物体的转动惯量。

成绩（满分30分）：指导教师签名：日期：2篇二：实验报告_复摆实验【实验题目】复摆实验【实验记录】1. 复摆中心g的位置：3. 计算重力加速度g:4?2t12?t22t12?t22= g2(h1?h2)2(h1?h2)g= 14. 作t-h图5. 利用mgth?4?ig?4?mh，作th~h关系图，考察其线形关系，由最小二乘法计 22222算g和复摆对重心的转动惯量ig。

重力加速度几种测量方法的比较引言：重力加速度是物理学中的一个十分重要的物理量，在地面上不同的地区，重力加速度g值不相同，它是由物体所在地区的纬度、海拔等因素决定，随着地球纬度和海拔高度的变化而变化，准确地确定它的量值，无论从理论上、还是科研上、生产上以及军事上都有极其重大的意义。

测量重力加速度的方法有很多，我所要做的就是通过学习前人的理论知识，经过思考，在现有的实验室条件下，进行实验，做出归纳和总结，提出自己的看法与体会。

且实验方法虽然多，但有的测量仪器的精确度受环境因素的影响比较大，不是每种方法都适用，所以有必要对测量方法进行研究，找出一种适合测量本地重力加速度的方法。

一、重力加速度的测量方法（一）用自由落体法测量重力加速度1.实验仪器：自由落体装置（如图一），数字毫秒计，光电门（两个），铁球。

图一自由落体装置2.实验原理、步骤、注意事项实验原理：设光电门A 、B 间的距离为s ，球下落到A 门时的速度为0v ，通过A 、B 间的时间为t ，则成立：2/20gt t v s += （1）两边除以t ,得：2//0gt v t s += （2）设t x =,t s y /=,则：2/0gx v y += （3）这是一直线方程，当测出若干不同s 的t 值，用t x =和t s y /=进行直线拟合，设所得斜率为b ，则由2/g b =可求出g ，b g 2=（4） 实验步骤：（1）调节实验装置的支架，使立柱为铅直，再使落球能通过A 门B 门的中点。

（2）测量A 、B 两光电门之间的距离s 。

（3）测量时间t 。

（4）计算各组的x ，y 值，用最小二乘法做直线拟合，求出斜率b 及其标准偏差b S 、)(b u （注意：在取b 的时，由于立柱调整不完善，落球中心未通过光电门的中点，立柱上米尺的误差均给s 值引入误差，也是b 的不确定度来源，一般此项不确定度（B 类评定）较小，可略去不计，所以b S b u =)(）。

山东理工大学物理实验报告实验名称： 复摆法侧重力加速度姓名：李 明 学号：05 1612 时间代码：110278 实验序号：19院系： 车辆工程系 专业： 车辆工程 级.班： 2 教师签名： 仪器与用具：复摆、秒表。

复摆，一块有刻度的匀质钢板，板面上从中心向两侧对称的开一些悬孔。

另有一固定刀刃架用以悬挂钢板。

调节刀刃水平螺丝，调节刀刃水平。

实验目的：①了解复摆小角摆动周期与回转轴到复摆重心距离的关系。

②测量重力加速度。

实验报告内容（原理预习、操作步骤、数据处理、误差分析、思考题解答）[实验原理]一个围绕定轴摆动的刚体就是复摆。

当复摆的摆动角θ很小时，复摆的振动可视为角谐振动。

根据转动定律有22dtd J J mgb θβθ-=-=即022=+θθJ m gbdtd 可知其振动角频率 Jmgb=ω 角谐振动的周期为mgbJT π2= （3.3.10） 式中J 为复摆对回转轴的转动惯量；m 为复摆的质量；b 为复摆重心至回转轴的距离；g 为重力加速度。

如果用Jc 表示复摆对过质心轴的转动惯量，根据平行轴定理有2mb Jc J += (3.3.11)将式（3.3.11）代入式（3.3.10）得mgbmb Jc T 22+=π（3.3.12） 以b 为横坐标，T 为纵坐标，根据实验测得b 、T 数据，绘制以质心为原点的T-b 图线，如图3.3.3所示。

左边一条曲线为复摆倒挂时的b T '-'曲线。

过T 轴上1T T =点作b 轴的平行线交两条曲线于点A 、B 、C 、D 。

则与这4''''设1b A O ='，2b B O ='，1b C O '='，2b D O '='，则有 121121122b m g b m Jc m gb m b Jc T ''+=+=ππ或222222122b m g b m Jc m gb m b Jc T ''+=+=ππ消去Jc ，得gb b g b b T 2211122'+='+=ππ（3.3.13） 将式（3.3.13）与单摆周期公式相比较 ，可知与复摆周期相同的单摆的摆长 11b b l '+=或 22b b l '+=，故称11b b '+（或22b b '+）为复摆的等值摆长。

《复摆法测重力加速度》
复摆法测重力加速度是求解单位体积上的重力加速度的一种有效方法。

它是以持续而
稳定的运动来测量小时间量单位面积上的重力加速度。

Polykarp Kusch在55年提出了这
一方法，它是基于动量定理和牛顿第二定律，通过复摆运动测定重力加速度。

它的过程为：1.线加速摆，由于重力的作用水平摆动的行程的比垂直摆动的行程更短，通过观察摆动的
次数，就可以把重力加速度确定下来。

2.重力倾斜试验，将摆设在体积不同的物体上，并
在水平面上量出和物体高度的关系，根据抛物线的斜率求出重力加速度。

3.交换法，重力
假设一定，将一把摆放在地球表面上，一把放入重力偏离地球表面的抛物线上，然后计算
水平摆动的次数，从而计算出重力加速度。

复摆法测重力加速度在研究地质或物理学的方面有很大的作用，它可以对小范围的地
底层数据进行处理，可以进行精确的地质或物理层次识别。

此外，由于它能够快速地测量
重力加速度，它也被用于量测空间中的重力，并制定运行空间中卫星的轨道，特别是用于
定义地球重力场表面和测量地形特征，如河床和海拔高度，从而把重力学与地理学息息相关。

复摆测重力加速度扈巧梅、杨德尚、周丽艳、包雪玉（吉首大学物理科学与信息工程学院）摘要：我们利用复摆测量重力加速度，研究该论述的方法的精确性、灵活性，以及分析误差因素。

关键字：重力加速度；复摆；精确性；灵活性Measuring the acceleration of gravity by compoundpendulumHu Qiaomei; Yang Deshang; Zhou Liyan; Bao Xeuyu（College of Physics Science and Information Engineering, Jishou University）Abstract:We measure the acceleration of gravity by compound pendulum. Then we discuss accuracy, flexibility and error component of the experiment.Keyword: Acceleration of gravity; Compound pendulum; Accuracy; Flexibility引言：重力加速度g在物理科学中是一个很中要的物理量参量。

1590年，意大利物理学家伽利略进行了世界上第一次重力测量。

发展至今，测重力加速度的方法多种多样，比如说自由落体、单摆、复摆、平抛运动、气垫导轨实验、凯特摆等方法测量，而根据实验室设备情况本文研究复摆。

1、实验目的（1）利用复摆精确地测量重力加速度；(2)用作图法处理实验数据；(3)分析实验的灵活性及误差因素。

2、实验仪器复摆装置、光电计时器、电子天平等3、实验原理复摆实验通常用于研究周期与摆轴位置的关系，并测定重力加速度。

复摆是一刚体绕固定水平轴在重力作用下作微小摆动的动力运动体系。

实验原理装置如图1,刚体绕固定轴O在竖直平面内作左右摆动，G是该物体的质心，与轴O 的距离为ｈ,θ为其摆动角度。

用三种方法测量重力加速度朱津纬1（1.复旦大学物理学系，上海市200433）摘要：本实验通过手机phyphox软件，用三种方法测量了重力加速度。

分别将落币法、复摆法和弹簧法所得的重力加速度结果与实际值比较，误差不超过4%。

1 引言随着科技的发展，如今智能手机功能越来越丰富。

许多应用软件全面地利用手机中传感器，可以用来实施物理实验[1,2]。

其中，“phyphox”是集合了很多实验项目的应用软件。

本实验将利用它来测量重力加速度。

重力加速度可通过多种方法进行测得。

如单摆法[3]，多管落球法[4]，和利用自由落体的方法[5]等。

在本实验中，重力加速度利用落币法、复摆法和弹簧法三种方法被测量，并与标准值比较。

2 实验原理首先，分别介绍三种方法的理论原理。

2.1 落币法该实验将利用“phyphox”中的“声控秒表”项目，测量硬币从不同高度ℎ自由落体所需的时间t。

通过对t−√ℎ数据线性拟合，得到重力加速度g=2斜率2。

如图1所示，硬币自由落体下落的高度为ℎ。

用水笔敲击直尺发出敲击声，设该时刻为t0。

经过微小时间差Δt（与高度无关，假设为常量），硬币开始下落，设该时刻为t1。

一段时间后，硬币落到地上，并发出与地面的碰撞声，设该时刻为t2。

“声控秒表”测量了两次声响的时间差t=t2−t0。

由自由落体公式可知ℎ=12g(t2−t1)2=12g(t−Δt)2，(2.1)即t=√2g√ℎ+Δt。

(2.2)因此t−√ℎ呈线性关系，斜率为√2g。

2.2 复摆法图1 落币法实验示意图该实验将利用“phyphox ”中的“单摆”项目，测量不同摆长L 复摆的摆动周期T 。

通过对T 2−L 2+bL+b 23(L+b 2)数据线性拟合，得到重力加速度g =4π2斜率。

如图2所示，长度为L 的细线与宽度为b 的手机组成复摆，以杆子为轴前后摆动。

设复摆的转动惯量为I ，手机（过中心水平轴）的转动惯量为I c =mb 212。

则由平行轴定理得I =I c +m(L +b2)2。

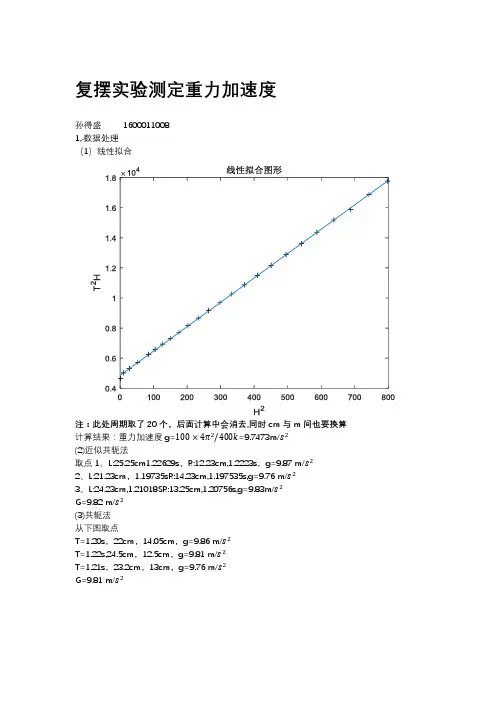
复摆实验测定重力加速度
孙得盛1600011008
1,·数据处理
（1）线性拟合
注：此处周期取了20个，后面计算中会消去,同时cm与m间也要换算计算结果：重力加速度g=100×4π2/400k=9.7473m/s2
(2)近似共轭法
取点1、L:25.25cm1.22629s，R:12.23cm,1.2223s，g=9.87 m/s2
2、L:21.23cm，1.19735sR:14.23cm,1.197535s,g=9.76 m/s2
3、L:24.23cm,1.21018SR:13.25cm,1.20756s,g=9.83m/s2
G=9.82 m/s2
(3)共轭法
从下图取点
T=1.20s，22cm，14.05cm，g=9.86 m/s2
T=1.22s,24.5cm，12.5cm，g=9.81 m/s2
T=1.21s，23.2cm，13cm，g=9.76 m/s2
G=9.81 m/s2
T——h图
2，讨论与分析
本实验3种方法之间的误差来源主要是复摆重心测定的误差，法1法2法3的差别也就是对这一误差的消除程度不同。

直线拟合并没有消除这个误差。

近似共轭由于数据不是刚好同周期导致引入修正量，但修正量中也涉及到复摆长所以也有一定误差。

共轭法由于是拟合作图，再选取同t轴高度，消除了大部分的复摆重心测量误差，得到的结果更精确。

从实验结果上看，也佐证了以上讨论。

（北京地区重力加速度g=9.80m/s2）.
附录：实验原始数据。

物理摆测重力加速度g值的实验研究本文根据物理摆的微振动理论，针对J—LD23型物理摆，用四种不同方法测量当地重力加速度,并利用计算机对测量数据进行分析。

第一种方法利用复摆的共轭性，采用Mathematica软件作图，从而找寻到共轭点，进而求出g值。

第二种方法根据复摆的周期公式，采用解方程组的方式求出g值。

第三种方法采用最小二乘法从测量数据中计算得到拟合直线方程，从而获得g值大小。

第四种方法采用凯特可逆摆测g值大小。

最后得到了四种不同方法所测出的g值，并对误差来源及四种方法的优劣进行了简要分析。

关键词：物理摆;周期;重力加速度；可逆摆。

1 前言在物理学中，重力加速度g是一个重要的地球物理常数。

它首先由伽利略（1564-1642）证明，如果忽略空气阻力的影响，所有落地物体都将以同一加速度下降，这个加速度称为重力加速度g。

1888年，法国军事测绘局使用新的方法进行了g值的测量,当时的测量结果为：g=9.80991m/s2。

1906年，德国的库能和福脱万勒用相同的方法在波茨坦作了g值的测量，作为国际重力网的参考点，即称为“波茨坦重力系统”的起点，其结果为g（波茨坦）=9.81274m/s2[1]。

地球上各点的加速度数值，主要与测点的纬度、高度和测点周围的地形，以及地球的潮汐、地球内部岩石密度的差异等有关。

重力加速度g值的准确测定对于计量学、精密物理测量、地球物理学、地震预报、重力探矿和空间科学等都具有重要意义[2]。

例如，不确定度为1×10-6的g 值，对绝对安培的影响为5×10-7；对绝对伏特、力和压力的影响为1×10-6；对水沸点温度的影响是3×10-4K。

观测g值的变化还可能对预报地震有密切的关系。

据有关方面报道，七级地震相对应的g值变化约为0.1×10-5m/s2[1]。

目前，许多国家都在探索用g值的变化作临震预报。

地下岩石和矿体密度的不同会引起地面重力加速度的相应的变化，从而可以进行重力探矿。

用凯特摆测量重力加速度实验日期：2011年12月17日实验者：实验名称：用凯特摆测量重力加速度实验原理：图1复摆示意图图1是复摆示意图，设一质量为m的刚体，其重心G到转轴O的距离为h，绕O轴的转动惯量为I，当摆幅很小时，刚体绕O轴摆动的周期T为：(1)式中g为当地的重力加速度设复摆绕通过重心G的轴的转动惯量为I G，当G轴与O轴平行时，有I=I G+mh2 (2)代入式（1）得：(3)对比单摆周期的公式，可得(4)称为复摆的等效摆长。

因此只要测出周期和等效摆长便可求得重力加速度。

上图是凯特摆摆杆的示意图。

对凯特摆而言，两刀口间的距离就是该摆的等效摆长l。

在实验中当两刀口位置确定后，通过调节A、B、C、D四摆锤的位置可使正、倒悬挂时的摆动周期T1和T2基本相等。

由公式（3）可得(5)(6)其中T1和h1为摆绕O轴的摆动周期和O轴到重心G的距离。

当T1≈T2时，h1+h2=l 即为等效摆长。

由式(5)和(6)消去I G，可得：(7)此式中，l、T1、T2都是可以精确测定的量，而h1则不易测准。

由此可知，a项可以精确求得，而b项则不易精确求得。

但当T1=T2以及 |2h1-l| 的值较大时，b项的值相对a项是非常小的，这样b项的不精确对测量结果产生的影响就微乎其微了。

一、实验目的：1.学习一种比较精确的测量重力加速度的方法。

2. 学习凯特摆的实验设计思想和技巧。

3. 选定两刀口间的距离，通过调节A、B、C、D四摆锤的位置，使得该摆以两个刀口为悬点的摆动周期基本相等。

二、实验所用仪器及使用方法实验仪器图1:凯特摆测量重力加速度实验仪器包括凯特摆、光电探头和多用数字测试仪。

图2:凯特摆凯特摆的两端共大小4个摆锤，调节摆锤的位置可以改变凯特摆的重心，两端相同的位置各有一个固定刀口。

实验之前需要先调节凯特摆的重心位置，重心调节完成的标志是：使用任何一个刀口时，凯特摆的摆动周期相同。

图3:凯特摆的大摆锤图4:凯特摆的小摆锤图5:固定刀口和V形刀承可将摆杆悬挂到支架上，使摆杆能在铅垂面内自由摆动。

凯特摆测重力加速度PB05204044 张雯 实验组别：20实验目的：(1)学习凯特摆的实验设计思想和技巧(2)掌握一种比较精确的测量重力加速度的方法实验仪器：凯特摆，光电探头，米尺，VAFN 多用数字测试仪实验原理：(1)复摆：设一质量为m 的刚体，其重心G 到转轴O 的距离为h ，绕O 轴的转动惯量为I ，当摆幅很小时，刚体绕O 轴摆动的周期T 为：(1)mghI T π2=式中g 为当地的重力加速度.设复摆绕通过重心G 的轴的转动惯量为IG ，当G 轴与O 轴平行时，有I=IG+mh2(2)代入式（1）得：(3)mghmh I T G 22+=π对比单摆周期的公式gl T π2=可得(4)mhmh I l G 2+=称为复摆的等效摆长。

因此只要测出周期和等效摆长便可求得重力加速度。

(2)凯特摆原理：下图是凯特摆摆杆的示意图。

对凯特摆而言，两刀口间的距离就是该摆的等效摆长l 。

在实验中当两刀口位置确定后，通过调节A 、B 、C 、D 四摆锤的位置可使正、倒悬挂时的摆动周期T1和T2基本相等。

由公式（3）可得(5)(6)12112mgh mh I T G +=π22222mgh mh I T G +=π其中T1和h1为摆绕O 轴的摆动周期和O 轴到重心G 的距离。

当T1≈T2时，h1+h2=l 即为等效摆长。

由式(5)和(6)消去IG ，可得：(7)()l h T T l T T g --++=12221222122224π此式中，l 、T1、T2都是可以精确测定的量，而h1则不易测准。

由此可知，a 项可以精确求得，而b 项则不易精确求得。

但当T1=T2以及 |2h1-l| 的值较大时，b 项的值相对a 项是非常小的，这样b 项的不精确对测量结果产生的影响就微乎其微了。

手写版预习报告与原始数据已递交数据处理：(1) 计算和的平均值与不确定度l 1h '由原始数据可得下表次数物理量123/l cm74.8874.9074.911/h cm29.5029.4529.43表一：- 数值表l 1ha) 计算的平均值与不确定度l 统计计算结果：3174.8874.9074.9174.89733ii ll cm =++===∑()0.0153l cmσ==的A 类不确定度：P=0.683 n=3 取=1.32l pt () 1.320.012A pu l t cm ==⨯=的B 类不确定度：钢卷尺 P=0.683l p 0.1cm k 1 C=3==A 仪0.1()10.0333B pu l K cm C==⨯=A 仪合成不确定度：（P=0.683）()0.035u l cm ===综上，实验测得 (P=0.683)()(74.8970.035)l l u l cm =±=±b) 计算的平均值与不确定度1h 统计计算结果： 311129.5029.4529.4329.46033ii hh cm=++===∑1()0.0361h cmσ==的A 类不确定度：P=0.683 n=3 取=1.321h pt 1() 1.320.028A pu h t cm ==⨯=的B 类不确定度：钢卷尺 P=0.6831h p 0.1cm k 1 C=3==A 仪10.1()10.0333B pu h K cm C ==⨯=A 仪合成不确定度：（P=0.6831()0.043u h cm ===）综上，实验测得(P=0.683)111()(29.4600.043)h h u h cm =±=±(2) 计算和的平均值与不确定度1T 2T 由原始数据可得下表次数物理量12345110/T s17.377417.375817.375717.377317.3755210/T s17.377617.379017.379517.376317.3788表二：摆动周期数值表a) 计算的平均值与不确定度1T 统计计算结果：3111101117.377417.375817.375717.377317.3755 1.73763105105ii T T s =++++=⨯=⨯=∑511()9.31010T sσ-==⨯的A 类不确定度：P=0.683 n=5 取=1.141T p t 51() 1.14 4.710A pu T t s-===⨯的B 类不确定度：多用数字测试仪 P=0.6831T p 0.0001s k 1 C=3==A 仪510.0001()1 3.3103B pu T K s C-==⨯=⨯A 仪合成不确定度：51() 5.710u T s-===⨯（P=0.683）综上，实验测得(P=0.683)111()(1.737630.00006)T T u T s =±=±b) 计算的平均值与不确定度2T 统计计算结果：3212101117.377617.379017.379517.376317.3788 1.73782105105i i T T s =++++=⨯=⨯=∑421() 1.31010T sσ-=⨯=⨯的A 类不确定度：P=0.683 n=5 取=1.142T pt 52() 1.14 6.610A pu T t s -===⨯的B 类不确定度：多用数字测试仪 P=0.6832T p 0.0001s k 1 C=3==A 仪520.0001()1 3.3103B pu T K s C-==⨯=⨯A 仪合成不确定度：52()7.410u T s-===⨯（P=0.683）综上，实验测得(P=0.683)222()(1.737820.00008)T T u T s =±=±(3)计算重力加速度的平均值与不确定度g 由公式 带入数值，得到重力加速度：2222212121422(2)T T T T a b g l h l π+-=+=+-g1222221221214422(2)T T T T g a b l h l ππ-⎡⎤-+==+⎢⎥+-⎢⎥⎣⎦122222173763 1.73782173763 1.73782420.748972(20.294600.74897)π-⎡⎤+-=⨯+⎢⎥⨯⨯⨯-⎣⎦..29.7906/m s =下面计算的不确定度g由于 的大小相对非常小221212(2)T T b h l -=-22122T T a l +=因此 12222122212842T T l g l T T ππ-⎡⎤+≈⨯=⎢⎥+⎣⎦两边取对数 22221222128ln ln 8ln ()l g ln l ln T T T T ππ==+-++两边取全微分11222222121222T dT T dT dg dl g l T TT T =--++因此有()u g g=得到的合成不确定度公式g ()u g g=9.7906=(P=0.683)20.0046/m s = 不确定度保留一位有效数字，因此：综上，实验测得=(P=0.683)g 2()(9.7910.005)/g u g m s ±=±误差分析：(1)本实验对周期的测量较精确，但是对等效摆长的测量却有很大的误差，由于钢卷尺较软，加之凯特摆形状的限制，对两刀口间距离（即）德德良存在很大误差。