大学物理机械波习题集附规范标准答案

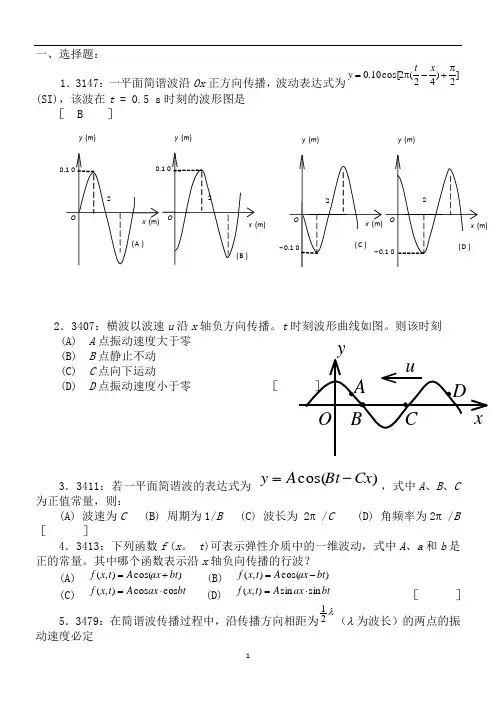
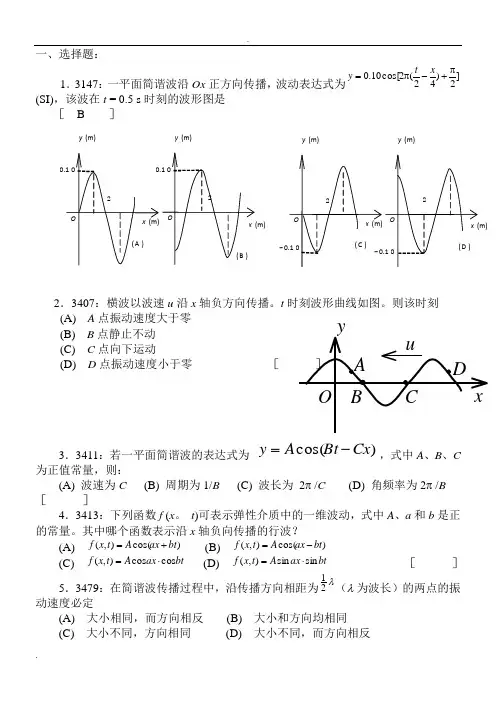
一、选择题：1．3147：一平面简谐波沿Ox 正方向传播，波动表达式为(SI)，该波在t = 0.5 s 时刻的波形图是［ B ］2．3407：横波以波速u 沿x 轴负方向传播。

t 时刻波形曲线如图。

则该时刻 (A) A 点振动速度大于零 (B) B 点静止不动(C) C 点向下运动(D) D 点振动速度小于零 ［ ］ 3．3411：若一平面简谐波的表达式为 ，式中A 、B 、C 为正值常量，则：(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B ［ ］4．3413：下列函数f (x 。

t )可表示弹性介质中的一维波动，式中A 、a 和b 是正的常量。

其中哪个函数表示沿x 轴负向传播的行波？(A) (B)(C) (D) ［ ］5．3479：在简谐波传播过程中，沿传播方向相距为（λ 为波长）的两点的振动速度必定]2)42(2cos[10.0π+-π=x t y )cos(Cx Bt A y -=)cos(),(bt ax A t x f +=)cos(),(bt ax A t x f -=bt ax A t x f cos cos ),(⋅=bt ax A t x f sin sin ),(⋅=λ21 x u A y B C D Ox (m) O 2 0.1 0y (m) ( A ) x (m) O 2 0.1 0 y (m) ( B )x (m) O 2- 0.1 0 y (m) ( C ) x (m)O 2 y (m)( D ) - 0.1 0(A) 大小相同，而方向相反 (B) 大小和方向均相同(C) 大小不同，方向相同 (D) 大小不同，而方向相反 ［ ］6．3483：一简谐横波沿Ox 轴传播。

若Ox 轴上P 1和P 2两点相距λ /8（其中λ 为该波的波长），则在波的传播过程中，这两点振动速度的(A) 方向总是相同 (B) 方向总是相反(C) 方向有时相同，有时相反 (D) 大小总是不相等 ［ ］7．3841：把一根十分长的绳子拉成水平，用手握其一端。

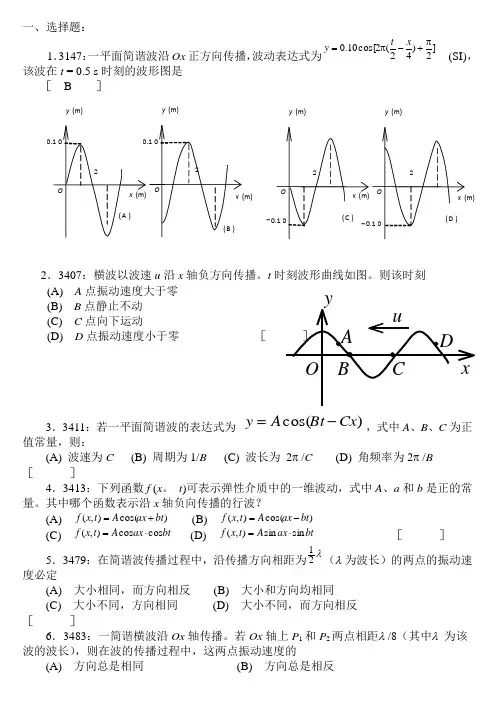
一、选择题：1．3147：一平面简谐波沿Ox 正方向传播，波动表达式为]2)42(2cos[10.0π+-π=x t y (SI)，该波在t = 0.5 s 时刻的波形图是［ B ］2．3407：横波以波速u 沿x 轴负方向传播。

t 时刻波形曲线如图。

则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 ［3．3411：若一平面简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C 为正值常量，则：(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B ［］4．3413：下列函数f (x 。

t )可表示弹性介质中的一维波动，式中A 、a 和b 是正的常量。

其中哪个函数表示沿x 轴负向传播的行波？(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D) btax A t x f sin sin ),(⋅= ［ ］5．3479：在简谐波传播过程中，沿传播方向相距为λ21（λ 为波长）的两点的振动速度必定(A) 大小相同，而方向相反 (B) 大小和方向均相同(C)大小不同，方向相同 (D) 大小不同，而方向相反 ［ ］6．3483：一简谐横波沿Ox 轴传播。

若Ox 轴上P 1和P 2两点相距λ /8（其中λ 为该波的波长），则在波的传播过程中，这两点振动速度的(A) 方向总是相同 (B) 方向总是相反y (m) y (m) - y (m) y (m)(C) 方向有时相同，有时相反 (D) 大小总是不相等 ［ ］7．3841：把一根十分长的绳子拉成水平，用手握其一端。

维持拉力恒定，使绳端在垂直于绳子的方向上作简谐振动，则 (A) 振动频率越高，波长越长(B) 振动频率越低，波长越长(C) 振动频率越高，波速越大 (D) 振动频率越低，波速越大 ［ ］ 8．3847：图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。

(完整版)机械波习题及答案波的形式传播波的图象认识机械波及其形成条件，理解机械波的概念，实质及特点，以及与机械振动的关系；理解波的图像的含义，知道波的图像的横、纵坐标各表示的物理量.能在简谐波的图像中指出波长和质点振动的振幅，会画出某时刻波的图像一、机械波⑴机械振动在介质中的传播形成机械波.⑵机械波产生的条件：①波源，②介质.二、机械波的分类⑴)横波：质点振动方向与波的传播方向垂直的波叫横波.横波有波峰和波谷.⑵纵波：质点振动方向与波的传播方向在同一直线上的波叫纵波.纵波有疏部和密部.三、机械波的特点(1)机械波传播的是振动形式和能量，质点只在各自的平衡位置附近振动，并不随波迁移.⑵介质中各质点的振动周期和频率都与波源的振动周期和频率相同⑶离波源近的质点带动离波源远的质点依次振动⑷所有质点开始振动的方向与波源开始振动的方向相同。

四、波长、波速和频率的关系⑴波长：两个相邻的且在振动过程中对平衡位置的位移总是相等的质点间的距离叫波长.振动在一个周期里在介质中传播的距离等于一个波长，对于横波：相邻的两个波峰或相邻的两个波谷之间的距离等于一个波长.对于纵波：相邻的两个密部中央或相邻的两个疏部中央之间的距离等于一个波长.⑵波速：波的传播速率叫波速.机械波的传播速率只与介质有关，在同一种均匀介质中，波速是一个定值，与波源无关.⑶频率：波的频率始终等于波源的振动频率.⑷波长、波速和频率的关系：v=λf=λ/T五、波动图像波动图象是表示在波的传播方向上，介质中各个质点在同一时刻相对平衡位置的位移，当波源做简谐运动时，它在介质中形成简谐波，其波动图象为正弦或余弦曲线.六、由波的图象可获取的信息⑴该时刻各质点的位移.⑵质点振动的振幅A．⑶波长.⑷若知道波的传播方向，可判断各质点的运动方向.如图7-32-1所示，设波向右传播，则1、4质点沿-y方向运动；2、3质点沿+y方向运动.⑸若知道该时刻某质点的运动方向，可判断波的传播方向.如图7-32-1中若质点4向上运动，则可判定该波向左传播.⑹若知波速v的大小。

第16单元 机械波（一）学号 姓名 专业、班级 课程班序号一 选择题[ C ]1.在下面几种说法中，正确的说法是： (A) 波源不动时，波源的振动周期与波动的周期在数值上是不同的 (B) 波源振动的速度与波速相同 (C) 在波传播方向上的任一质点振动相位总是比波源的相位滞后 (D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前[ A ]2. 一横波沿绳子传播时的波动方程为)104cos(05.0t x y ππ-= (SI)，则(A) 其波长为0.5 m (B) 波速为5 m ⋅s -1(C) 波速为25 m ⋅s -1 (D)频率为2 Hz[ C ]3. 一简谐波沿x 轴负方向传播，圆频率为ω，波速为u 。

设t = T /4时刻的波形如图所示，则该波的表达式为： (A) )/(cos u x t A y -=ω (B) ]2/)/([cos πω+-=u x t A y (C) )/(cos u x t A y +=ω (D) ])/([cos πω++=u x t A y[ D ]4. 一平面简谐波沿x 轴正向传播，t = T/4时的波形曲线如图所示。

若振动以余弦函数表示，且此题各点振动的初相取π-到π之间的值，则 (A) 0点的初位相为00=ϕ(B) 1点的初位相为 21πϕ-=(C) 2点的初位相为 πϕ=2(D) 3点的初位相为 23πϕ-=［ D ］5. 一平面简谐波在弹性媒质中传播，在媒质质元从平衡位置运动到最大位移处的过程中： (A) 它的动能转换成势能。

(B) 它的势能转换成动能。

(C) 它从相邻的一段质元获得能量其能量逐渐增大。

(D) 它把自己的能量传给相邻的一段质元，其能量逐渐减小。

二 填空题1.频率为100Hz 的波，其波速为250m/s ，在同一条波线上，相距为0.5m 的两点的相位差为52π. 2. 一简谐波沿x 轴正向传播。

1x 和2x 两点处的振动曲线分别如图(a)和(b)所示。

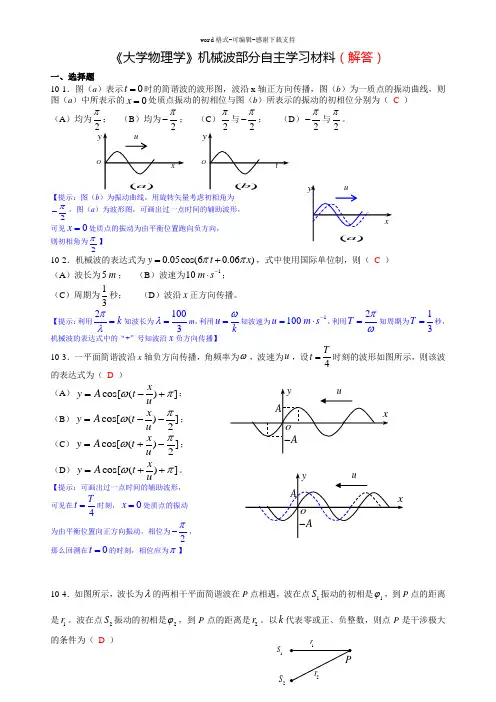
《大学物理学》机械波部分自主学习材料（解答）一、选择题10-1．图（a ）表示0t =时的简谐波的波形图，波沿x 轴正方向传播，图（b ）为一质点的振动曲线，则图（a ）中所表示的0x =处质点振动的初相位与图（b ）所表示的振动的初相位分别为（ C ） （A ）均为2π； （B ）均为π-； （C ）π与π-； （D ）2π-与2π。

【提示：图（b ）为振动曲线，用旋转矢量考虑初相角为2π-，图（a ）为波形图，可画出过一点时间的辅助波形，可见0x =处质点的振动为由平衡位置跑向负方向，则初相角为2π】10-2．机械波的表达式为0.05cos(60.06)y t x ππ=+，式中使用国际单位制，则（ C ） （A ）波长为5m ； （B ）波速为110m s -⋅；（C ）周期为13秒； （D ）波沿x 正方向传播。

【提示：利用2k πλ=知波长为1003λ=m ，利用u k ω=知波速为1100u m s -=⋅，利用2T πω=知周期为13T =秒，机械波的表达式中的“+”号知波沿x 负方向传播】10-3．一平面简谐波沿x 轴负方向传播，角频率为ω，波速为u ，设4Tt =时刻的波形如图所示，则该波的表达式为（ D ）（A ）cos[()]xy A t u ωπ=-+； （B ）cos[()]2x y A t u πω=--；（C ）cos[()]2x y A t u πω=+-；（D ）cos[()]xy A t uωπ=++。

【提示：可画出过一点时间的辅助波形，可见在4Tt =时刻，0x =处质点的振动为由平衡位置向正方向振动，相位为2π-，那么回溯在0t=的时刻，相位应为π】10-4．如图所示，波长为λ的两相干平面简谐波在P 点相遇，波在点1S 振动的初相是1ϕ，到P 点的距离是1r 。

波在点2S 振动的初相是2ϕ，到P 点的距离是2r 。

以k 代表零或正、负整数，则点P 是干涉极大的条件为（ D ）OO1S 2S r（A ）21r r k π-=； （B ）212k ϕϕπ-=； （C ）212122r r k ϕϕππλ--+=；（D ）122122r r k ϕϕππλ--+=。

⼤学物理机械波习题集附答案解析⼀、选择题：1．3147 ：⼀平⾯简谐波沿Ox 正⽅向传播，波动表达式为(SI) ，该波在 t = 0.5 s 时刻的波形图是［ B ］y 0.10 cos[ 2 ( t x ) ]2 4 2y (m) y (m) y (m)y (m)0.1 0 0.1 02 2 2 2O O Ox (m) Ox (m)x (m) x (m)(A )- 0.10 ( C ) (D )( B )-0.102．3407 ：横波以波速 u 沿 x 轴负⽅向传播。

t 时刻波形曲线如图。

则该时刻(A) A 点振动速度⼤于零yu(B) B 点静⽌不动A(C) C 点向下运动 D(D) D 点振动速度⼩于零［］C xO B3．3411 ：若⼀平⾯简谐波的表达式为y A cos(Bt Cx ) ，式中 A、B、C为正值常量，则：(A) 波速为 C (B) 周期为 1/B (C)波长为 2 /C (D) ⾓频率为 2 /B ［］4．3413 ：下列函数 f (x。

t)可表⽰弹性介质中的⼀维波动，式中A、a 和 b 是正的常量。

其中哪个函数表⽰沿x 轴负向传播的⾏波？(A) f (x,t ) Acos(ax bt ) (B)f (x,t) Acos(ax bt )(C) f (x,t) A cosax cosbt (D)f ( x,t)Asin ax sin bt ［］15．3479 ：在简谐波传播过程中，沿传播⽅向相距为2（为波长）的两点的振动速度必定(A) ⼤⼩相同，⽽⽅向相反(B) ⼤⼩和⽅向均相同(C) ⼤⼩不同，⽅向相同(D) ⼤⼩不同，⽽⽅向相反［］6．3483 ：⼀简谐横波沿 Ox 轴传播。

若 Ox 轴上 P1 和 P2 两点相距 /8（其中为该波的波长），则在波的传播过程中，这两点振动速度的(A) ⽅向总是相同(B) ⽅向总是相反(C) ⽅向有时相同，有时相反(D) ⼤⼩总是不相等［］7．3841 ：把⼀根⼗分长的绳⼦拉成⽔平y，⽤⼿握其⼀端。

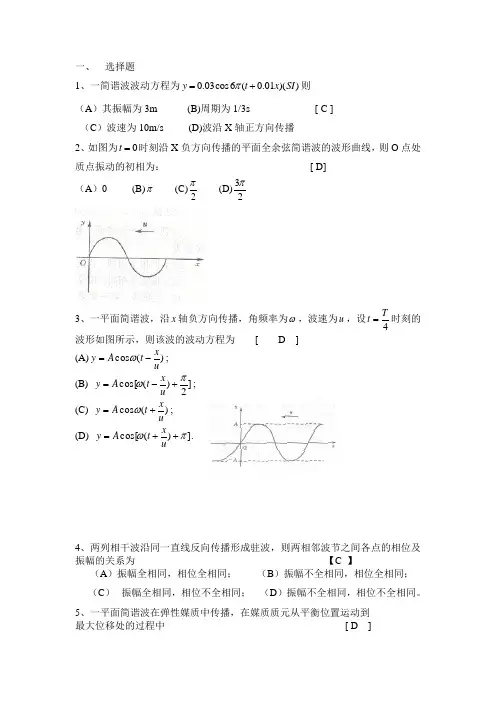
一、 选择题1、一简谐波波动方程为0.03cos6(0.01)()y t x SI π=+则 （A ）其振幅为3m (B)周期为1/3s [ C ] （C ）波速为10m/s (D)波沿X 轴正方向传播2、如图为0t =时刻沿X 负方向传播的平面全余弦简谐波的波形曲线，则O 点处质点振动的初相为： [ D] （A ）0 (B)π (C)2π (D)32π3、一平面简谐波，沿x 轴负方向传播，角频率为ω，波速为u ，设4Tt =时刻的波形如图所示，则该波的波动方程为 [ D ](A);)(cos uxt A y -=ω(B) ;]2)(cos[πω+-=u x t A y(C) ;)(cos u xt A y +=ω(D) ].)(cos[πω++=uxt A y4、两列相干波沿同一直线反向传播形成驻波，则两相邻波节之间各点的相位及振幅的关系为 【C 】（A ）振幅全相同，相位全相同； （B ）振幅不全相同，相位全相同； （C ）振幅全相同，相位不全相同； （D ）振幅不全相同，相位不全相同。

5、一平面简谐波在弹性媒质中传播，在媒质质元从平衡位置运动到 最大位移处的过程中 [ D ]（A ）它的动能转换为势能； （B ）它的势能转换为动能；（C ）它从相邻的一段质元获得能量，其能量逐渐增加； （D ）它的能量传给相邻的另一质元，其能量逐渐减小。

6、以平面余弦波波源得周期为s T 5.0=，它所激发得波得振幅为m 1.0，波长为m 10，取波源振动得位移恰好在正方向最大值时开始计时，波源所在处为原点，沿波传播方向为x 轴正方向，则2λ=x 处质点振动得表示式为[ A ] （A ）;)()4cos(1.0m t y ππ-= (B) ;)()22cos(1.0m t y ππ-=(C) ;)()(4cos 1.0m t y ππ-= (D) .)()2cos(1.0m t y ππ-=7、一平面简谐波沿Ox 正方向传播，波动表达式为]2)42(2cos[10.0π+-π=x t y(SI)，该波在t = 0.5 s 时刻的波形图是 ［ B ］8、横波以波速u 沿x 轴负方向传播．t 时刻波形曲线如图．则该时刻 ［ D ］ (A) A 点振动速度大于零． (B) B 点静止不动． (C) C 点向下运动． (D) D 点振动速度小于零．二、填空题（共18分，每题3分）。

机械波练习题一、选择题1．如图1所示，S 点为振源，其频率为100Hz ，所产生的横波向右传播，波速为80m/s ，P 、Q 是波传播途中的两点，已知SP=4.2m ，SQ=5.4m ．当S 通过平衡位置向上运动时 [ ]A ．P 在波谷，Q 在波峰B ．P 在波峰，Q 在波谷C ．P 、Q 都在波峰D ．P 通过平衡位置向上运动，Q 通过平衡位置向下运动．2．如图2所示，一列机械波沿x 轴传播，波速为16m/s ，某时刻的图象如图，由图象可知 A ．这列波波长为16m B ．这列波传播8m 需2s 时间 C ．x=4m 处质点的振幅为0 D ．x=6m 处质点将向y 轴正向运动3．a 、b 是一条水平绳上相距为L 的两点，一列简谐横波沿绳传播，其波长等于2L/3，当a 点经过平衡位置向上运动时，b 点 [ ]A ．经过平衡位置，向上运动B ．处于平衡位置上方位移最大处C ．经过平衡位置，向下运动D ．处于平衡位置下方位移最大处4．一列沿x 轴正方向传播的波，波速为6m/s ，振幅为2cm ，在某一时刻距波源5cm 的A 点运动到负最大位移时，距波源8cm 的B 点恰在平衡位置且向上运动．可知该波的波长λ，频率f 分别为A ．λ=12cm ，f=50HzB ．λ=4cm ，f=150HzC ．λ=12cm ，f=150HzD ．λ=4cm ，f=50Hz5．一列沿x 方向传播的横波，其振幅为A ，波长为λ，某一时刻波的图象如图3所示。

在该时刻，某一质点的坐标为(λ，0)，经过四分之一周期后，该质点的坐标为A ．(5/4)λ，0B ．λ ，－AC ．λ，AD ．(5/4)λ，A图 1图3图26．以下对波的说法中正确的是[ ]A ．频率相同的波叠加，一定可以发生稳定的干涉现象B ．横波可以在固体、液体和气体中传播C ．纵波不能用波的图象描述D ．波长和障碍物尺寸相近时，衍射现象明显7．图4所示为一列简谐波在t=7/4s 时的波动图象。

第16单元 机械波（一）学号 姓名 专业、班级 课程班序号一 选择题[ C ]1.在下面几种说法中，正确的说法是： (A) 波源不动时，波源的振动周期与波动的周期在数值上是不同的 (B) 波源振动的速度与波速相同 (C) 在波传播方向上的任一质点振动相位总是比波源的相位滞后 (D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前[ A ]2. 一横波沿绳子传播时的波动方程为)104cos(05.0t x y ππ-= (SI)，则(A) 其波长为0.5 m (B) 波速为5 m ⋅s -1(C) 波速为25 m ⋅s -1 (D)频率为2 Hz[ C ]3. 一简谐波沿x 轴负方向传播，圆频率为ω，波速为u 。

设t = T /4时刻的波形如图所示，则该波的表达式为： (A) )/(cos u x t A y -=ω (B) ]2/)/([cos πω+-=u x t A y (C) )/(cos u x t A y +=ω (D) ])/([cos πω++=u x t A y[ D ]4. 一平面简谐波沿x 轴正向传播，t = T/4时的波形曲线如图所示。

若振动以余弦函数表示，且此题各点振动的初相取π-到π之间的值，则 (A) 0点的初位相为00=ϕ(B) 1点的初位相为 21πϕ-=(C) 2点的初位相为 πϕ=2(D) 3点的初位相为 23πϕ-=［ D ］5. 一平面简谐波在弹性媒质中传播，在媒质质元从平衡位置运动到最大位移处的过程中： (A) 它的动能转换成势能。

(B) 它的势能转换成动能。

(C) 它从相邻的一段质元获得能量其能量逐渐增大。

(D) 它把自己的能量传给相邻的一段质元，其能量逐渐减小。

二 填空题1.频率为100Hz 的波，其波速为250m/s ，在同一条波线上，相距为0.5m 的两点的相位差为52π. 2. 一简谐波沿x 轴正向传播。

1x 和2x 两点处的振动曲线分别如图(a)和(b)所示。

一、选择题：1．3147：一平面简谐波沿Ox 正方向传播，波动表达式为]2)42(2cos[10.0π+-π=x t y (SI)，该波在t = 0.5 s 时刻的波形图是［ B ］2．3407：横波以波速u 沿x 轴负方向传播。

t 时刻波形曲线如图。

则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 ［3．3411：若一平面简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C为正值常量，则：(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B ［］4．3413：下列函数f (x 。

t )可表示弹性介质中的一维波动，式中A 、a 和b 是正的常量。

其中哪个函数表示沿x 轴负向传播的行波？(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D) bt axA t x f sin sin ),(⋅= ［ ］5．3479：在简谐波传播过程中，沿传播方向相距为λ21（λ 为波长）的两点的振动速度必定(A) 大小相同，而方向相反 (B) 大小和方向均相同(C) 大小不同，方向相同(D) 大小不同，而方向相反y (m) y (m) - y (m) y (m)［ ］6．3483：一简谐横波沿Ox 轴传播。

若Ox 轴上P 1和P 2两点相距λ /8（其中λ 为该波的波长），则在波的传播过程中，这两点振动速度的(A) 方向总是相同 (B) 方向总是相反(C) 方向有时相同，有时相反 (D) 大小总是不相等 ［ ］7．3841：把一根十分长的绳子拉成水平，用手握其一端。

维持拉力恒定，使绳端在垂直于绳子的方向上作简谐振动，则 (A) 振动频率越高，波长越长 (B) 振动频率越低，波长越长(C) 振动频率越高，波速越大 (D) 振动频率越低，波速越大 ［ ］ 8．3847：图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。

一、选择题：1．3147：一平面简谐波沿Ox 正方向传播，波动表达式为]2)42(2cos[10.0π+-π=x t y (SI)，该波在t = 0.5 s 时刻的波形图是［ B ］2．3407：横波以波速u 沿x 轴负方向传播。

t 时刻波形曲线如图。

则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 ［3．3411：若一平面简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C 为正值常量，则：(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B ［］4．3413：下列函数f (x 。

t )可表示弹性介质中的一维波动，式中A 、a 和b 是正的常量。

其中哪个函数表示沿x 轴负向传播的行波？(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D) bt axA t x f sin sin ),(⋅= ［ ］5．3479：在简谐波传播过程中，沿传播方向相距为λ21（λ 为波长）的两点的振动速度必定(A) 大小相同，而方向相反 (B) 大小和方向均相同(C) 大小不同，方向相同(D) 大小不同，而方向相反y (m) y (m) - y (m) y (m)［ ］6．3483：一简谐横波沿Ox 轴传播。

若Ox 轴上P 1和P 2两点相距λ /8（其中λ 为该波的波长），则在波的传播过程中，这两点振动速度的(A) 方向总是相同 (B) 方向总是相反(C) 方向有时相同，有时相反 (D) 大小总是不相等 ［ ］7．3841：把一根十分长的绳子拉成水平，用手握其一端。

维持拉力恒定，使绳端在垂直于绳子的方向上作简谐振动，则 (A) 振动频率越高，波长越长 (B) 振动频率越低，波长越长(C) 振动频率越高，波速越大 (D) 振动频率越低，波速越大 ［ ］ 8．3847：图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。

一. 选择题[C]1．（基础训练1）图14-10为一平面简谐波在t =2s 时刻的波形图，则平衡位置在P 点的质点的振动方程是(A)]31)2(cos[01.0π+-π=t y P (SI)．(B)]31)2(cos[01.0π++π=t y P (SI)．(C)]31)2(2cos[01.0π+-π=t y P (SI)．(D)]31)2(2cos[01.0π--π=t y P (SI)．【提示】由t=2s 波形，及波向X 轴负向传播，波动方程})2[(cos{0ϕω+-+-=ux x t A y ，ϕ为P 点初相。

以0x x =代入。

[C]2．（基础训练4）一平面简谐波在弹性媒质中传播，在某一瞬时，媒质中某质元正处于平衡位置，此时它的能量是（）(A)动能为零，势能最大．(B)动能为零，势能为零．(C)动能最大，势能最大．(D)动能最大，势能为零．【提示】在波动的传播过程中，任意时刻的动能和势能不仅大小相等而且相位相同，在平衡位置，动能最大，势能最大。

[D]3．（基础训练7）在长为L ，一端固定，一端自由的悬空细杆上形成驻波，则此驻波的基频波（波长最长的波）的波长为(A)L ．(B)2L ． (C)3L ．(D)4L ． 【提示】形成驻波，固定端为波节，自由端为波腹。

波长最长，4L λ=。

[D]4．（自测提高3）一平面简谐波以速度u 沿x 轴正方向传播，在t =t ＇时波形曲线如图14-24所示．则坐标原点O的振动方程为(A)]2)(cos[π+'-=t t b u a y ． (B)2)(2cos[π-'-π=t t b u a y ．图14-10图14-24(C)]2)(cos[π+'+π=t t b u a y ． (D)]2)(cos[π-'-π=t t bua y ．【提示】由图可知，波长为2b ，周期2=,b T u 频率=u b ωπ，在t =t ＇，o 点的相位为-2π。

机械波1．提示：1(,)cos[2()]t xy x t A T πϕλ=-+，2012(,)cos[2()]x t y x t A T λπϕλ+=-+，1sin[2()],dy t xv A dtTωπϕλ==--+2112sin[2()]x dy t v A v dtTλωπϕλ+==--+=-2．提示：波速取决于媒质的性质，振动速度是媒质中质元的运动速度3．提示：由图可知O 点处质元的运动方向向下，00,0,,t t y v A ω===-sin[2],dy t v A dtTωπϕ==-+0sin(0),2v A A πωϕωϕ=-+=-=4．提示：由图可知：8,160/,3,m u m s A m λ===则120,240uH Z v T νωππλ=====由图可知O 点处质元的运动方向向上，则当0,0,sin[2()],dy t xt x v A A dtT ωπϕωλ====--+=时可得2πϕ=-5．提示：在最大位移处，胁变最小，它的速度为0，因此动能为0，对于简谐波动能等于势能。

6．提示：对于A 点的上下运动可当作机械振动，在其偏离平衡位置最大位移处其动能为0，因此A 点在向平衡位置方向运动，则可知波沿X 轴负方向传播 7．提示：12,2πϕϕ-=2121122224r r πϕϕπϕπππλλ⎛⎫⎛⎫∆=---=--⨯=- ⎪ ⎪⎝⎭⎝⎭8．提示：由波腹条件22xk k x πλπλ=±⇒=±二、填空题 １．CB ，Bπ2，Cπ2，lC ，lC -提示：将已知波的方程与波的标准方程2(,)cos[]xy x t A t πωϕλ=-+或(,)cos[()]xy x t A t uωωϕ=-+对比可得波长和波速，位相差为：222[()][]t r d t r d cdπππωϕωϕλλλ-++--+==２．Lλπϕ2-；Nk k x x ∈±=,1λ；zk k x x ∈++=,)21(1λ。

第十机械波一. 选择题C1．基础训练1图14-10为一平面简谐波在t =2s 时刻的波形图;则平衡位置在P 点的质点的振动方程是A ]31)2(cos[01.0π+-π=t y P SI ．B ]31)2(cos[01.0π++π=t y P SI ．C ]31)2(2cos[01.0π+-π=t y P SI ．D ]31)2(2cos[01.0π--π=t y P SI ．提示由t=2s 波形;及波向X 轴负向传播;波动方程})2[(cos{0ϕω+-+-=ux x t A y ;ϕ为P 点初相..以0x x =代入.. C2．基础训练4一平面简谐波在弹性媒质中传播;在某一瞬时;媒质中某质元正处于平衡位置;此时它的能量是A 动能为零;势能最大．B 动能为零;势能为零．C 动能最大;势能最大．D 动能最大;势能为零．提示在波动的传播过程中;任意时刻的动能和势能不仅大小相等而且相位相同;在平衡位置;动能最大;势能最大..D3．基础训练7在长为L;一端固定;一端自由的悬空细杆上形成驻波;则此驻波的基频波波长最长的波的波长为AL ．B2L ． C3L ．D4L ． 提示形成驻波;固定端为波节;自由端为波腹..波长最长;4L λ=..D4．自测提高3一平面简谐波以速度u 沿x 轴正方向传播;在t =t ＇时波形曲线如图14-24所示．则坐标原点O 的振动方程为A ]2)(cos[π+'-=t t b u a y ． B 2)(2cos[π-'-π=t t bu a y ．C ]2)(cos[π+'+π=t t bu a y ．图14-10图14-24D ]2)(cos[π-'-π=t t b ua y ．提示由图可知;波长为2b;周期2=,b T u 频率=u b ωπ;在t =t ＇;o 点的相位为-2π.. 坐标原点O 的振动方程为]2)(cos[π-'-π=t t b u a yD5．自测提高6如图14-25所示;S 1和S 2为两相干波源;它们的振动方向均垂直于图面;发出波长为 的简谐波;P 点是两列波相遇区域中的一点;已知λ21=P S ;λ2.22=P S ;两列波在P 点发生相消干涉．若S 1的振动方程为)212cos(1π+π=t A y ;则S 2的振动方程为A )212cos(2π-π=t A y ．B )2cos(2π-π=t A y ．C )212cos(2π+π=t A y ．D 2cos(20.1)y A t =π-π．辅导书这里写错了 提示P 点两个振动的相位差为()()2010212r r πϕϕϕλ∆=---;发生相消干涉的条件为两列波频率相等、振动方向相同．．．．．．、振幅相同;相位差恒定并且 ()21,0,1,2,k k ϕπ∆=+=±±;有以上条件得到;S 2的振动方程为 C6．自测提高7在弦线上有一简谐波;其表达式是]3)2002.0(2cos[100.221π+-π⨯=-x t y SI 为了在此弦线上形成驻波;并且在x =0处为一波节;此弦线上还应有一简谐波;其表达式为：A ]3)2002.0(2cos[100.222π++π⨯=-x t y SI ． B ]32)2002.0(2cos[100.222π++π⨯=-x t y SI ．C ]34)2002.0(2cos[100.222π++π⨯=-x t y SI ．D ]3)2002.0(2cos[100.222π-+π⨯=-x t y SI ． 提示根据驻波的形成条件.. 二. 填空题7．基础训练10一平面简谐机械波在媒质中传播时;若一媒质质元在t 时刻的总机械能是10J;则在)(T t +T 为波的周期时刻该媒质质元的振动动能是______5J_____.. 提示k p E E =图14-258．基础训练16在真空中沿着z 轴负方向传播的平面电磁波;O 点处电场强度为)312cos(300π+π=t E x νSI;则O 点处磁场强度为__)3/2cos(796.0π+π-=t H y νA/m___________．在图14-18上表示出电场强度;磁场强度和传播速度之间的相互关系．提示电磁波特性..H E 和同相..H E 00με=..H E⨯为电磁波传播方向..9．基础训练17一列强度为I 的平面简谐波通过一面积为S 的平面;波速u与该平面的法线0n提示能流及波的强度定义..10．基础训练18一列火车以20 m/s 的速度行驶;若机车汽笛的频率为600Hz;一静止观测者在机车前和机车后所听到的声音频率分别为______637.5Hz_________和_____566.7Hz___________设空气中声速为340 m/s ． 提示RR S Su v u v νν+=- 11．自测提高11如图14-27所示;两相干波源S 1与S 2相距3 /4; 为波长．设两波在S 1S 2连线上传播时;它们的振幅都是A ;并且不随距离变化．已知在该直线上在S 1左侧各点的合成波强度为其中一个波强度的4倍;则两波源应满足的相位条件是_13+2ϕπ__．提示强度与振幅的平方成正比;所以可以判断S 1左侧各点为干涉增强点..根据干涉增强条件;得到213-=2ϕϕπ12．自测提高15有A 和B 两个汽笛;其频率均为404Hz ．A 是静止的;B 以3.3 m/s 的速度远离A ．在两个汽笛之间有一位静止的观察者;他听到的声音的拍频是已知空气中的声速为330 m/s____4Hz________．提示RR S Su v u v νν+=-;再利用拍频的定义.. 三.计算题图14-2713．基础训练21如图14-20所示为一平面简谐波在t =0时刻的波形图;设此简谐波的频率为250Hz;且此时质点P 的运动方向向上;求 1该波的表达式；2在距原点O 为100 m 处质点的振动方程与振动速度表达式．解：1由P 点的运动方向;可判定该波向右传播．原点O 处质点;t =0时 02/2cos x A A φ==;所以4/π-=φO 处振动方程为)41500cos(0ππ-=t A y m由图可判定波长 =200 m;故波动表达式为]41)200250(2cos[ππ--=x t A y m 2距O 点100 m 处质点的振动方程是)45500cos(1ππ-=t A y m 或13cos(500)4y A t =+ππm/s 振动速度表达式是5v 500sin(500)4A t =--πππm/s或3v 500sin(500)4A t =-+πππm/s14．基础训练22设1S 和2S 为两个相干波源;相距41波长;1S 比2S 的位相超前2π..若两波在1S 、2S 连线方向上的强度相同且不随距离变化;问1S 、2S 连线上在1S 外侧各点的合成波的强度如何 又在2S 外侧各点的强度如何解：由题目可知211-=2ϕϕπ;在1S 外侧任取一点P;P 点的相位为()()21212=-S P S P πϕϕϕπλ∆=---;满足干涉相消条件..所以在1S 、2S 连线上在1S 外侧各点的合成波的强度为零..同理;在2S 外侧任取一点Q;Q 点的相位为()()21212=0S Q S Q πϕϕϕλ∆=---;满足干涉增强条件..所以在1S 、2S 连线上在1S 外侧各点的合成波的强度为41I ..1I 为单个波的强度图14-19 图14-2015．基础训练23如图14-21;一平面波在介质中以波速u =20m/s 沿x 轴负方向传播;已知A 点的振动方程为t y π⨯=-4cos 1032SI ．1以A 点为坐标原点写出波的表达式；2以距A 点5 m 处的B 点为坐标原点;写出波的表达式． 解：1以A 点为坐标原点;波的表达式为-2310cos4()20xy t π=⨯+SI 2以距A 点5 m 处的B 点为坐标原点;波的表达式为2310cos[4()]20xt ππ-=⨯+-SI 16．基础训练27在弹性媒质中有一沿x 轴正向传播的平面波;其表达式为)214cos(01.0π-π-=x t y SI ．若在x =5.00 m 处有一媒质分界面;且在分界面处反射波相位突变 ;设反射波的强度不变;试写出反射波的表达式．解：反射波在x 点引起的振动相位为反射波表达式为)10214cos(01.0π-π+π+=x t y SI或10.01cos(4)2y t x ππ=++SI17．基础训练28正在报警的警钟;每隔0.5秒钟响一声;一声接一声地响着..有一个人在以60公里/小时的速度向警钟行驶的火车中;问这个人在5分钟内听到几响..解：由题目得到1100=2,330/,/,6S R s u m s v m s ν-==5分钟内听到560 2.1=630.3⨯⨯;听到的响声为630响..18．自测提高22在实验室中做驻波实验时;在一根两端固定长3 m 的弦线上以60Hz 的频率激起横向简谐波．弦线的质量为60×10-3 kg ．如要在这根弦线上产生有四个波腹的很强的驻波;必须对这根弦线施加多大的张力 .解：∵mTll m T Tu ===/μ① 又∵νλ=u ②由题意知λ214=l ∴l 21=λ③图14-21将③代入②得l u 21⋅=ν;代入①;得422l m Tl ν=; 241νml T =16260310604123=⨯⨯⨯⨯=-N 四．附加题19．自测提高24如图14-32;一圆频率为ω;振幅为A 的平面简谐波沿x 轴正方向传播;设在t=0时该波在原点O 处引起的振动使媒质元由平衡位置向y 轴的负方向运动;M 是垂直于x 轴波波长;设反的波密媒质反射面;已知4'47'λλ==PO OO ，λ为该射波不衰减;求：1入射波与反射波的波动方程；2P 点的振动方程.. 解：设O 处振动方程为)cos(0φω+=t A y 当t =0时;y 0=0;v 0<0;∴π=21φ∴)21cos(0π+=t A y ω 故入射波表达式为12cos()2y A tx在O ′处入射波引起的振动方程为由于M 是波密媒质反射面;所以O ′处反射波振动有一个相位的突变 ． ∴cos()y A t ππ2反t A ωcos =反射波表达式22cos[()]y A tOO x π)]47(2cos[x t A -π-=λλω 合成波为12y y y ]22cos[π+π-=x t A λω]22cos[π+π++x t A λω将P 点坐标λλλ234147=-=x 代入上述方程得P 点的振动方程图14-32。

一、选择题：1．3147：一平面简谐波沿Ox 正方向传播，波动表达式为]2)42(2cos[10.0π+-π=x t y (SI)，该波在t = 0.5 s 时刻的波形图是［ B ］2．3407：横波以波速u 沿x 轴负方向传播。

t 时刻波形曲线如图。

则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 ［3．3411：若一平面简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C为正值常量，则：(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B ［］4．3413：下列函数f (x 。

t )可表示弹性介质中的一维波动，式中A 、a 和b 是正的常量。

其中哪个函数表示沿x 轴负向传播的行波？(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D) bt axA t x f sin sin ),(⋅= ［ ］5．3479：在简谐波传播过程中，沿传播方向相距为λ21（λ 为波长）的两点的振动速度必定(A) 大小相同，而方向相反 (B) 大小和方向均相同(C) 大小不同，方向相同(D) 大小不同，而方向相反y (m) y (m) - y (m) y (m)［ ］6．3483：一简谐横波沿Ox 轴传播。

若Ox 轴上P 1和P 2两点相距λ /8（其中λ 为该波的波长），则在波的传播过程中，这两点振动速度的(A) 方向总是相同 (B) 方向总是相反(C) 方向有时相同，有时相反 (D) 大小总是不相等 ［ ］7．3841：把一根十分长的绳子拉成水平，用手握其一端。

维持拉力恒定，使绳端在垂直于绳子的方向上作简谐振动，则 (A) 振动频率越高，波长越长 (B) 振动频率越低，波长越长(C) 振动频率越高，波速越大 (D) 振动频率越低，波速越大 ［ ］ 8．3847：图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。