求阴影面积的常用方法
- 格式:docx
- 大小:148.45 KB
- 文档页数:6

总结:对于不规则图形面积的计算问题一般将它转化为若干基本规蒈则图形的组合,分析整体与部分的和、差关系,问题便得到解决.常用的基本方法有:蒇一、相加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面袁例如,下图中,要求整个图形的面积,只要先求出上面积,然后相加求出整个图形的面积..半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了薀衿羅二、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积袄.例如,下图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可差.蚀羆蚇蚃三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下页右螀的三角形,其面积直42、高是上图,欲求阴影部分的面积,通过分析发现它就是一个底是1?2?4?4。
:接可求为|2莇莂四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组袀例如,欲求下图中阴影部分面积,可以.合成一个新的图形,设法求出这个新图形面积即可. 把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了螈蒅袆袀五、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图膈如下图,求两个正方形中转化成若干个基本规则图形,然后再采用相加、相减法解决即可..此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便阴影部分的面积.芄膃羀六、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本蕿例如,如下图,欲求阴影部分的面积,只需把右边弓形切.规则图形,从而使问题得到解决.割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半肆羂七、平移法:这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成肀例如,如下图,欲求阴影部分面积,可先沿中间切.一个新的基本规则图形,便于求出面积开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。

求阴影面积的方法一、概述阴影面积是指在某个特定的时间段内,被某个物体所遮挡的区域。
在日常生活中,我们可以通过计算阴影面积来确定建筑物、树木等物体的高度或者角度。
本文将介绍几种常见的求阴影面积的方法。
二、水平杆法水平杆法也叫做“日晷法”,是一种比较古老但是依然有效的方法。
它需要一个水平放置的杆子和一个垂直放置的杆子。
1. 在一个晴朗无云的日子里,将水平杆竖立在地面上,使其与地面垂直。
然后用一根垂直杆子将水平杆上方投下的影子标记出来,并标记出时间和日期。
2. 等到太阳移动到另外一个位置时,再次用相同方式标记出新位置下水平杆上方投下的影子。
3. 根据两个时间点之间经过的时间以及两个影子之间距离变化量,可以计算出太阳高度角度。
4. 根据太阳高度角度以及地球半径等参数,可以计算出物体高度以及阴影面积。
三、三角测量法三角测量法是一种比较精确的测量方法,需要使用三角函数和仪器设备。
该方法适用于高度较高的物体,如建筑物、电线杆等。
1. 在地面上选定两个点,并测量它们之间的距离。
2. 用仪器测量物体顶部到地面的距离以及物体顶部到两个地面点之间形成的角度。
3. 根据三角函数计算出物体高度以及阴影面积。
四、数学模型法数学模型法是一种基于数学公式来计算阴影面积的方法。
该方法适用于平面场景或者建筑物表面等。
1. 确定光源位置以及场景中各个物体的位置和大小。
2. 根据光线传播规律,建立数学模型,计算出每个物体所投下的影子区域。
3. 将所有影子区域合并在一起,就可以得到整个场景中的阴影面积。
五、总结以上介绍了几种常见的求阴影面积的方法。
每种方法都有其适用范围和优缺点。
在实际应用中,需要根据具体情况选择合适的方法来进行测量。

求阴影部分面积的几种常用方法阴影部分的面积是指在形成的阴影中,被物体遮挡的部分面积。
计算阴影面积在多个领域中都有一定的应用,例如建筑设计、图像处理、计算机视觉等。
下面将介绍几种计算阴影部分面积的常用方法。
1.几何法几何法是最常见且简单的计算阴影面积的方法。
在平行光源的情况下,可以直接使用几何法计算阴影面积。
首先,需要知道光源的位置和物体的形状。
然后,可以通过光线和物体边缘的交点来确定阴影边缘,从而计算出阴影部分的面积。
这种方法在二维平面上的阴影计算中适用,但需要事先获得物体的准确形状和光源的位置。
2.正投影法正投影法是一种常用的计算阴影面积的方法。
在三维空间中,通过将物体和光源投影到一个平面上,然后计算投影面积来得到阴影的面积。
在计算阴影面积时,需要考虑物体的不透明度和光源的位置。
正投影法可以适用于复杂的物体和不同类型的光源。
3.体积投影法体积投影法是一种计算阴影面积的高级方法。
它首先将物体和光源之间的空间划分为多个体素(即体积像素),然后计算每个体素是否在物体的阴影区域中。
通过计算物体和光源之间的交点和遮挡关系,可以确定每个体素是否在阴影中。
最后,将位于阴影区域的体素的体积加总即可得到阴影的面积。
4.数值模拟法数值模拟法是一种计算阴影面积的复杂方法,它利用计算机模拟光线传播和物体与光线的相互作用。
该方法通过在计算机中建立一个模拟的三维场景,模拟光源的物理属性、物体的材质和几何形状,然后使用光线追踪算法模拟光线的传播和阴影的形成过程。
通过记录与阴影相关的信息,可以计算出阴影的面积。
综上所述,几何法、正投影法、体积投影法和数值模拟法是常用的计算阴影面积的方法。
选择适当的方法取决于具体的应用场景和需求。
不同的方法在准确性、计算复杂度和适用性方面存在差异,需要根据具体情况进行选择。

四种方法求阴影部分面积首先,我们可以使用几何方法来求解阴影部分的面积。
设阴影部分的形状为矩形,其底边的长度为a,高度为h。
阴影的边界可以用两条直线来表示,设直线1与x轴的交点为A,直线2与x轴的交点为B。
两条直线与x轴的交点之间的距离为b。
则阴影部分的面积可以用以下公式表示:A=(a+b)*h/2第二种方法是通过将阴影部分分割成多个小矩形来求解。
首先,我们将阴影部分分割成n个小矩形,每个小矩形的底边长度为ai,高度为hi。
则阴影部分的面积可以表示为以下公式的和:A = ∑(ai * hi)其中i的范围从1到n。
第三种方法是使用积分来求解。
假设阴影部分的形状可以用函数y=f(x)来表示。
要求阴影部分的面积,我们需要找到函数f(x)的定义域上的积分区间[a,b]。
A = ∫[a, b] f(x) dx最后一种方法是使用统计学方法来求解。
假设我们已经获得了一组阴影部分的随机样本,符合一定的分布规律。
我们可以使用这组样本数据来进行统计分析,得出阴影部分的面积的估计值。
首先,我们可以计算出这组样本数据的平均值和标准差。
然后,使用均值加减一个标准差的方法,来计算阴影部分的上下边界。
根据阴影部分的上下边界和样本数据的分布,我们可以得到阴影部分面积的估计值。
需要注意的是,这种方法求得的阴影部分面积只是一个估计值,可能存在一定的误差。
综上所述,我们可以用几何法、分割法、积分法和统计法来求解阴影部分的面积。
每种方法都有自己的优缺点和适用范围,选择合适的方法取决于具体情况和问题要求。

求阴影部分面积的方法在几何学中,求阴影部分的面积是一个常见的问题。
阴影部分的面积可以通过多种方法来计算,本文将介绍几种常用的方法。
一、几何图形分割法。
在几何图形分割法中,我们可以将阴影部分分割成几个简单的几何图形,然后分别计算每个图形的面积,最后将它们相加得到阴影部分的面积。
这种方法适用于较为规则的几何图形,如矩形、三角形等。
二、积分法。
对于较为复杂的曲线或曲面的阴影部分,我们可以利用积分法来求解。
通过建立适当的坐标系和积分限,我们可以将阴影部分的面积表示为一个定积分,通过积分计算得到阴影部分的面积。
三、几何变换法。
在一些特殊情况下,我们可以利用几何变换来求解阴影部分的面积。
例如,通过平移、旋转、镜像等几何变换,将阴影部分变换成一个已知的几何图形,然后计算这个已知几何图形的面积,最后根据几何变换的性质得到阴影部分的面积。
四、数值逼近法。
对于一些无法通过解析方法求解的阴影部分,我们可以利用数值逼近法来求解。
通过将阴影部分分割成若干小区域,然后分别计算每个小区域的面积,最后将它们相加得到阴影部分的面积的近似值。
五、利用计算机软件求解。
在现代科技条件下,我们还可以利用计算机软件来求解阴影部分的面积。
通过建立相应的数学模型,利用计算机软件进行数值计算,可以得到阴影部分的面积的精确值。
六、其他方法。
除了上述几种方法外,还有一些其他特殊的方法可以用来求解阴影部分的面积,如利用相似性、三角函数等性质来进行计算。
综上所述,求解阴影部分的面积涉及到多种方法,我们可以根据具体的情况选择合适的方法来进行计算。
在实际问题中,我们可以根据问题的特点和要求来选择合适的方法,从而求解阴影部分的面积。
希望本文介绍的方法对您有所帮助。

求图形面积的几种常用方法1、割补法:对于一些求不在一起的几块阴影面积的和,往往需要把它们通过剪割、拼补在一起,才便于计算,在剪割、拼补过程中,一定要注意割下来的图形和补上去的图形的形状、大小必须完全一样。
【例1】如图,每个小圆的半径是2厘米,求阴影部分的面积是多少平方厘米?【例2】右图中三个圆的半径都是4厘米,三个圆两两交于圆心。
求阴影部分的面积是多少平方厘米?2,重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可•例如,求下图中阴影部分面积3、加减法:注意观察,所求阴影部分的面积看是由哪几个图形相加,再减去哪个图形变可以得到。
我们把这种通过加、减就能求出它的面积的方法,我们的把它称为“加减法”【例3】如图,正方形的边长为4厘米,求阴影部分的面积是多少?使之组合成一个 原来【例4】如图,长方形的长为 12厘米,宽为8厘米,求阴影部分的面积是多少?4.辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线, 使不规则图形转化 成若干个基本规则图形,然后再采用相加、相减法解决即可 例如,求下图中阴影部分面积5, 平移法:这种方法是将图形中某一部分切割下来平行移动到一恰当位置, 新的基本规则图形,便于求出面积•例如,如下图,求阴影部分面积6. 对称添补法:这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形 图形面积就是这个新图形面积的一半 •例如,求下图中阴影部分的面积,7、旋转法:在求一些面积时,有时需要把某个图形进行一定方向的旋转,使之拼在一起, 变成另一个比较方便求的图形。
【例5】如图,梯形ABCD的上底是3厘米,下底是5厘米,高是4厘米,E是梯形的中点。
求阴影部分的面积是多少?8、等分法:就是将整个图形,平均分成若干份,再看所求的图形的面积占多少份,从而求得阴影部分的面积。
【例6】将三角形ABC的三条边分别向外延长一倍,得到一个大的六边形,已知三角形ABC【例7】如图,在正方形中,放置了两个小正方形,大正方形的面积是180平方厘米,求甲乙两个小正方形有面积各是多少?9、抓不变量:若甲比乙的面积大a,则甲和乙同时加上或减去相同的数,它们的大小不变,而图形发生变化,再通过变化后的图形进行求解,就可以使问题得到简便;若两个面积相等的图形,同时加上或差动相同的面积,则剩下的面积仍然相等。
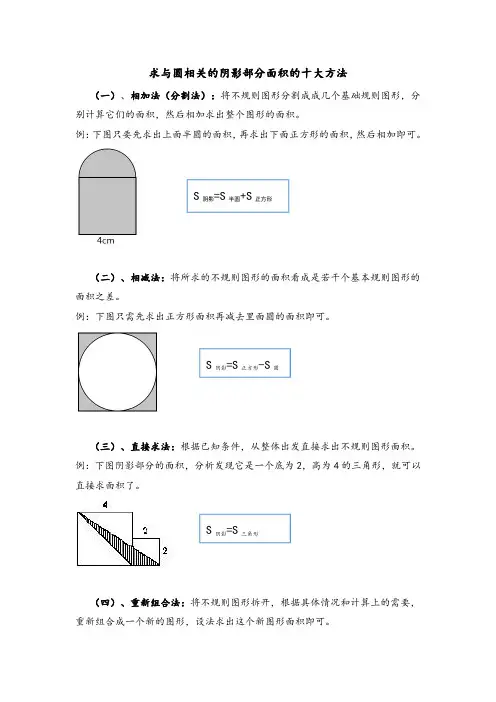
求与圆相关的阴影部分面积的十大方法(一)、相加法(分割法):将不规则图形分割成成几个基础规则图形,分别计算它们的面积,然后相加求出整个图形的面积。
例:下图只要先求出上面半圆的面积,再求出下面正方形的面积,然后相加即可。
(二)、相减法:将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。
例:下图只需先求出正方形面积再减去里面圆的面积即可。
(三)、直接求法:根据已知条件,从整体出发直接求出不规则图形面积。
例:下图阴影部分的面积,分析发现它是一个底为2,高为4的三角形,就可以直接求面积了。
(四)、重新组合法:将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可。
S 阴影=S 半圆+S 正方形S 阴影=S 正方形-S 圆S 阴影=S 三角形例:下图可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了。
(五)、辅助线法:根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可。
例:下图虽然可以用相减法解决,但不如添加一条辅助线后用直接法计算2个三角形面积之和更简便。
(六)、割补法:把原图形的一部分切割下来,补在图形中的另一部分,使之成为规则图形,从而使问题得到解决。
例:下图只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半。
(七)、平移法:将图形中某一部分切割下来,平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积。
S 阴影=S 正方形-S 圆S 阴影=S 正方形÷2S 阴影=S 三角形①+S 三角形②例:下图可先沿中间切开,把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
(八)、旋转法:将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度,贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积。

总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决.常用的基本方法有:一、相加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如,下图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了.二、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如,下图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可.三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下页右上图,欲求阴影部分的面积,通过分析发现它就是一个底是2、高是4的三角形,其面积直接可求为|:四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如,欲求下图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了.五、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可.如下图,求两个正方形中阴影部分的面积.此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便.六、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如,如下图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半.七、平移法:这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积.例如,如下图,欲求阴影部分面积,可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
八、旋转法:这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积.例如,欲求下图(1)中阴影部分的面积,可将左半图形绕B 点逆时针方向旋转180°,使A与C 重合,从而构成如右图(2)的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法:这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如,欲求下图中阴影部分的面积,沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。

-初中数学之求阴影面积方法总结一、公式法这属于最简单的方法,阴影面积是一个常规的几何图形,例如三角形、正方形等等。
简单举出2个例子:二、和差法攻略一直接和差法这类题目也比拟简单,属于一目了然的题目。
只需学生用两个或多个常见的几何图形面积进展加减。
攻略二构造和差法从这里开场,学生就要构建自己的数学图形转化思维了,学会通过添加辅助线进展求解。
三、割补法割补法,是学生拥有比拟强的转化能力后才能轻松运用的,否则学生看到这样的题目还是会无从下手。
尤其适用于直接求面积较复杂或无法计算时,通过对图形的平移、旋转、割补等,为利用公式法或和差法求解创造条件。
攻略一全等法攻略二对称法攻略三平移法攻略四旋转法小结:〔一〕解决面积问题常用的理论依据1、三角形的中线把三角形分成两个面积相等的局部。
2、同底同高或等底等高的两个三角形面积相等。
3、平行四边形的对角线把其分成两个面积相等的局部。
4、同底〔等底〕的两个三角形面积的比等于高的比。
同高〔或等高〕的两个三角形面积的比等于底的比。
5、根本几何图形面积公式:三角形、平行四边形、、菱形、矩形、梯形、圆、扇形。
6、相似三角形面积之比等于相似比的平方7、反比例函数中k的几何含义8、在直角坐标系中函数图像构成的图形面积常常利用图形顶点的坐标构造高去求面积〔二〕证明面积问题常用的证题思路和方法1、分解法:通常把一个复杂的图形,分解成几个三角形。
2、补全法:通过平移、旋转、翻折变换把分散的图形拼成一个规则的几何根本图形3、作平行线法:通过平行线找出同高〔或等高〕的三角形。
. z.。

求阴影部分面积的几种常用方法在计算机图形学和几何学中,计算阴影部分面积是一个常见的问题。
阴影可以通过光线投射到图形对象上而产生,阴影部分面积的计算是为了提供更真实的渲染效果或解决一些实际问题,比如遮挡检测、物体面积计算等。
下面将介绍几种常用的计算阴影部分面积的方法。
1.光线跟踪光线跟踪是一种广泛应用的方法,特别适用于计算实时渲染场景中的阴影。
该方法通过从光源发射光线,并对光线与物体之间的相交进行跟踪,来计算阴影部分面积。
如果一些光线与物体相交,说明该位置接收到光线,反之则处于阴影中。
通过跟踪足够多的光线,可以得到较为准确的阴影部分面积。
2.基于深度缓冲深度缓冲是一种常用的实时渲染技术,用于存储场景中各个像素的深度信息。
基于深度缓冲的阴影部分面积计算方法是,首先从光源的视角渲染场景并将深度信息保存到深度缓冲中。
然后,再从视点渲染场景,并在渲染每个像素时,通过比较当前像素的深度值与从光源视角计算得到的深度值,判断当前像素是否处于阴影中。
通过统计处于阴影的像素数量,可以得到阴影部分面积的估计。
3.包围盒计算包围盒计算是一种简化计算的方法,适用于对场景中的物体进行粗略的阴影部分面积估计。
该方法通过将物体简化为包围盒(bounding box),然后计算包围盒与光源的交叉部分得到阴影部分面积的估计。
这种方法虽然不够精确,但计算速度较快,适用于实时应用。
4.体素化计算体素化计算是一种将三维场景离散化为体素(voxel)的方法。
通过将场景中的物体表示为体素数组,并对体素进行遍历和计算,可以得到阴影部分面积的估计。
该方法在采样分辨率足够高的情况下,可以达到较高的计算精度,但也需要较大的计算开销。
5.基于图像处理的方法除了传统的计算几何的方法外,基于图像处理的方法也被广泛应用于阴影部分面积的计算。
例如,可以通过二值化图像并计算像素面积的方法,根据物体的阴影和非阴影部分的不同颜色值进行分割,然后统计阴影部分的像素数目来计算阴影部分面积。
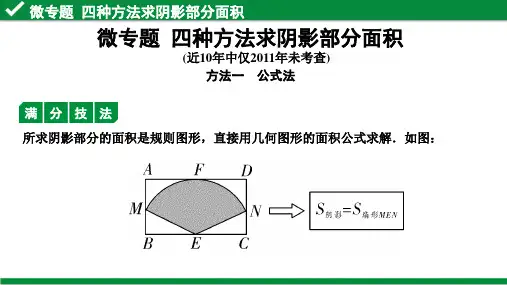
四种方法求阴影部分面积计算阴影面积是在几何学和物理学中的一个常见问题。
在这个问题中,我们需要找到两个或多个图形之间的重叠部分的面积。
这些图形可以是任何形状,包括圆形、矩形、三角形等。
在本文中,我将介绍四种不同的方法来计算阴影面积。
这些方法分别是几何法、分割法、积分法和数值法。
每种方法都有其优点和局限性,适用于不同类型的图形和场景。
1.几何法:几何法是最常见和直观的方法之一,适用于简单的图形。
它的基本思想是将图形转化为几何体,然后计算这些几何体的体积或面积。
对于平面图形,可以使用面积公式来计算。
例如,对于矩形,可以直接计算两个方向上的长度乘积;对于圆形,可以使用圆的半径和π来计算面积。
然后,通过找到两个图形的重叠部分,并计算其面积,可以得到阴影面积。
2.分割法:分割法是一种基于图形分割的方法,适用于复杂的图形。
它的思想是将图形分割成简单的几何体,然后计算这些几何体的面积,并将它们加在一起。
这种方法一般使用数学建模软件来进行计算。
例如,对于一个复杂的图形,可以将其分割成多个矩形或三角形,并计算它们的面积,然后将它们加在一起来得到阴影面积。
3.积分法:积分法是一种基于微积分的方法,适用于连续变化的图形。
它的基本思想是使用积分来计算曲线下面积。
对于阴影面积的计算,可以将两个图形的边界曲线表示为一个函数的形式,并计算它们之间的积分。
这种方法需要具备一定的数学知识和计算能力,但可以得到更准确的结果。
4.数值法:数值法是一种通过数值逼近的方法,适用于复杂的图形和场景。
它的思想是将图形离散化成有限个点或网格,并计算每个点或网格的面积,并将它们加在一起。
这种方法可以使用计算机程序进行计算,但结果的准确性依赖于离散化的精度。
通常情况下,离散化的精度越高,计算结果越准确。
综上所述,四种方法分别是几何法、分割法、积分法和数值法。
它们适用于不同类型的图形和场景,并具有不同的优点和局限性。
在实际应用中,我们可以根据具体情况选择合适的方法来计算阴影面积。
求阴影面积的几种常用方法1、直接用公式法例1、如图1,在Rt △ABC 中,∠A=90°,BC=4,点D 是BC 的中点,将△ABD 绕点A 按逆时针旋转90°,得△AB ’D ’,那么AD 在平面上扫过的区域(图中阴影部分)的面积是( )A. 4πB. 2π C.π D. 2π 分析:△ABD 绕点A 按逆时针旋转90°后,形成扇形ADD ’,且扇形的圆心角为90°,故可用扇形的面积公式直接求其面积。
解:∵∠A=90°, 点D 是BC 的中点,∴AD=21BC=2, ∴S 阴影=S 'ADD 扇形=3602902⨯π=π. 故选C.2、加减法.例2、如图2,正方形ABCD 的边长为a,那么阴影部分的面积为( ) A. 21πa 2 B. 41πa 2 C. 81πa 2 D. 161πa 2 分析:阴影部分的面积可以看作是扇形BCD 的面积减去半圆CD 的面积。
解:S 阴影=S CBD 扇形-S CD 半圆=360902a π-21π(2a )2 =41πa 2-81πa 2 =81πa 2. 所以本题答案选C.3、割补法例3、如图3,以BC 为直径,在半径为2且圆心角为90°的扇形内做半圆,交弦AB 于点D ,连接CD ,则阴影部分的面积是( )A. π-1B. π-2C. 21π-1D. 21π-2 分析:因为BC 为半圆的直径,所以CD ⊥AB ,CD=BD ,所以S CD 弓形= S BD 弓形,即S 阴影=S CAB 扇形-S ADC ∆.解:∵SCD 弓形= S BD 弓形∴S 阴影=S CAB 扇形-S ADC ∆⎪⎩⎪⎨⎧=+=+364423y x 22y x π⎪⎪⎨⎧-=-=918929ππyx =3602902⨯π-21×2×2 =π-1.故选A.4、等积变形法例4、如图4,已知半圆的直径AB=4cm ,点C 、D 是这个半圆的三等分点,则弦AC 、AD 和弧CD 围成的的阴影部分的面积为 cm 2.分析:因为C 、D 是半圆的三等分点,所以能够论证CD ∥AB ,所以S ACD ∆= S OCD ∆,所以S 阴影=S OCD 扇形解:连接OC 、OC 、CD∵C 、D 是半圆的三等分点,∴CD ∥AB∴S ACD ∆= S OCD ∆(同底等高),∴S 阴影=S OCD 扇形=3602602⨯π=32π. 5、覆盖法例5、如图5所示,正方形的边长为a ,分别以对角顶点为圆心,边长为半径画弧,则图中阴影部分的面积是多少?分析:阴影部分的面积可以看作是两个扇形的重叠部分。
求阴影面积的十种方法
阴影面积是指在光源照射下,物体投射出的阴影所覆盖的面积。
在几何学中,阴影面积是计算投影面积的一个重要概念。
对于不同形状的物体,计算其阴影面积有不同的方法,下面介绍几种常见的方法。
1. 直接计算法:对于简单的几何体,例如矩形、三角形、圆形等,可以根据相应的公式计算出其阴影面积。
2. 消影法:利用几何形体之间的消影关系计算阴影面积,这种方法适用于多个物体在同一平面上的情况。
3. 画图法:通过绘制物体投影图和阴影图,求出阴影面积。
4. 面积加减法:对于复杂物体,可以将其分解成若干个简单形体,再分别计算其阴影面积,最后将得到的结果加减得到总面积。
5. 数学模型法:利用数学模型模拟物体在光源照射下的投影过程,计算出阴影面积。
6. 三角网格法:使用三角网格模型计算阴影面积,适用于复杂非规则形状的物体。
7. 光线追踪法:通过模拟光线在场景中的传播方向,计算出阴影面积。
8. 蒙特卡罗法:通过随机生成光线投射到物体上,进行多次模拟,最终统计得到阴影面积。
9. 深度图法:通过产生一个深度图,依据深度图中的遮挡关系得出阴影区域,计算阴影面积。
10. 像素级法:将物体的每一个像素与光线相交,统计被覆盖的像素点,通过像素点的数量计算出阴影面积。
总之,计算阴影面积的方法主要取决于物体的形状和光源的位置,通过选择适合的方法,能够得到比较准确的结果。
初中数学专题复习——求阴影面积的常用方法计算平面图形的面积问题是常见题型,求平面阴影部分的面积是这类问题的难点。
不规则阴影面积常常由三角形、四边形、弓形、扇形和圆、圆弧等基本图形组合而成的,在解此类问题时,要注意观察和分析图形,会分解和组合图形。
介绍几种常用的方法。
1.转化法此法就是通过等积变换、平移、旋转、割补等方法将不规则的图形转化成面积相等的规则图形,再利用规则图形的面积公式,计算出所求的不规则图形的面积。
例1. 如图1,点C、D是以AB为直径的半圆O上的三等分点,AB=12,则图中由弦AC、AD和围成的阴影部分图形的面积为_________。
2.和差法有一些图形结构复杂,通过观察,分析出不规则图形的面积是由哪些规则图形组合而成的,再利用这些规则图形的面积的和或差来求,从而达到化繁为简的目的。
例2. 如图3是一个商标的设计图案,AB=2BC=8,为圆,求阴影部分面积。
3.重叠法就是把所求阴影部分的面积问题转化为可求面积的规则图形的重叠部分的方法。
这类题阴影一般是由几个图形叠加而成。
要准确认清其结构,理顺图形间的大小关系。
例3. 如图4,正方形的边长为a,以各边为直径在正方形内作半圆,求所围成阴影部分图形的面积。
4.补形法将不规则图形补成特殊图形,利用特殊图形的面积求出原不规则图形的面积。
例4. 如图5,在四边形ABCD中,AB=2,CD=1,,求四边形ABCD所在阴影部分的面积。
5.拼接法例5. 如图6,在一块长为a、宽为b的矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽都是c个单位),求阴影部分草地的面积。
6.特殊位置法例6. 如图8,已知两个半圆中长为4的弦AB与直径CD平行,且与小半圆相切,那么图中阴影部分的面积等于__________。
7.代数法将图形按形状、大小分类,并设其面积为未知数,通过建立方程或方程组来解出阴影部分面积的方法。
例7. 如图10,正方形的边长为a,分别以两个对角顶点为圆心、以a为半径画弧,求图中阴影部分的面积。
求阴影部分面积的方法在数学中,求阴影部分面积是一个常见的问题。
阴影部分面积的计算方法有很多种,下面我们将介绍几种常见的方法。
一、几何法。
几何法是最直观的求阴影部分面积的方法之一。
首先,我们需要将阴影部分与已知图形进行比较,找到相似的图形或者利用几何图形的性质来求解。
例如,如果阴影部分是一个三角形,我们可以利用三角形面积公式来计算阴影部分的面积。
如果阴影部分是一个不规则图形,我们可以将其分割成几个已知图形,然后分别计算它们的面积,最后将它们相加得到阴影部分的面积。
二、积分法。
积分法是一种比较高级的求阴影部分面积的方法。
如果阴影部分是一个曲线围成的区域,我们可以利用定积分的概念来求解。
首先,我们需要确定曲线的方程,并找到曲线与坐标轴之间的交点。
然后,利用定积分的性质,可以将曲线围成的区域分割成无穷小的矩形,然后将这些矩形的面积相加,即可得到阴影部分的面积。
三、投影法。
投影法是一种利用投影关系来求解阴影部分面积的方法。
如果阴影部分是一个立体图形在平面上的投影,我们可以利用投影的性质来求解。
首先,我们需要确定立体图形的形状和位置,然后利用投影的关系,可以将立体图形的面积投影到平面上,最后计算投影部分的面积即可得到阴影部分的面积。
四、数值逼近法。
数值逼近法是一种利用数值计算方法来求解阴影部分面积的方法。
如果阴影部分的形状比较复杂,难以用几何法或者积分法求解,我们可以利用数值计算方法来逼近阴影部分的面积。
例如,可以利用蒙特卡洛方法来进行随机抽样,然后利用抽样结果来估计阴影部分的面积。
以上就是几种常见的求阴影部分面积的方法,每种方法都有其适用的场景和计算步骤。
在实际问题中,我们可以根据具体情况选择合适的方法来求解阴影部分的面积。
希望本文的介绍对您有所帮助。
求阴影面积的常用方法
计算平面图形的面积问题是常见题型,求平面阴影部分的面积是这类问题的难 点。
不规则阴影面积常常由三角形、四边形、弓形、扇形和圆、圆弧等基本图形 组合而成的,在解此类问题时,要注意观察和分析图形,会分解和组合图形。
现 介绍几种常用的方法。
、转化法 此法就是通过等积变换、平移、旋转、割补等方法将不规则的图形转化成面积相 等的规则图形,再利用规则图形的面积公式,计算出所求的不规则图形的面积。
例1.如图1,点C 、D 是以AB 为直径的半圆0上的三等分点,AB=12则图中由 弦AC AD 和窗围成的阴影部分图形的面积为 _________________ 。
分析:连结CD OC OD 如图2o 易证AB//CD ,则曲仞和&OUD 的面积相等, 所以图中阴影部分的面积就等于扇形 OCD 勺面积。
易得,故
---------- =DJT
360
、和差法 有一些图形结构复杂,通过观察,分析出不规则图形的面积是由哪些规则图形组 合而成的,再利用这些规则图形的面积的和或差来求, 从而达到化繁为简的目的。
例2.如图3是一个商标的设计图案,AB=2BC=B /DF 为4圆,求阴影部分面积。
分析:经观察图3可以分解出以下规则图形:矩形 ABCD 扇形ADE 只迪 J 9°
用牢 +4x8-1x4x12 = % + S 360 2
'阴影='障屢伽+ £縫删g —' 所
以,
B
图1
6
三、重叠法就是把所求阴影部分的面积问题转化为可求面积的规则图形的重叠部分的方法。
这类题阴影一般是由几个图形叠加而成。
要准确认清其结构,理顺图形间的大小关系。
例3.如图4,正方形的边长为a,以各边为直径在正方形内作半圆,求所围成阴影部分图形的面积。
涮蔭
图4
解:因为4个半圆覆盖了正方形,而且阴影部分重叠了两次,所以阴影部分的面£=2心
(丝)2-/ =(壬-1)/
积等于4个半圆的面积和与正方形面积的差。
故 2 2 四、补
形法将不规则图形补成特殊图形,利用特殊图形的面积求出原不规则图形的面积。
例4.如图5,在四边形ABCD中AB=2 CD=1 Z占=A5 = ZD = 93,求四边形ABCD所在阴影部分的面积。
E
图5
解:延长BC AD,交于点E,因为厶a,厶5 = 90。
,所以N E=?0。
,又三EDC = 90。
,所以CE=2CD, DE = 43易求得朋=2希所以
1 1 H 衍
弘笔=£如-S =寸® EE-寸D DE = +
五、拼接法
例5.如图6,在一块长为a 、宽为b 的矩形草地上,有一条弯曲的柏油小路(小 路任何地方的水平宽都是c 个单位),求阴影部分草地的面积。
解:移动小半圆至两半圆同圆心位置,如图 9。
设切点为H,连结OH 、OB 由垂
解:(1)将“小路”沿着左右两个边界“剪去”; c
个单位;(3)得到一个新的矩形(如图7)。
水平方向的长变成了 ,所以草地的面积为 (2)将左侧的草地向右平移 由
于新矩形的纵向宽仍然为 b , b (a-c ) = ab - be。
六、特殊位置法
例6.如图8,已知两个半圆中长为4的弦AB 与直径CD 平行,且与小半圆相切, 那么图中阴影部分的面积等于 _____________________ 。
分析:在大半圆中,任意移动小半圆的位置,
将小半圆移动至两个半圆同圆心位置(如图
阴影部分面积都保持不变,所以可 9)。
图e
B
A
00) D
图9
BH = -AB = 2 r .
径定理,知2 。
又AB切小半圆于点H,故0H1AB,故OB^ - 0屮
七、代数法将图形按形状、大小分类,并设其面积为未知数,通过建立方程或方程组来解出阴影部分面积的方法。
例7.如图10,正方形的边长为a,分别以两个对角顶点为圆心、以a为半径画弧,求图中阴影部分的面积。
图10
解:设阴影部分的面积为x,剩下的两块形状、大小相同的每块面积为y,贝W
1
中正方形的面积是龙+O,而x+y是以半径为a的圆面积的「故有签+ W
X -hy =盂二(一一1)屮(—-
4 。
解得2 。
即阴影部分的面积是2 。
需要说明的是,在求阴影部分图形的面积问题时,要具体问题具体分析,从而选取一种合理、简捷的方法。
思考吧如图11,正方形的边长为1,以CD为直径在正方形内画半圆,再以点C 为圆心、1为半径画弧BD,则图中阴影部分的面积为
图H
二、组合图形
1四边形与圆组合
例6:如图,已知△ ABC 内接于O 0,且AB = BC = CA = 4cm ,则图中阴影部分的面积是
2
cm 。
B (C)
A,
fj O
例7:如图,A 、B 、C 、D 是圆周上的四点,且 AB + CD = A D ^
BC ,如果弦AB 的长为8, 弦CD 的长为4,那么图中两个弓形(阴影部分)的面积和是 ______________ 。
(兀取3)
5、环形
例&如图,在两个同心圆中, 影部分面积是
P 是大圆上任一点, PA 切小圆于点 A ,设PA = 4,则图中阴
6、扇形
例9:如图,在矩形ABCD 中, 于
P ,则图中阴影部分的面积为
AB = 1, ()
AD =,以 BC 的中点E 为圆心的 皿介与AD 相切 2兀
3兀
(计)匸(C )
厂(D )
例10:如图,四个正方形的边长都相等,其中阴影部分面积相等的图形个数是
(A )0;( B )2;( C ) 3;( D )4。
r '1
関
I
A
-l_ • •• 3 •一
2、圆与圆组合 例11:如图,AB 、AE 则图中阴影部分的面积为 分别为两个半圆的直径,弦 CD // AB ,且与小圆相切,若 CD = 12,
点*a
/ 、*'二汽沁八 f ——i : <—、、八-:-!
A E O B
例12:如图,设计一个商标图案 8cm ,以点为圆心,AD (如图阴影部分),在矩形 长为半径作半圆,则商标图案面积为 C
B
BC 的长为半径作 )
—"■
C C F
A O B
4、扇形与圆组合 例13:如图,o O 半径为 CED :则C ED
与CAD 所围成的阴影部分的面积是 ______________ ; 三、动态图形 1、 翻折 例14:矩形ABCD 的长、宽分别为 5和3,将顶点C 折过来,使它落在 为折痕),那么阴影部分的面积是 ____________________________________ ; 2、旋转 例15:如图,将边长为1的正方形ABCD 绕A 点按逆时针方向旋转 60°,得正方形A /
B /
C /
D /
, 则旋转前
后两个正方形重叠部分的面积是
2cm ,直径AB 垂直于直径 CD ,以B 为圆心, AB 上的C 点(DE。