过程控制第二章比例积分微分控制和其调节过程
- 格式:ppt
- 大小:578.50 KB
- 文档页数:3

过程控制仪表及控制系统课后习题答案(林德杰)2(总18页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--lxc第一章思考题与习题1-2 图为温度控制系统,试画出系统的框图,简述其工作原理;指出被控过程、被控参数和控制参数。
解:乙炔发生器中电石与冷水相遇产生乙炔气体并释放出热量。
当电石加入时,内部温度上升,温度检测器检测温度变化与给定值比较,偏差信号送到控制器对偏差信号进行运算,将控制作用于调节阀,调节冷水的流量,使乙炔发生器中的温度到达给定值。
系统框图如下:被控过程:乙炔发生器被控参数:乙炔发生器内温度控制参数:冷水流量1-3 常用过程控制系统可分为哪几类答:过程控制系统主要分为三类:1. 反馈控制系统:反馈控制系统是根据被控参数与给定值的偏差进行控制的,最终达到或消除或减小偏差的目的,偏差值是控制的依据。
它是最常用、最基本的过程控制系统。
2.前馈控制系统:前馈控制系统是根据扰动量的大小进行控制的,扰动是控制的依据。
由于没有被控量的反馈,所以是一种开环控制系统。
由于是开环系统,无法检查控制效果,故不能单独应用。
3. 前馈-反馈控制系统:前馈控制的主要优点是能够迅速及时的克服主要扰动对被控量的影响,而前馈—反馈控制利用反馈控制克服其他扰动,能够是被控量迅速而准确地稳定在给定值上,提高控制系统的控制质量。
3-4 过程控制系统过渡过程的质量指标包括哪些内容它们的定义是什么哪些是静态指标哪些是动态质量指标答:1. 余差(静态偏差)e :余差是指系统过渡过程结束以后,被控参数新的稳定值y(∞)与给定值c 之差。
它是一个静态指标,对定值控制系统。
希望余差越小越好。
2. 衰减比n:衰减比是衡量过渡过程稳定性的一个动态质量指标,它等于振荡过程的第一个波的振幅与第二个波的振幅之比,即:n <1系统是不稳定的,是发散振荡;n=1,系统也是不稳定的,是等幅振荡;n >1,系统是稳定的,若n=4,系统为4:1的衰减振荡,是比较理想的。


作 业第二章:2-6某水槽如题图2-1所示。
其中A 1为槽的截面积,R 1、R 2均为线性水阻,Q i 为流入量,Q 1和Q 2为流出量要求:(1)写出以水位h 1为输出量,Q i 为输入量的对象动态方程;(2)写出对象的传递函数G(s)并指出其增益K 和时间常数T 的数值。
图2-1解:1)平衡状态: 02010Q Q Q i +=2)当非平衡时: i i i Q Q Q ∆+=0;1011Q Q Q ∆+=;2022Q Q Q ∆+= 质量守恒:211Q Q Q dthd A i ∆-∆-∆=∆ 对应每个阀门,线性水阻:11R h Q ∆=∆;22R h Q ∆=∆ 动态方程:i Q R hR h dt h d A ∆=∆+∆+∆2113) 传递函数:)()()11(211s Q s H R R S A i =++1)11(1)()()(211+=++==Ts KR R S A s Q s H s G i这里:21121212111111R R A T R R R R R R K +=+=+=;2Q112-7建立三容体系统h 3与控制量u 之间的动态方程和传递数,见题图2-2。
解:如图为三个单链单容对像模型。
被控参考△h 3的动态方程: 3233Q Q dt h d c ∆-∆=∆;22R h Q ∆=∆;33R hQ ∆=∆; 2122Q Q dt h d c ∆-∆=∆;11R hQ ∆=∆ 111Q Q dth d c i ∆-∆=∆ u K Q i ∆=∆ 得多容体动态方程:uKR h dth d c R c R c R dt h d c c R R c c R R c c R R dt h d c c c R R R ∆=∆+∆+++∆+++∆333332211232313132322121333321321)()(传递函数:322133)()()(a s a s a s Ks U s H s G +++==; 这里:32132133213213321321332211232132131313232212111;c c c R R R kR K c c c R R R a c c c R R R c R c R c R a c c c R R R c c R R c c R R c c R R a ==++=++=2-8已知题图2-3中气罐的容积为V ,入口处气体压力,P 1和气罐 内气体温度T 均为常数。

⾃动控制原理第⼆章复习总结(第⼆版)第⼆章过程装备控制基础本章内容:简单过程控制系统的设计复杂控制系统的结构、特点及应⽤。
第⼀节被控对象的特性⼀、被控对象的数学描述(⼀)单容液位对象1.有⾃衡特性的单容对象2.⽆⾃衡特性的单容对象(⼆)双容液位对象1.典型结构:双容⽔槽如图2-5所⽰。
图2-5 双容液位对象图2-6 ⼆阶对象特性曲线2.平衡关系:⽔槽1的动态平衡关系为:3.⼆阶被控对象:1222122221)(Q K h dt dh T T dt h d T T ?=+++式(2-18)就是描述图2-5所⽰双容⽔槽被控对象的⼆阶微分⽅程式。
称⼆阶被控对象。
⼆、被控对象的特性参数(⼀)放⼤系数K(⼜称静态增益)(⼆)时间常数T(三)滞后时间τ(1).传递滞后τ0(或纯滞后):(2).容量滞后τc可知τ=τ0+τc。
三、对象特性的实验测定对象特性的求取⽅法通常有两种:1.数学⽅法2.实验测定法(⼀)响应曲线法:(⼆)脉冲响应法第⼆节单回路控制系统定义:(⼜称简单控制系统),是指由⼀个被控对象、⼀个检测元件及变送器、⼀个调节器和⼀个执⾏器所构成的闭合系统。
⼀、单回路控制系统的设计设计步骤:1.了解被控对象2.了解被控对象的动静态特性及⼯艺过程、设备等3.确定控制⽅案4.整定调节器的参数(⼀)被控变量的选择(⼆)操纵变量的选择(三)检测变送环节的影响(四)执⾏器的影响⼆、调节器的调节规律1.概念调节器的输出信号随输⼊信号变化的规律。
2.类型位式、⽐例、积分、微分。
(⼀)位式调节规律1.双位调节2.具有中间区的双位调节3.其他三位或更多位的调节。
(⼆)⽐例调节规律(P )1.⽐例放⼤倍数(K )2.⽐例度δ3.⽐例度对过渡过程的影响(如图2-24所⽰)4.调节作⽤⽐例调节能较为迅速地克服⼲扰的影响,使系统很快地稳定下来。
通常适⽤于⼲扰少扰动幅度⼩、符合变化不⼤、滞后较⼩或者控制精度要求不⾼的场合。
(三)⽐例积分调节规律(PI )1.积分调节规律(I )(1)概念:调节器输出信号的变化量与输⼊偏差的积分成正⽐==?t I t I dt t e T dt t e K t u 00)(1)()(式中:K I 为积分速度,T I 为积分时间。






第二章比例积分微分控制及其调节过程比例积分微分控制及其调节过程是控制工程中常用的一种控制方法,本文将介绍其基本概念、原理与调节过程。
1.比例积分微分控制的概念比例积分微分控制是一种基于反馈原理的控制方法。
它通过将被控对象的输出值与期望值之间的差异进行计算,并根据计算结果来调节控制器的输出信号,从而使被控对象的输出值趋于期望值。
在比例积分微分控制中,主要有三个调节参数:比例参数(Kp)、积分参数(Ti)和微分参数(Td)。
比例参数表示控制器输出的增益,积分参数表示控制器对偏差的累积处理,微分参数表示控制器对偏差变化率的处理。
2.比例积分微分控制的原理比例积分微分控制的原理可以用以下公式表示:u(t) = Kp * e(t) + Ki * ∫e(t) dt + Kd * de(t)/dt其中,u(t)表示控制器的输出信号,e(t)表示被控对象输出值与期望值的差异,Ki、Kd分别表示积分和微分参数。
比例控制项Kp*e(t)用来根据当前差异进行有限调整,即根据误差大小决定控制器输出的大小。
当误差较大时,比例控制项的影响较大,能够快速调整输出信号,使被控对象尽快趋于期望值。
积分控制项Ki * ∫e(t) dt用来累积误差的信息,即在一段时间内积累误差值,并加大对误差的修正力度。
积分项主要用于调节系统的静态误差,当系统存在静态误差时会积累一定量的误差,通过积分项可以消除这部分误差,使系统更加准确。
微分控制项Kd * de(t)/dt用来预测误差的变化趋势,即通过对误差的变化率进行检测和调整,可以提前对误差进行修正,从而提高系统的响应速度和稳定性。
3.比例积分微分控制的调节过程比例积分微分控制的调节过程主要包括以下几个步骤:(1)初始化控制器参数:设置比例参数Kp、积分参数Ti和微分参数Td的初值,并将控制器的输出信号初始化为0。
(2)测量被控对象的输出值:通过传感器等测量设备获取被控对象的输出值。
(3)计算误差:将被控对象的输出值与期望值进行比较,计算误差e(t)。
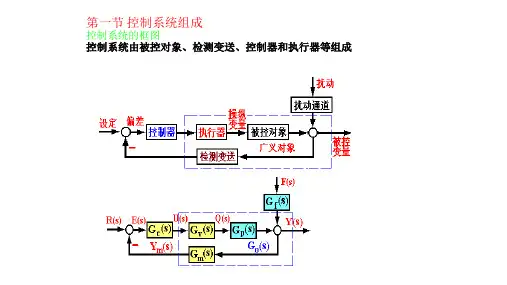
《过程控制》课程笔记第一章概论一、过程控制系统组成与分类1. 过程控制系统的基本组成过程控制系统主要由被控对象、控制器、执行器、检测仪表四个部分组成。
(1)被控对象:指生产过程中的各种设备、机器、容器等,它们是生产过程中需要控制的主要对象。
被控对象具有各种不同的特性,如线性、非线性、时变性等。
(2)控制器:控制器是过程控制系统的核心部分,它根据给定的控制策略,对检测仪表的信号进行处理,生成控制信号,驱动执行器动作,从而实现对被控对象的控制。
控制器的设计和选择直接影响控制效果。
(3)执行器:执行器是控制器与被控对象之间的桥梁,它接收控制器的信号,调节阀门的开度或者调节电机转速,从而实现对被控对象的控制。
执行器的响应速度和精度对控制系统的性能有很大影响。
(4)检测仪表:检测仪表用于实时测量被控对象的各项参数,如温度、压力、流量等,并将这些参数转换为电信号,传输给控制器。
检测仪表的准确性和灵敏度对控制系统的性能同样重要。
2. 过程控制系统的分类根据控制系统的结构特点,过程控制系统可以分为两大类:开环控制系统和闭环控制系统。
(1)开环控制系统:开环控制系统没有反馈环节,控制器根据给定的控制策略,直接生成控制信号,驱动执行器动作。
开环控制系统的优点是结构简单,成本低,但缺点是控制精度较低,容易受到外部干扰。
(2)闭环控制系统:闭环控制系统具有反馈环节,控制器根据检测仪表的信号,实时调整控制策略,生成控制信号,驱动执行器动作。
闭环控制系统的优点是控制精度高,抗干扰能力强,但缺点是结构复杂,成本较高。
二、过程控制系统性能指标1. 稳态误差:稳态误差是指系统在稳态时,输出值与设定值之间的差值。
稳态误差越小,表示系统的控制精度越高。
稳态误差可以通过调整控制器的参数来减小。
2. 动态性能:动态性能是指系统在过渡过程中,输出值随时间的变化规律。
动态性能指标包括上升时间、调整时间、超调量等。
动态性能的好坏直接影响到系统的响应速度和稳定性。
控制器的调节方式说明控制器是一种重要的设备,用来监控和调节各种过程和系统。
它们被广泛应用于工业、交通、医疗和家用设备等领域。
本文将介绍几种常见的控制器调节方式,包括比例控制、积分控制和微分控制,以及它们的应用场景和优势。
一、比例控制比例控制是最简单和最常用的控制方式之一。
它基于假设,即控制系统的输出与输入之间存在一个比例关系。
比例控制器根据偏差信号与设定值之间的差异,产生一个控制信号来调节输出。
调节信号的大小与偏差信号成正比。
这种控制方式适用于线性系统和快速响应的场景。
比例控制的公式可以表示为:输出 = Kp ×偏差其中,Kp是比例参数,表示控制器对偏差信号的增益。
较大的Kp 值会产生更大的调节效果,但可能引起系统不稳定。
因此,在实际应用中,需要根据具体系统进行参数的优化和调整。
二、积分控制积分控制是在比例控制的基础上引入积分动作的一种调节方式。
它通过累积偏差信号的积分值,来改善系统的稳态性能。
积分控制器可以消除偏差信号的持续存在,提高系统的精确度和稳定性。
它适用于对精确控制要求较高的场景。
积分控制的公式可以表示为:输出= Ki × ∫ 偏差 dt其中,Ki是积分参数,表示控制器对偏差信号的积分增益。
较大的Ki值会产生更大的调节效果,但也可能导致系统产生超调现象或不稳定。
因此,在应用中需要根据系统特性进行参数的调整和优化。
三、微分控制微分控制是在比例控制的基础上引入微分动作的一种调节方式。
它通过监测偏差信号的变化率,来预测系统未来的状态,并作出相应的调节。
微分控制器可以迅速响应系统的变化,提高系统的动态性能和抗干扰能力。
它适用于对快速响应和稳定性要求较高的场景。
微分控制的公式可以表示为:输出 = Kd × d(偏差)/dt其中,Kd是微分参数,表示控制器对偏差信号的变化率的增益。
较大的Kd值会产生更大的调节效果,但也可能引起系统产生震荡或不稳定。
因此,在应用中需要根据具体情况进行合理的参数选择和调整。
比例积分微分控制及其调节过程初学引言在自动控制系统中,比例积分微分控制(Proportional Integral Derivative Control, PID控制)被广泛应用于工业过程控制、机器人控制、飞行器操纵等各种领域。
本文将介绍比例积分微分控制的基本原理以及其调节过程初学。
1. 比例控制(Proportional Control)比例控制是 PID 控制中的第一个组成部分。
它的控制输出与误差信号(偏差)成正比。
其控制公式可以表示为:$$ \\text{Output}(t) = K_p \\cdot \\text{Error}(t) $$其中,K p是比例增益参数,$\\text{Error}(t)$ 表示当前的误差信号。
比例控制的作用是减小偏差信号,促使系统迅速稳定到给定的参考输入值。
然而,仅仅应用比例控制无法完全消除稳态误差。
2. 积分控制(Integral Control)积分控制是 PID 控制中的第二个组成部分。
它积累了误差信号的累积值,并将其乘以一个积分增益参数。
积分控制的目标是消除稳态误差。
积分控制的公式可以表示为:$$ \\text{Output}(t) = K_i \\cdot \\int_0^t{\\text{Error}(\\tau)d{\\tau}} $$其中,K i是积分增益参数。
通过调节积分增益参数,我们可以控制系统对于稳态误差的响应。
较高的积分增益会加速误差信号的积累,从而更快地消除稳态误差。
然而,过大的积分增益可能引起系统的超调或震荡。
3. 微分控制(Derivative Control)微分控制是 PID 控制中的第三个组成部分。
它对误差信号的变化率进行测量,并将其乘以一个微分增益参数。
微分控制的目标是抑制系统的超调以及提高系统的稳定性。
微分控制的公式可以表示为:$$ \\text{Output}(t) = K_d \\cdot \\frac{d\\text{Error}(t)}{dt} $$其中,K d是微分增益参数。