常用数字平方数速算表(初一必背)
- 格式:xlsx
- 大小:14.99 KB
- 文档页数:2

>> 平方数速算牢记常用平方数,特别是11~30以内数的平方,可以很好地提高计算速度:121、144、169、196、225、256、289、324、361、400441、484、529、576、625、676、729、784、841、900>> 尾数法速算资料分析试题当中牵涉的数据几乎都是通过近似后得到的结果,因此华图公务员考试研究中心老师建议考生在计算的时首先考虑首位估算,而尾数往往是微不足道的。
因此资料分析当中的尾数法只适用于未经近似或者不需要近似的计算之中。
历史数据证明,国家公务员考试行政职业能力测验试题中资料分析基本上不能用到尾数法,但在地方公务员考试行政职业能力测验的资料分析题,尾数法仍然可以有效地简化计算。
>> 错位相加/减A×9型速算技巧:A×9=A× 10-A;如:1949×9= 19490-1949=17541A×99型速算技巧:A×99=A×100-A;如:1949×99=194900-1949=192951A×11型速算技巧:A×11=A×10+A;如:1949×11= 19490+1949=21439A×101型速算技巧:A×101=A×100+A;如:1949×101=194900+1949=196849>> 乘/除以5、25、125的速算技巧A×5型速算技巧:A×5=10A÷2;A÷5型速算技巧:A÷5=0.1A×2如:1949×5=19490÷2=9745;1949÷5=194.9×2=389.8>> “首数互补尾数相同”型两数乘积速算技巧积的头=头×头+相同的尾;积的尾=尾×尾如:“38×78”,尾数均为“8”,首数“3”与“7”的和是“10”,互补所以乘积的首数为3×7+8=29,尾数为8×8=64,即38×78=2964如:“29×89”,尾数均为“9”,首数“2”与“8”的和是“10”,互补所以乘积的首数为2×8+9=25,尾数为9×9=81,即29×89=2581>> 平方差公式速算平方差公式:(a+b)(a-b)=a^2-b^2如:16×18=(17+1)×(17-1)=17^2-1=28831^2=31^2-1+1=30×32+1=961>> 实例详解【例1】假设某国外汇汇率以30.5%的平均速度增长,预计8年之后的外汇汇率大约为现在的多少倍?()A.3.4 B.4.5 C.6.8 D.8.4【答案】D【解析】(1+30.5%)^8=1.305^8≈1.3^8=(1.3^2)^4=1.69^4≈1.7^4=2.89^2≈2.9^2=8.41。

一到100的平方数顺口溜
(原创实用版)
目录
1.引言:介绍平方数顺口溜
2.一到十的平方数顺口溜
3.十一到一百的平方数顺口溜
4.结语:平方数顺口溜的趣味性和记忆效果
正文
1.引言:
在我国传统的数学教学中,有一种非常有趣的教学方法,那就是用顺口溜来帮助学生记忆一些常用的数学知识,如乘法口诀、加法口诀等。
其中,平方数顺口溜就是一道独特的风景线。
通过朗朗上口的诗句,让学生在轻松愉快的氛围中记住一到一百的平方数,既增强了学习的趣味性,又提高了记忆效果。
2.一到十的平方数顺口溜:
一到十的平方数分别是:1, 4, 9, 16, 25, 36, 49, 64, 81, 100。
为了让学生更容易记住这些数字,我们可以用如下的顺口溜来帮助他们记忆:
一一得一,二二得四,三三得九,四四十六,五五得二十五,六六三十六,七七四十九,八八六十四,九九八十一,一百大团圆。
3.十一到一百的平方数顺口溜:
十一到一百的平方数分别是:121, 144, 169, 196, 225, 256, 289, 324, 361, 400。
相应的顺口溜如下:
十一十一,一百二十一;十二十二,一百四十四;十三十三,一百六
十九;十四十四,一百九十六;十五十五,二百二十五;十六十六,二百五十六;十七十七,二百八十九;十八十八,三百二十四;十九十九,三百六十一;一百一百,大团圆。
4.结语:
平方数顺口溜的趣味性和记忆效果不言而喻。
通过这种寓教于乐的方式,让学生在轻松愉快的氛围中掌握知识,既能激发他们的学习兴趣,又能提高学习效率。

11-30以内整数平方的速算方法
一、11-19的平方的速算
定理1:设有11-19中某数,则此数的平方等于此数与它个位数字之和的10倍,再加上此数个位数字的平方。
例:172=(17+7)×10+72=240+49=289
二、21-29的平方的速算:
定理2:设有21-29中某数,则此数的平方等于此数与它个位数字之和的2倍乘以10,再加上此数个位数字的平方。
例:282=(28+8)×2×10+82=720+64=784
附:11-25的平方值
112=121122=144132=169142=196152=225162=256
172=289 182=324192=361212=441222=484 232=529
242=576 252=625 262=676 272=729 282=784 292=841
19×19的简便算法
例:13(被乘数)×12(乘数)=?
第一步:先把被乘数(13)跟乘数的个位数(2)加起来,13+2=15
第二步:然后把第一步的答案乘以10((也就是说后面加个0),第三步:再把被乘数的个位数(3)乘以乘数的个位数(2),2×3=6
第四步:把第二步和第三步的得数相加,就是最终答案。
150+6=156
就这样,用心算就可以很快地算出11×11到19×19了。

>> 平方数速算牢记常用平方数,特别是11~30以内数的平方,可以很好地提高计算速度:121、144、169、196、225、256、289、324、361、400441、484、529、576、625、676、729、784、841、900>> 尾数法速算资料分析试题当中牵涉的数据几乎都是通过近似后得到的结果,因此华图公务员考试研究中心老师建议考生在计算的时首先考虑首位估算,而尾数往往是微不足道的。
因此资料分析当中的尾数法只适用于未经近似或者不需要近似的计算之中。
历史数据证明,国家公务员考试行政职业能力测验试题中资料分析基本上不能用到尾数法,但在地方公务员考试行政职业能力测验的资料分析题,尾数法仍然可以有效地简化计算。
>> 错位相加/减A×9型速算技巧:A×9=A× 10-A;如:1949×9= 19490-1949=17541A×99型速算技巧:A×99=A×100-A;如:1949×99=194900-1949=192951A×11型速算技巧:A×11=A×10+A;如:1949×11= 19490+1949=21439A×101型速算技巧:A×101=A×100+A;如:1949×101=194900+1949=196849>> 乘/除以5、25、125的速算技巧A×5型速算技巧:A×5=10A÷2;A÷5型速算技巧:A÷5=0.1A×2如:1949×5=19490÷2=9745;1949÷5=194.9×2=389.8>> “首数互补尾数相同”型两数乘积速算技巧积的头=头×头+相同的尾;积的尾=尾×尾如:“38×78”,尾数均为“8”,首数“3”与“7”的和是“10”,互补所以乘积的首数为3×7+8=29,尾数为8×8=64,即38×78=2964如:“29×89”,尾数均为“9”,首数“2”与“8”的和是“10”,互补所以乘积的首数为2×8+9=25,尾数为9×9=81,即29×89=2581>> 平方差公式速算平方差公式:(a+b)(a-b)=a^2-b^2如:16×18=(17+1)×(17-1)=17^2-1=28831^2=31^2-1+1=30×32+1=961>> 实例详解【例1】假设某国外汇汇率以30.5%的平均速度增长,预计8年之后的外汇汇率大约为现在的多少倍?()A.3.4 B.4.5 C.6.8 D.8.4【答案】D【解析】(1+30.5%)^8=1.305^8≈1.3^8=(1.3^2)^4=1.69^4≈1.7^4=2.89^2≈2.9^2=8.41。

牢记常用平方数,特别是11~30以内数的平方,可以很好地提高计算速度:121、144、169、196、225、256、289、324、361、400441、484、529、576、625、676、729、784、841、900尾数法速算:因为资料分析试题当中牵涉到的数据几乎都是通过近似后得到的结果,所以一般我们计算的时候多强调首位估算,而尾数往往是微不足道的。
因此资料分析当中的尾数法只适用于未经近似或者不需要近似的计算之中。
历史数据证明,国考试题资料分析基本上不能用到尾数法,但在地方考题的资料分析当中,尾数法仍然可以有效地简化计算。
错位相加/减:A×9型速算技巧:A×9=A×10-A;如:743×9=7430-743=6687A×9.9型速算技巧:A×9.9=A×10+A÷10;如:743×9.9=7430-74.3=7355.7A×11型速算技巧:A×11=A×10+A;如:743×11=7430+743=8173A×101型速算技巧:A×101=A×100+A;如:743×101=74300+743=75043乘/除以5、25、125的速算技巧:A×5型速算技巧:A×5=10A÷2;A÷5型速算技巧:A÷5=0.1A×2例8739.45×5=87394.5÷2=43697.2536.843÷5=3.6843×2=7.3686A× 25型速算技巧:A×25=100A÷4;A÷ 25型速算技巧:A÷25=0.01A×4例7234×25=723400÷4=1808503714÷25=37.14×4=148.56A×125型速算技巧:A×125=1000A÷8;A÷125型速算技巧:A÷125=0.001A×8 例8736×125=8736000÷8=10920004115÷125=4.115×8=32.92减半相加:A×1.5型速算技巧:A×1.5=A+A÷2;例3406×1.5=3406+3406÷2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技巧:积的头=头×(头+1);积的尾=尾×尾例:“23×27”,首数均为“2”,尾数“3”与“7”的和是“10”,互补所以乘积的首数为2×(2+1)=6,尾数为3×7=21,即23×27=621两年混合增长率公式:如果第二期与第三期增长率分别为r1与r2,那么第三期相对于第一期的增长率为:r1+r2+r1× r2增长率化除为乘近似公式:如果第二期的值为A,增长率为r,则第一期的值A′:A′=A/1+r≈A×(1-r)(实际上左式略大于右式,r越小,则误差越小,误差量级为r2)平均增长率近似公式:如果N年间的增长率分别为r1、r2、r3……rn,则平均增长率:r≈r1+r2+r3+……rn/n(实际上左式略小于右式,增长率越接近,误差越小)求平均增长率时特别注意问题的表述方式,例如:1.“从2004年到2007年的平均增长率”一般表示不包括2004年的增长率;2.“2004、2005、2006、2007年的平均增长率”一般表示包括2004年的增长率。

牢记常用平方数,特别是11~30以内数的平方,可以很好地提高计算速度:121、144、169、196、225、256、289、324、361、400441、484、529、576、625、676、729、784、841、900尾数法速算:因为资料分析试题当中牵涉到的数据几乎都是通过近似后得到的结果,所以一般我们计算的时候多强调首位估算,而尾数往往是微不足道的。
因此资料分析当中的尾数法只适用于未经近似或者不需要近似的计算之中。
历史数据证明,国考试题资料分析基本上不能用到尾数法,但在地方考题的资料分析当中,尾数法仍然可以有效地简化计算。
错位相加/减:A×9型速算技巧:A×9=A×10-A;如:743×9=7430-743=6687A×9.9型速算技巧:A×9.9=A×10+A÷10;如:743×9.9=7430-74.3=7355.7A×11型速算技巧:A×11=A×10+A;如:743×11=7430+743=8173A×101型速算技巧:A×101=A×100+A;如:743×101=74300+743=75043乘/除以5、25、125的速算技巧:A×5型速算技巧:A×5=10A÷2;A÷5型速算技巧:A÷5=0.1A×2例8739.45×5=87394.5÷2=43697.2536.843÷5=3.6843×2=7.3686A× 25型速算技巧:A×25=100A÷4;A÷ 25型速算技巧:A÷25=0.01A×4例7234×25=723400÷4=1808503714÷25=37.14×4=148.56A×125型速算技巧:A×125=1000A÷8;A÷125型速算技巧:A÷125=0.001A×8 例8736×125=8736000÷8=10920004115÷125=4.115×8=32.92减半相加:A×1.5型速算技巧:A×1.5=A+A÷2;例3406×1.5=3406+3406÷2=3406+1703=5109“首数相同尾数互补”型两数乘积速算技巧:积的头=头×(头+1);积的尾=尾×尾例:“23×27”,首数均为“2”,尾数“3”与“7”的和是“10”,互补所以乘积的首数为2×(2+1)=6,尾数为3×7=21,即23×27=621两年混合增长率公式:如果第二期与第三期增长率分别为r1与r2,那么第三期相对于第一期的增长率为:r1+r2+r1× r2增长率化除为乘近似公式:如果第二期的值为A,增长率为r,则第一期的值A′:A′=A/1+r≈A×(1-r)(实际上左式略大于右式,r越小,则误差越小,误差量级为r2)平均增长率近似公式:如果N年间的增长率分别为r1、r2、r3……rn,则平均增长率:r≈r1+r2+r3+……rn/n(实际上左式略小于右式,增长率越接近,误差越小)求平均增长率时特别注意问题的表述方式,例如:1.“从2004年到2007年的平均增长率”一般表示不包括2004年的增长率;2.“2004、2005、2006、2007年的平均增长率”一般表示包括2004年的增长率。

常用数的平方表【原创版】目录1.引言2.平方表的定义和作用3.常用数的平方表的内容4.平方表的记忆方法5.结论正文1.引言平方表是一种数学工具,它列出了常用数字的平方值,对于数学运算和问题解决具有重要的参考价值。
无论是在学习、生活还是工作中,掌握平方表都是非常有益的。
本文将为大家介绍常用数的平方表,并提供一些记忆方法。
2.平方表的定义和作用平方表就是将 1 至 20(或更多)的数字自乘得到的结果排列成表格,方便人们查阅。
例如:1=1,2=4,3=9,4=16,以此类推。
平方表的作用主要体现在以下几个方面:(1)方便快速查阅数字的平方值,提高计算效率;(2)培养人们的数学思维能力和计算能力;(3)作为数学知识的补充,帮助人们更好地理解数学。
3.常用数的平方表的内容常用数的平方表如下:1=1 2=4 3=9 4=16 5=25 6=36 7=49 8=64 9=81 10=100 11=121 12=144 13=169 14=196 15=225 16=256 17=289 18=324 19=361 20=4004.平方表的记忆方法记忆平方表需要一定的时间和耐心,以下是一些建议的记忆方法:(1)联想法:将每个数字的平方值与生活中的事物、场景相联系,例如:2=4,可以联想到“二月二,龙抬头”;3=9,可以联想到“三九胃泰”。
(2)分组法:将平方表中的数字分为若干组,每组数字的平方值相差不大,例如:(1, 4, 9)、(16, 25, 36, 49)等,这样可以利用归纳法记忆。
(3)对比法:将相邻的数字进行比较,找到它们之间的规律,例如:4-3=7,5-4=9,6-5=11,可以发现每次增加 2。
(4)反复练习:利用碎片时间,反复查阅和记忆平方表,达到熟练掌握的程度。
5.结论常用数的平方表是学习数学和解决实际问题的重要工具,掌握它有助于提高我们的计算能力和数学思维。
通过联想法、分组法、对比法等记忆方法,我们可以轻松地记住平方表中的内容。

1到20的平方数表
(原创实用版)
目录
1.引言:介绍平方数表的定义和作用
2.范围:确定需要计算的平方数范围
3.计算:详细列出 1 到 20 的平方数
4.结论:总结 1 到 20 的平方数表
正文
平方数表是一个数学工具,它列出了从 1 到某个数字的所有整数的平方。
平方数表在数学中有着广泛的应用,例如在解决一些与平方数相关的问题时,可以使用平方数表来快速查找答案。
在本文中,我们将计算 1 到 20 的平方数表。
这个范围包括了从 1 到 20 的所有整数的平方。
下面是 1 到 20 的平方数表的详细计算结果:
1 的平方是 1,
2 的平方是 4,
3 的平方是 9,
4 的平方是 16,
5 的平方是 25,
6 的平方是 36,
7 的平方是 49,
8 的平方是 64,
9 的平方是 81,10 的平方是 100,11 的平方是 121,12 的平方是 144,13 的平方是 169,14 的平方是 196,15 的平方是 225,16 的平方是 256,17 的平方是 289,18 的平方是 324,19 的平方是 361,20 的平方是400。
因此,1 到 20 的平方数表包括了以上所有数字。
这个表可以帮助我们快速找到 1 到 20 的任何整数的平方。
总的来说,平方数表是一个有用的数学工具,它可以帮助我们解决一些与平方数相关的问题。
第1页共1页。
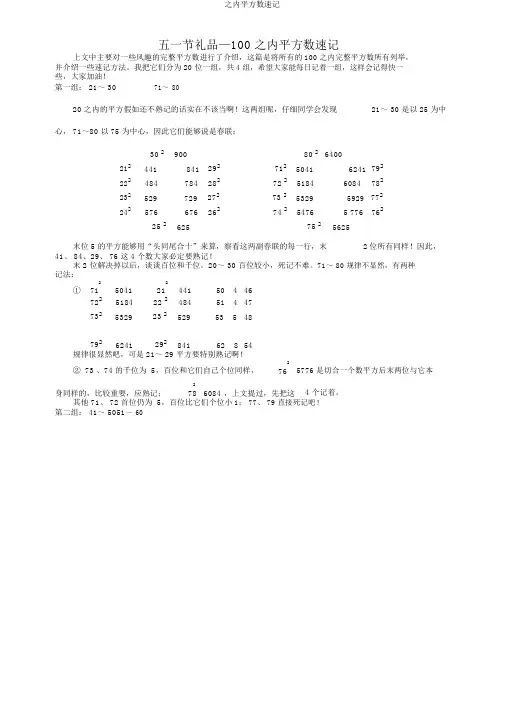
五一节礼品—100 之内平方数速记上文中主要对一些风趣的完整平方数进行了介绍,这篇是将所有的100 之内完整平方数所有列举,并介绍一些速记方法。
我把它们分为20 位一组,共4 组,希望大家能每日记着一组,这样会记得快一些,大家加油!第一组: 21~ 30 71~8020 之内的平方假如还不熟记的话实在不该当啊!这两组呢,仔细同学会发现21~ 30 是以 25 为中心, 71~80 以 75 为中心,因此它们能够说是春联:30 2 900 80 2 6400212 441 841 292 712 5041 6241 792222 484 784 282 72 2 5184 6084 782232 529 729 272 73 2 5329 5929 772242 576 676 262 74 2 5476 5 776 76225 2 625 75 2 5625末位 5 的平方能够用“头同尾合十”来算,察看这两副春联的每一行,末 2 位所有同样!因此,41、 84、29、 76 这 4 个数大家必定要熟记!末 2 位解决掉以后,谈谈百位和千位。
20~ 30 百位较小,死记不难。
71~ 80 规律不显然,有两种记法:25041 2441 50 4 46①71 21722 5184 22 2 484 51 4 47 732 5329 23 2 529 53 5 48792 6241 292 841 62 8 54 规律很显然吧,可是21~ 29 平方要特别熟记啊!② 73 、74 的千位为 5,百位和它们自己个位同样,25776 是切合一个数平方后末两位与它本76身同样的,比较重要,应熟记;2,上文提过,先把这 4 个记着。
78 6084其他 71、 72 首位仍为 5,百位比它们个位小1; 77、 79 直接死记吧!第二组: 41~ 5051~60上一组比较难记,下边来一组比较轻松的。
先记 51~ 60,这一组可用尾同头合十来算!512 2601 5 5 1 26 12 01 522 2704 5 5 2 27 2 2 04 532 2809 5 5 3 28 3 2 09 542 2916 5 5 4 29 4 2 16 552 3025 5 5 5 30 5 2 25 后边的几个规律留给大家自己来找吧!对于 41~ 50,其实和上述差不多,只可是用减法。