电化学阻抗谱等效电路串联并联原则

电阻的串并联与电路的等效电阻的应用电阻是电路中常见的元件之一，通过串联和并联电阻可以改变电路的总阻值。

在电路设计和分析中，了解电阻的串并联以及电路的等效电阻是非常重要的。

本文将介绍电阻的串并联原理，并探讨电路中等效电阻的应用。

1. 电阻的串联在电路中，当两个或更多的电阻依次连接在一起形成电路时，称为电阻的串联。

串联电阻的特点是电流在电阻之间依次流过，而电压在电阻上分配。

串联电阻的总阻值等于各个电阻的阻值之和。

假设电路中有两个串联的电阻R1和R2，则总电阻RT可以通过以下公式计算：RT = R1 + R2串联电阻的应用：- 串联电阻可以用于电路中的电流限制，通过选择合适的串联电阻阻值，可以限制电流在一定范围内，以保护电路中的其他元件免受过高电流的损害。

- 在电路中，串联电阻可以用于分压电路的设计。

通过选择不同阻值的串联电阻，可以将输入电压按照一定比例分压输出，实现电压降低的功能。

2. 电阻的并联当两个或更多的电阻同时连接在电路中，形成并联电路时，称为电阻的并联。

并联电阻的特点是电压相同，而电流分配到各个电阻上。

并联电阻的总阻值可以通过以下公式计算：1/RT = 1/R1 + 1/R2并联电阻的应用：- 并联电阻常用于电路中的功率分配。

例如，在LED灯串联电路中，为了保证每个LED获得相同的亮度，可以通过并联电阻使电流在各个LED之间均匀分配。

- 并联电阻还可以用于电路中的电流放大。

通过选择适当的并联电阻阻值，可以将电流放大到所需的范围，以满足电路的工作要求。

3. 电路的等效电阻在实际电路设计和分析中，我们常常需要将复杂的电路简化为一个等效电路，以便更好地理解和计算电路的行为。

等效电路是指具有相同输入和输出特性的简化电路。

对于串联电阻，其等效电阻为串联电阻的总和，即RT = R1 + R2，而对于并联电阻，其等效电阻可以通过公式1/RT = 1/R1 + 1/R2来计算。

等效电阻的应用：- 等效电阻可以用于简化复杂电路的计算和分析。

电化学原理与方法电化学阻抗谱电化学阻抗谱是电化学研究中常用的一种技术手段，它通过对样品施加交流电信号并测量相应的电流和电压，来研究电化学界面上的反应动力学过程。

本文将介绍电化学阻抗谱的基本原理、实验方法和应用。

首先，电化学阻抗谱的基本原理是基于交流电路理论。

当在电化学界面上施加交流电压信号时，该信号会引起电解质溶液中的离子迁移和电荷转移，从而导致交流电流的流动。

根据欧姆定律和基尔霍夫定律，可以将电化学阻抗谱通过等效电路模型描述为电阻、电感和电容的串、并联组合。

通过对等效电路模型的拟合，可以获得与电化学界面上的反应动力学相关的参数，如电荷转移电阻、界面电容等。

其次，电化学阻抗谱的实验方法包括三个方面的内容。

首先是实验设备的选择和准备。

通常使用电化学工作站来进行电化学阻抗谱实验，其中包括交流信号源，电位控制器，频率响应分析仪等设备。

其次是电极的选择和制备。

电极材料的选择应根据所研究体系的特性来确定，常见的电极材料包括铂、玻碳等。

制备电极时，需要将电极材料打磨至光滑，再进行活化处理。

最后是测量条件的确定。

包括施加的电压信号的幅值和频率，扫描电位的范围等。

最后，电化学阻抗谱在电化学研究中有着广泛的应用。

首先，它可以用来研究电极表面的活性位点分布和反应动力学。

通过测量不同频率下的阻抗谱，可以确定不同反应过程的速率常数和电荷转移步骤。

其次，电化学阻抗谱可以用于表征电化学界面的动态行为。

例如，可以通过观察阻抗谱中的截距和斜率来判断反应过程中的电化学反应控制机理。

另外，电化学阻抗谱还可以用于测定电极表面的电位分布和电解质溶液中的离子浓度分布等。

总之，电化学阻抗谱是一种非常有用的电化学研究方法，它可以用来研究电化学界面的反应动力学和界面行为。

通过对阻抗谱的测量和分析，可以得到与反应相关的重要参数。

在实验中，需要选择适当的设备和电极，并确定合适的测量条件。

电化学阻抗谱在材料科学、环境科学等领域中有着广泛的应用前景。

初中物理电学串联和并联电路的等效电阻在物理学中，电学是一个很重要的研究领域。

在电学中，串联和并联电路是两个基本的电路连接方式，我们经常使用它们来构建各种电子设备。

而在电路中，等效电阻是一个重要的概念，它表示了电路在电阻方面的性质。

本文将主要介绍初中物理中电学串联和并联电路的等效电阻的概念和计算方法。

1. 串联电路的等效电阻在串联电路中，电阻按照一定的顺序连接在一起，电流在每个电阻中是依次流过的。

串联电路的等效电阻是指将这些电阻替换为一个等效电阻，使得串联电路中的总电流等于等效电阻分压下的电流。

计算串联电路的等效电阻的方法为将各个电阻相加。

例如，假设我们有两个电阻R1和R2串联连接在一个电源上，我们需要计算它们的等效电阻。

根据串联电路的特点，电流依次通过R1和R2，所以它们的电流相等。

根据欧姆定律，电压V1和V2等于它们对应电阻的电流乘以电阻值，即V1=I*R1，V2=I*R2。

因此，总电压等于各个电阻电压的和，即V = V1 + V2 = I*R1 + I*R2 = I*(R1 + R2)。

根据欧姆定律，总电压等于总电流乘以等效电阻，即V = I*Req。

所以，我们可以得到等效电阻的计算公式为Req = R1 + R2。

在更复杂的串联电路中，我们可以按照这个方法依次计算各个电阻的电压并相加，最后求得等效电阻。

2. 并联电路的等效电阻在并联电路中，电阻的两端被平行地连接在一起，电流在各个电阻中是分流的。

与串联电路不同，电阻的电流并不相等，总电流等于各个分支电流的和。

并联电路的等效电阻是指将这些电阻替换为一个等效电阻，使得并联电路中的总电流等于等效电阻并流下的电流。

计算并联电路的等效电阻的方法为将各个电阻的倒数相加再取倒数。

例如，假设我们有两个电阻R1和R2并联连接在一个电源上，我们需要计算它们的等效电阻。

根据并联电路的特点，总电压相等于各个电阻的电压，即V = V1 = V2。

而根据欧姆定律，电流I等于总电压除以电阻，即I = V/R，所以I1 = V/R1，I2 = V/R2。

电阻的并联串联及等效变换 - 电工基础其中称为这些串联电阻的等效电阻。

它与这些串联电阻所起的作用是一样的。

可以看出，n个串联电阻吸取的总功率等于它们的等效电阻吸取的功率。

必大于任一个串联中的电阻。

电阻串联时，各电阻上的电压为此式称为电压安排公式，它表明各个串联电阻的电压与其电阻值成正比；或者说总电压按各个串联电阻的电阻值进行安排。

电阻串联电路应用广泛，常用来降压，调整电流、分压等。

二、电阻的并联电阻的并联：电路中两个或更多个电阻都连接在两个公共的结点间。

称为电阻的并联，电阻并联时，各并联电阻两端承受同一电压。

如图所示中n个电阻并联时，依据KVL有其中称为这些并联电阻的等效电导。

所以我们可以用一个电导等于的电阻来代替这n个并联电阻，如图（b）所示。

可以看出，n个并联电阻的总功率等于它们的等效电阻吸取的功率。

由于等效电阻，而各个并联电阻，故有这样有，即等效电阻总小于任意一个并联中的电阻。

电阻并联时，各电阻中的电流为上式称为电流的安排公式，它表明各个并联电阻中的电流与它们各自的电导成正比；或者说总电流按各个并联电阻的电导进行安排。

例如对于两个电阻的并联如图所示，依据上述结论，有即等效电阻为两分电流的安排关系为我们在此特殊提出两电阻的分流关系是由于我们在后续电路分析中经常要用到这个关系式。

三、电阻的混联既有电阻串联又有电阻并联的电路叫电阻混联电路。

这种电路在实际工作中应用广泛、形式多种多样。

如图所示。

分析混联电路，首先要弄清电路中各电阻的连接关系。

通过同一电流的各电阻肯定是串联关系；连接在共同两点之间的各支路肯定是并联关系；通常连接导线的电阻可忽视不计，因此电位相等的连接线可收缩为一点，反之，一个接点可拉长为一根导线。

依据以上三点，可将不易看清串并联关系的电路，改画整理成便于识别的电路，但连接关系不能变更。

如图（b），可将b点缩为一点即可看出，因而可得等效电阻，然后运用串、并联电路特点和欧姆定律进行分析和计算。

电阻电路中的电阻串并联组合与等效分析在电路中，电阻是一种常见的电子元件，它用来限制电流的流动。

电阻串联和并联是常见的电阻组合方式，在电路设计和分析中起着重要的作用。

本文将着重讨论电阻串并联的组合方式及其等效分析。

一、电阻串联电阻串联是指将多个电阻依次连接在电路中，电流依次通过它们。

在电阻串联中，电流在相邻电阻之间是相等的，而总电阻等于各个电阻之和。

例如，假设有三个电阻 R1、R2 和 R3，它们依次串联在一条电路中。

根据串联电阻的定义，总电阻 Rtotal 可以用以下公式表示：Rtotal = R1 + R2 + R3电流在每个电阻上的分布则可以用以下关系表示：I1 = I2 = I3其中，I1、I2 和 I3 分别代表电流在 R1、R2 和 R3 上的大小。

二、电阻并联电阻并联是指将多个电阻同时连接在电路中，电流在它们之间分流。

在电阻并联中，电压在相邻电阻之间是相等的，而总电阻的倒数等于各个电阻倒数之和的倒数。

例如，假设有三个电阻 R1、R2 和 R3，并联在一条电路中。

根据并联电阻的定义，总电阻 Rtotal 可以用以下公式表示：1 / Rtotal = 1 / R1 + 1 / R2 + 1 / R3电压在每个电阻上的分布则可以用以下关系表示：V1 = V2 = V3其中，V1、V2 和 V3 分别代表电压在 R1、R2 和 R3 上的大小。

三、电阻串并联组合在实际的电路中，常常需要将电阻通过串联和并联的方式组合起来。

通过合理的串并联组合，可以实现对电路的电阻值进行调整，以满足特定的电路要求。

例如，假设有两个电阻 R1 和 R2，我们可以通过串并联组合来实现不同的等效电阻。

1. 串联组合将 R1 和 R2 串联在一起，等效电阻为：Rtotal = R1 + R22. 并联组合将 R1 和 R2 并联在一起，等效电阻为：1 / Rtotal = 1 / R1 + 1 / R2通过对电阻的串并联组合，可以实现不同的等效电阻，从而满足电路设计和分析的要求。

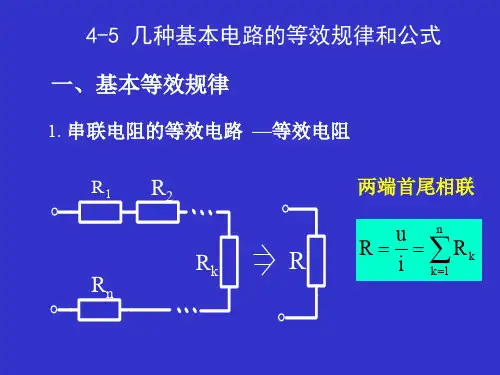
电阻串并联等效变换电阻串并联等效变换是电路中常用的一种技巧，可以将复杂的电路简化为一个等效电路，方便计算和分析。

本文将介绍电阻串并联等效变换的基本原理、方法和应用。

一、电阻串并联等效变换的基本原理电阻串并联等效变换的基本原理是根据欧姆定律和基尔霍夫定律，将一组电阻串联或并联起来，转化为一个等效电阻。

串联电阻的等效电阻为各电阻之和，即R=R1+R2+R3+...+Rn；并联电阻的等效电阻为各电阻的倒数之和的倒数，即1/R=1/R1+1/R2+1/R3+...+1/Rn。

二、电阻串并联等效变换的方法1. 串联电阻的等效变换方法将一组电阻串联起来，可以将其等效为一个等效电阻。

具体方法如下：（1）将电路中的电阻串联起来，组成一个电阻串。

（2）计算电阻串中各电阻之和，得到等效电阻R。

（3）将等效电阻R代替原电路中的电阻串。

2. 并联电阻的等效变换方法将一组电阻并联起来，可以将其等效为一个等效电阻。

具体方法如下：（1）将电路中的电阻并联起来，组成一个电阻并联。

（2）计算电阻并联中各电阻的倒数之和的倒数，得到等效电阻R。

（3）将等效电阻R代替原电路中的电阻并联。

三、电阻串并联等效变换的应用电阻串并联等效变换在电路分析和设计中具有广泛的应用，可以用于简化电路、计算电路参数和优化电路性能等方面。

1. 电路简化通过电阻串并联等效变换，可以将复杂的电路简化为一个等效电路。

这样可以减少计算量，提高计算精度，方便电路分析和设计。

2. 电路参数计算通过电阻串并联等效变换，可以方便地计算电路中的电阻、电流、电压等参数。

这对于电路分析和设计非常有用。

3. 电路性能优化通过电阻串并联等效变换，可以优化电路的性能，比如降低电路的功耗、提高电路的稳定性、改善电路的响应速度等。

总之，电阻串并联等效变换是电路分析和设计中常用的一种技巧，掌握了这种技巧，可以方便地简化电路、计算电路参数和优化电路性能，提高电路分析和设计的效率和精度。

电化学阻抗谱的原理电化学阻抗谱（Electrochemical Impedance Spectroscopy，EIS）是一种广泛应用于电化学研究和工程中的分析技术。

它通过测量电化学系统的频率响应来研究电化学过程的动力学和界面特性。

电化学阻抗谱是一种非破坏性的测试技术，可提供大量有用的信息，如电解质、电极材料、反应机制和电化学界面的性质。

电化学阻抗谱的原理基于电化学系统对交流（AC）电压的响应。

在电化学阻抗谱测试中，一个小幅度的交流电压信号被施加到电化学系统中，然后测量系统的响应。

这个信号可以是定频率的正弦信号或扫频信号，覆盖一定的频率范围。

根据欧姆定律，电化学系统的复电导G可以表示为系统的复阻抗Z的倒数，即G=1/Z。

复电导G的实部是电导（conductance），表示电流经过系统时的直流响应。

虚部是电容（capacitance）或电感（inductance），表示电流相位随频率变化的情况。

通过测量电化学系统对不同频率的电压的响应，可以得到电化学阻抗谱。

这个谱图是电化学系统在复平面上的表示，其中横轴表示实部，纵轴表示虚部。

谱图中的每个点表示系统在特定频率下的阻抗。

阻抗谱是电化学界面的“指纹”，可以提供关于界面化学反应、电荷转移和质量传递的信息。

在电化学阻抗谱中，存在多个特征频率点，对应着不同的电化学过程。

这些过程包括电解质的扩散、电荷传输、电极界面的反应等。

通过分析不同频率下的阻抗，可以确定系统的动力学特性。

例如，低频区域反映了控制电化学过程的质量传递和电极反应速率，高频区域反映了电容和电极界面的电荷转移。

电化学阻抗谱的分析方法主要有等效电路模型和特征谱分析。

等效电路模型是通过电路元件来模拟电化学界面的响应。

常见的等效电路模型包括Randles电路、Warburg元件和电解质电容等。

通过拟合实测的阻抗谱和选取最佳的等效电路模型参数，可以得到电化学过程的动力学参数和界面特性。

特征谱分析是通过直接分析阻抗谱来提取有用的信息。

电路中的串联和并联的规律电路是由一系列电子元件和导体连接而成的系统，串联和并联是电路中两种基本的连接方式。

串联和并联的规律是电路分析和设计的基础，对于理解电路中的电流和电压分布、电阻和电容等特性至关重要。

一、串联电路的规律串联电路是将多个电子元件依次连接在同一电路路径上的连接方式。

在串联电路中，电流只有一条路径可以流过，因此电流在各个电子元件中保持不变。

1. 电流规律：在串联电路中，电流大小相同。

根据基尔霍夫电流定律，电流的总和等于电流经过的各个元件中的电流之和。

2. 电压规律：在串联电路中，电压分配按照元件的电阻大小进行。

根据基尔霍夫电压定律，电压的总和等于电压经过的各个元件中的电压之和。

3. 等效电阻：串联电路的等效电阻等于各个电子元件的电阻之和。

由于电流只有一条路径可以流过，所以串联电路的总电阻等于各个电子元件的电阻之和。

二、并联电路的规律并联电路是将多个电子元件同时连接在两个节点上的连接方式。

在并联电路中，电流会分流经过各个电子元件，因此电流在各个元件中之和等于总电流。

1. 电流规律：在并联电路中，电流分配按照电阻的倒数进行。

根据基尔霍夫电流定律，电流的总和等于电流经过的各个元件中的电流之和。

2. 电压规律：在并联电路中，电压大小相同。

由于并联电路中各个电子元件是同时连接在两个节点上的，所以它们之间的电压是相等的。

3. 等效电阻：并联电路的等效电阻是各个电子元件电阻的倒数之和的倒数。

由于电流会分流，所以并联电路的总电阻小于各个电子元件的最小电阻。

总结：串联电路中，电流大小相同，电压按照电阻分配。

并联电路中，电流按照电阻的倒数分配，电压大小相同。

串联电路的等效电阻为各个电子元件电阻之和，而并联电路的等效电阻为各个电子元件电阻的倒数之和的倒数。

通过串联和并联的规律，我们能够计算电路中的电流、电压和电阻等重要参数，为电路的分析和设计提供了基础。

同时，这些规律也为我们理解电路中的能量分配、功率计算等提供了帮助。

电路中的串并联与等效电阻电路的串联、并联是电路中最基础的连接方式，通过串并联可以实现电路中电阻、电流和电压的灵活组合。

在电路中，串联是指将多个电阻、电容或电感连接在一条路径上，而并联则是将多个电阻、电容或电感连接在一个节点上。

本文将详细介绍电路中的串并联以及等效电阻的原理与计算方法。

一、串联电路的特点与计算方法串联电路是指将多个电阻依次连接在一起，电流在各个电阻之间依次流动。

串联电路中，电流相同，电压分配根据电阻值的大小进行。

计算串联电路的总电阻时，只需将各个电阻值相加即可。

例如，有三个电阻分别为R1、R2和R3，它们依次串联在一起。

则串联电路的总电阻Rt可由以下公式计算得出：Rt = R1 + R2 + R3当电路中的电阻数量较多时，可以通过计算器或电路模拟软件来快速计算总电阻。

二、并联电路的特点与计算方法并联电路是指多个电阻、电容或电感连接在一个节点上，电压在各个元件之间相同，电流分配根据元件的电阻值进行。

在计算并联电路的总电阻时，需要应用并联电阻的公式。

例如，有三个电阻分别为R1、R2和R3，并联在一个节点上。

则并联电路的总电阻Rt可由以下公式计算得出：1/Rt = 1/R1 + 1/R2 + 1/R3类似地，当并联电路中的元件数量较多时，可以借助计算器或电路模拟软件来快速计算总电阻。

三、串并联电路的等效电阻在电路中，多个电阻、电容或电感可以通过串联或并联的方式组合在一起，形成串并联电路。

对于串并联电路，可以通过等效电阻来简化分析与计算。

对于串联电路，它的等效电阻等于各个电阻值的总和，如前述所示。

对于并联电路，它的等效电阻可以应用并联电阻公式进行计算。

当电路中既存在串联又存在并联时，可以借助串并联电路的等效电阻进行分析。

可将各个串并联电路的等效电阻依次计算，最终得到整个电路的等效电阻。

四、电路中的等效电阻应用等效电阻在电路设计与分析中有着重要的应用。

通过等效电阻，可以将复杂的电路简化为一个电阻，从而简化计算与分析的复杂度。

电路中的串联与并联电流的分布与电阻的等效电路中的串联与并联是电路中常见的两种连接方式，它们对电流的分布和电阻的等效有着不同的影响。

本文将深入探讨串联与并联对电路的影响。

1. 串联电路的电流分布与等效电阻串联电路是将电子元件依次连接在同一路径上的电路。

在串联电路中，电流流过每个电子元件时都保持不变。

这是因为串联电路中的电流只有一个路径可走，所以电流分布相对简单。

例如，假设我们有三个电子元件A、B和C，它们依次连接在一个串联电路中。

电源提供的总电压将分别作用于A、B和C上，且电流在整个串联电路中保持恒定。

根据欧姆定律，我们知道电流等于电压除以电阻，所以我们可以得到如下公式：I = V / R_total其中，I代表电流，V代表总电压，R_total代表整个串联电路的总电阻。

由于串联电路中的电阻依次相连，所以整个电路的等效电阻为各电阻之和。

即：R_total = R1 + R2 + R3 + ...因此，串联电路中，每个电子元件的电阻对于整个电路的等效电阻起到了叠加的作用。

2. 并联电路的电流分布与等效电阻并联电路是将电子元件连接在各自独立的路径上的电路。

在并联电路中，电流在不同路径上分流，导致电流分布较为复杂。

假设我们有三个电子元件A、B和C，并联连接在一个电路中。

在并联电路中，电源提供的总电流将分别流过A、B和C。

根据欧姆定律，我们可以得到如下公式：I_total = I1 + I2 + I3 + ...其中，I_total代表总电流，I1、I2和I3分别代表经过元件A、B和C的电流。

并联电路中的等效电阻的计算有所不同。

根据欧姆定律，我们可以得到如下公式：1 / R_total = 1 / R1 + 1 / R2 + 1 / R3 + ...即，整个并联电路的等效电阻等于各电阻的倒数之和的倒数。

3. 串联与并联电路的比较串联与并联电路在电流的分布和等效电阻方面有着明显的区别。

首先，传联电路中的电流在整个电路中保持恒定，而并联电路中的电流在不同路径上分流。

电化学阻抗谱的串联电阻
电化学阻抗谱（EIS）是一种用来研究电化学系统的技术，可以
通过测量电极上的小信号交流电压和电流来获得电化学系统的信息。

而串联电阻是EIS中的一个重要参数，它是指在电化学系统中，电
解质溶液、电极表面以及电解质与电极之间的界面等部分所构成的
电阻的总和。

在电化学阻抗谱中，串联电阻通常用来描述电解质溶液的电阻、电极表面的电阻以及电解质与电极之间的界面电阻。

这些电阻会影
响电化学反应的进行，因此了解串联电阻对于理解电化学系统的动
力学行为非常重要。

串联电阻的大小可以反映出电化学系统中电子转移和离子传输
的难易程度。

较大的串联电阻通常意味着电子或离子的传输受到了
一定程度的限制，可能是由于电解质浓度低、电极表面有机物的吸附、电极表面的氧化还原反应等原因所致。

此外，串联电阻还可以提供有关电化学系统中界面的信息，比
如电解质与电极之间的反应速率、电解质的扩散系数等。

通过对串
联电阻的测量和分析，可以更深入地了解电化学系统的动力学特性，
为电化学过程的研究和应用提供重要参考。

总的来说，串联电阻在电化学阻抗谱中扮演着重要的角色，它反映了电化学系统中电子和离子传输的特性，对于深入理解电化学过程和优化电化学系统具有重要意义。