2018年中考数学总复习第三章函数第二节一次函数的图象与性质随堂演练

（东营专版）2019年中考数学复习第三章函数第二节一次函数的图象与性质要题随堂演练编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（东营专版）2019年中考数学复习第三章函数第二节一次函数的图象与性质要题随堂演练）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（东营专版）2019年中考数学复习第三章函数第二节一次函数的图象与性质要题随堂演练的全部内容。

一次函数的图象与性质要题随堂演练1．（2018·湘潭中考)若b＞0,则一次函数y＝－x＋b的图象大致是( ）2．（2017·德州中考）下列函数中，对于任意实数x1，x2，当x1＞x2时，满足y1＜y2的是( ）A．y＝－3x＋2 B．y＝2x＋1C．y＝2x2＋1 D．y＝－错误!3．（2018·枣庄中考）如图，直线l是一次函数y＝kx＋b的图象,如果点A（3，m）在直线l 上，则m的值为（）A．－5 B。

错误! C.错误! D．74．(2017·莱芜中考）对于实数a，b，定义符号min{a，b｝，其意义为:当a≥b时,min{a，b｝＝b；当a＜b时，min{a，b｝＝a.例如：min＝{2,－1}＝－1，若关于x的函数y＝min｛2x－1,－x＋3}，则该函数的最大值为( ）A.错误!B．1 C。

错误! D.错误!5．(2018·天津中考）将直线y＝x向上平移2个单位长度，平移后直线的解析式为______________。

6．(2018·十堰中考）如图，直线y＝kx＋b交x轴于点A，交y轴于点B,则不等式x(kx＋b）＜0的解集为________________．7．(2017·眉山中考）设点（－1,m）和点(错误!,n）是直线y＝(k2－1)x＋b(0＜k＜1）上的两个点，则m,n的大小关系为__________．8．(2018·广饶模拟)如图，一次函数的图象与x轴、y轴分别相交于点A，B，将△AOB沿直线AB翻折得△ACB。

第三章函数好题随堂演练1．(2018·天津)将直线y＝x向上平移2个单位长度，平移后直线的解析式为______________．2．如图，正比例函数y1＝k1x和一次函数y2＝k2x＋b的图象相交于点A(2，1)，当x＜2时，y1______y2.(填“＞”或“＜”)3．(2018·郴州)如图，在平面直角坐标系中，菱形OABC的一个顶点在原点处，且∠AOC＝60°，A点的坐标是(0，4)，则直线AC的表达式是____________．4．(2018·沈阳)在平面直角坐标系中，一次函数y＝kx＋b的图象如图所示，观察图象可得( )A．k＞0，b＞0 B．k＞0，b＜0C．k＜0，b＞0 D．k＜0，b＜05．(2018·常德)若一次函数y＝(k－2)x＋1的函数值y随x的增大而增大，则( )A．k＜2 B．k>2C．k>0 D．k＜06．若点A(m，n)在一次函数y＝3x＋b的图象上，且3m－n＞2，则b的取值范围为( )A．b＞2 B．b＞－2C．b＜2 D．b＜－27．(2018·昆明盘龙区模拟)如图，甲、乙两人以相同路线前往离学校12千米的地方参加植树活动．分析甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分钟)变化的函数图象，解决下列问题：(1)求出甲、乙两人所行驶的路程S 甲、S 乙与t 之间的关系式；(2)甲行驶10分钟后，甲、乙两人相距多少千米？参考答案1．y ＝x ＋2 2.＜3．y ＝－33x ＋4【解析】 如解图，过点C 作CD⊥OA 于D.∵四边形OABC 是菱形，∴OA＝OC ，∵∠AOC＝60°，∴△AOC 是等边三角形，∴OD＝AD ＝2，CD ＝3AD ＝23，∴点C 的坐标为(23，2)，设直线AC 的函数表达式为y ＝kx ＋b ，将点A(0，4)，点C(23，2)代入得⎩⎨⎧b ＝4，23k ＋b ＝2，解得⎩⎪⎨⎪⎧b ＝4，k ＝－33，故直线AC 的函数表达式为y ＝－33x ＋4.4．C 5.B 6.D7．解：(1)由图象设甲的解析式为：S 甲＝kt ，代入点(24，12)，解得：k ＝0.5；所以甲的解析式为：S 甲＝0.5t ；同理可设乙的解析式为：S 乙＝mt ＋b ，代入点(6，0)，(18，12)，可得：⎩⎪⎨⎪⎧6m ＋b ＝0，18m ＋b ＝12， 解得：⎩⎪⎨⎪⎧m ＝1，b ＝－6，所以乙的解析式为：S 乙＝t －6；(2)当t ＝10时，S 甲＝0.5×10＝5(千米)，S 乙＝10－6＝4(千米)， 5－4＝1(千米)，答：甲行驶10分钟后，甲、乙两人相距1千米．。

第二节一次函数好题随堂演练1．(2018·湘潭)若b＞0，则一次函数y＝－x＋b的图象大致是( )2．(2018·贵阳)一次函数y＝kx－1的图象经过点P，且y的值随x值的增大而增大，则点P的坐标可以为( )A．(－5，3) B．(1，－3)C．(2，2) D．(5，－1)3．(2017·陕西)若一个正比例函数的图象经过A(3，－6)，B(m，－4)两点，则m的值为( )A．2 B．8C．－2 D．－84．(2018·荆州)已知：将直线y＝x－1向上平移2个单位长度后得到直线y＝kx＋b，则下列关于直线y ＝kx＋b的说法正确的是( )A．经过第一、二、四象限B．与x轴交于(1，0)C．与y轴交于(0，1)D．y随x的增大而减小5．如图，一直线与两坐标轴的正半轴分别交于A，B两点，P是线段AB上任意一点(不包括端点)，过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10，则该直线的函数表达式是( )第5题图A．y＝x＋5 B．y＝x＋10C．y＝－x＋10 D．y＝－x＋56．已知正比例函数y＝kx的图象经过点A(－1，2)，则正比例函数的表达式为______________．7．(2018·眉山)已知点A(x1，y1)、B(x2，y2)在直线y＝kx＋b上，且直线经过第一、二、四象限，当x1＜x 2时，y 1与y 2的大小关系为______________．8．(2018·淮安)如图， 在平面直角坐标系中， 一次函数 y ＝kx ＋b 的图象经过点A ( －2，6 ) ，且与 x 轴相交于点 B ，与正比例函数 y ＝3x 的图象相交于点 C ，点 C 的横坐标为1.(1)求 k ，b 的值；(2)若点 D 在 y 轴负半轴上，且满足S △COD ＝13S △BOC ，求点 D 的坐标．第8题图9．(2018·宿迁)某种型号汽车油箱容量为40 L ，每行驶100 km 耗油10 L ，设一辆加满油的该型号汽车行驶路程为x(km )，行驶过程中油箱内剩余油量为y(L )．(1)求y 与x 之间的函数表达式；(2)为了有效延长汽车使用寿命，厂家建议每次加油时油箱剩余油量不低于油箱容量的14，按此建议，求该辆汽车最多行驶的路程．参考答案1．C 2.C 3.A 4.C 5.D6．y ＝－2x 7.y 1>y 28．解：(1)点C 的横坐标为1，且在y ＝3x 的图象上， ∴C 点坐标为(1，3)；将A ，C 点的坐标代入y ＝kx ＋b ，得⎩⎪⎨⎪⎧6＝－2k ＋b 3＝k ＋b， 解得k ＝—1，b ＝4.(2)直线AB 的解析式为y ＝－x ＋4，可求得B 点坐标为(4，0)，即OB ＝4，则S △BOC ＝12×4×3＝6. 所以S △COD ＝13×6＝2.由△OCD 的高为C 点的横坐标1，得12OD×1＝2，解得OD ＝4.故D 点坐标为(0，－4)． 9．解：(1)y ＝40－x 10； (2)由题意得：40－x 10≥40×14， 解得：x≤300，答：该辆汽车最多行驶的路程为300 km .。

中考专题总复习3---一次函数、反比例函数的图像、性质与应用★重点★正、反比例函数，一次函数的图象和性质。

一、平面直角坐标系1．各象限内点的坐标的特点2．坐标轴上点的坐标的特点3．关于坐标轴、原点对称的点的坐标的特点4．坐标平面内点与有序实数对的对应关系二、函数1 函数中的三个概念：常量，自变量，因变量。

2．表示方法：⑴解析法;⑵列表法;⑶图象法。

3．确定自变量取值范围的原则：⑴使代数式有意义;⑵使实际问题有意义。

4．画函数图象：⑴列表;⑵描点;⑶连线。

三、几种特殊函数 （定义→图象→性质） 1． 正比例函数⑴定义：y=kx(k ≠0) 或y/x=k 。

⑵图象：直线（过原点） ⑶性质：①k>0，…②k<0，… 2． 一次函数⑴定义：y=kx+b(k ≠0)⑵图象：直线过点（0,b ）—与y 轴的交点和（-b/k,0）—与x 轴的交点。

⑶性质：①k>0,…②k<0,… ⑷图象的四种情况： 4.反比例函数⑴定义：三种形式：1-==kx xky 或xy=k(k ≠0)。

⑵图象：双曲线（两支）—用描点法画出。

⑶性质：①k>0时，图象位于…，y 随x …;②k<0时，图象位于…，y 随x …;③两支曲线无限接近于坐标轴但永远不能到达坐标轴。

四、重要解题方法1． 用待定系数法求解析式（列方程[组]求解）2．利用图象一次（正比例）函数、反比例函数、 一．填空题 1．（2010年上海）一辆汽车在行驶过程中，路程 y （千米）与时间 x （小时）之间的函数关系如图3所示 当时 0≤x ≤1，y 关于x 的函数解析式为 y = 60 x ，那么当 1≤x ≤2时，y 关于x 的函数解析式为_____________.【答案】y=100x －40图32．（2010安徽蚌埠二中）已知点（1，3）在函数)0(>=x xky 的图像上。

正方形ABCD 的边BC 在x 轴上，点E 是对角线BD 的中点，函数)0(>=x xky 的图像又经过A 、E 两点，则点E 的横坐标为__________。

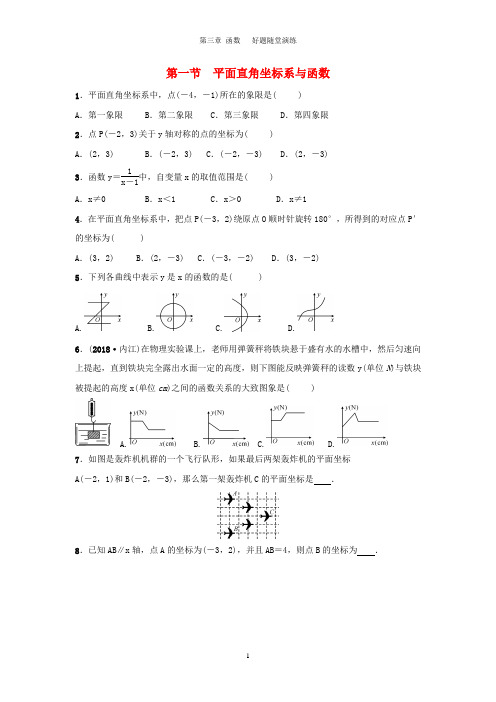
第一节平面直角坐标系与函数1．平面直角坐标系中，点(－4，－1)所在的象限是( ) A．第一象限 B．第二象限C．第三象限 D．第四象限2．点P(－2，3)关于y轴对称的点的坐标为( )A．(2，3) B．(－2，3)C．(－2，－3) D．(2，－3)3．函数y＝1x－1中，自变量x的取值范围是( )A．x≠0 B．x＜1 C．x＞0 D．x≠14．在平面直角坐标系中，把点P(－3，2)绕原点O顺时针旋转180°，所得到的对应点P′的坐标为( )A．(3，2) B．(2，－3)C．(－3，－2) D．(3，－2)5．下列各曲线中表示y是x的函数的是( )A. B. C. D.6．(2018²内江)在物理实验课上，老师用弹簧秤将铁块悬于盛有水的水槽中，然后匀速向上提起，直到铁块完全露出水面一定的高度，则下图能反映弹簧秤的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是( )A. B. C. D.7．如图是轰炸机机群的一个飞行队形，如果最后两架轰炸机的平面坐标A(－2，1)和B(－2，－3)，那么第一架轰炸机C的平面坐标是．8．已知AB∥x轴，点A的坐标为(－3，2)，并且AB＝4，则点B的坐标为．第二节 一次函数及其应用1．若一个正比例函数的图象经过A(3，－6)，B(m ，－4)两点，则m 的值为( )A ．2B ．8C ．－2D ．－82. 若点A(m ，n)在一次函数y ＝3x ＋b 的图象上，且3m －n ＞2，则b 的取值范围为( )A. b ＞2B. b ＞－2C. b ＜2D. b ＜－23．如图，一直线与两坐标轴的正半轴分别交于A ，B 两点，P 是线段AB 上任意一点(不包括端点)，过P 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10，则该直线的函数解析式是( )A ．y ＝x ＋5B ．y ＝x ＋10C ．y ＝－x ＋5D ．y ＝－x ＋104．如图，正比例函数y 1＝k 1x 和一次函数y 2＝k 2x ＋b 的图象相交于点A(2，1)，当x ＜2时，y 1y 2.(填“＞”或“＜”)5．如图，已知直线y 1＝－12x ＋1与x 轴交于点A ，与直线y 2＝－32x 交于点B. (1)求△AOB 的面积；(2)求y 1＞y 2时x 的取值范围．第三节 反比例函数1．已知反比例函数的解析式为y ＝|a|－2x，则a 的取值范围是( ) A ．a≠2 B．a≠－2 C ．a≠±2 D．a ＝±22．一司机驾驶汽车从甲地去乙地，他以平均80 km /h 的速度用了4 h 到达乙地，当他按原路匀速返回时，汽车的速度v km /h 与时间t h 的函数关系式是( )A ．v ＝320tB ．v ＝320tC ．v ＝20tD ．v ＝20t3．若ab<0，则正比例函数y ＝ax 与反比例函数y ＝b x在同一坐标系中的大致图象可能是( )A. B. C. D.4．如图，O 为坐标原点，菱形OABC 的顶点A 的坐标为(－3，4)，顶点C 在x 轴的负半轴上，函数y ＝k x(x ＜0)的图象经过顶点B ，则k 的值为( ) A ．－12 B ．－27 C ．－32 D ．－36第4题图 第5题图5．如图，它是反比例函数y ＝m －5x图象的一支，根据图象可知常数m 的取值范围是． 6．已知A(－4，y 1)、B(－1，y 2)是反比例函数y ＝－4x图象上的两个点，则y 1与y 2的大小关系为．7．如图，矩形OABC 的顶点A ，C 分别在x 轴、y 轴上，顶点B 在第一象限，AB ＝1，将线段OA 绕点O 逆时针方向旋转60°得到线段OP ，反比例函数y ＝k x(k≠0)的图象经过P ，B 两点，则k 的值为．8．如图，一次函数y 1＝kx ＋b 与反比例函数y 2＝m x(mk≠0)图象交于A(－4，2)，B(2，n)两点．(1)求一次函数和反比例函数的表达式；(2)求△ABO 的面积；(3)当x 取非零的实数时，试比较一次函数值与反比例函数值的大小．第四节 二次函数的图象与性质1．下列函数解析式中，一定为二次函数的是( )A ．y ＝3x －1B ．y ＝ax 2＋bx ＋cC ．s ＝2t 2－2t ＋1D ．y ＝x 2＋1x2．抛物线y ＝x 2＋2x ＋3的对称轴是( )A ．直线x ＝1B ．直线x ＝－1C ．直线x ＝－2D ．直线x ＝23．已知a≠0，函数y ＝a x 与y ＝－ax 2＋a 在同一直角坐标系中的大致图象可能是( ) A . B . C. D.4．写出一个y 关于x 的二次函数的解析式，且它的图象的顶点在y 轴上：．5．如图，抛物线y ＝ax 2与直线y ＝bx ＋c 的两个交点坐标分别为A(－2，4)，B(1，1)，则方程ax 2＝bx ＋c 的解是．6．若函数y ＝(a －1)x 2－4x ＋2a 的图象与x 轴有且只有一个交点，则a 的值为．7．已知：二次函数y ＝ax 2＋bx ＋c 图象上部分点的横坐标x 与纵坐标y 的对应值如表格所示，那么它的图象与y 轴的另一个交点坐标是．8．如图，二次函数y1的图象与x轴交于A，O两点，其中点O为坐标原点，顶点B的坐标为(－1，－1)．将其向右、向上平移得到抛物线y2，点B的对应点落在x轴上的点B′处，点A的对应点落在y轴上的点A′处．y1与y2相交于点C.(1)写出点A，B′的坐标，并求抛物线y2的函数解析式；(2)直接写出y2＞y1＞0的x的取值范围．第五节二次函数的简单综合1．如图，从地面竖直向上抛出一个小球，小球的高度h(单位：m)与小球运动时间t(单位：s)之间的关系式h＝30t－5t2，那么小球从抛出至回落到地面所需的时间是s.2．某农场拟建三间长方形种牛饲养室，饲养室的一面靠墙(墙长50 m)，中间用两道墙隔开(如图)．已知计划中的建筑材料可建墙的总长度为48 m，则这三间长方形种牛饲养室的总占地面积的最大值为m2.3.如图，已知抛物线y＝－x2＋mx＋3与x轴交于点A，B，与y轴交于点C，点B的坐标为(3，0)．(1)求m的值及抛物线的顶点坐标；(2)点P是抛物线对称轴l上的一个动点，当PA＋PC的值最小时，求点P的坐标．4．某大学生利用暑假40天社会实践参与了一家网店经营，了解到一种新型商品成本为20元/件，第x 天销售量为p 件，销售单价为q 元，经跟踪调查发现，这40天中p 与x 的关系保持不变．前20天(包含第20天)，q 与x 的关系满足关系式q ＝30＋ax ；从第21天到第40天中，q 是基础价与浮动价的和，其中基础价保持不变，浮动价与x 成反比．且得到了表中的数据．①请直接写出a 的值为；②从第21天到第40天中，求q 与x 满足的关系式；(3)若该网店第x 天获得的利润y 元，并且已知这40天里前20天中y 与x 的函数关系式为y ＝－12x 2＋15x ＋500. ①请直接写出这40天中p 与x 的关系式为：；②求这40天里该网店第几天获得的利润最大？参考答案第一节 平面直角坐标系与函数1．C 2.A 3.D 4.D 5.D 6.C 7.(2，－1)8．(1，2)或(－7，2)第二节 一次函数及其应用1．A 2.D 3.C 4.＜5．解：(1)把y ＝0代入y 1＝－12x ＋1，得－12x ＋1＝0， 解得x ＝2，∴点A 的坐标为(2，0)，∴OA＝2.∵直线y 1＝－12x ＋1与y 2＝－32x 交于点B ， ∴⎩⎪⎨⎪⎧y ＝－12x ＋1y ＝－32x ，解得⎩⎪⎨⎪⎧x ＝－1y ＝32， ∴点B 的坐标为(－1，32)． ∴S △AOB ＝12³OA³32＝12³2³32＝32. (2)由题图知，在点B 右侧，直线y 1＝－12x ＋1在直线y 2＝－32x 的上方，即 y 1＞y 2，∴当y 1＞y 2时，x 的取值范围是x ＞－1.第三节 反比例函数1．C 2.B 3.B 4.C 5.m ＞5 6.y 1＜y 2 7.4338．解：(1)∵一次函数y ＝kx ＋b 与反比例函数y ＝m x(mk≠0)图象交于 A(－4，2)，B(2，n)两点．∴n＝－82＝－4， 将A(－4，2)，B(2，－4)代入一次函数解析式：∴⎩⎪⎨⎪⎧2＝－4k ＋b －4＝2k ＋b ，解得⎩⎪⎨⎪⎧k ＝－1b ＝－2， 故一次函数的解析式为y ＝－x －2.将A(－4，2)代入反比例函数解析式得2＝m －4，解得m ＝－8， 故反比例函数函数解析式为y ＝－8x； (2)在y ＝－x －2中，令y ＝0，则x ＝－2，∴OC＝2，∴S △AOB ＝12³2³2＋12³2³4＝6; (3)根据两函数的图象可知：当x ＜－4时，y 1＞y 2；x ＝－4时，y 1＝y 2；当－4＜x ＜0时，y 1＜y 2;当0＜x ＜2时，y 1＞y 2；当x ＝2时，y 1＝y 2；x ＞2时，y 1＜y 2.第四节 二次函数的图象与性质1．C 2.B 3.D 4.y ＝x 2＋1(答案不唯一)5．－2，1 6.－1，1，2 7.(3，0)8．解：(1)点O 的坐标为(0，0)，点B 的坐标为(－1，－1)， 设抛物线y 1的函数解析式为y ＝a(x ＋1)2－1，将点(0，0)代入得a ＝1，∴抛物线y 1的函数解析式为y ＝(x ＋1)2－1，由对称性可知点A 的坐标为(－2，0)，由平移性质可知将A 平移到A′可知图象向右平移2个单位， 将点B 平移到点B′，则图象向上平移1个单位，从而点B 平移到点B′是先向右平移2个单位，再向上平移1个单位， 则点B′的坐标为(1，0)，抛物线y 2的函数解析式为y ＝(x －1)2.(2)联立y 1，y 2得(x ＋1)2－1＝(x －1)2，解得x ＝14. 由图象可知，当0＜x ＜14或x ＜－2时，y 2＞y 1＞0.第五节 二次函数的简单综合1．6 2.1443．解：(1)把B(3，0)代入得：0＝－32＋3m ＋3，解得：m ＝2，∴y＝－x 2＋2x ＋3.∵y＝－x 2＋2x ＋3＝－(x 2－2x ＋1)＋4＝－(x －1)2＋4，∴顶点坐标为(1，4)．(2)连接BC 并交抛物线对称轴l 于点P ，连接AP ，如解图，此时PA ＋PC 的值最小． 设Q 是直线l 上任意一点，连接AQ ，CQ ，BQ ，∵直线l 垂直平分AB ，∴AQ＝BQ ，AP ＝BP ，∴AQ＋CQ ＝BQ ＋CQ≥BC，BC ＝BP ＋CP ＝AP ＋CP ，即AQ ＋CQ≥AP＋CP.设直线BC 对应的函数解析式为y ＝kx ＋b(k≠0)，把(3，0)，(0，3)代入，得：⎩⎪⎨⎪⎧0＝3k ＋b ，3＝b ，∴⎩⎪⎨⎪⎧k ＝－1，b ＝3， ∴直线BC 对应的函数解析式为y ＝－x ＋3.当x ＝1时，y ＝－1＋3＝2.故当PA ＋PC 的值最小时，点P 的坐标为(1，2)．4．解：(1)0.5(2)设从第21天到第40天中， q 与x 满足的关系式为q ＝b ＋k x， ∴⎩⎪⎨⎪⎧b ＋k 21＝45b ＋k 35＝35，解得：⎩⎪⎨⎪⎧b ＝20k ＝525，∴q＝20＋525x ， (3)①p＝50－x ，②当1≤x≤20时，y ＝－12x 2＋15x ＋500，－b 2a＝15，当x ＝15时，y 最大＝612.5. 当21≤x≤40时，y ＝p(q －20)＝(50－x)²525x ＝26 250x－525， ∵y 随x 增大而减小，∴当x ＝21时，y 最大＝725.综上，这40天里该网店第21天获得的利润最大．。

河北省2０1８年中考数学总复习第三章函数第二节一次函数的图象与性质随堂演练编辑整理：尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（河北省20１８年中考数学总复习第三章函数第二节一次函数的图象与性质随堂演练）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉,前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为河北省2０１８年中考数学总复习第三章函数第二节一次函数的图象与性质随堂演练的全部内容。

一次函数的图象与性质随堂演练1.（2017·沈阳)在平面直角坐标系中,一次函数ｙ＝x－1的图象是( ）２．(2０1７·张家口二模）下列关于一次函数y＝－2ｘ+1的说法，其中正确的是（）A．图象经过第一、二、三象限B．图象经过点(-2，1）C．当ｘ＞1时,y＜０D.y随x的增大而增大3．(201７·上海)如果一次函数y＝ｋx+ｂ(k,b是常数,k≠0）的图象经过第一、二、四象限,那么ｋ，b应满足的条件是( )A.ｋ>0,且ｂ>0B.k<０，且ｂ＞0Ｃ.k＞0,且ｂ＜0 D.k＜0，且b<０4.（２017·济南）将一次函数y＝2x的图象向上平移２个单位后，当y>0时，x的取值范围是( )A.ｘ＞－1B.ｘ>１C．ｘ＞-2 D．ｘ>25.（201７·邢台一模）若关于x的一元二次方程x2-2ｘ＋kｂ+1＝0有两个不相等的实数根，则一次函数y＝ｋｘ＋b的大致图象可能是( )6．（２017·陕西)如图,已知直线ｌ1：y=-2x＋4与直线l2:ｙ＝kｘ＋b（k≠0)在第一象限交于点M。

若直线ｌ２与x轴的交点为A（-2,０),则ｋ的取值范围是（)A.-2＜k＜2 Ｂ.-2＜k＜0Ｃ.０＜ｋ＜４Ｄ.0＜k＜27．(20１7·裕华区模拟)如图,在平面直角坐标系中,点A,B,Ｃ，D是坐标轴上的点，且点C坐标是(0，－1),AB＝5,点(a，ｂ）在如图所示的阴影部分内部(不包括边界)．已知ＯＡ=OD＝4，则a的取值范围是( )8.(２01７·眉山)设点(－1,m)和点(＼ｆ(1,２)，n）是直线ｙ=(k2-1）x＋b(0<k＜1)上的两个点，则ｍ，n的大小关系为。

一次函数的图像和性质练习题一、填空题1.正比例函数(0)y kx k =≠一定经过 点，经过(1)， ，一次函数(0)y kx b k =+≠经过(0)， 点，(0) ，点． 2.直线26y x =-+与x 轴的交点坐标是 ，与y 轴的交点坐标是 。

与坐标轴围成的三角形的面积是 。

3.若一次函数(44)y mx m =--的图象过原点，则m 的值为 ．4.如果函数y x b =-的图象经过点(01)P ，，则它经过x 轴上的点的坐标为 ．5.一次函数3+-=x y 的图象经过点（ ，5）和（2， ）6.已知一次函数y=23x+m 和y=-21x+n 的图像都经过点A(-2,0), 且与y 轴分别交于B,C 两点,求△ABC 的面积。

7.某函数具有下面两条性质：（1）它的图象是经过原点的一条直线；（2）y 随x 的增大而减小．请你写出一个满足上述条件的函数8.在同一坐标系内函数y=2x 与y=2x+6的图象的位置关系是 ． 9.若直线y=2x+6与直线y=mx+5平行,则m=____________.10.在同一坐标系内函数y=ax+b 与y=3x+2平行，则a, b 的取值范围是 ．11.将直线y= -- 2x 向上平移3个单位得到的直线解析式是 ，将直线y= -- 2x 向下移3个单得到的直线解析式是 ．将直线y= -- 2x+3向下移2个单得到的直线解析式是 ． 12.一次函数(2)4y k x k =-+-的图象经过一、三、四象限，则k 的取值范围是 ． 13．已知点A(-4, a),B(-2,b)都在一次函数y=21x+k(k 为常数)的图像上,则a 与b 的大小关系是a____b(填”<””=”或”>”)14.直线y kx b =+经过一、二、三象限，则k ０，b ０，经过二、三、四象限，则有k 0，b 0，经过一、二、四象限，则有k 0，b 0．15.如果直线3y x b =+与y 轴交点的纵坐标为2-，那么这条直线一定不经过第 ------------象限． 16、直线152y x =-与轴的交点坐标是_______，与轴的交点坐标是_______. 17、直线23y x =-可以由直线2y x =沿轴_______而得到；直线32y x =-+可以由直线3y x =-轴_______而得到.18、已知一次函数()()634y m x n =++-. （1）当m______时，y 随x 的增大而减小；（2）当m______，n______时，函数图象与y 轴的交点在x 轴的下方； （3）当m______，n______时，函数图象过原点. 二、选择题1.已知函数(3)2y m x =+-，要使函数值y 随自变量x 的增大而减小，则m 的取值范围是（ ） Ａ．3m -≥Ｂ．3m >-Ｃ．3m -≤Ｄ．3m <-2.一次函数(1)5y m x =++中，y 的值随x 的减小而减小，则m 的取值范围是（ ） Ａ．1m >-Ｂ．1m <-Ｃ．1m =-Ｄ．1m <3．已知直线y kx b =+，经过点11()A x y ，和点22()B x y ，，若0k <，且12x x <，则1y 与2y 的大小关系是（ ）Ａ．12y y >Ｂ．12y y <Ｃ．12y y =Ｄ．不能确定4. 若直线23y mx m =--经过第二、三、四象限，则m 的取值范围是（ ） Ａ．32m <Ｂ．302m -<< Ｃ．32m >Ｄ．0m >5.一次函数31y x =-的图象不经过（ ）Ａ．第一象限Ｂ．第二象限 Ｃ．第三象限Ｄ．第四象限6.如果点P(a,b)关于x 轴的对称点p ,在第三象限,那么直线y=ax+b 的图像不经过 ( ) Ａ．第一象限 Ｂ．第二象限 Ｃ．第三象限 ........... Ｄ．第四象限 7.若一次函数y=kx+b 的图像经过(-2,-1)和点(1,2),则这个函数的图像不经过 ( ) Ａ．第一象限 Ｂ．第二象限 Ｃ．第三象限 ........... Ｄ．第四象限 8.下列图象中不可能是一次函数(3)y mx m =--的图象的是（ ）9．两个一次函数1y ax b =+与2y bx a =+，它们在同一直角坐标系中的图象可能是（ ）10yＤ．Ｃ．B ．A ．1x1x2Ｄ．Ｃ．B ． A ．A 、y=32x －8 B 、y=－x+3 C 、y=2x+5 D 、y=7x －6 11、在一次函数()15y m x =++中，的值随值的增大而减小，则的取值范围是（ ） A 、1m <- B 、1m >- C 、1m =- D 、1m <12、若一次函数b kx y +=的图象经过一、二、三象限,则b k ,应满足的条件是:（ ） A.0,0>>b k B.0,0<>b k C.0,0><b k D.0,0<<b k 13、将直线y=2x 向上平移两个单位，所得的直线是 （ ） A 、y=2x+2 B 、y=2x －2 C 、y=2（x －2） D 、y=2（x+2）14．汽车开始行驶时，油箱内有油40升，如果每小时耗油5升，则油箱内余油量y （升）与行驶时间t （时）的函数关系用图象表示应为下图中的（ ）15．李老师骑自行车上班，最初以某一速度匀速行进，•中途由于自行车发生故障，停下修车耽误了几分钟，为了按时到校，李老师加快了速度，仍保持匀速行进，如果准时到校．在课堂上，李老师请学生画出他行进的路程y•（千米）与行进时间t （小时）的函数图象的示意图，同学们画出的图象如图所示，你认为正确的是（ ）三、解答题1、在同一个直角坐标系中，画出函数21y x =-与34y x =-+的图象，并判断点A （1，1）、B （－2，10）是否在所画的图象上？在哪一个图象上？2.已知一次函数y=(3-k)x-2k+18, (1) k 为何值时,它的图像经过原点; (2) k 为何值时,它的图像经过点(0,-2);(3) k 为何值时,它的图像与y 轴的交点在x 轴的上方; (4) k 为何值时,它的图像平行于直线y=-x; (5) k 为何值时,y 随x 的增大而减小.3、已知一次函数y=kx+b （k 、b 为常数且k≠0）的图象经过点A （0，﹣2）和点B （1，0）， 求此函数的解析式4、求函数323-=x y 与x 轴、y 轴的交点坐标，并求这条直线与两坐标轴围成的三角形的面积.5、根据下列条件，确定函数关系式： （1）y 与x 成正比，且当x=9时，y=16；（2）y=kx+b 的图象经过点（3，2）和点（-2，1）．6、某摩托车的油箱最多可存油5升，行驶时油箱内的余油量y （升）与行驶的路程x(km)成一次函数关系，其图象如图。