基于线性二次最优LQR的直线倒立摆控制系统研究分析

桥式起重机吊重Fuzzy-LQR防摆控制器的设计李军;李学鋆【摘要】桥式起重机大小车联合运动可以提高作业效率,在其吊重防摆控制中加入大车运动更具工程意义.针对桥式起重机防摆定位控制具有非线性、强耦合、不确定等特点,设计Fuzzy-LQR控制吊重摆动.根据Lagrange方程建立三维动力学模型并在大小车运动方向对其进行解耦;通过信息融合技术将模糊控制器的多输入进行降维处理,解决模糊规则爆炸问题,结合LQR控制原理搭建Simulink仿真模型.选用CXTD16t-19.5m双梁桥式起重机进行仿真模拟,结果表明:运用Fuzzy-LQR分别控制解耦后的大小车运动或者大小车联合运动都能达到防摆定位的目的.【期刊名称】《机械设计与制造》【年(卷),期】2018(000)008【总页数】4页(P233-236)【关键词】桥式起重机;防摆控制;Fuzzy-LQR控制;LQR;模糊控制【作者】李军;李学鋆【作者单位】重庆交通大学机电与车辆工程学院,重庆 400074;重庆交通大学机电与车辆工程学院,重庆 400074【正文语种】中文【中图分类】TH161 引言起重机使用柔性绳索起吊重物使得结构轻便，提高了作业效率，但存在很大的安全隐患和控制问题。

为了推进起重机吊具的自动化控制和智能化控制，对起重机吊具的防摆定位控制进行研究具有十分重要的意义[1]。

针对起重机吊重防摆定位出现了PID控制、最优控制、滑模控制、模糊控制、神经网络控制、反步控制和无源控制等控制方法。

由于起重机吊重的非线性特性，单一的起重机吊重防摆定位控制方式存在各种不足，因此利用多种控制方法相结合，实现优势互补，可以弥补不足，提高控制精度和控制反应速度。

文献[2]建立了桥式起重机三维二自由度动力学模型、传递函数及建立仿真模型并通过解耦的处理方式利用小车控制吊重摆角，这种方式不仅可以快速控制摆角而且可以保证起重机定位。

最后实验仿真验证该方法可行，但存在抖振和严重超调。

（创新管理）倒立摆创新实验指导书倒立摆创新实验指导书－－线性二次最优LQR控制实验壹、实验目的让实验者了解且掌握线性二次最优控制LQR控制的原理和方法，学习如何使用最优控制算法对直线壹级倒立摆系统进行设计控制实验。

二、设计要求用最优控制算法设计控制器，使得当于小车上施加0.1ｍ的阶跃信号时，闭环系统的响应指标为：１.杆的上升时间小于2秒2.动态误差小于2％3.的超调量小于5％三、线性二次最优控制LQR基本原理及分析线性二次最优控制LQR基本原理为，由系统方程:确定下列最佳控制向量的矩阵K：u(t)=－K*x(t)使得性能指标达到最小值:式中Q——正定(或正半定)厄米特或实对称阵R——为正定厄米特或实对称阵图2-1最优控制LQR控制原理图方程右端第二项是考虑到控制能量的损耗而引进的，矩阵Q和R确定了误差和能量损耗的相对重要性。

且且假设控制向量u(t)是无约束的。

对线性系统：.根据期望性能指标选取Q和R，利用MATLAB命令lqr就能够得到反馈矩阵K的值。

K=lqr(A，B，Q，R)改变矩阵Q的值，能够得到不同的响应效果，Q的值越大(于壹定的范围之内)，系统抵抗干扰的能力越强，调整时间越短。

可是Q不能过大，其影响将于实验结果分析中阐述。

关于线性二次最优控制LQR的详细原理请参见现代控制理论的关联书籍。

四、实验步骤1)打开直线壹级倒立摆LQR实时控制模块，（进入MATLABSimulink实时控制工具箱“GoogolEducationProducts”打开“InvertedPendulum\LinearInvertedPendulum\Linear1-StageIPExperiment\LQRExp eriments”中的“LQRControlDemo”）图2-5直线壹级倒立摆LQR控制实时控制程序其中“LQRController”为LQR控制器模块，“RealControl”为实时控制模块，双击“LQRController”模块打开LQR控制器参数设置窗口如下：于“LQRController”模块上点击鼠标右键选择“Lookundermask”打开模型如下：双击“RealControl”模块打开实时控制模块如下图：其中“Pendulum”模块为倒立摆系统输入输出模块，输入为小车的速度“Vel”和“Acc”，输出为小车的位置“Pos”和摆杆的角度“Angle”。

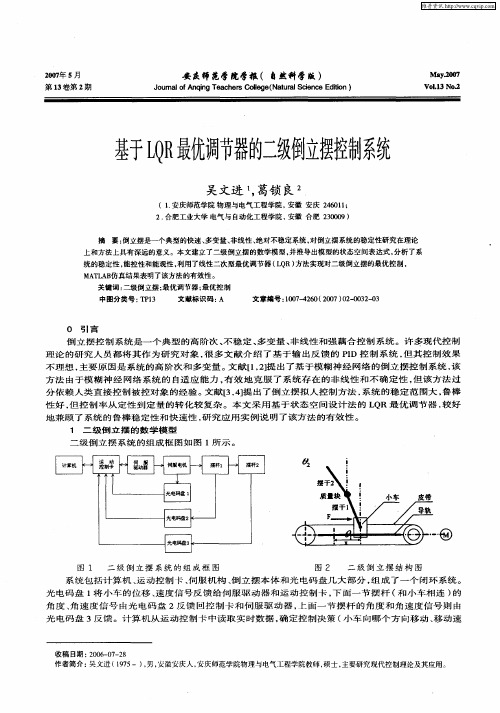
基于LQR的二级倒立摆控制系统研究摘要倒立摆系统是一个典型的多变量、非线性、强耦合和快速运动的高阶不稳定系统，它是检验各种新的控制理论和方法有效性的典型理想模型。

在其控制过程中，能有效地反映诸如镇定性、鲁棒性、随动性以及跟踪等许多关键问题。

本文主要研究二级倒立摆LQR控制方法。

首先建立了二级倒立摆的数学模型，然后对二级倒立摆的数学模型进行控制设计，应用遗传算法确定系统性能指标函数中的加权阵Q，R得到系统状态反馈控制矩阵。

最后，用MATLAB进行了系统仿真。

在几次凑试Q矩阵值后系统的响应结果都不尽如人意，于是采用遗传算法对Q矩阵优化。

仿真结果证明：经过遗传算法优系统响应能更加满足设计要求。

关键词二级倒立摆；LQR控制；遗传算法Research on double inverted pendulum controlsystem based on LQRAbstractThe inverted pendulum is a typical high order system, with multi- variable, non-linear, strong-coupling, fleet and absolutely instable. It is representative as an ideal model to prove new control theory and techniques. During the control process, pendulum can effectively reflect many key problems such as equanimity, robust, follow-up and track, therefore.This paper studies a control method of double inverted pendulum LQR. First of all, the mathematical model of the double inverted pendulum is established, then make a control design to double inverted pendulum on the mathematical model, and determine the system performance index weight matrix Q, R by using genetic algorithm in order to attain the system state feedback control matrix. Finally, the simulation of the system is made by MATLAB. After several test matrix Q value the results are not satisfactory response, then we optimize Q matrix by using Genetic Algorithm. Simulation results show: The system response can meet the design requirements effectively after Genetic Algorithm optimization.Key words Double inverted pendulum; LQR control; Genetic Algorithm.目录摘要 (I)Abstract (II)第1章绪论 (1)1.1引言 (1)1.2倒立摆设备简介 ..................................... 错误!未定义书签。

倒立摆实验报告实验人:2011年12月29日目录一．实验概述倒立摆简介 (3)倒立摆控制的目标与控制器设计方法 (3)实验装置简介 (3)二．实验内容实验对象建模 (4)控制器的设计、仿真与实验结果频率响应控制实验 (5)直线一级倒立摆 PID 控制实验 (13)直线一级倒立摆 LQR 控制实验 (17)三．小结 (21)一．实验概述1.倒立摆简介倒立摆控制系统是一个复杂的、不稳定的、非线性系统，是进行控制理论教学及开展各种控制实验的理想实验平台。

对倒立摆系统的研究能有效的反映控制中的许多典型问题：如非线性问题、鲁棒性问题、镇定问题、随动问题以及跟踪问题等。

通过对倒立摆的控制，用来检验新的控制方法是否有较强的处理非线性和不稳定性问题的能力。

同时，其控制方法在军工、航天、机器人和一般工业过程领域中都有着广泛的用途，如机器人行走过程中的平衡控制、火箭发射中的垂直度控制和卫星飞行中的姿态控制等。

2.倒立摆控制的目标与控制器设计方法。

倒立摆的控制问题就是使摆杆尽快地达到一个平衡位置，并且使之没有大的振荡和过大的角度和速度。

当摆杆到达期望的位置后，系统能克服随机扰动而保持稳定的位置。

本实验的控制对象是一级倒立摆,控制目标是实现起摆后摆杆稳定于倒立状态,有一定的抗干扰能力。

倒立摆系统的输入为小车的位移（即位置）和摆杆的倾斜角度期望值，计算机在每一个采样周期中采集来自传感器的小车与摆杆的实际位置信号，与期望值进行比较后，通过控制器处理得到控制量，再经数模转换驱动直流电机实现倒立摆的实时控制。

直流电机通过皮带带动小车在固定的轨道上运动，摆杆的一端安装在小车上，能以此点为轴心使摆杆能在垂直的平面上自由地摆动。

作用力u平行于铁轨的方向作用于小车，使杆绕小车上的轴在竖直平面内旋转，小车沿着水平铁轨运动。

当没有作用力时，摆杆处于垂直的稳定的平衡位置（竖直向下）。

为了使杆子摆动或者达到竖直向上的稳定，需要给小车一个控制力，使其在轨道上被往前或朝后拉动。

基于LQR控制的二级倒立摆系统研究作者：牛娟031210308王晨琳031210307王鹤彬031210312 学院：自动化指导老师：王晶、陆宁云摘要倒立摆系统是一种高阶次、不稳定、多变量、非线性、强耦合的系统，是进行控制理论研究的典型实验平台。

本文采用最优控制的方法设计二级倒立摆系统的控制器。

首先简要介绍了倒立摆以及倒立摆的几种常见控制方法，着重介绍了最优控制理论，其次对二级倒立摆系统进行了数学建模，最后对线性二次型最优控制原理进行了分析并使用MATLAB进行了仿真。

关键词：二级倒立摆，最优控制目录一、绪论 (3)1.1、倒立摆系统简介 (3)1.2、倒立摆系统的控制算法 (3)1.3、小结 (4)二、直线倒立摆的建模 (4)2.1、直线二级倒立摆的建模 (4)2.2、直线二级倒立摆的定性分析 (6)三、基于MATLAB的LQR仿真 (9)3.1、最优控制（LQR）简介 (9)3.2、线性二次型最有调节器原理 (9)3.3、MATLAB仿真 (10)3.4、SIMULINK仿真 (11)四、结束语 (13)4.1、小结 (13)4.2、未解决问题展望 (13)五、附录 (13)一、绪论1.1、倒立摆系统简介倒立摆系统是一种高阶次、不稳定、多变量、非线性、强耦合的系统，是进行控制理论研究的典型实验平台。

许多抽象的控制理论概念如系统稳定性、可控性和系统抗干扰能力等等，都可以通过倒立摆系统实验直观的表现出来。

在控制理论发展的过程中，某种控制理论的正确性及可行性需要通过设计一个控制器去控制一个典型的控制对象去加以验证。

倒立摆系统正是这样一种比较典型的控制对象。

最简单的倒立摆可由一个可在水平轨道上自由移动的小车和倒置摆铰链组成。

倒立摆的种类繁多，分类方法也多种多样：按结构来分有直线倒立摆，环形倒立摆，平面倒立摆；按级数来分有一级摆，二级摆，三级摆乃至更高级摆；按运动轨道来分有水平轨道倒立摆，倾斜轨道倒立摆；按控制电机数目来分有单电机倒立摆，多电机倒立摆。