2002-03年四川省初中数学竞赛

20XX 年全国初中数学联赛四川初赛试卷(3月21日下午2：30━4：30或3月22日上午9：00━11：00)1、若121≤≤-x ，则式子1449612222++++-++-x x x x x x 等于（ ） （A ）－4x ＋3 （B ）5 （C ）2x ＋3 （D ）4x ＋32、用三种边长相等的正多边形地砖铺地，其顶点拼在一起，刚好能完全铺满地面．已知正多边形的边数为x 、y 、z ，则zy x 111++的值为（ ） （A ）1 （B ）32 （C ）21 （D ）31 3、已知a 为非负整数，关于x 的方程0412=+---a x a x 至少有一个整数根，则a 可能取值的个数为（ ）（A ）4 （B ）3 （C ）2 （D ） 14、如图，设△ABC 和△CDE 都是正三角形，且∠EBD ＝62o ，则∠AEB 的度数是（ ）（A ）124o （B ）122o（C ）120o （D ）118o5、如图，直线x ＝1是二次函数y ＝ax 2＋bx ＋c 的图象的对称轴，则有（ ）（A ）a ＋b ＋c ＞0 （B ）b ＞a ＋c（C ）abc ＜0 （D ）c ＞2b6、已知x 、y 、z 是三个非负实数，满足3x ＋2y ＋z ＝5，x ＋y －z ＝2，若S ＝2x＋y －z ，则S 的最大值与最小值的和为（ ）（A ）5 （B ）6（C ）7 （D ）8二、填空题（本大题满分28分，每小题7分）1、已知a 是方程x 2－5x ＋1＝0的一个根，则44-+a a 的个位数字为_____________．2、在凸四边形ABCD 中，对角线AC 、BD 交于O 点，若S △OAD ＝4，S △OBC ＝9，则凸四边形ABCD 面积的最小值为__________________．3、实数x 、y 满足x 2－2x －4y ＝5，记t ＝x －2y ，则t 的取值范围为___________________．4、如图，△ABC 内接于⊙O ，且AB ＝AC ，直径AD 交BC 于E ，F 是OE 的中点．如果BD //CF ，BC ＝25，则线段CD 的长度为__________________．三、（本大题满分20分）已知方程x 2＋ax －b ＝0的根是a 和c ，方程x 2＋cx ＋d ＝0的根是b 和d ．其中，a 、b 、c 、d 为不同实数，求a 、b 、c 、d 的值．四、（本大题满分25分）如图，四边形A 1A 2A 3A 4内接于一圆，△A 1A 2A 3的内心是I 1，△A 2A 3A 4的内心是I 2，△A 3A 4A 1的内心是I 3．求证：（1）A 2、I 1、I 2、A 3四点共圆； （2）∠I 1I 2I 3＝90o ．五、（本大题满分25分）如图，将3枚相同硬币依次放入一个4×4的正方形格子中（每个正方形格子只能放1枚硬币）．求所放的3枚硬币中，任意两个都不同行且不同列的概率．20XX 年全国初中数学联赛四川初赛试卷参考答案及评分细则一、选择题（本题满分42分，每小题7分）1、B2、C3、B4、B5、D6、A二、填空题（本大题满分28分，每小题7分）1、72、253、29≤t 4、6三、（本大题20分）解：∵方程x 2＋ax －b ＝0的根是a 和c ，∴a ＋c ＝－a ，ac ＝－b∵x 2＋cx ＋d ＝0的根是b 和d ，∴b ＋d ＝－c ，bd ＝d ······································· 5分（一）若d ≠0，则由bd ＝d 知b ＝1由a ＋c ＝－a 知c ＝－2a ，由ac ＝－b 知－2a 2＝－1，解得22±=a ················· 10分 当22=a 时，2-=c 得d ＝－c －b ＝12-； ········································· （1） 当22-=a 时2=c ，得d ＝－c －b ＝12--． ······································ （2） 经验证，22±=a ，b ＝1，2 =c ，d ＝12-±是符合条件的两组解． ······· 15分 （二）若d ＝0，则b ＝－c ，由a ＋c ＝－a 知c ＝－2a ，由ac ＝－b 知ac ＝c若c ＝0，则a ＝0，这与a 、b 、c 、d 是不同的实数矛盾．若c ≠0，则a ＝1，再由c ＝－2a 知c ＝－2，从而b ＝－c ＝2经验证，a ＝1，b ＝2，c ＝－2，d ＝0也是符合条件的解． ······························· 20分四、（本大题25分）证明：（1）如图，连结I 1A 1，I 1A 2，I 1A 3，I 2A 2和I 2A 3∵I 1是△A 1A 2A 3的内心，∴∠I 1A 1A 2＝∠I 1A 1A 3＝21∠A 2A 1A 3 ∠I 1A 2A 1＝∠I 1A 2A 3＝21∠A 1A 2A 3，∠I 1A 3A 1＝∠I 1A 3A 2＝21∠A 1A 3A 2 ··················· 5分 延长A 1I 1交四边形A 1A 2A 3A 4外接圆于P ，则∠A 2I 1A 3＝∠A 2I 1P ＋∠PI 1A 3＝∠I 1A 1A 2＋∠I 1A 2A 1＋∠I 1A 1A 3＋∠I 1A 3A 1 ＝21(∠A 2A 1A 3＋∠A 1A 2A 3＋∠A 2A 3A 1)＋21∠A 2A 1A 3＝90o ＋21∠A 2A 1A 3 ··············· 10分 同理∠A 2I 2A 3＝90o ＋21∠A 2A 4A 3，又∵四边形A 1A 2A 3A 4内接于一圆 ∴∠A 2A 1A 3＝∠A 2A 4A 3，∴∠A 2I 1A 3＝∠A 2I 2A 3．∴A 2、I 1、I 2、A 3四点共圆． ······· 15分（2）又连结I 3A 4，则由（1）知A 3、I 2、I 3、A 4四点共圆∴∠I 1I 2A 3＝180o －∠I 1A 2A 3＝180o －21∠A 1A 2A 3 同理∠I 3I 2A 3＝180o －∠I 3A 4A 3＝180o －21∠A 1A 4A 3 ·········································· 20分 ∴∠I 1I 2I 3＝360o －(∠I 1I 2A 3＋∠I 3I 2A 3)＝21(∠A 1A 2A 3＋∠A 1A 4A 3)＝90o ················· 25分五、（本大题25分）解：1、计算总的放法数N ：第一枚硬币放入16个格子有16种放法；第二枚硬币放入剩下的15个格子有15种放法；第三枚硬币放入剩下的14个格子有14种放法．所以，总的放法数N ＝16×15×14＝3360． ············································ 10分2、计算满足题目要求的放法数m ：第一枚硬币放入16个格子有16种放法，与它不同行或不同列的格子有9个．因此，与第一枚硬币不同行或不同列的第二枚硬币有9种放法．与前两枚硬币不同行或不同列的格子有4个，第三枚硬币放入剩下的4个格子有4种放法．所以，满足题目要求的放法数m ＝16×9×4＝576． ································· 20分所求概率P ＝3561415164916=⨯⨯⨯⨯=N m ． ················································· 25分。

2002年全国初中数学竞赛试题一、选择题1．设a ＜b ＜0，a 2＋b 2＝4ab ，则ba ba -+的值为【 】 A 、3 B 、6 C 、2 D 、32．已知a ＝1999x ＋2000，b ＝1999x ＋2001，c ＝1999x ＋2002，则多项式a 2＋b 2＋c 2－ab －bc －ca 的值为【 】A 、0B 、1C 、2D 、33．如图，点E 、F 分别是矩形ABCD 的边AB 、BC 的中点，连AF 、CE 交于点G ，则ABCDAGCD S S 矩形四边形等于【 】A 、65 B 、54 C 、43 D 、32ABC DEF G4．设a 、b 、c 为实数，x ＝a 2－2b ＋3π，y ＝b 2－2c ＋3π，z ＝c 2－2a ＋3π，则x 、y 、z 中至少有一个值【 】A 、大于0B 、等于0C 、不大于0D 、小于0 5．设关于x 的方程ax 2＋(a ＋2)x ＋9a ＝0，有两个不等的实数根x 1、x 2，且x 1＜1＜x 2，那么a 的取值范围是【 】A 、72-＜a ＜52 B 、a ＞52 C 、a ＜72- D 、112-＜a ＜06．A 1A 2A 3…A 9是一个正九边形，A 1A 2＝a ，A 1A 3＝b ，则A 1A 5等于【 】 A 、22b a + B 、22b ab a ++ C 、()b a +21D 、a ＋b 二、填空题7．设x 1、x 2是关于x 的一元二次方程x 2＋ax ＋a ＝2的两个实数根，则(x 1－2x 2)(x 2－2x 1)的最大值为 。

8．已知a 、b 为抛物线y ＝(x －c)(x －c －d)－2与x 轴交点的横坐标，a ＜b ，则b c c a -+-的值为 。

9．如图，在△ABC 中，∠ABC ＝600，点P 是△ABC 内的一点，使得∠APB ＝∠BPC ＝∠CPA ，且PA ＝8，PC ＝6，则PB ＝ 。

“希望杯”全国数学竞赛（第1-23届）初一年级/七年级第一/二试题目录1.希望杯第一届（1990年）初中一年级第一试试题......................003-0052.希望杯第一届（1990年）初中一年级第二试试题......................010-0123.希望杯第二届（1991年）初中一年级第一试试题...... 0错误!未定义书签。

-0204.希望杯第二届（1991年）初中一年级第二试试题...... 0错误!未定义书签。

-0265.希望杯第三届（1992年）初中一年级第一试试题...... 0错误!未定义书签。

-0326.希望杯第三届（1992年）初中一年级第二试试题...... 0错误!未定义书签。

-0407.希望杯第四届（1993年）初中一年级第一试试题...... 0错误!未定义书签。

-0508.希望杯第四届（1993年）初中一年级第二试试题...... 0错误!未定义书签。

-0589.希望杯第五届（1994年）初中一年级第一试试题...... 0错误!未定义书签。

-06610.希望杯第五届（1994年）初中一年级第二试试题..... 0错误!未定义书签。

-07311.希望杯第六届（1995年）初中一年级第一试试题..... 0错误!未定义书签。

-080 12希望杯第六届（1995年）初中一年级第二试试题..... 0错误!未定义书签。

-08713.希望杯第七届（1996年）初中一年级第一试试题..... 0错误!未定义书签。

-09814.希望杯第七届（1996年）初中一年级第二试试题....... 错误!未定义书签。

-10515.希望杯第八届（1997年）初中一年级第一试试题....... 错误!未定义书签。

-11316.希望杯第八届（1997年）初中一年级第二试试题....... 错误!未定义书签。

-12017.希望杯第九届（1998年）初中一年级第一试试题....... 错误!未定义书签。

1991年全国初中数学联合竞赛决赛试题第一试 一、选择题本题共有8个小题，每小题都给出了（A ）、（B ）（C ）、（D ）四个答案结论，其中只有一个是正确的．请把正确结论的代表字母写在题后的圆括号内．１． 设等式y a a x a y a a x a ---=-+-)()(在实数范围内成立，其中a ，x ，y 是两两不同的实数，则22223y xy x y xy x +--+的值是（A ）3 ； （B ）31； （C ）2； （D ）35． 答（ ）２． 如图，AB ‖EF ‖CD ，已知AB =20，CD =80，BC =100，那么EF 的值是（A ） 10； （B ）12；（C ） 16； （D ）18． 答（ ）３． 方程012=--x x 的解是（A ）251±； （B ）251±-； （C ）251±或251±-； （D ）251±-±． 答（ ）４．已知：)19911991(2111n n x --=（n 是自然数）．那么n x x )1(2+-，的值是（Ａ）11991-； （Ｂ）11991--；（Ｃ）1991)1(n -； （Ｄ）11991)1(--n ． 答（ ）５． 若M n 1210099321=⨯⨯⨯⨯⨯ ，其中Ｍ为自然数，n 为使得等式成立的最大的自然数，则Ｍ（Ａ）能被２整除，但不能被３整除； （Ｂ）能被３整除，但不能被２整除； （Ｃ）能被４整除，但不能被３整除； （Ｄ）不能被３整除，也不能被２整除． 答（ ）６． 若a ，c ，d 是整数，b 是正整数，且满足c b a =+，d c b =+，a d c =+，那么d c b a +++的最大值是（Ａ）1-；（Ｂ）5-；（Ｃ）0；（Ｄ）１． 答（ ）７． 如图，正方形OPQR 内接于ΔABC ．已知ΔAOR 、ΔBOP 和ΔCRQ 的面积分别是11=S ，32=S 和13=S ，那么，正方形OPQR 的边长是（Ａ）2；（Ｂ）3；（Ｃ）2 ；（Ｄ）3． 答（ ）８． 在锐角ΔABC 中，1=AC ，c AB =， 60=∠A ，ΔABC 的外接圆半径R ≤1，则（Ａ）21< c < 2 ； （Ｂ）0< c ≤21； 答（ ）11=S 3S =132=S（C ）c > 2； （D ）c = 2． 答（ ） 二、填空题１．Ｅ是平行四边形ABCD 中BC 边的中点，AE 交对角线BD 于G ，如果ΔBEG 的面积是１，则平行四边形ABCD 的面积是 ．２．已知关于x 的一元二次方程02=++c bx ax 没有实数解．甲由于看错了二次项系数，误求得两根为２和４；乙由于看错了某一项系数的符号，误求得两根为－１和４，那么，=+acb 32 ． 3．设m ，n ，p ，q 为非负数，且对一切x >０，qpn m x x x x )1(1)1(+=-+恒成立，则４．四边形ABCD 中，∠ ABC 135=，∠BCD 120=，AB 6=，BC 35-=，CD = 6，则AD = ．第二试x + y ， x － y ， x y ，yx四个数中的三个又相同的数值，求出所有具有这样性质的数对（x , y ）．二、ΔABC 中，AB ＜AC ＜BC ，D 点在BC 上，E 点在BA 的延长线上，且BD ＝BE ＝AC ，ΔBDE 的外接圆与ΔABC 的外接圆交于F 点（如图）．求证：BF ＝AF ＋CF三、将正方形ABCD 分割为 2n 个相等的小方格（n 是自然数），把相对的顶点A ，C 染成红色，把B ，D 染成蓝色，其他交点任意染成红、蓝两色中的一种颜色．证明：恰有三个顶点同色的小方格的数目必是偶数．1992年全国初中数学联合竞赛决赛试题 第一试 一.选择题本题共有8个题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.满足1=+-ab b a 的非负整数),(b a 的个数是(A)1; (B)2; (C)3; (D)4.2.若0x 是一元二次方程)0(02≠=++a c bx ax 的根,则判别式ac b 42-=∆与平方式20)2(b ax M +=的关系是(A)∆>M (B)∆=M (C)∆>M ; (D)不确定. 3.若01132=+-x x ,则44-+x x 的个位数字是(A)1; (B)3; (C)5; (D)7. 答( )4.在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为(A)7; (B)6; (C)5; (D)4. 答( )5.如图,正比例函数)0(>==a ax y x y 和的图像与反比例函数)0(>=k xk y 的图像分别相交于A 点和C 点.若AOB Rt ∆和COD ∆的面积分别为S 1和S 2,则S 1与S 2的关系是(A)21S S > (B)21S S = (C)21S S < (D)不确定答( )6.在一个由88⨯个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为1S ,把圆周经过的所有小方格的圆内部分的面积之和记为2S ,则21S S 的整数部分是 (A)0; (B)1; (C)2; (D)3. 答( )7.如图,在等腰梯形ABCD 中, AB //CD ,AB=2CD , ︒=∠60A ,又E 是底边AB 上一点,且FE=FB=AC , FA=AB .则AE :EB 等于(A)1:2 (B)1:3 (C)2:5 (D)3:10 答( )8.设9321,,,,x x x x ⋅⋅⋅均为正整数,且921x x x <⋅⋅⋅<<,220921=+⋅⋅⋅++x x x ,则当54321x x x x x ++++的值最大时,19x x -的最小值是(A)8; (B)9; (C)10; (D)11. 答( ) 二.填空题1.若一等腰三角形的底边上的高等于18cm ,腰上的中线等15cm ,则这个等腰三角形的面积等于________________.2.若0≠x ,则xx x x 44211+-++的最大值是__________.3.在ABC ∆中,B A C ∠∠=∠和,90 的平分线相交于P 点，又AB PE ⊥于E 点，若3,2==AC BC ，则=⋅EB AE .4.若b a ,都是正实数，且0111=+--b a b a ，则=+33)()(baa b . 第二试一、设等腰三角形的一腰与底边的长分别是方程062=+-a x x 的两根，当这样的三角形只有一个时，求a 的取值范围.二、如图，在ABC ∆中，D AC AB ,=是底边BC 上一点，E 是线段AD 上一点，且A CED BED ∠=∠=∠2.求证：CD BD 2=.三、某个信封上的两个邮政编码M 和N 均由0，1，2，3，5，6这六个不同数字组成，现有四个编码如下：A ：320651B ：105263C ：612305D ：316250已知编码A 、B 、C 、D 各恰有两个数字的位置与M 和N 相同.D 恰有三个数字的位置与M 和N 相同.试求：M 和N. 1993年全国初中数学联合竞赛决赛试题 第一试 一.选择题本题共有8个小题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.多项式1612+-x x 除以12-x 的余式是(A)1; (B)-1; (C)1-x ; (D)1+x ;2.对于命题Ⅰ.内角相等的圆内接五边形是正五边形.Ⅱ.内角相等的圆内接四边形是正四边形,以下四个结论中正确的是 (A)Ⅰ,Ⅱ都对 (B)Ⅰ对,Ⅱ错 (C)Ⅰ错,Ⅱ对. (D)Ⅰ,Ⅱ都错. 3.设x 是实数,11++-=x x y .下列四个结论: Ⅰ.y 没有最小值;Ⅱ.只有一个x 使y 取到最小值;Ⅲ.有有限多个x (不止一个)使y 取到最大值; Ⅳ.有无穷多个x 使y 取到最小值. 其中正确的是(A)Ⅰ (B)Ⅱ (C)Ⅲ (D)Ⅳ 4.实数54321,,,,x x x x x 满足方程组其中54321,,,,a a a a a 是实常数,且54321a a a a a >>>>,则54321,,,,x x x x x 的大小顺序是(A)54321x x x x x >>>>; (B)53124x x x x x >>>>; (C)52413x x x x x >>>>; (D)24135x x x x x >>>>. 5.不等式73)1(12+<-<-x x x 的整数解的个解(A)等于4 (B)小于4 (C)大于5 (D)等于5 6.在ABC ∆中,BC AO O A =∠,,是垂心是钝角, 则)cos(OCB OBC ∠+∠的值是 (A)22-(B)22(C)23 (D)21-. 答( )7.锐角三角ABC 的三边是a , b , c ,它的外心到三边的距离分别为m , n , p ,那么m :n :p 等于(A)cb a1:1:1; (B)c b a :: (C)C B A cos :cos :cos (D)C B A sin :sin :sin . 答( ) 8.13333)919294(3-+-可以化简成 (A))12(333+; (B))12(333- (C)123- (D)123+ 答( ) 二.填空题1. 当x 变化时,分式15632212++++x x x x 的最小值是___________.2.放有小球的1993个盒子从左到右排成一行,如果最左面的盒里有7个小球,且每四个相邻的盒里共有30个小球,那么最右面的盒里有__________个小球.3.若方程k x x =--)4)(1(22有四个非零实根,且它们在数轴上对应的四个点等距排列,则k =____________.4.锐角三角形ABC 中,︒=∠30A .以BC 边为直径作圆,与AB ,AC 分别交于D , E ,连接DE , 把三角形ABC 分成三角形ADE与四边形BDEC ,设它们的面积分别为S 1, S 2,则S 1:S 2=___________.第二试一.设H 是等腰三角形ABC 垂心,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积HBC ABC S S ∆∆⋅的值变小,变大,还是不变?证明你的结论.二.ABC ∆中, BC =5, AC =12, AB =13, 在边AB ,AC 上分别取点D , E , 使线段DE 将ABC ∆分成面积相等的两部分.试求这样的线段DE 的最小长度.三.已知方程0022=++=++b cx x c bx x 及分别各有两个整数根21,x x 及21,x x '',且,021>x x 021>''x x . (1)求证:;0,0,0,02121<'<'<<x x x x (2)求证:1-b ≤c ≤1+b ; (3)求c b ,所有可能的值.1994年全国初中数学联赛试题 第一试(4月3日上午8：30—9：30)考生注意：本试共两道大题，满分80分.一、选择题（本题满分48分，每小题6分）本题共有8个小题都给出了A ，B 、C ，D ，四个结论，其中只有一个是正确的，请把你认为正确结论的代表字母写在题后答案中的圆括号内，每小题选对得6分；不选、选错或选出的代表字母超过一个（不论是否写在圆括号内），一律得0分.〔答〕( )2．设a,b,c是不全相等的任意实数，若x=a2-bc,y=b2-ca,z=c2-ab,则x,y,zA．都不小于0 B．都不大于0C．至少有一个小0于D．至少有一个大于0 〔答〕( )3．如图1所示，半圆O的直径在梯形ABCD的底边AB上，且与其余三边BC，CD，DA相切，若BC=2，DA=3，则AB的长A．等于4 B．等于5C．等于6 D．不能确定〔答〕( )A．1 B．-1 C．22001D．-22001〔答〕( )5．若平行直线EF，MN与相交直线AB，CD相交成如图2所示的图形，则共得同旁内角A．4对B．8对C．12对D．16对〔答〕( )〔答〕( )7．设锐角三角形ABC的三条高AD，BE，CF相交于H。

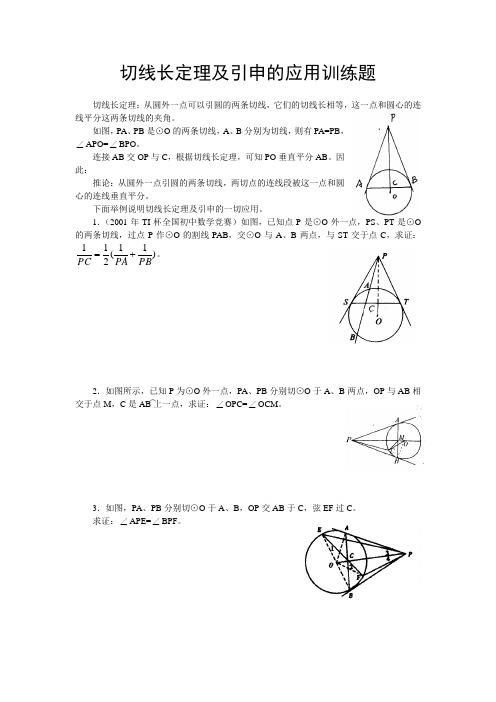
切线长定理及引申的应用训练题切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分这两条切线的夹角。

如图，PA 、PB 是⊙O 的两条切线，A 、B 分别为切线，则有PA=PB ，∠APO=∠BPO 。

连接AB 交OP 与C ，根据切线长定理，可知PO 垂直平分AB 。

因此：推论：从圆外一点引圆的两条切线，两切点的连线段被这一点和圆心的连线垂直平分。

下面举例说明切线长定理及引申的一切应用。

1．（2001年TI 杯全国初中数学竞赛）如图，已知点P 是⊙O 外一点，PS 、PT 是⊙O 的两条切线，过点P 作⊙O 的割线PAB ，交⊙O 与A 、B 两点，与ST 交于点C ，求证：)11(211PBPA PC +=。

2．如图所示，已知P 为⊙O 外一点，PA 、PB 分别切⊙O 于A 、B 两点，OP 与AB 相交于点M ，C 是AB 上一点，求证：∠OPC=∠OCM 。

3．如图，PA 、PB 分别切⊙O 于A 、B ，OP 交AB 于C ，弦EF 过C 。

求证：∠APE=∠BPF 。

（4．（2002年四川省初中数学竞赛）如图，P是⊙O外一点，PA与⊙O切于A，PBC是⊙O 的割线，AD PO于D。

求证：PB：BD=PC：CD。

5．（2006年全国初中数学竞赛试题）如图，点P为⊙O的两条切线，切点分别为A、B。

过点A作PB的平行线，交⊙O于点C，连接PC，交⊙O于点E；连接AE，并延长AE交PB于点K。

求证：PE·AC=CE·KB。

6、如图,圆O的直径为10,在圆O上位于直径AB的异侧有定点C和动点P,已知BC:CA=4:3,点P在半圆弧AB上运动(不与A、B重合),过C作CP的垂线CD交PB的延长线于D点. （1）求证：AC.CD=PC.BC；（2）当点P运动到孤AP的中点时，求CD的长；（3）当点P运动到什么位置时，△PCD的面积最大？并求出这个最大面积.7、如图,在⊙O中,直径AB的两侧有定点C和动点P,点P在孤AB上运动(不与A、B重合),过点C作CP的垂线,与PB的延长线交于点Q.（1）试猜想：△PCQ与△ACB具有何种关系？（不要求证明）（2）当点P运动到什么位置时，△ABC≌△PCB？并给出证明。

光荣榜2002~2003学年度获得各项奖励学生名单：一、获国家、省级奖励：广东省优秀学生：杨淳佳广东省三好学生：肖跃第十九届全国中学生物理竞赛（广东赛区）奖项：二等奖：林伟曾楚铕三等奖：吴为丹许于春黄凯特陈煊陈秀丰肖健雄吴传文陈悦晖许作舟中国化学学会2002年全国高中学生化学竞赛（广东赛区）奖项：二等奖：陈淑如赵建明林绍杰三等奖：谢琳潘颖炜中国生物学会2002年全国高中学生生物联赛（广东赛区）奖项：二等奖：黄俊柅三等奖：章楷琛李绵第三届全国中小学生电脑制作活动竞赛（广东赛区）奖项：一等奖：肖健雄（高中组程序设计）一等奖：郑亮亮（高中组程序设计）二等奖：李伟铿（高中组网页制作）三等奖：陈其孜（高中组电脑绘画）全国普及法律常识办公室组织的“争做遵纪守法小公民”征文比赛：一等奖：詹美林（作品：《遵纪守法，从身边小事做起》）第二届广东省中小学生学习航天航空科技知识征文比赛奖项：二等奖：肖健雄第17届广东省青少年科技创新大赛：三等奖：黄钰妮王岚王诗涛第17届广东省青少年科技创新大赛科学幻想绘画：二等奖：蔡怡斐2003年全国初中数学联合竞赛：全国三等奖：赖建沆（市二等奖）2003年全国初中化学竞赛：二等奖：温晰陈轩－1－三等奖：张锷广东省中学生现场作文竞赛初中组：二等奖：肖妍琳广东省传统项目学校田径比赛：学校田径队获金、银、铜牌各一枚。

教育艺术杂志社主办的第三届手拉手中国青少年作文大赛：二等奖：刘泓第一届广东省少年儿童发明奖：计算机科学作品潮州市一等奖：黄浩杰第十八届广东省青少年科技创新大赛科学幻想绘画比赛：李奕东《未来的资源》获三等奖二、获2002年潮汕星河奖名单：李炫：获第十三届潮汕星河奖学业一等奖李黄煌：获第十三届潮汕星河奖学业一等奖张帆驰：获第十三届潮汕星河奖学业一等奖谢泽林：获第十三届潮汕星河奖学业二等奖肖健雄：获第十三届潮汕星河奖科技二等奖三、潮州市市级奖励名单：市级优秀学生干部、“三好生”、优秀团员：优秀学生干部：肖健雄黄凯特杨淳佳蔡树蓁王义烔谢琳翁振佳林石楷蔡润辉程佳凌沈熙黄钰妮刘塽张锷黄静佳“三好生”：肖跃吴佳贤杨煊吴俊陈烁杭刘真陈俊榕潘锦谢瑾黄静燕翁翠芬卢莹章林冰温晰王诗涛佘桂娜优秀团员：吴溯李绵陈洁陈少锐杜健陈盼庄奕吴诺林继玲苏昕郑焕钊2003年全国初中数学联合竞赛：潮州市三等奖：张锷吴垠吴键温晰2003年潮州市初中生作文现场赛：一等奖黄志扬陈铠南－2－二等奖陈欢许安婍三等奖吴思瀚林锂依洪师菡谢晓绵2002年潮州市运动会田径比赛获奖项目：田径队获团体总分第二名高中男子：100Ｍ第一名：陈依煌200Ｍ第二名：陈依煌100Ｍ第六名：林铮800Ｍ第二名：郭宜1500Ｍ第三名：郭宜110Ｍ栏第二名：陈烁400Ｍ栏第三名：陈烁跳高第二名：陈锐鹏4×100Ｍ第二名：4×400Ｍ第三名：（超市纪录）高中女子：100Ｍ第一名：余小洁200Ｍ第一名：余小洁100Ｍ第三名：吴佳新200Ｍ第四名：吴佳新跳高第三名：陈娟跳远第四名：陈娟潮州市中学生乒乓球比赛：学校乒乓球队获男子团体冠军、女子团体亚军，并包囊男子单打冠、亚军。

2002年全国初中数学竞赛试题及解析一、选择题1．设a ＜b ＜0，a 2＋b 2＝4ab ，则ba ba -+的值为【 】 A 、3 B 、6 C 、2 D 、32．已知a ＝1999x ＋2000，b ＝1999x ＋2001，c ＝1999x ＋2002，则多项式a 2＋b 2＋c 2－ab －bc －ca 的值为【 】A 、0B 、1C 、2D 、33．如图，点E 、F 分别是矩形ABCD 的边AB 、BC 的中点，连AF 、CE 交于点G ，则A B C DA G C D S S 矩形四边形等于【 】 A 、65 B 、54 C 、43 D 、32ABC DEF G4．设a 、b 、c 为实数，x ＝a 2－2b ＋3π，y ＝b 2－2c ＋3π，z ＝c 2－2a ＋3π，则x 、y 、z 中至少有一个值【 】A 、大于0B 、等于0C 、不大于0D 、小于0 5．设关于x 的方程ax 2＋(a ＋2)x ＋9a ＝0，有两个不等的实数根x 1、x 2，且x 1＜1＜x 2，那么a 的取值范围是【 】 A 、72-＜a ＜52 B 、a ＞52 C 、a ＜72- D 、112-＜a ＜06．A 1A 2A 3…A 9是一个正九边形，A 1A 2＝a ，A 1A 3＝b ，则A 1A 5等于【 】 A 、22b a + B 、22b ab a ++ C 、()b a +21D 、a ＋b 二、填空题7．设x 1、x 2是关于x 的一元二次方程x 2＋ax ＋a ＝2的两个实数根，则(x 1－2x 2)(x 2－2x 1)的最大值为 。

8．已知a 、b 为抛物线y ＝(x －c)(x －c －d)－2与x 轴交点的横坐标，a ＜b ，则b c c a -+-的值为 。

9．如图，在△ABC 中，∠ABC ＝600，点P 是△ABC 内的一点，使得∠APB ＝∠BPC ＝∠CPA ，且PA ＝8，PC ＝6，则PB ＝ 。

2002年四川省初中数学竞赛一试一、选择题（每小题6分，共36分）1、若x<1，则|+|等于（）（A）1 （B）3-2x (C) 2x-3 (D) -22、如图，一个长为10米的梯子斜靠在墙上，梯子的顶端距地面的垂直距离为8米，如果梯子的顶端下滑1米，那么梯子的底端的滑动距离（）（A）等于1米（B）大于1米（C）小于1米（D）不能确定3、设a,b 都是正实数且，那么的值为（）（A ）（B ）（C ）（D ）4、若x1,x2是方程x2+2x-k=0的两个不相等的实数根，则x +x-2是（）（A）正数（B）零（C）负数（D）不大于零的数5、如果等腰梯形的下底与对角线长都是10厘米，上底与梯形的高相等，则上底的长是（）厘米。

（A）5（B）6（C）5 （D）6 6、关于的两个方程x2+4mx+4m2+2m+3=0,x2+(2m+1)x+m2=0中至少有一个方程有实根，则m的取值范围是（）（A）-<m<-（B）m≤-或m≥-（C）-<m<（D）m≤-或m ≥二、填空题（每小题9分，共54分）1、如果y=++2，则2x+y= .2、设a是一个无理数，且a,b满足ab+a-b=0，则b= .3、在一长8米宽6米的花园中欲挖一面积为24米2的矩形水池，且使四边所留走道的宽度相同，则该矩形水池的周长应为米。

2ABCDE34O4、如图，D、E分别是ABC的AC、AB边上的点，BD、CE相交于点O，若S△OCD=2，S△OBE=3，S△OBC=4，那么S ADOE= 。

5、如图，立方体的每个面上都写有一个自然数，并的是质数a，12的对面写的是质数b，15的对面写的是质数c，则a2+b2+c2-ab-ac-bc= .6、△ABC的一边为5，另外两边的长恰好是方程2x2-12x+m=0的两个根，则m的取值范围 .三、（20分）某公司生产电脑，1997年平均每台生产成本为5000元，并以纯利润20%标定出厂价，1998年开始，公司国强管理和技术改造，从而生产成本逐年降低，2001年每台电脑出厂价仅为1997年出厂价的80%，但公司却得到50%的利润，求以1997年生产成本为基数，1997年2001年生产成本平均每年降低的百分数（精确到0.01）.(计算时：=1.414, =1.732, =2.236)四、（20分）如图，P是⊙O外一点，PA与⊙O切于A，PBC是⊙O的割线，AD⊥PO于D，求证：PB：BD=PC：CD.AC五、（20分）将最小的31个自然数分成A、B两组，10在A组中，如果把10从A组移到B组，则A组中各数的算术平均数增加，B组的各数的算术平均数也增加，问A 组中原有多少个数？。

2002年全国初中数学竞赛试题一、选择题1．设a ＜b ＜0，a2＋b2＝4ab ，则ba ba -+的值为【 】 A 、3 B 、6 C 、2 D 、3Bq20xL2kEI 2．已知a ＝1999x ＋2000，b ＝1999x ＋2001，c ＝1999x ＋2002，则多项式a2＋b2＋c2－ab －bc －ca 的值为【 】Bq20xL2kEI A 、0 B 、1 C 、2 D 、3Bq20xL2kEI 3．如图，点E 、F 分别是矩形ABCD 的边AB 、BC 的中点，连AF 、CE 交于点G ，则ABCDAGCD S S 矩形四边形等于【 】A 、65 B 、54 C 、43 D 、32Bq20xL2kEI AB C DEF G4．设a 、b 、c 为实数，x ＝a2－2b ＋3π，y ＝b2－2c ＋3π，z ＝c2－2a ＋3π，则x 、y 、z 中至少有一个值【 】Bq20xL2kEI A 、大于0 B 、等于0 C 、不大于0 D 、小于0Bq20xL2kEI 5．设关于x 的方程ax2＋(a ＋2>x ＋9a ＝0，有两个不等的实数根x1、x2，且x1＜1＜x2，那么a 的取值范围是【 】Bq20xL2kEI A 、72-＜a ＜52 B 、a ＞52 C 、a ＜72- D 、112-＜a ＜0 6．A1A2A3…A9是一个正九边形，A1A2＝a ，A1A3＝b ，则A1A5等于【 】A 、22b a +B 、22b ab a ++C 、()b a +21 D 、a ＋b 二、填空题7．设x1、x2是关于x 的一元二次方程x2＋ax ＋a ＝2的两个实数根，则(x1－2x2>(x2－2x1>的最大值为 。

Bq20xL2kEI8．已知a、b为抛物线y＝(x－c>(x－c－d>－2与x轴交点的横坐标，a＜b，则bcca-+-的值为。

Bq20xL2kEI 9．如图，在△ABC中，∠ABC＝600，点P是△ABC内的一点，使得∠APB＝∠BPC＝∠CPA，且PA＝8，PC＝6，则PB＝。