【全国百强校word】河北省衡水中学2017届高三上学期一轮复习第六周周测地理试题

参考答案1．A 试题分析：由220x x -≥有02x ≤≤，所以集合[]0,2A =，=(-,0)(2,+)R C A ∞∞U ；当x R∈时，20xy =>，所以集合(0,+)B =∞,则=B A C R I )((2,)+∞,故选A.2．C 试题分析：22(1)1121(1)(1)i z i i i i i i i i +=+=+=++=+--+,所以z 的共轭复数12z i =- 3．D 试题分析：相关系数r 越接近于1和残差平方和m 越小，两变量A B 、的线性相关性越强4．C 试题分析：本程序框图的功能是求5121814121+⋅⋅⋅+++的值, 而9115122=,所以当9n =时要执行循环体,10n =时不执行循环体,输出S ,得出结果,故?10≥n ,选C.5．A 试题分析：由题意设双曲线方程为22221(0,0)x y a b a b-=>>，则离心率c e a ===，所以222a b =，焦点(,0)c ±到渐近线by x a=±的距离为1bc b c ===，所以22a =，双曲线方程为1222=-y x ,故选A.6．C 试题分析：此几何体是底面为正方形的长方体,由正视图有底面对角线为4,所以底边边长为,由侧视图有高为3,该几何体的外接球球心为体对角线的中点,设其外接球半径为R ,则25R ==,52R =,表面积22544254S R πππ==⨯=,故选C.7．B 试题分析：设增量为30302916305390229d S d d ⨯⇒=⨯+=⇒=，故选B. 8．C 试题分析：选项A, 若βα⊥，β⊂m ，则m α⊂或m αP 或m 与α相交,A 错；选项B, 若βα∥，α∥m ，则β∥m 或m β⊂,B 错；选项C,若βα∥，α⊥m ，则β⊥m ,C 正确；选项D, 若α∥m ，β∥m ，则βα∥或α与β相交,D 错.故选C.9．B 试题分析：对于①命题“若)(x f 是周期函数，则)(x f 是三角函数”的否命题是“若)(x f 不是周期函数，则)(x f 不是三角函数”，①错；对于②,命题“存在0,2>-∈x x R x ”的否定是“对于任意2,0x R x x ∈-≤” ,②错；对于③，在ABC ∆中，当B A sin sin >时，由正弦定理sin sin a bA B=有a b >，由大边对大角有A B >,当A B >时,得a b >，由正弦定理有B A sin sin >，所以“B A sin sin >”是“B A >”成立的充要条件,③正确；对于④，举例函数2()(2016)f x x =-，在)2017,2015(上有零点2016x =，但(2015)(2017)10f f ⋅=>不符合.故只有1个正确.10．C 试题分析：当04k <<时，椭圆焦点在x 轴上，224,a b k ==，c ==离心率2c e a ==，由112e <<有03k <<；当4k >时，椭圆焦点在y 轴上，22,4,a k b c ===e =，112e <<有163k >.故实数k 的范围是03k <<或163k >,选C. 11．D 试题分析：由已知有，第二年的年销售收入为70%(70)(11.8)1%x x x ⋅+--万元，商场对该商品征收的管理费记为70%,(70)(11.8)%(0)1%x y y x x x x ⋅=+->-，则14y ≥，所以70%(70)(11.8)%141%x x x x ⋅+-≥-，化简得212200x x -+≤，所以210x ≤≤，故x 得最大值为10 12．B 试题分析：设(,)M t kt 为函数kx x f =)(上的一点,则(,)M t kt 关于直线e y =的对称点为(,2)N t e kt -在函数)1(2ln 2)(2e x ee x x g ≤≤+=上,所以22ln 2e kt t e -=+,22ln 1()t k t e t e =-≤≤,则22ln 2't k t -=,所以k 在1,e e ⎡⎫⎪⎢⎣⎭上为减函数,在(2,e e ⎤⎦上为增函数,所以当t e =时min2ln 2e k e e=-=-,当1t e =时max 12ln21e k e e=-=,故22k e e -≤≤,选B. 13．38试题分析：由题意所有可能的情况有44=16⨯种情况，函数b a y x+=的图象经过第三象限时，{},a b 配对的情况有{}{}{}{}11,2,,2,2,2,2,1,3,2,3,132⎧⎫⎧⎫------⎨⎬⎨⎬⎩⎭⎩⎭共6种情况，故函数的图象经过第三象限的概率为63168=.14．5,53⎡⎫-⎪⎢⎣⎭试题分析：由已知的不等式组,画出可行域如图阴影部分,三角形三个顶点坐标分别为3(2,)2,(2,1)-,12(,)33,当z 取不同值时, 122--=y x z 表示的是斜率为1的平行直线系,经过点12(,)33时,z 取最小值53-,在经过点(2,1)-时,取最大值5,由于不等式2x <表示的区域不包括直线2x =,所以不能取到最大值5,故z 的取值范围是5,53⎡⎫-⎪⎢⎣⎭.15．2016试题分析：由已知有2121a b a a ==,322a b a =,所以32212a a b b b ==,由433ab a =有433123a a b b b b ==,同理得1231n n a b b b b -=L ,所以211220a b b b =L ,而数列{}n b 为等比数列,故110102112201202191011()()()(2016)2016a b b b b b b b b b ====L L .16．322⎡⎤⎢⎥⎣⎦，试题分析：由已知条件,建立平面直角坐标系,如图,则(0,2),(0,0),(2,0)A B C ，线段AC 方程为20(02)x y x +-=≤≤，设(,2),(,2)M a a N b b --,a b <,由2=MN 有1b a -=,所以(1,1)N a a +-,由于N M ,为AC 边上两个动点,所以01a ≤≤,且213(,2)(1,1)(1)(2)(1)2()22BM BN a a a a a a a a a ⋅=-⋅+-=++--=-+u u u u r u u u r ,当12a =时,有最小值32,当0a =或1a =,有最大值2.故BN BM ⋅的取值范围为322⎡⎤⎢⎥⎣⎦，17解：（1）所以32=a ，2=∴d ，12-=∴n a n ，………..3分2n S n =………6分（2）.12分18.解：（1）由题意可得2632718x y ==，所以7x =，3y =. ……………………3分 （2）记从中层抽取的3人为1b ，2b ，3b ，从高管抽取的2人为1c ，2c ，则抽取的5人中选2人的基本事件有：12(,)b b ，13(,)b b ，11(,)b c ，12(,)b c ，23(,)b b ，21(,)b c ，22(,)b c ，31(,)b c ，32(,)b c ，12(,)c c 共10种. ……8分设选中的2人都来自中层的事件为A ，则A 包含的基本事件有：12(,)b b ，13(,)b b ，23(,)b b 错误!未找到引用源。

河北省衡水中学2016～2017学年度第6周周测物理试题第1卷二、选择题：本题共8小题,每小题6分,在每小题给出的四个选项中,第14—18题只有一项符合题目要求,第19～21题至少有两项符合题目要求。

全部选对的得6分,选对但不全的得3分,有选错的得0分。

14.下列关于电磁感应现象的认识,正确的是( ) A.它最先是由奥斯特通过实验发现的 B.它说明了电能生磁C.它是指变化的磁场产生电流的现象D.它揭示了电流受到安培力的原因15.质量为m 、长为L 的直导体棒放置于四分之一光滑圆弧轨道上,整个装置处于竖直向上磁感应强度为B 的匀强磁场中,直导体棒中通有恒定电流,平衡时导体棒与圆弧圆心的连线与竖直方向成600角,其截面图如图所示。

则关于导体棒中的电流方向、大小分析正确的是( )A.向外,BL m g 3 B.向外,BL m g33 C.向里,BL m g 33 D.向里,BLm g3 16.有一静电场,其电势随x 坐标的改变而改变,变化的图线如图所示。

若将一带负电的粒子(重力不计)从坐标原点0由静止释放,粒子沿x 轴运动,电场中P 、Q 两点的坐标分别为1mm 、4mm 。

下列说法正确的是( )A.粒子经过P 点和Q 点时,加速度大小相等、方向相反B.粒子经过P点与Q点时,电场力做功的功率相等C.粒子经过P点与Q点时,动能相等D.粒子在P点的电势能为正值17.如图所示,传送带足够长,与水平面间的夹角α＝370,并以v＝10m/s的速度逆时针匀速转动着,在传送带的A端轻轻地放一个质量为m＝lkg的小物体,若己知物体与传送带之间的动摩擦因数μ＝0.5,(g＝10m/s2,sin370＝0.6,cos370＝0.8)则下列有关说法正确的是( )A.在放上小物体的第1s内,系统产生50J的热量B.在放上小物体的第1s内,至少给系统提供能量70J才能维持传送带匀速转动C.小物体运动1s后加速度大小为2m/s2D.小物体运动1s后,受到的摩擦力大小不适用公式F＝μF N18.2013年12月2日,我国成功发射“嫦娥三号”探月卫星,如图所示为“嫦娥三号”飞行轨道示意图.“嫦娥三号”任务全过程主要经历5个关键飞控阶段,分别是：发射及入轨段；地月转移段；环月段；动力下降段；月面工作段.其中在环月段时要从圆轨道变换到椭圆轨道.下列说法正确的是( )A.“嫦娥三号”的发射速度大于11.2 km/sB.由圆轨道变换到椭圆轨道时,“嫦娥三号”要加速C.由圆轨道变换到椭圆轨道时,“嫦娥三号”绕月球运动的周期减小D.“嫦娥三号”在动力下降段处于失重状态19.如图所示,匀强磁场的方向竖直向下,磁场中有光滑的水平桌面,在桌面上平放着内壁光滑.底部有带电小球的试管。

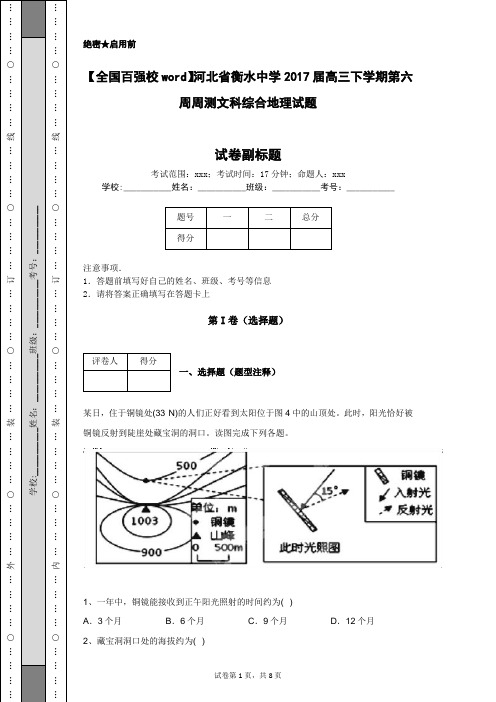
绝密★启用前【全国百强校word 】河北省衡水中学2017届高三下学期第六周周测文科综合地理试题试卷副标题考试范围：xxx ；考试时间：17分钟；命题人：xxx学校:___________姓名：___________班级：___________考号：___________注意事项．1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、选择题（题型注释）某日，住于铜镜处(33°N)的人们正好看到太阳位于图4中的山顶处。

此时，阳光恰好被铜镜反射到陡崖处藏宝洞的洞口。

读图完成下列各题。

1、一年中，铜镜能接收到正午阳光照射的时间约为( ) A ．3个月B ．6个月C ．9个月D ．12个月2、藏宝洞洞口处的海拔约为( )A ．990米B ．790米C ．590米D ．390米近年来，我国部分城市遭遇暴雨时，立交桥下、低洼地区往往积木成灾，出现交通中断，甚至财产损失、人员伤亡等现象，影响城市正常运转。

读右图“某城区降雨径流与不透水面积关系图”回答下列问题。

3、该城区( )A ．降雨量相同，不透水面积比例越大，径流量越小B ．径流量相同，不透水面积比例越大，降水量越大C ．不透水面积比例越大，单位降水量产生径流越大D ．降雨量越大，不同透水面积比例对应的地表径流的差值越小 4、为降低城市暴雨带来的损失，城市施工建设应采用的措施( ) ①增强预报、预警 ②扩大绿地面积 ③完善蓄水，排水系统 ④改进路面材料透水性 ⑤提高个人防范意识 A ．①③③④B ．②③④C ．①②③④⑤D ．③④⑤下面图Ⅰ中Pa 为晨昏线，图Ⅱ是图Ⅰ中的对应河段厦其附近的等潜水位线圈，图Ⅲ中的年径流量曲线图是从图Ⅱ中A 、E 两处测得的，读图回答问题。

5、关于图Ⅰ的说法，正确的是( )A ．位于北半球，PQ 为昏线B ．位于南半球，PQ 为晨线C ．PQ 间的实际距离约为20KmD ．图中河流径流的季节变化小6、．关于河流EF 段、CD 段的说法，正确的是( ) A ．EF 段流向为由北向南，CD 段河水补给潜水 B ．EF 段流向为由北向南，CD 段河水潜水补给河水 C ．EF 段流向为由南向北，CD 段河水潜水补给河水 D ．EF 段流向为由南向北，CD 段河水补给潜水7、比较a 、b 、c 、d 的数值大小( ) A. a>b>c>d B. a<b<c<d C. a=b=c=d下图为云南高黎贡山北段植物物种丰富度随海拔变化示意图，读图回答下列问题。

试卷第1页，共9页绝密★启用前【全国百强校word 】河北省衡水中学2017届高三高考模拟信息卷（四）文综地理试题 （带解析）试卷副标题考试范围：xxx ；考试时间：24分钟；命题人：xxx学校:___________姓名：___________班级：___________考号：___________注意事项．1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、选择题（题型注释）下图为我国某区域等高线地形图，读图回答下列各题1、图中A 、B 两地的地质构造分别对应下图的试卷第2页，共9页………线…………○……………线…………○……A. ②③B. ①②C. ③④D. ①③2、图中B 区域北侧的高原主要地貌类型及民居说法正确的是 A ．喀斯特地貌 竹楼 B ．雅丹地貌 土楼 C ．黄土地貌 窑洞D ．丹霞地貌 蒙古包中泰铁路合作项目原计划全长900km ，纵贯泰国中部，在其东北部的廊开与中老铁路对接，经老挝磨丁和中国磨憨抵达昆明，共同构成泛亚铁路中线。

2016年3月25日泰国交通部长突然宣布，出于对贷款利率等因素的考虑，泰国决定自筹资金投资中泰铁路项目建设工程，不敢再向中方贷款。

虽然仍将使用中国技术、信号系统和列车，但工程将使用泰国企业作为分包商，原材料、设备和劳动力也将来自泰国。

泰国政府同时决定，仅建设曼谷-呵叻段一段，设计时速250km 。

下图为泛亚铁路规划线路图。

读图和材料，完成下列各题。

试卷第3页，共9页3、泛亚铁路建设的主导因素是 A ．市场B ．政策C ．资源D ．科技4、泰国境内曼谷-呵叻一段高铁线路长度约 A ．50kmB ．250kmC ．450kmD ．650km5、中国高铁迅速走向世界，除中国政府大力支持外，其竞争优势还包括①勘测设计时间短，施工先进 ②技术最先进，生产制造能力最强③运营成本低，经验丰富④快速而安全，建设成本较低⑤融资门槛低，贷款利率低 A ．①②③B ．①②⑤C ．②③④D ．①③④下面分别是1984～2013年中国经济重心、人口重心演变轨迹示意图，据此完成下列各题。

A.圆环中产生逆时针方向地电流。

则下列判断正确地是(1)实验时他们先调整垫木地位置,使不挂配重片时小车能在倾斜地长木板上做匀速直线运动,这样做地目地是；(1)该学生接线中错误和不规范地做法是A.滑动变阻器不起变阻作用能E pm = 0.8J,已知小物块与水平面间地动摩擦因数μ=0.5,g取10m/s2。

求:(1)小物块从A点运动至B点地时间。

(2)小物块经过圆弧轨道上地C点时,对轨道地压力大小。

(3)C、D两点间地水平距离L。

25. (18分)如图甲所示,两金属板M、N水平放置组成平行板电容器,在M板中央开有小孔O,再将两个相同地绝缘弹性挡板P、Q对称地放置在M板上方,且与M板夹角均为60°,两挡板地下端在小孔O左右两侧。

现在电容器两板间加电压大小为U地直流电压,在M板上方加上如图乙所示地、垂直纸面地交变磁场,以方向垂直纸面向里为磁感应强度地正值,其值为B0,磁感应强度为负值时大小为B x,但B x未知。

现有一质量为m、电荷量为+q、不计重力地带电粒子,从N金属板中央A点由静止释放,t=0时刻,粒子刚好从小孔O进入上方磁场中,在t1时刻粒子第一次撞到左挡板P上,紧接着在t1+t2时刻粒子撞到了右挡板Q上,然后粒子又从O点竖直向下返回平行金属板间,接着再返回磁场做前面所述地运动。

粒子与挡板碰撞前后电量不变,沿板面地分速度不变,垂直于板面地分速度大小不变、方向相反,不计碰撞地时间及磁场变化产生地感应影响。

求:(1)粒子第一次到达挡板P时地速度大小。

(2)图乙中磁感应强度B x地大小。

(3)两金属板M和N之间地距离d。

(二)选考题:共45分。

请考生从给出地2道物理题、2道化学题、2道生物题中每科任选一题作答。

如果多答, 则每学科按所答地第一题计分。

33.[物理——选修3 —3](15分）(1)(6分)分子间同时存在相互作用地引力和斥力,分子力则是它们地合力（即表现出来地力）。

关于分子②图甲所示是汽缸水平放置达到地平衡状态24、（1）小物块恰好从B点沿切线方向进入轨道。

河北省衡水中学2017届高三上学期期中考试英语试卷本试卷分为第I卷（选择题）和第II卷（非选择题）两部分, 共150分。

考试时间120分钟。

第I卷 (共90分)注意事项:1．答第一卷前,考生务必将自己地姓名、考号、考试科目用铅笔涂写在答题卡上。

2．选出每小题解析后,用铅笔把答题卡上对应题目地解析标号涂黑。

如需改动,用橡皮擦干净后,再选涂其它解析标号。

不能答在本试卷上,否则无效。

第一部分听力（共两节,满分20分）第一节（共5个小题；每小题1分,满分5分）听下面5段对话。

每段对话后有一个小题,从每题所给地A、B、C三个选项中选出最佳选项,并标在试卷地相应位置。

听完每段对话后,你都有10秒钟地时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. Where is the woman going now?A. To the library.B. To a coffee shop.C. To the supermarket.2. What does the man care about most?A. Earning some extra money.B. Keeping the environment clean.C. Helping out the corner shop.3. When is the woman’s birthday?A. In May.B. In April.C. In March.4. What is the man doing?A. Playing with his daughter.B. Playing a joke on the woman.C. Playing a game on his smartphone.5. Why is the woman’s French so good?A. She has been studying for ten years.B. She was born in France.C. She works hard at it.第二节:听下面5段对话或独白。

2n++⨯，n++⨯2nn+2n n ++-PDBD D =，平面EAC （Ⅱ）解：∵PD ∥EAC 平面PBD OE ，BD 中点，∴ABCD 是菱形，ADPD D =，∴123PAD S ∆⨯⨯20．（本小题满分13分）22为直径的圆的外部，则0OA OB ⋅>，∴()()112212,,OA OB x y x y y y ==)()(244kx x x k x -+-+()21643k k =+)()0,+∞()>成立1f x河北省衡水中学2017届高三上学期六调数学（文科）试卷解析一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．【考点】并集及其运算．【分析】求出集合A，然后求解并集即可．【解答】解：集合A={x|y=lg（x﹣3）}={x|x＞3}，B={x|x≤5}，则A∪B=R．故选：D．2．【考点】复数代数形式的乘除运算．【分析】利用复数的运算法则、共轭复数的定义即可得出．【解答】解：复数z====，则=﹣1﹣i．故选：D．3．【考点】五点法作函数y=Asin（ωx+φ）的图象．【分析】先将函数变形，再利用三角函数的图象的平移方法，即可得到结论．【解答】解：∵函数y=sin（2x﹣）=sin[2（x﹣）]，∴为了得到函数y=sin（2x﹣）的图象，可以将函数y=sin2x的图象向右平移个单位长度故选A．4．【考点】双曲线的简单性质．【分析】由双曲线方程求出三参数a，b，c，再根据离心率e=求出离心率．【解答】解：由题意，m2﹣4＜0且m≠0，∵m∈Z，∴m=1∵双曲线的方程是y2﹣x2=1∴a2=1，b2=3，∴c2=a2+b2=4∴a=1，c=2，∴离心率为e==2．故选：B．5．【考点】线性回归方程．【分析】根据表格中所给的数据，求出这组数据的横标和纵标的平均值，表示出这组数据的样本中心点，根据样本中心点在线性回归直线上，代入得到关于m的方程，解方程即可．【解答】解：∵根据所给的表格可以求出==4．5，==∵这组数据的样本中心点在线性回归直线上，∴=0.7×4．5+0.35，∴m=3，故选：D．6．【考点】程序框图．【分析】模拟执行如图所示的程序框图，得出y的值是以3为周期的函数，当i=2014=671×3+1时终止循环，求出输出的y值．【解答】解：执行如图所示的程序框图，如下；y=2，i=1；y=1﹣=，i=2；y=1﹣=﹣1，i=3；y=1﹣=2，i=4；…；∴y的值是以3为周期的函数，则当i=2014=671×3+1时，终止循环，且输出的结果为y=2．故选：D．7．【考点】利用导数研究函数的单调性．【分析】先求导，再根据函数的奇偶性排除A，B，再根据函数值得变化趋势得到答案．【解答】解：∵f（x）=x2sinx+xcosx，∴f′（x）=x2cosx+cosx，∴f′（﹣x）=（﹣x）2cos（﹣x）+cos（﹣x）=x2cosx+cosx=f′（x），∴其导函数f′（x）为偶函数，图象关于y轴对称，故排除A，B，当x→+∞时，f′（x）→+∞，故排除D，故选：C．8．【考点】几何概型．【分析】根据题意，画出由曲线y=x+1与纵轴及直线y=2所围成的封闭图形区域D（阴影部分），以及不等式组所确定的区域E，计算阴影面积与正方形面积比即可．【解答】解：画出由曲线y=x+1与纵轴及直线y=2所围成的封闭图形区域D（阴影部分），以及不等式组所确定的区域E，如图所示，则在区域E内随机取一点，该点恰好在区域D的概率为：P==．故选：C．9．【考点】简单空间图形的三视图．【分析】根据几何体的三视图，得出该几何体是什么图形，从而求出结果．【解答】解：根据几何体的三视图知，该几何体为三棱锥，底面△ABC为俯视图中的直角三角形，∠BAC=90°，其中AC=4，AB=3，BC=5，PB⊥底面ABC，且PB=5，∴∠PBC=∠PBA=90°，∴最长的棱为PC，在Rt△PBC中，由勾股定理得，PC===5．故选：C．10．【考点】函数y=Asin（ωx+φ）的图象变换．【分析】由f（x）的图象经过点P（0，），且﹣＜θ＜，可得θ=，又由g（x）的图象也经过点P（0，），可求出满足条件的φ的值【解答】函数f（x）=sin（2x+θ）（﹣＜θ＜）向右平移φ个单位，得到g（x）=sin（2x+θ﹣2φ），因为两个函数都经过P（0，），所以sinθ=，又因为﹣＜θ＜，所以θ=，所以g（x）=sin（2x+﹣2φ），sin（﹣2φ）=，所以﹣2φ=2kπ+，k∈Z，此时φ=kπ，k∈Z，或﹣2φ=2kπ+，k∈Z，此时φ=kπ﹣，k∈Z，故选：C．11．【考点】轨迹方程．【分析】利用椭圆的定义判断点P的轨迹是以A．F 为焦点的椭圆，求出A、B的值，即得椭圆的方程．【解答】解：由题意得圆心F（1，0），半径等于2，|PA|=|PB|，∴|PF|+|PA|=|PF|+|PB|=|BF|=半径2＞|AF|，故点P的轨迹是以A．F 为焦点的椭圆，2a=2，c=1，∴b=，∴椭圆的方程为=1．故选D．12．【考点】利用导数研究函数的单调性；抽象函数及其应用．【分析】根据不等式恒成立，利用参数分类法进行转化为a≥x﹣x2lnx在≤x≤2上恒成立，构造函数h（x）=x﹣x2lnx，求函数的导数，利用函数单调性和导数之间的关系求出函数的最值即可．【解答】解：函数g（x）的导数g′（x）=3x2﹣2x=x（3x﹣2），∴函数g（x）在[，]上递减，则[，2]上递增，g（[）=，g(2)=8﹣4﹣5=﹣1，若对任意的，都有f（x1）﹣g（x2）≥2成立，即当≤x≤2时，f（x）≥1恒成立，即恒成立，即a≥x﹣x2lnx在≤x≤2上恒成立，令h（x）=x﹣x2lnx，则h′（x）=1﹣2xlnx﹣x，h′′（x）=﹣3﹣2lnx，当在≤x≤2时，h′′（x）=﹣3﹣2lnx＜0，即h′（x）=1﹣2xlnx﹣x在≤x≤2上单调递减，由于h′(1)=0，∴当≤x≤1时，h′（x）＞0，当1≤x≤2时，h′（x）＜0，∴h（x）≤h(1)=1，∴a≥1．故选：B．二、填空题：本题共4小题，每小题5分，满分20分，将答案填在答题纸上13．【考点】球的体积和表面积．【分析】直六棱柱的外接球的直径为直六棱柱中最长的对角线，可得直六棱柱的外接球的直径，即可求出外接球的体积．【解答】解：直六棱柱的外接球的直径为直六棱柱中最长的对角线，∵一个直六棱柱的底面是边长为2的正六边形，侧棱长为3，∴直六棱柱的外接球的直径为5，∴外接球的半径为，∴外接球的表面积为=25π．故答案为：25π．14．【考点】简单线性规划．【分析】作出题中不等式组表示的平面区域，得如图的△ABC及其内部，再将目标函数z=x﹣y对应的直线进行平移，可得当x=3，y=5时，z=x﹣y取得最小值．【解答】解：作出不等式组表示的平面区域，得到如图的△ABC及其内部，其中A（1，1），B（7，1），C（3，5）设z=F（x，y）=x﹣y，将直线l：z=x﹣y进行平移，当l经过点C时，目标函数z达到最小值∴z最小值=F（3，5）=﹣2故答案为：﹣215．【考点】数量积表示两个向量的夹角．【分析】由条件利用两个向量的数量积的定义求得的值，由此求得的值，可得||的值，再利用两个向量的夹角公式求得向量与+2的夹角．【解答】解：∵向量，的夹角为60°，且||=2，||=1，则=||•||•cos60°=2×1×=1，再由=+4+4=4+4+4=12，可得||==2．设向量与+2的夹角为θ，则cosθ====．再由0≤θ≤π可得θ=，故答案为．16．【考点】基本不等式在最值问题中的应用．【分析】（a﹣c）2+（b﹣d）2的几何意义是点（b，a）到点（d，c）的距离的平方，而点（b，a）在曲线y=3x ﹣ln（x+1）上，点（d，c）在直线y=2x+上．故（a﹣c）2+（b﹣d）2的最小值就是曲线上与直线y=2x+平行的切线到该直线的距离的平方．利用导数求出曲线上斜率为2的切线方程，再利用两平行直线的距离公式即可求出最小值．【解答】解：由ln（b+1）+a﹣3b=0，得a=3b﹣ln（b+1），则点（b，a）是曲线y=3x﹣ln（x+1）上的任意一点，由2d﹣c+=0，得c=2d+，则点（d，c）是直线y=2x+上的任意一点，因为（a﹣c）2+（b﹣d）2表示点（b，a）到点（d，c）的距离的平方，即曲线上的一点与直线上一点的距离的平方，所以（a﹣c）2+（b﹣d）2的最小值就是曲线上的点到直线距离的最小值的平方，即曲线上与直线y=2x+平行的切线到该直线的距离的平方．y'=，令y'=2，得x=0，此时y=0，即过原点的切线方程为y=2x，则曲线上的点到直线距离的最小值的平方=1．故答案为：1．三、解答题：解答应写出文字说明、证明过程或演算步骤．17．【考点】数列的求和；数列递推式．【分析】(1)根据条件利用等比数列的公式，求出公差，即可求数列{a n}的通项公式；(2)求得数列{b n}的通项公式，采用乘以公比错位相减法即可求得数列{b n}的前n项和T n．18．【考点】独立性检验的应用．【分析】（Ⅰ）随机调查这个班的一名学生，有50种情况，抽到不积极参加班级工作且学习积极性不高的学生，有19种情况，即可求出概率；（Ⅱ）利用列举法确定基本事件的个数，即可求出两名学生中有1名男生的概率是多少？（Ⅲ）求出K2，与临界值比较，即可得出结论．19．【考点】棱柱、棱锥、棱台的体积；平面与平面垂直的判定．【分析】（Ⅰ）由已知得AC⊥PD，AC⊥BD，由此能证明平面EAC⊥平面PBD．（Ⅱ）由已知得PD∥OE，取AD中点H，连结BH，由此利用，能求出三棱锥P﹣EAD的体积．20．【考点】直线与圆锥曲线的综合问题；椭圆的简单性质；抛物线的简单性质．【分析】（Ⅰ）设点G的坐标为（x0，y0），列出关于x0，y0，p的方程组，即可求解抛物线方程．（Ⅱ）利用已知条件推出m、n的关系，设（x1，y1）、B（x2，y2），联立直线与椭圆方程，利用韦达定理以及判别式大于0，求出K的范围，通过原点O在以线段AB为直径的圆的外部，推出，然后求解k的范围即可．21．【考点】利用导数求闭区间上函数的最值；利用导数研究函数的极值．【分析】（Ⅰ）对函数g（x）求导，得到g'（x）=0，得到极值点，求出极值．（Ⅱ）不妨设x2＞x1，则等价于：f（x2）﹣f（x1）＜h（x2）﹣h （x1），即f（x2）﹣h（x2）＜f（x1）﹣h（x1），分离参数，利用导数求最值求出参数范围即可．请考生在22．23两题中任选一题作答，如果多做，则按所做的第一题记分．[选修4-4：坐标系与参数方程] 22．【考点】简单曲线的极坐标方程；参数方程化成普通方程．【分析】(1)由曲线A的极坐标方程得到ρ2（3+sin2θ）=12，由此能求出曲线A的普通方程，由曲线B是过点P（﹣1，1），倾斜角为的直线，能求出曲线B的一个参数方程．(2)设|PM|=|t1|，|PN|=|t2|，把，代入中得，，由此利用韦达定理能求出|MP|+|NP|的值．[选修4-5：不等式选讲]23．【考点】绝对值不等式的解法；函数恒成立问题．【分析】（Ⅰ）先求出f（x）的表达式，得到关于x的不等式组，解出即可；（Ⅱ）问题转化为：a+1＞（f （x））min，求出f（x）的最小值，从而求出a的范围即可．。

2016-2017学年度上学期高三年级六调考试理数试卷第Ⅰ卷一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知21zi i=++,则复数z =（ ） A ．13i - B ． 13i -- C ．13i -+ D ．13i + 2. 已知命题()()()()122121:,,0p x x R f x f x xx ∀∈--≥，则p ⌝是（ ）A ．()()()()122121,,0x x R f x f x xx ∃∉--<B ． ()()()()122121,,0x x R f x f x xx ∃∈--< C ． ()()()()122121,,0x x R f x f x xx ∀∉--<D ．()()()()122121,,0x x R f x f x xx ∀∈--<3.已知()f x 是奇函数，且()()2f x f x -=，当[]2,3x ∈时，()()2log 1f x x =-，则13f ⎛⎫= ⎪⎝⎭（ ） A ． 22log 3- B ． 22log 3log 7- C ．22log 7log 3- D ．2log 32- 4.直线3y kx =+与圆()()22234x y -+-=相交于,M N 两点，若23MN ≥，则k 的取值范围是 （ ） A ．3,04⎡⎤-⎢⎥⎣⎦ B ．2,03⎡⎤-⎢⎥⎣⎦ C. 3,3⎡⎤-⎣⎦ D ．33,33⎡⎤-⎢⎥⎣⎦5.如图，若4n =时，则输出的结果为（ ）A ．37 B ． 67 C. 49D ．5116.已知一个底面为正六边形，侧棱长都相等的六棱锥的正视图与俯视图如图所示，若该几何体的底面边长为2，侧棱长为7，则该几何体的侧视图可能是 （ ）A ．B ．C. D ．7.已知,A B 为双曲线E 的左，右顶点，点M 在E 上，ABM ∆为等腰三角形，且顶角为120°，则E 的离心率为 （ ）A ． 2B ． 2 C. 3 D ．58. 已知,x y 满足约束条件102202x y x y y -+≥⎧⎪-+≤⎨⎪≤⎩，则23z x y =-的最小值为（ ）A ． -6B ．-3 C. -4 D ．-2 9. 已知向量,a b 满足()1,2,3,2a b a b ==-=，则2a b +=（ ）A ． 22B ．17 C. 15 D ．2510. 若数列{}n a 满足11a =，且对于任意的*n N ∈都有11n n a a n +=++，则122016111a a a +++等于（ ） A ．20162017 B ．20152016 C. 40302016 D ．4032201711.如图是函数()2f x x ax b =++的部分图象，则函数()()ln g x x f x '=+的零点所在的区间是（ ）A ． 11,42⎛⎫⎪⎝⎭ B ．1,12⎛⎫⎪⎝⎭C. ()1,2 D ．()2,3 12.已知函数()()xx f x x R e=∈，若关于x 的方程()()210f x mf x m -+-=恰好有4个不相等的实数根，则实数m 的取值范围为 （ ）A ． 11,1e ⎛⎫+ ⎪⎝⎭ B ． 20,2e e ⎛⎫ ⎪ ⎪⎝⎭ C. 21,12e e ⎛⎫+ ⎪ ⎪⎝⎭D ．2,12e e ⎛⎫ ⎪ ⎪⎝⎭ 第Ⅱ卷二、填空题:本题共4小题,每小题5分，满分20分，将答案填在答题纸上13.如图，利用随机模拟的方法可以估计图中由曲线22x y =与两直线2x =及0y =所围成的阴影部分的面积:S ①先产生两组01的增均匀随机数，()(),a rand b rand ==；②产生N 个点(),x y ，并统计满足条件22x y <的点(),x y 的个数1N ，已知某同学用计算器做模拟试验结果，当1000N =时，1332N =，则据此可估计S 的值为 ．（保留小数点后三位）14.《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为：弧田面积()212=⨯弦矢+矢.弧田，由圆弧和其所对弦所围成.公式中“弦”指圆弧对弦长，“矢”等于半径长与圆心到弦的距离之差，按照上述经验公式计算所得弧田面积与实际面积之间存在误差.现有圆心角为23π，弦长等于9米的弧田.按照《九章算术》中弧田面积的经验公式计算所得弧田面积与实际面积的差为 ．（实际面积-弧田面积）15.已知{}n a 满足()*211112311,,4444nn n n n n a a a n N S a a a a -+⎛⎫=+=∈=++++ ⎪⎝⎭，类比课本中推导等比数列前n 项和公式的方法，可求得45nn n S a -= ． 16.已知三棱锥0,90,O ABC BOC OA -∠=⊥平面BOC ，其中10AB =，13BC =，5,,,,AC O A B C =四点均在球S 的表面上，则球S 的表面积为 ． 三、解答题 ：解答应写出文字说明、证明过程或演算步骤.17. （本小题满分12分）如图，在ABC ∆中，030,25,B AC D ∠==是边AB 上一点．（1）求ABC ∆中，030,25,B AC D ∠==是边AB 上一点； （2）若2,CD ACD =∆的面积为4，ACD ∠为锐角，求BC 的长． 18. （本小题满分12分）四棱锥P ABCD -中，底面ABCD 为直角梯形，090ADC BCD ∠=∠=，2,3BC CD ==，04,60PD PDA =∠=，且平面PAD ⊥平面ABCD ．（1）求证：AD PB ⊥；（2）在线段PA 上是否存在一点M ，使二面角M BC D --的大小为6π，若存在，求出PM PA的值；若不存在，请说明理由．19. （本小题满分12分）某校高三一次月考之后，为了为解数学学科的学习情况，现从中随机抽出若干名学生此次的数学成绩，按成绩分组，制成了下面频率分布表： 组号 分组频数 频率 第一组[)90,1005 0.05 第二组 [)100,110 35 0.35 第三组 [)110,120 30 0.30 第四组 [)120,130 20 0.20 第五组 [)130,140100.10合计100 1.00（1）试估计该校高三学生本次月考的平均分；（2）如果把表中的频率近似地看作每个学生在这次考试中取得相应成绩的概率，那么从所有学生中采用逐个抽取的方法任意抽取3名学生的成绩，并记成绩落在[)110,130中的学生数为ξ， 求：①在三次抽取过程中至少有两次连续抽中成绩在[)110,130中的概率； ②ξ的分布列和数学期望．（注：本小题结果用分数表示） 20. （本小题满分12分）已知抛物线()2:20C x py p =>的焦点为F ，过抛物线上一点P 作抛物线C 的切线l 交x 轴于点D ，交y 轴于点Q ，当2FD =时，060PFD ∠=． （1）判断PFQ ∆的形状，并求抛物线C 的方程；（2）若,A B 两点在抛物线C 上，且满足0AM BM +=，其中点()2,2M ，若抛物线C 上存在异于A B 、的点H ，使得经过A B H 、、三点的圆和抛物线在点H 处有相同的切线，求点H 的坐标． 21. （本小题满分12分） 设函数()()()()ln ,01m x n f x x g x m x +==>+．（1）当1m =时，函数()y f x =与()y g x =在1x =处的切线互相垂直，求n 的值；（2）若函数()()y f x g x =-在定义域内不单调，求m n -的取值范围； （3）是否存在正实数a ，使得()202axa x f f e f x a ⎛⎫⎛⎫+≤⎪ ⎪⎝⎭⎝⎭对任意正实数x 恒成立？若存在，求出满足条件的实数a ；若不存在，请说明理由．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22. （本小题满分10分）选修4-4：坐标系与参数方程极坐标系与直角坐标系xOy 有相同的长度单位，以原点为极点，以x 轴正半轴为极轴，曲线1C 的极坐标方程为4sin ρθ=，曲线2C 的参数方程为cos sin x m t y t αα=+⎧⎨=⎩（t 为参数，0απ≤<），射线,,44ππθϕθϕθϕ==+=-与曲线1C 交于（不包括极点O ）三点,,A B C ．（1）求证：2OB OC OA +=；（2）当512πϕ=时，,B C 两点在曲线2C 上，求m 与α的值． 23. （本小题满分10分）选修4-5：不等式选讲 已知函数()32f x a x x =--+． （1）若2a =，解不等式()3f x ≤；（2）若存在实数x ，使得不等式()122f x a x ≥-++成立，求实数a 的取值范围．试卷答案一、选择题1-5: ABDDC 6-10: CACBD 11、12：BC二、填空题13. 1.328 14. 27327928π--15. 5n 16. 14π 三、解答题17.解：（1）∵在ABC ∆中，030,25B AC ∠==，∴由余弦定理，得222202cos AC AB BC AB BC ABC ==+-∠()22323AB BC AB BC AB BC =+-≥-，∴()20202323AB BC ≤=+-，当且仅当AB BC =时，取等号，∴()1sin 5232ABC S AB BC B ∆=≤+, ∴ABC ∆的面积的最大值为()523+；（2）设ACD θ∠=，在ACD ∆中，∵2,CD ACD =∆的面积为4，ACD ∠为锐角， ∴11sin 252sin 422ACD S AC CD θθ∆==⨯⨯=， ∴25sin 5θ=， ∴5cos 5θ=， 由余弦定理，得22252cos 20485165AD AC CD AC CD θ=+-=+-⨯=， ∴4AD =． 由正弦定理，得sin sinA AD CD θ=，∴42sin sin A θ=， ∴5sin 5A =， 此时sin sin BC AC A B =， ∴sin 4sin AC A BC B==， ∴BC 的长为4．18.解：（1）过点B 作//BO CD ，交AD 于O ，连接OP ． ∵0//,90,//OB AD BC ADC BCD CD ∠=∠=， ∴四边形OBCD 是矩形，∴,2OB AD OD BC ⊥==， ∵04,60PD PDA =∠=， ∴2202cos6023OP PD OD PD OD =+-=，∴222OP OD PD +=，∴OP OD ⊥， 又OP ⊂平面,OPB OB ⊂平面,OPB OPOB O =，∴AD ⊥平面OPB ，∵PB ⊂平面OPB ， ∴AD PB ⊥；（2）∵平面PAD ⊥平面ABCD ，平面PAD平面,ABCD AD OP AD =⊥， ∴OP ⊥平面ABCD ．以O 为原点，以,,OA OB OP 所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系，如图所示，则()()0,3,0,2,3,0B C -，假设存在点(),0,M m n ，使得二面角M BC D --的大小为6π， 则()(),3,n ,2,0,0MB m BC =--=-．设平面BCM 的一个法向量为(),,m x y z =，则0m BC m MB ⎧=⎪⎨=⎪⎩，∴2030x mx y nz -=⎧⎪⎨-+-=⎪⎩，令1y =，得30,1,m n ⎛⎫= ⎪ ⎪⎝⎭， ∵OP ⊥平面ABCD ，∴()0,0,1n =为平面ABCD 的一个法向量．∴233cos ,231m nn m n m nn ===+，解得1n =，∴123163623PM PO PA PO ---===． 19.解：（1）本次月考数学学科的平均分为59535105301152012510135114.5100⨯+⨯+⨯+⨯+⨯=；（2）由表，知成绩落在[)110,130中的概率为12，①设A 表示事件“在三次抽取过程中至少有两次连续抽中成绩在[)110,130中”． 则()1111131222228P A ⎛⎫=⨯+-⨯⨯= ⎪⎝⎭， 所以在三次抽取过程中至少有两次连续抽中成绩在[)110,130中的概率为38； ②ξ的可能取值为0，1，2，3()303110128P C ξ⎛⎫==-= ⎪⎝⎭，()21311311228P C ξ⎛⎫==⨯⨯-= ⎪⎝⎭，()212311321228P C ξ⎛⎫⎛⎫==⨯⨯-= ⎪ ⎪⎝⎭⎝⎭()33311328P C ξ⎛⎫=== ⎪⎝⎭ ξ的分布列为 ξ 0123P 18383818()13313012388882E ξ=⨯+⨯+⨯+⨯=，或13,2B ξ⎛⎫⎪⎝⎭，则()32E ξ=．20.解：（1）设()11,P x y ，则切线l 的方程为2112x x y x p p =-，且2112x y p=， 所以()111,0,0,,22x p D Q y FQ y ⎛⎫-=+⎪⎝⎭，12pPF y =+，所以FQ FP =，所以PFQ ∆为等腰三角形，且D 为PQ 的中点， 所以DF PQ ⊥，因为02,60DF PFD =∠=， 所以060QFD ∠=，所以12p=，得2p =， 所以抛物线方程为24x y =；（2）由已知，得,A B 的坐标分别为()()0,0,4,4，设()()0000,0,4H x y x x ≠≠，AB 的中垂线方程为4y x =-+，①AH 的中垂线方程为200428x y x x =-++，②联立①②，解得圆心坐标为 ：2200004432,88x x x x N ⎛⎫+++- ⎪⎝⎭， 由012NHx k =-，得32000280x x x --=， 因为000,4x x ≠≠，所以02x =-， 所以H 点坐标为()2,1-． 21.解：（1）当1m =时，()()211ng x x -'=+，∴()y g x =在1x =处的切线斜率14nk -=， 由()1f x x '=，得()11f '=，∴1114n-⨯=-，∴5n =． （2）易知函数()()y f x g x =-的定义域为()0,+∞，又()()()()()()()()222212121111111x m n x m n x m n x y f x g x x x x x x +--++--+⎡⎤-⎣⎦'''=-=-==+++，由题意，得()121x m n x+--+的最小值为负， ∴()14m n ->．（注：结合函数()2211y x m n x =+--+⎡⎤⎣⎦图象同样可以得到）， ∴()()21144m n m n +-⎡⎤⎣⎦≥->∴()14m n +->，∴3m n ->；（3）令()()2ln 2ln ln ln 22ax a x h x f f e f ax a ax x x a x a ⎛⎫⎛⎫=+=-+- ⎪ ⎪⎝⎭⎝⎭，其中0,0x a >>，则()1ln 2ln h x a a a x a x '=--+，则()1ln 2ln k x a a a x a x =--+，则()22110aax k x x x x +'=--=-<，∴()k x 在区间()0,+∞内单调递减，且()0k x =在区间()0,+∞内必存在实根，不妨设()00k x =，即()0001ln 2ln 0k x a a a x a x =--+=，可得001ln ln 21x a ax =+-，（*）则()h x 在区间()00,x 内单调递增，在区间()0x +∞内单调递减，∴()()0max h x h x =，()()()00001ln21ln h x ax a ax x =---，将（*）式代入上式，得()00012h x ax ax =+-．根据题意()000120h x ax ax =+-≤恒成立， 又∵0012ax ax +≥，当且仅当001ax ax =时，取等号， ∴00012,1ax ax ax +==，∴01x a =，代入（*）式，得1ln ln 2a a =，即12a a =，又0a >， ∴22a =，∴存在满足条件的实数a ，且22a =．22.解：（1）依题意4sin OA ϕ=，4sin ,4sin 44OB OC ππϕϕ⎛⎫⎛⎫=+=- ⎪ ⎪⎝⎭⎝⎭，则()()4sin 4sin 22sin cos 22sin cos 44OB OC ππϕϕϕϕϕϕ⎛⎫⎛⎫+=++-=++- ⎪ ⎪⎝⎭⎝⎭42sin 2OA ϕ==；（2）当512πϕ=时，,B C 两点的极坐标分别为223,,2,36ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭，化为直角坐标为()()3,3,3,1B C -， 曲线2C 是经过点(),0m ，且倾斜角为α的直线，又因为经过点,B C 的直线方程为323y x =-+， 所以523,6m πα==．23.解：（1）不等式()3f x ≤，化为2323x x --+≤，则22323x x x ≤-⎧⎨-++≤⎩或2232323x x x ⎧-<≤⎪⎨⎪---≤⎩或233223x x x ⎧>⎪⎨⎪---≤⎩， 解得3742x -≤≤，∴不等式()3f x ≤的解集为37|42x x ⎧⎫-≤≤⎨⎬⎩⎭；（2）不等式()122f x a x ≥-++等价于3321a x x a --+≥-， 即3361x a x a --+≥-，又()()3363366x a x x a x a --+≤--+=+， 若存在实数x ，使得不等式()122f x a x ≥-++成立， 则61a a +≥-，解得52a ≥-，∴实数a 的取值范围是5,2⎡⎫-+∞⎪⎢⎣⎭．。

河北省衡水中学2017届上学期高三年级六调考试理科综合本试题卷共12页，38题（含选考题）。

全卷满分300分，考试用时150分钟。

注意事项：1、答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2、选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3、非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4、选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。

答案写在答题卡上对应的答题区域内，写在试题卷、草稿纸和答题卡上的非答题区域无效。

5、考试结束后，请将本试题卷和答题卡一并上交。

可能用到的相对原子质量：H 1 C 12 N 14 O 16 F 19 Na 23 Mg 24 Al 27Si 28 S 32 Cl 35.5 K 39 Ca 40 Cr 52 Fe 56 Cu 64 Br 80 I 127 Ba 137第Ⅰ卷一、选择题：本题共13小题，每小题6分，共78分。

每小题只有一个选项符合题目要求。

1．下列有关细胞结构的说法正确的是A．高尔基体通过产生囊泡来增加膜面积B．染色体解螺旋形成染色质的同时，DNA分子双链也随之解旋C．在洋葱根尖分生区细胞有丝分裂末期高尔基体参与了赤道板的形成D．液泡内含有糖类、无机盐、色素和蛋白质等物质，可以调节植物细胞内部的环境2．下列关于细胞生命历程的叙述正确的是A．细胞的有丝分裂对生物性状的遗传有贡献B．恶性肿瘤细胞有无限增殖的特性，所以不易被化疗药物杀死C．细胞周期中染色质DNA和染色体DNA一样容易复制D．细胞在癌变过程中，细胞膜上甲胎蛋白和癌胚抗原等糖蛋白的含量会减少3．下列有关生物学实验的描述正确的是A．在电子显微镜下拍摄到的叶绿体的结构照片属于物理模型B．用无水乙醇提取分离绿叶中的色素，溶解度越大的色素在滤纸条上扩散速度越快C．用苏丹Ⅳ染液无法检测生物组织中维生素D的存在D．在观察细胞内DNA和RNA分布的实验中，可使用酒精来改变细胞膜通透性，加速染色剂进入细胞4．下列有关内环境稳态的叙述正确的是A．肾小管通过主动运输吸收水的过程受抗利尿激素的调节B．饥饿时，血液流经肝脏后血糖浓度会增加C．突触前膜释放的乙酰胆碱通过胞吞进入下一个神经元发挥作用D．神经递质在核糖体中合成，经由内质网和高尔基体加工后通过胞吐作用由突触前膜释放，这体现了生物膜的流动性5．“发展经济不应以破坏环境为代价”已经成为人类的共识，要保护生态系统，应走一条可持续发展的道路，为此，人们在广大的山区进行人工植树造林，在许多城市建造了湿地公园。