小升初常考-长方体和正方体题型
- 格式:doc
- 大小:286.50 KB
- 文档页数:16

完整版)长方体正方体经典题型汇总1.这个长方体的棱长总和是64分米。
2.这个长方体框架的高是15分米。
3.需要42厘米长的塑料带。
4.这个正方体的棱长是4厘米。
5.这个长方体的棱长总和是30分米。
6.这个长方体框架的高是20厘米。
7.这个正方体的棱长是28米÷4=7米。
8.这个长方体的棱长总和是21厘米。
9.每个正方体木块的棱长总和是40厘米。
1.至少需要36平方分米铁皮。
2.这张商标纸的面积是320平方厘米。
3.原来正方形铁皮的面积是625平方厘米。
4.这个长方体的表面积是162平方厘米。
5.粉刷水泥的面积是63平方米,需要252千克水泥。
6.至少需要480平方厘米铁皮,12节需要5760平方厘米铁皮。
7.20个这样的长方体需要400平方厘米的硬纸。
1.商标纸面积问题:一盒饼干长20厘米,宽15厘米,高30厘米。
要在它的四周贴上高6厘米的商标纸,求商标纸的面积。
解:首先计算长方体的表面积,即2(长×宽+长×高+宽×高),得到2(20×15+20×30+15×30)=2700平方厘米。
然后计算加上商标纸后的长方体的表面积,即2[(20+2×6)×(15+2×6)+(20+2×6)×(30+2×6)+(15+2×6)×(30+2×6)] =2×(32×27+32×42+27×42)=2×3024=6048平方厘米。
商标纸的面积即为加上商标纸后的表面积减去原表面积,即6048-2700=3348平方厘米。
2.侧面积问题:一个长方体侧面积是360平方厘米,高是9厘米,长是宽的3倍。
求它的表面积。
解:由题可得,长方体的宽为120/9=40厘米,长为3×40=120厘米。
因此,长方体的表面积为2(40×9+120×9+40×120)=2×(360+1080+4800)=2×6240=平方厘米。

小升初数学专项练习试题长方体正方体题型归纳
考试复习最忌心浮气躁,急于求成。
指导复习的教师,应给学生一种乐观、镇定、自信的精神面貌。
要扎扎实实地复习,一步一步地前进,下文为大家准备了小升初数学专项练习试题。
1.在括号里填上合适的单位名称。
(1)一块橡皮的体积大约是6( )。
(2)集装箱的体积大约是40( )。
(3)水桶的容积大约是12( )。
(4)一个西瓜的体积大约是4( )。
(5)教室的面积大约是56( )。
(6)一本数学书的体积约是320( )。
2.单位换算
3.05立方米=( )立方分米 60毫升=( )升
450立方厘米=( )升 ( )立方分米=800毫升
710毫升=( )升=( )立方分米
3.7升=( )立方分米( )立方厘米
4.一种冷藏车的车厢是长方体,从里面量,长4米,宽1.7米,高1.8米。
它的容积是多少立方米?
5.一块正方体石料,棱长8分米。
这块石料的体积是多少立方分米?如果1立方分米的石料重2.7千克,这块石料重多少千克?
为大家推荐的小升初数学专项练习试题,还满意吗?相信大家都会仔细阅读,加油哦!。
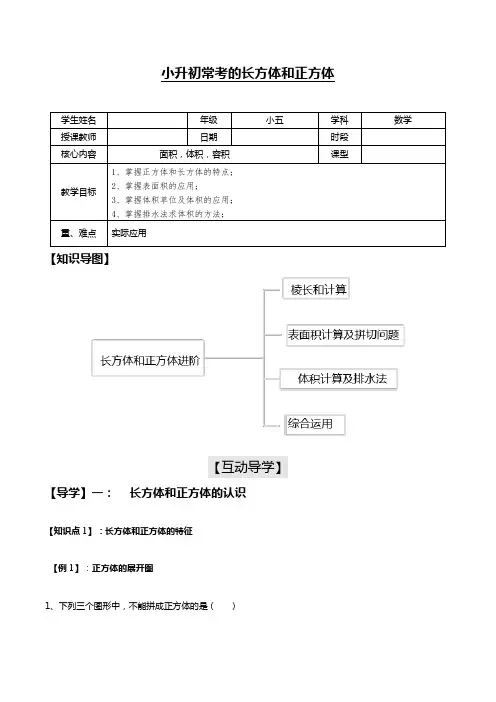
小升初常考的长方体和正方体学生姓名年级小五学科数学授课教师日期时段核心内容面积,体积,容积课型教学目标1、掌握正方体和长方体的特点;2、掌握表面积的应用;3、掌握体积单位及体积的应用;4、掌握排水法求体积的方法;重、难点实际应用【知识导图】【互动导学】【导学】一:长方体和正方体的认识【知识点1】:长方体和正方体的特征【例1】:正方体的展开图1、下列三个图形中,不能拼成正方体的是()① ② ③2、右图是一个正方体的展开图。
在这个正方体中,与面相对的是( )面,与面相对的是( ), ( )面与( )面是相对的面。
3、下图中哪两个字所在的面,是正方体中相对的面?4. 右图是正方体的一个平面展开图,将它折成正方体后, (1)1号面和( )号面相对; (2)2号面和( )号面相对; (3)3号面和( )号面相对。
【例3】:长方体的展开图(1)这是一个长方体的展开图,前面的面积是( )平方厘米,右面的面积是( )平方厘米, 上面的面积是( )厘米。
da bce f后(2)右图是一个长方体的展开图,这个长方体上面的面是 ( ),右面的面是( )。
A 、长4cm ,宽2cmB 、长4cm ,宽1.5cmC 、长2cm ,宽1.5cmD 、边长2cm(3)沿下图中的虚线折叠,可以围成一个长方体。
围成的这个长方体的体积是多少立方厘米?【例题】4:一个正方体的6个面分别涂着红、黄、蓝、白、黑、绿六种颜色,根据下面的三种摆法,判断哪种颜色的对面涂着哪种颜色。
练习1:根据一个正方体的三种不同的摆法,判断出相对的两个面上的字母各是什么?【例题】5:一个装书的纸皮箱,长55厘米,宽35厘米,高20厘米,如果要用封口纸条把这箱书封扎好(如图),需用多长的封口纸条?(接头处不计)黄4 红2蓝5 黑4 蓝白 绿 白红 F 4 D 2A 5B 6A 2C ECD【知识点2】:正方体的染色问题(1)三个面都染色:必定在顶点上;(2)两个面染色:必定在棱上;(3)一个面染色:必定在面上。

长方体正方体专项训练应用题一、长方体正方体的基本概念1. 长方体- 长方体有6个面,每个面都是长方形(可能有两个相对的面是正方形),相对的面完全相同。
- 长方体有12条棱,相对的棱长度相等,可以分为三组,每组有4条棱。
- 长方体有8个顶点。
2. 正方体- 正方体是特殊的长方体,它的6个面都是正方形,且6个面完全相同。
- 正方体有12条棱,12条棱的长度都相等。
- 正方体有8个顶点。
二、长方体正方体的表面积相关应用题1. 题目- 一个长方体的长是5厘米,宽是4厘米,高是3厘米,求这个长方体的表面积。
- 解析:- 长方体表面积公式为S=(ab + ah+bh)×2(其中a为长,b为宽,h为高)。
- 把a = 5厘米,b = 4厘米,h = 3厘米代入公式。
- 首先计算ab=5×4 = 20平方厘米,ah = 5×3=15平方厘米,bh=4×3 = 12平方厘米。
- 然后(ab + ah+bh)×2=(20 + 15+12)×2=(35 + 12)×2 = 47×2=94平方厘米。
2. 题目- 一个正方体的棱长为6分米,求它的表面积。
- 解析:- 正方体表面积公式为S = 6a^2(其中a为棱长)。
- 把a = 6分米代入公式,S=6×6^2=6×36 = 216平方分米。
三、长方体正方体的体积相关应用题1. 题目- 一个长方体的长是8米,宽是5米,高是4米,求这个长方体的体积。
- 解析:- 长方体体积公式为V=abh(其中a为长,b为宽,h为高)。
- 把a = 8米,b = 5米,h = 4米代入公式,V = 8×5×4=40×4 = 160立方米。
2. 题目- 一个正方体的棱长为7厘米,求它的体积。
- 解析:- 正方体体积公式为V=a^3(其中a为棱长)。
- 把a = 7厘米代入公式,V=7^3=7×7×7 = 343立方厘米。
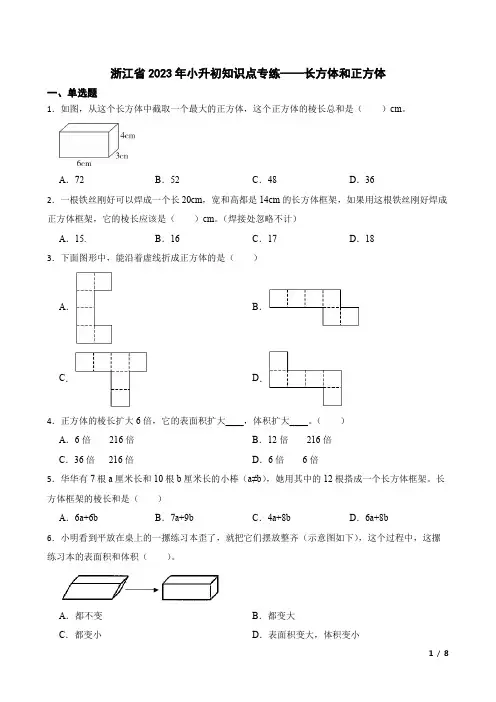
浙江省2023年小升初知识点专练——长方体和正方体一、单选题1.如图,从这个长方体中截取一个最大的正方体,这个正方体的棱长总和是()cm。
A.72B.52C.48D.362.一根铁丝刚好可以焊成一个长20cm,宽和高都是14cm的长方体框架,如果用这根铁丝刚好焊成正方体框架,它的棱长应该是()cm。
(焊接处忽略不计)A.15.B.16C.17D.183.下面图形中,能沿着虚线折成正方体的是()A.B.C.D.4.正方体的棱长扩大6倍,它的表面积扩大____,体积扩大____。
()A.6倍216倍B.12倍216倍C.36倍216倍D.6倍6倍5.华华有7根a厘米长和10根b厘米长的小棒(a≠b),她用其中的12根搭成一个长方体框架。
长方体框架的棱长和是()A.6a+6b B.7a+9b C.4a+8b D.6a+8b6.小明看到平放在桌上的一摞练习本歪了,就把它们摆放整齐(示意图如下),这个过程中,这摞练习本的表面积和体积()。
A.都不变B.都变大C.都变小D.表面积变大,体积变小7.一个长6分米,宽4分米,高5分米的长方体盒子,最多能放()个棱长是2分米的正方体的木块。
A.15B.14C.13D.128.用两个长4厘米,宽3厘米,高2厘来的长方体拼成个大长方体,这个大长方体的表面积最大是()平方厘米。
A.104B.98C.92D.88二、填空题9.正方体的棱长扩大到原来的5倍,它的表面积扩大到原来的倍,它一个面的面积扩大到原来的倍,它的体积扩大到原来倍.10.要做一个长6分米、宽4分米、高2分米的无盖玻璃鱼缸,用角钢做它的框架,至少需要角钢分米,把它放在桌面上,占平方分米.11.把1.2米的长方体材料(如图),平均锯成3段,表面积比原来增加2.4平方分米,原来这根木料的体积是立方分米。
12.一个长方体的体积是80立方厘米,它的长是4厘米,宽是5厘米,高是,它的表面积是,如果把这个长方体削成一个最大的正方体,正方体的体积是。

浙教版2023年小升初数学长方体和正方体知识点专练(含答案)一、单选题1.3个棱长是1厘米的正方体小方块排成一行后,它的表面积是()A.18平方厘米B.16平方厘米C.14平方厘米2.一个正方体的木料,它的底面积是10平方厘米,把它横截成4段相同的长方体,表面积增加()平方厘米。
A.60B.40C.303.观察下边展开图应该正方体的展开图A.B.C.4.把一个表面积是96平方米的正方体锯成两个长方体后,表面积增加了()平方米。
A.8B.16C.325.一个长方体的长是4厘米,宽是3.5厘米,高是1.5厘米,它的底面的面积是()平方厘米。
A.6B.14C.5.25D.216.用同样的金属制成一个棱长5dm的正方体油桶和一个长12.5dm、宽5dm、深2dm的长方体油桶,它们的体积相比()。
A.正方体大B.长方体大C.同样大D.无法比较7.一个长方体相交于同一个顶点的三条棱,长度的比是3:2:1,这三条棱长的和是12厘米,体积是()立方厘米。
A.48B.96C.24D.3848.一个长方体无盖鱼缸的长是30厘米,宽20厘米,高25厘米,这个鱼缸的用料是()A.21平方厘米B.31平方分米C.31平方厘米二、填空题9.把一个正方体锯成两个完全一样的长方体,每个长方体的表面积是24平方厘米,原来正方体的表面积是平方厘米。
10.把4个棱长是2dm的正方体顺次拼成一排,变成一个长方体,则表面积减少dm2.11.至少要个小正方体才能拼成一个大正方体,如果一个小正方体的棱长是3厘米,那么这样一个大正方体的表面积是平方厘米,体积是立方厘米。
12.一个长方体的前面和上面的面积之和是39平方厘米,它的长、宽、高都是质数,那么长方体的体积是.13.做一个下面规格的抽屉,至少需要平方米的木板。
(图中单位:厘米)14.图中小正方体的棱长是1厘米.下图的表面积是.(图中单位:厘米)15.用3个棱长是1厘米的小正方体拼成一个长方体.这个长方体的表面积是。
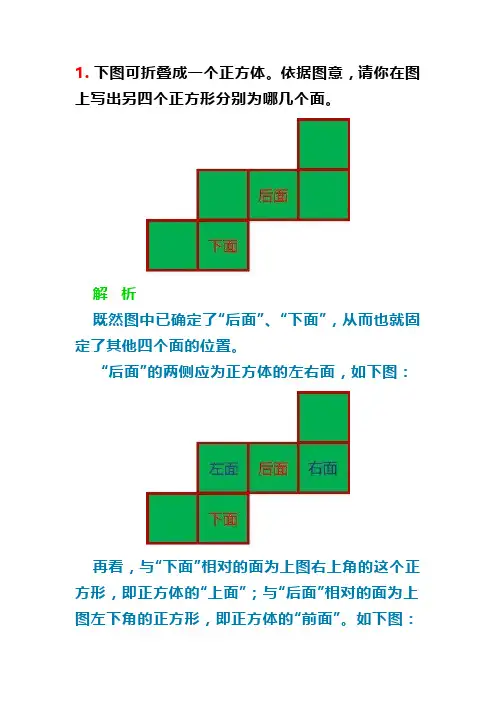
1. 下图可折叠成一个正方体。
依据图意,请你在图上写出另四个正方形分别为哪几个面。
解析既然图中已确定了“后面”、“下面”,从而也就固定了其他四个面的位置。
“后面”的两侧应为正方体的左右面,如下图:再看,与“下面”相对的面为上图右上角的这个正方形,即正方体的“上面”;与“后面”相对的面为上图左下角的正方形,即正方体的“前面”。
如下图:2.下图由五个正方形拼成,如果再添一个同样大小的正方形,应该放置在哪儿,才可将下图折叠成一个正方体?请将添加的正方形拼入下图。
解析可折叠成正方体的六个正方形的摆放结构有3类情况。
其一,以4个正方形(在同一条直线上)为主体,另两个正方形必须分布在两侧,。
其二,以三个正方形为主体,有以下四种结构:其三,以两个正方形为主体,其结构如阶梯状:再回到本题,如果添加一个正方形,使其成为4个正方形为主体,有以下2种添加方法:如果添加一个正方形,使其成为3个正方形为主体,有以下2种添加方法:所以,此题有以上四个答案3.用长299mm,宽为253mm的长方形装饰板拼一个正方形,至少要用多少块?解析由题意知,最少装饰板块数,只能拼出最小的正方形。
这个正方形边长应是装饰板长与宽的最小公倍数。
299与253的公因数不明显,最好用“碾转相除法"(本园地有相关知识专题讲解,可查阅)先求出二者的最大公因数。
299÷253=1 (46)253÷46=5 (23)46÷23=2 (整除为止)最后的除数23就是299与253的最大公因数。
再求299与253的最小公倍数:23×13×11=3289因而,拼出的正方形的边长应为3289mm。
由上式知,用装饰板长299mm拼出正方形边长3289mm所需块数为13;用装饰板宽253mm拼出正方形边长3289mm所需块数为11。
因此,要拼一个边长为3289mm的正方形所用装饰板至少的块数为:13×11=143块4. 一个长方体前面的面积为105平方厘米,右面的面积为56平方厘米,求这个长方体的表面积。


1. 一个长方体的长、宽、高分别为卫米、勺米、4米。
如果高增加2米,新的长方体体积比原来增加()立方米,表面积增加()平方米。
考查目的:计算长方体的表面积和体积。
答案,-1_r〔解析:因为长方体的底面大小不变(长、宽不变),高增加2米,新的长方体体积比原来增加的体积,即为同样底面积且高为2米的长方体的体积,根据“长方体的体积=长乂宽X高”可求得新长方体体积比原来增加的体积。
表面积增加的部分是高为2米的新长方体4个侧面的面积,即(2也+ 2^)x2 = 4(应十技)。
2.棱长1厘米的小正方体至少需要()个可拼成一个较大的正方体。
需要()个这样的小正方体可拼成一个棱长为1分米的大正方体,如果把这些小正方体依次排成一排,可以排成()米考查目的:长方体和正方体的特征,体积单位和长度单位之间的进率答案:8,1000, 10解析:每个小正方体的棱长都是1厘米,则其体积是1立方厘米,可以用它组成棱长是2厘米的正方体,这样就需要2X2X2 = 8 (个)小正方体。
棱长1 分米的大正方体体积是1立方分米,需要1 000个棱长1厘米的小正方体拼成,将这些小正方体依次排成一排,长度就是1 000个棱长1厘米的小正方体的边长 之和。
正方形都相同)后,沿虚线折起来,做成没有盖子的长方体铁盒,该铁盒的长是( )cm,宽是( )cm ,高是( )cm,表面积是( ) cm 2,容积是( )cm 3°(铁皮厚度不计) ;; 20 cm|| I ■■P ------------------- 40 cm --------------------- 彳考查目的:计算长方体的表面积和体积。
答案:30,10,5,700, 1 500。
解析:结合题意观察图形可知,这个铁盒的长、宽、高分别是( 40-5X 2) 厘米、(20-5X 2)厘米、5厘米,再利用长方体的表面积公式 &=(辭十皿十航汽2 和长方体的体积公式F = “品分别计算即可。

《长方体和正方体》主要题型一、长方体和正方体之间相互等量转换知识点:一定要清楚不变的量是什么练习:1、用一根铁丝刚好焊成一个棱长8厘米的正方体框架,如果用这根铁丝焊成一个长10厘米、宽7厘米的长方体框架,它的高应该是多少厘米?2、已知一本书是长方体形状,它的长是10厘米,宽是3厘米,高是8厘米,现在有一个与这本书表面积相同的正方体,求这个正方体的棱长之和二、棱长的变化引起表面积和体积的变化。
知识点:要清楚哪一条棱在变,哪一条棱不变练习:1、一个长方体,如果高增加2厘米就成了正方体,而且表面积要增加56平方厘米,原来这个长方体的体积是多少立方厘米?2、一个长方体,高截去2厘米,表面积就减少了48平方厘米,剩下部分成为一个正方体,求原长方体的体积?3、一个长方体,如果长减少2厘米就成了一个正方体,而且表面积要减少56平方厘米。
原来这个长方体的体积是多少立方厘米?4、一个长方体,长a分米,宽b分米,高h分米,如果高减少3分米,这个长方体表面积比原来减少()平方分米?体积比原来减少()立方分米?三、段的变化知识点:截1次,产生2个面(即表面积增加了2个面)练习:1、一个长方体长2米,截面是边长3厘米的正方形,将这个长方体木料锯成五段后,表面积一共增加了多少平方厘米?2、将一个长3米的长方体木料平均截成3段,表面积一共增加了0.36平方分米,这根木料的体积是多少立方分米?四、正方体拼知识点:拼表面积发生变化,体积不变练习:1、用8个棱长都是2厘米的正方体拼成一个长方体(包括正方体),拼成的长方体的表面积最多是多少平方厘米?最少是多少平方厘米?2、用12个棱长都是2厘米的正方体拼成一个长方体,一共有多少种拼法,每种拼法拼成的长方体的表面分别是多少?3、用四个棱长都是3厘米的正方体拼成一个长方体,拼成的长方体的表面积可能是多少?五、长方体切、拼1、将一个长8厘米,宽6厘米,高5厘米的长方体切成两个小长方体,表面积最多增加多少平方厘米?最少增加多少平方厘米?2、将三个长8厘米,宽6厘米,高5厘米的长方体拼成一个大长方体,表面积最多减少多少平方厘米?最少减少多少平方厘米?3、把一个长16 厘米,宽12厘米,高8厘米的长方体木块,锯成若干个小正方体,(没有剩余)至少可以锯成多少个这样的小正方体?表面积一共增加多少平方方厘米?六、挖知识点:清楚是哪一个位置被挖走,比较前后增加了几个面,减少了几个面1、用8个小正方体木块拼成一个大的正方体,如果拿走1个小方块,它的表面积和原来比( )。
-小升初长方体和正方体专项试题-人教版一、解答题(题型注释)别是6分米、4分米、26分米,正方体的体积是多少立方分米?2.一个正方体水箱的容积是125立方分米,把这一满水箱水全部注入到一长方体水箱内。
已知长方体水箱长10分米,宽5分米,这个水箱内的水深多少分米?3.一个长方体长4米,宽4米,高1.5米,这个长方体的表面积是多少?4.在如图上添上若干个正方形,使它成为一个正方体表面积的展开图,并求出这个正方体的表面积和体积.(正方形边长2厘米)5.按要求涂一涂6.加上一条线段,使下面的图形变成我们认识的图形。
7.下面是由几个正方体拼成的模型,请把从不同角度看到的形状画在下面的方格里。
8.学校新建了一个游泳池,长50米,宽20米,深2米,水深1.5米.这个游泳池占地多少平方米?池内水的体积是多少立方米?9.一块正方体石料棱长是6分米,这块石料的体积是多少立方分米?如果1立方分米石料的质量是2.7千克,这块石料的质量是多少千克?参数答案1.解:(6+4+26)×4=144(分米)144÷12=12(分米)正方体的体积=棱长×棱长×棱长=12×12×12=1728(立方分米)答:正方体的体积是1728立方分米。
【解析】1.长方体12条棱长的总长度,12条棱分别为:4条长,4条宽,4条高。
正方体有12条棱,并且长度都是一样的。
2.125÷(10×5)=2.5(分米)答:这个水箱内的水深2.5分米。
【解析】2. 125÷(10×5)=2.5(分米)答:这个水箱内的水深2.5分米。
3.解:(4×4+4×1.5+4×1.5)×2=(16+6+6)×2=28×2=56(平方米)答:这个长方体的表面积是56平方米.【解析】3.长方体的表面积=(长×宽+长×高+宽×高)×2,把数据代入计算即可解答.本题考查了长方体表面积公式的应用,关键是掌握表面积公式.4.解:正方体的表面积=2×2×6=24(平方厘米),正方体的体积=23=8(立方厘米).答:这个正方体的表面积和体积分别是24平方厘米、8立方厘米.【解析】4.根据正方体的展开图,1﹣4﹣1型,补上3个小正方形,是它能够折成正方体,根据正方体的表面积=棱长×棱长×6求出正方体的表面积,根据体积=棱长3,求出体积,据此解答即可.此题考查正方体的展开图、表面积和体积,解决此题的关键是,熟悉正方体的展开图的类型,记住表面积体积的计算方法.5.解:【解析】5.6.解:【解析】6.7.【解析】7.8.解:50×20=1000(平方米)1000×1.5=1500(立方米)答:这个游泳池占地1000平方米,池内水的体积是1500立方米.【解析】8.用游泳池的长乘宽即可求出游泳池的占地面积,用占地面积乘水的深度即可求出池内水的体积.9.6×6×6=216(立方分米),216×2.7=583.2(千克)【解析】9.正方体的体积=棱长x棱长x棱长,。
长方体和正方体基本题型归纳1.鱼缸表面积问题:一个长90厘米、宽30厘米、高60厘米的长方体无盖玻璃鱼缸,制作这个鱼缸至少需要多大面积的玻璃?2.排气管道问题:一节横截面为正方形,边长为2厘米的排气管道长1米,制作这样一节排气管道至少需要多少平方米的铁皮?3.粉刷房间问题:一间长5米、宽4米、高3米的房间,门窗面积为8平方米,这间房的粉刷面积是多少?4.加工机套问题:制作1000个洗衣机机套(没有低面),每台洗衣机的长、宽、高分别为59.5厘米、42.5厘米、80厘米,至少需要多少平方米的布料?5.游泳池贴瓷砖问题:一个长50米、宽25米、深2.5米的游泳池,四周和低面都需要贴瓷砖,共需要多少平方米的瓷砖?6.长方体体积问题:一个底面积为20平方厘米、高为8厘米的长方体,体积是多少?7.截长方体成正方体问题:将一个长12厘米、宽10厘米、高5厘米的长方体截成一个体积最大的正方体,这个正方体的体积是多少?8.长方体表面积问题:一根2米长的长方体木块,平均截成两段后表面积增加了0.6平方米,原来长方体木块的体积是多少?9.游泳池注水问题:往一个长50米、宽30米的游泳池中注水,如果每小时能注水200平方米,多少时间才能使水深达2.4米?10.蓄水池问题:挖一个长10米、宽8米、深5米的长方体蓄水池,其占地面积、蓄水量、贴瓷砖面积和水位线长度分别是多少?11.长方体体积问题:一个长3米、宽0.5米、厚0.12米的长方体木料,其体积是多少?合多少立方分米?12.土坑问题:建筑工地要挖一个长50米、宽30米、深0.5米的长方体土坑,挖出多少方的土?13.方木体积问题:家具厂订购500根横截面面积为24平方分米、长为3米的方木,这些木料共多少方?14.围墙问题:一道长15厘米、厚24厘米、高3米的围墙需要多少块砖?15.木地板问题:一间长5米、宽3米的房间地面铺设了2厘米厚的木地板,至少需要多少立方米的木材。
小升初复习试卷:长方体与正方体一、填空题:(24分,每题2分)1. 1020立方厘米=________立方分米5.05升=________ 升________ 毫升3立方分米70立方厘米=________ 毫升3平方千米=________公顷。
520.73立方分米=________升________毫升4.06公顷=________平方米。
2. 我在正面看到的是,它可能是________.3. 一个长方体和正方体的棱长之和相等,已知长方体的长是6厘米,宽是4厘米,高是2厘米,正方体的体积是________立方厘米。
4. 1立方分米的1个正方体可以分成________个1立方厘米的小正方体,如果把这些小正方体排成一排,一共长________分米。
5. 将棱长是1分米的正方体铁块镕铸成一个底面是长方形(长20厘米、宽10厘米)的长方体铁块。
这个长方体铁块的表面积是________平方厘米。
6. 一个长方体的长是8分米,把它分成两个相等的正方体后,表面积比原来增加________.7. 一个长方体的表面积是40平方厘米,把它平均分开,正好成为两个相等的正方体,每个正方体的表面积是________ 平方厘米;体积是________立方厘米。
8. 把6个棱长1厘米的正方体木块拼成一个长方体,这个长方体的体积是________立方厘米,表面积是________平方厘米或________平方厘米。
9. 把一个长24厘米,宽18厘米,高9厘米的长方体木块截成同样大小的正方体木块(不许有剩余),最少可以截成________块。
10. 有一个长10厘米、宽8厘米、高5厘米的长方体木块,这个长方体的体积是________立方厘米,如果把它锯成棱长是3厘米的小正方体木块,共可以锯成________块。
11. 一个长方体,体积是200立方分米,若将它沿横截方向截成5段,表面积就增加160平方分米,这个长方体的长是________ 分米。
专题20《长方体和正方体》2022年小升初数学真题汇编专项复习(全国通用)考试时间:60分钟满分:100分一、填空题(共10题;共19分)1.把一个长8分米、宽6分米、高10分米的长方体木块削成一个最大的圆锥。
这个圆锥的体积是立方分米,削去部分的体积是立方分米。
2.一个游泳池长50米,宽25米,高3米,如果往游泳池中放2.5米深的水,一共放水立方米,合立方分米,合升.3.把一个长方体木块的高截去2厘米后剩下部分是一个正方体,这时表面积比原来减少56平方厘米。
这个正方体的表面积是平方厘米,体积是立方厘米。
4.一个圆柱,它的底面积不变,如果高增加2 cm,表面积就增加62.8 c㎡,那么这个圆柱的底面积是c㎡。
5.一个长方体,长6分米,宽和高都是2分米,这个长方体底面的面积是平方分米,这个长方体右面的面积是平方分米,它的体积是立方分米.6.将3个棱长为3厘米的正方体拼成一个长方体后,长方体的表面积比原来三个正方体的表面积之和减少了。
7.一个长方体的高减小2厘米后,成为一个正方体,那么表面积就减小48平方厘米,这个正方体的体积是立方厘米.8.把一个棱长是6dm的正方体铁块锻造成一个长方体后,长方体的底面积是24dm2,那么它的高是()dm。
9.一个长方体玻璃水箱,长15厘米,宽10厘米,高20厘米。
小明向空水箱中慢慢注水,水在长方体水箱中形成长方体。
当长方体水箱中第一次出现正方形面时,小明注入了毫升的水;当第二次出现正方形面时,水与玻璃的接触面积是平方厘米。
10.下图是用棱长1厘米的小正方体拼成的,下图中物体表面积是平方厘米,体积是立方厘米。
至少再加个小正方体,就变成一大的正方体。
二、单选题(共8题;共16分)11.一个长方体形状的玻璃容器,从里面量长为50厘米,宽为40厘米,高为45厘米。
向容器里注水,当容器内的水体第1次出现正方形面时,容器里有水()升。
A.90B.100C.80D.8112.下面()能围成正方体。
习题讲解(相应题型的练习)
棱长加深拓展:
如图,有一个长5分米、宽和高都是3分米的长方体硬纸箱,如果用绳子将箱子横着捆两道,长着捆一道,打结处共用2分米。
一共要用绳子多长?
、
表面积:
4、如图,把一个长方体木料沿着虚线正好锯成3个完全一样的小正方体后,表面积增加了48平方分米。
这根木料的表面积是多少平方分米?
容积体积转化:
5、一个正方体水箱容积是343立方分米,把这一满水箱的水全部注入到一个长方体水箱内,已知长方体水箱长10分米,宽7分米,这个水箱内的水深多少分米?
7、有一只长150厘米,宽50厘米,高40厘米的水盒,里面装满水,这时放入一块高和长都是20厘米的长方体石块,水溢出4升,这块石头的宽是多少厘米?
8、一个玻璃鱼缸,长10分米,宽6分米,高8分米,鱼缸中原有水深7分米,现在一块假山石放入水中并浸没,水溢出48升.这块假石的体积有多少立方米?
9、把10升水倒入一个长2.5分米,宽2分米,高6分米的长方体水缸中。
⑴这时水面的高度离容器口有多少分米?
⑵此时,将一个正方体铁块全部浸入水中,水面离容器口还有2.4分米,你能求出正方体铁块的棱长吗?
(单位:cm)
30。
小升初常考的长方体和正方体学生姓名年级小五学科数学授课教师日期时段核心内容面积,体积,容积课型教学目标1、掌握正方体和长方体的特点;2、掌握表面积的应用;3、掌握体积单位及体积的应用;4、掌握排水法求体积的方法;重、难点实际应用【知识导图】【互动导学】【导学】一:长方体和正方体的认识【知识点1】:长方体和正方体的特征【例1】:正方体的展开图1、下列三个图形中,不能拼成正方体的是()① ② ③2、右图是一个正方体的展开图。
在这个正方体中,与面相对的是( )面,与面相对的是( ), ( )面与( )面是相对的面。
3、下图中哪两个字所在的面,是正方体中相对的面?4. 右图是正方体的一个平面展开图,将它折成正方体后, (1)1号面和( )号面相对; (2)2号面和( )号面相对; (3)3号面和( )号面相对。
【例3】:长方体的展开图(1)这是一个长方体的展开图,前面的面积是( )平方厘米,右面的面积是( )平方厘米, 上面的面积是( )厘米。
(2)右图是一个长方体的展开图,这个长方体上面的面是 ( ),右面的面是( )。
da bce f后A 、长4cm ,宽2cmB 、长4cm ,宽C 、长2cm ,宽D 、边长2cm(3)沿下图中的虚线折叠,可以围成一个长方体。
围成的这个长方体的体积是多少立方厘米?【例题】4:一个正方体的6个面分别涂着红、黄、蓝、白、黑、绿六种颜色,根据下面的三种摆法,判断哪种颜色的对面涂着哪种颜色。
练习1:根据一个正方体的三种不同的摆法,判断出相对的两个面上的字母各是什么【例题】5:一个装书的纸皮箱,长55厘米,宽35厘米,高20厘米,如果要用封口纸条把这箱书封扎好(如图),需用多长的封口纸条(接头处不计)黄红蓝黑蓝白 绿白红 F D2A5 BA2C ECD【知识点2】:正方体的染色问题(1)三个面都染色:必定在顶点上;(2)两个面染色:必定在棱上;(3)一个面染色:必定在面上。
立体图形题型1:长方体的表面积例1:食堂的长方体烟囱是用铁皮制成的,求用了多少铁皮,就是求 ( )。
A.体积 B.表面积 C.四个面的面积 D.五个面的面积【答案】C例2:把一个棱长是4dm的正方体,分成相等的两个长方体后,表面积增加了________平方分米。
【分析】切成两个相等的长方体后,表面积会增加两个正方形的面,由此计算即可。
4×4×2=32(平方分米)【答案】4×4×2=32(平方分米)故答案为32例3:制作一个长、宽、高分别是5厘米、4厘米、3厘米的长方体纸盒,需要准备(______)种大小不同的长方形,其中最大的长方形的面积是(_______)平方厘米,最小的是(_______)平方厘米。
【分析】长方体是由六个面组成,分成3组,每组二个面是相同的,所以是准备3种大小不同的长方形。
这里求的“最大的长方形的面积”是指一个“面”的面积,最大的是面积是5×4=20平方厘米,最小的是4×3=12平方厘米。
【答案】3 20 12例4:一间教室长9m,宽6m,高4m,要粉刷房顶和四壁,扣除门窗和黑板的面积26m2。
若每平方米用涂料0.45kg,粉刷这间教室需要涂料多少千克?【分析】粉刷教室只有5个面,一个底面和四个侧面,根据长方体表面积公式计算出表面积,减去门窗和黑板的面积就是需要粉刷的面积,再乘每平方米需要涂料的质量即可求出需要涂料的总重量.【答案】解:(9×6+6×4×2+4×9×2-26)×0.45=(54+48+72-26)×0.45=148×0.45=66.6(kg)答:粉刷这间教室需要涂料66.6千克。
题型2:正方体的表面积例5:两个正方体的棱长比是3∶5,它们的表面积比是( )。
A.9∶25 B.3∶5 C.18∶30【答案】A例6:一个正方体的棱长和48dm,正方体表面积是(______)dm2.【分析】由棱长和求棱长,再求表面积解:棱长为48÷12=4dm,表面积为4×4×6=96dm2.【答案】96例7:木工做一只棱长是5分米的正方体无盖木箱至少用木板多少平方分米?【答案】解:5χ5χ5=125平方分米。
小升初常考的长方体和正方体学生姓名年级小五学科数学授课教师日期时段核心内容面积,体积,容积课型教学目标1、掌握正方体和长方体的特点;2、掌握表面积的应用;3、掌握体积单位及体积的应用;4、掌握排水法求体积的方法;重、难点实际应用【知识导图】【互动导学】【导学】一:长方体和正方体的认识【知识点1】:长方体和正方体的特征【例1】:正方体的展开图1、下列三个图形中,不能拼成正方体的是()①②③2、右图是一个正方体的展开图。
在这个正方体中,与面相对的是( )面,与面相对的是( ), ( )面与( )面是相对的面。
3、下图中哪两个字所在的面,是正方体中相对的面?4. 右图是正方体的一个平面展开图,将它折成正方体后, (1)1号面和( )号面相对; (2)2号面和( )号面相对; (3)3号面和( )号面相对。
【例3】:长方体的展开图(1)这是一个长方体的展开图,前面的面积是( )平方厘米,右面的面积是( )平方厘米, 上面的面积是( )厘米。
(2)右图是一个长方体的展开图,这个长方体上面的面是 ( ),右面的面是( )。
A 、长4cm ,宽2cmB 、长4cm ,宽1.5cmC 、长2cm ,宽1.5cmD 、边长2cm(3)沿下图中的虚线折叠,可以围成一个长方体。
围成的这个长方体的体积是多少立方厘米?da bcef后【例题】4:一个正方体的6个面分别涂着红、黄、蓝、白、黑、绿六种颜色,根据下面的三种摆法,判断哪种颜色的对面涂着哪种颜色。
练习1:根据一个正方体的三种不同的摆法,判断出相对的两个面上的字母各是什么?【例题】5:一个装书的纸皮箱,长55厘米,宽35厘米,高20厘米,如果要用封口纸条把这箱书封扎好(如图),需用多长的封口纸条?(接头处不计)【知识点2】:正方体的染色问题 (1)三个面都染色:必定在顶点上; (2)两个面染色:必定在棱上; (3)一个面染色:必定在面上。
黄4 红2蓝5 黑4 蓝白 绿 白红 F 4 D 2A 5B 6A 2C ECD【例题】1:一个棱长10厘米的正方体木块,表面涂满了红色,把它切成棱长1厘米的小正方体。
问:在这些小正方体中,(1)3个面涂有红色的有多少个?(2)2个面涂有红色的有多少个?(3)1个面涂有红色的有多少个?(4)6个面都没有涂色的有多少个?练习1:下图由9个棱长为1厘米的正方体搭成的,将这个立体图形表面涂上红色。
其中只有三面涂上红色的正方体有()个,只有四面涂上红色的正方体有()个。
【导学】二:长方体和正方体的表面积和体积【知识点1】:长方体和正方体的表面积和体积变化规律【例题】1:变化规律(1)一个长方体的长、宽、高都扩大2倍,它的表面积就(),体积扩大()倍。
(2)一个正方体的棱长扩大2倍,则表面积就(),体积扩大()倍。
(3)大正方体棱长是小正方体棱长的2倍,大正方体表面积是小正方体表面积的()倍。
【知识点2】:长方体正方体的切割与拼接【例题】1:一个长方体底面是一个边长为20厘米的正方形,高为40厘米,如果把它的高增加5厘米,它的表面积会增加多少?练习1:有一个长方体,如果把高增加3cm后,就变成一个正方体,表面积就会增加96cm2。
求这个长方体的体积。
练习2:把一个长方体截去一个高为8厘米的长方形后,剩下的部分是一个正方体。
正方体的表面积比原来长方体的表面积减少320平方厘米。
求原来长方体的体积。
练习3:一个长方体木块,从上部和下部分别增加高为3厘米和2厘米的长方体,变成一个正方体,表面积增加了360平方厘米。
原来长方体的体积是多少立方厘米?【例题】2:把一根长80厘米,宽5厘米,高3厘米的长方体木料锯成长都是40厘米的两段,表面积比原来增加了多少平方厘米。
练习1:一个长方体正好可以切成5个同样大小的正方体,切成的5个正方体的表面积比原来长方表面积多了200平方厘米,求原来长方体的表面积?【例题】3:把一个正方体木块锯成3个大小一样的小长方体后,表面积增加了36平方厘米。
原来正方体的表面积是多少?练习1:把一个长方体和一个正方体拼成一个新的长方体,这个新长方体的表面积比原来的长方体的表面积增加了80平方厘米,求正方体的表面积。
练习2:用两个棱长是3厘米的正方体,拼成一个长方体,它的表面积比两个正方体的表面积少多少平方厘米,这个长方体的表面积是多少平方厘米。
练习3:把一根长2米的方木(底面是正方形)锯成三段,表面积增加5.67平方分米,原来这根方木的体积是多少立方分米?【例题】4:把棱长12厘米的正方体切割成棱长是3厘米的小正方体,可以切割成多少块?练习1:一个棱长为6厘米的正方体木块,如果把它锯成棱长为2厘米的小正方体,表面积增加了多少平方厘米?练习2:有一个棱长是1米的正方体木块,如果把它锯成相等的8个小正方体,表面积增加多少平方米?【例题】5:把一个长为10分米,宽为6分米,高为8分米的长方形,切割成相等的两个长方体,有几种切法,那中增加的表面积最多?哪种增加的表面积最少?练习1:把两个相同的长方体拼成一个大的长方体,已知小长方体的长是8cm,宽是6cm,高是3cm。
有几种拼法,分别求出拼成的大长方形的面积?练习2:用两个长6厘米,宽3厘米,高1厘米的长方体拼成一个表面积尽可能小的正方体,这个拼成的长方体的表面积是()平方厘米。
练习3:用4个棱长是3厘米的正方体,拼成一个长方体,有几种拼法,每种拼法长方体的表面积比四个正方体的表面积和减少了多少平方厘米。
练习4:一个长方体的长、宽、高分别是6厘米、5厘米和4厘米,若把它切割成三个体积相等的小长方体,这三个小长方体表面积的和最大是多少平方厘米?【例题】6:练习如下图,一个正方体被切成12个大大小小的长方体,这些长方体表面积的总和是350平方厘米,求原来正方体的表面积和体积。
练习1:一张长方形铁皮,长25分米,宽20分米。
在这张长方形铁皮的四个角上各剪去一个边长是5分米的正方形,然后折成一个长方体铁盒,这个铁盒的体积是多少?【知识点2】打孔问题【例题1】一个长方体被挖掉一小块(如图),下面说法完全正确的是()。
A.体积减少,表面积也减少。
B.体积减少,表面积增加。
C.体积减少,表面积不变。
【例题2】求下面零件的表面积。
(单位:厘米)练习1:一个棱长为4分米的正方体,分别在前后、左右、上下各面的中心位置,挖去一个棱长为1分米的小正方体。
挖完后得到的形体,它的表面积是多少平方分米?练习2:下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为0.5厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为0.25厘米,那么最后得到的立体图形的表面积是多少平方厘米?【知识点3】组合图形问题【例题1】一个零件形状大小如下图:算一算,它的表面积是多少平方厘米?(单位:厘米)【知识点4】三视图法求面积【例1】右图是由棱长1厘米的正方体拼成的图形,它的表面积是()㎝²,体积是()㎝³。
至少需要这样的小正方体()个才能拼成一个大的正方体。
【例2】如右图所示,由三个正方体木块粘合而成的模型,它们的棱长分别为1米、2米、4米,要在表面涂刷油漆,如果大正方体的下面不涂油漆,则模型涂刷油漆的面积是多少平方米?练习1:如图,棱长分别为厘米、厘米、厘米、厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是多少平方厘米?(希望杯真题)【导学】三:排水法求不规则物体的体积【例题】1:一个密封的玻璃缸,存水的空间长为6dm,宽为4dm,高为5dm,缸里的水深为3dm。
现将缸竖起来,现在的水深是多少?练习1:有两个水池,甲水池长8分米、宽6分米、水深3分米,乙水池空着,它长6分米、宽和高都是4分米。
现在要从甲水池中抽一部分水到乙水池,使两个水池中水面同样高。
问水面高多少?【例题】2:在一个棱长2分米的正方体的玻璃容器里,向容器里倒入5升水,再把一块石头投入水中,这时量得容器内水深15厘米,石头的体积是多少立方厘米?练习1:把一个土豆放入长15厘米,宽10厘米的长方体容器里,水面由12厘米上升到16厘米,土豆的体积是多少?【例题】3:一个长方体的容器,底面积是16平方分米,装的水高6分米,现放入一个体积是24立方分米的铁块。
这时的水面高多少?练习1:把一个体积为80立方厘米的铁块浸在底面积为20平方厘米的长方体容器中,水面高度为10厘米,如果把铁块捞出后,水面高多少?练习2:有一个边长为5cm的正方体铁块,浸没在一个盛水的长方体容器中。
取出铁块后,水面下降了0.5cm,求这个长方体的底面积是多少平方厘米?【例题】4:有甲、乙、丙三个正方体水池,它们内边长分别是5米、3米、1米,把两堆碎石分别沉没在乙、丙两个水池的水里,它们的水面分别升高了4厘米和2厘米。
如果将这两堆碎石都沉没在甲水池的水里,甲水池的水面升高了多少厘米?练习1:一个长方体容器内装满水。
现有大、中、小三个铁球,第一次把小球沉入水中;第二次把小球取出,把中球沉入水中;第三次把中球取出,把小球和大球一起沉入水中。
已知每次从容器中溢出的水量情况是:第二次是第一次的3倍,第三次是第一次的2.5倍。
求大球的体积是小球的多少倍?【例题】5:用一个底面是边长8厘米的正方形,高为16厘米的长方体容器,测量一个球形铁块的体积,容器中装的水距杯口还有2厘米。
当铁块放入容器中,有部分水溢出,当把铁块取出后,水面下降5厘米,求球形铁块的体积。
练习1:一个长方体玻璃缸,从里面量长为8dm,宽为6dm,高为4dm,里面的水深2.8dm。
现在要放进去一个棱长为4dm的正方体铁块,玻璃缸内的水会溢出来多少?练习2:有一个正方体容器,边长为25厘米,里面注满了水,有一根长50厘米,横截面是12平房里面的长方体铁棒,先将铁棒垂直插入水中,水会溢出多少立方厘米?。