第7章回转体的平衡

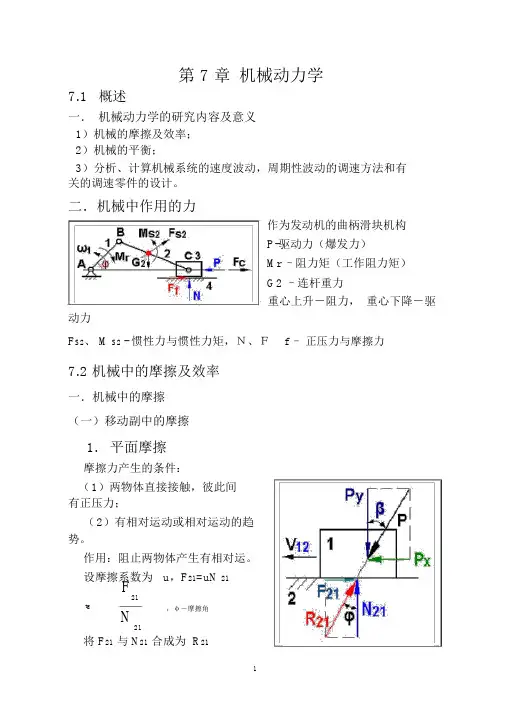
第 7 章机械动力学7.1概述一．机械动力学的研究内容及意义1）机械的摩擦及效率；2）机械的平衡；3）分析、计算机械系统的速度波动，周期性波动的调速方法和有关的调速零件的设计。

二．机械中作用的力作为发动机的曲柄滑块机构P-驱动力（爆发力）Mr –阻力矩（工作阻力矩）G2 –连杆重力重心上升－阻力，重心下降－驱动力F S2、 M S2 - 惯性力与惯性力矩，Ｎ、Ｆ f –正压力与摩擦力7.2 机械中的摩擦及效率一．机械中的摩擦（一）移动副中的摩擦1.平面摩擦摩擦力产生的条件：（1）两物体直接接触，彼此间有正压力；（2）有相对运动或相对运动的趋势。

作用：阻止两物体产生有相对运。

设摩擦系数为u，F21=uN 21F21tg，φ－摩擦角N21将 F21与 N21合成为 R21R21－总反力（全反力）P X P分解为 P和 P ，tgX Y P Y（ P X P sin、 P Y P cos ）F21P X，有F21tgY 方向平衡： Py=N 21，即：tg tg P Xtg讨论：①总反力 R21恒与相对速度V 12成 90° +φ②当β >φ， P X > F21，滑块作加速运动；当β =φ， P X = F21，动则恒动，静则恒静；当β <φ， P X < F21，原来运动，作减速运动，原来静止，永远静止，称自锁。

③ 自锁条件：β≤φβ=φ，条件自锁（静止）；β<φ，无条件自锁。

2.斜面摩擦斜面机构如图，滑块置于升角α的斜面上，摩擦角为φ，作用于滑块上的铅垂力为Q，求滑块等速上升和下降时所需水平平衡力P 和 P’。

（1）求等速上升水平平衡力 PP－驱动力， Q－阻力PQ R 21 0 ，tg ()P，P Qtg () （1）Q（ 2）求等速下降水平平衡力 P ’Q －驱动力， P ’－阻力P'Q R 21 0 ，tg () P '，P 'Qtg () （2）Q讨论：① 欲求下滑 （反行程） P ’，只需将式 （ 1）中 P →P ’，φ→ (－φ )② 下滑时，当α >φ， P ’为平衡力α <φ， P ’为负，成为驱动力的一部分，该条件下，若无 P ’，则无论 Q 多大，滑块不下滑，称自锁，自锁条件：α≤φ。

第七章 势流理论（二）本章主要讨论：轴对称有势流动和机翼绕流的有关理论。

§7.1 轴对称流动一条曲线绕轴旋转一周形成的物体形状称为旋成体。

当来流沿旋成体中轴线方向绕流旋成体时，通过中轴线的各子午面上的流动均相同，这种流动称为轴对称流动。

比如，均匀流绕圆球的流动。

对于无旋轴对称流动，存在速度势函数φ和流函数ψ 。

但，速度势函数φ是调和函数，流函数 ψ 不是调和函数。

采用柱坐标(r ,θ,x )，设 x 轴为对称轴，流动参数不随 θ 变化。

),,(t x r v v r r = ),,(t x r v v x x =不可压缩流体的轴对称势流应该满足：()()0=∂∂+∂∂xrv r rv x r 连续性方程：0=∂∂-∂∂r v x v xr 无旋条件： 如果存在物体壁面S ，速度应该在物面上满足边界条件：0=v 物面法向流速为零：∞=V 无穷远处流速：求解不可压缩流体轴对称势流问题的主要任务就是寻求满足以上方程组和边界条件的速度矢量。

有两种数学求解途经:rxV ∞轴对称轴途径一：0122222=∂∂+∂∂+∂∂=∇xr r r φφφφ控制方程：0=V 物面无穿透条件：∞=V 无穷远处来流：xv rv x r ∂∂=∂∂=φφ,这里：速度势函数φ是调和函数，可以采用叠加法求解。

途径二：0122222=∂∂+∂∂-∂∂=x r r r D ψψψψ控制方程：0=V 物面无穿透条件：∞=V 无穷远处来流：rr v xr v x r ∂∂=∂∂-=ψψ1,1这里：流函数函数Ψ不是调和函数，称为斯托克斯函数。

但它是线性的，也可采用叠加法求解。

一.基本的轴对称势流：1.均匀直线流：0,,0===∞θv V v v x r∞=∂∂==∂∂=V x v r v x r φφ,0 x V ∞=∴φ∞=∂∂==∂∂-=V r r v x r v x r ψψ1,01又 221r V ∞=∴ψ2.空间点源(汇)流：(0 , 0)处有一点源 Q ： R v R Q 24π=()22244xr QR Q v R +==ππ如图，有：()22224sin xr rx r Q v v r R r +⋅+===∂∂∴πθφ()22224cos xr xx r Q v v x R x +⋅+===∂∂∴πθφ 2214xr Q +⋅-=∴πφ()23224x r rxQrv r x +==∂∂πψ又：()232224x r Qr rv x r +=-=∂∂πψ且：224x r xQ +⋅-=∴πψ 22224,14xr xQ xr Q +⋅-=+⋅-=πψπφ即：当点源在 x 0 点（轴对称轴上），速度势函数和流函数为：()()22022414x x r x x Q x x r Q -+-⋅-=-+⋅-=πψπφ 3.空间偶极子流：0lim 0>=∆∞→→∆M x Q Q x 令：()()23222222220414114limx r x M x r x M x x x r xr x Q Q x +⋅-=⎪⎪⎭⎫⎝⎛+∂∂=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∆∆-+-+∆=∞→→∆πππφ令：()23224x r x M +⋅-=∴πφ ()232224x r r M +⋅=πψ亦可得：当偶极子在 x 0 点（轴对称轴上），速度势函数和流函数为：()[]()[]232322222044x x r r M x x r x x M-+⋅=-+-⋅-=πψπφ*二.均匀来流绕圆球体的流动：采用球坐标（R ，θ，λ）。

机械基础第2版习题答案第7章第七单元支承零部件练习题一、名词解释1．轴轴是支承传动件（如齿轮、蜗杆、带轮、链轮等）的零件。

2．曲轴曲轴是指将回转运动转变为往复直线运动（或将往复直线运动转变为回转运动）的轴。

3．软轴软轴是由几层紧贴在一起的钢丝构成，可将扭矩（扭转及旋转）灵活地传递到任意位置的轴。

4．心轴心轴是指工作时仅承受弯矩作用而不传递转矩的轴。

5．转轴转轴是指工作时既承受弯矩又承受转矩的轴。

6．传动轴传动轴是指工作时仅传递转矩而不承受弯矩的轴。

7．轴承轴承是用来支承轴或轴上回转零件的部件。

8．滑动轴承滑动轴承是工作时轴承和轴颈的支承面间形成直接或间接滑动摩擦的轴承。

9．滚动轴承滚动轴承是将运转的轴与轴座之间的滑动摩擦变为滚动摩擦，从而减少摩擦损失的一种精密的机械元件。

二、填空题1．支承零部件主要包括轴和轴承，它们是组成机器不可缺少的重要零部件。

2．轴是支承传动件的零件，轴上被支承的部位称为轴颈，轴的功用是支承回转零部件，并使回转零部件具有确定的位置，传递运动和扭矩。

3．轴承是支承轴颈的支座，轴承的功用是保持轴的旋转精度，减少轴与支承件之间的摩擦磨损。

4．轴按其形状进行分类，可分为直轴、曲轴和软轴（或挠性轴、钢丝软轴）三类。

5．轴的结构包括轴颈、轴头、轴身三部分。

6．根据轴承工作时摩擦性质的不同，轴承分为滑动轴承和滚动轴承两大类。

7．滑动轴承根据承受载荷方向的不同，可分为向心滑动轴承和推力滑动轴承两大类。

8．滑动轴承通常由轴承座、轴瓦（或轴套）、润滑装置和密封装置等组成。

9．常用的轴瓦分为整体式轴瓦和剖分式轴瓦两种结构。

10．滑动轴承的失效形式主要有磨粒磨损、刮伤、胶合（咬粘）、疲劳、腐蚀等。

11．滚动轴承一般由内圈、外圈、滚动体和保持架组成。

12．常见的滚动体有球、短圆柱滚子、长圆柱滚子、球面滚子、圆锥滚子、螺旋滚子、滚针等多种。

13．滚动轴承的分类方法很多，按滚动轴承所能承受的载荷方向或公称接触角进行分类，可分为向心滚动轴承和推力滚动轴承。

习题7-1 如图所示的滚齿机工作台传动机构，已知各轮齿数为z1=15,z2=28,z3=15, z4=35，z 9=40及被切齿轮B的齿数为64，求传动比i75.题7-1图题7-2图7-2 如图所示轮系中，已知各轮齿数为z1=20,z2=25,z2′=20,z3=40，z3′=35，z4=40,z4′=2（右旋）, z5=60, z5′=20(模数m=4mm)。

若n1=500r/min，求齿条6的线速度v的大小和方向。

7-3如图所示轮系中，已知z1=z3′=20, z3=z5=60.试求（1）齿轮2和齿轮4的齿数z2和z 4；（2）传动比i15题7-3图题7-4图7-4 如图所示钟表传动机构，N为发条盘，E为擒纵轮，S、M与H分别为秒针、分针和时针。

已知z1=72，z2=12，z3=64，z4=8，z5=60，z6=8，z7=60，z8=6，z9=8，z10=24，z11=6，z 12=24。

求秒针与分针的传动比iＳＭ及分针与时针的传动比iＭＨ。

7-5 如图所示轮系，已知各轮齿数z1=60，z2=20，z2′=30，z3=15；在图a中,若已知n 3=150r/min，n1=50r/min，n3和n1转向如图所示，求nＨ的大小和转向。

在图b中，若已知n 3=150r/min，n1=50r/min，转向如图所示，求nＨ的大小和转向。

题7-5图7-6 如图所示的手动起重葫芦，各齿轮齿数分别为z1=30,z2=15,z2′=18,z3=54，求手动链轮S和起重链轮H的传动比iＳＨ。

题7-6图题7- 7图7-7如图所示的液压回转台传动机构，已知z2=15，马达M的转速（指马达转子相对其壳体的转速）n Ｍ=12r/min ，回转台H 的转速（与马达转速n Ｍ相反）n Ｈ=－１.5r/min ，求齿轮1的齿数。

7-8如图所示的手动齿轮机构。

已知各轮齿数z 1=z 2′=40, z 2=z 3=38,求手柄转速n Ｈ与齿轮1转速n 1的传动比i Ｈ１。

机械原理孙恒课后答案【篇一：机械原理(第七版) 孙桓主编第7章】ss=txt>1.设某机器的等效转动惯量为常数，则该机器作匀速稳定运转的条件是，作变速稳定运转的条件是。

2.机器中安装飞轮的原因，一般是为了，同时还可获得的效果。

3.在机器的稳定运转时期，机器主轴的转速可有两种不同情况，即稳定运转，在前一种情况，机器主轴速度是，在后一种情况，机器主轴速度是。

4.机器中安装飞轮的目的是和。

7.机器等效动力学模型中的等效质量(转动惯量)是根据的原则进行转化的，因而它的数值除了与各构件本身的质量（转动惯量)有关外，还与。

8.机器等效动力学模型中的等效力(矩)是根据则进行转化的，等效质量(转动惯量)是根据的原则进行转化的。

9.机器等效动力模型中的等效力(矩)是根据的原则进行转化的，因而它的数值除了与原作用力(矩)的大小有关外，还与有关。

10.若机器处于起动(开车)阶段，则机器的功能关系应是，机器主轴转速的变化情况将是。

11.若机器处于停车阶段，则机器的功能关系应是，机器主轴转速的变化情况将是。

12.用飞轮进行调速时，若其它条件不变，则要求的速度不均匀系数越小，飞轮的转动惯量将越，在满足同样的速度不均匀系数条件下，为了减小飞轮的转动惯量，应将飞轮安装在轴上。

13.当机器运转时，由于负荷发生变化使机器原来的能量平衡关系遭到破坏，引起机器运转速度的变化，称为，为了重新达到稳定运转，需要采用来调节。

14.在机器稳定运转的一个运动循环中，运动构件的重力作功等于因为。

15.机器运转时的速度波动有速度波动两种，前者采用，后者采用进行调节。

16.若机器处于变速稳定运转时期，机器的功能特征应有，它的运动特征是。

17.当机器中仅包含机构时，等效动力学模型中的等效质量(转动惯量)是常量，若机器中包含机构时，等效质量(转动惯量)是机构位置的函数。

18.设作用于机器从动件上的外力(矩)为常量，且当机器中仅包含机构时，等效到主动件上的等效动力学模型中的等效力(矩)亦是常量，若机器中包含机构时，等效力(矩)将是机构位置的函数。