【必考题】初三数学下期中第一次模拟试卷(及答案)(1)
- 格式:doc
- 大小:790.50 KB
- 文档页数:20

【必考题】九年级数学下期中一模试题含答案(1)一、选择题1.如图,以O为圆心,任意长为半径画弧,与射线OM交于点A,再以A为圆心,AO长为半径画弧,两弧交于点B,画射线OB.则cos∠AOB的值等于()A.B.C.D.2.如图,用放大镜看△ABC,若边BC的长度变为原来的2倍,那么下列说法中,不正确的是().A.边AB的长度也变为原来的2倍;B.∠BAC的度数也变为原来的2倍;C.△ABC的周长变为原来的2倍;D.△ABC的面积变为原来的4倍;3.在Rt△ABC中,∠ACB=90°,AB=5,tan∠B=2,则AC的长为()A.1B.2C.5D.254.用放大镜观察一个五边形时,不变的量是()A.各边的长度 B.各内角的度数 C.五边形的周长 D.五边形的面积5.河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比1:3,则AC的长是( )A.10米B.53米C.15米D.103米6.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为()A .五丈B .四丈五尺C .一丈D .五尺7.如图,BC 是半圆O 的直径,D ,E 是»BC上两点,连接BD ,CE 并延长交于点A ,连接OD ,OE ,如果70A ∠︒=,那么DOE ∠的度数为( )A .35︒B .38︒C .40︒D .42︒8.如图,AB 是⊙O 的直径,弦CD 交AB 于点P ,AP=2,BP=6,∠APC=30°,则CD 的长为( )A .15B .25C .215D .89.如图,在矩形ABCD 中,DE AC ⊥于E ,设ADE α∠=,且3cos 5α=,5AB =,则AD 的长为( )A .3B .163C .203D .16510.如图,在平行四边形中,点在边上,与相交于点,且,则与的周长之比为( )A .1 : 2B .1 : 3C .2 : 3D .4 : 911.若△ABC ∽△A′B′C′且34AB A B ='',△ABC 的周长为15cm ,则△A′B′C′的周长为( )cm. A .18B .20C .154D .80312.如图,在△ABC 中,M 是AC 的中点,P ,Q 为BC 边上的点,且BP=PQ=CQ ,BM 与AP,AQ分别交于D,E点,则BD∶DE∶EM等于A.3∶2∶1B.4∶2∶1C.5∶3∶2D.5∶2∶1二、填空题13.如图,在一段坡度为1∶2的山坡上种树,要求株距(即相邻两株树之间的水平距离)为6米,那么斜坡上相邻两株树之间的坡面距离为____米.14.如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为________.15.利用标杆CD测量建筑物的高度的示意图如图所示,使标杆顶端的影子与建筑物顶端的影子恰好落在地面的同一点E.若标杆CD的高为1.5米,测得DE=2米,BD=16米,则建筑物的高AB为_____米.16.若△ABC∽△A’B’C’,且△ABC与△A’B’C’的面积之比为1:4,则相似比为____.17.如图,在平面直角坐标系中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为13,点A,B,E在x轴上,若正方形BEFG的边长为6,则点C的坐标为________.18.如图,四边形ABCD、CDEF、EFGH都是正方形,则∠1+∠2= .19.如图,矩形ABCD 的顶点,A C 都在曲线ky x=(常数0k ≥,0x >)上,若顶点D 的坐标为()5,3,则直线BD 的函数表达式是_.20.如图,为了测量某棵树的高度,小明用长为2m 的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点距离相距6m ,与树相距15m ,则树的高度为_________m.三、解答题21.等腰Rt PAB V 中,90PAB ∠=o ,点C 是AB 上一点(与A B 、不重合),连接PC ,将线段PC 绕点C 顺时针旋转90o ,得到线段DC .连接, PD BD . 探究PBD ∠的度数,以及线段AB 与BD BC 、的数量关系.(1)尝试探究:如图(1)PBD ∠= ;AB BC AC =+= ;(2)类比探索:如图(2),点C 在直线AB 上,且在点B 右侧,还能得出与(1)中同样的结论么?请写出你得到的结论并证明:22.如图,小明同学在东西方向的环海路A 处,测得海中灯塔P 在它的北偏东60°方向上,在A 的正东200米的B 处,测得海中灯塔P 在它的北偏东30°方向上.问:灯塔P 到环海路的距离PC约等于多少米?(取1.732,结果精确到1米)23.如图,AD是△ABC的中线,tan B=13,cos C=22,AC=2.求:(1)BC的长;(2)sin ∠ADC的值.24.某天上午7:30,小芳在家通过滴滴打车软件打车前往动车站搭乘当天上午8:30的动车.记汽车的行驶时间为t小时,行驶速度为v千米/小时(汽车行驶速度不超过60千米/小时).根据经验,v,t的一组对应值如下表:V(千米/小时)2030405060T(小时)0.60.40.30.250.2(1)根据表中的数据描点,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;(2)若小芳从开始打车到上车用了10分钟,小芳想在动车出发前半小时到达动车站,若汽车的平均速度为32千米/小时,小芳能否在预定的时间内到达动车站?请说明理由;(3)若汽车到达动车站的行驶时间t满足0.3<t<0.5,求平均速度v的取值范围.25.如图,在△ABC中,D、E分别是边AC、BC的中点,F是BC延长线上一点,∠F=∠B.(1)若AB=10,求FD的长;(2)若AC=BC,求证:△CDE∽△DFE.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】【分析】根据作图可以证明△AOB是等边三角形,则∠AOB=60°,据此即可求解.【详解】连接AB,由图可知:OA=0B,AO=AB∴OA=AB=OB,即三角形OAB为等边三角形,∴∠AOB=60°,∴cos∠AOB=cos60°=.故选B.【点睛】本题主要考查了特殊角的三角函数值,正确理解△ABC是等边三角形是解题的关键.2.B解析:B【解析】【分析】根据相似三角形的判定和性质,可得出这两个三角形相似,相似三角形的周长之比等于相似比,面积之比等于相似比的平方.【详解】解:∵用放大镜看△ABC,若边BC的长度变为原来的2倍,∴放大镜内的三角形与原三角形相似,且相似比为2∴边AB的长度也变为原来的2倍,故A正确;∴∠BAC的度数与原来的角相等,故B错误;∴△ABC的周长变为原来的2倍,故C正确;∴△ABC的面积变为原来的4倍,故D正确;故选B【点睛】本题考查了相似三角形的性质,相似三角形的周长之比等于相似比,面积之比等于相似比的平方.3.B解析:B【解析】【分析】根据正切的定义得到BC=12AC,根据勾股定理列式计算即可.【详解】在Rt△ABC中,∠ACB=90°,tan∠B=2,∴ACBC=2,∴BC=12 AC,由勾股定理得,AB2=AC2+BC2)2=AC2+(12AC)2,解得,AC=2,故选B.【点睛】本题考查的是锐角三角函数的定义、勾股定理,掌握锐角A的对边a与邻边b的比叫做∠A的正切是解题的关键.4.B解析:B【解析】解:∵用一个放大镜去观察一个三角形,∴放大后的三角形与原三角形相似,∵相似三角形的对应边成比例,∴各边长都变大,故此选项错误;∵相似三角形的对应角相等,∴对应角大小不变,故选项B正确;.∵相似三角形的面积比等于相似比的平方,∴C选项错误;∵相似三角形的周长得比等于相似比,∴D选项错误.故选B.点睛:此题考查了相似三角形的性质.注意相似三角形的对应边成比例,相似三角形的对应角相等,相似三角形的面积比等于相似比的平方,相似三角形的周长得比等于相似比.5.B解析:B【解析】【分析】Rt△ABC中,已知了坡比是坡面的铅直高度BC与水平宽度AC之比,通过解直角三角形即可求出水平宽度AC的长.【详解】Rt△ABC中,BC=5米,tanA=1:3;∴AC=BC÷tanA=53米;故选:B.【点睛】此题主要考查学生对坡度坡角的掌握及三角函数的运用能力.6.B解析:B【解析】【分析】根据同一时刻物高与影长成正比可得出结论.【详解】设竹竿的长度为x尺,∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,∴1.5 150.5x,解得x=45(尺),故选B.【点睛】本题考查了相似三角形的应用举例,熟知同一时刻物髙与影长成正比是解答此题的关键.7.C解析:C【解析】【分析】连接CD,由圆周角定理得出∠BDC=90°,求出∠ACD=90°-∠A=20°,再由圆周角定理得出∠DOE=2∠ACD=40°即可,【详解】连接CD,如图所示:∵BC是半圆O的直径,∴∠BDC=90°,∴∠ADC=90°,∴∠ACD=90°-∠A=20°,∴∠DOE=2∠ACD=40°,故选C.【点睛】本题考查了圆周角定理、直角三角形的性质;熟练掌握圆周角定理是解题的关键.8.C解析:C【解析】【分析】作OH⊥CD于H,连结OC,如图,根据垂径定理由OH⊥CD得到HC=HD,再利用AP=2,BP=6可计算出半径OA=4,则OP=OA-AP=2,接着在Rt△OPH中根据含30°的直角三角形的性质计算出OH=12OP=1,然后在Rt△OHC中利用勾股定理计算出CH=15,所以CD=2CH=215.【详解】作OH⊥CD于H,连结OC,如图,∵OH⊥CD,∴HC=HD,∵AP=2,BP=6,∴AB=8,∴OA=4,∴OP=OA﹣AP=2,在Rt△OPH中,∵∠OPH=30°,∴∠POH=30°,∴OH=12OP=1,在Rt△OHC中,∵OC=4,OH=1,∴22=15OC OH∴15故选C.【点睛】本题主要考查圆中的计算问题,熟练掌握垂径定理、含30°的直角三角形的性质以及勾股定理等知识点,掌握数形结合的思想是解答的关键9.C解析:C 【解析】 【分析】根据矩形的性质可知:求AD 的长就是求BC 的长,易得∠BAC =∠ADE ,于是可利用三角函数的知识先求出AC ,然后在直角△ABC 中根据勾股定理即可求出BC ,进而可得答案. 【详解】解:∵四边形ABCD 是矩形,∴∠B =∠BAC =90°,BC=AD ,∴∠BAC +∠DAE =90°, ∵DE AC ⊥,∴∠ADE +∠DAE =90°,∴∠BAC =ADE α∠=, 在直角△ABC 中,∵3cos 5α=,5AB =,∴25cos 3AB AC α==,∴AD=BC 203==. 故选:C. 【点睛】本题考查了矩形的性质、勾股定理和解直角三角形的知识,属于常考题型,熟练掌握矩形的性质和解直角三角形的知识是解题关键.10.C解析:C 【解析】 【分析】根据已知可得到相似三角形,从而可得到其相似比,再根据相似三角形的周长比等于相似比就可得到答案. 【详解】∵四边形ABCD 是平行四边形, ∴DC ∥AB ,CD=AB . ∴△DFE ∽△BFA , ∵DE :EC=1:2, ∴EC :DC=CE :AB=2:3, ∴C △CEF :C △ABF =2:3. 故选C .11.B解析:B 【解析】∵△ABC ∽△A ′B ′C ′,∴34ABC AB A B C A B ''=''='V V 的周长的周长,∵△ABC 的周长为15cm ,∴△A ′B ′C ′的周长为20cm .故选B .12.C解析:C【解析】【分析】过A 作AF ∥BC 交BM 延长线于F ,设BC=3a ,则BP=PQ=QC=a ;根据平行线间的线段对应成比例的性质分别求出BD 、BE 、BM 的长度,再来求BD ,DE ,EM 三条线段的长度,即可求得答案.【详解】过A 作AF ∥BC 交BM 延长线于F ,设3BC a =,则BP PQ QC a ===;∵AM CM =,AF ∥BC , ∴1AF AM BC CM==, ∴3AF BC a ==,∵AF ∥BP , ∴133BD BP a DF AF a ===, ∴34DF BF BD ==, ∵AF ∥BQ , ∴2233BE BQ a EF AF a ===, ∴23EF BE =,即25BF BE =, ∵AF ∥BC , ∴313BM BC a MF AF a===, ∴BM MF =,即2BF BM =, ∴235420BF BF BF DE BE BD =-=-=,22510BF BF BF EM BM BE =-=-=, ∴3::::?53242010BF BF BF BD DE EM ==::. 故选:C .【点睛】本题考查了平行线分线段成比例定理以及比例的性质,正确作出辅助线是关键.二、填空题13.3米【解析】【分析】利用垂直距离:水平宽度得到水平距离与斜坡的比把相应的数值代入即可【详解】解:∵坡度为1:2且株距为6米∴株距:坡面距离=2:∴坡面距离=株距×(米)【点睛】本题是将实际问题转化为解析:【解析】【分析】利用垂直距离:水平宽度得到水平距离与斜坡的比,把相应的数值代入即可.【详解】解:∵坡度为1:2=6米,∴株距:坡面距离=2∴坡面距离=株距=【点睛】本题是将实际问题转化为直角三角形中的数学问题,可把条件和问题放到直角三角形中,进行解决.要注意坡度是坡角的正切函数.14.【解析】已知BC=8AD是中线可得CD=4在△CBA和△CAD中由∠B=∠DAC∠C=∠C可判定△CBA∽△CAD根据相似三角形的性质可得即可得AC2=CD•BC=4×8=32解得AC=4解析:【解析】已知BC=8, AD是中线,可得CD=4,在△CBA和△CAD中,由∠B=∠DAC,∠C=∠C,可判定△CBA∽△CAD,根据相似三角形的性质可得AC CDBC AC=,即可得AC2=CD•BC=4×8=32,解得.15.5【解析】【分析】根据同一时刻同一地点物高与影长成正比列式求得CD 的长即可【详解】解:∵AB∥CD∴△EBA∽△ECD∴即∴AB=135(米)故答案为:135【点睛】此题主要考查相似三角形的性质解题解析:5【解析】【分析】根据同一时刻同一地点物高与影长成正比列式求得CD的长即可.【详解】解:∵AB∥CD,∴△EBA∽△ECD,∴CD ED AB EB =,即1.52216AB =+, ∴AB =13.5(米).故答案为:13.5【点睛】 此题主要考查相似三角形的性质,解题的关键是熟知相似三角形的判定与性质.16.1:2【解析】【分析】由△ABC 相似△A′B′C′面积比为1:4根据相似三角形的面积比等于相似比的平方即可求解【详解】解:∵△ABC 相似△A′B′C′面积比为1:4∴△ABC 与△A′B′C′的相似比解析:1:2【解析】【分析】由△ABC 相似△A ′B ′C ′,面积比为1:4,根据相似三角形的面积比等于相似比的平方,即可求解.【详解】解:∵△ABC 相似△A ′B ′C ′,面积比为1:4,∴△ABC 与△A ′B ′C ′的相似比为:1:2,故答案为: 1:2.【点睛】本题主要考查的是相似三角形的性质,解决本题的关键是要熟知相似三角形面积的比等于相似比的平方.17.【解析】【分析】直接利用位似图形的性质结合相似比得出AB 的长进而得出△OAD ∽△OBG 进而得出AO 的长即可得出答案【详解】∵正方形BEFG 的边长是6∴∵两个正方形的相似比为∴∴∵AD ∥BG ∴△OAD解析:(3,2)【解析】【分析】直接利用位似图形的性质结合相似比得出AB 的长,进而得出△OAD ∽△OBG ,进而得出AO 的长,即可得出答案.【详解】.∵正方形BEFG 的边长是6,∴6BE EF ==. ∵两个正方形的相似比为13, ∴163CB CB EF ==. ∴2AB BC ==,.∵AD ∥BG ,∴△OAD ∽△OBG ,∴13OA OB =,即213OB OB -=. ∴3OB =.∴点C 的坐标为(3,2). 【点睛】本题主要考查了位似变换以及相似三角形的判定与性质,正确得出AO 的长是解题关键. 18.45°【解析】【分析】首先求出线段ACAFAG 的长度(用a 表示)求出两个三角形对应边的比进而证明△ACF ∽△GCA 问题即可解决【详解】设正方形的边长为a 则AC=∵∴∵∠ACF=∠ACF ∴△ACF ∽△解析:45°.【解析】【分析】首先求出线段AC 、AF 、AG 的长度(用a 表示),求出两个三角形对应边的比,进而证明△ACF ∽△GCA ,问题即可解决.【详解】设正方形的边长为a ,则=,∵ACCF a==CG AC == ∴AC CG CF AC=, ∵∠ACF=∠ACF ,∴△ACF ∽△GCA ,∴∠1=∠CAF ,∵∠CAF+∠2=45°,∴∠1+∠2=45°.点睛:该题以正方形为载体,主要考查了相似三角形的判定及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.19.【解析】【分析】利用矩形的性质和反比例函数图象上点的坐标特征得到A (3)C (5)所以B ()然后利用待定系数法求直线BD 的解析式【详解】∵D(53)∴A(3)C (5)∴B()设直线BD 的解析式为y=m 解析:35y x =【解析】【分析】利用矩形的性质和反比例函数图象上点的坐标特征得到A (3k ,3),C (5,5k ),所以B (3k ,5k ),然后利用待定系数法求直线BD 的解析式. 【详解】 ∵D (5,3),∴A (3k ,3),C (5,5k ), ∴B (3k ,5k ), 设直线BD 的解析式为y=mx+n , 把D (5,3),B (3k ,5k )代入得 5335m n k k m n ==+⎧⎪⎨+⎪⎩,解得350m n ⎧⎪⎨⎪⎩==, ∴直线BD 的解析式为35y x =. 故答案为35y x =. 【点睛】本题考查了反比例函数图象上点的坐标特征:反比例函数y=k x(k 为常数,k≠0)的图象是双曲线,图象上的点(x ,y )的横纵坐标的积是定值k ,即xy=k .也考查了矩形的性质.20.7【解析】设树的高度为m 由相似可得解得所以树的高度为7m解析:7【解析】设树的高度为x m ,由相似可得6157262x +==,解得7x =,所以树的高度为7m 三、解答题21.(1)90o,2BC BD +;(2)结论:90PBD ∠=︒,2AB BD BC =-,理由详见解析【解析】【分析】(1)由题意得:△PCD 为等腰直角三角形,且∠PCD=90°则∠CPD=45°=∠APB ,证明△PAC ∽△PBD ,得出∠PBD=∠PAC=90°,2AC BD =,因此2AC BD =,即可得出结论;(2)由题意得:△PCD 为等腰直角三角形,且∠PCD=90°则∠CPD=45°=∠APB ,证明△PAC ∽△PBD ,得出∠PBD=∠PAC=90°,AC BD =,因此AC =,即可得出结论.【详解】解:(1)PCD QV 为等腰直角三角形,且90PCD ∠=︒, 45CPD APB ∴∠=︒=∠,CPD BPC APB BPC ∴∠+∠=∠+∠,即BPD APC ∠=∠, 又PA PB =Q ,~PAC PBD ∴∆∆2=,2AC BD ∴=,∴2AC BD =,∴2AB BC AC BC BD =+=+,故答案为90o ,BC +,(2)结论:90PBD ∠=︒; 2AB BD BC =-;理由如下: PCD QV 为等腰直角三角形,且90PCD ∠=︒,45CPD APB ∴∠=︒=∠,CPD BPC APB BPC ∴∠+∠=∠+∠,即BPD APC ∠=∠, 又PA PC PB PD==Q ,PAC PBD ∴V V ∽2=,90PBD PAC ∴∠=∠=︒,2AC BD =,2AC BD ∴=,2AB AC BC BD BC ∴=-=-. 【点睛】 本题是相似形综合题,主要考查了等腰直角三角形的性质、相似三角形的判定与性质等知识;熟练掌握等腰直角三角形的性质,证明三角形相似是解决问题的关键.22.173米【解析】【分析】由外角的性质可以得到∠PAC=∠APB,从而有PB=AB=200,在Rt△PBC中,由三角函数定义可以求出PC的长.【详解】解:由题意,可得∠PAC=30°,∠PBC=60°.∴∠APB=∠PBC=∠PBC-∠PAC=30°.∴∠PAC=∠APB.∴PB=AB=200.在Rt△PBC中,∠PCB=90°,∠PBC=60°,PB=200,∴PC=PBsin∠PBC=34002003346.42⨯==≈173(米).答:灯塔P到环海路的距离PC约等于173米.考点:解直角三角形的应用-方向角问题.23.(1)BC=4;(2)sin ∠ADC=2 2.【解析】(1)如图,作AE⊥BC,∴CE=AC•cos C=1,∴AE=CE=1,1 tan3B=,∴BE=3AE=3,∴BC=4;(2)∵AD是△ABC的中线,∴DE=1,∴∠ADC=45°,∴2 sin2ADC∠=.24.(1)v=12t;(2)若汽车的平均速度为32千米/小时,小芳不能在预定的时间内到达动车站;(3)平均速度v的取值范围是24<v<40【解析】【分析】(1)根据表格中数据,可知v是t的反比例函数,设v=kt,利用待定系数法求出k即可;(2)根据时间t=13小时,求出速度,即可判断;(3)根据自变量的取值范围,求出函数值的取值范围即可.【详解】(1)根据表格中数据,可知v=kt,∵v=20时,t=0.6,∴k=20×0.6=12,∴v=12t(t≥0.2).(2)∵1﹣16-12=13,∴t=13时,v=1213=36>32,∴若汽车的平均速度为32千米/小时,小芳不能在预定的时间内到达动车站;(3)∵0.3<t<0.5,∴24<v<40,答:平均速度v的取值范围是24<v<40.【点睛】本题考查反比例函数的应用,待定系数法等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于基础题.25.(1) FD=5; (2)证明见解析.【解析】【分析】(1)利用三角形中位线的性质得出DE∥AB,进而得出∠DEC =∠B,即可得出FD=DE,即可得出答案;(2)利用等腰三角形的性质和平行线的性质得出∠B=∠A=∠CED=∠CDE,即可得出∠CDE=∠F,即可得出△CDE∽△DFE.【详解】解:(1)∵D、E分别是AC、BC的中点,∴DE//AB,DE=12AB=5又∵DE//AB,∴∠DEC= ∠B.而∠F= ∠B,∴∠DEC =∠B,∴FD=DE=5;(2)∵AC=BC,∴∠A=∠B.又∠CDE=∠A,∠CED= ∠B,∴∠CDE=∠B.而∠B=∠F,∴∠CDE=∠F,∠CED=∠DEF,∴△CDE∽△DFE.【点睛】此题主要考查了相似三角形的判定与性质以及等腰三角形的性质和平行线的性质等知识,熟练利用相关性质是解题关键.。
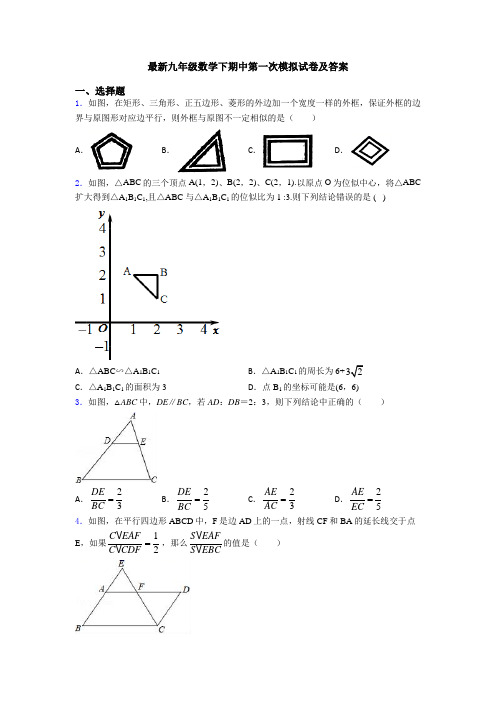
最新九年级数学下期中第一次模拟试卷及答案一、选择题1.如图,在矩形、三角形、正五边形、菱形的外边加一个宽度一样的外框,保证外框的边界与原图形对应边平行,则外框与原图不一定相似的是()A.B.C.D.2.如图,△ABC的三个顶点A(1,2)、B(2,2)、C(2,1).以原点O为位似中心,将△ABC 扩大得到△A1B1C1,且△ABC 与△A1B1C1的位似比为1 :3.则下列结论错误的是 ( )A.△ABC∽△A1B1C1B.△A1B1C1的周长为6+32C.△A1B1C1的面积为3D.点B1的坐标可能是(6,6)3.如图,△ABC中,DE∥BC,若AD:DB=2:3,则下列结论中正确的()A.23DEBC=B.25DEBC=C.23AEAC=D.25AEEC=4.如图,在平行四边形ABCD中,F是边AD上的一点,射线CF和BA的延长线交于点E,如果12C EAFC CDF=VV,那么S EAFS EBCVV的值是()A.12B.13C.14D.195.如图,△OAB∽△OCD,OA:OC=3:2,∠A=α,∠C=β,△OAB与△OCD的面积分别是S1和S2,△OAB与△OCD的周长分别是C1和C2,则下列等式一定成立的是()A.32OBCD=B.32αβ=C.1232SS=D.1232CC=6.如图,过反比例函数的图像上一点A作AB⊥轴于点B,连接AO,若S△AOB=2,则的值为()A.2 B.3 C.4 D.57.如图,ABC△与ADEV相似,且ADE B∠=∠,则下列比例式中正确的是()A.AE ADBE DC=B.AE ABAB AC=C.AD ABAC AE=D.AE DEAC BC=8.如图▱ABCD,F为BC中点,延长AD至E,使:1:3DE AD=,连结EF交DC于点G,则:DEG CFGS S∆V=()A.2:3B.3:2C.9:4D.4:99.已知2x=3y,则下列比例式成立的是()A.B.C.D.10.已知点P是线段AB的黄金分割点(AP>PB),AB=4,那么AP的长是()A.252-B.25-C.251-D.52-11.下列变形中:①由方程125x-=2去分母,得x﹣12=10;②由方程29x=92两边同除以29,得x=1;③由方程6x﹣4=x+4移项,得7x=0;④由方程2﹣5362x x-+=两边同乘以6,得12﹣x﹣5=3(x+3).错误变形的个数是()个.A.4B.3C.2D.112.给出下列函数:①y=﹣3x+2;②y=3x;③y=2x2;④y=3x,上述函数中符合条作“当x>1时,函数值y随自变量x增大而增大“的是()A.①③B.③④C.②④D.②③二、填空题13.已知反比例函数21kyx+=的图像经过点(2,1)-,那么k的值是__.14.一天,小青想利用影子测量校园内一根旗杆的高度,在同一时刻内,小青的影长为2米,旗杆的影长为20米,若小青的身高为1.60米,则旗杆的高度为__________米.15.计算:cos245°-tan30°sin60°=______.16.若△ABC∽△A’B’C’,且△ABC与△A’B’C’的面积之比为1:4,则相似比为____.17.如图,点D、E、F分别位于△ABC的三边上,满足DE∥BC,EF∥AB,如果AD:DB=3:2,那么BF:FC=_____.18.如图,l 1∥l 2∥l 3,AB=25AC ,DF=10,那么DE=_________________.19.如图,小军、小珠之间的距离为2.7 m ,他们在同一盏路灯下的影长分别为1.8 m ,1.5 m ,已知小军、小珠的身高分别为1.8 m ,1.5 m ,则路灯的高为____m.20.如图所示的网格是正方形网格,点P 到射线OA 的距离为m ,点P 到射线OB 的距离为n ,则m __________ n .(填“>”,“=”或“<”)三、解答题21.如图,等边ABC ∆中,D 、E 、F 分别是AB 、AC 、BC 上的点,连接CD 、EF 交于点G ,且60CGF ∠=︒.(1)请直接写出图中所有与BDC ∆相似的三角形(任选一对证明);(2)若45EF DC =,试求AE EC 的值.22.如图,小明同学在东西方向的环海路A 处,测得海中灯塔P 在它的北偏东60°方向上,在A 的正东200米的B 处,测得海中灯塔P 在它的北偏东30°方向上.问:灯塔P 到环海路的距离PC 约等于多少米?(取1.732,结果精确到1米)23.如图,某市郊外景区内一条笔直的公路l 经过A 、B 两个景点,景区管委会又开发了风景优美的景点C .经测量,C 位于A 的北偏东60︒的方向上,B 的北偏东30°的方向上,且10AB km =.(1)求景点B 与C 的距离.(2)求景点A 与C 的距离.(结果保留根号)24.已知:△ABC 在直角坐标平面内,三个顶点的坐标分别为A (0,3)、B (3,4)、C (2,2)(正方形网格中每个小正方形的边长是一个单位长度).(1)画出△ABC 向下平移4个单位长度得到的△A 1B 1C 1,点C 1的坐标是 ; (2)以点B 为位似中心,在网格内画出△A 2B 2C 2,使△A 2B 2C 2与△ABC 位似,且位似比为2:1,点C 2的坐标是 .25.如图,l 1∥l 2∥l 3,AB=3,AD=2,DE=4,EF=7.5.求BC 、BE 的长?【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】根据相似多边形的判定定理对各个选项进行分析,从而确定最后答案.【详解】正五边形相似,因为它们的边长都对应成比例、对应角都相等,符合相似的条件,故A不符合题意;锐角三角形、菱形的原图与外框相似,因为其对应角均相等,对应边均对应成比例,符合相似的条件,故B、D不符合题意;矩形不相似,因为其对应角的度数一定相同,但对应边的比值不一定相等,不符合相似的条件,故A符合题意;故选C.【点睛】本题主要考查了相似图形判定,解决本题的关键是要注意边数相同、各角对应相等、各边对应成比例的两个多边形是相似多边形.2.C解析:C【解析】【分析】根据位似图的性质可知,位似图形也是相似图形,周长比等于位似比,面积比等于位似比的平方,对应边之比等于位似比,据此判断即可.【详解】A. △ABC∽△A1B1C1,故A正确;B. 由图可知,AB=2-1=1,BC=2-1=1,,所以△ABC的周长为,由周长比等于位似比可得△A1B1C1的周长为△ABC周长的3倍,即6+B正确;C. S△ABC=1111=22⨯⨯,由面积比等于位似比的平方,可得△A1B1C1的面积为△ABC周长的9倍,即19=4.52⨯,故C错误;D. 在第一象限内作△A1B1C1时,B1点的横纵坐标均为B的3倍,此时B1的坐标为(6,6),故D正确;故选C.【点睛】本题考查位似三角形的性质,熟练掌握位似的定义,以及位似三角形与相似三角形的关系是解题的关键.3.B解析:B【解析】【分析】运用平行线分线段成比例定理对各个选项进行判断即可.【详解】∵AD:DB=2:3,∴ADAB=25.∵DE∥BC,∴DEBC=ADAB=25,A错误,B正确;AE AC =ADAB=25,C错误;AE EC =ADDB=23,D错误.故选B.【点睛】本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.4.D解析:D【解析】分析:根据相似三角形的性质进行解答即可.详解:∵在平行四边形ABCD中,∴AE∥CD,∴△EAF∽△CDF,∵12EAFCDFCCVV,=∴12 AFDF=,∴11123 AFBC==+,∵AF∥BC,∴△EAF∽△EBC,∴21139EAFEBCSS⎛⎫==⎪⎝⎭VV,故选D.点睛:考查相似三角形的性质:相似三角形的面积比等于相似比的平方.5.D解析:D【解析】A选项,在△OAB∽△OCD中,OB和CD不是对应边,因此它们的比值不一定等于相似比,所以A选项不一定成立;B 选项,在△OAB ∽△OCD 中,∠A 和∠C 是对应角,因此αβ=,所以B 选项不成立; C 选项,因为相似三角形的面积比等于相似比的平方,所以C 选项不成立;D 选项,因为相似三角形的周长比等于相似比,所以D 选项一定成立.故选D.6.C解析:C【解析】试题分析:观察图象可得,k >0,已知S △AOB =2,根据反比例函数k 的几何意义可得k=4,故答案选C.考点:反比例函数k 的几何意义.7.D解析:D【解析】【分析】利用相似三角形性质:对应角相等、对应边成比例,可得结论.【详解】由题意可得,A ABC DE ∽△△,所以AE DE AC BC=, 故选D .【点睛】在书写两个三角形相似时,注意顶点的位置要对应,即若ABC A B C '''∽△△,则说明点A 的对应点为点'A ,点B 的对应点B ',点C 的对应点为点C '. 8.D解析:D【解析】【分析】先设出DE x =,进而得出3AD x =,再用平行四边形的性质得出3BC x =,进而求出CF ,最后用相似三角形的性质即可得出结论.【详解】解:设DE x =,∵:1:3DE AD =,∴3AD x =,∵四边形ABCD 是平行四边形,∴//AD BC ,BC AD 3x ==,∵点F 是BC 的中点, ∴1322CF BC x ==, ∵//AD BC ,∴DEG CFG ∆∆∽,∴224392DEGCFGS DE xS CF x⎛⎫⎪⎛⎫===⎪⎪⎝⎭ ⎪⎝⎭VV,故选:D.【点睛】此题主要考查了相似三角形的判定和性质,平行四边形的性质,中点的定义,表示出CF是解本题的关键.9.C解析:C【解析】【分析】把各个选项依据比例的基本性质,两内项之积等于两外项之积,已知的比例式可以转化为等积式2x=3y,即可判断.【详解】A.变成等积式是:xy=6,故错误;B.变成等积式是:3x+3y=4y,即3x=y,故错误;C.变成等积式是:2x=3y,故正确;D.变成等积式是:5x+5y=3x,即2x+5y=0,故错误.故选C.【点睛】本题考查了判断两个比例式是否能够互化的方法,即转化为等积式,判断是否相同即可.10.A解析:A【解析】根据黄金比的定义得:12APAB=,得1422AP=⨯= .故选A.11.B解析:B【解析】【分析】根据方程的不同特点,从计算过程是否正确、方法应用是否得当等方面加以分析.【详解】①方程125x-=2去分母,两边同时乘以5,得x﹣12=10,故①正确.②方程29x=92,两边同除以29,得x=814;要注意除以一个数等于乘以这个数的倒数,故②错误.③方程6x﹣4=x+4移项,得5x=8;要注意移项要变号,故③错误.④方程2﹣5362x x-+=两边同乘以6,得12﹣(x﹣5)=3(x+3);要注意去分母后,要把是多项式的分子作为一个整体加上括号,故④错误.故②③④变形错误.故选B.【点睛】在解方程时,要注意以下问题:(1)去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号;(2)移项时要变号.12.B解析:B【解析】分析:分别利用一次函数、正比例函数、反比例函数、二次函数的增减性分析得出答案.详解:①y=﹣3x+2,当x>1时,函数值y随自变量x增大而减小,故此选项错误;②y=3x,当x>1时,函数值y随自变量x增大而减小,故此选项错误;③y=2x2,当x>1时,函数值y随自变量x增大而减小,故此选项正确;④y=3x,当x>1时,函数值y随自变量x增大而减小,故此选项正确.故选B.点睛:本题主要考查了一次函数、正比例函数、反比例函数、二次函数的性质,正确把握相关性质是解题的关键.二、填空题13.【解析】【分析】将点的坐标代入可以得到-1=然后解方程便可以得到k的值【详解】∵反比例函数y=的图象经过点(2-1)∴-1=∴k=−;故答案为k=−【点睛】本题主要考查函数图像上的点满足其解析式可以解析:32 k=-【解析】【分析】将点的坐标代入,可以得到-1=212k+,然后解方程,便可以得到k的值.【详解】∵反比例函数y=21kx+的图象经过点(2,-1),∴-1=21 2 k+∴k =− 32; 故答案为k =−32.【点睛】本题主要考查函数图像上的点满足其解析式,可以结合代入法进行解答14.16【解析】【分析】易得△AOB∽△ECD 利用相似三角形对应边的比相等可得旗杆OA 的长度【详解】解:∵OA⊥DACE⊥DA∴∠CED=∠OAB=90°∵CD∥OE∴∠CDA=∠OBA∴△AOB∽△E 解析:16 【解析】【分析】易得△AOB ∽△ECD ,利用相似三角形对应边的比相等可得旗杆OA 的长度.【详解】解:∵OA ⊥DA ,CE ⊥DA ,∴∠CED=∠OAB=90°,∵CD ∥OE ,∴∠CDA=∠OBA ,∴△AOB ∽△ECD ,∴CE OA 16OA ,DE AB 220==, 解得OA=16.故答案为16. 15.0【解析】【分析】直接利用特殊角的三角函数值代入进而得出答案【详解】=故答案为0【点睛】此题主要考查了特殊角的三角函数值正确记忆相关数据是解题关键解析:0【解析】【分析】直接利用特殊角的三角函数值代入进而得出答案.【详解】2cos 45tan30sin60︒-︒︒=223311022=-= .故答案为0.【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.16.1:2【解析】【分析】由△ABC相似△A′B′C′面积比为1:4根据相似三角形的面积比等于相似比的平方即可求解【详解】解:∵△ABC相似△A′B′C′面积比为1:4∴△ABC与△A′B′C′的相似比解析:1:2【解析】【分析】由△ABC相似△A′B′C′,面积比为1:4,根据相似三角形的面积比等于相似比的平方,即可求解.【详解】解:∵△ABC相似△A′B′C′,面积比为1:4,∴△ABC与△A′B′C′的相似比为:1:2,故答案为: 1:2.【点睛】本题主要考查的是相似三角形的性质,解决本题的关键是要熟知相似三角形面积的比等于相似比的平方.17.3:2【解析】因为DE∥BC所以因为EF∥AB所以所以故答案为:3:2解析:3:2【解析】因为DE∥BC,所以32AD AEDB EC==,因为EF∥AB,所以23CE CFEA BF==,所以32BFFC=,故答案为: 3:2.18.【解析】试题解析::∵l1∥l2∥l3∴∵AB=AC∴∴∵DF=10∴∴DE=4 解析:【解析】试题解析::∵l1∥l2∥l3,∴AB DE AC DF=.∵AB=25 AC,∴25 ABAC=,∴25 DEDF=.∵DF=10,∴2 105 DE=,∴DE=4.19.3【解析】试题分析:如图∵CD ∥AB ∥MN ∴△ABE ∽△CDE △ABF ∽△MNF ∴即解得:AB=3m 答:路灯的高为3m 考点:中心投影解析:3【解析】试题分析:如图,∵CD ∥AB ∥MN ,∴△ABE ∽△CDE ,△ABF ∽△MNF , ∴,CD DE FN MN AB BE FB AB ==, 即1.8 1.8 1.5 1.5,1.8 1.5 2.7AB BD AB BD==++-, 解得:AB=3m ,答:路灯的高为3m .考点:中心投影.20.>【解析】【分析】由图像可知在射线上有一个特殊点点到射线的距离点到射线的距离于是可知利用锐角三角函数即可判断出【详解】由题意可知:找到特殊点如图所示:设点到射线的距离点到射线的距离由图可知【点睛】本 解析:>【解析】【分析】由图像可知在射线OP 上有一个特殊点Q ,点Q 到射线OA 的距离2QD =,点Q 到射线OB 的距离1QC =,于是可知AOP BOP ∠>∠ ,利用锐角三角函数sin sin AOP BOP ∠>∠ ,即可判断出m n >【详解】由题意可知:找到特殊点Q ,如图所示:设点Q 到射线OA 的距离QD ,点Q 到射线OB 的距离QC由图可知QD =1QC =∴ sin QD AOP OP ∠==1sin QC BOP OP OP ∠== ∴sin sin AOP BOP ∠>∠, ∴m n OP OP> ∴m n >【点睛】本题考查了点到线的距离,熟知在直角三角形中利用三角函数来解角和边的关系是解题关键.三、解答题21.(1)GFC CFE ∆∆、;(2)14 【解析】【分析】(1)根据等边三角形的性质及∠CGF=60°,可以得出∠B=∠ACB=∠CGF=60°,可以得出△BDC ∽△GFC ∽△CFE ;(2)由(1)△BDC ∽△CFE 可以得出EF CE DC BC = ,再根据条件45EF DC =和三角形ABC 是等边三角形和线段的转化,就可以得出AE EC 的值. 【详解】解:(1)GFC CFE ∆∆、∵等边ABC ∆,∴∠B=∠ACB =60°∵60CGF ∠=︒∴∠B=∠ACB=∠CGF又∵∠DCB=∠FCG∴GFC BDC ∆∆∽∵∠EFC=∠GFC∴GFC CFE ∆∆∽∴GFC CFE BDC ∆∆∽∽△(2)∵△BDC ∽△CFE454541,54EF CE DC BCEF DC CE BC CE AE AC EC ∴==∴=∆∴∴==Q Q 等边ABC AC=BC即【点睛】 本题考查了相似三角形的判定与性质,等边三角形的性质.22.173米【解析】【分析】由外角的性质可以得到∠PAC=∠APB ,从而有PB=AB=200,在Rt △PBC 中,由三角函数定义可以求出PC 的长.【详解】解:由题意,可得∠PAC=30°,∠PBC=60°.∴∠APB=∠PBC=∠PBC -∠PAC=30°.∴∠PAC=∠APB .∴PB=AB=200.在Rt △PBC 中,∠PCB=90°,∠PBC=60°,PB=200,∴PC=PBsin ∠PBC=400346.42⨯==≈173(米). 答:灯塔P 到环海路的距离PC 约等于173米.考点:解直角三角形的应用-方向角问题.23.(1)BC=10km ;【解析】【分析】(1)由题意可求得∠C =30°,进一步根据等角对等边即可求得结果;(2)分别在Rt BCD ∆和Rt ACD ∆中利用锐角三角函数的知识解直角三角形即可求得结果.【详解】解:(1)过点C 作CD ⊥直线l ,垂足为D ,如图所示.根据题意,得:30CAD ∠=︒,60CBD ∠=︒,∴∠C =∠CBD -∠CAD =30°,∴∠CAD =∠C ,∴BC =AB =10km .(2) 在Rt BCD ∆中,sin CD CBD BC ∠=,∴sin 60CD BC ==o g , 在Rt ACD ∆中,1sin 2CD CAD AC ∠==,∴2AC CD ==.【点睛】本题考查了解直角三角形的应用,属于基本题型,熟练掌握锐角三角函数的知识是解题的关键.24.(1)画图见解析,(2,-2);(2)画图见解析,(1,0);【解析】【分析】(1)将△ABC向下平移4个单位长度得到的△A1B1C1,如图所示,找出所求点坐标即可;(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,如图所示,找出所求点坐标即可.【详解】(1)如图所示,画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是(2,-2);(2)如图所示,以B为位似中心,画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是(1,0),故答案为(1)(2,-2);(2)(1,0)【点睛】此题考查了作图-位似变换与平移变换,熟练掌握位似变换与平移变换的性质是解本题的关键.25.BC=6,BE=5【解析】【分析】根据平行线分线段成比例定理得BFBE=3BC=24,则可计算出BC=6,BF=12BE,然后利用12BE+BE=7.5求出BE的长.【详解】∵l1∥l2∥l3,∴FBBE=ABBC=ADDE,即BFBE=3BC=24,∴BC=6,BF=12BE,∴12BE+BE=7.5,∴BE=5.【点睛】本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.。

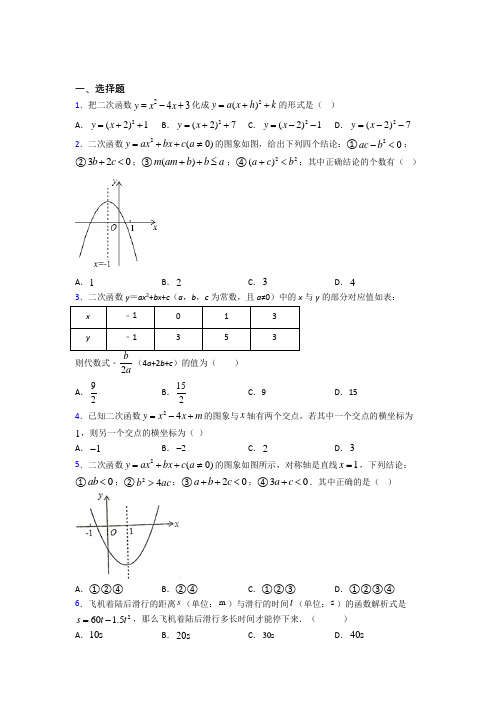
一、选择题1.一次函数y =ax +b 与二次函数y =ax 2+bx +c 在同一坐标系中的图象可能是( ) A . B .C .D .2.二次函数2y x bx c =++的图象经过坐标原点O 和点()7,0A ,直线AB 交y 轴于点()0,7B -,动点(),C x y 在直线AB 上,且17x <<,过点C 作x 轴的垂线交抛物线于点D ,则CD 的最值情况是( )A .有最小值9B .有最大值9C .有最小值8D .有最大值8 3.已知二次函数2(2)1y mx m x =+--(m 为常数,且0m ≠),( )A .若0m >,则1x <,y 随x 的增大而增大B .若0m >,则1x >,y 随x 的增大而减小C .若0m <,则1x <,y 随x 的增大而增大D .若0m <,则1x >,y 随x 的增大而减小 4.二次函数y =ax 2+bx +c 的图象如图所示,下列结论中正确的有①abc >0;②b 2﹣4ac <0;③2a >b ;④(a +c )2<b 2;⑤a ﹣2b +4c >0.( )A .1个B .2个C .3个D .4个5.小凯在画一个开口向上的二次函数图象时,列出如下表格: x… -1 0 1 2 … y … 1 2 1 1 …A .(-1,1)B .(0,2)C .(1,1)D .(2,1) 6.如图,抛物线2(0)y ax bx c a =++≠与x 轴交于点()4,0,其对称轴为直线1x =,结合图像给出下列结论:①0b <;②420a b c -+>;③当2x >时,y 随x 的增大而增大;④所以正确关于x 的一元二次方程20ax bx c ++=有两个不相等的实数根.其中正确的结论有( )A .1个B .2个C .3个D .4个7.下列不等式成立的是( )A .sin60°<sin45°<sin30°B .cos30°<cos45°<cos60°C .tan60°<tan45°<tan30°D .sin30°<cos45°<tan60°8.如图,某河堤迎水坡AB 的坡比tan 1:3CAB i =∠=,堤高5BC m =,则坡面AB 的长是( )A .5mB .10mC .53mD .8m9.如图,传送带和地面所成斜坡AB 的坡度为1∶2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为( )A .5米B 5C .25D .45 10.在Rt ABC 中,90C ∠=︒,5AB =,4BC =,则tan A 的值为( )A .35B .45C .34D .4311.如图,在44⨯的正方形方格图形中,小正方形的顶点称为格点,ABC 的顶点都在格点上,则BAC ∠的正弦值是( )A .12B .55C .255D .无法确定 12.如图,一个斜坡长130m ,坡顶离水平地面的距离为50m ,那么这个斜坡与水平地面夹角的正切值等于( )A .513B .1213C .512D .1312二、填空题13.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,则关于x 的一元二次方程2ax bx c ++0(0)a =≠的根为___________.14.抛物线23(2)4=---y x 的顶点坐标是______.15.在平面直角坐标系中,把抛物线22y x =+先绕其顶点旋转180︒后,再向右平移2个单位,向下平移3个单位后的抛物线解析式为__________.16.已知二次函数221y x =-,如果y 随x 的增大而增大,那么x 的取值范围是__________.17.如图,测角仪CD 竖直放在距建筑物AB 底部8m 的位置,在D 处测得建筑物顶端A 的仰角为50°.若测角仪CD 的高度是1.5m ,则建筑物AB 的高度约为_____m .(结果精确到个位,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)18.如图,正方形ABCD的边长为4,E为AB边上一点,tan∠ADE=34,M为ED的中点,过点M作DE的垂线,交边AD于点P,若点N在射线PM上,且由点E、M、N组成的三角形与△AED相似,则PN的长为______.19.如图,在△ABC中,∠BAC=90°,AB=AC=5,将△ABC折叠,使点B落在AC边上的点D处,EF为折痕,若sin∠CFD的值为23,则BE=_____.20.如图,一艘轮船在小岛A的北偏东60°方向且距小岛80海里的B处,沿正西方向航行一定时间后到达小岛的北偏西45°的C处,则该船航行的路程为_____海里.三、解答题21.商店销售某商品,销售中发现,该商品每天的销售量y(个)与销售单价x(元/个)之间存在如图所示的关系,其中成本为20元/个.(1)求y与x之间的函数关系式.(2)为了保证每天利润不低于1300元,单价不高于30元/个,那么商品的销售单价应该定在什么范围?22.如图(1),已知抛物线C1:y=﹣x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线C2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D (0,﹣2).(1)求抛物线C2的解析式;(2)点P(m,0)为线段AB上一动点(不与A、B重合),过点P作y轴的平行线交抛物线C1于点M,交抛物线C2于点N.①请用含m的代数式分别表示点M、N的坐标;②设四边形OMEN的面积为S,求S关于m的函数关系式,并求出当S的最大值以及此时m的值;③在点P移动的过程中,若CM=DN≠0,则m的值为.(3)如图(2),点Q(0,n)为y轴上一动点(0<n<4),过点Q作x轴的平行线依次交两条抛物线于点R、S、T、U,则TU﹣RS=.23.如图,一农户要建一矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用27m长的建筑材料围成,为了方便进出,在垂直于住房墙的一边留一个1m宽的门.所围成矩形猪舍的长、宽分别为多少时,猪舍的面积最大,最大面积是多少?24.如图,△ABC 中,BD 平分∠ABC ,E 为BC 上一点,∠BDE=∠BAD=90°,(1)求证:BD 2=BA·BE ; (2)若AB=6,BE=8,求CD 的长.25.计算下列各小题(1)2245603060cos tan tan cos ︒+︒⋅︒-︒;(2)()23tan 308cos 451tan 60︒+︒+-︒.26.如图,已知△OAB ,点A 的坐标为(2,2),点B 的坐标为(3,0).(1)求sin ∠AOB 的值;(2)若点P 在y 轴上,且△POA 与△AOB 相似,求点P 的坐标.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【分析】先由一次函数y ax b =+的图象得到a 、b 的正负,再与二次函数2y ax bx c =++的图象的开口方向、对称轴位置相比较即可做出判断.【详解】解:A 、由抛物线可知,a <0,x =﹣2b a <0,得b <0,由直线可知,a >0,b >0,故本选项错误;B 、由抛物线可知,a <0,x =﹣2b a <0,得b <0,由直线可知,a <0,b <0,故本选项正确;C 、由抛物线可知,a >0,x =﹣2b a >0,得b <0,由直线可知,a >0,b >0,故本选项错误;D 、由抛物线可知,a <0,x =﹣2b a<0,得b <0,由直线可知,a <0,b >0,故本选项错误.故选:B .【点睛】本题主要考查一次函数的图象、二次函数2y ax bx c =++的图象与性质,熟练掌握两函数图象与解析式的系数的关系是解答的关键. 2.B解析:B【分析】根据待定系数法求得抛物线的解析式和AB 的解析式,设(,7)C x x -,则2(,7)D x x x -,根据图象的位置即可得出2(4)9CD x =--+,根据二次函数的性质即可求得.【详解】 解:二次函数2y x bx c =++的图象经过坐标原点O 和点(7,0)A , ∴04970c b c =⎧⎨++=⎩,解得70b c =-⎧⎨=⎩, ∴二次函数为27y x x =-,(7,0)A ,(0,7)B -,∴直线AB 为:7y x =-,令277x x x -=-,解得:11x =,27x =,∴点E 的横坐标为1,则点C 始终在点D 上方,设(,7)C x x -,则2(,7)D x x x -,2227(7)87(4)9CD x x x x x x ∴=---=-+-=--+,17x ∴<<范围内,有最大值9,故选:B .【点睛】本题考查了二次函数的性质,待定系数法求一次函数的解析式,求二次函数的解析式,表示出CD 的关系式是解题的关键.3.D解析:D【分析】先求出二次函数图象的对称轴,然后根据m 的符号分类讨论,结合图象的特征即可得出结论.【详解】 该二次函数图象的对称轴为直线21122m x m m -=-=-+, 若0m >,对于22m x m -=-无法判断其符号,故A 、B 选项不一定正确; 若0m <,则202m x m -=-<,即22m m--<1,且抛物线的开口向下, ∴当1x >时,y 随x 的增大而减小,故选:D .【点睛】此题考查的是二次函数的图象及性质,解决此题的关键是分类讨论确定对称轴的位置,再结合开口方向进行综合分析.4.C解析:C【分析】由函数图象可知a <0,对称轴﹣1<x <0,图象与y 轴的交点c >0,函数与x 轴有两个不同的交点;即可得出b ﹣2a >0,b <0;△=b 2﹣4ac >0;再由图象可知当x =1时,y <0,即a +b +c <0;当x =﹣1时,y >0,即a ﹣b +c >0;当x =﹣12时,y >0,即14a ﹣12b +c >0,即可求解.【详解】解:由函数图象抛物线开口向下,对称轴﹣1<x <0,图象与y 轴的交点c >0, ∴a <0,2b a -<0,c >0, ∴b <0,∴abc >0,故①正确;∵函数与x 轴有两个不同的交点,∴△=b 2﹣4ac >0,故②错误; ∵2b a->﹣1, ∴2a <b ,故③错误;当x =1时,y <0,即a +b +c <0;当x =﹣1时,y >0,即a ﹣b +c >0;∴(a +b +c )(a ﹣b +c )<0,即(a +c )2<b 2;故④正确;∵x =﹣12时,y >0, ∴14a ﹣12b +c >0,即a ﹣2b +4c >0,故⑤正确; 故选:C .【点睛】此题考查二次函数的图象,根据图象确定式子的正负,正确理解函数图象,由图象得到相关信息,掌握二次函数的性质,根的判别式与图象的关系是解题的关键.5.A解析:A【分析】观察图表数据,根据二次函数的对称性即可判断出计算错误的一组数据,然后再利用二次函数的增减性得出结论.【详解】解:观察y 值发现y =1时x 有三个不同的值,因此这三个值中必有一对计算错误.由二次函数的对称性:如果(-1,1),(1,1)是图象的两个对称点,那么根据描点得到这个函数图象的开口应该是向下的.同理若(-1,1),(2,1)是两个对称点,那么该函数图象的开口也是向下的,所以(1,1),(2,1)是图象的两个对称点,因此该图像的对称轴为直线032x =,根据二次函数的增减性,当开口向上时,在对称轴的左边,y 随x 的增大而减小,所以1x =-时,y 一定是大于1的,故选A .【点睛】本题考查了二次函数的图象,找出图表数据特点,根据函数的对称性解答即可,熟练掌握二次函数的图象和性质,是解答的关键.6.C解析:C【分析】根据抛物线的开口方向、对称轴、顶点坐标、增减性以及与x 轴y 轴的交点,综合判断即可.【详解】解:抛物线开口向上,因此a >0,抛物线的对称轴为x=-2b a=1,所以0b <,所以①正确;抛物线的对称轴为x=1,与x 轴的一个交点为(4,0),则另一个交点(-2,0),于是4a-2b+c=0,所以②不正确;x >1时,y 随x 的增大而增大,所以③正确;抛物线与x 轴有两个不同的交点,因此一元二次方程20ax bx c ++=有两个不相等的实数根,所以④正确;综上所述,正确的结论有①③④.故答案为:C .【点睛】本题考查二次函数的图形和性质,掌握二次函数的图形和系数之间的关系是正确判断的前提. 7.D解析:D【分析】根据特殊角三角函数值,可得答案.【详解】解:A 、sin60°=2,sin45°=2,sin30°=12 ,故A 不成立;B 、cos30°cos45°=2,cos60°=12,故B 不成立;C 、tan60°,tan45°=1,tan30°,故C 不成立;D 、sin30°=12,cos45°,tan60°D 成立; 故选:D .【点睛】 本题考查了特殊角三角函数值,熟记特殊角三角函数值是解题的关键.8.B解析:B【分析】根据坡比求出AC 的长度,再利用勾股定理求出AB 即可.【详解】解:∵tan 3CAB BC i AC ==∠=,5BC m =, ∴53AC =m , ∴2222(53)510AB AC BC m =+=+=, 故选:B . 【点睛】此题考查解直角三角形的实际应用,勾股定理,熟记坡比的计算公式是解题的关键. 9.C解析:C【分析】作BC ⊥底面于点C ,根据坡度的概念、勾股定理列式计算即可;【详解】作BC ⊥底面于点C ,设BC x =,∵传送带和底面所成斜坡AB 的坡度为1∶2,∴2AC x =,由勾股定理得:222AC BC AB +=,即()222210x x +=,解得:25x =,即25BC =.故答案选C .【点睛】本题主要考查了解直角三角形的应用-坡度坡角问题,准确计算是解题的关键. 10.D解析:D【分析】由勾股定理算出AC 的值,然后根据正切函数的定义即可得到解答.【详解】解:由勾股定理可得:2222543AC AB BC =-=-=,∴tanA=43BC AC =, 故选D .【点睛】 本题考查解直角三角形,熟练掌握勾股定理及三角函数的定义是解题关键.11.B解析:B【分析】先根据勾股定理的逆定理判断出ABC 的形状,再由锐角三角函数的定义即可得出结论.【详解】解:2223425AB =+=,2222420AC =+=,222125BC =+=,222AC BC AB ∴+=,ABC ∴为直角三角形,且90ACB ∠=︒,则5sin BC BAC AB ∠==, 故选:B .【点睛】本题考查的是勾股定理的逆定理以及锐角三角函数的定义,熟知在一个三角形中,如果两条边长的平方之和等于第三边长的平方,那么这个三角形是直角三角形是解答此题的关键. 12.C解析:C【分析】如图(见解析),先利用勾股定理求出AC 的长,再根据正切三角函数的定义即可得.【详解】如图,由题意得:130,50,90,AB m BC m C A ==∠=︒∠是斜坡与水平地面的夹角, 由勾股定理得:22120AC AB BC m =-=, 则505tan 12012BC A AC ===, 即这个斜坡与水平地面夹角的正切值等于512, 故选:C .【点睛】本题考查了勾股定理、正切,熟练掌握正切三角函数的定义是解题关键.二、填空题13.x1=-1x2=3【分析】关于x 的一元二次方程ax2+bx+c=0(a≠0)的根即为二次函数y=ax2+bx+c (a≠0)的图象与x 轴的交点的横坐标【详解】解:根据图象知抛物线y=ax2+bx+c (解析:x 1=-1,x 2=3【分析】关于x 的一元二次方程ax 2+bx+c=0(a≠0)的根即为二次函数y=ax 2+bx+c (a≠0)的图象与x 轴的交点的横坐标.【详解】解:根据图象知,抛物线y=ax 2+bx+c (a≠0)与x 轴的一个交点是(-1,0),对称轴是x=1. 设该抛物线与x 轴的另一个交点是(x ,0),则12x -=1, 解得,x=3,即该抛物线与x 轴的另一个交点是(3,0),所以关于x 的一元二次方程ax 2+bx+c=0(a≠0)的根为x 1=-1,x 2=3.故答案是:x 1=-1,x 2=3.【点睛】本题考查了抛物线与x 轴的交点,解题时,注意抛物线y=ax 2+bx+c (a≠0)与关于x 的一元二次方程ax 2+bx+c=0(a≠0)间的转换. 14.【分析】根据题目中的抛物线可以写出该抛物线的顶点坐标本题得以解决【详解】解:∵物线∴该抛物线的顶点坐标为(2-4)故答案为:(2-4)【点睛】本题考查了二次函数的性质解题的关键是明确题意利用二次函数 解析:(2,4)-【分析】根据题目中的抛物线,可以写出该抛物线的顶点坐标,本题得以解决.【详解】解:∵物线23(2)4=---y x ,∴该抛物线的顶点坐标为(2,-4),故答案为:(2,-4).【点睛】本题考查了二次函数的性质,解题的关键是明确题意,利用二次函数的性质解答. 15.【分析】先求出抛物线绕其顶点旋转后解析式再根据平移规律即可求解【详解】解:抛物线先绕其顶点旋转后解析式为将抛物线向右平移个单位向下平移个单位后的抛物线解析式为故答案为:【点睛】本题考查了抛物线图象与解析:2(2)1=---y x【分析】先求出抛物线22y x =+绕其顶点旋转180︒后解析式,再根据平移规律即可求解.【详解】解:抛物线22y x =+先绕其顶点旋转180︒后解析式为22y x =-+,将抛物线22y x =-+向右平移2个单位,向下平移3个单位后的抛物线解析式为()212y x =---.故答案为:2(2)1=---y x【点睛】本题考查了抛物线图象与几何变换,熟知二次函数图象旋转与平移规律是解题关键. 16.【分析】由于抛物线y=2x2-1的对称轴是y 轴所以当x≥0时y 随x 的增大而增大【详解】解:∵抛物线y=2x2-1中a=2>0∴二次函数图象开口向上且对称轴是y 轴∴当x≥0时y 随x 的增大而增大故答案为解析:0x ≥【分析】由于抛物线y=2x 2-1的对称轴是y 轴,所以当x≥0时,y 随x 的增大而增大.【详解】解:∵抛物线y=2x 2-1中a=2>0,∴二次函数图象开口向上,且对称轴是y 轴,∴当x≥0时,y 随x 的增大而增大.故答案为:0x ≥.【点睛】本题考查了抛物线y=ax 2+b 的性质:①图象是一条抛物线;②开口方向与a 有关;③对称轴是y 轴;④顶点(0,b ).17.11【分析】根据题意作辅助线DE ⊥AB 然后根据锐角三角函数可以得到AE 的长从而可以求得AB 的长本题得以解决【详解】解:作DE ⊥AB 于点E 由题意可得DE =CD =8m ∵∠ADE =50°∴AE =DE•ta解析:11【分析】根据题意,作辅助线DE ⊥AB ,然后根据锐角三角函数可以得到AE 的长,从而可以求得AB 的长,本题得以解决.【详解】解:作DE ⊥AB 于点E ,由题意可得,DE =CD =8m ,∵∠ADE =50°,∴AE =DE •tan50°≈8×1.19=9.52(m ),∵BE=CD=1.5m,∴AB=AE+BE=9.52+1.52=11.2≈11(m),故答案为:11.【点睛】本题考查了解直角三角形的应用-仰角俯角问题,解答本题的关键是明确题意,利用数形结合的思想解答.18.0或或【分析】首先根据tan∠ADE=求得AE=3根据勾股定理求出DE=5由M为ED的中点得DM=EM=根据tan∠ADE=求得PM=然后分三种情况根据相似三角形的性质即可求解【详解】解:∵正方形A解析:0或154或12524【分析】首先根据tan∠ADE=34求得AE=3,根据勾股定理求出DE=5,由M为ED的中点得DM=EM=52,根据tan∠ADE=34求得PM=158,然后分三种情况,根据相似三角形的性质即可求解.【详解】解:∵正方形ABCD的边长为4,tan∠ADE=AEAD=34,AE=3,∴22345+=,∵M为ED的中点,∴DM=EM=52,∴在Rt△PMD中,PM=DM∙an∠ADE=52×34=158,如图:点N 在线段PM 上,1EMN DAE △∽△时1MN EM AE DA =,即15234MN =, ∴1158MN =, ∴111515088PN PM MN =-=-=; 点N 在线段PM 的延长线上,2EMN DAE △∽△时2MN EM AE DA =,即25234MN =, ∴2158MN =, ∴22151515884PN PM MN =+=+=; 点N 在线段PM 的延长线上,3EMN EAD △∽△时3MN EM AD EA =,即35243MN =, ∴3103MN =, ∴3315101258324PN PM MN =+=+=. 故答案为:0或154或12524. 【点睛】本题考查正方形的性质,相似三角形的性质,利用正切值求边长,熟练掌握相似三角形的性质是解题的关键.19.3【分析】由题意得△BEF ≌△DEF 故∠EDF=∠B ;由三角形的外角性质即可解决【详解】解:∵在△ABC 中∠BAC=90°AB=AC=5∴∠B=∠C 设BE=x ∵AB=5∴AE=AB-BE=5-x ∵将解析:3【分析】由题意得△BEF ≌△DEF ,故∠EDF=∠B ;由三角形的外角性质,即可解决.【详解】解:∵在△ABC 中,∠BAC=90°,AB=AC=5,∴∠B=∠C ,设BE=x ,∵AB=5∴AE=AB-BE=5-x ,∵将△ABC 折叠,使点B 落在AC 边上的点D 处,∴△BEF ≌△DEF∴BE=DE=5-x ,∠B=∠EDF=∠C∵∠ADE+∠EDF=∠C+∠DFC∴∠ADE=∠DFC∴sin ∠CFD=sin ∠ADE=523AE x DE x -==, 解得,x=3,即,BE=3故答案为:3【点睛】主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用全等三角形的性质、三角形外角性质等知识来解决问题. 20.(40+40)【分析】过A 作AQ ⊥BC 于Q ∠BAQ =60°∠CAQ =45°AB =80海里在直角三角形ABQ 中求出AQBQ 再在直角三角形AQC 中求出CQ 再根据BC =CQ+BQ 即可得出答案;【详解】解:解析:(【分析】过A 作AQ ⊥BC 于Q ,∠BAQ =60°,∠CAQ =45°,AB =80海里,在直角三角形ABQ 中求出AQ 、BQ ,再在直角三角形AQC 中求出CQ ,再根据BC =CQ+BQ 即可得出答案;【详解】解:过A 作AQ ⊥BC 于Q ,由题意得:AB =80,在直角三角形ABQ 中,∠BAQ =60°,∴∠B =90°﹣60°=30°,∴AQ =12AB =40,BQ =3AQ =403, 在直角三角形AQC 中,∠CAQ =45°,∴CQ =AQ =40,∴BC =BQ+CQ =(40+403)海里.故答案为:(40+403)【点睛】本题考查了解直角三角形的应用中的方向角问题、等腰直角三角形的性质、含30°角的直角三角形的性质等知识;通过解直角三角形得出CQ 和BQ 是解决问题的关键.三、解答题21.(1)1003400y x =-+;(2)每个不低于21元且不高于30元【分析】(1)观察图形,找出点的坐标,再利用待定系数法即可求出y 与x 之间的函数关系式; (2)设每天的销售利润为w 元,根据利润=每个的利润×销售数量,即可得出w 关于x 的函数关系式,利用二次函数图象上点的坐标特征可求出当w =1300时x 的值,再利用二次函数的性质即可解决问题.【详解】解:(1)设y 与x 的函数关系式为y =kx +b ,将(25,900),(28,600)代入y =kx +b ,得2590028600k b k b +=⎧⎨+=⎩, 解得1003400k b =-⎧⎨=⎩, ∴y 与x 的函数关系式为y =-100x +3400;(2)设该商品每天的销售利润为w 元,由题意得w =(x -20)•y=(x -20)(-100x +3400)=-100x 2+5400x -68000当w =1300时,即-100x 2+3600x -68000=1300,解得:121x =,233x =,画出每天利润w 关于销售单价x 的函数关系图象如解图,又∵单价不高于30元/个,∴当该商品的销售单价每个不低于21元,且不高于30元时,可保证每天利润不低于1300元.【点睛】本题考查了待定系数法求一次函数解析式以及二次函数的应用,解题的关键是:(1)根据点的坐标,利用待定系数法求出y与x之间的函数关系式;(2)利用二次函数图象上点的坐标特征,求出当y=1300时x的值.22.(1)y=12x2﹣32x﹣2;(2)①M(m,﹣m2+2m+3),N(m,12m2﹣32m﹣2);②S AMBN=﹣3m2+7m+10(﹣1<m<3),当m=76时,S AMBN有最大值,最大值=169 12;③1或73;(3)1.【分析】(1)令抛物线l1:y=0,可求得点A和点B的坐标,然后设设抛物线l2的解析式为y=a (x+1)(x-4),将点D的坐标代入可求得a的值,从而得到抛物线的解析式.(2)①利用待定系数法可得,M(m,-m2+2M+3),N(M,12m2-32m-2).②由点A和点B的坐标可求得AB的长,依据S AMBN=12AB•MN列出S与x的函数关系,从而可得到当S有最大值时,m的值,于是可得结论.③CM与DN不平行时,可证明四边形CDNM为等腰梯形,然后可证明GM=HN,列出关于m的方程,于是可求得点P的坐标;当CM∥DN时,四边形CDNM为平行四边形.故此DC=MN=5,从而得到关于m的方程,从而可得结论.(3)设S,T的横坐标分别为x1,x2,设R,U的横坐标分别为x3,x4.利用根与系数的关系解决问题即可.【详解】解:(1)∵令﹣x2+2x+3=0,解得:x1=﹣1,x2=3,∴A(﹣1,0),B(3,0),设抛物线l2的解析式为y=a(x+1)(x﹣4),∵将D(0,﹣2)代入得:﹣4a=﹣2,∴a=12, ∴抛物线的解析式为y=12x 2﹣32x ﹣2. (2)①由题意P (m ,0),可得M (m ,﹣m 2+2m +3),N (m ,12m 2﹣32m ﹣2). ②如图1所示:∵A (﹣1,0),B (3,0),∴AB =4,∵P (m ,0),M (m ,﹣m 2+2m +3),N (m ,12m 2﹣32m ﹣2), ∵MN ⊥AB ,∴S AMBN =12AB •MN =﹣3m 2+7m +10(﹣1<m <3), ∴当m =76时,S AMBN 有最大值,最大值=16912. ③如图2所示:作CG ⊥MN 于G ,DH ⊥MN 于H ,如果CM 与DN 不平行.∵DC ∥MN ,CM =DN ,∴四边形CDNM 为等腰梯形.∴∠DNH =∠CMG .在△CGM 和△DNH 中,DNH CMG DHN CGM DN CM ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△CGM ≌△DNH (AAS ),∴MG=HN.∴PM﹣PN=1.∵P(m,0),则M(m,﹣m2+2m+3),N(m,12m2﹣32m﹣2).∴(﹣m2+2m+3)+(12m2﹣32m﹣2)=1,解得:m1=0(舍去),m2=1.当CM∥DN时,如图3所示:∵DC∥MN,CM∥DN,∴四边形CDNM为平行四边形.∴DC=MN=5∴﹣m2+2m+3﹣(12m2﹣32m﹣2)=5,∴m1=0(舍去),m2=73,综上所述,m的值为1或73.故答案为:1或73.(3)设S,T的横坐标分别为x1,x2,设R,U的横坐标分别为x3,x4.则TU=x4﹣x2,RS=x1﹣x3,∴TU﹣RS=(x4﹣x2)﹣(x1﹣x3)=(x3+x4)﹣(x1+x2),由﹣x 2+2x +3=n ,可得,x 2﹣2x ﹣3+n =0,∴x 1+x 2=2, 由12x 2﹣32x ﹣2=n ,可得x 2﹣3x ﹣4﹣2n =0, ∴x 3+x 4=3,∴TU ﹣RS =(x 3+x 4)﹣(x 1+x 2)=3﹣2=1,故答案为:1.【点睛】本题属于二次函数综合题,考查了二次函数的性质,待定系数法,全等三角形的判定和性质,一元二次方程的根与系数的关系等知识,解题的关键是学会构建二次函数解决最值问题,学会利用参数,构建一元二次方程解决问题,属于中考压轴题.23.矩形猪舍的长、宽分别为12米、8米时,猪舍的面积最大,最大面积是96平方米.【分析】设猪舍的宽为m x ,则长为(2721)m x -+,由题意可得2(2721)2(7)98y x x x =-+=--+,然后再根据二次函数的性质进行求最大值即可;【详解】设猪舍的宽为m x ,则长为(2721)m x -+,由题意得2(2721)2(7)98y x x x =-+=--+,对称轴为7x =, 272112x -+≤,27210x -+>,814x ∴≤<,在22(7)98y x =--+中,∵20-<,∴在对称轴右侧y 随着x 的增大而减小,所以当8x =米时,即矩形猪舍的长、宽分别为12米、8米时,猪舍的面积最大,最大面积是96平方米.【点睛】本题考查了二次函数的应用,矩形的面积公式的运用及二次函数的性质,解答时寻找题目的等量关系是关键;24.(1)见解析;(2)【分析】(1)根据角平分线定义可证得∠ABD=∠EBD ,再根据相似三角形的判定证明△BAD ∽△BDE ,然后根据相似三角形的性质即可证得结论;(2)根据(1)中结论求得BD 长,再根据勾股定理求得AD 长,进而可求得∠ABD=30°,即∠ABC=60°,利用锐角三角函数求得AC 长,即可求得CD 长.【详解】解:(1)∵BD 平分∠ABC ,∴∠ABD=∠EBD ,又∵∠BDE=∠BAD=90°,∴△BAD ∽△BDE ,∴BD :BE=BA :BD ,即BD 2=BA·BE ; (2)∵由(1)可知,BD 2=BE·BA ,且AB=6,BE=8 , ∴∴AD 2=BD 2-AB 2=12 即AD=,∵sin ∠ABD=AD BD =12, ∴∠ABD=30°,又∠ABD=∠EBD ,∴∠ABC=60° ,∴CA=BA×tan60°,∴【点睛】本题考查相似三角形的判定与性质、锐角三角函数、勾股定理、角平分线的定义,熟练掌握相似三角形的判定与性质是解答的关键.25.(1)32;(2)1. 【分析】(1)直接利用特殊角的三角函数值代入得出答案;(2)直接利用特殊角的三角函数值代入得出答案;【详解】(1)22cos 45tan 60tan 30cos60︒+︒︒-︒=21222⎛⎫⨯+ ⎪ ⎪⎝⎭=131132=11=23222⨯+-+- .(2)3tan 3045︒+︒+=32=)1+=412. 【点睛】本题考查了特殊角的三角函数值,熟练掌握知识点是解题的关键;26.(1)22;(2)点P的坐标为(0,3)或(0,83).【分析】(1)证明∠AOB=45°,可得结论.(2)分两种情形,利用相似三角形的性质分别求解即可.【详解】解:(1)如图,过点A作AH⊥OB于H.∵A(2,2),∴AH=OH=2,∴∠AOB=45°,∴sin∠AOB=22.(2)由(1)可知,∠AOP=∠AOB=45°,OA=2,当△AOP′∽△AOB时,OAOA=OPOB,可得OP′=OB=3,∴P′(0,3),当△AOP∽△BOA时,OAOB=OPOA,∴2322,∴OP=83,∴P(0,83),综上所述,满足条件的点P的坐标为(0,3)或(0,83).【点睛】本题考查相似三角形的性质,解直角三角形等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.。
一、选择题1.把二次函数243y x x =-+化成2()y a x h k =++的形式是( )A .2(2)1y x =++B .2(2)7y x =++C .2(2)1y x =--D .2(2)7y x =-- 2.二次函数2(0)y ax bx c a =++≠的图象如图,给出下列四个结论:①20ac b -<;②320b c +<;③()m am b b a ++≤;④22()a c b +<;其中正确结论的个数有( )A .1B .2C .3D .4 3.二次函数y =ax 2+bx +c (a ,b ,c 为常数,且a ≠0)中的x 与y 的部分对应值如表: x﹣1 0 1 3 y﹣1 3 5 3 则代数式﹣2a (4a +2b +c )的值为( ) A .92 B .152 C .9 D .154.已知二次函数24y x x m =-+的图象与x 轴有两个交点,若其中一个交点的横坐标为1,则另一个交点的横坐标为( )A .1-B .2-C .2D .35.二次函数2(0)y ax bx c a =++≠的图象如图所示,对称轴是直线1x =,下列结论:①0ab <;②24b ac >;③20a b c ++<;④30a c +<.其中正确的是( )A .①②④B .②④C .①②③D .①②③④ 6.飞机着陆后滑行的距离s (单位:m )与滑行的时间t (单位:s )的函数解析式是260 1.5s t t =-,那么飞机着陆后滑行多长时间才能停下来.( )A .10sB .20sC .30sD .40s7.如图,△ABC 中,AB =AC =13,BC =10,则sin B =( )A .512B .1013C .513D .12138.如图,在直角△BAD 中,延长斜边BD 到点C ,使得BD=2DC ,连接AC ,如果5tanB 3=,则tan CAD ∠的值是( )A .3B .3C .13D .15 9.cos45°的值为( ) A .1 B .12 C .22 D .32 10.如图,在国旗台DF 上有一根旗杆AF ,国庆节当天小明参加升旗仪式,在B 处测得旗杆顶端的仰角为37°,小明向前走4米到达点E ,经过坡度为1的坡面DE ,坡面的水平距离是1米,到达点D ,测得此时旗杆顶端的仰角为53°,则旗杆的高度约为( )米.(参考数据:sin370.6︒≈,cos370.8︒≈,tan370.75︒≈)A .6.29B .4.71C .4D .5.3311.已知在Rt △ABC 中,∠C =90°,AC 15AB =4,则cos B 的值是( ) A 15B .13 C .14 D 1512.如图,菱形ABCD 的边长是2,∠B=120°,P 是对角线AC 上一个动点,E 是CD 的中点,则PE +PD 的最小值为( )A .2B .3C .2D .5二、填空题13.如图,二次函数2y ax bx c =++与反比例函数k y x=的图象相交于点()()()1231,1,3,A y B y C y -、、三个点,则不等式2kax bx c x ++>的解是____.14.已知抛物线22y x x n =-+与x 轴只有一个公共点,则n =__________.15.一个盒子中装有分别写上数字1,2,﹣4的三个大小形状相同的白球,现摇匀后从中随机摸出一个球,将上面的数字记作a ,不放回.再从中随机摸出一个球,将上面的数字记作b ,则a ,b 的值使得抛物线y =ax 2+bx +3的对称轴在y 轴右侧的概率为_____. 16.若方程20ax bx c ++=的两个根是3-和1,那么二次函数2y ax bx c =++的图象的对称轴是直线x = _____________________17.如图所示,在△ABC 中,∠ACB =90°,CD 是AB 边上的中线,AC =6,CD =5,则sin A 等于________.18.如图是某数学兴趣小组设计用手电简来测量某古城墙高度的示意图,在点P 处放一水平的平面镜,光线从点A 出发经平面镜反射后刚好射到古城墙CD 的顶端C 处,已知AB ⊥BD ,CD ⊥BD ,且测得AB =4m ,BP =6m ,PD =12m ,那么该古城墙CD 的高度是_____.19.如图,矩形ABCD 的四个顶点分别在直线3421,,,l l l l 上.若这四条直线相互平行且相邻直线的间距均为1,若α=30°,则矩形ABCD 的面积为_________.20.已知在Rt ABC 中,90C ∠=︒,1cot 3B =,2BC =,那么AC =_____________. 三、解答题21.在平面直角坐标系xOy 中,二次函数y =ax 2+2x ﹣3a (a ≠0)交x 轴于A 、B 两点(点A 在点B 的左侧),且抛物线的对称轴为直线x =﹣1.(1)求此抛物线的解析式及A 、B 两点坐标;(2)若抛物线交y 轴于点C ,顶点为D ,求四边形ABCD 的面积.22.已知抛物线2y ax c =+经过点()0,2A 和点()1,0B -.(1)求抛物线的解析式;(2)将(1)中的抛物线平移,使其顶点坐标为()2,1,平移后的抛物线与x 轴的两个交点分别为点,C D (点C 在点D 的左边).求点,C D 的坐标;(3)将(1)中的抛物线平移,设其顶点的纵坐标为m ,平移后的抛物线与x 轴两个交点之间的距离为n .若15m <≤,直接写出n 的取值范围.23.在平面直角坐标系中,抛物线212y x bx c =++经过点(4,0)A -,点M 为抛物线的顶点,点B 在y 轴上,且OA OB =,直线AB 与抛物线在第一象限交于点()2,6C ,如图.(1)求抛物线的解析式;(2)求直线AB 的函数解析式、点M 的坐标和ABO ∠的余弦值.(3)连接OC ,若过点O 的直线交线段AC 于点P ,将AOC △的面积分成1:2的两部分,求点P 的坐标为______.24.在△ABC 中,∠ACB =90°,CA =CB =2,点P 是边AB 的中点,连接CP . (1)如图①,∠B 的大小= (度),AB 的长= ,CP 的长= ;(2)延长BC 至点O ,使OC =2BC ,将△ABC 绕点O 逆时针旋转α(0°<α<180°)得到△A'B'C',点A ,B ,C ,P 的对应点分别为A',B',C',P'.①图②,当α=30°时,求点C′到直线OB 的距离及点C'到直线AB 的距离;②当C′P'与△ABC 的一条边平行时,求点P'到直线AC 的距离(直接写出结果即可).25.某数学小组开展了一次测量小山高度的活动,如图,该数学小组从地面A 处出发,沿坡角为53°的山坡AB 直线上行一段距离到达B 处,再沿着坡角为22°的山坡BC 直线上行600米到达C 处,通过测量数据计算出小山高CD =612m ,求该数学小组行进的水平距离AD (结果精确到1m ).(参考数据:sin22°≈0.37,cos22°≈0.92,cos53°≈0.6,tan53°≈1.3)26.(120182sin 30|12(2020)2π-⎛⎫︒-+-- ⎪⎝⎭(2)解方程:(3)(1)3x x x --=-(3)先化简,再求值:21111x x x x -⎛⎫-÷ ⎪++⎝⎭,其中 1.x =【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】利用配方法先提出二次项系数,在加上一次项系数的一半的平方来凑完全平方式,即可把一般式转化为顶点式.【详解】解:()()22243443421y x x x x x =-+=-++-=--. 故选:C .【点睛】此题考查了二次函数的顶点式,掌握利用配方法将二次函数一般式转化为顶点式是解题的关键.2.D解析:D【分析】利用二次函数图象的相关知识与函数系数的联系,需要根据图形,逐一判断.【详解】解:∵抛物线开口向下,所以a<0,与y 轴交于正半轴,所以c >0,∴ac<0,∵b²≥0,∴20ac b -<,∴①正确;∵把x=1代入抛物线得:y=a+b+c <0,∴2a+2b+2c <0,∵-2b a-=-1, ∴b=2a , ∴3b+2c <0,∴②正确;∵抛物线的对称轴是直线x=-1,∴y=a-b+c 的值最大,即把x=m 代入得:y=am 2+bm+c≤a -b+c ,∴am 2+bm+b≤a ,即m (am+b )+b≤a ,∴③正确;∵a+b+c <0,a-b+c >0,∴(a+c+b )(a+c-b )<0,则(a+c )2-b 2<0,即(a+c )2<b 2,故④正确;故选:D .【点睛】本题考查了二次函数图象与系数的关系,在解题时要注意二次函数的系数与其图象的形状,对称轴,特殊点的关系,也要掌握在图象上表示一元二次方程ax 2+bx+c=0的解的方法,同时注意特殊点的运用.3.B解析:B【分析】由当x=0和x=3时y 值相等,可得出二次函数图象的对称轴为直线x=32,进而可得出2b a -的值,由x=1时y=5,可得出当x=2时y=5,即4a+2b+c=5,再将2b a -=32及4a+2b+c=5代入2b a -(4a+2b+c )中即可求出结论. 【详解】解:∵当x =0和x =3时,y 值相等,∴二次函数图象的对称轴为直线x =32, ∴3=22b a -. ∵当x =1时,y =5,∴当x =2×32﹣1=2时,y =5, ∴4a +2b +c =5. ∴2b a -(4a +2b +c )=32×5=152. 故选:B .【点睛】本题考查了二次函数图象上点的坐标特征以及二次函数的性质,利用二次函数的性质及二次函数图象上点的坐标特征,找出2b a-和(4a+2b+c )的值是解题的关键. 4.D解析:D【分析】函数的对称轴为:x=-22b a=,一个交点的坐标为(1,0),则另一个交点的坐标为(3,0),即可求解.【详解】 解:∵二次函数y=x 2-4x+m 中a=1,b=-4,∴函数的对称轴为:x=-22b a=, ∵一个交点的坐标为(1,0)与另一个交点的坐标关于对称轴对称,∴另一个交点的坐标为(3,0),即另一个交点的横坐标为3.故选:D .【点睛】本题考查的是抛物线与x 轴的交点,主要考查函数图象上点的坐标特征,要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法,及这些点代表的意义及函数特征. 5.C解析:C【分析】根据函数的图像分别确定各项系数的正负,再由对称轴和与x 轴的交点即可解题.【详解】∵抛物线开口向上,∴a>0,∵抛物线与y 轴的交点在x 轴下方,∴c<0,抛物线的对称轴为直线x=-b 2a =10>,即02<b a0a >0b ∴<∴ab<0,所以①正确;∵抛物线与x 轴有2个交点,∴△=b 2-4ac>0,所以②正确;∵x=1时,y<0,∴a+b+c<0,而c<0,∴a+b+2c<0,所以③正确;∵抛物线的对称轴为直线x=-b 2a=1, ∴b=-2a ,而x=-1时,y>0,即a-b+c>0,∴a+2a+c>0,即30a c +>所以④错误.故选C .本题考查了二次函数的图像与性质,属于简单题,熟悉二次函数的图像性质是解题关键. 6.B解析:B【分析】当s取最大值时,飞机停下来,求函数最大值时的自变量即可.【详解】∵当s取最大值时,飞机停下来,∴t=6022( 1.5)ba-=-⨯-=20,故选:B.【点睛】本题考查了二次函数应用-飞机着陆问题,熟练把问题转化为二次函数的最值问题是解题的关键.7.D解析:D【分析】过点A作AD⊥BC,垂足为D,求出AD长,再根据三角函数的意义计算即可.【详解】解:过点A作AD⊥BC,垂足为D,∵AB=AC=13,BC=10,∴BD=CD=5,AD=2212AB BD-=,sin B=1213 ADAB=,故选:D.【点睛】本题考查了等腰三角形的性质和三角函数,解题关键是作高构建直角三角形,利用三角函数的意义进行计算.8.D解析:D延长AD ,过点C 作CE ⊥AD ,垂足为E ,由5tanB 3=,即53AD AB =,设AD =5x ,则AB =3x ,利用相似三角形的判定可证△CDE ∽△BDA ,由相似三角形的性质可得:12CE DE CD AB AD BD ===,进而可得CE =32x ,DE =52x ,从而可求得tan ∠CAD 的值. 【详解】 解:如图,延长AD ,过点C 作CE ⊥AD ,垂足为E ,∵5tanB 3=,即53AD AB =, ∴设AD =5x ,则AB =3x , ∵∠CDE =∠BDA ,∠CED =∠BAD ,∴△CDE ∽△BDA ,∴12CE DE CD AB AD BD ===, ∴CE =32x ,DE =52x , ∴AE =152x , ∴tan ∠CAD =15CE AE =. 故选:D .【点睛】 本题考查了锐角三角函数的定义、相似三角形的判定和性质等知识,解题的关键是:正确添加辅助线,将∠CAD 放在直角三角形中.9.C解析:C【分析】直接根据特殊角的三角函数值即可得出结论;【详解】∵2cos 452=° , 故选:C .【点睛】本题考查了特殊角的三角函数值,熟记各特殊角度的三角函数值是解答此题的关键. 10.A解析:A【分析】过点D 作DG ⊥BC ,根据题意可得DG=FC=1,再根据题意可证ADF ~BAC ,最后相似三角形的性质即可求解.【详解】解:过点D 作DG ⊥BC∵坡度为1的坡面DE ,∴∠DEG =45°∵EG =1∴DG=FC=1∵∠ADF=53°∴∠DAF=∠B=37°∴ADF ~BAC令AF=x ,则DF=GC=0.75x0.75410.751x x x x =+++ 解得:x 6.29≈故选:A .【点睛】此题主要考查锐角的三角函数、相似三角形的判定与性质,熟练进行逻辑推理是解题关键.11.C解析:C【分析】首先利用勾股定理计算出BC 长,再根据余弦定义可得答案.【详解】解:如图:∵∠C =90°,AC =15,AB =4,∴BC =22AB AC -=1615-=1, ∴cosB =BC AB =14, 故选:C .【点睛】此题主要考查了锐角三角函数定义,解题的关键是掌握余弦:锐角B 的邻边a 与斜边c 的比叫做∠B 的余弦,记作cosB .12.B解析:B【详解】∵四边形ABCD 是菱形,∴点B 与点D 关于直线AC 对称.如图,连接BE 与AC 相交于点P ,由轴对称确定最短路线问题,BE 的长度即为PE+PD 的最小值,连接BD.∵∠B=120°,∴∠BCD=180°−120°=60°.又∵BC=CD ,∴△BCD 是等边三角形.∵E 是CD 的中点,3sin 6023BE BC =⋅=⨯= . 故选B.二、填空题13.或【分析】不等式的解集对应图象上面为二次函数图象比反比例函数图象高的部分找出x 的范围即可【详解】解:不等式的解对应图象上面为二次函数图象比反比例函数图象高的部分∴不等式的解为或故答案为:或【点睛】本 解析:10x -<<或13x <<【分析】不等式的解集对应图象上面为二次函数图象比反比例函数图象高的部分,找出x 的范围即可.【详解】 解:不等式2k ax bx c x++>的解对应图象上面为二次函数图象比反比例函数图象高的部分,∴不等式2k ax bx c x++>的解为10x -<<或13x <<, 故答案为:10x -<<或13x <<.【点睛】本题考查利用函数图象解不等式,即比较图象的高低.14.【分析】由抛物线与x 轴只有一个公共点可知对应的一元二次方程根的判别式△=b2−4ac =0由此即可得到关于n 的方程解方程即可求得n 的值【详解】解:∵抛物线与x 轴只有一个公共点∴△=4−4×1×n =0解解析:1【分析】由抛物线22y x x n =-+与x 轴只有一个公共点可知,对应的一元二次方程220x x n -+=根的判别式△=b 2−4ac =0,由此即可得到关于n 的方程,解方程即可求得n 的值.【详解】解:∵抛物线22y x x n =-+与x 轴只有一个公共点,∴△=4−4×1×n =0,解得n =1.故答案为:1.【点睛】此题主要考查了抛物线与x 轴的交点问题,利用二次函数根的判别式的和抛物线与x 轴的交点个数建立方程是解题的关键.15.【分析】根据题意画出树状图然后根据对称轴位于y轴的右侧找出满足条件的结果数即可求解【详解】解:根据题意画树状图如下:共有6种等可能的结果二次函数y =ax2+bx+3的对称轴为要保证对称轴在y 轴的右侧 解析:23【分析】根据题意画出树状图,然后根据对称轴位于y轴的右侧,找出满足条件的结果数即可求解.【详解】解:根据题意画树状图如下:共有6种等可能的结果,二次函数y =ax 2+bx +3的对称轴为2b x a =-, 要保证对称轴在y 轴的右侧,即b x 02a=->, 则满足条件的结果有(1,-4)、(2,-4)、(-4,1)、(-4,2),∴概率为4263P ==, 故答案为:23. 【点睛】本题考查利用树状图求概率、抛物线的对称轴,解题的关键是根据题意画出树状图. 16.【分析】先根据题意得出抛物线与x 轴的交点坐标再由两点坐标关于抛物线的对称轴对称即可得出结论【详解】解:∵方程ax2+bx+c=0的两个根是-3和1∴二次函数y=ax2+bx+c 的图象与x 轴的交点分别解析:1-【分析】先根据题意得出抛物线与x 轴的交点坐标,再由两点坐标关于抛物线的对称轴对称即可得出结论.【详解】解:∵方程ax 2+bx+c=0的两个根是-3和1,∴二次函数y=ax 2+bx+c 的图象与x 轴的交点分别为(-3,0),(1,0).∵此两点关于对称轴对称,∴对称轴是直线x=312-+=-1. 故答案为:-1.【点睛】本题考查的是抛物线与x 轴的交点,熟知抛物线与x 轴的交点与一元二次方程根的关系是解答此题的关键. 17.【分析】根据直角三角形斜边上的中线等于斜边的一半可得CD=AD 再根据勾股定理求出BC 的长然后根据再根据勾股定理求出BC 的长然后根据正弦的定义求出∠A 的正弦即为sinA 的值【详解】解:∵CD 是AB 边上解析:45【分析】根据直角三角形斜边上的中线等于斜边的一半可得CD=AD ,再根据勾股定理求出BC 的长,然后根据再根据勾股定理求出BC 的长,然后根据正弦的定义求出∠A 的正弦,即为sin A 的值.【详解】解:∵CD 是AB 边上的中线,∴CD=AD∴AB=2CD=2×5=10∴8== ∵sin A=84105BC AB == 【点睛】本题考查了锐角三角函数的定义,直角三角形斜边上的中线等于斜边的一半的性质, 再根据勾股定理求出BC 的长,,然后根据正弦的定义求出∠A 的正弦是解本题的关键. 18.8米【分析】根据光的反射原理得到∠APB=∠CPD 在直角三角形中利用等角的正切值相等建立等式求解即可【详解】根据光的反射原理得到∠APB=∠CPD ∴tan ∠APB=tan ∠CPD ∴∴解得CD=8故应解析:8米.【分析】根据光的反射原理,得到∠APB=∠CPD ,在直角三角形中,利用等角的正切值相等建立等式求解即可.【详解】根据光的反射原理,得到∠APB=∠CPD ,∴tan ∠APB =tan ∠CPD , ∴AB CD PB PD=, ∴4612CD =, 解得CD=8,故应填8米.【点睛】 本题考查了物理背景下的三角函数问题,熟练掌握光的反射原理,三角函数的定义是解题的关键.19.【分析】过B 点作直线EF 与平行线垂直与l2交于点E 与l3交于点F 得AB=2进而求得矩形的面积;【详解】解:如图过B 作于E 点交于F 点∵∴∠又∵相邻直线的间距均为1∴BF=EF=1则∴又∵矩形ABCD 中解析:83 【分析】过B 点作直线EF 与平行线垂直,与l 2交于点E ,与l 3交于点F .得AB=2,43BC =.进而求得矩形的面积;【详解】解:如图,过B 作2BE l ⊥于E 点,交2l 于F 点∵34//l l∴∠=30BAF α∠=︒又∵相邻直线的间距均为1,∴BF=EF=1 则1sin 2BF AB α== ∴2212AB BF ==⨯=又∵矩形ABCD 中,∠90ABC =° 而∠+90ABF α∠=︒∴30EBC α∠=∠=︒,且BE=2 ∴3cos 2BE EBC BC ∠== ∴34323BC BE ===则S 矩形ABCD=AB×BC=483233= 83 【点睛】 本题考查了矩形的性质、直角三角形中三角函数的应用,锐角三角函数值的计算等知识,根据平行线之间的距离构造全等的直角三角形是关键.20.6【分析】根据三角函数的定义即可求解【详解】∵cotB=∴AC==3BC=6故答案是:6【点睛】此题考查锐角三角函数的定义及运用解题关键在于掌握在直角三角形中锐角的正弦为对边比斜边余弦为邻边比斜边正解析:6【分析】根据三角函数的定义即可求解.【详解】∵cotB=BCAC,∴AC=13BC BCcotB=3BC=6.故答案是:6.【点睛】此题考查锐角三角函数的定义及运用,解题关键在于掌握在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边,余切为邻边比对边.三、解答题21.(1)y=x2+2x﹣3,A(﹣3,0),B(1,0);(2)四边形ABCD的面积是9【分析】(1)根据抛物线对称轴方程x=b2a求得a的值,继而确定函数解析式;将二次函数解析式转换为交点式,直接写出A、B两点坐标;(2)由抛物线解析式求得点C、D的坐标,然后利用分割法求得四边形ABCD的面积.【详解】解:(1)根据题意知,抛物线的对称轴为x=﹣22a=﹣1,则a=1.故该抛物线解析式是:y=x2+2x﹣3.因为y=x2+2x﹣3=(x+3)(x﹣1),所以A(﹣3,0),B(1,0);(2)如图:由(1)知,A(﹣3,0),B(1,0),由抛物线y=x2+2x﹣3知,C(0,﹣3).∵y=x2+2x﹣3=(x+1)2﹣4,∴D(﹣1,﹣4),E(﹣1,0).∴AE =2,OC =3,OE =1,OB =1,ED =4,∴S 四边形ABCD =S △BOC +S 梯形OEDC +S △DAE =12×1×3+12(3+4)×1+12×2×4=9. 即四边形ABCD 的面积是9.【点睛】本题考查了抛物线与x 轴的交点以及二次函数的性质,得出各点的坐标是解答本题的突破口,另外注意将不规则图形的面积转化为几个规则图形的面积和进行求解.22.(1)222y x =-+;(2)2,0,222C D ⎛⎫⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭;(3n <≤【分析】(1)把点A 、B 的坐标分别代入函数解析式,列出关于a 、c 的方程组,通过解方程求得它们的值;(2)根据平移的规律写出平移后抛物线的解析式,然后令0y =,则解关于x 的方程,即可求得点C 、D 的横坐标;(3)根据抛物线与x 轴两个交点之间的距离为21||x x -的关系来即可求n 的取值范围;【详解】解:(1)抛物线2y ax c =+经过点(0,2)A 和点(1,0)B -, ∴20c a c =⎧⎨+=⎩, 解得:22a c =-⎧⎨=⎩, ∴此抛物线的解析式为222y x =-+;(2)此抛物线平移后顶点坐标为(2,1),∴抛物线的解析式为22(2)1y x =--+,令0y =,即22(2)10x --+=,解得 12x =+22x =-, 点C 在点D 的左边,(C ∴ 22-0),(2D +,0); (3)设平移后抛物线的解析式是22y x m =-+,该抛物线与x 轴的两交点横坐标为1x ,2x ,整理为:220x m -=.此时120x x +=,122m x x =-.则21||x x n -==.当1m =时,n =当5m =时,n =.所以,nn <≤【点睛】本题考查了待定系数法求二次函数解析式,二次函数图象的几何变换.要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.会利用方程求抛物线与坐标轴的交点.23.(1)2122y x x =+;(2)4y x =+,()2,2M --,cos 2ABO ∠=;(3)(2,2)P -或(0,4)【分析】(1)将点A 、C 的坐标代入抛物线表达式,求出b 、c 的值,即可求解抛物线的解析式; (2)点A (−4,0),OB =OA =4,故点B (0,4),利用待定系数法求出AB 的表达式,并根据二次函数关系式,可求得点M 的坐标,并由函数关系式得ABO ∠的度数,即可求出ABO ∠的余弦值;(3)OP 将△AOC 的面积分成1:2的两部分,则可利用高相等时,面积比等于底之比得13AP AC =或23AC ,得出13p c y y =或23p c y y =,即可求解. 【详解】解:(1)将点A 、C 的坐标代入抛物线表达式得:11640214262b c b c ⎧⨯-+=⎪⎪⎨⎪⨯++=⎪⎩, 解得20b c =⎧⎨=⎩, 故抛物线的解析式为:2122y x x =+. (2)点(4,0)A -,4OB OA ==,故点(0,4)B ,设直线AB 的解析式为y =kx +4,将点A 坐标代入得,−4k +4=0,∴k =1.∴直线AB 的表达式为:y =x +4. 对于2122y x x =+,函数的对称轴为2x =-,故点()2,2M --,则45ABO ∠=︒,故cos 2ABO ∠=. (3)∵OP 将AOC △的面积分成1:2的两部分, ∴13OAP OAC S S =△△或23OAP OAC S S =△△, 则13AP AC =或23AP AC =. ①13AP AC =,则13p c y y =, 即163p y =. 解得2p y =.当2p y =时,42x +=解得2x =-, ②23AP AC =,则23p c y y =, 即236py =. 解得4p y =.当4p y =时,44x +=,解得0x =,故点(2,2)P -或(0,4).故答案为:(2,2)P -或(0,4).【点睛】本题属于二次函数综合题,考查了待定系数法求函数的解析式、二次函数的图象与性质、面积的计算等,掌握待定系数法、二次函数的图象与性质等相关知识并能灵活应用其解决问题是解题的关键.24.(1)45,2)①点C′到直线OB 的距离为2,点C′到直线AB 的距离为;②4﹣或或5【分析】(1)根据三角形内角和定理以及勾股定理,直角三角形斜边中线的性质求解即可.(2)①过点C′作C′D ⊥OB ,垂足为点D ,过点C′作C′E ⊥AB ,交BA 的延长线于点E ,连接AC′,解直角三角形求出C′D ,C′E 即可.②分三种情形:如图③﹣1中,当P′C′∥AC 时,延长P′C′交OB 于H .如图③﹣2中,如图当P′C′∥AB 时,过点P′作P′H ⊥OB 交BO 的延长线于H ,交A′C′于T .如图③﹣3中,当P′C′∥BC 时,延长B′A′交BO 于H ,分别画出图形求解即可.【详解】解:(1)在△ABC中,∠ACB=90°,CA=CB=2,∴∠B=∠A=45°,∵sinB=CAAB =22,∴AB=22,∵点P是边AB的中点,∴CP=12AB=2,故答案为45,22,2.(2)①过点C′作C′D⊥OB,垂足为点D,过点C′作C′E⊥AB,交BA的延长线于点E,连接AC′,∵将△ABC绕点O逆时针旋转a得到△A′B′C′,∴OC′=OC=2BC=2×2=4,在R△OC′D中,∠O=30°,∴C′D=12OC′=12×4=2,∴点C′到直线OB的距离为2,OD2OC D'242-=3;∵C′D⊥OB,∠ACB=90°,∴∠C′DB=∠ACB=90°,∴AC∥C′D,∵C′D=2,AC=2,C′D=AC,∴四边形C′DCA是平行四边形,∴C′A=DC=OC﹣OD=4﹣3C′A∥DC,∴∠EAC'=∠B=45°,∠EC′A=90°﹣∠EAC′=90°﹣45°=45°,∴∠EAC′=∠EC′A∴C′E=AE,在Rt△AC′E中,∵C′E2+AE2=C′A2,∴C′E2=22C A,∴C′E=22C′A=22(4﹣23)=22﹣6.∴点C′到直线AB的距离为22﹣6;②如图③﹣1中,当P′C′∥AC时,延长P′C′交OB于H.∵P′H∥AC,∴∠OHC′=∠ACO=90°,∵∠OC′H=∠B′C′P′=45°,∴OH=OC′•cos45°=22,∴CH=OC﹣OH=4﹣22.∴点P'到直线AC的距离为4﹣22.如图③﹣2中,如图当P′C′∥AB时,过点P′作P′H⊥OB交BO的延长线于H,交A′C′于T.由题意四边形OHTC′是矩形,OH=C′T=1,∴CH=OC+OH=1+4=5,∴点P'到直线AC的距离为5.如图③﹣3中,当P′C′∥BC时,延长B′A′交BO于H,可得OH=OB′•cos45°=2,∴CH =32+4,∴点P'到直线AC 的距离为4+32.综上所述,点P'到直线AC 的距离为4﹣22或4+32或5.【点睛】本题考查了作图-旋转变换,解直角三角形,直角三角形斜边中线的性质等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题.25.852m【分析】过B 作BE ⊥CD 于点E ,过B 作BH ⊥AD 于点H ,通过证明四边形BEDH 是矩形,得到DE =BH ,BE =DH ,再根据三角函数的性质,分别计算得BE 、AH 的长,即可完成求解.【详解】如图,过B 作BE ⊥CD 于点E ,过B 作BH ⊥AD 于点H又∵CD AD ⊥∴//BH ED ,//EB DH ,90EDH ∠=︒∴四边形BEDH 是矩形,∴DE =BH ,BE =DH ,在Rt △BCE 中,∵BC =600,∠CBE =22°∴CE =BC•sin22°=600×0.37=222m ,BE =BC•cos22°=600×0.92=552m∴DH =BE =552m∵CD =612m ,∴BH =DE =CD-CE =612-222=390m在Rt △ABH 中,∵∠BAH =53°∴tan53°=BH AH ∴AH 3901.3==300m ∴AD =AH+DH =300+552=852m∴该数学小组行进的水平距离AD 为852m .【点睛】本题考查了矩形、三角函数的知识;解题的关键是熟练掌握矩形、三角函数的性质,从而完成求解.26.(13;(2)122,3x x ==;(3)11x --,2-. 【分析】(1)先逐项化简,再算加减即可;(2)先整理成一般形式,再用因式分解法求解即可;(3)先根据分式的运算法则化简,再把 1.x =代入计算; 【详解】解:(12012sin 30|1(2020)2π-⎛⎫︒-+-- ⎪⎝⎭=(121412⨯++-=1141+-3;(2)(3)(1)3x x x --=-,整理,得x 2-5x+6=0,∴(x-2)(x-3)=0∴122,3x x ==;(3)21111x x x x -⎛⎫-÷ ⎪++⎝⎭, =211111x x x x x x++⎛⎫-⨯ ⎪++-⎝⎭ =()111x x x x x +-⨯+- =11x --,当1x =时,=.原式=【点睛】本题考查了实数的混合运算,特殊角的三角函数值,解一元二次方程,分式的化简求值,二次根式的除法和加法等知识,熟练掌握各知识点是解答本题的关键.。

【常考题】初三数学下期中第一次模拟试卷及答案一、选择题1.如图,△ABC的三个顶点A(1,2)、B(2,2)、C(2,1).以原点O为位似中心,将△ABC 扩大得到△A1B1C1,且△ABC 与△A1B1C1的位似比为1 :3.则下列结论错误的是 ( )A.△ABC∽△A1B1C1B.△A1B1C1的周长为6+32C.△A1B1C1的面积为3D.点B1的坐标可能是(6,6)2.用放大镜观察一个五边形时,不变的量是()A.各边的长度 B.各内角的度数 C.五边形的周长 D.五边形的面积3.如图,平面直角坐标系中,点A是x轴上任意一点,BC平行于x轴,分别交y=3x(x>0)、y=kx(x<0)的图象于B、C两点,若△ABC的面积为2,则k值为()A.﹣1B.1C.12-D.124.已知点C在线段AB上,且点C是线段AB的黄金分割点(AC>BC),则下列结论正确的是()A.AB2=AC•BC B.BC2=AC•BC C.AC 51-BC D.BC51-AC5.如图,在同一平面直角坐标系中,反比例函数y=kx与一次函数y=kx﹣1(k为常数,且k>0)的图象可能是()A.B.C.D.6.反比例函数kyx=与1(0)y kx k=-+≠在同一坐标系的图象可能为()A.B.C.D.7.河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比1:3,则AC的长是( )A.10米B.53米C.15米D.103米8.如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=()A.1:3 B.1:4 C.2:3 D.1:29.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为()A.五丈B.四丈五尺C.一丈D.五尺10.如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5m,EF=0.25m,目测点D到地面的距离DG=1.5m,到旗杆的水平距离DC=20m,则旗杆的高度为( )A .105 mB .(105 1.5)+ mC .11.5mD .10m11.如图,阳光从教室的窗户射入室内,窗户框AB 在地面上的影子长DE =1.8m ,窗户下沿到地面的距离BC =1m ,EC =1.2m ,那么窗户的高AB 为( )A .1.5mB .1.6mC .1.86mD .2.16m12.如图,ABC △与ADE V 相似,且ADE B ∠=∠,则下列比例式中正确的是( )A .AE AD BE DC =B .AE AB AB AC = C .AD AB AC AE = D .AE DE AC BC= 二、填空题13.如图,是由一些大小相同的小正方体搭成的几何体分别从正面看和从上面看得到的平面图形,则搭成该几何体的小正方体最多是_______个.14.如图,点A 在双曲线y=2x 上,点B 在双曲线y= 5x上,且AB ∥y 轴,C ,D 在y 轴上,若四边形ABCD 为平行四边形,则它的面积为________.15.如图,矩形ABCD 中,AD=2,AB=5,P 为CD 边上的动点,当△ADP 与△BCP 相似时,DP=__.16.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是______步.17.如图所示的网格是正方形网格,点P 到射线OA 的距离为m ,点P 到射线OB 的距离为n ,则m __________ n .(填“>”,“=”或“<”)18.如图,若点 A 的坐标为 ()1,3 ,则 sin 1∠ =________.19.如图,为了测量某棵树的高度,小明用长为2m 的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点距离相距6m ,与树相距15m ,则树的高度为_________m.20.已知线段AB 的长为10米,P 是AB 的黄金分割点(AP >BP ),则AP 的长_____米.(精确到0.01米)三、解答题21.小明想利用影长测量学校旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长是1.4米;此时,他发现旗杆AB的一部分影子BD落在地面上,另一部分影子CD落在楼房的墙壁上,分别测得BD=11.2米,CD=3米,求旗杆AB的高度.22.在学习了矩形这节内容之后,明明同学发现生活中的很多矩形都很特殊,如我们的课本封面、A4 的打印纸等,这些矩形的长与宽之比都为2:1,我们将具有这类特征的矩形称为“完美矩形”如图(1),在“完美矩形”ABCD 中,点P 为AB 边上的定点,且AP=AD.(1)求证:PD=AB.(2)如图(2),若在“完美矩形“ABCD 的边BC 上有一动点E,当BECE的值是多少时,△PDE 的周长最小?(3)如图(3),点Q 是边AB 上的定点,且BQ=BC.已知AD=1,在(2)的条件下连接DE 并延长交AB 的延长线于点F,连接CF,G 为CF 的中点,M、N 分别为线段QF 和CD 上的动点,且始终保持QM=CN,MN 与DF 相交于点H,请问GH 的长度是定值吗?若是,请求出它的值,若不是,请说明理由.23.已知锐角三角形ABC内接于⊙O(AB>AC),AD⊥BC于点D,BE⊥AC于点E,AD、AE交于点F.(1)如图1,若⊙O直径为10,AC=8,求BF的长;(2)如图2,连接OA,若OA=F A,AC=BF,求∠OAD的大小.24.如图,在四边形ABCD中,AC平分∠DAB,AC2=AB•AD,∠ADC=90°,点E为AB的中点.(1)求证:△ADC∽△ACB.(2)若AD=2,AB=3,求的值.25.如图,平面直角坐标系xOy中,A(2,1),B(3,﹣1),C(﹣2,1),D(0,2).已知线段AB绕着点P逆时针旋转得到线段CD,其中C是点A的对应点.(1)用尺规作图的方法确定旋转中心P,并直接写出点P的坐标;(要求保留作图痕迹,不写作法)(2)若以P为圆心的圆与直线CD相切,求⊙P的半径【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】根据位似图的性质可知,位似图形也是相似图形,周长比等于位似比,面积比等于位似比的平方,对应边之比等于位似比,据此判断即可.【详解】A. △ABC∽△A1B1C1,故A正确;B. 由图可知,AB=2-1=1,BC=2-1=1,2,所以△ABC的周长为2,由周长比等于位似比可得△A1B1C1的周长为△ABC周长的3倍,即6+B正确;C. S△ABC=1111=22⨯⨯,由面积比等于位似比的平方,可得△A1B1C1的面积为△ABC周长的9倍,即19=4.52⨯,故C错误;D. 在第一象限内作△A1B1C1时,B1点的横纵坐标均为B的3倍,此时B1的坐标为(6,6),故D正确;故选C.【点睛】本题考查位似三角形的性质,熟练掌握位似的定义,以及位似三角形与相似三角形的关系是解题的关键.2.B解析:B【解析】解:∵用一个放大镜去观察一个三角形,∴放大后的三角形与原三角形相似,∵相似三角形的对应边成比例,∴各边长都变大,故此选项错误;∵相似三角形的对应角相等,∴对应角大小不变,故选项B正确;.∵相似三角形的面积比等于相似比的平方,∴C选项错误;∵相似三角形的周长得比等于相似比,∴D选项错误.故选B.点睛:此题考查了相似三角形的性质.注意相似三角形的对应边成比例,相似三角形的对应角相等,相似三角形的面积比等于相似比的平方,相似三角形的周长得比等于相似比.3.A解析:A【解析】【分析】连接OC、OB,如图,由于BC∥x轴,根据三角形面积公式得到S△ACB=S△OCB,再利用反比例函数系数k的几何意义得到12×|3|+12•|k|=2,然后解关于k的绝对值方程可得到满足条件的k的值.【详解】连接OC、OB,如图,∵BC∥x轴,∴S△ACB=S△OCB,而S△OCB=12×|3|+12•|k|,∴12×|3|+12•|k|=2,而k<0,∴k=﹣1,故选A.【点睛】本题考查了反比例函数系数k的几何意义:在反比例函数y=kx图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是12|k|,且保持不变.4.D解析:D 【解析】【分析】根据黄金分割的定义得出512BC ACAC AB==,从而判断各选项.【详解】∵点C是线段AB的黄金分割点且AC>BC,∴512BC ACAC AB==,即AC2=BC•AB,故A、B错误;51-AB,故C错误;51-AC,故D正确;故选D.【点睛】本题考查了黄金分割,掌握黄金分割的定义和性质是解题的关键.5.B解析:B【解析】当k>0时,直线从左往右上升,双曲线分别在第一、三象限,故A、C选项错误;∵一次函数y=kx-1与y轴交于负半轴,∴D选项错误,B选项正确,故选B.6.B解析:B【解析】【分析】根据反比例函数和一次函数的性质逐个对选项进行分析即可.【详解】A 根据反比例函数的图象可知,k>0,因此可得一次函数的图象应该递减,但是图象是递增的,所以A错误;B根据反比例函数的图象可知,k>0,,因此一次函数的图象应该递减,和图象吻合,所以B正确;C根据反比例函数的图象可知,k<0,因此一次函数的图象应该递增,并且过(0,1)点,但是根据图象,不过(0,1),所以C错误;D根据反比例函数的图象可知,k<0,因此一次函数的图象应该递增,但是根据图象一次函数的图象递减,所以D错误.故选B【点睛】本题主要考查反比例函数和一次函数的性质,关键点在于系数的正负判断,根据系数识别图象.7.B解析:B【解析】【分析】Rt△ABC中,已知了坡比是坡面的铅直高度BC与水平宽度AC之比,通过解直角三角形即可求出水平宽度AC的长.【详解】Rt△ABC中,BC=5米,tanA=1;∴AC=BC÷故选:B.【点睛】此题主要考查学生对坡度坡角的掌握及三角函数的运用能力.8.D解析:D【解析】解:在平行四边形ABCD中,AB∥DC,则△DFE∽△BAE,∴DF:AB=DE:EB.∵O为对角线的交点,∴DO=BO.又∵E为OD的中点,∴DE=14DB,则DE:EB=1:3,∴DF:AB=1:3.∵DC=AB,∴DF:DC=1:3,∴DF:FC=1:2.故选D.9.B解析:B【解析】【分析】根据同一时刻物高与影长成正比可得出结论.【详解】设竹竿的长度为x尺,∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,∴ 1.5150.5x =, 解得x=45(尺),故选B .【点睛】本题考查了相似三角形的应用举例,熟知同一时刻物髙与影长成正比是解答此题的关键.10.C解析:C【解析】【分析】确定出△DEF 和△DAC 相似,根据相似三角形对应边成比例求出AC ,再根据旗杆的高度=AC+BC 计算即可得解.【详解】解:∵∠FDE=∠ADC ,∠DEF=∠DCA=90°,∴△DEF ∽△DAC , ∴CDE CD EF A = , 即:0.50.2520AC = , 解得AC=10,∵DF 与地面保持平行,目测点D 到地面的距离DG=1.5米,∴BC=DG=1.5米,∴旗杆的高度=AC+BC=10+1.5=11.5米.故选:C .【点睛】本题考查了相似三角形的应用,主要利用了相似三角形对应边成比例,准确确定出相似三角形是解题的关键.11.A解析:A【解析】∵BE ∥AD ,∴△BCE ∽△ACD , ∴CB CE AC CD =,即 CB CE AB BC DE EC=++, ∵BC=1,DE=1.8,EC=1.2 ∴1 1.21 1.8 1.2AB =++ ∴1.2AB=1.8,∴AB=1.5m .故选A .12.D解析:D【解析】【分析】利用相似三角形性质:对应角相等、对应边成比例,可得结论.【详解】由题意可得,A ABC DE ∽△△,所以AE DE AC BC=, 故选D .【点睛】在书写两个三角形相似时,注意顶点的位置要对应,即若ABC A B C '''∽△△,则说明点A 的对应点为点'A ,点B 的对应点B ',点C 的对应点为点C '. 二、填空题13.7【解析】【分析】首先利用从上面看而得出的俯视图得出该几何体的第一层是由几个小正方体组成然后进一步根据其从正面看得出的主视图得知其第二层最多可以放几个小正方体然后进一步计算即可得出答案【详解】根据俯 解析:7【解析】【分析】首先利用从上面看而得出的俯视图得出该几何体的第一层是由几个小正方体组成,然后进一步根据其从正面看得出的主视图得知其第二层最多可以放几个小正方体,然后进一步计算即可得出答案.【详解】根据俯视图可得出第一层由5个小正方体组成;再结合主视图,该正方体第二层最多可放2个小正方体,∴527+=,∴最多是7个,故答案为:7.【点睛】本题主要考查了三视图的运用,熟练掌握三视图的特性是解题关键.14.3【解析】试题分析:由AB ∥y 轴可知AB 两点横坐标相等设A (m )B (m )求出AB=﹣=再根据平行四边形的面积公式进行计算即可得=•m=3考点:反比例函数系数k 的几何意义解析:3【解析】试题分析:由AB∥y轴可知,A、B两点横坐标相等,设A(m,2m),B(m,5m),求出AB=5m﹣2m=3m,再根据平行四边形的面积公式进行计算即可得ABCDSY=3m•m=3.考点:反比例函数系数k的几何意义15.1或4或25【解析】【分析】需要分类讨论:△APD∽△PBC和△PAD∽△PBC根据该相似三角形的对应边成比例求得DP的长度【详解】设DP=x则CP=5-x本题需要分两种情况情况进行讨论①当△PAD解析:1或4或2.5.【解析】【分析】需要分类讨论:△APD∽△PBC和△PAD∽△PBC,根据该相似三角形的对应边成比例求得DP的长度.【详解】设DP=x,则CP=5-x,本题需要分两种情况情况进行讨论,①、当△PAD∽△PBC时,AD BC = DP CP∴225xx=-,解得:x=2.5;②、当△APD∽△PBC时,ADCP=DPBC,即25x-=2x,解得:x=1或x=4,综上所述DP=1或4或2.5【点晴】本题主要考查的就是三角形相似的问题和动点问题,首先将各线段用含x的代数式进行表示,然后看是否有相同的角,根据对应角的两边对应成比例将线段写成比例式的形式,然后分别进行计算得出答案.在解答这种问题的时候千万不能出现漏解的现象,每种情况都要考虑到位.16.【解析】【分析】如图根据正方形的性质得:DE∥BC则△ADE∽△ACB列比例式可得结论【详解】如图∵四边形CDEF是正方形∴CD=EDDE∥CF设ED=x则CD =xAD=12-x∵DE∥CF∴∠AD解析:60 17.【解析】【分析】如图,根据正方形的性质得:DE∥BC,则△ADE∽△ACB,列比例式可得结论.【详解】如图,∵四边形CDEF是正方形,∴CD=ED ,DE ∥CF ,设ED=x ,则CD=x ,AD=12-x ,∵DE ∥CF ,∴∠ADE=∠C ,∠AED=∠B ,∴△ADE ∽△ACB , ∴DE BC =AD AC , ∴x 5=12-x 12, ∴x=6017, 故答案为6017.【点睛】本题考查了相似三角形的判定和性质、正方形的性质,设未知数,构建方程是解题的关键.17.>【解析】【分析】由图像可知在射线上有一个特殊点点到射线的距离点到射线的距离于是可知利用锐角三角函数即可判断出【详解】由题意可知:找到特殊点如图所示:设点到射线的距离点到射线的距离由图可知【点睛】本 解析:>【解析】【分析】由图像可知在射线OP 上有一个特殊点Q ,点Q 到射线OA 的距离2QD =Q 到射线OB 的距离1QC =,于是可知AOP BOP ∠>∠ ,利用锐角三角函数sin sin AOP BOP ∠>∠ ,即可判断出m n >【详解】由题意可知:找到特殊点Q ,如图所示:设点Q 到射线OA 的距离QD ,点Q 到射线OB 的距离QC 由图可知2QD =,1QC = ∴ 2sin QD AOP OP ∠== ,1sin QC BOP OP OP ∠== ∴sin sin AOP BOP ∠>∠,∴m n OP OP> ∴m n >【点睛】本题考查了点到线的距离,熟知在直角三角形中利用三角函数来解角和边的关系是解题关键.18.【解析】【分析】根据勾股定理可得OA 的长根据正弦是对边比斜边可得答案【详解】如图由勾股定理得:OA==2sin ∠1=故答案为解析:3 【解析】 【分析】根据勾股定理,可得OA 的长,根据正弦是对边比斜边,可得答案.【详解】如图,由勾股定理,得:OA =22OB AB +=2.sin ∠1=3AB OA =,故答案为3.19.7【解析】设树的高度为m 由相似可得解得所以树的高度为7m 解析:7【解析】设树的高度为x m,由相似可得6157262x+==,解得7x=,所以树的高度为7m20.18【解析】【分析】根据黄金分割定义:列方程即可求解【详解】解:设AP为x米根据题意得整理得x2+10x﹣100=0解得x1=5﹣5≈618x2=﹣5﹣5(不符合题意舍去)经检验x=5﹣5是原方程的解析:18【解析】【分析】根据黄金分割定义:AP BPAB AP=列方程即可求解.【详解】解:设AP为x米,根据题意,得x10 10x x -=整理,得x2+10x﹣100=0解得x1=55﹣5≈6.18,x2=﹣55﹣5(不符合题意,舍去)经检验x=55﹣5是原方程的根,∴AP的长为6.18米.故答案为6.18.【点睛】本题考查了黄金分割的概念,熟练掌握黄金比是解答本题的关键.三、解答题21.旗杆AB的高度是11米.【解析】【分析】作CE⊥AB于E,可得矩形BDCE,利用同一时刻物高与影长的比一定得到AE的长度,加上CD的长度即为旗杆的高度.【详解】解:作CE⊥AB于E,∵DC⊥BD于D,AB⊥BD于B,∴四边形BDCE为矩形,∴CE=BD=11.2米,BE=DC=2米,∵同一时刻物高与影长所组成的三角形相似,∴AEEC=11.4,即11.2AE=11.4,解得AE=8,∴AB=AE+EB=8+3=11(米).答:旗杆AB的高度是11米.【点睛】考查相似三角形的应用;作出相应辅助线得到矩形是解决本题的难点;用到的知识点为:同一时刻物高与影长的比一定.22.(1)证明见解析(2)222-(3)2【解析】【分析】(1)根据题中“完美矩形”的定义设出AD与AB,根据AP=AD,利用勾股定理表示出PD,即可得证;(2)如图,作点P关于BC的对称点P′,连接D P′交BC于点E,此时△PDE的周长最小,设AD=PA=BC=a,表示出AB与CD,由AB-AP表示出BP,由对称的性质得到BP=BP′,由平行得比例,求出所求比值即可;(3)GH=2,理由为:由(2)可知BF=BP=AB-AP,由等式的性质得到MF=DN,利用AAS得到△MFH≌△NDH,利用全等三角形对应边相等得到FH=DH,再由G为CF中点,得到HG为中位线,利用中位线性质求出GH的长即可.【详解】(1)在图1中,设AD=BC=a,则有AB=CD=2a,∵四边形ABCD是矩形,∴∠A=90°,∵PA=AD=BC=a,∴PD=22AD PA+=2a,∵AB=2a,∴PD=AB;(2)如图,作点P关于BC的对称点P′,连接DP′交BC于点E,此时△PDE的周长最小,设AD=PA=BC=a,则有2,∵BP=AB-PA,∴2a-a,∵BP′∥CD,∴22BE BPCE CD===;(3),理由为:由(2)可知BF=BP=AB-AP,∵AP=AD,∴BF=AB-AD,∵BQ=BC,∴AQ=AB-BQ=AB-BC,∵BC=AD,∴AQ=AB-AD,∴BF=AQ,∴QF=BQ+BF=BQ+AQ=AB,∵AB=CD,∴QF=CD,∵QM=CN,∴QF-QM=CD-CN,即MF=DN,∵MF∥DN,∴∠NFH=∠NDH,在△MFH和△NDH中,{MFH NDHMHF NHDMF DN∠∠∠∠===,∴△MFH≌△NDH(AAS),∴FH=DH,∵G为CF的中点,∴GH是△CFD的中位线,∴GH=12CD=12×.【点睛】此题属于相似综合题,涉及的知识有:相似三角形的判定与性质,全等三角形的判定与性质,勾股定理,三角形中位线性质,平行线的判定与性质,熟练掌握相似三角形的性质是解本题的关键.23.(1)BF=6;(2)∠OAD=30°.【解析】【分析】(1)如图1中,作⊙O的直径CM,连接AM,BM.利用勾股定理求出AM,证明四边形AMBF是平行四边形即可解决问题;(2)如图2中,作⊙O 的直径CM ,连接AM ,BM ,设AD 交CM 于J .证明AO ⊥CM .推出∠OAD =∠BCM ,解直角三角形求出∠BCM 即可解决问题.【详解】(1)如图1中,作⊙O 的直径CM ,连接AM ,BM .∵CM 是直径,∴∠CAM =∠CBM =90°,∵CM =10,AC =8,∴AM =22CM AC -=22108-=6,∵AD ⊥CB ,BE ⊥AC ,∴∠ADC =∠MBC =90°,∠BEC =∠MAC =90°,∴AD ∥BM ,AM ∥BE ,∴四边形AMBF 是平行四边形,∴BF =AM =6.(2)如图2中,作⊙O 的直径CM ,连接AM ,BM ,设AD 交CM 于J .由(1)可知四边形AMBF 是平行四边形,∴AM =BF ,AF =BM∵AC =BF ,∴AC =AM ,∵∠MAC =90°,MO =OC ,∴AO ⊥CM ,∵AD ⊥BC ,∴∠AOJ =∠CDJ =90°,∵∠AJO =∠CJD ,∴∠DCJ =∠JAO ,∵AF =OA ,AF =BM ,∴OA =BM ,∴CM =2BM ,∵∠CBM=90°,∴sin∠BCM=BMCM=12,∴∠BCM=30°,∴∠OAD=∠BCM=30°.【点睛】本题属于圆综合题,考查了圆周角定理,平行四边形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线面构造特殊四边形解决问题.24.(1)证明见解析;(2).【解析】【分析】(1)根据角平分线的定义得到∠DAC=∠CAB,根据相似三角形的判定定理证明;(2)根据相似三角形的性质得到∠ACB=∠ADC=90°,根据直角三角形的性质得到 CE=AE,根据等腰三角形的性质、平行线的判定定理证明=,由相似三角形的性质列出比例式,计算即可.【详解】(1)证明:∵AC 平分∠DAB,∴∠DAC=∠CAB,∵AC2=AB•AD,∴=,∴△ADC∽△ACB;(2)∵△ADC∽△ACB,∴∠ACB=∠ADC=90°,∵点 E 为 AB 的中点,∴CE=AE= AB= ,∴∠EAC=∠ECA,∴∠DAC=∠EAC,∴∠DAC=∠ECA,∴CE∥AD;∴==,∴=.【点睛】本题考查的是直角三角形的性质、平行线的判定、相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理是解题的关键.25.(1)如图点P即为所求.见解析;(2)以P为圆心的圆与直线CD相切,⊙P的半径为65.【解析】【分析】(1)作相对AC,BD的垂直平分线,两条垂直平分线的交点P即为所求.(2)作PE⊥CD于E,求出点E的坐标,利用相似三角形的性质求出PE即可.【详解】(1)如图点P即为所求.(2)作PE⊥CD于E,设AC交PD于K.∵∠CDO=∠PDE,∠CKD=∠PED=90°,∴△COD∽△PED,∴COPE=CDPD,∴2PE5∴PE=55,∵以P为圆心的圆与直线CD相切,∴⊙P 65.【点睛】本题考查作图,相似三角形的判定和性质,切线的性质等知识,解题的关键是熟练掌握基本知识.。
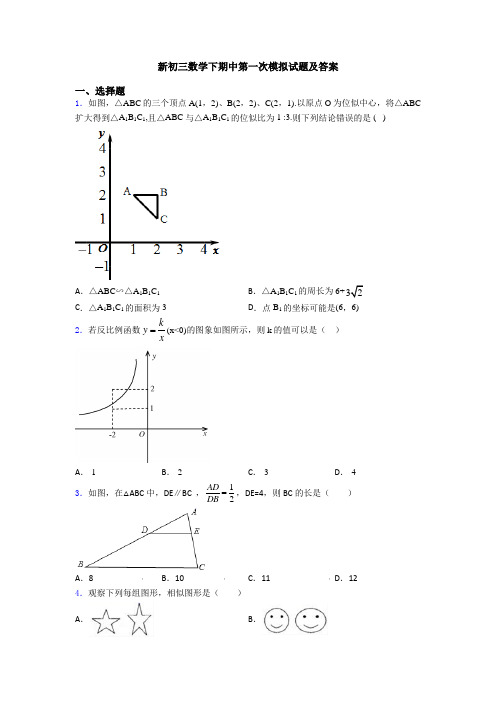
新初三数学下期中第一次模拟试题及答案一、选择题1.如图,△ABC的三个顶点A(1,2)、B(2,2)、C(2,1).以原点O为位似中心,将△ABC 扩大得到△A1B1C1,且△ABC 与△A1B1C1的位似比为1 :3.则下列结论错误的是 ( )A.△ABC∽△A1B1C1B.△A1B1C1的周长为6+32C.△A1B1C1的面积为3D.点B1的坐标可能是(6,6)2.若反比例函数kyx=(x<0)的图象如图所示,则k的值可以是()A.-1B.-2C.-3D.-43.如图,在△ABC中,DE∥BC ,12ADDB=,DE=4,则BC的长是()A.8 B.10 C.11 D.12 4.观察下列每组图形,相似图形是()A.B.C .D .5.如图▱ABCD ,F 为BC 中点,延长AD 至E ,使:1:3DE AD =,连结EF 交DC 于点G ,则:DEG CFG S S ∆V =( )A .2:3B .3:2C .9:4D .4:96.如图,一张矩形纸片ABCD 的长BC =xcm ,宽AB =ycm ,以宽AB 为边剪去一个最大的正方形ABEF ,若剩下的矩形ECDF 与原矩形ABCD 相似,则x y 的值为( )A .512-B .512+C .2D .212+ 7.河堤横断面如图所示,堤高BC =5米,迎水坡AB 的坡比1:3,则AC 的长是( )A .10米B .53米C .15米D .103米8.《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )A .五丈B .四丈五尺C .一丈D .五尺9.如图,△ABC 中AB 两个顶点在x 轴的上方,点C 的坐标是(﹣1,0),以点C 为位似中心,在x 轴的下方作△ABC 的位似图形△A′B′C′,且△A′B′C′与△ABC 的位似比为2:1.设点B 的对应点B′的横坐标是a ,则点B 的横坐标是( )A .12a -B .1(1)2a -+C .1(1)2a --D .1(3)2a -+ 10.如图,在矩形ABCD 中,DE AC ⊥于E ,设ADE α∠=,且3cos 5α=,5AB =,则AD 的长为( )A .3B .163C .203D .16511.如图,已知△ABC 的三个顶点均在格点上,则cosA 的值为( )A 3B 5C 23D 25 12.若270x y -=. 则下列式子正确的是( )A .72x y =B .27x y =C .27x y =D .27x y = 二、填空题13.如图,在平面直角坐标系中,已知点A 、B 的坐标分别为(8,0)、(0,3C 是AB 的中点,过点C 作y 轴的垂线,垂足为D ,动点P 从点D 出发,沿DC 向点C 匀速运动,过点P 作x 轴的垂线,垂足为E ,连接BP 、EC .当BP 所在直线与EC 所在直线垂直时,点P 的坐标为____14.如图,在2×2的网格中,以顶点O 为圆心,以2个单位长度为半径作圆弧,交图中格线于点A ,则tan ∠ABO 的值为_____.15.已知AB ∥CD ,AD 与BC 相交于点O.若BO OC =23,AD =10,则AO =____.16.学校校园内有块如图所示的三角形空地,计划将这块空地建成一个花园,以美化环境,预计花园每平方米造价为30元,学校建这个花园至少需要投资________元.17.若a b =34,则a b b+=__________. 18.在 ABC V 中, 6AB = , 5AC = ,点D 在边AB 上,且 2AD = ,点E 在边AC 上,当 AE = ________时,以A 、D 、E 为顶点的三角形与 ABC V 相似.19.已知线段a =2厘米,c =8厘米,则线段a 和c 的比例中项b 是______厘米.20.如图,将矩形ABCD 折叠,折痕为EF ,BC 的对应边B'C′与CD 交于点M ,若∠B′MD=50°,则∠BEF 的度数为_____.三、解答题21.如图,有一路灯杆AB (底部B 不能直接到达),在灯光下,小华在点D 处测得自己的影长DF =3m ,沿BD 方向到达点F 处再测得自己的影长FG =4m .如果小华的身高为1.5m ,求路灯杆AB 的高度.22.如图,已知反比例函数y =k x 的图象经过点A (4,m ),AB ⊥x 轴,且△AOB 的面积为2. (1)求k 和m 的值; (2)若点C (x ,y )也在反比例函数y =k x 的图象上,当-3≤x ≤-1时,求函数值y 的取值范围.23.如图,点P 是菱形ABCD 的对角线BD 上一点,连接CP 并延长,交AD 于点E ,交BA 的延长线于点F .(1)求证:2PC PE PF =g ;(2)若菱形边长为8,2PE =,6EF =,求FB 的长.24.如图,在平面直角坐标系xOy 中,直线y =x +b 与双曲线y =k x相交于A ,B 两点, 已知A (2,5).求:(1)b 和k 的值;(2)△OAB 的面积.25.已知锐角三角形ABC 内接于⊙O (AB >AC ),AD ⊥BC 于点D ,BE ⊥AC 于点E ,AD 、AE 交于点F .(1)如图1,若⊙O直径为10,AC=8,求BF的长;(2)如图2,连接OA,若OA=F A,AC=BF,求∠OAD的大小.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】根据位似图的性质可知,位似图形也是相似图形,周长比等于位似比,面积比等于位似比的平方,对应边之比等于位似比,据此判断即可.【详解】A. △ABC∽△A1B1C1,故A正确;B. 由图可知,AB=2-1=1,BC=2-1=1,2,所以△ABC的周长为2,由周长比等于位似比可得△A1B1C1的周长为△ABC周长的3倍,即6+32B正确;C. S△ABC=1111=22⨯⨯,由面积比等于位似比的平方,可得△A1B1C1的面积为△ABC周长的9倍,即19=4.52⨯,故C错误;D. 在第一象限内作△A1B1C1时,B1点的横纵坐标均为B的3倍,此时B1的坐标为(6,6),故D正确;故选C.【点睛】本题考查位似三角形的性质,熟练掌握位似的定义,以及位似三角形与相似三角形的关系是解题的关键.2.C解析:C【解析】【分析】由图像可知,反比例函数与线段AB 相交,由A 、B 的坐标,可求出k 的取值范围,即可得到答案.【详解】如图所示:由题意可知A (-2,2),B (-2,1),∴1-2⨯2<<-2⨯k ,即4-<<-2k故选C.【点睛】本题考查反比例函数的图像与性质,由图像性质得到k 的取值范围是解题的关键.3.D解析:D【解析】【分析】 根据AD DB =12,可得AD AB =13,再根据DE ∥BC ,可得DE BC =AD AB ; 接下来根据DE=4,结合上步分析即可求出BC 的长.【详解】 ∵AD DB =12, ∴AD AB =13, ∵在△ABC 中,DE ∥BC , ∴DE BC =AD AB =13. ∵DE=4,∴BC=3DE=12.故答案选D.【点睛】 本题考查了平行线分线段成比例的知识,解题的关键是熟练的掌握平行线分线段成比例定理.解析:D【解析】【分析】根据相似图形的定义,形状相同,可得出答案.【详解】解:A 、两图形形状不同,故不是相似图形;B 、两图形形状不同,故不是相似图形;C 、两图形形状不同,故不是相似图形;D 、两图形形状相同,故是相似图形;故选:D .【点睛】本题主要考查相似图形的定义,掌握相似图形形状相同是解题的关键.5.D解析:D【解析】【分析】先设出DE x =,进而得出3AD x =,再用平行四边形的性质得出3BC x =,进而求出CF ,最后用相似三角形的性质即可得出结论.【详解】解:设DE x =,∵:1:3DE AD =,∴3AD x =,∵四边形ABCD 是平行四边形,∴//AD BC ,BC AD 3x ==,∵点F 是BC 的中点, ∴1322CF BC x ==, ∵//AD BC , ∴DEG CFG ∆∆∽, ∴224392DEGCFG S DE x S CF x ⎛⎫ ⎪⎛⎫=== ⎪ ⎪⎝⎭ ⎪⎝⎭V V , 故选:D .【点睛】此题主要考查了相似三角形的判定和性质,平行四边形的性质,中点的定义,表示出CF 是解本题的关键.6.B【解析】【分析】根据相似多边形对应边的比相等,可得到一个方程,解方程即可求得.【详解】∵四边形ABCD是矩形,∴AD=BC=xcm,∵四边形ABEF是正方形,∴EF=AB=ycm,∴DF=EC=(x﹣y)cm,∵矩形FDCE与原矩形ADCB相似,∴DF:AB=CD:AD,即:x y y y x -=∴xy=2,故选B.【点睛】本题考查了相似多边形的性质、矩形的性质、翻折变换的性质;根据相似多边形对应边的比相等得出方程是解决本题的关键.7.B解析:B【解析】【分析】Rt△ABC中,已知了坡比是坡面的铅直高度BC与水平宽度AC之比,通过解直角三角形即可求出水平宽度AC的长.【详解】Rt△ABC中,BC=5米,tanA=1;∴AC=BC÷故选:B.【点睛】此题主要考查学生对坡度坡角的掌握及三角函数的运用能力.8.B解析:B【解析】【分析】根据同一时刻物高与影长成正比可得出结论.【详解】设竹竿的长度为x尺,∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,∴ 1.5150.5x =, 解得x=45(尺),故选B .【点睛】本题考查了相似三角形的应用举例,熟知同一时刻物髙与影长成正比是解答此题的关键.9.D解析:D【解析】【分析】设点B 的横坐标为x ,然后表示出BC 、B′C 的横坐标的距离,再根据位似变换的概念列式计算.【详解】设点B 的横坐标为x ,则B 、C 间的横坐标的长度为﹣1﹣x ,B′、C 间的横坐标的长度为a+1,∵△ABC 放大到原来的2倍得到△A′B′C ,∴2(﹣1﹣x )=a+1,解得x =﹣12(a+3), 故选:D .【点睛】 本题考查了位似变换,坐标与图形的性质,根据位似变换的定义,利用两点间的横坐标的距离等于对应边的比列出方程是解题的关键.10.C解析:C【解析】【分析】根据矩形的性质可知:求AD 的长就是求BC 的长,易得∠BAC =∠ADE ,于是可利用三角函数的知识先求出AC ,然后在直角△ABC 中根据勾股定理即可求出BC ,进而可得答案.【详解】解:∵四边形ABCD 是矩形,∴∠B =∠BAC =90°,BC=AD ,∴∠BAC +∠DAE =90°, ∵DE AC ⊥,∴∠ADE +∠DAE =90°,∴∠BAC =ADE α∠=,在直角△ABC 中,∵3cos 5α=,5AB =,∴25cos 3AB AC α==,∴AD=BC 203==. 故选:C.【点睛】本题考查了矩形的性质、勾股定理和解直角三角形的知识,属于常考题型,熟练掌握矩形的性质和解直角三角形的知识是解题关键.11.D解析:D【解析】【分析】【详解】过B 点作BD ⊥AC ,如图,由勾股定理得,AB=221310+=,AD=222222+=,cosA=AD AB =2210=25, 故选D .12.A解析:A【解析】【分析】 直接利用比例的性质分别判断即可得出答案.【详解】∵2x -7y =0,∴2x =7y .A .72x y =,则2x =7y ,故此选项正确; B .27x y =,则xy =14,故此选项错误; C .27x y =,则2y =7x ,故此选项错误; D .27x y =,则7x =2y ,故此选项错误. 故选A .【点睛】本题考查了比例的性质,正确将比例式变形是解题的关键.二、填空题13.(1)【解析】【分析】先根据题意求得CD和PE的长再判定△EPC∽△PDB 列出相关的比例式求得DP的长最后根据PEDP的长得到点P的坐标【详解】由题意可知OB=2AO=8∵CD⊥BOC是AB的中点∴解析:(1,3)【解析】【分析】先根据题意求得CD和PE的长,再判定△EPC∽△PDB,列出相关的比例式,求得DP的长,最后根据PE、DP的长得到点P的坐标.【详解】由题意可知,OB=23,AO=8,∵CD⊥BO,C是AB的中点,∴BD=DO=12BO==PE,CD=12AO=4.设DP=a,则CP=4﹣a,当BP所在直线与EC所在直线第一次垂直时,∠FCP=∠DBP,又∵EP⊥CP,PD⊥BD,∴∠EPC=∠PDB=90°,∴△EPC∽△PDB.DP DBPE PC∴=∴33=,∴a1=1,a2=3(舍去).∴DP=1,∵PE=3,∴P(1,3).考点:1相似三角形性质与判定;2平面直角坐标系.14.2+3【解析】【分析】连接OA过点A作AC⊥OB于点C由题意知AC=1OA=OB=2从而得出OC=OA2-AC2=3BC=OB﹣OC=2﹣3在Rt△ABC中根据tan∠ABO=ACBC可得答案【详解解析:2+.【解析】【分析】连接OA ,过点A 作AC⊥OB 于点C ,由题意知AC=1、OA=OB=2,从而得出OC==、BC=OB ﹣OC=2﹣,在Rt△ABC 中,根据tan∠ABO=可得答案.【详解】如图,连接OA ,过点A 作AC⊥OB 于点C ,则AC=1,OA=OB=2,∵在Rt△AOC 中,OC==, ∴BC=OB﹣OC=2﹣,∴在Rt△ABC 中,tan∠ABO==2+. 故答案是:2+.【点睛】 本题考查了解直角三角形,根据题意构建一个以∠ABO 为内角的直角三角形是解题的关键.15.【解析】∵AB∥CD 解得AO=4故答案是:4【点睛】运用了平行线分线段成比例定理灵活运用定理找准对应关系是解题的关键解析:【解析】∵AB ∥CD ,223103AO BO AO OD OC AO ∴===-,即, 解得,AO=4,故答案是:4.【点睛】运用了平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.16.【解析】【分析】如图所示作BD⊥CA 于D 则在直角△ABD 中可以求出BD 然后求出△ABC 面积;根据单价可以求出总造价【详解】如图所示AB=10AC=30∠BAC=120°作BD⊥CA 于D 则在直角△AB解析:6750【解析】【分析】如图所示,作BD ⊥CA 于D ,则在直角△ABD 中可以求出BD ,然后求出△ABC 面积;根据单价可以求出总造价.【详解】如图所示,3AC=30,∠BAC=120°,作BD ⊥CA 于D ,则在直角△ABD中,∠BAD=60°,∴BD=ABsin60°=15,∴△ABC面积=12×AC×BD=225.又因为每平方米造价为30元,∴总造价为30×225=6750(元).【点睛】此题主要考查了运用三角函数定义解直角三角形,关键是通过作辅助线把实际问题转化为数学问题,抽象到解直角三角形中解题.17.【解析】【分析】由比例的性质即可解答此题【详解】∵∴a=b∴=故答案为【点睛】此题考查了比例的基本性质熟练掌握这个性质是解答此题的关键解析:7 4【解析】【分析】由比例的性质即可解答此题.【详解】∵34ab=,∴a=34 b,∴a bb+=3744b b bb b+=,故答案为7 4【点睛】此题考查了比例的基本性质,熟练掌握这个性质是解答此题的关键.18.【解析】当时∵∠A=∠A∴△AED∽△ABC此时AE=;当时∵∠A=∠A∴△AD E∽△ABC此时AE=;故答案是:解析:512 35或【解析】当AE AB AD AC=时, ∵∠A=∠A , ∴△AED ∽△ABC ,此时AE=·621255AB AD AC ⨯==; 当AD AB AE AC=时, ∵∠A=∠A ,∴△ADE ∽△ABC ,此时AE=·52563AC AD AB ⨯==; 故答案是:12553或. 19.4【解析】∵线段b 是ac 的比例中项∴解得b =±4又∵线段是正数∴b =4点睛:本题考查了比例中项的概念利用比例的基本性质求两条线段的比例中项的时候负数应舍去解析:4【解析】∵线段b 是a 、c 的比例中项,∴216b ac ==,解得b =±4,又∵线段是正数,∴b =4. 点睛:本题考查了比例中项的概念,利用比例的基本性质求两条线段的比例中项的时候,负数应舍去.20.70°【解析】【分析】设∠BEF=α则∠EFC=180°﹣α∠DFE=∠BEF=α∠CFE=40°+α依据∠EFC=∠EFC 即可得到180°﹣α=40°+α进而得出∠BEF 的度数【详解】∵∠C=∠C解析:70°【解析】【分析】设∠BEF=α,则∠EFC=180°﹣α,∠DFE=∠BEF=α,∠C'FE=40°+α,依据∠EFC=∠EFC',即可得到180°﹣α=40°+α,进而得出∠BEF 的度数.【详解】∵∠C'=∠C=90°,∠DMB'=∠C'MF=50°,∴∠C'FM=40°,设∠BEF=α,则∠EFC=180°﹣α,∠DFE=∠BEF=α,∠C'FE=40°+α,由折叠可得,∠EFC=∠EFC',∴180°﹣α=40°+α,∴α=70°,∴∠BEF=70°,故答案为:70°.【点睛】本题考查了矩形的性质、折叠的性质,熟练掌握相关的性质是解题的关键.三、解答题21.路灯杆AB 的高度是6m .【解析】【分析】在同一时刻物高和影长成正比,根据相似三角形的性质即可解答.【详解】解:∵CD ∥EF ∥AB ,∴可以得到△CDF ∽△ABF ,△ABG ∽△EFG , ∴,CD DF FE FG AB BF AB BG==, 又∵CD =EF , ∴DF FG BF BG=, ∵DF =3m ,FG =4m ,BF =BD +DF =BD +3,BG =BD +DF +FG =BD +7,∴3437DB BD =++, ∴BD =9,BF =9+3=12, ∴1.5312AB =, 解得AB =6. 答:路灯杆AB 的高度是6m .【点睛】考查了相似三角形的应用和中心投影.只要是把实际问题抽象到相似三角形中,利用相似三角形的性质对应边成比例就可以求出结果.22.(1) k =4, m =1;(2)当-3≤x ≤-1时,y 的取值范围为-4≤y ≤-43. 【解析】【分析】【详解】试题分析:(1)根据反比例函数系数k 的几何意义先得到k 的值,然后把点A 的坐标代入反比例函数解析式,可求出k 的值;(2)先分别求出x=﹣3和﹣1时y 的值,再根据反比例函数的性质求解.试题解析:(1)∵△AOB 的面积为2,∴k=4,∴反比例函数解析式为4y x=,∵A (4,m ),∴m=44=1; (2)∵当x=﹣3时,y=﹣43; 当x=﹣1时,y=﹣4,又∵反比例函数4y x =在x <0时,y 随x 的增大而减小,∴当﹣3≤x≤﹣1时,y 的取值范围为﹣4≤y≤﹣43. 考点:反比例函数系数k 的几何意义;反比例函数图象上点的坐标特征.23.(1)见解析;(2) 16=FB .【解析】【分析】(1)可由相似三角形AEP FAP ∆∆∽对应边成比例进行求解,也可由平行线分线段成比例定理进行求解,两者均可;(2)由题中已知线段的长度,结合(1)中的结论,再由平行线分线段成比例,即可得出结论.【详解】(1)证明:Q 四边形ABCD 是菱形,DC DA ∴=,ADP CDP ∠=∠,//DC AB ,又DP Q 是公共边,DAP DCP ∴∆≅∆,PA PC ∴=,DAP DCP ∠=∠,由//DC FA 得,F DCP ∠=∠,F DAP ∴∠=∠,又EPA APF ∠=∠QAEP FAP ∴∆∆∽,∴PA:PF=PE :PA ,2PA PE PF ∴=g2PC PE PF ∴=g .(2)2PE =Q ,6EF =,8PF ∴=,2PC PE PF =Q g ,216PC ∴=,4PC ∴=//DC FB Q ∴FB PF DC PC=, 又8DC =, ∴884FB =16FB ∴=.【点睛】本题主要考查了全等三角形的判定及性质以及菱形的性质和相似三角形的判定及性质问题,能够熟练掌握.24.(1)b=3,k=10;(2)S △AOB =212. 【解析】 (1)由直线y=x+b 与双曲线y=k x相交于A 、B 两点,A (2,5),即可得到结论; (2)过A 作AD⊥x 轴于D ,BE⊥x 轴于E ,根据y=x+3,y=10x,得到(-5,-2),C (-3,0).求出OC=3,然后根据三角形的面积公式即可得到结论. 解:(1)把()2,5A 代入y x b =+.∴52b =+∴3b =.把()2,5A 代入k y x =,∴52k =, ∴10k =.(2)∵10y x =,3y x =+. ∴103x x=+时,2103x x =+, ∴12x =,25x =-.∴()5,2B --.又∵()3,0C -,∴AOB AOC BOC S S S =+V V V 353222⨯⨯=+ 10.5=. 25.(1)BF =6;(2)∠OAD =30°.【解析】【分析】 (1)如图1中,作⊙O 的直径CM ,连接AM ,BM .利用勾股定理求出AM ,证明四边形AMBF 是平行四边形即可解决问题;(2)如图2中,作⊙O 的直径CM ,连接AM ,BM ,设AD 交CM 于J .证明AO ⊥CM .推出∠OAD =∠BCM ,解直角三角形求出∠BCM 即可解决问题.【详解】(1)如图1中,作⊙O 的直径CM ,连接AM ,BM .∵CM 是直径,∴∠CAM =∠CBM =90°,∵CM =10,AC =8,∴AM =22CM AC -=22108-=6,∵AD ⊥CB ,BE ⊥AC ,∴∠ADC =∠MBC =90°,∠BEC =∠MAC =90°,∴AD ∥BM ,AM ∥BE ,∴四边形AMBF 是平行四边形,∴BF =AM =6.(2)如图2中,作⊙O 的直径CM ,连接AM ,BM ,设AD 交CM 于J .由(1)可知四边形AMBF 是平行四边形,∴AM =BF ,AF =BM ∵AC =BF ,∴AC =AM ,∵∠MAC =90°,MO =OC ,∴AO ⊥CM ,∵AD ⊥BC ,∴∠AOJ =∠CDJ =90°,∵∠AJO =∠CJD ,∴∠DCJ =∠JAO ,∵AF =OA ,AF =BM ,∴OA =BM ,∴CM =2BM ,∵∠CBM =90°,∴sin ∠BCM =BM CM =12, ∴∠BCM =30°,∴∠OAD =∠BCM =30°.【点睛】 本题属于圆综合题,考查了圆周角定理,平行四边形的判定和性质,解直角三角形等知识,解题的关键是学会添加常用辅助线面构造特殊四边形解决问题.。
【好题】初三数学下期中第一次模拟试题(及答案) 一、选择题1.若反比例函数kyx(x<0)的图象如图所示,则k的值可以是()A.-1B.-2C.-3D.-42.如图,在同一平面直角坐标系中,反比例函数y=kx与一次函数y=kx﹣1(k为常数,且k>0)的图象可能是()A.B.C.D.3.如图,在正方形ABCD中,N为边AD上一点,连接BN.过点A作AP⊥BN于点P,连接CP,M为边AB上一点,连接PM,∠PMA=∠PCB,连接CM,有以下结论:①△PAM∽△PBC;②PM⊥PC;③M、P、C、B四点共圆;④AN=AM.其中正确的个数为()A.4B.3C.2D.14.如图,△OAB∽△OCD,OA:OC=3:2,∠A=α,∠C=β,△OAB与△OCD的面积分别是S1和S2,△OAB与△OCD的周长分别是C1和C2,则下列等式一定成立的是()A.32OBCD=B.32αβ=C.1232SS=D.1232CC=5.已知线段a、b、c、d满足ab=cd,把它改写成比例式,错误的是()A.a:d=c:b B.a:b=c:d C.c:a=d:b D.b:c=a:d6.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为()A.15B.25C.215D.87.如图,在矩形ABCD中,DE AC⊥于E,设ADEα∠=,且3cos5α=,5AB=,则AD的长为()A.3B.163C.203D.1658.图(1)所示矩形ABCD中,BC x=,CD y=,y与x满足的反比例函数关系如图(2)所示,等腰直角三角形AEF的斜边EF过点C,M为EF的中点,则下列结论正确的是()A.当3x=时,EC EM<B.当9y=时,EC EM<C.当x增大时,EC CF⋅的值增大D.当x增大时,BE DF⋅的值不变9.如图,将一个Rt△ABC形状的楔子从木桩的底端点P处沿水平方向打入木桩底下,使木桩向上运动,已知楔子斜面的倾斜角为20°,若楔子沿水平方向前移8cm(如箭头所示),则木桩上升了()A.8tan20°B.C.8sin20°D.8cos20°10.如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5m,EF=0.25m,目测点D到地面的距离DG=1.5m,到旗杆的水平距离DC=20m,则旗杆的高度为( )mA.105 m B.(105 1.5)C.11.5m D.10m11.如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影子长DE=1.8m,窗户下沿到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为()A.1.5m B.1.6m C.1.86m D.2.16m12.下列四个几何体中,主视图与左视图相同的几何体有()A.1个B.2个C.3个D.4个二、填空题13.如图,在一段坡度为1∶2的山坡上种树,要求株距(即相邻两株树之间的水平距离)为6米,那么斜坡上相邻两株树之间的坡面距离为____米.14.若反比例函数y =﹣的图象经过点A(m ,3),则m 的值是_____.15.如图,△ABC 中,AD 是中线,BC=8,∠B=∠DAC ,则线段 AC 的长为________.16.如图,点A 在双曲线y =6x(x >0)上,过点A 作AB ⊥x 轴于点B ,点C 在线段AB 上且BC :CA =1:2,双曲线y =k x (x >0)经过点C ,则k =_____.17.如图,小军、小珠之间的距离为2.7 m ,他们在同一盏路灯下的影长分别为1.8 m ,1.5 m ,已知小军、小珠的身高分别为1.8 m ,1.5 m ,则路灯的高为____m.18.把边长分别为1和2的两个正方形按如图所示的方式放置,则图中阴影部分的面积是_____.19.在 ABC V 中, 6AB = , 5AC = ,点D 在边AB 上,且 2AD = ,点E 在边AC 上,当 AE = ________时,以A 、D 、E 为顶点的三角形与 ABC V 相似.20.已知线段AB 的长为10米,P 是AB 的黄金分割点(AP >BP ),则AP 的长_____米.(精确到0.01米)三、解答题21.已知四边形ABCD 中,E ,F 分别是AB ,AD 边上的点,DE 与CF 交于点G.(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证:DE AD CF CD=;(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得DE ADCF CD=成立?并证明你的结论.22.如图,∠ABD=∠BCD=90°,AB•CD=BC•BD,BM∥CD交AD于点M.连接CM交DB于点N.(1)求证:△ABD∽△BCD;(2)若CD=6,AD=8,求MC的长.23.如图,在Rt△ABC中,CD,CE分别是斜边AB上的高,中线,BC=a,AC=b.(1)若a=3,b=4,求DE的长;(2)直接写出:CD=(用含a,b的代数式表示);(3)若b=3,tan∠DCE=13,求a的值.24.如图,AB是⊙O直径,BC⊥AB于点B,点C是射线BC上任意一点,过点C作CD 切⊙O于点D,连接AD.(1)求证:BC=CD;(2)若∠C=60°,BC=3,求AD的长.25.如图,直线y=12x+2与双曲线y=k x相交于点A (m ,3),与x 轴交于点C . (1)求双曲线的解析式;(2)点P 在x 轴上,如果△ACP 的面积为3,求点P 的坐标.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】由图像可知,反比例函数与线段AB 相交,由A 、B 的坐标,可求出k 的取值范围,即可得到答案.【详解】如图所示:由题意可知A (-2,2),B (-2,1),∴1-2⨯2<<-2⨯k ,即4-<<-2k故选C.【点睛】本题考查反比例函数的图像与性质,由图像性质得到k 的取值范围是解题的关键.2.B解析:B【解析】当k>0时,直线从左往右上升,双曲线分别在第一、三象限,故A、C选项错误;∵一次函数y=kx-1与y轴交于负半轴,∴D选项错误,B选项正确,故选B.3.A解析:A【解析】【分析】根据互余角性质得∠PAM=∠PBC,进而得△PAM∽△PBC,可以判断①;由相似三角形得∠APM=∠BPC,进而得∠CPM=∠APB,从而判断②;根据对角互补,进而判断③;由△APB∽△NAB得AP ANBP AB=,再结合△PAM∽△PBC便可判断④.【详解】解:∵AP⊥BN,∴∠PAM+∠PBA=90°,∵∠PBA+∠PBC=90°,∴∠PAM=∠PBC,∵∠PMA=∠PCB,∴△PAM∽△PBC,故①正确;∵△PAM∽△PBC,∴∠APM=∠BPC,∴∠CPM=∠APB=90°,即PM⊥PC,故②正确;∵∠MPC+∠MBC=90°+90°=180°,∴B、C、P、M四点共圆,∴∠MPB=∠MCB,故③正确;∵AP⊥BN,∴∠APN=∠APB=90°,∴∠PAN+∠ANB=90°,∵∠ANB+∠ABN=90°,∴∠PAN=∠ABN,∵∠APN=∠BPA=90°,∴△PAN∽△PBA,∴AN PA BA PB=,∵△PAM∽△PBC,∴Al AP BC BP=,∴AN AM AB BC=,∵AB=BC,∴AM=AN,故④正确;故选:A.【点睛】本题考查了相似三角形的判定和性质,正方形的性质、四点共圆,同角的余角相等,判断出PM⊥PC是解题的关键.4.D解析:D【解析】A选项,在△OAB∽△OCD中,OB和CD不是对应边,因此它们的比值不一定等于相似比,所以A选项不一定成立;B选项,在△OAB∽△OCD中,∠A和∠C是对应角,因此αβ=,所以B选项不成立;C选项,因为相似三角形的面积比等于相似比的平方,所以C选项不成立;D选项,因为相似三角形的周长比等于相似比,所以D选项一定成立.故选D.5.B解析:B【解析】【分析】根据比例的基本性质:两外项之积等于两内项之积.对选项一一分析,选出正确答案.【详解】解:A、a:d=c:b⇒ab=cd,故正确;B、a:b=c:d⇒ad=bc,故错误;C、d:a=b:c⇒dc=ab,故正确;D、a:c=d:b⇒ab=cd,故正确.故选B.【点睛】本题考查比例的基本性质,解题关键是根据比例的基本性质实现比例式和等积式的互相转换.6.C解析:C【解析】【分析】作OH⊥CD于H,连结OC,如图,根据垂径定理由OH⊥CD得到HC=HD,再利用AP=2,BP=6可计算出半径OA=4,则OP=OA-AP=2,接着在Rt△OPH中根据含30°的直角三角形的性质计算出OH=12OP=1,然后在Rt△OHC中利用勾股定理计算出CH=15,所以CD=2CH=215.【详解】作OH⊥CD于H,连结OC,如图,∵OH⊥CD,∴HC=HD,∵AP=2,BP=6,∴AB=8,∴OA=4,∴OP=OA﹣AP=2,在Rt△OPH中,∵∠OPH=30°,∴∠POH=30°,∴OH=12OP=1,在Rt△OHC中,∵OC=4,OH=1,∴22=15OC OH∴15故选C.【点睛】本题主要考查圆中的计算问题,熟练掌握垂径定理、含30°的直角三角形的性质以及勾股定理等知识点,掌握数形结合的思想是解答的关键7.C解析:C【解析】【分析】根据矩形的性质可知:求AD 的长就是求BC 的长,易得∠BAC =∠ADE ,于是可利用三角函数的知识先求出AC ,然后在直角△ABC 中根据勾股定理即可求出BC ,进而可得答案.【详解】解:∵四边形ABCD 是矩形,∴∠B =∠BAC =90°,BC=AD ,∴∠BAC +∠DAE =90°, ∵DE AC ⊥,∴∠ADE +∠DAE =90°,∴∠BAC =ADE α∠=,在直角△ABC 中,∵3cos 5α=,5AB =,∴25cos 3AB AC α==,∴AD=BC 203==. 故选:C.【点睛】本题考查了矩形的性质、勾股定理和解直角三角形的知识,属于常考题型,熟练掌握矩形的性质和解直角三角形的知识是解题关键.8.D解析:D【解析】【分析】由于等腰直角三角形AEF 的斜边EF 过C 点,则△BEC 和△DCF 都是直角三角形;观察反比例函数图像得出反比例函数解析式为y=9x;当x =3时,y =3,即BC=CD=3,根据等腰直角三角形的性质得,CF=3,则C 点与M 点重合;当y =9时,根据反比例函数的解析式得x =1,即BC=1,CD=9,所以,而;利用等腰直角三角形的性质BE•DF=BC•CD=xy ,然后再根据反比例函数的性质得BE•DF=9,其值为定值;由于x =2xy ,其值为定值.【详解】解:因为等腰直角三角形AEF 的斜边EF 过C 点,M 为EF 的中点,所以△BEC 和△DCF 都是直角三角形;观察反比例函数图像得x =3,y =3,则反比例解析式为y=9x.A 、当x =3时,y =3,即BC=CD=3,所以,,C 点与M 点重合,则EC=EM ,所以A 选项错误;B 、当y =9时,x =1,即BC=1,CD=9,所以,,,所以B 选项错误;C 、因为x y =2×xy =18,所以,EC•CF 为定值,所以C 选项错误;D 、因为BE•DF=BC•CD=xy =9,即BE•DF 的值不变,所以D 选项正确.故选:D .【点睛】本题考查了动点问题的函数图像:先根据几何性质得到与动点有关的两变量之间的函数关系,然后利用函数解析式和函数性质画出其函数图像,注意自变量的取值范围.9.A解析:A【解析】【分析】根据已知,运用直角三角形和三角函数得到上升的高度为:8tan20°.【详解】设木桩上升了h 米,∴由已知图形可得:tan20°=8h , ∴木桩上升的高度h =8tan20°故选B. 10.C解析:C【解析】【分析】确定出△DEF 和△DAC 相似,根据相似三角形对应边成比例求出AC ,再根据旗杆的高度=AC+BC 计算即可得解.【详解】解:∵∠FDE=∠ADC ,∠DEF=∠DCA=90°,∴△DEF ∽△DAC , ∴CDE CD EF A = , 即:0.50.2520AC = , 解得AC=10,∵DF 与地面保持平行,目测点D 到地面的距离DG=1.5米,∴BC=DG=1.5米,∴旗杆的高度=AC+BC=10+1.5=11.5米.故选:C .【点睛】本题考查了相似三角形的应用,主要利用了相似三角形对应边成比例,准确确定出相似三角形是解题的关键.11.A解析:A【解析】∵BE ∥AD ,∴△BCE ∽△ACD ,∴CB CEAC CD=,即CB CEAB BC DE EC=++,∵BC=1,DE=1.8,EC=1.2∴1 1.21 1.8 1.2 AB=++∴1.2AB=1.8,∴AB=1.5m.故选A.12.D解析:D【解析】解:①正方体的主视图与左视图都是正方形;②球的主视图与左视图都是圆;③圆锥主视图与左视图都是三角形;④圆柱的主视图和左视图都是长方形;故选D.二、填空题13.3米【解析】【分析】利用垂直距离:水平宽度得到水平距离与斜坡的比把相应的数值代入即可【详解】解:∵坡度为1:2且株距为6米∴株距:坡面距离=2:∴坡面距离=株距×(米)【点睛】本题是将实际问题转化为解析:35米【解析】【分析】利用垂直距离:水平宽度得到水平距离与斜坡的比,把相应的数值代入即可.【详解】解:∵坡度为1:2,22125+=,且株距为6米,∴株距:坡面距离=2:5∴坡面距离=株距×535=(米).【点睛】本题是将实际问题转化为直角三角形中的数学问题,可把条件和问题放到直角三角形中,进行解决.要注意坡度是坡角的正切函数.14.﹣2【解析】∵反比例函数y=-6x的图象过点A(m3)∴3=-6m解得=-2解析:﹣2【解析】∵反比例函数的图象过点A(m,3),∴,解得.15.【解析】已知BC=8AD是中线可得CD=4在△CBA和△CAD中由∠B=∠DAC∠C=∠C可判定△CBA∽△CAD根据相似三角形的性质可得即可得AC2=CD•BC=4×8=32解得AC=4解析:42【解析】已知BC=8, AD是中线,可得CD=4,在△CBA和△CAD中,由∠B=∠DAC,∠C=∠C,可判定△CBA∽△CAD,根据相似三角形的性质可得AC CDBC AC,即可得AC2=CD•BC=4×8=32,解得AC=42.16.2【解析】【分析】根据反比例函数系数k的几何意义即可得到结论【详解】解:连接OC∵点A在双曲线y=(x>0)上过点A作AB⊥x轴于点B∴S△OAB=×6=3∵BC:CA=1:2∴S△OBC=3×=1解析:2【解析】【分析】根据反比例函数系数k的几何意义即可得到结论.【详解】解:连接OC,∵点A在双曲线y=6x(x>0)上,过点A作AB⊥x轴于点B,∴S△OAB=12×6=3,∵BC:CA=1:2,∴S△OBC=3×13=1,∵双曲线y=kx(x>0)经过点C,∴S△OBC=12|k|=1,∴|k |=2,∵双曲线y =k x (x >0)在第一象限, ∴k =2,故答案为2.【点睛】本题考查了反比例函数的图象与性质,反比例函数图象上点的坐标特征,反比例函数系数k 的几何意义,熟练掌握反比例函数系数k 的几何意义是解题的关键. 17.3【解析】试题分析:如图∵CD∥AB∥MN∴△ABE∽△CDE△ABF∽△MNF∴即解得:AB=3m 答:路灯的高为3m 考点:中心投影解析:3【解析】试题分析:如图,∵CD ∥AB ∥MN ,∴△ABE ∽△CDE ,△ABF ∽△MNF ,∴,CD DE FN MN AB BE FB AB ==, 即1.8 1.8 1.5 1.5,1.8 1.5 2.7AB BD AB BD==++-, 解得:AB=3m ,答:路灯的高为3m .考点:中心投影.18.【解析】【分析】由正方形的性质易证△ABC ∽△FEC 可设BC=x 只需求出BC 即可求出图中阴影部分的面积【详解】如图所示:设BC =x 则CE =1﹣x ∵AB ∥EF ∴△ABC ∽△FEC ∴=∴=解得x =∴阴影解析:16【解析】【分析】由正方形的性质易证△ABC ∽△FEC ,可设BC=x ,只需求出BC 即可求出图中阴影部分的面积.【详解】如图所示:设BC =x ,则CE =1﹣x ,∵AB∥EF,∴△ABC∽△FEC∴ABEF=BCCE,∴12=x1x-解得x=13,∴阴影部分面积为:S△ABC=12×13×1=16,故答案为:16.【点睛】本题主要考查正方形的性质及三角形的相似,本题要充分利用正方形的特殊性质.利用比例的性质,直角三角形的性质等知识点的理解即可解答.19.【解析】当时∵∠A=∠A∴△AED∽△ABC此时AE=;当时∵∠A=∠A∴△AD E∽△ABC此时AE=;故答案是:解析:512 35或【解析】当AE ABAD AC=时,∵∠A=∠A,∴△AED∽△ABC,此时AE=·621255 AB ADAC⨯==;当AD ABAE AC=时,∵∠A=∠A,∴△ADE∽△ABC,此时AE=·52563 AC ADAB⨯==;故答案是:125 53或.20.18【解析】【分析】根据黄金分割定义:列方程即可求解【详解】解:设A P为x米根据题意得整理得x2+10x﹣100=0解得x1=5﹣5≈618x2=﹣5﹣5(不符合题意舍去)经检验x=5﹣5是原方程的解析:18【解析】【分析】根据黄金分割定义:AP BPAB AP=列方程即可求解.【详解】解:设AP为x米,根据题意,得x10 10x x -=整理,得x2+10x﹣100=0解得x1=﹣5≈6.18,x2=﹣5(不符合题意,舍去)经检验x=5是原方程的根,∴AP的长为6.18米.故答案为6.18.【点睛】本题考查了黄金分割的概念,熟练掌握黄金比是解答本题的关键.三、解答题21.(1)详见解析;(2)当∠B+∠EGC=180°时,DE ADCF DC=成立,理由详见解析.【解析】【分析】(1)根据矩形的性质可得∠A=∠ADC=90°,由DE⊥CF可得∠ADE=∠DCF,即可证得△ADE∽△DCF,从而证得结论;(2)在AD的延长线上取点M,使CM=CF,则∠CMF=∠CFM.根据平行线的性质可得∠A=∠CDM,再结合∠B+∠EGC=180°,可得∠AED=∠FCB,进而得出∠CMF=∠AED即可证得△ADE∽△DCM,从而证得结论;【详解】解:(1)∵四边形ABCD是矩形,∴∠A=∠ADC=90°,∵DE⊥CF,∴∠ADE=∠DCF,∴△ADE∽△DCF,∴DE AD CF DC=(2)当∠B+∠EGC=180°时,DE ADCF DC=成立,证明如下:在AD的延长线上取点M,使CM=CF,则∠CMF=∠CFM.∵AB∥CD.∴∠A=∠CDM.∵AD∥BC,∴∠CFM=∠FCB.∵∠B+∠EGC=180°,∴∠AED=∠FCB,∴∠CMF=∠AED,∴△ADE∽△DCM,∴DE ADCM DC=,即DE ADCF DC=.【点睛】本题是相似形综合题目,考查了相似三角形的判定与性质、等腰三角形的性质以及平行线的性质,熟练掌握等腰三角形的性质,证明三角形相似是解决问题的关键.22.(1)见解析;(2)MC=7.【解析】【分析】(1)由两组边成比例,夹角相等来证明即可;(2)由相似三角形的性质得边成比例,进而利用勾股定理求得BC,再判定∠MBC=90°,最后由勾股定理求得MC的值即可.【详解】(1)证明:∵AB•CD=BC•BD∴ABBC=BDCD在△ABD和△BCD中,∠ABD=∠BCD=90°∴△ABD∽△BCD;(2)∵△ABD∽△BCD∴ADBD=BDCD,∠ADB=∠BDC又∵CD=6,AD=8∴BD2=AD•CD=48∴BC22BD CD-4836-3∵BM∥CD∴∠MBD=∠BDC,∠MBC=∠BCD=90°∴∠ADB=∠MBD,且∠ABD=90°∴BM=MD,∠MAB=∠MBA∴BM=MD=AM=4∴MC22BC BM+1216+7.【点睛】此题主要考查相似三角形的判定与性质,解题的关键是熟知相似三角形的判定定理与勾股定理的运用.23.(1)710;(2)2222ab a b a b++;(3)101-. 【解析】【分析】(1)求出BE ,BD 即可解决问题.(2)利用勾股定理,面积法求高CD 即可.(3)根据CD =3DE ,构建方程即可解决问题.【详解】解:(1)在Rt △ABC 中,∵∠ACB =90°,a =3,b =4, ∴2235,cos 5BC AB a b B AC ∴=+===. ∵CD ,CE 是斜边AB 上的高,中线,∴∠BDC =90°,15BE AB 22==. ∴在Rt △BCD 中, 39cos 355BD BC B =⋅=⨯= 5972510DE BE BD ∴=-=-=(2)在Rt △ABC 中,∵∠ACB =90°,BC =a ,AC =b , 2222AB BC AC a b ∴=+=+ABC 11S AB CD AC BC 22=⋅=⋅V Q 222222AC BC ab a b CD AB a b a b⋅+∴===++2222a b a b ++. (3)在Rt △BCD 中,22222cos BD BC B a a b a b =⋅==++∴222222222122DE BE BD a b a b a b=-=+=++, 又1tan 3DE DCE CD ∠==, ∴CD =3DE 22222232a b a b =++.∵b =3, ∴2a =9﹣a 2,即a 2+2a ﹣9=0.由求根公式得110a=-±(负值舍去),即所求a的值是101-.【点睛】本题考查解直角三角形的应用,直角三角形斜边中线的性质,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.24.(1)证明见解析;(2)3.【解析】【分析】(1)根据切线的判定定理得到BC是⊙O的切线,再利用切线长定理证明即可;(2)根据含30°的直角三角形的性质、正切的定义计算即可.【详解】(1)∵AB是⊙O直径,BC⊥AB,∴BC是⊙O的切线,∵CD切⊙O于点D,∴BC=CD;(2)连接BD,∵BC=CD,∠C=60°,∴△BCD是等边三角形,∴BD=BC=3,∠CBD=60°,∴∠ABD=30°,∵AB是⊙O直径,∴∠ADB=90°,∴AD=BD•tan∠ABD=3.【点睛】本题考查了切线的性质、直角三角形的性质、圆周角定理,掌握圆的切线垂直于经过切点的半径是解题的关键.25.(1)6yx=(2)(-6,0)或(-2,0).【解析】分析:(1)把A点坐标代入直线解析式可求得m的值,则可求得A点坐标,再把A点坐标代入双曲线解析式可求得k的值,可求得双曲线解析式;(2)设P(t,0),则可表示出PC的长,进一步表示出△ACP的面积,可得到关于t 的方程,则可求得P点坐标.详解:(1)把A点坐标代入y=12x+2,可得:3=12m+2,解得:m=2,∴A(2,3).∵A点也在双曲线上,∴k=2×3=6,∴双曲线解析式为y=6x;(2)在y=12x+2中,令y=0可求得:x=﹣4,∴C(﹣4,0).∵点P在x轴上,∴可设P点坐标为(t,0),∴CP=|t+4|,且A(2,3),∴S△ACP=12×3|t+4|.∵△ACP的面积为3,∴12×3|t+4|=3,解得:t=﹣6或t=﹣2,∴P点坐标为(﹣6,0)或(﹣2,0).点睛:本题主要考查函数图象的交点,掌握函数图象的交点坐标满足每个函数解析式是解题的关键.。
【好题】初三数学下期中第一次模拟试卷(含答案)一、选择题1.如图,在矩形、三角形、正五边形、菱形的外边加一个宽度一样的外框,保证外框的边界与原图形对应边平行,则外框与原图不一定相似的是( )A .B .C .D .2.用放大镜观察一个五边形时,不变的量是( )A .各边的长度B .各内角的度数C .五边形的周长D .五边形的面积3.如图,菱形OABC 的顶点A 的坐标为(3,4),顶点C 在x 轴的正半轴上,反比例函数y=k x (x >0)的图象经过顶点B ,则反比例函数的表达式为( )A .y=12xB .y=24xC .y=32xD .y=40x4.如图,在平行四边形ABCD 中,F 是边AD 上的一点,射线CF 和BA 的延长线交于点E ,如果12C EAF C CDF =V V ,那么S EAF S EBCV V 的值是( )A .12B .13C .14D .19 5.若37a b =,则b a a-等于( ) A .34 B .43 C .73 D .37 6.已知点C 在线段AB 上,且点C 是线段AB 的黄金分割点(AC >BC ),则下列结论正确的是( )A.AB2=AC•BC B.BC2=AC•BC C.AC=512-BC D.BC=512-AC7.如图,D是△ABC的边BC上一点,已知AB=4,AD=2.∠DAC=∠B,若△ABD的面积为a,则△ACD的面积为()A.a B.a C.a D.a8.在△ABC中,若=0,则∠C的度数是()A.45°B.60°C.75°D.105°9.如图,过反比例函数的图像上一点A作AB⊥轴于点B,连接AO,若S△AOB=2,则的值为()A.2 B.3 C.4 D.510.如图,△ABC中AB两个顶点在x轴的上方,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C′,且△A′B′C′与△ABC的位似比为2:1.设点B的对应点B′的横坐标是a,则点B的横坐标是()A.12a-B.1(1)2a-+C.1(1)2a--D.1(3)2a-+11.若反比例函数2yx=-的图象上有两个不同的点关于y轴的对称点都在一次函数y=-x+m的图象上,则m的取值范围是()A.22m>B.-22m<C.22-22m m>或<D.-2222m<<12.下列变形中:①由方程125x-=2去分母,得x﹣12=10;②由方程29x=92两边同除以29,得x=1;③由方程6x﹣4=x+4移项,得7x=0;④由方程2﹣5362x x-+=两边同乘以6,得12﹣x﹣5=3(x+3).错误变形的个数是()个.A.4B.3C.2D.1二、填空题13.如图,在一段坡度为1∶2的山坡上种树,要求株距(即相邻两株树之间的水平距离)为6米,那么斜坡上相邻两株树之间的坡面距离为____米.14.若点A(m,2)在反比例函数y=的图象上,则当函数值y≥-2时,自变量x的取值范围是____.15.如图是由棱长相等的小立方体摆成的几何体的主视图与俯视图,根据视图可以判断组成这个几何体至少要________个小立方体.16.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的P点处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为________米.17.将三角形纸片△ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=8,BC=10,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是______________.18.若ab=34,则a bb+=__________.19.近视眼镜的度数(y度)与镜片焦距(x米)呈反比例,其函数关系式为120.yx=如果近似眼镜镜片的焦距0.3x=米,那么近视眼镜的度数y为______.20.小刚身高1.7m,测得他站立在阳光下的影子长为0.85m,紧接着他把手臂竖直举起,测得影子长为1.1m,那么小刚举起的手臂超出头顶的高度为________m.三、解答题21.如图,铁路MN和公路PQ在点O处交汇,∠QON=30°,在点A处有一栋居民楼,AO=320m,如果火车行驶时,周围200m以内会受到噪音的影响,那么火车在铁路MN上沿ON方向行驶时.(1)居民楼是否会受到噪音的影响?请说明理由;(2)如果行驶的速度为72km/h,居民楼受噪音影响的时间为多少秒?22.如图,某市郊外景区内一条笔直的公路a经过三个景点A、B、C,•景区管委会又开发了风景优美的景点D,经测量,景点D位于景点A的北偏东30′方向8km处,•位于景点B的正北方向,还位于景点C的北偏西75°方向上,已知AB=5km.(1)景区管委会准备由景点D向公路a修建一条距离最短的公路,不考试其他因素,求出这条公路的长.(结果精确到0.1km).(2)求景点C与景点D之间的距离.(结果精确到1km)(参考数据:3=1.73,5=2.24,sin53°=0.80,sin37°=0.60,tan53°=1.33,tan37°=0.75,sin38°=0.62,sin52°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73).23.如图,直线123l //l //l ,直线AC 依次交1l 、2l 、3l 于A 、B 、C 三点,直线DF 依次交1l 、2l 、3l 于D 、E 、F 三点,若AB 4AC 7=,DE 2=,求EF 的长.24.已知:在四边形ABCD 中,对角线AC 、BD 相交于点E ,且AC ⊥BD ,作BF ⊥CD ,垂足为点F ,BF 与AC 交于点C ,∠BGE=∠ADE .(1)如图1,求证:AD=CD ;(2)如图2,BH 是△ABE 的中线,若AE=2DE ,DE=EG ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE 面积的2倍.25.已知:如图,在正方形ABCD 中,P 是BC 上的点,Q 是CD 上的点,且∠AQP =900, 求证:△ADQ ∽△QCP .【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】根据相似多边形的判定定理对各个选项进行分析,从而确定最后答案.【详解】正五边形相似,因为它们的边长都对应成比例、对应角都相等,符合相似的条件,故A不符合题意;锐角三角形、菱形的原图与外框相似,因为其对应角均相等,对应边均对应成比例,符合相似的条件,故B、D不符合题意;矩形不相似,因为其对应角的度数一定相同,但对应边的比值不一定相等,不符合相似的条件,故A符合题意;故选C.【点睛】本题主要考查了相似图形判定,解决本题的关键是要注意边数相同、各角对应相等、各边对应成比例的两个多边形是相似多边形.2.B解析:B【解析】解:∵用一个放大镜去观察一个三角形,∴放大后的三角形与原三角形相似,∵相似三角形的对应边成比例,∴各边长都变大,故此选项错误;∵相似三角形的对应角相等,∴对应角大小不变,故选项B正确;.∵相似三角形的面积比等于相似比的平方,∴C选项错误;∵相似三角形的周长得比等于相似比,∴D选项错误.故选B.点睛:此题考查了相似三角形的性质.注意相似三角形的对应边成比例,相似三角形的对应角相等,相似三角形的面积比等于相似比的平方,相似三角形的周长得比等于相似比.3.C解析:C【解析】【分析】过A作AM⊥x轴于M,过B作BN⊥x轴于N,根据菱形性质得出OA=BC=AB=OC,AB ∥OC,OA∥BC,求出∠AOM=∠BCN,OM=3,AM=4,OC=OA=AB=BC=5,证△AOM ≌△BCN,求出BN=AM=4,CN=OM=3,ON=8,求出B点的坐标,把B的坐标代入y=kx求出k即可.【详解】过A作AM⊥x轴于M,过B作BN⊥x轴于N,则∠AMO=∠BNC=90°,∵四边形AOCB是菱形,∴OA=BC=AB=OC,AB∥OC,OA∥BC,∴∠AOM=∠BCN,∵A(3,4),∴OM=3,AM=4,由勾股定理得:OA=5,即OC=OA=AB=BC=5,在△AOM 和△BCN 中AMO BNC AOM BCN OA BC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AOM ≌△BCN(AAS),∴BN=AM=4,CN=OM=3,∴ON=5+3=8,即B 点的坐标是(8,4),把B 的坐标代入y=kx 得:k=32,即y=32x, 故答案选C.【点睛】 本题考查了菱形的性质,解题的关键是熟练的掌握菱形的性质.4.D解析:D【解析】分析:根据相似三角形的性质进行解答即可.详解:∵在平行四边形ABCD 中,∴AE ∥CD ,∴△EAF ∽△CDF , ∵12EAF CDF C C V V ,= ∴12AF DF =, ∴11123AF BC ==+, ∵AF ∥BC ,∴△EAF ∽△EBC , ∴21139EAF EBC S S ⎛⎫== ⎪⎝⎭V V , 故选D.点睛:考查相似三角形的性质:相似三角形的面积比等于相似比的平方. 5.B解析:B【解析】由比例的基本性质可知a=37b,因此b aa-=347337b bb-=.故选B. 6.D解析:D 【解析】【分析】根据黄金分割的定义得出512BC ACAC AB-==,从而判断各选项.【详解】∵点C是线段AB的黄金分割点且AC>BC,∴51BC ACAC AB-==,即AC2=BC•AB,故A、B错误;∴AC=51-AB,故C错误;BC=51-AC,故D正确;故选D.【点睛】本题考查了黄金分割,掌握黄金分割的定义和性质是解题的关键.7.C解析:C【解析】【分析】【详解】解:∵∠DAC=∠B,∠C=∠C,∴△ACD∽△BCA,∵AB=4,AD=2,∴△ACD的面积:△ABC的面积为1:4,∴△ACD的面积:△ABD的面积=1:3,∵△ABD的面积为a,∴△ACD的面积为a,故选C.【点睛】本题考查相似三角形的判定与性质,掌握相关性质是本题的解题关键.8.C解析:C【解析】【分析】根据非负数的性质可得出cosA及tanB的值,继而可得出A和B的度数,根据三角形的内角和定理可得出∠C的度数.【详解】由题意,得 cosA=,tanB=1,∴∠A=60°,∠B=45°,∴∠C=180°-∠A-∠B=180°-60°-45°=75°.故选C.9.C解析:C【解析】试题分析:观察图象可得,k>0,已知S△AOB=2,根据反比例函数k的几何意义可得k=4,故答案选C.考点:反比例函数k的几何意义.10.D解析:D【解析】【分析】设点B的横坐标为x,然后表示出BC、B′C的横坐标的距离,再根据位似变换的概念列式计算.【详解】设点B的横坐标为x,则B、C间的横坐标的长度为﹣1﹣x,B′、C间的横坐标的长度为a+1,∵△ABC放大到原来的2倍得到△A′B′C,∴2(﹣1﹣x)=a+1,解得x=﹣12(a+3),故选:D.【点睛】本题考查了位似变换,坐标与图形的性质,根据位似变换的定义,利用两点间的横坐标的距离等于对应边的比列出方程是解题的关键.11.C解析:C【解析】【分析】根据题意可知反比例函数2y x =-的图象上的点关于y 轴的对称的点在函数2y x =上,由此可知反比例函数2y x=的图象与一次函数y=-x+m 的图象有两个不同的交点,继而可得关于x 的一元二次方程,再根据根的判别式即可求得答案.【详解】 ∵反比例函数2y x =-上有两个不同的点关于y 轴对称的点在一次函数y =-x +m 图象上, ∴反比例函数2y x=与一次函数y =-x +m 有两个不同的交点, 联立得2y x y x m⎧=⎪⎨⎪=-+⎩,消去y 得:2x m x =-+, 整理得:220x mx -+=,∵有两个不同的交点∴220x mx -+=有两个不相等的实数根,∴△=m 2-8>0,∴m >m <故选C.【点睛】本题考查了反比例函数图象上点的坐标特征,关于x 轴、y 轴对称的点的坐标,熟练掌握相关内容、正确理解题意是解题的关键.12.B解析:B【解析】【分析】根据方程的不同特点,从计算过程是否正确、方法应用是否得当等方面加以分析.【详解】 ①方程125x -=2去分母,两边同时乘以5,得x ﹣12=10,故①正确. ②方程29x =92,两边同除以29,得x =814;要注意除以一个数等于乘以这个数的倒数,故②错误.③方程6x ﹣4=x +4移项,得5x =8;要注意移项要变号,故③错误.④方程2﹣5362x x -+=两边同乘以6,得12﹣(x ﹣5)=3(x +3);要注意去分母后,要把是多项式的分子作为一个整体加上括号,故④错误.故②③④变形错误.故选B .【点睛】在解方程时,要注意以下问题:(1)去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号;(2)移项时要变号.二、填空题13.3米【解析】【分析】利用垂直距离:水平宽度得到水平距离与斜坡的比把相应的数值代入即可【详解】解:∵坡度为1:2且株距为6米∴株距:坡面距离=2:∴坡面距离=株距×(米)【点睛】本题是将实际问题转化为解析:35米【解析】【分析】利用垂直距离:水平宽度得到水平距离与斜坡的比,把相应的数值代入即可.【详解】解:∵坡度为1:2,22125+=,且株距为6米,∴株距:坡面距离=2:5∴坡面距离=株距×535=(米).【点睛】本题是将实际问题转化为直角三角形中的数学问题,可把条件和问题放到直角三角形中,进行解决.要注意坡度是坡角的正切函数.14.x≤-2或x>0【解析】【分析】先把点A(m2)代入解析式得A(22)再根据反比例函数的对称性求出A点关于原点的对称点A(-2-2)再根据函数图像即可求出函数值y≥-2时自变量的取值【详解】把点A(解析:x≤-2或x>0【解析】【分析】先把点A(m,2)代入解析式得A(2,2),再根据反比例函数的对称性求出A点关于原点的对称点A’(-2,-2),再根据函数图像即可求出函数值y≥-2时自变量的取值.【详解】把点A(m,2)代入y=,得A(2,2),∵点A(2,2)关于原点的对称点A’为(-2,-2),故当函数值y≥-2时,自变量x的取值范围为x≤-2或x>0.【点睛】此题主要考查反比例函数的图像,解题的关键是利用反比例函数的中心对称性.15.8【解析】由俯视图可以看出组成这个几何体的底面小正方体有5个由主视图可知第二层最少有2个第三层最少有1个所以组成这个几何体的小正方体的个数最少为5+2+1=8个点睛:本题主要考查学生由三视图判断几何解析:8【解析】由俯视图可以看出组成这个几何体的底面小正方体有5个,由主视图可知第二层最少有2个,第三层最少有1个,所以组成这个几何体的小正方体的个数最少为5+2+1=8个.点睛:本题主要考查学生由三视图判断几何体,同时也体现了对空间想象能力方面的考查.做题要掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”.16.5【解析】根据题意画出图形构造出△PCD∽△PAB利用相似三角形的性质解题解:过P作PF⊥AB交CD于E交AB于F如图所示设河宽为x米∵AB∥CD∴∠PDC=∠PBF∠PCD=∠PAB∴△PDC∽△解析:5【解析】根据题意画出图形,构造出△PCD∽△PAB,利用相似三角形的性质解题.解:过P作PF⊥AB,交CD于E,交AB于F,如图所示设河宽为x米.∵AB∥CD,∴∠PDC=∠PBF,∠PCD=∠PAB,∴△PDC∽△PBA,∴AB PF CD PE=,∴AB15x CD15+=,依题意CD=20米,AB=50米,∴15205015x=+,解得:x=22.5(米).答:河的宽度为22.5米.17.5或(答对一个得1分)【解析】根据△B′FC与△ABC相似时的对应情况有两种情况:①B′FC∽△ABC时B′FAB=CF/BC又因为AB=AC=8BC=10BF=BF所以解得BF=;②△B′CF∽△解析:5或(答对一个得1分)【解析】根据△B′FC与△ABC相似时的对应情况,有两种情况:① B′FC∽△ABC时,B′F AB ="CF/BC" ,又因为AB=AC=8,BC=10,B'F=BF,所以10810BF BF-=,解得BF=;②△B′CF∽△BCA时,B′F/BA ="CF/CA" ,又因为AB=AC=8,BC=10,B'F=CF,BF=B′F,又BF+FC=10,即2BF=10,解得BF=5.故BF的长度是5或.18.【解析】【分析】由比例的性质即可解答此题【详解】∵∴a=b∴=故答案为【点睛】此题考查了比例的基本性质熟练掌握这个性质是解答此题的关键解析:7 4【解析】【分析】由比例的性质即可解答此题.【详解】∵34ab=,∴a=34 b,∴a bb+=3744b b bb b+=,故答案为7 4【点睛】此题考查了比例的基本性质,熟练掌握这个性质是解答此题的关键.19.400【解析】分析:把代入即可算出y的值详解:把代入故答案为400点睛:此题主要考查了反比例函数的定义本题实际上是已知自变量的值求函数值的问题比较简单解析:400【解析】分析:把0.3x =代入120y x =,即可算出y 的值. 详解:把0.3x =代入120x, 400y =,故答案为400.点睛:此题主要考查了反比例函数的定义,本题实际上是已知自变量的值求函数值的问题,比较简单.20.5【解析】【分析】根据同一时刻身长和影长成比例求出举起手臂之后的身高与身高做差即可解题【详解】解:设举起手臂之后的身高为x 由题可得:17:085=x :11解得x=22则小刚举起的手臂超出头顶的高度为解析:5【解析】【分析】根据同一时刻身长和影长成比例,求出举起手臂之后的身高,与身高做差即可解题.【详解】解:设举起手臂之后的身高为x由题可得:1.7:0.85=x :1.1,解得x=2.2,则小刚举起的手臂超出头顶的高度为2.2-1.7=0.5m【点睛】本题考查了比例尺的实际应用,属于简单题,明确同一时刻的升高和影长是成比例的是解题关键.三、解答题21.(1)居民楼会受到噪音的影响;(2)影响时间应是12秒.【解析】【分析】(1)作AC ⊥ON 于C ,利用含30度的直角三角形三边的关系得到AC =12AO =160,则点A 到MN 的距离小200,从而可判断学校会受到影响;(2)以A 为圆心,100为半径画弧交MN 于B 、D ,如图,则AB =AD =200,利用等腰三角形的性质得BC =CD ,接下来利用勾股定理计算出BC =120,所以BD =2BC =240,然后利用速度公式计算出学校受到的影响的时间.【详解】(1)如图:过点A 作AC ⊥ON ,∵∠QON =30°,OA =320米,∴AC =160米,∵AC <200,∴居民楼会受到噪音的影响;(2)以A为圆心,200m为半径作⊙A,交MN于B、D两点,即当火车到B点时直到驶离D点,对居民楼产生噪音影响,∵AB=200米,AC=160米,∴由勾股定理得:BC=120米,由垂径定理得BD=2BC=240米,∵72千米/小时=20米/秒,∴影响时间应是:240÷20=12秒.【点睛】此题是解直角三角形的应用,主要考查的是垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.22.(1)景点D向公路a修建的这条公路的长约是3.1km;(2)景点C与景点D之间的距离约为4km.【解析】【详解】解:(1)如图,过点D作DE⊥AC于点E,过点A作AF⊥DB,交DB的延长线于点F,在Rt△DAF中,∠ADF=30°,∴AF=12AD=12×8=4,∴DF=22228443AD AF-=-=,在Rt△ABF中BF=2222AB AF54-=-=3,∴BD=DF﹣BF=43﹣3,sin∠ABF=45 AFAB=,在Rt△DBE中,sin∠DBE=DBBD,∵∠ABF=∠DBE,∴sin∠DBE=45,∴DE=BD•sin∠DBE=45×(43﹣3)=163125-≈3.1(km),∴景点D向公路a修建的这条公路的长约是3.1km;(2)由题意可知∠CDB=75°,由(1)可知sin∠DBE=45=0.8,所以∠DBE=53°,∴∠DCB=180°﹣75°﹣53°=52°,在Rt △DCE 中,sin ∠DCE=DB DC ,∴DC= 3.1sin 520.79DE ︒=≈4(km ), ∴景点C 与景点D 之间的距离约为4km . 23.5【解析】【分析】 利用平行线分线段成比例定理得到AB DE AC DF=,然后把有关数据代入计算即可. 【详解】 123l //l //l Q ,直线AC 依次交1l 、2l 、3l 于A 、B 、C 三点,直线DF 依次交1l 、2l 、3l 于D 、E 、F 三点,AB DE AC DF ∴=, AB 4AC 7=Q ,DE 2=, 427DF∴=, 解得:DF 3.5=,EF DF DE 3.52 1.5∴=-=-=.【点睛】本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.24.(1)证明见解析;(2)△ACD 、△ABE 、△BCE 、△BHG .【解析】分析:(1)由AC⊥BD、BF⊥CD 知∠ADE+∠DAE=∠CGF+∠GCF,根据∠BGE=∠ADE=∠CGF 得出∠DAE=∠GCF 即可得;(2)设DE=a ,先得出AE=2DE=2a 、EG=DE=a 、AH=HE=a 、CE=AE=2a ,据此知S △ADC =2a 2=2S △ADE ,证△ADE≌△BGE 得BE=AE=2a ,再分别求出S △ABE 、S △ACE 、S △BHG ,从而得出答案.详解:(1)∵∠BGE=∠ADE,∠BGE=∠CGF,∴∠ADE=∠CGF,∵AC⊥BD、BF⊥CD,∴∠ADE+∠DAE=∠CGF+∠GCF,∴∠DAE=∠GCF,∴AD=CD;(2)设DE=a ,则AE=2DE=2a ,EG=DE=a ,∴S △ADE =12AE ×DE=12×2a ×a=a 2, ∵BH 是△ABE 的中线,∴AH=HE=a,∵AD=CD、AC⊥BD,∴CE=AE=2a,则S△ADC=12AC•DE=12•(2a+2a)•a=2a2=2S△ADE;在△ADE和△BGE中,∵AED BEG DE GEADE BGE ∠∠⎧⎪⎨⎪∠∠⎩===,∴△ADE≌△BGE(ASA),∴BE=AE=2a,∴S△ABE=12AE•BE=12•(2a)•2a=2a2,S△ACE=12CE•BE=12•(2a)•2a=2a2,S△BHG=12HG•BE=12•(a+a)•2a=2a2,综上,面积等于△ADE面积的2倍的三角形有△ACD、△ABE、△BCE、△BHG.点睛:本题主要考查全等三角形的判定与性质,解题的关键是掌握等腰三角形的判定与性质及全等三角形的判定与性质.25.证明见解析【解析】试题分析:本题利用等角的余角相等得出一对相等的角,加上直角得出相似三角形.试题解析:在Rt△ADQ与Rt△QCP中,∵∠AQP=90°,∴∠AQP+∠PQC=90°,又∵∠PQC+∠QPC=90°,∴∠AQP=∠QPC,∴Rt△ADQ∽Rt△QCP.。
一、选择题1.如图,在菱形ABCD 中,660AB DAB =∠=︒,,A ,E 分别交BC 、BD 于点E 、F ,2CE =,连接CF ,以下结论:①ABF CBF ≌;②点E 到AB 的距离是23;③ADF 与EBF △的面积比为3∶2:④ABF 的面积为为183,其中正确的是( )A .①④B .①③④C .①②④D .①②③④2.如图,已知D 、E 分别为AB 、AC 上的两点,且DE ∥BC ,AE=2CE ,AB=12,则AD 的长为( )A .4B .6C .5D .83.如图,在矩形、三角形、正五边形、菱形的外边加一个宽度一样的外框,保证外框的边界与原图形对应边平行,则外框与原图一定相似的有( )A .1个B .2个C .3D .4个4.如图,已知////AB CD EF ,它们依次交直线1l 、2l 于点A 、D 、F 和点B 、C 、E ,如果:3:1AD DF =,10BE =,那么CE 等于( )A .103B .203C .52D .1525.如图,地面上点A 处有一只兔子,距它10米的B 处有一根高1.6米的木桩,大树、木桩和兔子刚好在一条直线上.一只老鹰在9.6米高的树顶上刚好看见兔子,则大树C 离木桩B( )米.A .60B .50C .40D .456.如图,在矩形OABC 中,点A 和点C 分别在y 轴和x 轴上.AC 与BO 交于点D ,过点C 作CE BD ⊥于点E ,2DE BE =.若5CE =,反比例函数(0,0)ky k x x=>>经过点D ,则k =( )A .2B .352C .36D .307.如图,正比例函数y ax =的图象与反比例函数ky x=的图象相交于A ,B 两点,其中点A 的横坐标为2,则不等式kax x<的解集为( )A .2x <-或2x >B .2x <-或02x <<C .20x -<<或02x <<D .20x -<<或2x >8.如图,直线l x ⊥轴于点P ,且与反比例函数11(0)k y x x=>及22(0)ky x x =>的图象分别交于点A ,B ,连接OA ,OB ,已知△OAB 的面积为2,则12k k -的值为( )A .2B .3C .4D .59.若反比例函数()2221m y m x -=-的图象在第二、四象限,则m 的值是( )A .-1或1B .小于12的任意实数 C .-1D .不能确定10.如图,函数ky x=与2(0)y kx k =-+≠在同一平面直角坐标系中的图像大致( ) A . B .C .D .11.函数ky x=与y kx k =-(0k ≠)在同一平面直角坐标系中的大致图象是( ) A . B . C . D .12.给出下列函数:①y =﹣3x +2:②y =3x ;③y =﹣5x:④y =3x ,上述函数中符合条件“当x >1时,函数值y 随自变量x 增大而增大”的是( ) A .①③ B .③④ C .②④ D .②③二、填空题13.如图,点О是正方形ABCD 的中心,DE 与О相切于点E ,连接,BE 若10,DE =102BE =О的面积是________________.14.如图,AB 是⊙O 的直径,点C 在圆上,直线l 经过点C ,且l ∥AB ,P 为直线l 上一个动点,若AC =4,BC =3,以点P ,A ,C 为顶点的三角形与△ABC 相似,则PC =_____.15.△ABC 的三边长分别为7、6、2,△DEF 的两边分别为1、3,要使△ABC ∽△DEF ,则△DEF 的第三边长为______.16.如图,90A B ∠=∠=︒,AB a ,AD BC <,在边AB 上取点P ,使得PAD △,PBC 与PDC △两两相似,则AP 长为___________.(结果用含a 的代数式表示)17.如图,直线y =34-x +6与反比例函数y =kx(k >0)的图象交于点M 、N ,与x 轴、y 轴分别交于点B 、A ,作ME ⊥x 轴于点E ,NF ⊥x 轴于点F ,过点E 、F 分别作EG ∥AB ,FH ∥AB ,分别交y 轴于点G 、H ,ME 交HF 于点K ,若四边形MKFN 和四边形HGEK 的面积和为12,则k 的值为_____.18.如图,直线3y x =-+与y 轴交于点A ,与反比例函数()0ky x x=<的图象交于点C ,过点C 作CB x ⊥轴于点B ,若3AO BO =,则k 的值为________.19.如图,平面直角坐标系中,等腰Rt ABC ∆的顶点.A B 分别在x 轴、y 轴的正半轴,90,ABC =∠CA x ⊥轴, 点C 在函数()0k y x x=>的图象上.若2,AB =则k 的值为_____.20.从﹣3,﹣2,﹣1,0,1,2这6个数中任意取出一个数记作k ,则既能使函数y =k x的图象经过第一、第三象限,又能使关于x 的一元二次方程x 2﹣kx +1=0有实数根的概率为_____.参考答案三、解答题21.如图,在平面直角坐标系中,O 为坐标原点,点A 在x 轴的正半轴上,△AOB 为等腰三角形,且OA =OB ,B (8,6),过点B 作y 轴的垂线,垂足为D ,点C 在线段BD 上,点D 关于直线OC 的对称点在腰OB 上.(1)求AB 的长; (2)求点C 的坐标;(3)点P 从点C 出发,以每秒1个单位的速度沿折线CB ﹣BA 运动;同时点Q 从A 出发,以每秒1个单位的速度沿AO 向终点O 运动,当一点停止运动时,另一点也随之停止运动.设△BPQ 的面积为S ,运动时间为t ,求S 与t 的函数关系式.22.已知:△ABC 在坐标平面内,三个顶点的坐标为A (0,3)、B (3,4)、C (2,2).(正方形网格中,每个小正方形边长为1个单位长度) (1)画出△ABC 向下平移4个单位得到的△A 1B 1C 1;(2)以B 为位似中心,在网格中画出△A 2BC 2,使△A 2BC 2与△ABC 位似,且位似比2:1,直接写出C 2点坐标是 ; (3)△A 2BC 2的面积是 平方单位.23.已知y 是x 的反比例函数,且当x =4时,1y =-. (1)求y 与x 之间的函数解析式; (2)求当132x -≤≤-时,y 的取值范围. 24.如图,一次函数y 1=kx +b (k ≠0)和反比例函数()20my m x=≠的图象相交于点A (﹣4,2),B (n ,﹣4)(1)求一次函数和反比例函数的表达式; (2)观察图象,直接写出不等式y 1<y 2的解集.25.如图,在平面直角坐标系xOy 中,已知四边形DOBC 是矩形,且D (0,4),B (6,0).若反比例函数11k y x=(x >0)的图象经过线段OC 的中点A ,交DC 于点E ,交BC 于点F .设直线EF 的解析式为y 2=k 2x+b . (1)求反比例函数和直线EF 的解析式;(温馨提示:平面上有任意两点M (x 1,y 1)、N (x 2,y 2),它们连线的中点P 的坐标为(121222x x y y ++,))(2)求△OEF 的面积; (3)请结合图象直接写出不等式k 2x -b ﹣1k x>0的解集.26.如图1,在矩形ABCD中,AD=2,点E是AD的中点,连接BE,且BE⊥AC交AC于点F.(1)求证:△EAB∽△ABC;(2)求AB,EF的长;(3)如图2,连接DF,BD,求DFBD的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据菱形的性质得出△ABF和△CBF全等的条件,从而可判断①成立;过点E作EG⊥AB,过点F作MH⊥AB,求得EG的长度,则可判断②是否成立;由AD∥BE,可判定△ADF∽△EBF,由相似三角形的性质可得△ADF与△EBF的面积比,从而可判断③是否成立;利用相似三角形的性质和等边三角形的性质,可求得△ABF在AB边上的高,进而求得△ABF的面积,则可判断④是否成立.【详解】解:∵四边形ABCD是菱形,AB=6,∴BC=AB=6,∵∠DAB=60°,∴AB=AD=DB=6,∠ABD=∠DBC=60°,在△ABF与△CBF中,AB BC ABF FBC BF BF =⎧⎪∠=∠⎨⎪=⎩, ∴△ABF ≌△CBF (SAS ),故①成立;如图,过点E 作EG ⊥AB 延长线于点G ;过点F 作MH ⊥AB 交AB ,CD 于点H ,M , 则由菱形的对边平行可得MH ⊥CD ,∵CE=2,BC=6,∠ABC=120°, ∴BE=6-2=4,∠EBG=60° ∵EG ⊥AB ,∴33= 故②成立;∵AD ∥BE , ∴△ADF ∽△EBF , ∴2269()(),44ADF EBF S AD S BE ∆∆=== 故③不成立; ∵△ADF ∽△EBF ,32DF AD FB EB ∴== ∵DB=6, ∴BF= 125∴FH=125×32=635, ∴S △ABF =12AB•FH=16318362⨯=, 故④成立.综上所述,一定成立的有①②④. 故选:C . 【点睛】本题考查了菱形的性质、全等三角形的判定、相似三角形的判定与性质及三角形的面积计算,熟练掌握相关性质及定理是解题的关键.2.D解析:D 【分析】先根据平行线分线段成比例定理得出比例式,代入后得出AD=23AB ,代入求出即可. 【详解】 解:∵DE ∥BC ,∴AD AEAB AC =, ∵AE=2CE ,∴2223AE CE AC EC EC ==+ 又AB=12,∴AD=23AB=8, 故选:D . 【点睛】本题考查了平行线分线段成比例定理,能根据定理得出正确的比例式是解此题的关键.3.C解析:C 【分析】根据相似多边形的判定定理对各个选项进行分析,从而确定最后答案. 【详解】矩形的原图与外框不相似,因为其对应角的度数一定相同,但对应边的比值不一定相等,不符合相似的条件;锐角三角形的原图与外框相似,因为其对应角均相等,对应边均对应成比例,符合相似的条件;正五边形相似,因为它们的边长都对应成比例、对应角都相等,符合相似的条件; 菱形的原图与外框相似,因为其对应角均相等,对应边均对应成比例,符合相似的条件. 综上,外框与原图一定相似的有3个, 故选:C . 【点睛】本题主要考查了相似图形的概念,注意边数相同、各角对应相等、各边对应成比例的两个多边形是相似多边形.4.C解析:C 【分析】根据平行线分线段成比例得到BC ADCE DF=,代入已知解答即可.【详解】解:∵////AB CD EF , ∴BC ADCE DF =, ∵:3:1AD DF =,10BE =, ∴1031CE CE -=, 解得:CE=52, 故选:C . 【点睛】本题考查平行线分线段成比例、比例的性质,掌握平行线分线段成比例是解答的关键,注意对应线段的顺序.5.B解析:B 【分析】如图,证明△ABE ∽△ACD ,根据相似三角形的性质列式求解即可. 【详解】 解:如图,根据题意得,△ABE ∽△ACD , ∴AB BEAC CD= ∵AB=10m ,BE=1.6m ,CD=9.6m∴10 1.6=9.6AC ∴AC=60m∴BC=AC-AB=60-10=50m 故选:B . 【点睛】此题主要考查了相似三角形的应用,善于观察题目的信息是解题以及学好数学的关键.6.B解析:B 【分析】作DF ⊥OC 于F ,根据矩形的性质和相似三角形的性质求得OD=3,OE=5,根据勾股定理求得30OC =,然后通过三角形相似求得DF 和OF ,从而求得D 的坐标,代入解析式即可求得k 的值.【详解】解:作DF ⊥OC 于F ,在矩形OABC 中,∠OCB=90°,OD=BD ,90,OCE BCE ∴∠+∠=︒∵CE ⊥OB ,90,CEO BEC ∴∠=∠=︒90,OCE COE ∴∠+∠=︒,COE BCE ∴∠=∠,COE BCE ∴∽,CE OE BE CE∴= ∴2,CE BE OE =∵2DE BE =,5,CE = 设,BE x =则DE=2x ,3,OD BD x ==∴OE=5x ,∴255,x x =解得,x=1(负根舍去),∴OD=3,OE=5,∴()22225530,OC OE CE =+=+= ∵∠OFD=∠OEC=90°,∠DOF=∠EOC ,∴△DOF ∽△COE , ∴,DF OF OD CE OE OC== 5530OF == ∴30622OF DF ==∴D 的坐标为⎝⎭, ∵反比例函数k y x =(k >0,x >0)经过点D ,∴222k == 故选:B .【点睛】本题考查了矩形的性质,勾股定理,三角形相似的判定和性质,反比例函数图象上点的坐标特征,求得D 的坐标是解题的关键.7.B解析:B【分析】先根据反比例函数与正比例函数的性质求出B 点横坐标,再由函数图象可得k ax x <,求出x 的取值范围即可.【详解】∵正比例函数y ax =的图象与反比例函数k y x =的图象相交于A ,B 两点, ∴A ,B 两点坐标关于原点对称,∵点A 的横坐标为2,∴B 点的横坐标为-2, ∵k ax x<, ∴在第一和第三象限,正比例函数y ax =的图象在反比例函数k y x=的图象的下方, ∴2x <-或02x <<,故选:B .【点睛】 本题考查了反比例函数与一次函数的交点问题,关键是掌握正比例函数与反比例函数图象交点关于原点对称.8.C解析:C【分析】据反比例函数k 的几何意义可知:△AOP 的面积为12k ,△BOP 的面积为22k ,由题意可知△AOB 的面积为12k −22k . 【详解】根据反比例函数k 的几何意义可知:△AOP 的面积为12k ,△BOP 的面积为22k , ∴△AOB 的面积为12k −22k , ∴12k −22k =2, ∴k 1-k 2=4,故选:C .【点睛】本题考查反比例函数k 的几何意义,解题的关键是正确理解k 的几何意义,本题属于中等题型,9.C解析:C【分析】根据反比例函数的定义列出方程221m -=-且210m -<求解即可.【详解】解:22(21)m y m x -=-是反比例函数,∴221m -=-,210m -≠,解之得1m =±.又因为图象在第二,四象限,所以210m -<, 解得12m <,即m 的值是1-. 故选:C .【点睛】 对于反比例函数()0k y k x=≠.(1)0k >,反比例函数图像分布在一、三象限;(2)k 0< ,反比例函数图像分布在第二、四象限内.10.B解析:B【分析】先根据反比例函数的图像,判断k 的符号,然后再判断一次函数的图像.【详解】A 中,反比例函数经过一、三象限,故k >0,则一次函数应经过一、二、四象限,错误;B 中,反比例函数经过一、三象限,故k >0,则一次函数应经过一、二、四象限,正确;C 中,反比例函数经过二、四象限,故k <0,则一次函数应经过一、二、三象限,错误;D 中,反比例函数经过二、四象限,故k <0,则一次函数应经过一、二、三象限,错误; 故选:B .【点睛】本题考查一次函数与反比例函数图像的性质,解题关键是通过函数的系数符号,判断函数图象经过的象限.11.C解析:C【分析】分k>0和k<0两种情况确定正确的选项即可.【详解】当k:>0时,反比例函数的图象位于第一、三象限,一次函数的图象交 y轴于负半轴,y 随着x的增大而增大,A选项错误,C选项符合;当k<0时,反比例函数的图象位于第二、四象限,一次函数的图象交y轴于正半轴,y 随着x的增大而增减小,B. D均错误,故选:C.【点睛】此题考查反比例函数的图象,一次函数的图象,熟记函数的性质是解题的关键.12.B解析:B【分析】分别利用一次函数、正比例函数、反比例函数的增减性分析得出答案.【详解】解:①y=﹣3x+2,当x>1时,函数值y随自变量x增大而减小,故此选项不符合题意;②y=3x,当x>1时,函数值y随自变量x增大而减小,故此选项不符合题意;③y=﹣5x,当x>1时,函数值y随自变量x增大而增大,故此选项符合题意;④y=3x,当x>1时,函数值y随自变量x增大而增大,故此选项符合题意;故选:B.【点睛】此题考查一次函数、正比例函数、反比例函数,正确把握相关性质是解题关键.二、填空题13.25【分析】连接EO可知EO⊥ED延长DE到点F作BF⊥DF根据题意可知△DEO∽△DFB在△EFB中根据勾股定理求解得出半径的长然后再根据圆的面积公式求解即可;【详解】如图:连接EO可知EO⊥ED解析:25π【分析】连接EO,可知EO⊥ED,延长DE到点F,作BF⊥DF,根据题意可知△DEO∽△DFB,在△EFB中,222EB EF FB=+,根据勾股定理求解得出半径的长,然后再根据圆的面积公式求解即可;【详解】如图:连接EO ,可知EO ⊥ED ,延长DE 到点F ,作BF ⊥DF ,∵∠FDB=∠EDO ,∠DEO=∠DFB ,∴△DEO ∽△DFB ,∵EO=r ,ED=10,EB=102, ∵DO=OB ,∴12DO EO DE DB FB DF===, ∴EF=10,FB=2r , 在△EFB 中,222EB EF FB =+,()22102=1004r +,∴ r=5,∴ 圆的面积为225r ππ=,故答案为:25π【点睛】本题考查了圆的面积公式、相似三角形的判定、勾股定理等知识,熟练掌握这些公式是解题的关键;14.32或5【分析】先根据勾股定理求出AB 的长由l ∥AB 可得∠ACP =∠A 所以以点PAC 为顶点的三角形与△ABC 相似只有两种情况或根据对应边成比例列式求出PC 的长【详解】∵AB 是⊙O 的直径∴∠ACB =9解析:3.2或5【分析】先根据勾股定理求出AB 的长,由l ∥AB ,可得∠ACP =∠A ,所以以点P ,A ,C 为顶点的三角形与△ABC 相似只有两种情况,ABCCAP 或ABC CPA ,根据对应边成比例列式求出PC 的长.【详解】∵AB 是⊙O 的直径,∴∠ACB =90°,在Rt △ABC 中,AC =4,BC =3,∴AB =5,∵l ∥AB ,∴∠ACP =∠A ,当以点P ,A ,C 为顶点的三角形与△ABC 相似,①ABC CAP , ∴AB AC CA CP =,则544CP=,解得 3.2CP =, ②ABC CPA , ∴AB AC CP CA =,则544CP =,解得5CP =, 综上可知若△ABC 与△PAC 相似,则PC =3.2或5.故答案为:3.2或5.【点睛】本题考查圆周角定理和相似三角形的存在性问题,解题的关键是利用分类讨论的思想根据相似三角形对应边成比例求出要求的线段长.15.35【分析】根据△ABC ∽△DEF 得到结合△ABC 的三边长分别为762△DEF 的两边分别为13可以得到△DEF 的两边13分别与△ABC 的两边26是对应边得到两三角形相似比为可以求出△DEF 的第三边【解析:3.5【分析】根据△ABC ∽△DEF ,得到AB AC BC DE DF EF==,结合△ABC 的三边长分别为7、6、2,△DEF 的两边分别为1、3,可以得到△DEF 的两边1、3分别与△ABC 的两边2,6是对应边,得到两三角形相似比为12,可以求出△DEF 的第三边. 【详解】解:∵要使△ABC ∽△DEF ,需AB AC BC DE DF EF==, ∵△ABC 的三边长分别为7、6、2,△DEF 的两边分别为1、3,∴△DEF 的两边1、3分别与△ABC 的两边2,6是对应边,∴两三角形相似比为12, ∴△DEF 的第三边长为:7×12=3.5. 故答案为:3.5.【点睛】本题考查了相似三角形的性质,根据两三角形相似,结合两三角形的线段长求出相似比是解题的关键.16.或【分析】根据△PAD △PBC 都是直角三角形△PAD △PBC △PDC 两两相似利用相似三角形性质分类讨论即可;【详解】∵△PAD △PBC 都是直角三角形△PAD △PBC △PDC 两两相似∴△PDC 是直角三 解析:12a 或13a 【分析】 根据△PAD ,△PBC 都是直角三角形,△PAD ,△PBC ,△PDC 两两相似,利用相似三角形性质分类讨论即可;【详解】∵△PAD ,△PBC 都是直角三角形,△PAD ,△PBC ,△PDC 两两相似,∴△PDC 是直角三角形,当90DPC ∠=︒时,∴90APD BPC ∠+∠=︒,∵90BPC BCP ∠+∠=︒,∴APD BCP ∠=∠,∵90A B ∠=∠=︒,∴△△APD BCP ,当△△APD PDC 时,∴APD PDC ∠=∠,此时CD ∥AB ,90ADC ∠=︒,四边形ABCD 是矩形,∴AD=BC ,与题意矛盾,故不存在这种情况;当△△APD PCD 时,∴ADP PDC ∠=∠,APD PCD ∠=∠,∴PCD BCP ∠=∠,过点P 作PM CD ⊥于M ,∴90PMD A ∠=∠=︒,90PMC B ∠=∠=︒,在△PAD 和△PMD 中,A PMD ADP MDP PD PD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△△PAD PMD ≅,∴PA=PM ,在△PBC 和△PMC 中,B PMC BCP MCP CP CP ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△△PBC PMC ≅,∴PB=PM , ∴12PA PB AB ==, ∵AB a , ∴12AP a =; 当90PDC ∠=︒时, 当△△△ADPDCP BCP 时,60APD DPC BPC ∠=∠=∠=︒,∴30ADP ∠=︒, ∴12AP PD =, 在△DPC 和△BPC 中,PDC B DPC BPC PC PC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△△DPC BPC ≅,∴PD=PB , ∴12AP PB =, ∴1133AP AB a ==; ∴AP 的长为12a 或13a . 【点睛】 本题主要考查了相似三角形的性质应用,结合全等三角形证明求解是解题的关键. 17.9【分析】容易知道四边形ANFHAMEGAMKH 为平行四边形根据MN 在反比例函数的图象上利用平行四边形的面积公式就可以求出它们的面积从而确定两者的数量关系【详解】解:∵HF ∥ANNF ∥MEEG ∥AM解析:9.【分析】容易知道四边形ANFH 、AMEG 、AMKH 为平行四边形,根据M 、N 在反比例函数的图象上,利用平行四边形的面积公式就可以求出它们的面积,从而确定两者的数量关系.【详解】解:∵HF ∥AN ,NF ∥ME ,EG ∥AM∴四边形ANFH 、AMEG 、AMKH 为平行四边形,∴S 平行四边形AMEG =ME•OE =k ,S 平行四边形ANFH =NF•OF =k ,则S 平行四边形AMEG +S 平行四边形ANFH =2k , ∵四边形MKFN 和四边形HGEK 的面积和为12,∴2S 平行四边形AMKH +12=2k ,∴S 平行四边形AMKH =k ﹣6,设点M 、N 的坐标分别为(x 1,y 1),(x 2,y 2),将y =34-x+6与反比例函数y =k x联立并整理得:3x 2﹣24x+4k =0, ∴x 1+x 2=8,x 1x 2=43k , 则S 平行四边形AMKH =k ﹣6=MK•x 1=NF•x 1=x 1y 2=x 1(﹣34x 2+6)=﹣34x 1x 2+6x 1=﹣k+6x 1, ∴6x 1=2k ﹣6,即x 1=13k ﹣1,则x 2=8﹣x 1=9﹣13k , ∴x 1x 2=43k =(13k ﹣1)(9﹣13k ), 解得:k =9,故答案为9.【点睛】本题考查了反比例函数的问题,掌握反比例函数的图象以及性质、平行四边形的性质以及判定定理、平行四边形的面积公式、韦达定理是解题的关键.18.-4【分析】先求出点A 的坐标然后表示出AOBO 的长度根据AO=3BO 求出点C 的横坐标代入直线解析式求出纵坐标用待定系数法求出反比例函数解析式【详解】解:∵直线与y 轴的交点A 的坐标为∴∵∴轴∴点C 的横解析:-4【分析】先求出点A 的坐标,然后表示出AO 、BO 的长度,根据AO=3BO ,求出点C 的横坐标,代入直线解析式求出纵坐标,用待定系数法求出反比例函数解析式.【详解】解:∵直线3y x =-+与y 轴的交点A 的坐标为()0,3,∴3AO =.∵3AO BO =,∴1BO =,CB x ⊥轴∴点C 的横坐标为1-.把1x =-代入3y x =-+,得()134y =--+=,∴点C 的坐标为()1,4-,把()1,4C -代入k y x=,得4k =-. 故答案是:-4.【点睛】本题考查的是反比例函数与一次函数的交点问题,根据题意确定点C 的横坐标并求出纵坐标是解题的关键. 19.4【分析】根据等腰三角形的性质和勾股定理求出AC 的值根据等面积法求出OA 的值OA 和AC 分别是点C 的横纵坐标又点C 在反比例函数图像上即可得出答案【详解】∵△ABC 为等腰直角三角形AB=2∴BC=2解得解析:4【分析】根据等腰三角形的性质和勾股定理求出AC 的值,根据等面积法求出OA 的值,OA 和AC 分别是点C 的横纵坐标,又点C 在反比例函数图像上,即可得出答案.【详解】∵△ABC 为等腰直角三角形,AB=2∴BC=2,AC ==1122BC AB OA AC ⨯⨯=⨯⨯ 112222OA ⨯⨯=⨯⨯解得:∴点C 的坐标为 又点C 在反比例函数图像上 ∴4k ==故答案为4.【点睛】本题考查的是反比例函数,解题关键是根据等面积法求出点C 的横坐标.20.【分析】确定使函数的图象经过第一三象限的k 的值然后确定使方程有实数根的k 值找到同时满足两个条件的k 的值即可【详解】解:这6个数中能使函数y =的图象经过第一第三象限的有12这2个数∵关于x 的一元二次方解析:16【分析】确定使函数的图象经过第一、三象限的k 的值,然后确定使方程有实数根的k 值,找到同时满足两个条件的k 的值即可.【详解】解:这6个数中能使函数y =k x的图象经过第一、第三象限的有1,2这2个数, ∵关于x 的一元二次方程x 2﹣kx +1=0有实数根,∴k 2﹣4≥0,解得k ≤﹣2或k ≥2,能满足这一条件的数是:﹣3、﹣2、2这3个数,∴能同时满足这两个条件的只有2这个数, ∴此概率为16, 故答案为:16. 三、解答题21.(1);(2)()3,6;(3)()()231505510t t S t ⎧-+≤≤=≤< 【分析】(1)过点B 作BH OA ⊥,根据勾股定理求出OB ,BH ,再根据已知条件得出OA ,AH ,即可得解;(2)由点B 坐标及BD 垂直y 轴可得OD=6,BD=8,再根据已知条件90CD B CD O CDO ''∠=∠=∠=︒,设点C 的横坐标为c ,则BC=8-c ,在根据勾股定理即可得解;(3)先求出AB 的长,计算点P 运动到终点A 和点Q 运动到终点O 的时间,取更小的时间t 的最大值,由于点P 在折线CB-BA 上运动且BC=5,所以t=5为分解分两种情况讨论即可;【详解】(1)过点B 作BH OA ⊥,∵点B 的坐标为(8,6),BD 垂直y 轴,∴BD=OH=8,DO=BH=6, ∴228610OB =+=,∵OB=OA ,∴AH=OA-OH=10-8=2,∴2262210AB =+=;(2)如图,设点D 关于直线OC 的对称点为D ,连接DD ',∴OC 垂直平分DD ',∴OD OD '=,CD CD '=,CD O CDO '∠=∠, 由(1)知OD=6,OB=10, ∴6OD '=,∴1064BD OB OD ''=-=-=,设CD CD c '==,则8BC c =-,∵△Rt BCD '中,222BD CD BC ''+=,∴()22248c c +=-, 解得3c =,∴点C 的坐标为()3,6.(3)由(1)可知210AB =,∵835BC =-=,∴点P 沿折线CB-BA 运动所用的时间内为5210+,∵10<5210+,∴010t ≤≤,当05t ≤≤,点P 在线段CB 上,如图所示,∴5PB BC CP t =-=-,∴()1165=15322S PB BH t t =⨯=⨯⨯--, 当5<t 10≤,点P 在线段BA 上,如图,∴5BP t =-,AQ t =,过点Q 作QG AB ⊥于点G ,∴90AGQ AHB ∠=∠=︒,∵QAG BAH ∠=∠,∴△△AGQAHB , ∴QG AQ BH AB=, ∴310210BH AQ QG AB ===, ∴()2113103101052210204S PB QG t t ==-=-;综上所述:()()231505*********t t S t t t ⎧-+≤≤⎪=⎨-≤⎪<. 【点睛】本题主要考查了相似三角形的判定与性质,勾股定理,轴对称的性质,准确分析计算是解题的关键.22.(1)图见解析;(2)图见解析,2C (1,0);(3)10【分析】(1)利用平移的性质得出对应点的坐标即可画出平移后的图形;(2)利用位似图形的性质得出对应点的坐标即可画出平移后的图形,进而可得点C 2的坐标;(3)根据所画图形判断出△A 2BC 2为等腰直角三角形,利用三角形的面积公式即可求解.【详解】解:(1)如图所示:△A 1B 1C 1,即为所求;(2)如图所示:△A 2BC 2即为所求,C 2点坐标为(1,0),故答案为:(1,0);(3)∵A 2C 2=BC 2=224225+=,A 2B=2262210+=,∴A 2C 22+BC 22= A 2B 2,∴△A 2BC 2是等腰直角三角形,且∠A 2C 2B=90°,∴△A 2BC 2的面积位为:12×(25)2=10平方单位, 故答案为:10.【点睛】本题考查平移变换和位似变换的性质、勾股定理及其逆定理、三角形的面积公式,掌握变换性质,正确得出变换后的对应点的位置是解答的关键.23.(1)4y x =-;(2)4y 83≤≤. 【分析】(1)利用待定系数法确定反比例函数的解析式即可;(2)根据自变量的取值范围确定函数值的取值范围即可.【详解】解:(1)设反比例函数的解析式为k y x =, ∵当x=4,y=-1,∴k=-1×4=-4,∴反比例函数的解析式为4y x =-; (2)当x=-3时,43y =,当x=-12时,y=8, ∴当-3≤x≤-12时,y 的取值范围是43≤y≤8. 【点睛】本题考查了反比例函数的性质,求得反比例函数的解析式是解答本题的关键. 24.(1) y =﹣x ﹣2,;(2) x >2或﹣4<x <0【分析】将点A (﹣4,2)代入2m y x=,求反比例函数解析式,再求得B 的坐标,将A 与B 两点坐标代入y 1=kx +b ,即可求解;(2)y 1<y 2,在图象中找反比例函数图象在一次函数图象上方的部分即可.【详解】 (1)将点A (﹣4,2)代入2m y x =, ∴m =﹣8,∴y =8x -,将B (n ,﹣4)代入y =8x -,∴n =2,∴B (2,﹣4), 将A (﹣4,2),B (2,﹣4)代入y 1=kx +b ,得到2442k b k b =-+⎧⎨-=+⎩, ∴12k b =-⎧⎨=-⎩, ∴y =﹣x ﹣2,(2)由图象直接可得:x >2或﹣4<x <0;【点睛】本题考查一次函数和反比例函数图象和性质;熟练待定系数法求函数解析式是解题的关键.25.(1)62,53y y x x ==-+(2)454(3)x <-6或-1.5<x <0 【分析】 (1)根据点A 是OC 的中点,可得A (3,2),可得反比例函数解析式为y 1=6x ,根据E (32,4),F (6,1),运用待定系数法即可得到直线EF 的解析式为y=-23x+5; (2)过点E 作EG ⊥OB 于G ,根据点E ,F 都在反比例函数y 1=6x 的图象上,可得S △EOG =S △OBF ,再根据S △EOF =S 梯形EFBG 进行计算即可;(3)根据点E ,F 关于原点对称的点的坐标分别为(-1.5,-4),(-6,-1),可得不等式k 2x-b-1k x>0的解集为:x <-6或-1.5<x <0. 【详解】(1)∵D (0,4),B (6,0),∴C (6,4),∵点A 是OC 的中点,∴A (3,2), 把A (3,2)代入反比例函数y 1=1k x ,可得k 1=6, ∴反比例函数解析式为y 1=6x , 把x=6代入y 1=6x ,可得y=1,则F (6,1), 把y=4代入y 1=6x ,可得x=32,则E (32,4), 把E (32,4),F (6,1)代入y 2=k 2x+b ,可得 2234216k b k b⎧+⎪⎨⎪+⎩==,解得2235k b ⎧-⎪⎨⎪⎩==, ∴直线EF 的解析式为y=-23x+5; (2)如图,过点E 作EG ⊥OB 于G ,∵点E ,F 都在反比例函数y 1=6x 的图象上, ∴S △EOG =S △OBF ,∴S △EOF =S 梯形EFBG =12(1+4)×92=454; (3)由图象可得,点E ,F 关于原点对称的点的坐标分别为(-1.5,-4),(-6,-1), ∴由图象可得,不等式k 2x-b-1k x >0的解集为:x <-6或-1.5<x <0. 【点睛】本题主要考查了反比例函数与一次函数交点问题以及矩形性质的运用,求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解.解题时注意运用数形结合思想得到不等式的解集.26.(1)见解析;(2)2AB =3EF ;(33【分析】(1)根据矩形的性质得出90EAB ABC ∠=∠=︒和∠AEB =∠BAC ,即可证明结论; (2)由(1)的结论,得AB EA BC AB=,即可求出AB 的长,再由勾股定理求出BE 的长,再由△AEF ∽△CBF ,即可求出EF 的长; (3)由△AFE ∽△CFB 得12EF AE BF CB ==,证明3ED EF BE ED==,则△DEF ∽△BED ,即可求出结果.【详解】解:(1)∵四边形ABCD 为矩形,∴90BAE CBA ∠=∠=︒ ,AD ∥BC ,AD =BC ,AB ∥CD ,AB =CD ,∴90BAC CAE ∠+∠=︒,∵BE ⊥AC ,∴90CAE AEB ∠+∠=︒,∴∠AEB =∠BAC ,∴△EAB ∽△ABC ;(2)由(1)知△EAB ∽△ABC ,∴AB EA BC AB=, ∵AD =2,点E 是AD 的中点, ∴AE =1,BC =2, ∴22AB AE BC =⋅=, ∴AB =在Rt △ABE 中,BE =, ∵AD ∥BC ,∴△AEF ∽△CBF , ∴12EF AE BF CB ==,∴13EF BE ==; (3)∵AD ∥BC , ∴△AFE ∽△CFB , ∴12EF AE BF CB ==, ∴3BE EF ==∴ED EF BE ED ==, ∵∠DEB =∠FED , ∴△DEF ∽△BED , ∴DF EF BD ED =,∴DF BD = 【点睛】本题考查相似三角形的性质和判定,解题的关键是掌握相似三角形的性质和判定.。
一、选择题1.如图,在ABC ∆中,E 为BC 边上的一点,F 为AC 边上的一点,连接BF ,AE ,交于点D ,若D 为BF 的中点,CF 2AF =,则:BE CE 的值为( )A .1:2B .1:3C .1:4D .2:32.如图,AB 为⊙O 的直径,AC 交⊙O 于E 点,BC 交⊙O 于D 点,CD =BD ,∠C =70°,现给出以下四个结论:①∠A =45°;②AC =AB ;③AE =BE ;④2CE •AB =BC 2,其中正.确.结论有( )A .1个B .2个C .3个D .4个3.如图,△ABC 、△FGH 中,D 、E 两点分别在AB 、AC 上,F 点在DE 上,G 、H 两点在BC 上,且DE ∥BC ,FG ∥AB ,FH ∥AC ,若BG :GH :HC=4:6:5,则△ADE 与△FGH 的面积比为何?( )A .2:1B .3:2C .5:2D .9:4第II 卷(非选择题)请点击修改第II 卷的文字说明参考答案4.如图,在ABC 中,点D 、E 分别在边AB 、AC 上,则在下列五个条件中:①AED B ∠=∠;②//DE BC ;③AD AEAC AB=;④AD BC DE AC ⋅=⋅,能满足ADE ACB 的条件有( )A .1个B .2个C .3个D .4个5.已知P 是线段AB 的黄金分割点,且51AB =+,则AP 的长为( ).A .2B .51-C .2或51-D .35-6.如图,在△ABC 中,∠ACB =90°,CD ⊥AB ,垂足为D ,延长至点G ,连接BG ,过点A 作AF ⊥BG ,垂足为F ,AF 交CD 于点E ,则下列错误的是( )A .AD ACAC AB= B .AD CDCD BD= C .DE CDCD DG= D .EG BDEF BG= 7.一次函数y kx b =+和反比例函数xby k =的部分图象在同一坐标系中可能为( ) A . B . C . D .8.已知点A (x 1,y 1)、B (x 2,y 2)、C (x 3,y 3)是函数y =﹣2x图象上的点,且x 1<0<x 2<x 3,则y 1,y 2,y 3的大小关系是( ) A .y 1>y 2>y 3B .y 1<y 2<y 3C .y 1>y 3>y 2D .无法确定9.下列函数是y 关于x 的反比例函数的是( ) A .y =11x + B .y =21x C .y =﹣12xD .y =﹣2x 10.反比例函数ky x=经过点(2,1),则下列说法错误..的是( )A .2k =B .函数图象分布在第一、三象限C .当0x >时,y 随x 的增大而增大D .当0x >时,y 随x 的增大而减小11.已知11(,)x y ,22(,)x y , 33(,)x y 是反比例函数2y x=-的图象上的三个点,且120x x <<,30x >,则123,,y y y 的大小关系是( )A .213y y y <<B .312y y y <<C .123y y y <<D .321y y y <<12.如图,双曲线ky x=经过Rt BOC ∆斜边上的中点A ,且与BC 交于点D ,若BOD 6S ∆=,则k 的值为( )A .2B .4C .6D .8二、填空题13.如图,点P 是ABC 的重心,过P 作BC 的平行线,分别交AC ,AB 于点D ,E ,作//DF EB ,交CB 于点F ,若ABC 的面积为227cm ,则DFC △的面积为______2cm .14.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”.如图,P 为AB 的黄金分割点()AP PB >,如果AB 的长度为8cm ,那么AP 的长度是_____________.15.如图,在ABC 中,点D 是线段BC 的黄金分割点(DC BD >),若ABD △的面积是252-,则ABC 的面积是_______.16.若()0a b a c b ck k c b a+++===≠, 则k 的值为______. 17.近视眼镜的度数y (度)与镜片焦距x (米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数y 与镜片焦距x 之间的函数关系式为________.(无需确定x 的取值范围)18.如果一个正比例函数的图像与反比例函数-1y x=交于A (x 1,y 1),B (x 2,y 2),那么(x 1-x 2)(y 1-y 2)=____________.19.如图,反比例函数(0)ky x x=>经过,A B 两点,过点A 作AC y ⊥轴于点C ,过点B 作BD y ⊥轴于点D ,过点B 作轴BE x ⊥于点E ,连接AD ,已知 =2,=2AC BE ,=16BEOD S 矩形,则 ACD S =_____.20.如图,在平面直角坐标系中,反比例函数y=kx(k≠0),经过▱ABCD 的顶点B .D ,点A 的坐标为(0,-1),AB ∥x 轴,CD 经过点(0,2),▱ABCD 的面积是18,则点C 的坐标是______.三、解答题21.如图,AB 是ABC 的内接圆O 的直径,点D 在半圆上,DC 与AB 交于点E ,12∠=∠,过点C 作CF DC ⊥交DB 的延长线于点F ,交圆O 于点G .(1)当105DF =,:1:2AE EC =时,求圆O 的半径.(2)在(2)的条件下,连接DG 交BC 于点M ,则:OMB DGF S S =△△______.(直接写出答案)22.如图,在ABC 中,正方形EFGH 内接于ABC ,点E F 、在边AB 上,点G H 、分别在BC AC 、上,且2EF AE FB =⋅, (1)求证:90C ∠=︒(2)求证:AH CG AE FB ⋅=⋅.23.如图,已知点O 是坐标原点,B 、C 两点的坐标分别为(3,-1),(2,1).(1)以O 点为位似中心在y 轴的左侧将△OBC 放大到原图的2倍(即新图与原图的相似比为2),画出对应的△OB ꞌC ꞌ;(2)若△OBC 内部一点M 的坐标为(a ,b ),则点M 对应点M ′的坐标是 ; (3)求出变化后△OB ꞌC ꞌ的面积 . 24.如图,一次函数y=ax+b 的图象与反比例函数y=kx的图象交于M (-3,1),N (1,n )两点.(1)求这两个函数的表达式;(2)过动点C (m ,0)且垂直于x 轴的直线与一次函数及反比例函数的图象分别交于D 、E 两点,当点E 位于点D 上方时,直接写出m 的取值范围. 25.如图,已知反比例函数y =kx的图象经过点A (4,m ),AB ⊥x 轴,且△AOB 的面积为2. (1)求k 和m 的值;(2)若点C (x ,y )也在反比例函数y =kx的图象上,当-3≤x ≤-1时,求函数值y 的取值范围.26.如图在平面直角坐标系xOy 中,函数14(0)y x x=>的图象与一次函数2y kx k =-的图象的交点为(,2)A m . (1)求一次函数的解析式;(2)设一次函数y kx k =-的图象与y 轴交于点B ,若点P 是x 轴上一点,且满足PAB ∆的面积是6,求点P 的坐标.【参考答案】***试卷处理标记,请不要删除一、选择题 1.B 解析:B 【分析】过点F 作FG//BC 交AE 于点G ,证明DFGDBE ∆∆可得FG BE =,再由//FG BC 可证得13BE GF AF CE CE AC ===,故可得结论. 【详解】解:过点F 作FG//BC 交AE 于点G∵D 是BF 的中点, ∴DB DF = ∵//FG BC ∴DFGDBE ∆∆∴1FG DFBE DB == ∴FG BE = 又∵//FG BC ∴F C EC G AFA = ∵CF 2AF = ∴3AC AF =∴13BE GF AF CE CE AC === 故选:B . 【点睛】此题主要考查了相似三角形的判定与性质以及平行线分线段成比例定理,熟练掌握相关定理与性质是解答此题的关键.2.B解析:B【分析】连结AD、BE,DE,如图,根据圆周角定理得∠ADB=90°,则AD⊥BC,加上CD=BD,根据等腰三角形的判定即可得到AC=AB;再根据等腰三角形的性质和三角形内角和定理可计算出∠BAC=40°;由AB为直径得到∠AEB=90°,则∠ABE=50°,根据圆周角定理可判断AE BE≠;接着证明△CED∽△CBA,利用相似比得到CD CEAC BC=,然后利用等线段代换即可判断④.【详解】解:连接AD,∵AB是⊙O的直径,∴∠ADB=90°.∵CD=BD,∴AD是BC的垂直平分线,∴AC=AB,故②正确;∵AC=AB,∴∠ABC=∠C=70°,∴∠BAC=40°,故①错误;连接BE,DE,∵AB为⊙O的直径,∴∠AEB=90°,∵∠BAC=40°,∴∠ABE=50°,∴∠BAC≠∠ABE,∴AE≠BE,∴AE BE≠,故③错误;∵四边形ABDE是圆内接四边形,∴∠CDE=∠CAB,∴△CDE∽△CAB,∴CD CEAC BC=,∴CE•AC=CD·BC,∴CE•AB=12BC·BC,∴2CE •AB =BC 2,故④正确. 故选B . 【点睛】本题考查了相似三角形的判定和性质,圆周角定理,根据题意作出辅助线,构造出圆周角是解题的关键.3.D解析:D 【解析】分析:只要证明△ADE ∽△FGH ,可得2⎛⎫= ⎪⎝⎭△△FGH ADE S DE S GH ,由此即可解决问题. 详解:∵BG :GH :HC=4:6:5,可以假设BG=4k ,GH=6k ,HC=5k , ∵DE ∥BC ,FG ∥AB ,FH ∥AC ,∴四边形BGFD 是平行四边形,四边形EFHC 是平行四边形,∴DF=BG=4k ,EF=HC=5k ,DE=DF+EF=9k ,∠FGH=∠B=∠ADE ,∠FHG=∠C=∠AED , ∴△ADE ∽△FGH ,∴2299=64ADE FGHS DE k SGH k ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭.故选D .点睛:本题考查相似三角形的判定和性质,平行四边形的判定和性质等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.4.B解析:B 【分析】根据相似三角形的判定逐个判断即可得. 【详解】①在ADE 和ACB △中,AED BA A ∠=∠⎧⎨∠=∠⎩,ADEACB ∴,则条件①能满足;②//DE BC ,ADE ABC ∴,则条件②不能满足;③在ADE 和ACB △中,AD AEAC AB A A⎧=⎪⎨⎪∠=∠⎩,ADEACB ∴,则条件③能满足;④由AD BC DE AC ⋅=⋅得:AD DEAC BC=, 对应的夹角ADE ∠与C ∠不一定相等,∴此时ADE 和ACB △不一定相似,则条件④不能满足;综上,能满足的条件有2个, 故选:B . 【点睛】本题考查了相似三角形的判定,熟练掌握判定方法是解题关键.5.C解析:C 【分析】若点P 是靠近点B 的黄金分割点,则12AP AB =,然后代入数据计算即可;若点P 是靠近点A 的黄金分割点,先求出BP ,再利用线段的和差即可求出AP . 【详解】解:若P 是靠近点B 的黄金分割点,则)12AP AB ===;若P 是靠近点A 的黄金分割点,则)12BP AB ===,∴121AP AB BP =-=-=; 故选:C . 【点睛】是解题的关键. 6.D解析:D 【分析】通过证明△ACD ∽△ABC ,可得AD AC AC AB =,通过证明△ACD ∽△CBD ,可得AD CDCD BD=,通过△ADE ∽△GDB ,△ACD ∽△CBD ,可得DE CDCD DG=,通过证明△GEF ∽△GBD ,可得=EG BGEF BD ,即可求解. 【详解】解:∵CD ⊥AB ,∴∠ADC =∠CDB =90°, ∴∠BCD +∠ABC =90°, ∵∠ACB =90°,∴∠ACD +∠BCD =90°, ∴∠ACD =∠ABC ,又∵∠ACB =∠ADC =90°, ∴△ACD ∽△ABC ,∴AD AC AC AB=, 故A 选项不合题意;∵∠ACD =∠ABC ,∠ADC =∠BDC ,∴△ACD ∽△CBD , ∴AD CD CD BD= 故B 选项不合题意;∵AF ⊥BG ,∴∠AFB =90°,∴∠FAB +∠GBA =90°,∵∠GDB =90°,∴∠G +∠GBA =90°,∴∠G =∠FAB ,又∵∠ADE =∠GDB =90°,∴△ADE ∽△GDB , ∴=AD DE GD BD, ∴AD •BD =DE •DG ,∵△ACD ∽△CBD , ∴=AD CD CD BD, ∴CD 2=AD •BD ,∴CD 2=DE •DG , ∴DE CD CD DG=, 故C 选项不合题意;∵∠G =∠G ,∠EFG =∠GDB =90°,∴△GEF ∽△GBD , ∴=EG BG EF BD故D 选项符合题意,故选:D .【点睛】本题主要考查相似三角形的判定及其性质,解题的关键是熟练掌握相似三角形的判定方法及其性质.7.C解析:C【分析】运用一次函数和反比例函数的图象性质逐项分析即可.先观察反比函数看k 、b 是同号还是异号,再由一次函数图象判断k 、b 是同号还是异号,如果两者相一致就是正确选项,否则是错误选项.【详解】【点睛】 此题考查反比例函数和一次函数的图象特点.其关键是要弄清图象特点与关系式中k 、b 同号还是异号.8.C解析:C【分析】根据反比例函数图象上点的坐标特征得到y 1=12x -,y 2=22x -,y 3=32x -,然后根据x 1<0<x 2<x 3比较y 1,y 2,y 3的大小.【详解】点(x 1,y 1),(x 2,y 2),(x 3,y 3)都是2y x =-的图象上的点, ∴y 1=12x -,y 2=22x -,y 3=32x -, 而x 1<0<x 2<x 3,∴y 1>y 3>y 2.故选:C .【点睛】本题考查了反比例函数图象上点的坐标特征:熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.9.C【分析】直接利用反比例函数的定义分别判断得出答案.【详解】解:A 、y =11x +是y 与x+1成反比例,故此选项不合题意; B 、y =21x,是y 与x 2成反比例,不符合反比例函数的定义,故此选项不合题意; C 、y =﹣12x ,符合反比例函数的定义,故此选项符合题意; D 、y =﹣2x 是正比例函数,故此选项不合题意. 故选:C .【点睛】本题考查了反比例函数的定义,正确把握定义是解题的关键.10.C解析:C【分析】将点(2,1)代入k y x=中求出k 值,再根据反比例函数的性质对四个选项逐一分析即可. 【详解】 将点(2,1)代入k y x=中,解得:k=2, A .k=2,此说法正确,不符合题意; B .k=2﹥0,反比例函数图象分布在第一、三象限,此书说法正确,不符合题意; C .k=2﹥0且x ﹥0,函数图象位于第一象限,且y 随x 的增大而减小,此说法错误,符合题意;D .k=2﹥0且x ﹥0,函数图象位于第一象限,且y 随x 的增大而减小,此说法正确,不符合题意;故选:C .【点睛】本题考查了反比例函数的性质,熟练掌握反比例函数的性质,理解函数图象上的点与解析式的关系是解答的关键.11.B解析:B【分析】 先根据反比例函数2y x=-的系数20-<判断出函数图象在二、四象限,在每个象限内,y 随x 的增大而增大,再根据120x x <<,30x >,判断出1y 、2y 、3y 的大小.解:反比例函数2y x=-中,20k =-<, ∴此函数的图象在二、四象限,在每一象限内y 随x 的增大而增大,∵120x x <<,30x >30y ,210y y >>,∴312y y y <<,故选:B .【点睛】本题考查了二次函数图象上点的坐标特征.用到的知识点为:k 0<时,反比例函数k y x=图象的分支在二、四象限,在第四象限的函数值总小于在第二象限的函数值;在同一象限内,y 随x 的增大而增大. 12.B解析:B【分析】 设,k A x x ⎛⎫ ⎪⎝⎭,根据A 是OB 的中点,可得22,k B x x ⎛⎫ ⎪⎝⎭,再根据BC OC ⊥,点D 在双曲线k y x =上,可得2,2k D x x ⎛⎫ ⎪⎝⎭,根据三角形面积公式列式求出k 的值即可. 【详解】 设,k A x x ⎛⎫ ⎪⎝⎭ ∵A 是OB 的中点 ∴22,k B x x ⎛⎫ ⎪⎝⎭∵BC OC ⊥,点D 在双曲线k y x =上 ∴2,2k D x x ⎛⎫ ⎪⎝⎭∴BOD 112322222k k S BD OC x k x x ∆⎛⎫=⨯⨯=⨯-⨯= ⎪⎝⎭ ∵BOD 6S ∆= ∴3642k =÷= 故答案为:B .【点睛】 本题考查了反比例函数的几何问题,掌握反比例函数的性质、中点的性质、三角形面积公式是解题的关键.二、填空题13.3【分析】连接AP并延长交BC于G由重心的性质得AP:PG=2:1由DE//BC根据平行线分线段成比例定理可得AD:DC=AP:PG=2:1于是CD:AC=1:3再由DF//AB得出△DFC∽△AB解析:3【分析】连接AP并延长交BC于G.由重心的性质得,AP:PG=2:1.由DE//BC,根据平行线分线段成比例定理可得AD:DC=AP:PG=2:1,于是CD:AC=1:3.再由DF//AB,得出△DFC∽△ABC,根据相似三角形的性质得出S△DFC:S△ABC=1:9.【详解】解:连接AP并延长交BC于G.由重心的性质得,AP:PG=2:1.∵DE//BC,∴AD:DC=AP:PG=2:1,∴CD:AC=1:3.∵DF//AB,∴△DFC∽△ABC,∴S△DFC:S△ABC=1:9,∴S△DFC=1×S△ABC=3cm2.9故答案为:3.【点睛】本题考查了三角形重心的性质,平行线分线段成比例定理,相似三角形的判定与性质,难度适中.准确作出辅助线是解题的关键.14.()cm【分析】利用黄金分割的定义计算出AP【详解】为的黄金分割点故答案为:()cm【点睛】此题考查黄金分割的定义黄金分割物体的较大部分等于与整体的解析:(454)cm【分析】利用黄金分割的定义计算出AP.【详解】P 为AB 的黄金分割点()AP PB >,()118422AP AB cm ∴==⨯=故答案为:(4)cm.【点睛】. 15.【分析】根据黄金分割的定义以及等高的两个三角形面积之比等于底之比即可求出的面积【详解】解:∵在中点是线段的黄金分割点()∴∵的面积是∴的面积故答案为:【点睛】本题考查了黄金分割的概念也考查了三角形的解析:2【分析】根据黄金分割的定义,以及等高的两个三角形面积之比等于底之比,即可求出ABC 的面积.【详解】解:∵在ABC 中,点D 是线段BC 的黄金分割点(DC BD >),∴BD BC 1==: ∵ABD △的面积是2∴ABC 的面积()22==故答案为:2.【点睛】本题考查了黄金分割的概念,也考查了三角形的面积公式,解题的关键是正确理解黄金分割的概念.16.或2【分析】根据等式的性质可得2(a+b+c )=k (a+b+c )根据因式分解可得a+b+c=0或k=2根据分式的性质可得答案【详解】解:由得b+c=ak①a+c=bk②a+b=ck③①+②+③得2(解析:1-或2【分析】根据等式的性质,可得2(a+b+c )=k (a+b+c ),根据因式分解,可得a+b+c=0或k=2,根据分式的性质,可得答案.【详解】 解:由()0a b a c b c k k c b a+++===≠,得 b+c=ak ①,a+c=bk ②,a+b=ck ③,①+②+③,得2(a+b+c )=k (a+b+c ),移项,得2(a+b+c )-k (a+b+c )=0,因式分解,得(a+b+c )(2-k )=0a+b+c=0或k=2,当0a b c ++=时,a b c +=-,1a b c k c c+-===-, ∴1k =-或2.故答案为:1-或2.【点睛】本题考查了比例的性质,利用等式的性质得出2(a+b+c )=k (a+b+c )是解题关键,又利用了分式的性质.17.【解析】根据题意得xy =025×400=100∴ 解析:100y x =【解析】根据题意得xy =0.25×400=100,∴100y x=. 18.-4【分析】由AB 为正比例函数的图像与反比例函数的交点则其坐标关于原点对称所以可得x1=-x2y1=-y2最后替换后计算即可【详解】解:∵A (x1y1)B (x2y2)为上的点∴x1y1=-1x2y2解析:-4【分析】由A 、B 为正比例函数的图像与反比例函数-1y x =的交点,则其坐标关于原点对称,所以可得x 1=-x 2,y 1=-y 2,最后替换后计算即可.【详解】解:∵A (x 1,y 1),B (x 2,y 2)为-1y x =上的点 ∴x 1y 1=-1, x 2y 2=-1,∵正比例函数的图像与反比例函数-1y x=的两交点A (x 1,y 1),B (x 2,y 2) ∴A 、B 关于原点对称,∴x 1=-x 2,y 1=-y 2,∴(x 1-x 2)(y 1-y 2)=(-x 2-x 2)(-y 2-y 2)=-2 x 2 (-2 y 2)=4 x 2y 2=-4故答案为-4.【点睛】本题考查了反比例函数与正比例函数的交点问题,掌握正比例函数与反比例函数的两交点坐标关于原点对称是解答本题的关键.19.【分析】过点A 作AH ⊥x 轴于点H 交BD 于点F 则四边形ACOH 和四边形ACDF 均为矩形根据S 矩形BEOD=16可得k 的值即可得到矩形ACOH 和矩形ACDF 的面积进而求出S △ACD 【详解】解:过点A 作A解析:6【分析】过点A 作AH ⊥x 轴于点H ,交BD 于点F ,则四边形ACOH 和四边形ACDF 均为矩形,根据S 矩形BEOD =16,可得k 的值,即可得到矩形ACOH 和矩形ACDF 的面积,进而求出S △ACD .【详解】解:过点A 作AH ⊥x 轴于点H ,交BD 于点F ,则四边形ACOH 和四边形ACDF 均为矩形∵S 矩形BEOD =16,反比例函数()0k y x x=>经过点B ∴k=16 ∵反比例函数()0k y x x=>经过点A ∴S 矩形ACOH =16∵AC=2∴OC=16÷2=8 ∴CD=OC-OD=OC-BE=8-2=6∴S 矩形ACDF =2×6=12∴S △ACD =12S 矩形ACDF =12×12=6. 故答案为6.【点睛】 本题主要考查了反比例函数系数k 的几何意义和性质. 通过矩形的面积求出k 的值是解本题的关键.20.(32)【分析】如图先求出AE 的长再根据平行四边形的面积可求出ABCD的长从而可知点B 坐标然后利用待定系数法可求出反比例函数的解析式最后利用函数解析式可求出点D 坐标从而根据CD 的长可求出点C 的横坐标 解析:(3,2)【分析】如图,先求出AE 的长,再根据平行四边形的面积可求出AB 、CD 的长,从而可知点B 坐标,然后利用待定系数法可求出反比例函数的解析式,最后利用函数解析式可求出点D 坐标,从而根据CD 的长可求出点C 的横坐标,即可得出答案.【详解】如图,由题意得,2(1)3,,AE AE AB AB CD =--=⊥=,点C 、D 纵坐标均为2 ABCD S AE AB AE CD ∴=⋅=⋅,即3318AB CD ==解得6AB CD ==∴点B 坐标为(6,1)B -将点(6,1)B -代入反比例函数的解析式得16k =- 解得6k =-则反比例函数的解析式为6y x =-令2y =得62x-=,解得3x =- (3,2)D ∴-设点C 坐标为(,2)C a(3)6CD a ∴=--=,解得3a =(3,2)C ∴故答案为:(3,2).【点睛】本题考查了平行四边形的面积、利用待定系数法求反比例函数的解析式等知识点,根据平行四边形的面积求出AB 的长,从而得出点B 坐标是解题关键.三、解答题21.(1)254;(2)544【分析】(1)连接AD,利用“HL”证明Rt△ADB≅Rt△ACB,推出AB⊥DC,DE=CE,再证明BE为△DCF 的中位线,利用锐角三角函数的定义得到AD1BD2=,再利用勾股定理即可求得⊙O 的半径;(2)同理先求得DE=5, DC=10,利用勾股定理可求得CG=152,证明△OBM~△GCM,推出56OMMG=,推出OBMGBM56SS=,设OBM5S a=,则GBM6S a=,利用三角形的中线平分此三角形的面积,即可推出DGF44S a=,即可求得答案.【详解】(1)连接AD,∵∠1=∠2,∴AD=AC,∵AB为⊙O的直径,∴∠ADB=∠ACB=90︒,∴Rt△ADB≅Rt△ACB(HL),∴DB=CB,∠1=∠3,∴AB⊥DC,∴DE=CE,∵CF⊥DC,∴BE∥FC,∴BE为△DCF的中位线,∴DB=12DF=5∵AE:EC=1:2,∴AE AD1tan3tan1EC BD2∠∠====,∴552∴()222252555522AD BD⎛⎫+=+=⎪⎝⎭,∴⊙O的半径为254;(2)连接BG ,∵CF ⊥DC ,∴∠ACG=90︒,∴DG 为⊙O 的直径, ∵DE 1tan 3EB 2∠==, ∴EB=2DE ,∵222DE EB BD +=,即(222455DE DE +=, ∴DE=5,则DC=2DE=10, ∵222DC CG GD +=,即22225102CG ⎛⎫+= ⎪⎝⎭, ∴CG=152, ∵BO ∥GC ,∴△OBM ~△GCM , ∴OM OB MG CG=, 则25541562OM OB MG CG ===, ∴OBM GBM 56S S =, 设OBM 5Sa =,则GBM 6S a =, ∴GBO 5611Sa a a =+=, ∵点O 为直径DG 的中点, ∴DBO GBO 11SS a ==, ∴DBG GBO 222S S a ==, ∵点B 为线段DF 的中点,DGF DBG 244S S a ==,∴OBM DGF 554444S a S a ==. 故答案为:544. 【点睛】 本题考查了圆周角定理,相似三角形的判定和性质,勾股定理的应用,三角形中位线的判定和性质,三角形的中线的性质等知识点,解题的关键是灵活运用所学知识解决问题. 22.(1)证明见解析(2)证明见解析【分析】(1)由已知可得RT △AEH ∽RT △GFB ,从而可得∠A+∠B=∠FGB+∠B=90°,进一步得到∠C=180°-90°=90°;(2)根据由(1)所得RT △AEH ∽RT △HCG 的性质和已知条件可以得到解答.【详解】(1)证明:由已知,EF=EH=GF ,∴由2EF AE FB =⋅可得:AE EF EF FB =,即AE EH GF FB=, 又四边形 EFGH 是正方形 ,∴∠AEH=∠GFB=90°,∴RT △AEH ∽RT △GFB ,∴∠A=∠FGB ,∴∠A+∠B=∠FGB+∠B=90°,∴∠C=180°-90°=90°; (2)∵四边形 EFGH 是正方形 ,∴HG ∥AB ,∴∠A=∠CHG ,又∠AEH=∠C=90°,∴RT △AEH ∽RT △HCG ,∴,?·AH EH AH CG HG EH HG GC==, 由已知得:EF=EH=GH ,∴2··AH CG EF AE FB ==.【点睛】本题考查正方形与相似三角形的综合应用,灵活运用相似三角形的判定和性质是解题关键.23.(1)见解析;(2)(-2a ,-2b );(3)10【分析】(1)把B 、C 的横纵坐标都乘以-2得到B′、C′的坐标,然后描点即可;(2)利用(1)中对应点的关系求解;(3)先计算△OBC 的面积,然后利用相似的性质把△OBC 的面积乘以4得到△OB ꞌC ꞌ的面积.【详解】(1)如下图,△OB ꞌC ꞌ为所作;(2)点M 对应点M ′的坐标为(-2a ,-2b );(3)''11144(23212131)10222OB C OCB S S ∆∆==⨯⨯-⨯⨯-⨯⨯-⨯⨯=. 【点睛】本题考查了作图、位似变换,熟练应用以原点为位似中心的两位似图形对应点的坐标的关系确定变换后对应点的坐标,然后描点得到变换后的图形.24.(1)y=3x -;2y x =--;(2)m >1或-3<m <0 【分析】(1)把M 代入反比例函数的解析式即可求得k 的值,然后求得n 的值,利用待定系数法即可求得一次函数的解析式;(2)先画出两函数的图象,再根据两函数图象的上下位置关系结合交点的横坐标即可得出m 的取值范围.【详解】(1)∵点M (-3,1)和N (1,n )在反比例函数k y x =的图象上, ∴3k =-,3n =-.∴反比例函数表达式为3x=-, 点N 的坐标为N (1,3-),∵点M (-3,1)和N (1,3-)在一次函数y ax b =+的图象上,∴313a b a b -+=⎧⎨+=-⎩, 解得12a b =-⎧⎨=-⎩, ∴一次函数表达式为2y x =--; (2)一次函数2y x =--的图象与反比例函数3y x =-的图象相交于点M (-3,1)和N (1,3-),观察函数图象可知:若过动点C (m ,0)且垂直于x 轴的直线分别与反比例函数图象和一次函数图象交于E 、D 两点,当点E 位于点D 上方时,则m 的取值范围是:m >1或-3<m <0.【点睛】本题是反比例函数与一次函数的综合题,考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征以及待定系数法求函数解析式,根据两函数图象的上下位置关系找出不等式的解集是解题的关键.25.(1) k =4, m =1;(2)当-3≤x ≤-1时,y 的取值范围为-4≤y ≤-43. 【详解】试题分析:(1)根据反比例函数系数k 的几何意义先得到k 的值,然后把点A 的坐标代入反比例函数解析式,可求出k 的值;(2)先分别求出x=﹣3和﹣1时y 的值,再根据反比例函数的性质求解.试题(1)∵△AOB 的面积为2,∴k=4,∴反比例函数解析式为4y x =,∵A (4,m ),∴m=44=1; (2)∵当x=﹣3时,y=﹣43; 当x=﹣1时,y=﹣4,又∵反比例函数4y x =在x <0时,y 随x 的增大而减小,∴当﹣3≤x≤﹣1时,y 的取值范围为﹣4≤y≤﹣43. 考点:反比例函数系数k 的几何意义;反比例函数图象上点的坐标特征.26.(1)22y x =-;(2)(4,0),(2,0)-.【分析】(1)将点A 的坐标代入反比例函数解析式中即可求出m ,然后将点A 的坐标代入一次函数解析式中即可求出结论;(2)将三角形以x 轴为分界线,分为两个三角形,先求出点C 和点B 的坐标,再把两个三角形的面积相加即可求出CP 的长,从而求出结论.【详解】(1)根据题意,将点(,2)A m 代入4y x=, 得:42m=, 解得:2m =,即点(2,2)A , 将点(2,2)A 代入y kx k =-,得:22k k =-,解得:2k =,∴一次函数的解析式为22y x =-;(2)如图,将y=0代入22y x =-,解得x=1;将x=0代入22y x =-,解得y=-2;∴一次函数22y x =-与x 轴的交点为(1,0)C ,与y 轴的交点为(0,2)B -,ABP ACP BPC S S S ∆∆∆=+,∴1122622CP CP ⨯+⨯=, 解得3CP =,则P 点坐标为(4,0),(2,0)-.【点睛】本题考查了反比例函数与一次函数的交点问题,求出函数解析式并熟悉点的坐标与图形的关系是解题的关键.。
【必考题】初三数学下期中第一次模拟试卷(及答案)(1)一、选择题1.下列说法正确的是( )A .小红小学毕业时的照片和初中毕业时的照片相似B .商店新买来的一副三角板是相似的C .所有的课本都是相似的D .国旗的五角星都是相似的2.如图,123∠∠∠==,则图中相似三角形共有( )A .1对B .2对C .3对D .4对 3.已知点C 在线段AB 上,且点C 是线段AB 的黄金分割点(AC >BC ),则下列结论正确的是( )A .AB 2=AC •BC B .BC 2=AC •BC C .AC =512-BCD .BC =512-AC 4.如图,过反比例函数的图像上一点A 作AB ⊥轴于点B ,连接AO ,若S △AOB =2,则的值为( )A .2B .3C .4D .5 5.如果两个相似三角形对应边之比是1:3,那么它们的对应中线之比是( )A .1:3B .1:4C .1:6D .1:9 6.在同一直角坐标系中,函数k y x=和y=kx ﹣3的图象大致是( ) A . B . C .D .7.如图,△ABC 中AB 两个顶点在x 轴的上方,点C 的坐标是(﹣1,0),以点C 为位似中心,在x 轴的下方作△ABC 的位似图形△A′B′C′,且△A′B′C′与△ABC 的位似比为2:1.设点B 的对应点B′的横坐标是a ,则点B 的横坐标是( )A .12a -B .1(1)2a -+C .1(1)2a --D .1(3)2a -+ 8.图(1)所示矩形ABCD 中,BC x =,CD y =,y 与x 满足的反比例函数关系如图(2)所示,等腰直角三角形AEF 的斜边EF 过点C ,M 为EF 的中点,则下列结论正确的是( )A .当3x =时,EC EM <B .当9y =时,EC EM <C .当x 增大时,EC CF ⋅的值增大D .当x 增大时,BE DF ⋅的值不变9.若△ABC ∽△A′B′C′且34AB A B ='',△ABC 的周长为15cm ,则△A′B′C′的周长为( )cm.A .18B .20C .154D .80310.如图,小明同学用自制的直角三角形纸板DEF 测量树的高度AB ,他调整自己的位置,设法使斜边DF 保持水平,并且边DE 与点B 在同一直线上.已知纸板的两条边DF =50cm ,EF =30cm ,测得边DF 离地面的高度AC =1.5m ,CD =20m ,则树高AB 为( )A.12m B.13.5m C.15m D.16.5m11.如图,在△ABC中,M是AC的中点,P,Q为BC边上的点,且BP=PQ=CQ,BM与AP,AQ分别交于D,E点,则BD∶DE∶EM等于A.3∶2∶1B.4∶2∶1C.5∶3∶2D.5∶2∶112.如图,一张矩形纸片ABCD的长BC=xcm,宽AB=ycm,以宽AB为边剪去一个最大的正方形ABEF,若剩下的矩形ECDF与原矩形ABCD相似,则xy的值为()A.512-B.512+C.2D.212+二、填空题13.如图,P(m,m)是反比例函数9yx=在第一象限内的图象上一点,以P为顶点作等边△PAB,使AB落在x轴上,则△POB的面积为_____.14.如图,已知一次函数y=kx﹣3(k≠0)的图象与x轴,y轴分别交于A,B两点,与反比例函数y=12x(x>0)交于C点,且AB=AC,则k的值为_____.15.如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,23),C 是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线垂直时,点P的坐标为____16.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左侧墙上与地面成60°角时,梯子顶端距离地面23米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为_____米(结果保留根号).17.将一副三角板按如图1位置摆放,使得两块三角板的直角边AC和MD重合.已知AB="AC=8" cm,将△MED绕点A(M)逆时针旋转60°后(图2),两个三角形重叠(阴影)部分的面积是 cm2.18.小华为了求出一个圆盘的半径,他用所学的知识,将一宽度为2cm的刻度尺的一边与圆盘相切,另一边与圆盘边缘两个交点处的读数分别是“4”和“16”(单位:cm),请你帮小华算出圆盘的半径是_____cm.19.小刚身高1.7m ,测得他站立在阳光下的影子长为0.85m ,紧接着他把手臂竖直举起,测得影子长为1.1m ,那么小刚举起的手臂超出头顶的高度为________m .20.如图是一个圆柱体的三视图,由图中数据计算此圆柱体的侧面积为________.(结果保留π)三、解答题21.已知:如图,四边形ABCD 的对角线AC 和BD 相交于点E ,AD=DC ,DC 2=DE•DB ,求证:(1)△BCE ∽△ADE ;(2)AB•BC=BD•BE .22.如图,在△ABC 中,∠B=90°,AB=4,BC=2,以AC 为边作△ACE ,∠ACE=90°,AC=CE ,延长BC 至点D ,使CD=5,连接DE .求证:△ABC ∽△CED .23.如图,在ABC V 中,AB AC =,点E 在边BC 上移动(点E 不与点B ,C 重合),满足DEF B ∠=∠,且点D 、F 分别在边AB 、AC 上.(1)求证:BDE CEF △∽△.(2)当点E 移动到BC 的中点时,求证:FE 平分DFC ∠.24.如图,AB与CD相交于点O,△OBD∽△OAC,ODOC=35,OB=6,S△AOC=50,求:(1)AO的长;(2)求S△BOD25.如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E、F.求证:四边形AFGE与四边形ABCD相似.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【解析】【分析】观察图形,看它们的形状是否相同,形状相同的两个图形是相似图形.【详解】A.小明上幼儿园时的照片和初中毕业时的照片,形状不相同,不相似;B.商店新买来的一副三角板,形状不相同,不相似;C.所有的课本都是相似的,形状不相同,不相似;D .国旗的五角星都是相似的,形状相同,相似.故选D .【点睛】本题考查了相似图形,相似图形是指形状相同的图形,仔细观察看每组图形是否相同,如果相同就相似,否则就不相似.2.D解析:D【解析】【分析】根据已知及相似三角形的判定定理,找出题中存在的相似三角形即可.【详解】∵∠1=∠2,∠C =∠C ,∴△ACE ∽△ECD ,∵∠2=∠3,∴DE ∥AB ,∴△BCA ∽△ECD ,∵△ACE ∽△ECD ,△BCA ∽△ECD ,∴△ACE ∽△BCA ,∵DE ∥AB ,∴∠AED =∠BAE ,∵∠1=∠2,∴△AED ∽△BAE ,∴共有4对,故此选D 选项.【点睛】本题考查学生对相似三角形判断依据的理解掌握,也考察学生的看图分辨能力.3.D解析:D【解析】【分析】根据黄金分割的定义得出BC AC AC AB ==,从而判断各选项. 【详解】∵点C 是线段AB 的黄金分割点且AC >BC ,∴12BC AC AC AB ==,即AC 2=BC•AB,故A 、B 错误;∴AC=12AB ,故C 错误;AC ,故D 正确; 故选D .【点睛】本题考查了黄金分割,掌握黄金分割的定义和性质是解题的关键.4.C解析:C【解析】试题分析:观察图象可得,k >0,已知S △AOB =2,根据反比例函数k 的几何意义可得k=4,考点:反比例函数k的几何意义.5.A解析:A【解析】∵两个相似三角形对应边之比是1:3,∴它们的对应中线之比为1:3.故选A.点睛: 本题考查相似三角形的性质,相似三角形的对应边、对应周长,对应高、中线、角平分线的比,都等于相似比,掌握相似三角形的性质及灵活运用它是解题的关键.6.A解析:A【解析】【分析】根据一次函数和反比例函数的特点,k≠0,所以分k>0和k<0两种情况讨论.当两函数系数k取相同符号值,两函数图象共存于同一坐标系内的即为正确答案.【详解】分两种情况讨论:①当k>0时,y=kx﹣3与y轴的交点在负半轴,过一、三、四象限,反比例函数的图象在第一、三象限,没有图像符合要求;②当k<0时,y=kx﹣3与y轴的交点在负半轴,过二、三、四象限,反比例函数的图象在第二、四象限,A符合要求.故选A.【点睛】本题考查了反比例函数的图象性质和一次函数的图象性质,关键是由k的取值确定函数所在的象限.7.D解析:D【解析】【分析】设点B的横坐标为x,然后表示出BC、B′C的横坐标的距离,再根据位似变换的概念列式计算.【详解】设点B的横坐标为x,则B、C间的横坐标的长度为﹣1﹣x,B′、C间的横坐标的长度为a+1,∵△ABC放大到原来的2倍得到△A′B′C,∴2(﹣1﹣x)=a+1,解得x=﹣12(a+3),【点睛】本题考查了位似变换,坐标与图形的性质,根据位似变换的定义,利用两点间的横坐标的距离等于对应边的比列出方程是解题的关键.8.D解析:D【解析】【分析】由于等腰直角三角形AEF的斜边EF过C点,则△BEC和△DCF都是直角三角形;观察反比例函数图像得出反比例函数解析式为y=9x;当x=3时,y=3,即BC=CD=3,根据等腰直角三角形的性质得,CF=3,则C点与M点重合;当y=9时,根据反比例函数的解析式得x=1,即BC=1,CD=9,所以,而;利用等腰直角三角形的性质BE•DF=BC•CD=xy,然后再根据反比例函数的性质得BE•DF=9,其值为定值;由于x=2xy,其值为定值.【详解】解:因为等腰直角三角形AEF的斜边EF过C点,M为EF的中点,所以△BEC和△DCF都是直角三角形;观察反比例函数图像得x=3,y=3,则反比例解析式为y=9x.A、当x=3时,y=3,即BC=CD=3,所以,,C点与M点重合,则EC=EM,所以A选项错误;B、当y=9时,x=1,即BC=1,CD=9,所以,,,所以B选项错误;C、因为x y=2×xy=18,所以,EC•CF为定值,所以C选项错误;D、因为BE•DF=BC•CD=xy=9,即BE•DF的值不变,所以D选项正确.故选:D.【点睛】本题考查了动点问题的函数图像:先根据几何性质得到与动点有关的两变量之间的函数关系,然后利用函数解析式和函数性质画出其函数图像,注意自变量的取值范围.9.B解析:B【解析】∵△ABC∽△A′B′C′,∴34 ABC ABA B C A B''=''='VV的周长的周长,∵△ABC的周长为15cm,∴△A′B′C′的周长为20cm.故选B.10.D解析:D【解析】利用直角三角形DEF 和直角三角形BCD 相似求得BC 的长后加上小明同学的身高即可求得树高AB .【详解】∵∠DEF=∠BCD=90°,∠D=∠D ,∴△DEF ∽△DCB , ∴BC DC EF DE=, ∵DF=50cm=0.5m ,EF=30cm=0.3m ,AC=1.5m ,CD=20m ,∴由勾股定理求得DE=40cm ,∴200.30.4BC =, ∴BC=15米,∴AB=AC+BC=1.5+15=16.5(米).故答案为16.5m .【点睛】本题考查了相似三角形的应用,解题的关键是从实际问题中整理出相似三角形的模型.11.C解析:C 【解析】 【分析】过A 作AF ∥BC 交BM 延长线于F ,设BC=3a ,则BP=PQ=QC=a ;根据平行线间的线段对应成比例的性质分别求出BD 、BE 、BM 的长度,再来求BD ,DE ,EM 三条线段的长度,即可求得答案.【详解】过A 作AF ∥BC 交BM 延长线于F ,设3BC a =,则BP PQ QC a ===;∵AM CM =,AF ∥BC ,∴1AF AM BC CM==, ∴3AF BC a ==,∵AF ∥BP ,∴133BD BP a DF AF a ===,∴34DF BF BD ==, ∵AF ∥BQ , ∴2233BE BQ a EF AF a ===, ∴23EF BE =,即25BF BE =, ∵AF ∥BC , ∴313BM BC a MF AF a===, ∴BM MF =,即2BF BM =, ∴235420BF BF BF DE BE BD =-=-=,22510BF BF BF EM BM BE =-=-=, ∴3::::?53242010BF BF BF BD DE EM ==::. 故选:C .【点睛】 本题考查了平行线分线段成比例定理以及比例的性质,正确作出辅助线是关键.12.B解析:B【解析】【分析】根据相似多边形对应边的比相等,可得到一个方程,解方程即可求得.【详解】∵四边形ABCD 是矩形,∴AD =BC =xcm ,∵四边形ABEF 是正方形,∴EF =AB =ycm ,∴DF =EC =(x ﹣y )cm ,∵矩形FDCE 与原矩形ADCB 相似,∴DF :AB =CD :AD , 即:x y y y x-=∴x y 故选B .【点睛】本题考查了相似多边形的性质、矩形的性质、翻折变换的性质;根据相似多边形对应边的比相等得出方程是解决本题的关键.二、填空题13.【解析】【详解】如图过点P作PH⊥OB于点H∵点P(mm)是反比例函数y=在第一象限内的图象上的一个点∴9=m2且m>0解得m=3∴PH=OH=3∵△PAB 是等边三角形∴∠PAH=60°∴根据锐角三解析:9332+.【解析】【详解】如图,过点P作PH⊥OB于点H,∵点P(m,m)是反比例函数y=9x在第一象限内的图象上的一个点,∴9=m2,且m>0,解得,m=3.∴PH=OH=3.∵△P AB是等边三角形,∴∠P AH=60°.∴根据锐角三角函数,得AH=3.∴OB=3+3∴S△POB=12OB•PH=9332+.14.k=【解析】试题分析:如图:作CD⊥x轴于D则OB∥CD∴△AOB∽△ADC∴∵AB=AC∴OB=CD由直线y=kx﹣3(k≠0)可知B(0﹣3)∴OB=3∴CD=3把y=3代入y=(x>0)解得x解析:k=3 2【解析】试题分析:如图:作CD⊥x轴于D,则OB∥CD,∴△AOB∽△ADC,∴,∵AB=AC,∴OB=CD,由直线y=kx﹣3(k≠0)可知B(0,﹣3),∴OB=3,∴CD=3,把y=3代入y=(x>0)解得,x=4,∴C(4,3),代入y=kx ﹣3(k≠0)得,3=4k ﹣3,解得k=, 故答案为.考点:反比例函数与一次函数的交点问题.15.(1)【解析】【分析】先根据题意求得CD 和PE 的长再判定△EPC ∽△PDB 列出相关的比例式求得DP 的长最后根据PEDP 的长得到点P 的坐标【详解】由题意可知OB=2AO=8∵CD ⊥BOC 是AB 的中点∴解析:(1,3)【解析】【分析】先根据题意求得CD 和PE 的长,再判定△EPC ∽△PDB ,列出相关的比例式,求得DP 的长,最后根据PE 、DP 的长得到点P 的坐标.【详解】由题意可知,OB=23,AO=8,∵CD ⊥BO ,C 是AB 的中点,∴BD=DO=12BO==PE ,CD=12AO=4. 设DP=a ,则CP=4﹣a ,当BP 所在直线与EC 所在直线第一次垂直时,∠FCP=∠DBP , 又∵EP ⊥CP ,PD ⊥BD ,∴∠EPC=∠PDB=90°, ∴△EPC ∽△PDB.DP DB PE PC ∴= 343a =-, ∴a 1=1,a 2=3(舍去).∴DP=1,∵3,∴P (13.考点:1相似三角形性质与判定;2平面直角坐标系.16.【解析】【分析】本题需要分段求出巷子被分成的两部分再加起来即可先在直角三角形ABC中用正切和正弦分别求出BC和AC(即梯子的长度)然后再在直角三角形DCE中用∠DCE的余弦求出DC然后把BC和DC加解析:222【解析】【分析】本题需要分段求出巷子被分成的两部分,再加起来即可.先在直角三角形ABC中,用正切和正弦,分别求出BC和AC(即梯子的长度),然后再在直角三角形DCE中,用∠DCE 的余弦求出DC,然后把BC和DC加起来即为巷子的宽度.【详解】解:如图所示:3米,∠ACB=60°,∠DCE=45°,AC=CE.则在直角三角形ABC中,ABBC=tan∠ACB=tan60°3AB AC =sin∠ACB=sin60°3∴BC3233=2,AC32332=4,∴直角三角形DCE中,CE=AC=4,∴CDCE=cos45°=2,∴CD=CE×22=4×22=22,∴BD=2+22,故答案为:2+22.【点睛】本题需要综合应用正切、正弦.余弦来求解,注意梯子长度不变,属于中档题.17.【解析】【分析】分析:设BCAD交于点G过交点G作GF⊥AC与AC交于点F根据AC=8就可求出GF的长从而求解【详解】解:设BCAD交于点G过交点G 作GF⊥AC与AC交于点F设FC=x则GF=FC=解析:48-163【解析】【分析】分析:设BC,AD交于点G,过交点G作GF⊥AC与AC交于点F,根据AC=8,就可求出GF的长,从而求解.【详解】解:设BC,AD交于点G,过交点G作GF⊥AC与AC交于点F,设FC=x,则GF=FC=x,∵旋转角为60°,即可得∠FAG=60°,∴AF=GFcot∠FAG=33x.所以x+3x=8,则x=12-43.所以S△AGC=12×8×(12-43)=48-16318.10【解析】【分析】如图先利用垂径定理得BD=6再利用勾股定理建立方程求解即可得出结论【详解】如图记圆的圆心为O连接OBOC交AB于D∴OC⊥ABBD=AB由图知AB=16﹣4=12cmCD=2cm解析:10【解析】【分析】如图,先利用垂径定理得,BD=6,再利用勾股定理建立方程求解即可得出结论.【详解】如图,记圆的圆心为O,连接OB,OC交AB于D,∴OC⊥AB,BD=12 AB,由图知,AB=16﹣4=12cm,CD=2cm,∴BD=6,设圆的半径为r,则OD=r﹣2,OB=r,在Rt△BOD中,根据勾股定理得,OB2=AD2+OD2,∴r2=36+(r﹣2)2,∴r=10cm,故答案为10.【点睛】本题考查了垂径定理的应用,勾股定理,正确添加辅助线构造出直角三角形是解本题的关键.19.5【解析】【分析】根据同一时刻身长和影长成比例求出举起手臂之后的身高与身高做差即可解题【详解】解:设举起手臂之后的身高为x由题可得:17:085=x:11解得x=22则小刚举起的手臂超出头顶的高度为解析:5【解析】【分析】根据同一时刻身长和影长成比例,求出举起手臂之后的身高,与身高做差即可解题.【详解】解:设举起手臂之后的身高为x由题可得:1.7:0.85=x:1.1,解得x=2.2,则小刚举起的手臂超出头顶的高度为2.2-1.7=0.5m【点睛】本题考查了比例尺的实际应用,属于简单题,明确同一时刻的升高和影长是成比例的是解题关键.20.24π【解析】解:由图可知圆柱体的底面直径为4高为6所以侧面积=4π×6=24π故答案为24π点睛:本题考查了立体图形的三视图和学生的空间想象能力圆柱体的侧面积公式根据主视图判断出圆柱体的底面直径与解析:24π【解析】解:由图可知,圆柱体的底面直径为4,高为6,所以,侧面积=4π×6=24π.故答案为24π.点睛:本题考查了立体图形的三视图和学生的空间想象能力,圆柱体的侧面积公式,根据主视图判断出圆柱体的底面直径与高是解题的关键.三、解答题21.(1)见解析;(2)见解析.【解析】【分析】(1)由∠DAC=∠DCA,对顶角∠AED=∠BEC,可证△BCE∽△ADE.(2)根据相似三角形判定得出△ADE∽△BDA,进而得出△BCE∽△BDA,利用相似三角形的性质解答即可.【详解】证明:(1)∵AD=DC,∴∠DAC=∠DCA,∵DC2=DE•DB,∴=,∵∠CDE=∠BDC,∴△CDE∽△BDC,∴∠DCE=∠DBC,∴∠DAE=∠EBC,∵∠AED=∠BEC,∴△BCE∽△ADE,(2)∵DC2=DE•DB,AD=DC∴AD2=DE•DB,同法可得△ADE∽△BDA,∴∠DAE=∠ABD=∠EBC,∵△BCE∽△ADE,∴∠ADE=∠BCE,∴△BCE∽△BDA,∴=,∴AB•BC=BD•BE.【点睛】本题考查了相似三角形的判定与性质.关键是要懂得找相似三角形,利用相似三角形的性质求解.22.证明见解析【解析】【分析】由已知易证∠BAC=∠ECD,在Rt△ABC中由已知可得2225AB BC+=,结合AB=4,CD=5,可证得AB CEAC CD=,由此即可由“两边对应成比例,且夹角相等的两三角形相似”得到△ABC∽△CED.【详解】∵∠B=90°,AB=4,BC=2,∴ 2225 AC AB BC=+=∵ CE=AC,∴ 5CE=∵ CD=5,∴ AB ACCE CD=.∵∠B=90°,∠ACE=90°,∴∠BAC+∠BCA=90°,∠BCA+∠DCE=90°.∴∠BAC=∠DCE.∴△ABC∽△CED.23.见解析【解析】试题分析:(1)由三角形内角和定理可得:∠BDE=180°-∠B-∠DEB,∠CEF=180°-∠DEF-∠DEB,结合∠B=∠DEF,可得∠BDE=∠CEF;由AB=AC可得∠B=∠C,由此即可证得:△BDE ∽△CEF;(2)由(1)中结论:△BDE∽△CEF可得:BE DECF EF=,结合BE=EC可得:CE DECF EF=,再结合∠C=∠B=∠DEF,证得:△DEF∽△ECF,由此可得∠DFE=∠EFC,从而得到结论EF 平分∠DFC.试题解析:(1)∵AB AC =,∴B C ∠=∠,∵180BDE B DAB ∠=︒-∠-∠,180CEF DEF DEB ∠=︒-∠-∠,∵DEF B ∠=∠,∴BDE CEF ∠=∠,BDE CEF V V ∽.(2)∵BDE CEF V V ∽, ∴BE DE CF EF=, ∵E 是BC 中点,BE CE =, ∴CE DE CF EF=, ∵DEF B C ∠=∠=∠,∴DEF ECF V V ∽,∴DFE CFE ∠=∠,∴EF 平分DFC ∠.24.(1)10;(2)18.【解析】【分析】(1)根据相似三角形对应边之比相等可得BO AO =DO CO =35,再代入BO =6可得AO 长; (2)根据相似三角形的面积的比等于相似比的平方可得BOD AOC S S V V =925,进而可得S △BOD . 【详解】解:(1)∵△OBD ∽△OAC , ∴BO AO =DO CO =35∵BO =6,∴AO =10;(2)∵△OBD ∽△OAC ,DO CO =35 ∴BOD AOC S S V V =925∵S △AOC =50,∴S △BOD =18.【点睛】此题主要考查相似三角形的性质,解题的关键是熟知相似三角形的面积之比等于相似比的平方.25.证明见解析.【解析】【分析】由正方形的性质可知;AC 平分∠DAB ,然后由角平分线的性质可知GE=GF ,从而可证明四边形EGFA 为正方形,故此四边形AFGE 与四边形ABCD 相似;【详解】解:∵四边形ABCD 是正方形,AC 是对角线,∴∠DAC =∠BAC =45°. 又∵GE ⊥AD ,GF ⊥AB ,∴EG =FG ,且AE =EG ,AF =FG .∴AE =EG =FG =AF ,∴四边形AFGE 为正方形. ∴AF AB =FG BC =GE CD =AE AD, 且∠EAF =∠DAB ,∠AFG =∠ABC ,∠FGE =∠BCD ,∠AEG =∠ADC.∴四边形AFGE 与四边形ABCD 相似.。