清华大学2018年全国优秀大学生计算法学主题夏令营

清华大学地球系统科学系保研夏令营通知清华大学地球系统科学系保研夏令营通知清华大学地球系统科学系2018年保研夏令营通知已经公布，为了方便考生了解相关内容，本文是店铺搜索整理的关于2018年清华大学地球系统科学系保研夏令营通知，供参考阅读，希望对大家有所帮助!想了解更多相关信息请持续关注我们店铺!清华大学地球系统科学系(以下简称“地学系”)将于2017年6月3 - 5日在北京清华大学举行全国优秀大学生夏令营活动。

夏令营旨在增进国内高校优秀本科生对地球系统科学和全球变化研究领域的了解、对清华地学学科的'认识，并从中选拔优秀学生继续深造。

在夏令营期间，营员将与清华地学系教授进行面对面交流，通过互动讨论等形式，促进师生之间的相互了解，感受地学系的国际化教学科研氛围;同时为2017年接收免试推荐研究生(2018年9月入学)进行初步遴选工作(正式拟录取工作将根据清华大学统一安排在2017年秋季学期开学初进行)。

本届夏令营只招收攻读博士学位的学生。

清华大学地学系提供所有参加者在夏令营期间的伙食费用，并为外地参加者提供住宿和来程(火车硬座)路费(需提供车票)。

一、申请资格1、申请者应为“985”或“211”大学在校大气科学、生态学(含植物学、土壤化学)、海洋科学、计算机科学、地理学、环境科学、经济学、数学、物理学或相关专业三年级(2018年毕业)学生。

2、学习成绩优异，本科前三年(或前5学期)总评成绩排名在本校同年级本专业前10%之内;或者虽然成绩不在前10%之内，但在其他方面有优异表现者——例如选修经济学第二学位且成绩优异、有突出的研究成果等——亦可申请。

3、对地学学科有浓厚兴趣，有志于大气、海洋、生态、计算地球科学、地理学等学科领域的研究应用工作，并有较强或潜在的能力。

4、应有两名副教授以上职称教师的书面推荐信。

5、英语水平良好。

二、申请材料1、申请表：见附件一。

附专业排名证明。

申请者只能申请一个专业，同时申请两个以上专业者，材料不予受理。

清华大学2018保送生拟录取名单(159人)的更新!清华大学2018保送生拟录取名单(159人)毕业学校保送特征院校考核成绩院校考核合格标准北师大附属实验奥赛国家队集训学生计算机类（计算机科学与技术）清华附中奥赛国家队集训学生计算机类（计算机科学实验班）清华附中奥赛国家队集训学生计算机类（计算机科学实验班）人大附中奥赛国家队集训学生临床医学类（医学实验班）人大附中奥赛国家队集训学生计算机类（计算机科学与技术）人大附中奥赛国家队集训学生理科试验班类（化生（生物科学））人大附中奥赛国家队集训学生理科试验班类（数理（数学与应用数学））人大附中奥赛国家队集训学生理科试验班类（数理（数学与应用数学））南开中学奥赛国家队集训学生计算机类（计算机科学与技术）石家庄市第二中学奥赛国家队集训学生计算机类（计算机科学与技术）石家庄外国语学校外国语中学优秀学生综合成绩：250分综合成绩250分石家庄外国语学校外国语中学优秀学生综合成绩：262分综合成绩250分石家庄外国语学校外国语中学优秀学生综合成绩：271.5分综合成绩250分石家庄二中实验学校奥赛国家队集训学生理科试验班类（化生（生物科学衡水第一中学奥赛国家队集训学生理科试验班类（化生（生物科学衡水第一中学奥赛国家队集训学生理科试验班类（数理（基础科学班衡水第一中学奥赛国家队集训学生临床医学类（医学实验班）山西大学附中奥赛国家队集训学生理科试验班类（化生（生物科学））辽宁省实验中学奥赛国家队集训学生计算机类（计算机科学实验班）大连二十四中奥赛国家队集训学生工科试验班类（环境、化工与新材料）长春外国语学校外国语中学优秀学生综合成绩：265.5分综合成绩250分吉大附中奥赛国家队集训学生计算机类（计算机科学与技术）东北师大附中奥赛国家队集训学生理科试验班类（经济、金融与管理）东北师大附中奥赛国家队集训学生理科试验班类（化生（生物科学））东北师大附中奥赛国家队集训学生计算机类（计算机科学与技术）东北师大附中奥赛国家队集训学生计算机类（计算机科学与技术）上海市上海中学奥赛国家队集训学生理科试验班类（经济、金融与管理上海市上海中学奥赛国家队集训学生计算机类（计算机科学实验班）上海外国语大学附属外国语学校外国语中学优秀学生综合成绩：272分综合成绩250分华东师范大学第二附属中学奥赛国家队集训学生理科试验班类数理数学与应用数学华东师范大学第二附属中学奥赛国家队集训学生临床医学类（医学实验班）南京外国语学校奥赛国家队集训学生计算机类（计算机科学与技术）南京外国语学校奥赛国家队集训学生计算机类（计算机科学与技术）南京外国语学校外国语中学优秀学生综合成绩：262.5分综合成绩250分南京外国语学校外国语中学优秀学生综合成绩：277.5分综合成绩250分南京外国语学校奥赛国家队集训学生计算机类（计算机科学与技术）南京外国语学校奥赛国家队集训学生计算机类（计算机科学与技术）南京外国语学校外国语中学优秀学生综合成绩：264.5分综合成绩250分南京外国语学校外国语中学优秀学生综合成绩：271分综合成绩250分南京外国语学校外国语中学优秀学生综合成绩：287.5分综合成绩250分英语（世界文学与文化实验班）南京外国语学校外国语中学优秀学生综合成绩：269.5分综合成绩250分南京外国语学校外国语中学优秀学生综合成绩：257.5分综合成绩250分南京外国语学校外国语中学优秀学生综合成绩：258分综合成绩250分南京外国语学校外国语中学优秀学生综合成绩：255.5分综合成绩250分南京外国语学校外国语中学优秀学生综合成绩：263分综合成绩250分南京外国语学校外国语中学优秀学生综合成绩：275分综合成绩250分南京外国语学校外国语中学优秀学生综合成绩：281.5分综合成绩250分南京外国语学校外国语中学优秀学生综合成绩：261分综合成绩250分南京外国语学校外国语中学优秀学生综合成绩：285分综合成绩250分南京师大附中奥赛国家队集训学生理科试验班类（化生（生物科学））常州高级中学奥赛国家队集训学生计算机类（计算机科学与技术）淮阴中学奥赛国家队集训学生计算机类（计算机科学与技术）杭州二中奥赛国家队集训学生理科试验班类（化生（生物科学））杭州二中奥赛国家队集训学生计算机类（计算机科学实验班）杭州二中奥赛国家队集训学生计算机类（计算机科学与技术）学军中学奥赛国家队集训学生计算机类（计算机科学实验班）杭州学军中学奥赛国家队集训学生临床医学类（协和）学军中学奥赛国家队集训学生计算机类（计算机科学与技术）学军中学奥赛国家队集训学生计算机类（计算机科学与技术）乐成寄宿中学奥赛国家队集训学生理科试验班类（经济、金融与管理）乐成寄宿中学奥赛国家队集训学生工科试验班类（机械、航空与动力（钱班））乐成寄宿中学奥赛国家队集训学生计算机类（计算机科学实验班）乐成寄宿中学奥赛国家队集训学生计算机类（计算机科学实验班）绍兴一中奥赛国家队集训学生理科试验班类（数理（数学与应用数学））金华一中奥赛国家队集训学生临床医学类（医学实验班）合肥一中奥赛国家队集训学生计算机类（计算机科学与技术）淮南二中奥赛国家队集训学生计算机类（计算机科学与技术）淮北一中奥赛国家队集训学生临床医学类（医学实验班）福州三中奥赛国家队集训学生计算机类（计算机科学与技术）泉州七中奥赛国家队集训学生理科试验班类（化生（生物科学））泉州七中奥赛国家队集训学生临床医学类（医学实验班）福州一中奥赛国家队集训学生计算机类（计算机科学与技术）莆田一中奥赛国家队集训学生计算机类（计算机科学实验班）刘越千子江西省南昌市外国语学校外国语中学优秀学生综合成绩：276分综合成绩250分南昌市外国语学校外国语中学优秀学生综合成绩：279分综合成绩250分英语（世界文学与文化实验班）南昌外国语学校外国语中学优秀学生综合成绩：273.5分综合成绩250分南昌市外国语学校外国语中学优秀学生综合成绩：257分综合成绩250分江西科技学院附中奥赛国家队集训学生理科试验班类（化生（生物科学））上饶中学奥赛国家队集训学生理科试验班类（化生（生物科学））历城二中奥赛国家队集训学生理科试验班类（化生（生物科学））胜利一中奥赛国家队集训学生计算机类（计算机科学与技术）潍坊一中奥赛国家队集训学生临床医学类（协和）寿光现代中学奥赛国家队集训学生理科试验班类（化生（生物科学））临沂一中奥赛国家队集训学生临床医学类（协和）临沂一中奥赛国家队集训学生理科试验班类（化生（生物科学））河南省实验中学奥赛国家队集训学生理科试验班类（化生（生物科学））郑州外国语学校外国语中学优秀学生综合成绩：264.5分综合成绩250分郑州外国语学校外国语中学优秀学生综合成绩：277.5分综合成绩250分郑州外国语学校外国语中学优秀学生综合成绩：260.5分综合成绩250分郑州外国语学校外国语中学优秀学生综合成绩：272分综合成绩250分郑州外国语学校外国语中学优秀学生综合成绩：274分综合成绩250分英语（世界文学与文化实验班）郑州外国语学校外国语中学优秀学生综合成绩：262分综合成绩250分郑州外国语学校外国语中学优秀学生综合成绩：282.5分综合成绩250分郑州外国语学校外国语中学优秀学生综合成绩：267分综合成绩250分郑州外国语学校外国语中学优秀学生综合成绩：252分综合成绩250分郑州外国语奥赛国家队集训学生理科试验班类（经济、金融与管理）郑州外国语奥赛国家队集训学生理科试验班类（化生（生物科学））郑州外国语学校外国语中学优秀学生综合成绩：263分综合成绩250分郑州外国语奥赛国家队集训学生理科试验班类（化生（生物科学））郑州外国语奥赛国家队集训学生理科试验班类（化生（生物科学））郑州外国语学校外国语中学优秀学生综合成绩：263.5分综合成绩250分郑州外国语学校外国语中学优秀学生综合成绩：262.5分综合成绩250分郑州外国语奥赛国家队集训学生理科试验班类（化生（生物科学河南师大附中奥赛国家队集训学生理科试验班类（化生（生物科学））安阳一中奥赛国家队集训学生计算机类（计算机科学与技术）武汉二中奥赛国家队集训学生计算机类（计算机科学与技术）武汉外国语学校外国语中学优秀学生综合成绩：271.5分综合成绩250分武汉外国语学校外国语中学优秀学生综合成绩：251分综合成绩250分武汉外国语学校外国语中学优秀学生综合成绩：262分综合成绩250分武汉外国语学校外国语中学优秀学生综合成绩：260分综合成绩250分武汉外国语学校外国语中学优秀学生综合成绩：256.5分综合成绩250分武汉外国语学校外国语中学优秀学生综合成绩：268.5分综合成绩250分武汉外国语学校外国语中学优秀学生综合成绩：306.5分综合成绩250分武汉外国语学校外国语中学优秀学生综合成绩：255分综合成绩250分华师一附中奥赛国家队集训学生计算机类（计算机科学实验班）华师一附中奥赛国家队集训学生计算机类（计算机科学实验班）黄冈中学奥赛国家队集训学生理科试验班类（化生（生物科学））广州六中奥赛国家队集训学生计算机类（计算机科学与技术）华南师大附中奥赛国家队集训学生理科试验班类（化生（生物科学））深圳中学奥赛国家队集训学生计算机类（计算机科学实验班）深圳中学奥赛国家队集训学生计算机类（计算机科学实验班）深圳外国语学校外国语中学优秀学生综合成绩：256分综合成绩250分深圳市外国语学校高中部外国语中学优秀学生综合成绩：301分综合成绩250分英语（世界文学与文化实验班）深圳外国语学校外国语中学优秀学生综合成绩：284.5分综合成绩250分英语（世界文学与文化实验班）深圳外国语学校外国语中学优秀学生综合成绩：280.5分综合成绩250分英语（世界文学与文化实验班）汕头市金山中学奥赛国家队集训学生计算机类（计算机科学与技术）汕头市金山中学奥赛国家队集训学生计算机类（计算机科学与技术）中山一中奥赛国家队集训学生理科试验班类（化生（生物科学））柳州高级中学奥赛国家队集训学生工科试验班自动化工业工程自动化巴蜀中学奥赛国家队集训学生工科试验班类（机械、航空与动力（钱班））巴蜀中学奥赛国家队集训学生理科试验班类（化生（生物科学））重庆一中奥赛国家队集训学生计算机类（计算机科学实验班）重庆八中奥赛国家队集训学生计算机类（计算机科学实验班）重庆南开中学奥赛国家队集训学生理科试验班类（化生（化学））重庆南开中学奥赛国家队集训学生理科试验班类（化生（生物科学））石室中学奥赛国家队集训学生计算机类（计算机科学与技术）成都市外国语学校外国语中学优秀学生综合成绩：251.5分综合成绩250分成都市外国语学校外国语中学优秀学生综合成绩：263.5分综合成绩250分成都市外国语学校外国语中学优秀学生综合成绩：294分综合成绩250分英语（世界文学与文化实验班）成都市外国语学校外国语中学优秀学生综合成绩：287分综合成绩250分英语（世界文学与文化实验班）成都市外国语学校外国语中学优秀学生综合成绩：283.5分综合成绩250分英语（世界文学与文化实验班）成都市外国语学校外国语中学优秀学生综合成绩：263.5分综合成绩250分成都市外国语学校外国语中学优秀学生综合成绩：285分综合成绩250分英语（世界文学与文化实验班）成都市外国语学校外国语中学优秀学生综合成绩：271分综合成绩250分英语（世界文学与文化实验班）成都市外国语学校外国语中学优秀学生综合成绩：269分综合成绩250分成都市外国语学校外国语中学优秀学生综合成绩：280.5分综合成绩250分成都外国语奥赛国家队集训学生计算机类（计算机科学实验班）成都市外国语学校外国语中学优秀学生综合成绩：281分综合成绩250分成都市外国语学校外国语中学优秀学生综合成绩：260.5分综合成绩250分成都市外国语学校外国语中学优秀学生综合成绩：271.5分综合成绩250分英语（世界文学与文化实验班）成都七中奥赛国家队集训学生工科试验班类（环境、化工与新材料）成都七中奥赛国家队集训学生理科试验班类（经济、金融与管理）成都七中奥赛国家队集训学生理科试验班类（经济、金融与管理）成都七中奥赛国家队集训学生理科试验班类（数理（能源实验班成都七中奥赛国家队集训学生理科试验班类（经济、金融与管理）成都七中。

2018年全国普通高校学科竞赛排行榜内竞赛项目随着我国教育改革的不断深化和高等教育的快速发展，各类学科竞赛在高校教育中扮演着越来越重要的角色。

学科竞赛既是学生综合能力的重要展示评台，也是高校学科发展和创新能力的重要评价标准。

近年来，各类学科竞赛活动在全国各地开展，参与人数不断增加，竞赛项目也日益丰富多样。

2018年，全国普通高校学科竞赛排行榜内竞赛项目涵盖了各个学科领域，涉及数学、物理、化学、信息技术、工程技术、生命科学、地球科学、经济管理等多个方面。

本文将从这些方面对2018年全国普通高校学科竞赛排行榜内的竞赛项目进行介绍和分析。

一、数学竞赛1. 数学建模竞赛：数学建模竞赛是一项集数学理论、实验科学和工程技术于一体的学术性竞赛活动，其目的是培养学生综合运用所学知识的能力，提高学生的创新素质和实践能力。

该竞赛项目在2018年全国普通高校学科竞赛排行榜内占据重要位置，吸引了众多高校和学生的关注与参与。

2. 数学竞赛（数学奥赛）：数学竞赛是选拔和培养数学人才的重要途径，也是促进数学教育改革和提高教学质量的有效手段。

数学竞赛分为国际数学奥林匹克竞赛、全国青少年数学奥林匹克竞赛、全国中学生数学竞赛等不同级别，按芳龄和学历划分，吸引了大量数学爱好者的参与。

二、物理竞赛1. 物理竞赛（物理奥赛）：物理竞赛是一个历史悠久的学科竞赛项目，旨在选拔和培养物理学人才，促进物理学科教学与科研的交流与发展。

全国青少年物理奥林匹克竞赛、全国高中生物理竞赛等是物理竞赛的重要组成部分，吸引了众多对物理学感兴趣的学生积极参与。

2. 物理建模竞赛：物理建模竞赛是一项将数学建模与物理领域相结合的竞赛活动，旨在培养学生的实际动手能力、科研创新能力和团队合作精神。

该竞赛项目在2018年全国普通高校学科竞赛排行榜内获得了广泛关注，成为了物理学科领域一个重要的竞赛项目。

三、化学竞赛1. 化学竞赛（化学奥赛）：化学竞赛旨在选拔和培养优秀的化学人才，促进化学学科的教学与科研水平提高。

一、介绍随着计算机科学与技术的不断发展，越来越多的学子们选择走上计算机科学与技术的道路。

对于大部分想要继续深造的学生来说，保研成为了一个非常重要的选择。

为了更好地了解保研情况，许多高校都会举办计算机保研夏令营。

本文将针对2023年的计算机保研夏令营时间进行汇总和介绍。

二、清华大学计算机保研夏令营1. 时间：2023年7月10日-7月15日2. 介绍：清华大学计算机系将于2023年7月10日至7月15日举办计算机保研夏令营。

夏令营将安排专业课程学习、导师指导、实验室参观等活动，学生将有机会与清华大学计算机系的老师和学长学姐面对面交流，深入了解研究生生活和研究方向，同时也可以增加对保研流程的了解和实践经验。

三、北京大学计算机保研夏令营1. 时间：2023年7月20日-7月25日2. 介绍：北京大学计算机科学与技术学院将于2023年7月20日至7月25日举办计算机保研夏令营。

夏令营内容包括专业课程学习、导师座谈、实验室见习等环节。

学生将有机会与北京大学计算机科学与技术学院的老师和学长学姐进行深入交流，了解研究生的学习和生活环境，为未来的保研之路提供有力支持。

四、上海交通大学计算机保研夏令营1. 时间：2023年7月30日-8月4日2. 介绍：上海交通大学计算机系将于2023年7月30日至8月4日举办计算机保研夏令营。

此次夏令营将提供包括专业课程学习、导师指导、实验室参观等内容。

学生将有机会与上海交通大学计算机系的老师和学长学姐面对面交流，全面了解研究生学习和研究环境，并积累保研经验。

五、总结随着计算机领域的不断发展，越来越多的学生选择走上保研的道路。

各高校计算机保研夏令营为学生提供了一个全面了解研究生学习和生活环境的机会，也为学生积累保研经验提供了宝贵的机遇。

希望同学们能够充分利用夏令营的机会，为自己的保研之路做出更加明智的选择。

六、浙江大学计算机保研夏令营1. 时间：2023年8月10日-8月15日2. 介绍：浙江大学计算机科学与技术学院将于2023年8月10日至8月15日举办计算机保研夏令营。

1.首先，我要说明的是我本人是南京大学软件学院本科生，所以对于外校生的保研经历可能了解的并不是很清楚，经验只供参考。

今年夏令营共四天，第一天是报到入营，第二天是讲座和导师介绍，第三天是面试和机考，第四天是自己与联系的导师进行交流，夏令营结束。

其中最重要的是第三天的面试和机考。

面试本次是老师事先分好组，然后每个组内的人抽签决定面试顺序，每个组的不同就是面试老师的不同。

我是本组第二个面试，但其实比较水，我就被问了两个问题，英文自我介绍和项目经历。

可能还会被问到的问题是最喜欢哪门课，一些软件工程专业的名词解释等。

外校学生可能会问一些其他的？机考按照惯例是两道题，一道面向对象的题目，一道算法题。

面向对象的题目就考你一些软件工程基本知识，弄清各个类之间的关系，面向测试用例编程即可，今年的是银行，账户，用户，事务之间的关系。

算法题大概是leetcode上easy到medium之间的难度，不是很难。

本校外校的题目应该是一样的。

如果是学硕的话要提前联系导师！以上就是我参加本次夏令营的感受了。

2.2018北大软微软工夏令营保研经历因为自己当初在选择要保到软微的时候曾经花费了大量的时间在网上寻找相关的保研经验，但是相关信息极度匮乏，导致我直到去夏令营报到才知道了整个流程，也是在听完了宣讲才清楚了软微的确切情况。

我很菜，和其他写保研去清华北大经验帖的大佬相比可以说是菜出了翔，英语很烂，没什么科研项目，没什么牛逼的竞赛经历，只是一个埋头学习书本知识的苦行僧，除了还能拿得出手的成绩排名为一无所有，这也是为什么会选择去这个在清北所有学院里看起来是最弱的软微。

曾经的经历让我想要写一篇文章来帮助未来想保研去软微软工的同学，同时也记录一下我的保研经历。

接下来我会介绍为保研做的准备和参加夏令营的经历，着重是软微软件工程夏令营的相关情况。

本文更多的是个人经历的记录，并没有什么鸡汤经验分享，至于读者能够获得什么样的帮助这要看个人感悟了，当然你也可以把这当作闲时的一个乐子。

2018年清华大学自主招生暨领军计划试题1．已知函数x e a x x f )()(2+=有最小值，则函数a x x x g ++=2)(2的零点个数为（ ） A ．0 B ．1 C ．2 D ．取决于a 的值 【答案】C【解析】注意)()(/x g e x f x=，答案C ．2． 已知ABC ∆的三个内角C B A ,,所对的边为c b a ,,．下列条件中，能使得ABC ∆的形状唯一确定的有（ ）A ．Z c b a ∈==,2,1B ．B bC a C c A a A sin sin 2sin sin ,1500=+=C ．060,0sin cos )cos(cos sin cos ==++C C B C B C B A D ．060,1,3===A b a【答案】AD ．3．已知函数x x g x x f ln )(,1)(2=-=，下列说法中正确的有（ ） A ．)(),(x g x f 在点)0,1(处有公切线B ．存在)(x f 的某条切线与)(x g 的某条切线平行C ．)(),(x g x f 有且只有一个交点D ．)(),(x g x f 有且只有两个交点【答案】BD【解析】注意到1-=x y 为函数)(x g 在)0,1(处的切线，如图，因此答案BD ．4．过抛物线x y 42=的焦点F 作直线交抛物线于B A ,两点，M 为线段AB 的中点．下列说法中正确的有（ ）A ．以线段AB 为直径的圆与直线23-=x 一定相离 B ．||AB 的最小值为4 C ．||AB 的最小值为2D ．以线段BM 为直径的圆与y 轴一定相切 【答案】AB【解析】对于选项A ，点M 到准线1-=x 的距离为||21|)||(|21AB BF AF =+，于是以线段AB 为直径的圆与直线1-=x 一定相切，进而与直线23-=x 一定相离；对于选项B ，C ，设)4,4(2a a A ，则)1,41(2a a B -，于是2414||22++=a a AB ，最小值为4．也可将||AB 转化为AB 中点到准线的距离的2倍去得到最小值；对于选项D ，显然BD 中点的横坐标与||21BM 不一定相等，因此命题错误． 5．已知21,F F 是椭圆)0(1:2222>>=+b a by a x C 的左、右焦点，P 是椭圆C 上一点．下列说法中正确的有（ ） A ．b a 2=时，满足02190=∠PF F 的点P 有两个 B ．b a 2>时，满足02190=∠PF F 的点P 有四个C ．21F PF ∆的周长小于a 4D ．21F PF ∆的面积小于等于22a【答案】ABCD ．【解析】对于选项A ，B ，椭圆中使得21PF F ∠最大的点P 位于短轴的两个端点；对于选项C ，21PF F ∆的周长为a c a 422<+；选项D ，21PF F ∆的面积为22212121212||||21sin ||||21a PF PF PF F PF PF =⎪⎭⎫ ⎝⎛+≤∠⋅． 6．甲、乙、丙、丁四个人参加比赛，有两花获奖．比赛结果揭晓之前，四个人作了如下猜测： 甲：两名获奖者在乙、丙、丁中； 乙：我没有获奖，丙获奖了； 丙：甲、丁中有且只有一个获奖； 丁：乙说得对．已知四个人中有且只有两个人的猜测是正确的，那么两个获奖者是（ ） A ．甲B ．乙C ．丙D ．丁【答案】BD【解析】乙和丁同时正确或者同时错误，分类即可，答案：BD ．7．已知AB 为圆O 的一条弦（非直径），AB OC ⊥于C ，P 为圆O 上任意一点，直线PA 与直线OC 相交于点M ，直线PB 与直线OC 相交于点N ．以下说法正确的有（ ） A ．P B M O ,,,四点共圆 B ．N B M A ,,,四点共圆 C ．N P O A ,,,四点共圆D ．以上三个说法均不对【答案】AC【解析】对于选项A ，OPM OAM OBM ∠=∠=∠即得；对于选项B ，若命题成立，则MN 为直径，必然有MAN ∠为直角，不符合题意；对于选项C ，MAN MOP MBN ∠=∠=∠即得．答案：AC ．8．C B A C B A cos cos cos sin sin sin ++>++是ABC ∆为锐角三角形的（ ） A ．充分非必要条件 B ．必要非充分条件 C ．充分必要条件D ．既不充分也不必要条件【答案】B【解析】必要性：由于1cos sin )2sin(sin sin sin >+=-+>+B B B B C B π，类似地，有1sin sin ,1sin sin >+>+A B A C ，于是C B A C B A cos cos cos sin sin sin ++>++．不充分性：当4,2ππ===C B A 时，不等式成立，但ABC ∆不是锐角三角形．9．已知z y x ,,为正整数，且z y x ≤≤，那么方程21111=++z y x 的解的组数为（ ） A ．8B ．10C ．11D ．12【答案】B 【解析】由于xz y x 311121≤++=，故63≤≤x ． 若3=x ，则36)6)(6(=--z y ，可得)12,12(),15,10(),18,9(),24,8(),42,7(),(=z y ； 若4=x ，则16)4)(4(=--z y ，可得)8,8(),12,6(),20,5(),(=z y ； 若5=x ，则6,5,320,211103=≤≤+=y y y z y ，进而解得)10,5,5(),,(=z y x ； 若6=x ，则9)3)(3(=--z y ，可得))6,6(),(=z y ． 答案：B ．10．集合},,,{21n a a a A Λ=，任取A a a A a a A a a n k j i i k k j j i ∈+∈+∈+≤<<≤,,,1这三个式子中至少有一个成立，则n 的最大值为（ ） A ．6B ．7C ．8D ．9【答案】B11．已知000121,61,1===γβα，则下列各式中成立的有（ ） A ．3tan tan tan tan tan tan =++αγγββα B ．3tan tan tan tan tan tan -=++αγγββαC ．3tan tan tan tan tan tan =++γβαγβαD ．3tan tan tan tan tan tan -=++γβαγβα【答案】BD【解析】令γβαtan ,tan ,tan ===z y x ，则3111=+-=+-=+-zxzx yz y z xy x y ，所以)1(3),1(3),1(3zx z x yz y z xy z y +=-+=-+=-，以上三式相加，即有3-=++zx yz xy ．类似地，有)11(311),11(311),11(311+=-+=-+=-zxx z yz z y xy y x ，以上三式相加，即有3111-=++=++xyzz y x zx yz xy ．答案BD ． 12．已知实数c b a ,,满足1=++c b a ，则141414+++++c b a 的最大值也最小值乘积属于区间（ ）A ．)12,11(B ．)13,12(C ．)14,13(D ．)15,14(【答案】B【解析】设函数14)(+=x x f ，则其导函数142)(/+=x x f ，作出)(x f 的图象，函数)(x f 的图象在31=x 处的切线321)31(7212+-=x y ，以及函数)(x f 的图象过点)0,41(-和)7,23(的割线7174+=x y ，如图，于是可得321)31(7212147174+-≤+≤+x x x ，左侧等号当41-=x 或23=x 时取得； 右侧等号当31=x 时取得．因此原式的最大值为21，当31===c b a 时取得；最小值为7，当23,41=-==c b a 时取得，从而原式的最大值与最小值的乘积为)169,144(37∈．答案B ．13．已知1,1,,,222=++=++∈z y x z y x R z y x ，则下列结论正确的有（ ） A ．xyz 的最大值为0 B ．xyz 的最大值为274- C ．z 的最大值为32D ．z 的最小值为31-【答案】ABD14．数列}{n a 满足)(6,2,1*1221N n a a a a a n n n ∈-===++，对任意正整数n ，以下说法中正确的有（ ）A ．n n n a a a 221++-为定值 B ．)9(mod 1≡n a 或)9(mod 2≡n aC ．741-+n n a a 为完全平方数D ．781-+n n a a 为完全平方数 【答案】ACD 【解析】因为2112221122213226)6(++++++++++++-=--=-n n n n n n n n n n n a a a a a a a a a a a n n n n n n n a a a a a a a 22121122)6(++++++-=+-=，选项A 正确；由于113=a ，故76)6(2121121221-=+-=--=-++++++n n n n n n n n n n n a a a a a a a a a a a ，又对任意正整数恒成立，所以211211)(78,)(74n n n n n n n n a a a a a a a a +=--=-++++，故选项C 、D 正确．计算前几个数可判断选项B 错误．说明：若数列}{n a 满足n n n a pa a -=++12，则n n n a a a 221++-为定值．15．若复数z 满足11=+zz ，则z 可以取到的值有（ ） A ．21B ．21-C ．215- D ．215+ 【答案】CD 【解析】因为11||1||=+≤-zz z z ，故215||215+≤≤-z ，等号分别当i z 215+=和i z 215-=时取得．答案CD ． 16． 从正2016边形的顶点中任取若干个，顺次相连构成多边形，若正多边形的个数为（ ） A ．6552 B ．4536 C ．3528 D ．2016 【答案】C【解析】从2016的约数中去掉1，2，其余的约数均可作为正多边形的边数．设从2016个顶点中选出k 个构成正多边形，这样的正多边形有k2016个，因此所求的正多边形的个数就是2016的所有约数之和减去2016和1008．考虑到732201625⨯⨯=，因此所求正多边形的个数为352810082016)71)(931)(32168421(=--++++++++．答案C ．17．已知椭圆)0(12222>>=+b a b y a x 与直线x y l x y l 21:,21:21-==，过椭圆上一点P 作21,l l 的平行线，分别交21,l l 于N M ,两点．若||MN 为定值，则=ba（ ） A ．2B ．3C ．2D ．5【答案】C【解析】设点),(00y x P ，可得)2141,21(),2141,21(00000000y x y x N y x y x M +--++，故意2020441||y x MN +=为定值，所以2,1641422===b a b a ，答案：C ．说明：（1）若将两条直线的方程改为kx y ±=，则kb a 1=；（2）两条相交直线上各取一点N M ,，使得||MN 为定值，则线段MN 中点Q 的轨迹为圆或椭圆．18． 关于y x ,的不定方程y x 21652=+的正整数解的组数为（ ） A ．0B ．1C ．2D ．3【答案】B19．因为实数的乘法满足交换律与结合律，所以若干个实数相乘的时候，可以有不同的次序．例如，三个实数c b a ,,相乘的时候，可以有Λ),(),(,)(,)(ca b ab c c ba c ab 等等不同的次序．记n 个实数相乘时不同的次序有n I 种，则（ ）A ．22=IB ．123=IC ．964=ID ．1205=I 【答案】B【解析】根据卡特兰数的定义，可得1121221)!1(!1------=⋅==n n n n nn n n C n n C nA C I ．答案：AB ． 关于卡特兰数的相关知识见《卡特兰数——计数映射方法的伟大胜利》．20．甲乙丙丁4个人进行网球淘汰赛，规定首先甲乙一组、丙丁一组进行比赛，两组的胜者争夺冠军．4个人相互比赛的胜率如表所示：表中的每个数字表示其所在的选手击败其所在列的选手的概率，例如甲击败乙的概率是0.3，乙击败丁的概率是0.4．那么甲刻冠军的概率是 ． 【答案】0.165【解析】根据概率的乘法公式 ，所示概率为165.0)8.05.03.05.0(3.0=⨯+⨯．21．在正三棱锥ABC P -中，ABC ∆的边长为1．设点P 到平面ABC 的距离为x ，异面直线CP AB ,的距离为y ．则=∞→y x lim ．【答案】23【解析】当∞→x 时，CP 趋于与平面ABC 垂直，所求极限为ABC ∆中AB 边上的高，为23． 22．如图，正方体1111D C B A ABCD -的棱长为1，中心为A A E A BC BF O 1141,21,==，则四面体OEBF 的体积为 ．【答案】196【解析】如图，EBF G EBF O OEBF V V V --==21961161212111=⋅==--B BCC E GBF E V V ．23．=+-⎰-dx x x n n )sin 1()(22012ππ ．【答案】0【解析】根据题意，有0)sin 1()sin 1()(21222012=+=+-⎰⎰---dx x x dx x x n n n n ππππ．24．实数y x ,满足223224)(y x y x =+，则22y x +的最大值为 ． 【答案】1【解析】根据题意，有22222322)(4)(y x y x y x +≤=+，于是122≤+y x ，等号当2122==y x 时取得，因此所求最大值为1．25．z y x ,,均为非负实数，满足427)23()1()21(222=+++++z t x ，则z y x ++的最大值与最小值分别为 ． 【答案】2322- 【解析】由柯西不等式可知，当且仅当)0,21,1(),,(=z y x 时，z y x ++取到最大值23．根据题意，有41332222=+++++z y x z y x ，于是,)(3)(4132y z y x z y x +++++≤解得2322-≥++z y x ．于是z y x ++的最小值当)2322,0,0(),(-=yz x 时取得，为2322-． 26．若O 为ABC ∆内一点，满足2:3:4::=∆∆∆COA BOC AOB S S S ，设AC AB AO μλ+=，则=+μλ ．【答案】23【解析】根据奔驰定理，有329492=+=+μλ．27．已知复数32sin32cosππiz+=，则=+++2223zzzz．【答案】132i-【解析】根据题意，有iizzzzzz232135sin35cos122223-=+=-=+=+++ππ．28．已知z为非零复数，zz40,10的实部与虚部均为不小于1的正数，则在复平面中，z所对应的向量OP的端点P运动所形成的图形的面积为.【答案】20010033003π+-【解析】设),(Ryxyixz∈+=，由于2||4040zzz=，于是⎪⎪⎩⎪⎪⎨⎧≥+≥+≥≥,140,140,110,1102222yxyyxxyx如图，弓形面积为1003100)6sin6(20212-=-⋅⋅πππ，四边形ABCD的面积为100310010)10310(212-=⋅-⋅.于是所示求面积为30031003200)1003100()1003100(2-+=-+-ππ.29．若334tan=x，则=+++xxxxxxxxxxxcossincos2cossin2cos4cos2sin4cos8cos4sin．3【解析】根据题意，有xxxxxxxxxxxcossincos2cossin2cos4cos2sin4cos8cos4sin+++38tantan)tan2(tan)2tan4(tan)4tan8(tan==+-+-+-=xxxxxxxx．30．将16个数：4个1，4个2，4个3，4个4填入一个44⨯的数表中，要求每行、每列都恰好有两个偶数，共有种填法．【答案】44100031．设A 是集合}14,,3,2,1{Λ的子集，从A 中任取3个元素，由小到大排列之后都不能构成等差数列，则A 中元素个数的最大值为 ．【答案】8【解析】一方面，设},,,{21k a a a A Λ=，其中141,*≤≤∈k N k ．不妨假设k a a a <<<Λ21． 若9≥k ，由题意，7,33513≥-≥-a a a a ，且1335a a a a -≠-，故715≥-a a ．同理759≥-a a ．又因为1559a a a a -≠-，所以1519≥-a a ，矛盾！故8≤k ．另一方面，取}14,13,11,10,5,4,2,1{=A ，满足题意．综上所述，A 中元素个数的最大值为8．。

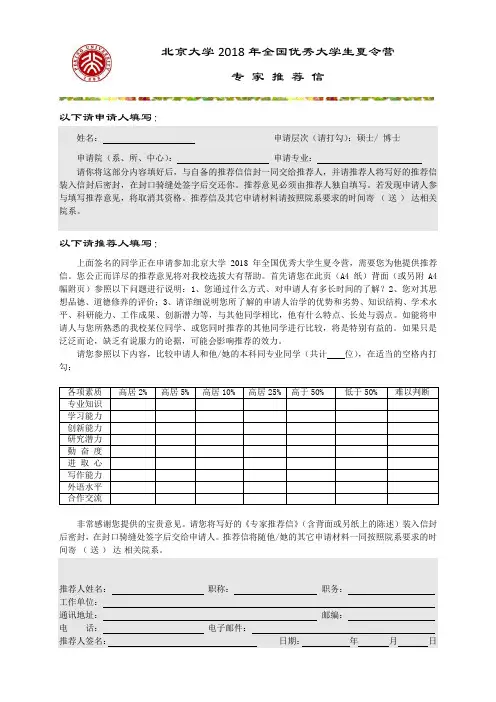
北京大学2018年全国优秀大学生夏令营
专家推荐信
以下请申请人填写：
姓名：申请层次（请打勾）：硕士/ 博士
申请院（系、所、中心）：申请专业：
请你将这部分内容填好后，与自备的推荐信信封一同交给推荐人，并请推荐人将写好的推荐信装入信封后密封，在封口骑缝处签字后交还你。

推荐意见必须由推荐人独自填写。

若发现申请人参与填写推荐意见，将取消其资格。

推荐信及其它申请材料请按照院系要求的时间寄（送）达相关院系。

以下请推荐人填写：
上面签名的同学正在申请参加北京大学2018年全国优秀大学生夏令营，需要您为他提供推荐信。

您公正而详尽的推荐意见将对我校选拔大有帮助。

首先请您在此页（A4纸）背面（或另附A4幅附页）参照以下问题进行说明：1、您通过什么方式、对申请人有多长时间的了解？2、您对其思想品德、道德修养的评价；3、请详细说明您所了解的申请人治学的优势和劣势、知识结构、学术水平、科研能力、工作成果、创新潜力等，与其他同学相比，他有什么特点、长处与弱点。

如能将申请人与您所熟悉的我校某位同学、或您同时推荐的其他同学进行比较，将是特别有益的。

如果只是泛泛而论，缺乏有说服力的论据，可能会影响推荐的效力。

请您参照以下内容，比较申请人和他/她的本科同专业同学（共计位），在适当的空格内打勾：
非常感谢您提供的宝贵意见。

请您将写好的《专家推荐信》（含背面或另纸上的陈述）装入信封后密封，在封口骑缝处签字后交给申请人。

推荐信将随他/她的其它申请材料一同按照院系要求的时间寄（送）达相关院系。

请推荐人在此面填写对申请人的推荐意见
2。

重庆大学光电工程学院推荐优秀应届本科毕业生免试攻读硕士研究生实施办法（2016年9月修订稿）为贯彻落实教育部及重庆大学关于推荐优秀应届本科毕业生免试攻读硕士研究生的有关文件精神，培养和造就综合素质高、创新能力强、基础扎实的专门人才，鼓励本科学生树立良好的学风，突出个性发展，切实贯彻落实以人为本、因材施教的育人方针，结合我院实际，制订本办法。

一、指导原则坚持公平、公正、公开；坚持知识、能力、素质并重，倡导学生德、智、体全面发展。

二、工作机构1、学院成立由院长任组长，由本科教学、研究生、学生工作分管负责人和系主任、教师代表及相关工作人员组成的推免工作组。

2、推免工作组下设三个小组：（1）学习成绩核算小组：由教学秘书、教务人员等相关工作人员组成，主要负责申请者学习成绩绩点核算及课程缺考、补考及学分等情况核实工作；（2）专业能力测评小组：由系主任召集相关专家及工作人员组成，主要负责分专业对入围的申请者进行专业能力测评。

（3）综合素质测评小组：由学办主任、团委书记、辅导员等组成，主要负责对申请者进行政审、综合素质测评及综合成绩绩点核算。

三、推荐条件（一）基本条件1、纳入国家普通本科招生计划录取的应届本科毕业生(不含专升本、第二学士学位、独立学院学生)，完清学费，具有正式学籍。

2、品德优良，遵纪守法，身心健康；诚实守信，学风端正，无任何考试作弊和剽窃他人学术成果及违法违纪受处分记录。

3、按期完成前三年本专业教育教学计划规定的课程，成绩优异，名列前茅，且全国大学外语四级考试成绩达到425分及以上，或托福≥550分（或网考≥80分），或雅思≥5.5（体育、艺术类通过学校大学基础英语（1-4））。

所有课程无缺考；前三学年补考门次不超过1门次（高等数学、大学物理无补考）。

（二）优选条件1、符合《重庆大学推荐优秀应届本科毕业生免试攻读硕士学位研究生工作管理办法（试行）》（重大校[2014]268号）所规定的优先推荐条件的，按照学校规定办法推荐。

清华叉院直博夏令营流程清华叉院直博夏令营流程简介清华叉院直博夏令营是一项面向优秀本科生的夏季培训活动，旨在为有意向申请清华大学研究生的同学提供机会，体验研究生学术环境，并与优秀的研究生导师进行学术交流。

流程安排参加清华叉院直博夏令营的同学将经历以下流程：1.报名申请–在指定时间内，按要求填写并提交夏令营报名申请。

–提交个人简历、成绩单、推荐信等相关材料。

2.初审筛选–夏令营组织委员会对报名申请进行初步筛选。

–根据综合素质和学术表现，选拔出具备参与资格的同学。

3.公布名单–初审通过的同学将在指定时间内收到夏令营邀请函。

–在指定渠道公布夏令营参与名单。

4.宣讲会和学术交流–夏令营开始前，将举行一次宣讲会，介绍清华叉院的研究方向和导师团队。

–在夏令营期间，安排专题讲座和学术交流活动，邀请叉院导师和学生分享他们的研究经验和成果。

5.实验室参观–组织不同研究方向的实验室参观活动。

–同学们有机会亲身体验清华叉院实验室的学术氛围和科研环境。

6.项目实践–夏令营期间，安排一个小型项目实践环节。

–同学们在导师的指导下，亲自参与项目研究，锻炼科研能力和创新思维。

7.学术论坛和评选–夏令营结束时，举行学术论坛，同学们有机会展示自己的项目成果。

–在评委的评选下，选出优秀的项目，并颁发奖项。

8.结营仪式–清华叉院直博夏令营圆满结束。

–对参与夏令营的同学进行结营仪式，并发放结业证书。

总结通过清华叉院直博夏令营的流程安排，参与的同学有机会深入了解清华叉院的学术理念和科研氛围，与优秀的研究生导师和同学进行交流和合作，提升自己的学术能力和专业素养。

夏令营的项目实践环节更是锻炼同学们的科研能力和创新意识。

让我们期待这个有益的夏季培训活动！报名申请•在指定时间内，填写并提交夏令营报名申请。

•准备个人简历、成绩单、推荐信等相关材料。

•注意填写要求，确保信息准确完整。

初审筛选•夏令营组织委员会对报名申请进行初步筛选。

•综合素质和学术表现会成为选拔的主要依据。

清华大学计算法学清华大学计算法学是一门多学科交叉的研究领域，该学科主要涵盖理论计算机科学、实验计算机科学、应用计算机科学、人工智能等相关领域的基本理论与应用知识。

此外，也经常涉及到计算机科学中的设计和分析技术的内容。

清华大学计算法学领域的研究重点在于理论尖端的计算机理论，以及基于实际用途，有效应用理论计算机科学中的方法和技术来解决实际问题，如计算、科学计算、计算机科学、网络计算、信息处理、自动控制、机器学习和人工智能，以及对算法质量度量标准和优化方法的研究。

从理论计算机科学的角度，清华大学计算法学主要研究证明机器可通过有限的时间和空间解决的问题的理论性质，以及计算机系统的可靠性、效率、信誉和安全性等方面的理论研究。

同时，也开展了对现代数据算法、流形算法、计算复杂性理论和网络算法优化等方面的理论研究。

实验计算机科学，是清华大学计算法学领域的重点，主要围绕具体的算法的设计和实现，以及测试相关的理论方法和实践经验，开展研究和开发工作。

例如，在深度学习、机器学习、计算机视觉和自然语言的算法领域，将实现新的先进算法，提高它们的效率并使它们能够更好地应用到现实世界中。

应用计算机科学，清华大学计算法学主要偏向于软件开发，探索从计算机问题中提取算法，并将其应用于市场需求上。

同时，也重视与计算机科学应用领域之间的交互，对程序设计语言和软件设计技术进行研究，提供更强大的计算机系统，提高软件的可重复性、可维护性和可扩展性。

在人工智能方面，清华大学计算法学主要关注机器学习算法的理论和实践，近几年也开展了若干课题，如智能推理、多智能体系统、认知机器人学和自然语言质量等方面的应用研究，也开发了一些机器学习算法和模型，为企业提供更为实用的解决方案来优化自动化运营。