- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解析:因为v=s′=3t2+2t,所以此物体在t=3时的瞬时速度为 3×32+2×3= 33.故选D.
10
2.曲线y=x3在原点处的切线( B ) (A)不存在 (B)有1条,其方程为y=0 (C)有1条,其方程为x=0 (D)有2条,其方程为x=0和y=0
11
3.函数 y= 1 在区间[1,2],[2,3],[3,4]的平均变化率分别为 k1,k2,k3,则( A )
13
5.如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)= .
解析:由题意知切线的斜率k=f′(5)=-1,f(5)=-5+8=3, 所以f(5)+f′(5)=3-1=2. 答案:2
14
6.已知曲线y=ln x的切线过原点,则此切线的斜率为
.
答案: 1 e
15
2
知识链条完善
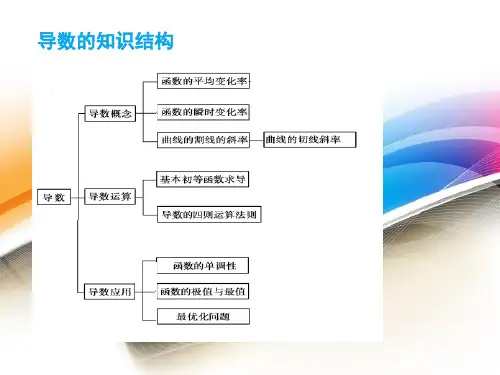
网络构建
把散落的知识连起来
一、函数的平均变化率
1.概念:对于函数 y=f(x), f x2 f x1 = y ,叫做函数 y=f(x)从 x1 到 x2 的
x2 x1
x
平均 变
化率.
2.几何意义:函数y=f(x)图象上两点(x1,f(x1)),(x2,f(x2))连线的 斜率 . 3.物理意义:函数y=f(x)表示变速运动的质点的运动方程,就是该质点在[x1,x2] 上的 平均 速度.
高频考点突破
6
2.与导数几何意义有关的结论 (1)切点既在曲线上,也在切线上,切点的坐标同时适合曲线方程和切线方程. (2)求曲线y=f(x)在点P(x0,f(x0))处的切线方程,点P(x0,f(x0))为切点,当切线 斜率存在(即f(x)在x=x0处可导)时,切线方程为y-f(x0)=f′(x0)(x-x0);当切线 斜率不存在(即f(x)在x=x0处不可导)时,切线方程为x=x0. (3) 已 知 曲 线 f(x) 的 切 线 斜 率 为 k, 则 切 点 (x0,f(x0)) 的 横 坐 标 x0 就 是 方 程 f′(x0)=k的解. (4)奇函数的导数是偶函数,偶函数的导数是奇函数. (5)周期函数的导数仍是周期函数,其周期与原函数的周期相同.
7
三、基本初等函数的导数公式 原函数
f(x)=c(c 为常数) f(x)=xα(α∈Q*)
f(x)=sin x f(x)=cos x f(x)=ax(a>0,且 a≠1)
f(x)=ex
f(x)=logax(a>0,且 a≠1)
f(x)=ln x
8
导函数 f′(x)=0 f′(x)= αxα-1 f′(x)= cos x f′(x)= -sin x f′(x)= axln a f′(x)= ex
x
(A)k1<k2<k3 (C)k3<k2<k1
(B)k2<k1<k3 (D)k1<k3<k2
解析:k1= 1 -1=- 1 ,k2= 1 - 1 =- 1 ,k3= 1 - 1 =- 1 ,所以 k1<k2<k3,故选 A.
2
2 3 2 l与直线x+4y-8=0垂直,则l的方程为( A ) (A)4x-y-3=0 (B)x+4y-5=0 (C)4x-y+3=0 (D)x+4y+3=0
3
二、导数的概念
1.函数 y=f(x)在 x=x0 处的导数 (1)定义
称函数 y=f(x)在 x=x0处的瞬时变化率 lim y = lim f x0 x f x0 为函数 y=f(x)在 x=x0
x x 0
x 0
x
处的导数,记作 f′(x0)或 y′ |xx0 ,即 f′(x0)=
4
2.函数 f(x)的导函数
称函数 f′(x)= lim f x x f x 为 f(x)的导函数.
x 0
x
5
拓展空间
1.概念理解 (1)导数即为自变量改变量趋近0时,函数平均变化率的极限. (2)f′(x0)表示函数f(x)在x=x0处的导数值;(f(x0))′是函数值f(x0)的导数,而函 数值f(x0)是一个常数,其导数一定为0,即(f(x0))′=0. (3)曲线y=f(x)在点P(x0,y0)处的切线是指P为切点,切线斜率为k=f′(x0)的切 线,是唯一的一条切线.曲线y=f(x)过点P(x0,y0)的切线,是指切线经过P点.点P 可以是切点,也可以不是切点,而且这样的直线可能有多条. (4)曲线未必在其切线的“同侧”,例如直线y=0(即x轴)是曲线y=x3在点(0,0) 处的切线. (5)直线与曲线公共点的个数不是曲线的切线的本质特征,直线与曲线只有一 个公共点,不能说明直线就是曲线的切线,反之,直线是曲线的切线,也不能说明 直线与曲线只有一个公共点,例如曲线y=x3在点(1,1)处的切线y=3x-2与曲线 y=x3还有一个交点(-2,-8).
lim y = lim f x0 x f x0 .
x x 0
x 0
x
(2)几何意义
函数f(x)在x=x0处的导数f′(x0)的几何意义是在曲线y=f(x)上点(x0,f(x0)) 处的 切线的斜率 (瞬时速度就是位移函数s(t)对时间t的导数).相应地,切 线方程为 y-f(x0)=f′(x0)(x-x0) .
第十四章 导数及其应用 第一节 导数的概念及其几何意义
1
备考方向明确
方向比努力更重要
复习目标 1.导数概念的实际背景. 2.曲线的切线的定义、导数的几何意义、理解导 数的概念. 3.根据导数的定义求函数 y=c(c 为常数),y=x,
y= 1 ,y=x2,y=x3,y= x 的导数. x
学法指导
1.理解导数的概念,会利用导数的 定义,求一些简单函数的导数. 2.熟记基本初等函数的导数公式. 3.正确区分曲线在某点处的切线与 过某点的切线.
f′(x)= 1 x ln a
f′(x)= 1 x
拓展空间 公式理解 利用公式求导时要特别注意不要将幂函数与指数函数的导数公式混淆,幂函 数的求导公式为(xn)′=nxn-1,而指数函数的求导公式为(ax)′=axln a.
9
温故知新
1.若物体的运动方程是s=t3+t2-1,t=3时物体的瞬时速度是( D ) (A)27 (B)31 (C)39 (D)33