下载文档原格式
![材料力学习题解答[第三章]](https://img.taocdn.com/s1/m/ffe185e2551810a6f52486fd.png)
材料力学第三章答案材料力学第三章答案【篇一：材料力学习题册答案-第3章扭转】是非判断题二、选择题0 b 2t?d316?1?? ? b wp??d316?1?? ?2c wp??d316?1?? ? d w3p??d316?1?? ?46.对于受扭的圆轴，关于如下结论：①最大剪应力只出现在横截面上；②在横截面上和包含杆件的纵向截面上均无正应力；③圆轴内最大拉应力的值和最大剪应力的值相等。
现有四种答案，正确的是（ a ）a ②③对b①③对c①②对d 全对7.扭转切应力公式?mnp?i?适用于（d）杆件。
pa 任意杆件；b 任意实心杆件；c 任意材料的圆截面；d 线弹性材料的圆截面。
9.若将受扭实心圆轴的直径增加一倍，则其刚度是原来的（ d a 2倍； b 4倍； c 8倍； d 16倍。
三、计算题1.试用截面法求出图示圆轴各段内的扭矩t，并作扭矩图2.图示圆轴上作用有四个外力偶矩me1 =1kn/m, me2 =0.6kn/m,）me3= me4 =0.2kn/m, ⑴试画出该轴的扭矩图；⑵若me1与me2的作用位置互换，扭矩图有何变化？(1)(2)解：me1与me2的作用位置互换后，最大扭矩变小。
3.如图所示的空心圆轴，外径d=100㎜，内径d=80㎜，m=6kn/m,m=4kn/m.请绘出轴的扭矩图，并求出最大剪应力解：扭矩图如上，则轴面极惯性矩id4?d4)(1004?804)(10?3)4p=?(32??32?5.8?10?6m4㎜，l=500tr4?103?50?103ip5.8?104．图示圆形截面轴的抗扭刚度为g ip，每段长1m,试画出其扭矩图并计算出圆轴两端的相对扭转角。
ab+ad=cdab=t1l?90?gipgipad=bc=t2l100gipgipcd=t3l40gipgip?90?100?4050?gipgip【篇二：《材料力学》第3章扭转习题解】[习题3-1] 一传动轴作匀速转动，转速n?200r/min，轴上装有五个轮子，主动轮ii输入的功率为60kw，从动轮，i，iii，iv，v依次输出18kw，12kw，22kw和8kw。
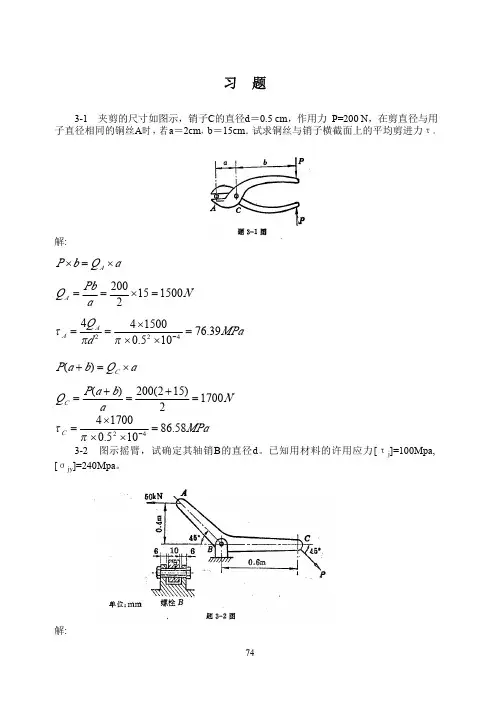
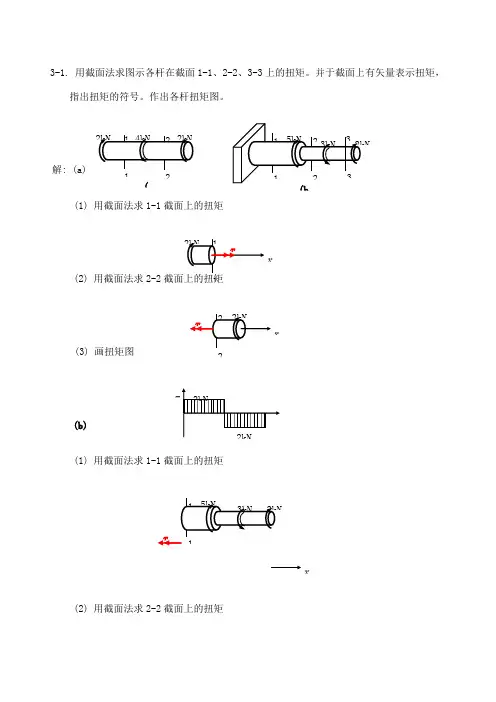
3-1. 用截面法求图示各杆在截面1-1、2-2、3-3上的扭矩。
并于截面上有矢量表示扭矩，指出扭矩的符号。
作出各杆扭矩图。
解: (a)(1) 用截面法求1-1截面上的扭矩(2) 用截面法求2-2(3) 画扭矩图(b)(1) 用截面法求1-1截面上的扭矩(2) 用截面法求2-2截面上的扭矩(21 x2xT xT 1x(3) 用截面法求3-3截面上的扭矩(4) 画扭矩图3.3. 直径D =50 mm10 mm 处的切应力，并求横截面上的最大切应力。
解: (1) 圆轴的极惯性矩点的切应力(2) 圆轴的抗扭截面系数 截面上的最大切应力注：截面上的切应力成线性分布，所以也可以用比例关系求最大切应力。
3.4. 发电量为1500 kW 的水轮机主轴如图示。
D =550 mm ，d =300 mm ，正常转速n =250 r/min 。
材料的许用剪应力[τ]=500 MPa 。
试校核水轮机主轴的强度。
解：(1) 计算外力偶矩(2) 计算扭矩 (3) 2T 4kN.(4) 强度校核强度足够。
注：强度校核类问题，最后必需给出结论。
3-5. 图示轴AB 的转速n =120 r/min ，从B 轮输入功率P =44.1 kW ，功率的一半通过锥形齿轮传送给轴C ，另一半由水平轴H 输出。
已知D 1=60 cm ，D 2=24 cm ，d 1=10 cm ，d 2=8 cm ，d 3=6 cm ，[τ]=20 MPa 。
试对各轴进行强度校核。
解：（1（2（3）计算抗扭截面系数 （4）强度校核强度足够。
3-6. 图示阶梯形圆轴直径分别为d 1=40 mm ，d 2=70 mm ，轴上装有三个带轮。
已知由轮3输入的功率为P 3=30 kW ，轮1输出的功率为P 1=13 kW ，轴作匀速转动，转速n =200 r/min ，[θ]=2 o /m 。
试校核轴的强度和刚度。
解：(1) 计算外力偶矩(2) 计算扭矩(3)(4) 强度校核强度足够。
第三章扭转之阳早格格创做一、利害推断题1.圆杆受扭时，杆内各面处于杂剪切状态. （×）2.杆件受扭时，横截里上的最大切应力爆收正在距截里形心最近处. （×）3.薄壁圆管战空心圆管的扭转切应力公式真足一般. （×）4.圆杆扭转化形真量上是剪切变形. （×）5.非圆截里杆没有克没有及应用圆截里杆扭转切应力公式，是果为非圆截里杆扭转时“仄截里假设”没有克没有及创造. （√）6.资料相共的圆杆，他们的剪切强度条件战扭转强度条件中，许用应力的意思相共，数值相等. （×）7.切应力互等定理仅适用于杂剪切情况. （×）8.受扭杆件的扭矩，仅与杆件受到的转矩（中力奇矩）有闭，而与杆件的资料及其横截里的大小、形状无闭. （√）9.受扭圆轴正在横截里上战包罗轴的纵背截里上均无正应力. （√）10.受扭圆轴的最大切应力只出当前横截里上. （×）11.受扭圆轴内最大推应力的值战最大切应力的值相等. （√）12.果木料沿纤维目标的抗剪本领好，故若受扭木量圆杆的轴线与木料纤维目标仄止，当扭距达到某一极限值时，圆杆将沿轴线目标出现裂纹. （×）二、采用题1.内、中径之比为α的空心圆轴，扭转时轴内的最大切应力为τ，那时横截里上内边沿的切应力为（ B）A τ；B ατ；C 整； D（2.真心圆轴扭转时，没有爆收伸服的极限扭矩为T，若将其横截里里积减少一倍，则极限扭矩为（ C ）3.二根受扭圆轴的曲径战少度均相共，但是资料C分歧，正在扭矩相共的情况下，它们的最大切应力τ、τ战扭转角ψ、ψ之间的闭系为（ B ）τ2,φ1=φτ2,φ2,φ1=φ2,φ24.阶梯圆轴的最大切应力爆收正在（ D ）A 扭矩最大的截里；B 曲径最小的截里；C 单位少度扭转角最大的截里；D 没有克没有及决定.5.空心圆轴的中径为D，内径为d, α=d／D,其抗扭截里系数为（ D ）6.对付于受扭的圆轴，闭于如下论断：①最大剪应力只出当前横截里上；②正在横截里上战包罗杆件的纵背截里上均无正应力； ③圆轴内最大推应力的值战最大剪应力的值相等. 现有四种问案，精确的是（ A ）A ②③对付B ①③对付C ①②对付D 齐对付D ）杆件.A 任性杆件；B 任性真心杆件；C 任性资料的圆截里；D 线弹性资料的圆截里.θ与（A ）无闭.A 杆的少度；B 扭矩；C 资料本量；D 截里几许本量.9.若将受扭真心圆轴的曲径减少一倍，则其刚刚度是本去的（ D ）A 2倍；B 4倍；C 8倍；D 16倍.三、估计题1.试用截里法供出图示圆轴各段内的扭矩T ，并做扭矩图⑴试画出该轴更？.3.如图所示的空心圆轴，中径D=100㎜，内径d=80㎜，l=500㎜，M=6kN/m,M=4kN/m. 请画出轴的扭矩图，并供出最大剪应力解：扭矩图如上，则轴里极惯性矩I P则最大剪应力τmax4．图示圆形截里轴的抗扭刚刚度为1m,试画出其扭矩图并估计出圆轴二端的相对付扭转角.解：φAD=φAB+φBC+φCD φφ所以φ5.如图所示的阶梯形传动轴中，A轮输进的转矩M=800N•m,B﹑C战D轮输出的转矩分别为==300N•m，=200N•m.传动轴的许用切应力[τ]=400Mpa,许用扭转角[θ]=1°/m,资料的剪切弹性模量G=80Gpa.⑴试根据轴的强度条件战刚刚度条件，决定传动轴各段的曲径.⑵若将传动轴改为等截里空心圆轴，并央供内中曲径之比α=d/D=0.6,试决定轴的中径；并比较二种情况下轴的沉量.解： （1τ］对付于AB 段共理得AC 段的d 段d 所以d 1应与值38.5mm ，d 2应与值43.7mm,d 36.图示的传动轴少l=510㎜，曲径D=50㎜.现将此轴的一段钻成内径d=25㎜的内腔，而余下一段钻成d=38㎜的内腔.若资料的许用切应力[τ]=70Mpa,试供：⑵若央供二段轴内的扭转角相等，则二段的少度应分别为几？与，ρ即7.如图所示钢轴AD 的资料许用切应力[τ]=50Mpa ，切变模量G=80Gpa,许用扭转角[θ°／m.效率正在轴上的转矩M=800N •m ，1200N •m ，M=400N •m.试安排此轴的曲径. 解：由题意轴中最大扭矩为800N •Mg 根据轴的强度条件ττ］ 所以根据轴的刚刚度条件所以即轴的曲径应与值43.4mm.8. 钻探机钻杆中经D=60㎜,内径d=㎜,功率P=7.355KW ，轴的转速n=180r/min,杆钻进土层的深度l=40m,资料的切变模量G=80Gpa ，许用切应力[τ]=40Mpa ，假设土壤对付钻杆的阻力沿少度匀称分散，试供： ⑴土壤对付钻杆单位少度的阻力矩m ； ⑵做钻杆的扭矩图，并举止强度校核；⑶估计A 、B 截里的相对付扭转角.解：（1）由ML-T=0 则(2)扭矩图如图所示（3）二端截里的相对付扭转角为Φ感动土木0902班石李、臧明近共教！。
第一章 绪论1-1 连续介质假设的条件是什么？答：所研究问题中物体的特征尺度L ，远远大于流体分子的平均自由行程l ，即l/L<<1。
1-2 设稀薄气体的分子自由行程是几米的数量级，问下列二种情况连续介质假设是否成立？ （1）人造卫星在飞离大气层进入稀薄气体层时； （2）假象地球在这样的稀薄气体中运动时。
答：（1）不成立。
（2）成立。
1-3 粘性流体在静止时有没有切应力？理想流体在运动时有没有切应力？静止流体没有粘性吗？ 答：（1）由于0=dy dv ，因此0==dydvμτ，没有剪切应力。
（2）对于理想流体，由于粘性系数0=μ，因此0==dydvμτ，没有剪切应力。
（3）粘性是流体的根本属性。
只是在静止流体中，由于流场的速度为0，流体的粘性没有表现出来。
1-4 在水池和风洞中进行船模试验时，需要测定由下式定义的无因次数（雷诺数）νUL=Re ，其中U 为试验速度，L 为船模长度，ν为流体的运动粘性系数。
如果s m U /20=，m L 4=，温度由C ︒10增到C ︒40时，分别计算在水池和风洞中试验时的Re 数。
（C ︒10时水和空气的运动粘性系数为410013.0-⨯和410014.0-⨯，C ︒40时水和空气的运动粘性系数为4100075.0-⨯和410179.0-⨯）。
答：C ︒10时水的Re 为：()()72410154.6/10013.04)/(20Re ⨯=⨯⨯==-sm m s m ULν。
C ︒10时空气的Re 为：()()72410714.5/10014.04)/(20Re ⨯=⨯⨯==-sm m s m ULν。
C ︒40时水的Re 为：()()82410067.1/100075.04)/(20Re ⨯=⨯⨯==-sm m s m ULν。
C ︒40时空气的Re 为：()()62410469.4/10179.04)/(20Re ⨯=⨯⨯==-sm m s m ULν。
第 3 章扭转思考题3-1何谓扭矩？扭矩的正负号如何规定的？如何计算扭矩？答轴在外力偶矩作用下，由截面法求出的横截面上分布内力向截面形心简化的合力（力偶矩）称为扭矩。
对扭矩T的正负规定为：若按右手螺旋法则把T表示为矢量，当矢量方向与截面的外法线n的方向一致时，T为正；反之为负。
用截面法计算扭矩，注意截面位置应偏离外力偶矩作用面。
3-2薄壁圆筒、圆轴扭转切应力公式分别是如何建立的？假设是什么？公式的应用条件是什么？答等厚薄壁圆筒在两端垂直于轴线的平面内作用大小相等而转向相反的外力偶M e所做试验结果现象表明，当薄壁圆筒扭转时，其横截面和包含轴线的纵向截面上都没有正应力，横截面上只有切应力⎜，因为筒壁的厚度 ™很小，可以假设沿薄壁圆筒筒壁厚度切应力不变。
又因在同一圆周上各点情况完全相同，应力也就相同，从而建立薄壁圆筒扭转切应力计算公式；在圆轴两端施加一对大小相等、方向相反的外力偶。
从实验中观察到的现象，假设轴变形后，横截面仍保持平面，其形状、大小与横截面间的距离均不改变，而且半径仍为直线（圆轴扭转平面假设），连同胡克定律和静力平衡条件推出圆轴扭转切应力计算公式。
公式应用条件为线弹性材料、小变形、等截面（锥度不大的变截面可近似用）。
3-3试述纯剪切和薄壁圆筒扭转变形之间的差异及相互关系。
答单元体 4 个互相垂直的面上只作用切应力的状态称为纯剪切；薄壁圆筒扭转变形时（忽略厚度影响）筒壁各点的应力状态为纯剪切。
3-4试述剪切胡克定律与拉伸（压缩）胡克定律之间的异同点及3 个弹性常量E, G, ⎧之间关系。
答剪切胡克定律⎜ = G©（反映角度的变化）与拉伸（压缩）胡克定律 ⎛ = E∑（反映长度的变化）皆为应力与应变成正比关系。
3 个弹性常量E, G, ⎧之间关系为G =E2(1 + ⎧ )。
3-5圆轴扭转时如何确定危险截面、危险点及强度条件？答等截面圆轴扭转时的危险截面为扭矩最大的横截面，变截面圆轴扭转时的危险截面在其扭矩与扭转截面系数比值最大的横截面；其危险点在该横截面的外边缘。
强度条件为⎜ max = T maxW pδ [⎜ ]3-6金属材料圆轴扭转破坏有几种形式？答塑性金属材料和脆性金属材料扭转破坏形式不完全相同。
塑性材料试件在外力偶作用下，先出现屈服，最后沿横截面被剪断，如图 a 所示；脆性材料试件受扭时，变形很小，最后沿与轴线约45°方向的螺旋面断裂，如图 b 所示。
T (x ) GI p (x ) T GI p 思考题 3-6 解图3-7 从强度方面考虑，空心圆轴为何比实心圆轴合理？答 对于相同的横截面面积（即用相同量材料），空心圆轴比实心圆轴的抗扭截面系数大， 从而强度高。
3-8 如何计算扭转变形？怎样建立刚度条件？什么样的构件需要进行刚度校核？ 答 （1）写出扭矩方程或扭矩图；相距 l 的两截面间的扭转角d ∏ = d x l l上式适用于等截面圆轴和截面变化不大的圆锥截面轴。
对等截面圆轴，若在长 l 的两横截面 间的扭矩 T 为常量，则∏ =Tl GI p圆轴扭转的刚度条件为max δ [⎝ ]对于等截面圆轴为⎝ max =T max GI pδ [⎝ ] 或⎝ max = T maxGI p⋅ 180︒ π δ [⎝ ]3-9 矩形截面轴的自由扭转切应力分布与扭转变形有何特点？如何计算最大扭转切应力与扭转变形？答轴扭转时，横截面边缘上各点的切应力都与截面边界相切，且 4 个角点处的切应力 为零；最大切应力⎜ max 发生在截面长边的中点处，而短边中点处的切应力⎜ 1 是短边上的最 大切应力。
其计算公式为⎜ max =T W t=T〈hb 2⎜ 1 = ©⎜ max（2）矩形截面杆扭转时，其横截面不再保持平面而发生翘曲。
杆件两端相对扭转角∏ =Tl G ®hb 3 TlGI t3-10 两根直径相同而长度和材料均不同的圆轴 1，2，在相同扭转作用下，试比较两者 最大切应力及单位长度扭转角之间的大小关系，答最大切应力相同；单位长度扭转角不同。
3-11 同一变速箱中的高速轴一般较细，低速轴较粗，这是为什么？答同一变速箱中的高速轴与低速轴指相对转速高低，其传递的功率相同（不计功率损耗），啮合处线速度相同。
要啮合处产生相同的线速度，则高速轴的啮合半径就较小；又因为啮合处相互作用力相同，该作用力对啮合半径就较小的高速轴线产生的外力偶矩就较小，从而在高速轴中产生的扭矩较小，故高速轴可做得较细。
3-12图示轴A和套筒B牢固地结合在一起，两者切变模量分别为G A和G B，两端受扭转力偶矩，为使轴和套筒承受的扭转相同而必须满足的条件是什么？思考题3-12 图答设套筒B的内、外径分别为d和D，则两者切变模量须满足下列关系：G B G A =D 4 d 4d 43-13 试画出空心圆轴扭转时，横截面上切应力分布规律图。
答思考题3-14 解图3-14 图示组合轴，中心部分为钢，外圈为铜。
两种材料紧密组合成一整体，若该轴受扭后，全部处于线弹性范围，试画出其横截面上的应力分布图。
思考题3-14 图思考题3-14 解图答3-15图示3 种闭口薄壁截面杆承受扭转作用，若3 种截面的横截面积A，壁厚 ™和承受的扭矩T均相同，则其扭转切应力最大和最小的各是哪种截面？思考题3-15 图答 ⎜ c max > ⎜ b max > ⎜ a max3-16图示承受扭矩的3 种截面形式，试分别画出其切应力沿壁厚的分布规律。
思考题3-16 图= 9549 ⋅ = 191 N ⊕ mM A = 9549 ⋅ = 9549 ⋅ = 1337 N ⊕ m习 题3-1求图示各轴的扭矩图，并指出其最大值。
(a)(a1)(c)(c1)解 (a) T max = 2M e ； (c) T max = 40 kN ⊕ m ；（b ） T max = M e(d) T max = 4 kN ⊕ m (b)(b1)(d)(d1)3-2图(a)所示某传动轴，转速 n = 500 r/min ，轮 A 为主动轮，输入功率 P A = 70 kW ，轮 B ，轮 C 与轮 D 为从动轮，输出功率分别为 P B = 10 kW ， P C = P D = 30 kW 。
（1）求轴内的最大扭矩；（2）若将轮 A 与轮 C 的位置对调，试分析对轴的受力是否有利。
(a)(b)解 （1） M B = 9549 ⋅P Bn10 500 P A 70n 500= 9549 ⋅ = 573 N ⊕ mπd1π d 2 = < ⎜ max 2M D = M C = 9549 ⋅ 用截面法如图(b)所示：P Cn30500AB段AC段CD段T1 = M B = 191 N ⊕ mT2 = M B M A = 1146 N ⊕ m T3 = M D = 573 N ⊕ m由以上结果得T max = 1146 N ⊕ m（2）若将轮A与轮C位置对调，则T1，T3值不变，而T2 = M B + M C = 764 N ⊕ mT max = 764 N ⊕ m其绝对值比第（1）种情况小，即对轴的受力有利。
3-3 试绘出图示截面上切应力的分布图，其中T为截面的扭矩。
(a1) (b1) (c1)3-4 图示圆截面轴，AB与BC段的直径分别为d1与d 2，且d1 = 4d 2 / 3。
求轴内的最大扭转切应力。
解BC段⎜ max 2 = M eW p2 = 16M eπd 23AB段⎜ max1 = 2M eW p1= 16 ⋅ 2M e3= 32M e4 3 313.5M eπd 23( ϒ 40 / π ⋅ 42 ⋅ 10 ⋅ '1 ∞≤ ƒM e = 189 MPa41 ⋅1⋅10 2π 75 ⋅10= 2.52 ⋅10 rad 8 ⋅1.5 ⋅10 3 ⋅ 50 ⋅10 3 4 ⋅ + 2 = 458 MPa 8FD (4c + 2) 8(4c 3) 解 （1）⎜ max = = 50πd[⎜ ]= 373 MPa < [⎜ ],安全。
8FD 8 ⋅1.5 ⋅10 3 ⋅ 50 ⋅10 3⎜ max = ⎜ max 2 =16M eπd 233-5一受扭等截面薄壁圆管，外径 D = 42 mm ，内径d = 40 mm ，两端受扭力矩 Me = 500 N ⊕ m ，切变模量 G = 75 GPa 。
试计算圆管横截面与纵截面上的扭转切应力，并计算管表面纵线的倾斜角。
解 （1）⎜ max =M e W p=16M eπD 3 1 〈 4)=16 ⋅ 5003 94' 42 ∞ = 194 MPa（2）若考虑薄壁 ，可求其平均扭转切应力⎜ =讨论：误差或=2πR 2™194 189194194 189194 500 292 ⋅ 100% = 2.6% < 5%⋅100% = 2.6% < 5%故薄壁管一般均用简化公式求平均切应力。
（3） © = ⎜ G = 189 ⋅10 6933-6 设有 1 密圈螺旋弹簧，承受轴向载荷 F = 1.5 kN 作用。
设弹簧的平均直径D = 50 mm ，弹簧丝的直径 d = 8 mm ，弹簧丝材料的许用切应力 [⎜ ] = 450 MPa ，试校核弹簧的强度。
50 3π ⋅ 83 ⋅10 9 ⋅ 4 ⋅ 38 = ⋅ 100% = 1.78% < 5% 450强度满足（工程中误差小于 5%，认为技术满足要求）。
（2）用简化公式= πd 3 π ⋅ 83 ⋅10 9讨论：由于 c = D d = 50 8 = 6.25 < 10 ,故应用解（1）中修正公式计算（（1）（2）计算值相差较大）。
3-7一圆截面等直杆试样，直径d = 20 mm ，两端承受外力偶矩 Me = 150 N ⊕ m 作用。
设由试验测得标距 l 0 = 100 mm 内轴的相对扭转角 ∏ = 0.012 rad ，试确定切变模量 G 。
解∏ = Tl 0 GI p =M e l 0 GI p许用切应力 [⎜ ] = 80 MPa ，单位长度许用扭转角 [⎝ ] = 1.0 / m ，切变模量 G = 80 GPa 。
试T = 9549 ⋅ = 9549 ⋅ = 2546 N ⊕ mδ [⎝ ] πd π G [⎝ ] = 6.56 ⋅ 10 m = 65.6 mm [⎜ ] = 80 MPa ， G = 80 GPa ， [⎝ ] = 1.2 / m 。
试校核轴的强度和刚度。
[⎜ ]πD d 4 80 4G =M e l 0∏I p=M e l 0 ∏ ⊕ πd4150 ⋅ 0.1⋅ 32 0.012π ⋅ 20 4 ⋅10 12= 79.6 GPa3-8设有 1 圆截面传动轴，轴的转速n = 300 r/min ，传递功率 P = 80 kW ，轴材料的︒设计轴的直径。
