下载文档原格式
平行四边形面积四等分的方法概述说明1. 引言1.1 概述本文将探讨平行四边形面积四等分的方法，该问题涉及到如何将一个平行四边形分割成四个具有相同面积的部分。
通过研究和介绍不同的解决方法，我们可以深入理解这一几何难题，并找到有效的解决方案。
1.2 文章结构本文主要包括五个部分：引言、正文、方法介绍、实验与结果以及结论和展望。
接下来的正文部分将详细介绍平行四边形面积四等分问题，并对不同方法进行系统性的介绍和比较。
实验与结果部分将设计相关实验并进行数据分析。
最后，我们将总结主要研究结论并提出改进方向。
1.3 目的本文旨在描述并总结目前已知的平行四边形面积四等分方法，为读者提供一个全面了解该问题以及解决方案的资源。
同时，本研究也希望通过实验与结果的讨论，能够对各种方法的优劣进行评估，并提出进一步改进策略。
通过这一工作，我们期望能够为学术研究和实践中遇到类似问题的读者提供有价值的参考和启示。
2. 正文平行四边形是一种具有特殊性质的四边形，其两组对边分别平行且相等长度。
本篇文章旨在介绍平行四边形面积四等分的方法。
首先，我们需要了解什么是面积四等分。
所谓面积四等分，指的是将一个平行四边形划分为四个面积相等的部分。
这是一个具有一定难度的几何问题，但通过合理的方法与技巧，我们可以轻松地实现这一目标。
接下来，我们将介绍三种常用的方法来实现平行四边形面积的四等分。
3.1 方法一：对角线法该方法是最直观也最简单的一种方法。
即通过连接平行四边形的两组对角线，将其划分为两个不重叠的三角形。
由于三角形面积公式为底乘以高再除以2，因此使得两个三角形面积相等即可实现面积四等分。
3.2 方法二：高度法这种方法依托于平行四边形内部垂直相交线段之间长度之比与面积之比的关系。
通过找到合适位置并画出垂直交线段，在确定好长度比例后进行切割即可达到面积四等分的目标。
3.3 方法三：三角形切割法该方法利用平行四边形可以视为两个相等的三角形之和。
图形与面积专题1、小方桌面的边长是1米，把它的四边撑开，就成了一张圆桌面（如图）。
求圆桌面的面积。
2、把底面半径是6厘米，高10厘米的圆柱体切割成若干等分，拼成一个近似的长方体。
在这个切拼过程中，体积与表面积有没有发生变化？如果没有发生变化，请说明理由。
如果发生变化，请计算增加或减少的数量。
3、我们都知道：圆的周长与直径的比值就是圆周率。
它是一个无限不循环小数，用字母Л表示。
但你未必知道“圆方率”，就让我们一起来探索吧！【探索】把一个棱长a厘米的正方体削成一个最大的圆柱体。
求这个圆柱体与正方体体积和表面积比。
（计算涉及圆周率，直接用Л表示）4、如图已知扇形的半径OA=OB=4厘米，45∠=°，AC垂直OB于点C。
A O B那么图中阴影部分的面积是多少平方厘米？（4分）5、如图三角形ABC中，EF平行于BC，AB=4AE，求三角形甲、乙、丙的面积之比？6、如右图正方形的面积是36平方厘米，△ABC的面积比△ACE的面积大2平方厘米。
DE的长度是多少厘米？7、如图，圆的半径是2厘米，请分别求出大正方形和小正方形的面积。
8、如图：求图中阴影部分的面积。
（单位：厘米）9、已知正方形的面积是80平方厘米，求圆的面积。
10、求右图阴影部分的周长和面积。
（单位：厘米）11、求下图中阴影部分面积。
（单位：厘米）12、如图，正方形的边长和圆的直径都是313、如下图所示的长方形中，三角形ADE 与四边形DEBF 、三角形CDF 面积相等，求三角形DEF 的面积是多少？C DF14、在一个棱长为8cm的正方体玻璃缸种，盛有一定深度的水，将棱长为4cm 的正方体铁片放入缸中。
（1）若缸中水深为6cm，则水会上升多少？（2）若缸中水深为2cm，则水深上升多少？15、求图中阴影部分的面积（单位：厘米）16、如图，梯形ABCD的面积是45平方厘米，下底AB=10厘米，高6厘米，三角形DOC的面积为5平方厘米，求三角形AOB的面积。
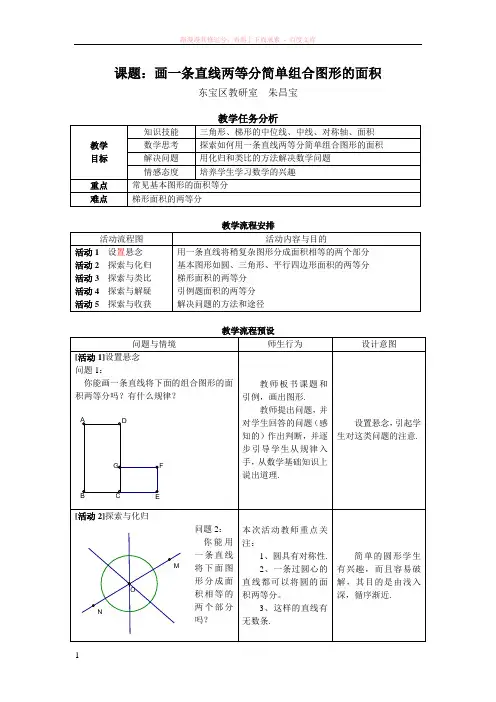
课题：画一条直线两等分简单组合图形的面积东宝区教研室 朱昌宝教学 目标 知识技能三角形、梯形的中位线、中线、对称轴、面积 数学思考 探索如何用一条直线两等分简单组合图形的面积 解决问题 用化归和类比的方法解决数学问题 情感态度培养学生学习数学的兴趣重点 常见基本图形的面积等分 难点 梯形面积的两等分教学流程安排活动流程图 活动内容与目的活动1 设置悬念 活动2 探索与化归 活动3 探索与类比 活动4 探索与解疑 活动5 探索与收获 用一条直线将稍复杂图形分成面积相等的两个部分 基本图形如圆、三角形、平行四边形面积的两等分 梯形面积的两等分 引例题面积的两等分 解决问题的方法和途径问题与情境师生行为 设计意图[活动1]设置悬念 问题1：你能画一条直线将下面的组合图形的面积两等分吗？有什么规律？教师板书课题和引例，画出图形.教师提出问题，并对学生回答的问题（感知的）作出判断，并逐步引导学生从规律入手，从数学基础知识上说出道理.设置悬念，引起学生对这类问题的注意.[活动2]探索与化归问题2： 你能用一条直线将下面图形分成面积相等的两个部分吗？本次活动教师重点关注：1、圆具有对称性.2、一条过圆心的直线都可以将圆的面积两等分。
3、这样的直线有无数条.简单的圆形学生有兴趣，而且容易破解，其目的是由浅入深，循序渐近.EDAB CG FOMN问题与情境师生行为 设计意图问题3：你能用一条直线将下列图形的面积两等分吗？说明理由.［活动3］探索与类比用一条直线两等分矩形、正方形的面积.本次活动教师重点关注：1、两等分三角形的面积至少有三条，目前学生易接受理论支撑是“等底等高的两个三角形面积等积”..2、平行四边形两等分面积只要找到中心对称点，任意过对称中心点的直线都可以将其面积两等分,这样的直线有无数条.3、引导学生关注两等分平行四边形的数学基础知识（分析思路和说理是重点）.4、用类比的思想讨论矩形和正方形两等分面积.三角形和平行四边形（含短形和正方形）也是最简单的图形，其目的在于找规律，说理由，用类此的思想同时解决矩形和正方形的等分问题，有一般包涵特殊的思想.问题4：讨论,是否过梯形的O 点作任意一条直线就可以将梯形的面积两等分 教师关注要点： 1、梯形中位线不能将梯形面积两等分（直观法或等高不等底的两个梯形面积不相等）.2、过梯形两底的中点的连线可以将梯形面积两等分,为什么？ 突出转化的思想，把梯形转化为三角形和平行四边形来考虑，一方面培养学生解决问题的途径（化难为易,应用旧知），另一方面又加强了知识简单的相互联系，灵活运用,达到开发思维的目的.编制这一个活动，给出了两种方法，再对梯形的一般性进行研究，特别是“过上、下底且经过梯形中位线的中点”这三个要素进行讨论，有利于培养学生思维的缜密和严谨，方法一：作梯形的中位线能等分两个相等的面积吗？为什么？3、取AB 中点E ，连接BE 交CB 的延长线于F ，由于S △ADE =S △FBE ，再作FC 中点G ，直线DG 将梯形面积两等分（学生说明理由）.方法二：把梯形转化为三角形来等分GFEA C BDDBACODACBF E A CB D方法三：作AD 、BC 中点的连线A CBD4、学生说明理由有利于培养学生在特殊圆形中求一般规律，在一般图形中求特殊解法.举反例是一种反证思想，培养学生发散思维，求异思维，对于问题的理解将更加深入.方法四：把梯形转化为平行四边形来等分5、同转化为三角形道理一样（学生说明理由）.方法五：取中位线的中点，在什么条件下作一直线将梯形面积两等分？6、条件：过上下底边并且经过中点的直线可以将梯形面积两等分（要求学生从多个角度说明理由）.7、讨论：两等分平行四边形和梯形有什么不同？在条件上有哪些限制，举反例.问题先简单后复杂，解题先易后难，加强思维培养，提高解题能力.[活动4]探索与解疑 解答引例O 2O 1EDABCGF方法一：作两矩形的对角线，两交点O 1O 2连接的直线即为所作.学生实践、教师关注要点：把这个组合图形分成两个基本图形，再利用以上所学的结论(分开看). 基于以上活动、支手实践和规律探索，学生基本上可以从方法一、方法二中解决问题，对于方法三和利用梯形存在困难，因此观察图形特点，从“分”和“补”两个方面通盘考虑问题，使问题的解决更加灵活，手段更加多样，道理更加充分，思路更加清晰. 通过交流，让学生用自FGE A CBDE FA CBD方法二：作两矩形的对角线，两交点O 1O 2连接的直线即为所作.己的语言清楚表达解决问题的过程，提高语言表达能力.方法三：作矩形ABEH 和矩形GFHD 的对角线，O 1O 2所在的直线平分这个组合图形补全图形，从整体入手。
