初中数学竞赛专题分类解析第四讲：平行四边形和梯形讲义

平行四边形和梯形一、平行四边形平行四边形是一种特殊的四边形，具有一些独特的性质和特征。

在数学和几何学中，学习平行四边形的性质和应用是非常重要的。

1. 定义和特征平行四边形是一个四边形，其中相对的两边是平行的，并且相对的两条边相等。

平行四边形的定义可以表述如下：•两对相对边平行：即AB || CD，AB || CD，且AB ≠ CD。

•两对相对边相等：即AB = CD，AD = BC。

2. 性质和公式平行四边形具有以下性质和公式：•相对角相等：平行四边形的相对角相等，即∠A = ∠C，∠B =∠D。

•对角线分割成等长的线段：平行四边形的对角线交于O点，且AO = OC，BO = OD。

•对角线互相平分：平行四边形的对角线互相平分，即AO = OC = BO = OD。

•面积公式：平行四边形的面积可表示为S = 底边长 × 高，其中高指的是从底边到对顶边的垂直距离。

3. 应用平行四边形的性质和特征在实际生活中有许多应用。

以下是其中几个常见的应用场景：•建筑设计：平行四边形的结构稳定性使其在建筑设计中被广泛应用，例如桥梁、楼房等。

•工程测量：在工程测量中，平行四边形的性质可以用于测量地面的倾斜度以及其他距离和角度的测量。

•图像处理：在图像处理中，平行四边形的性质可以用于图像的纠偏、校正和变形处理。

二、梯形梯形是一种特殊的四边形，具有一些与平行四边形相似的性质。

了解梯形的定义和特征对于数学和几何学的学习是很重要的。

1. 定义和特征梯形是一个四边形，其中有两条平行边，称为底边和顶边，其他两条非平行边称为腰边。

梯形的定义可以表述如下：•有两条平行边：即AB || CD，且AB ≠ CD。

•有两条非平行边：即AD ≠ BC。

2. 性质和公式梯形具有以下性质和公式：•相邻角补角为180°：梯形的相邻内角的补角之和为180°，即∠A + ∠B = 180°，∠C + ∠D = 180°。

平行四边形和梯形知识点归纳1.平行四边形的定义及性质平行四边形是指具有两对对边平行的四边形。

以下是平行四边形的一些性质：-对角线相互平分-对角线相等-相邻角互补（和为180度）-同位角相等-任意一对相邻内角互补-对边相等2.平行四边形的判定方法判定一个四边形是否为平行四边形可以使用以下方法：-两组对边分别平行-对角线互相平分-一组对边相等且对角线互相分割成相等的部分3.梯形的定义及性质梯形是指至少有一对对边平行的四边形。

以下是梯形的一些性质：-底边平行-顶角互补（和为180度）-一对对边相等的梯形为等腰梯形-高线平行于底边且等于底边长度乘以高线对应的比例4.梯形的判定方法判定一个四边形是否为梯形可以使用以下方法：-一对对边平行-一对对边相等且没有其他平行边-底边长度与高线长度成比例5.平行四边形和梯形的应用5.1平行四边形的应用平行四边形的性质和判定方法在几何学的各个分支中常常被应用，例如：-在解决平面图形的计算问题中，我们经常会遇到平行四边形的形状，通过了解平行四边形的性质和判定方法，可以更快地解决问题。

-在建筑和土木工程中，平行四边形的形状常常出现，例如建筑物的立面图等。

了解平行四边形的性质可以帮助我们更好地设计和构建建筑物。

5.2梯形的应用梯形也在几何学的各个领域中被广泛应用，例如：-在计算梯形的面积时，我们可以通过将梯形分割成平行四边形和直角三角形，从而简化计算。

-在图形的投影中，梯形的形状常常出现，通过了解梯形的性质，可以更好地理解和分析图像的特点。

结论平行四边形和梯形是几何学中重要的概念，它们具有独特的性质和判定方法。

通过了解这些知识点，我们可以更好地理解和应用于实际问题中。

在解决几何学问题时，熟练掌握平行四边形和梯形的性质和判定方法是非常重要的。

希望通过本文库文档的详细介绍，您对平行四边形和梯形有了更深入的理解。

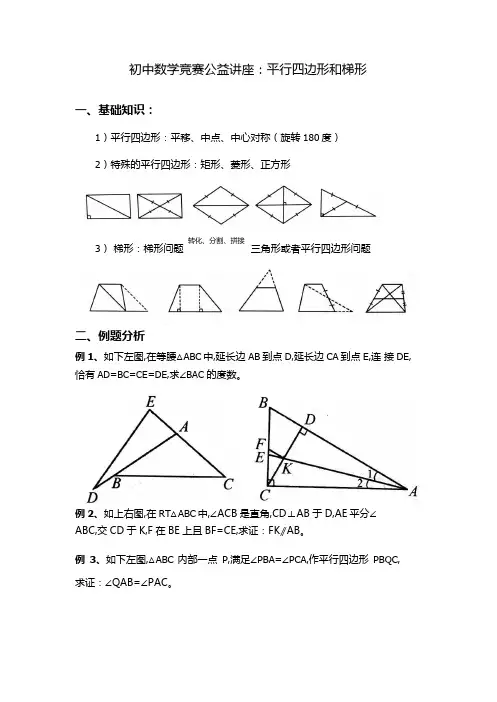
初中数学竞赛公益讲座：平行四边形和梯形一、基础知识：1）平行四边形：平移、中点、中心对称（旋转 180 度）2）特殊的平行四边形：矩形、菱形、正方形3） 梯形：梯形问题 转化、分割、拼接 三角形或者平行四边形问题二、例题分析例 1、如下左图,在等腰△ABC 中,延长边 AB 到点 D ,延长边 CA 到点 E ,连 接 DE ,恰有 AD=BC=CE=DE ,求∠BAC 的度数。

例 2、如上右图,在 RT △ABC 中,∠ACB 是直角,CD⊥AB 于 D,AE 平分∠ ABC,交 CD 于 K,F 在 BE 上且 BF=CE,求证：FK ⫽AB 。

例 3、如下左图,△ABC 内部一点 P ,满足∠PBA=∠PCA ,作平行四边形 PBQC , 求证：∠QA B=∠PAC 。

例4、如上右图,已知A、B 是两个定点,C 是位于直线AB 某一侧的一个动点, 分别以AC、BC 为边,在△ABCDE 外部作正方形CADI、CBEF,求证无论C 点在什么位置上,DE 的中点M 的位置不变。

例5、如下左图,梯形ABCD 中,AB⫽CD,BC⊥CD,AB=2,CD=4,点E 是BC 上的一个动点,连接并延长EA 到点F,使得EF:AE=2:1,连接并延长ED 到点G,使得EG:ED=3:2,以EF 和EG 为临边作平行四边形EFHG,连接EH 交AD 于点P,1）求EH 的最小长度；2）求证：P 是定点。

例6、如上右图,四边形ABCD 中,点E、F 分别在边AB、CD 上,连接BF、CE 交于点P,连接AF、DE 交于点Q,若四边形EQFP 是平行四边形,求证：四边形ABCD 是梯形。

例 7、如下图,等腰梯形ABCD,对角线AC 与BD 交于点O,M 、N 分别为腰AB 和CD 上的点,且AM=CN,连接MN 分别交BD、AC 于点P、Q,求证：MP=QN。

三、练习题1、如下左图,在锐角△ABC 中,作高BD 和EC,过B、C 分别作ED 的垂线BF和CG,求证：EF=DG2、如上右图,在直角梯形ABCD 中,∠A和∠B是直角,AB=2,点P 为AB 的中点,连接PC、PD,若∠PDC 也是直角,就△PCD 面积的最小值。

初三数学复习教案平行四边形与梯形的性质与判定一、平行四边形的性质与判定1. 平行四边形的定义平行四边形是指四边形的对边是平行的四边形。

具体而言，如果一个四边形的对边两两平行，则它可以被称为平行四边形。

2. 平行四边形的性质（1）对边相等：平行四边形的对边长度相等。

（2）对角线相交：平行四边形的对角线相交于一点，并且这个交点将对角线分为两条相等的线段。

（3）同位角相等：平行四边形的内角与外角以及同位角之间互相相等。

（4）对角矩形：如果一个平行四边形的所有内角都是直角，则它可以被称为对角矩形。

3. 平行四边形的判定（1）对边相等判定：如果一个四边形的对边长度相等，则它是一个平行四边形。

（2）对角线比例判定：如果一个四边形的两条对角线被一条直线分成比例相等的线段，则它是一个平行四边形。

二、梯形的性质与判定1. 梯形的定义梯形是指有两个平行边的四边形，这两个平行边被称为梯形的底边，而两个非平行边被称为梯形的腰。

2. 梯形的性质（1）底角相等：梯形的两个底角相等。

（2）腰角相等：梯形的两个腰角相等。

（3）对腰异侧角互补：梯形的对腰异侧角互为补角。

（4）对角矩形：如果一个梯形的两个连续内角互为补角，则它可以被称为对角矩形。

3. 梯形的判定（1）底边平行判定：如果一个四边形的两个非平行边被一条直线分成比例相等的线段，则它是一个梯形。

（2）腰长比例判定：如果一个四边形的两个非平行边长度成比例，则它是一个梯形。

总结：平行四边形和梯形是初三数学中重要的几何概念。

通过了解平行四边形和梯形的性质与判定方法，我们可以更好地理解和应用这些概念，解决与其相关的数学问题。

在做题和复习时，我们应该熟练掌握平行四边形和梯形的定义、性质和判定方法，灵活运用于解题过程中。

这样可以提高我们的数学解题能力，更好地应对考试和学习中的数学难题。

了解平行四边形和梯形的性质平行四边形和梯形是初中数学中的基本几何概念。

它们具有一些独特的性质和规律，对于我们深入理解几何形状的特点和应用具有重要意义。

本文将介绍平行四边形和梯形的定义、性质及相关的数学定理。

1. 平行四边形的性质平行四边形是由四条边和四个角组成的几何形状，具有以下性质：1.1 对边平行性质平行四边形的对边两两平行，即任意一对相对的边都是平行的。

1.2 对角线性质平行四边形的对角线互相平分，即对角线的交点将对角线分成两等分。

1.3 同底角性质平行四边形的对边平行，所以同一边上的两个相邻内角和是180度。

1.4 同位角性质平行四边形的对边平行，所以对应的内角是相等的。

2. 梯形的性质梯形也是由四条边和四个角组成的几何形状，具有以下性质：2.1 底边平行性质梯形的底边是两边中较长的边，梯形的两个底边是平行的。

2.2 上底角性质梯形的两个上底角是相等的。

2.3 下底角性质梯形的两个下底角是相等的。

2.4 对角线性质梯形的对角线互相平分，即对角线的交点将对角线分成两等分。

3. 相关定理在研究平行四边形和梯形的性质时，还有一些重要的定理需要了解：3.1 平行四边形的性质定理如果一个四边形的对边是平行的并且相等，则这个四边形是平行四边形。

3.2 梯形的性质定理如果一个四边形有两个边是平行的，那么这个四边形是梯形。

3.3 梯形的中线定理在梯形中，两个中线的长度相等，且平行于底边。

3.4 万能定理如果一个四边形的一对对边是平行且相等，那么这个四边形是平行四边形。

总结：通过了解平行四边形和梯形的定义、性质，我们可以更深入地理解这两种几何形状的特点。

平行四边形的对边平行，对角线互相平分，同位角相等；梯形的底边平行，对角线互相平分，上底角相等，下底角相等。

同时，还有一些相关的数学定理可以应用于求解问题。

掌握这些知识，有助于我们在解题过程中灵活运用几何概念，提高数学能力。

认识平行四边形与梯形平行四边形和梯形是几何学中常见的两种特殊四边形。

它们具有独特的性质和特点，在数学中起到重要的应用和作用。

本文将介绍平行四边形和梯形的定义、性质以及它们的区别。

一、平行四边形平行四边形是指具有两组对边分别平行的四边形。

下面给出平行四边形的定义和性质。

1. 定义平行四边形的定义是：具有两组对边分别平行的四边形。

2. 性质（1）相对边相等：平行四边形的对边长度相等。

（2）相对角相等：平行四边形的对角线所夹的角相等。

（3）同位角相等：同位角是指相邻并位于同一边的两个内角，平行四边形的同位角相等。

（4）对角线的交点连线是平分线：对于平行四边形ABCD，其对角线AC和BD的交点O，连接OA、OB、OC、OD，这四条线段互相平分。

（5）对边平行：平行四边形的对边互相平行。

二、梯形梯形是指具有一对平行边的四边形。

下面给出梯形的定义和性质。

1. 定义梯形的定义是：具有一对平行边的四边形。

2. 性质（1）底角相等：梯形的两个底角相等。

（2）顶角相等：梯形的两个顶角相等。

（3）对边平行：梯形的对边互相平行。

（4）对角线的交点连线是中位线：对于梯形ABCD，其对角线AC 和BD的交点O，连接OA、OB、OC、OD，这四条线段相互平分。

三、平行四边形与梯形的区别尽管平行四边形和梯形都是具有平行边的四边形，但它们的不同之处在于：平行四边形的对边长度相等，而梯形的两个底角和两个顶角相等。

以ABCD为例，若AB∥CD，BC∥AD，且AB=CD，BC ≠ AD，则ABCD是平行四边形，反之若两个底角相等，两个顶角相等，但底边和顶边不平行，则ABCD是梯形。

四、总结平行四边形和梯形是几何学中的两个重要概念。

平行四边形具有对边平行、相对边相等、同位角相等和对角线互相平分等性质；而梯形具有对边平行、底角相等、顶角相等和对角线互相平分等性质。

通过对它们的认识和理解，我们能更好地应用它们解决实际问题。

通过本文的学习，我们对平行四边形和梯形有了更深入的了解。

平行四边形专题讲义一、学习目标 复习平行四边形、特殊平行四边形性质与判定，能利用它们进行计算或证明. 二、学习重难点 重点：性质与判定的运用；难点：证明过程的书写。

三、本章知识结构图1．平行四边形是特殊的 ；特殊的平行四边形包括 、 、 。

2．梯形 （是否）特殊平行四边形， （是否）特殊四边形。

3．特殊的梯形包括 梯形和 梯形。

4、本章学过的四边形中，属于轴对称图形的有 ；属于中心对称图形的有 。

四、复习过程 （一）知识要点1：平行四边形的性质与判定1.平行四边形的性质：（1）从边看：对边 ，对边 ； （2）从角看：对角 ，邻角 ； （3）从对角线看：对角线互相 ； （4）从对称性看：平行四边形是 图形。

2、平行四边形的判定：（1）判定1：两组对边分别 的四边形是平行四边形。

（定义）（2）判定2：两组对边分别 的四边形是平行四边形。

（3）判定3：一组对边 且 的四边形是平行四边形。

（4）判定4：两组对角分别 的四边形是平行四边形。

（5）判定5：对角线互相 的四边形是平行四边形。

【基础练习】1.已知□ABCD 中，∠B =70°，则∠A =____，∠C =____，∠D =____．2.已知O 是ABCD 的对角线的交点，AC =38 mm ，BD =24 mm,AD =14 mm ，那么△BOC 的周长等于__ __.3.如图1，ABCD 中，对角线AC 和BD 交于点O ，若AC =8，BD =6，则边AB 长的取值范围是（ ）. A.1＜AB ＜7 B.2＜AB ＜14 C.6＜AB ＜8 D.3＜AB ＜44.不能判定四边形ABCD 为平行四边形的题设是（ ） A.AB=CD,AD=BC B.ABCD C.AB=CD,AD ∥BC D.AB ∥CD,AD ∥BC5.在ABCD 中，AE ⊥BC 于E ，AF ⊥CD 于F ，AE=4，AF=6，ABCD 的周长为40，则ABCD 的面积是 （ ） A 、36 B 、48 C 、 40 D 、24【典型例题】例1、若平行四边形ABCD 的周长是20cm,△AOD 的周长比△ABO 的周长大6cm.求AB,AD 的长. F DA OA B CDOA DDC AB E F M NBE F C AD例2、 如图，已知四边形ABCD 是平行四边形，∠BCD 的平分线CF 交边AB 于F ，∠ADC 的平分线DG 交边AB 于G 。

初三数学平行四边形；梯形；矩形知识精讲北师大版【同步教育信息】一. 本周教学内容：1. 平行四边形2. 梯形3. 矩形二. 教学目标：1. 熟练的掌握与平行四边形、梯形、矩形相关的性质及判定定理，并灵活应用到具体问题当中。

2. 进一步掌握几何题的证明方法，发展同学们的推理论证能力。

三、重点及难点：重点：平行四边形、梯形、矩形性质与判定的应用，并在解决问题中，发展推理意识。

难点：证明过程与推理过程的严密性。

四. 课堂教学［知识要点］1. 主要概念：三角形的中位线：连接三角形两边中点的线段叫做三角形的中位线。

2. 主要定理：（1）平行四边形的性质定理①平行四边形的对边相等。

②平行四边形的对角相等。

③平行四边形的对角线互相平分。

（2）平行四边形的判定方法①平行四边形的定义：两组对边分别平行的四边形是平行四边形。

②两组对边分别相等的四边形是平行四边形。

③一组对边平行且相等的四边形是平行四边形。

④两组对角分别相等的四边形是平行四边形。

⑤对角线互相平分的四边形是平行四边形。

（3）等腰梯形的性质定理①等腰梯形在同一底上的两个角相等。

②等腰梯形的两条对角线相等。

（4）等腰梯形的判定定理：同一底上的两个角相等的梯形是等腰梯形。

（5）三角形的中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半。

（6）其他定理：夹在两条平行线间的平行线段相等。

（7）矩形的性质定理与判定定理矩形的四个角都是直角。

矩形的对角线相等。

有三个角是直角的四边形是矩形。

对角线相等的平行四边形是矩形。

（8）直角三角形的性质定理与判定定理直角三角形斜边上的中线等于斜边的一半。

如果一个三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。

【典型例题】例1. 如图在平行四边形ABCD 中，EF 过点O ，说明①AE 与CF 什么关系？②四边形AECF 是什么四边形？解：①AE=CF证明：∵四边形ABCD 为平行四边形 ∴AO=CO ，AD//BC ∴∠DAC=∠ACB 在△AOE 和△COF 中⎪⎩⎪⎨⎧∠=∠=∠=∠COF AOE COAO ACB DAC CFAE COFAOE =∴∆≅∆∴②四边形AECF 是平行四边形 证明：连接AF 、ECOFOE COFAOE =∴∆≅∆又∵OA=OC∴四边形AECF 是平行四边形。

平行四边形和梯形一、平行四边形。

1. 定义，平行四边形是一个具有两对对边平行的四边形。

也就是说，它的对边是平行的，且对边长度相等。

2. 性质，平行四边形的对角线相互平分，对角线的长度相等。

平行四边形的相邻角互补，即相邻两个角的和为180°。

平行四边形的对边相等，对角线互相垂直。

3. 应用，平行四边形在日常生活中有着广泛的应用，比如建筑设计、地图绘制、家具制作等。

在数学中，平行四边形也是一种常见的几何形状，我们可以通过平行四边形的性质来解决一些几何问题。

二、梯形。

1. 定义，梯形是一个具有两条平行边的四边形。

梯形的两条平行边被称为上底和下底，两条非平行边被称为斜边。

2. 性质，梯形的对角线不相等，且对角线的交点将梯形分成两个三角形。

梯形的上底和下底的中线平行且等长。

梯形的上底和下底的和等于梯形的周长。

3. 应用，梯形在日常生活中也有着广泛的应用，比如梯形的形状可以用来设计楼梯、房顶等。

在数学中，梯形也是一个常见的几何形状，我们可以通过梯形的性质来解决一些几何问题。

比较分析。

1. 相同点，平行四边形和梯形都是四边形，都有着两条平行边。

2. 不同点，平行四边形的对边相等，对角线相互平分，对角线相等；梯形的上底和下底的中线平行且等长，对角线不相等。

3. 应用，平行四边形和梯形在日常生活和数学中都有着广泛的应用，但具体的应用场景和解决问题的方法有所不同。

结论。

通过对平行四边形和梯形的介绍和比较分析，我们可以看出它们都是重要的几何形状，有着各自独特的特点和性质。

在日常生活和数学中，我们可以通过对它们的认识和理解来解决一些实际问题。

因此，对平行四边形和梯形的学习和掌握对于我们的生活和工作都是非常重要的。

希望通过本文的介绍，读者能够更好地理解和运用平行四边形和梯形，为我们的生活和学习带来更多的帮助。

中小学1对1课外辅导专家武汉龙文教育学科辅导讲义授课对象授课教师授课时间授课题目平行四边形——梯形课型复习课使用教具讲义、纸笔教学目标会应用学会和认识梯形的基本性质和定理基本定理和性质解决一般问题教学重点和难点梯形相关问题的综合应用以及辅助线的做法参考教材（人教版）八年级数学下册教学流程及授课详案知识点小结㈠、有关概念1、梯形：一组对边平行而另一组对边不平行的四边形叫做梯形。

2、梯形的底、梯形的高、梯形的腰；3、直角梯形：一腰垂直于底的梯形叫做直角梯形。

4、等腰梯形：两腰相等的梯形叫做等腰梯形。

5、梯形的中位线：连结梯形两腰中点的线段叫做梯形中位线。

㈡、等腰梯形的性质；1、等腰梯形性质定理1：等腰梯形在同一底上的两个角相等。

2、等腰梯形性质定理2：等腰梯形的两条对角线相等。

3、梯形中位线定理：梯形中位线平行于两底，并且等于两底和的一半㈢、等腰梯形的判定；1、等腰梯形的判定定理l。

：在同一个底上的两个底角相等的梯形是等腰梯形。

2、等腰梯形的判定定理2：对角线相等的梯形是等腰梯形。

研究等腰梯形常用的方法有：化为一个等腰三角形和一个平行四边形；或两个全等的直角三角形和一矩形；或作对角线的平行线交下底的延长线于一点；或延长两腰交于一点。

典型例题[例1]( 1 )下列语句中错误的是 ( )A．只有一组对边平行的四边形是梯形B．有一组对边平行而另一组对边不平行的四边形是梯形C．有一组对边平行的四边形是梯形D．一组对边平行且不相等的四边形是梯形( 2 )下面结论：①等腰梯形中不可能有直角；②直角梯形中不可能有等腰；③等腰梯形是对称图形，其中结论正确的是 (只填序号)。

一、平移1、平移一腰：从梯形的一个顶点作一腰的平行线，把梯形转化为一个三角形和一个平行四边形。

［例1］如图1，梯形ABCD 的上底AB=3，下底CD=8，腰AD=4，求另一腰BC 的取值范围。

图1析解：过点B 作BM//AD 交CD 于点M ，则梯形ABCD 转化为△BCM 和平行四边形ABMD 。

学习指南如何理解初中数学中的平行四边形与梯形数学在初中阶段是一门重要且基础的学科，其中平行四边形和梯形是初中数学中的基本图形。

本文将详细介绍这两个图形的概念、性质以及解题方法，帮助学生更好地理解和应用。

一、平行四边形1. 概念介绍平行四边形是指具有以下性质的四边形：两组对边分别平行且长度相等。

简而言之，就是有两对边是平行且长度相等的四边形。

2. 性质探究平行四边形有一些重要的性质，我们来逐一探究：（1）对边性质：平行四边形的对边是平行的。

（2）相邻角性质：平行四边形的相邻两个内角是补角，即它们的和为180°。

（3）对角线性质：平行四边形的对角线相互等分，并且交点的连线是对角线的中点。

3. 解题方法在解平行四边形的问题时，我们需要运用以上性质并合理利用图形知识进行推理。

（1）已知条件推断：当我们已知一些条件时，可以根据平行四边形的性质推断出其他信息。

（2）辅助线引入：在解题过程中，可以通过引入辅助线来简化问题，使得平行四边形的性质更加明显。

（3）利用相似性质：当平行四边形与其他几何图形构成相似关系时，可以利用相似性质求解问题。

二、梯形1. 概念介绍梯形是指具有以下性质的四边形：两边平行，但两腰长不相等。

简而言之，就是两条平行边不等长的四边形。

2. 性质探究梯形也有一些重要的性质，我们来逐一探究：（1）底角性质：梯形的底角是对边所对的内角，是补角。

（2）等腰梯形性质：如果梯形的两腰长相等，则称为等腰梯形。

等腰梯形的底角相等，顶角也相等。

（3）中位线性质：梯形的两条非平行边中点的连线是梯形两对边中点的连线，并且中位线与底边平行且长度为底边两侧边长之和的一半。

3. 解题方法在解梯形相关问题时，我们可以运用以下方法：（1）积分法：计算梯形的面积时，我们可以将其分解为两个三角形和一个矩形，然后利用面积计算公式进行计算。

（2）利用相似性质：当梯形与其他几何图形构成相似关系时，可以利用相似性质求解问题。

平行四边形和梯形简介在几何学中，平行四边形和梯形是两种常见的多边形。

它们在数学和实际应用中都有广泛的应用。

本文将介绍平行四边形和梯形的定义、性质以及计算公式，帮助读者更好地理解和运用这两种多边形。

平行四边形定义平行四边形是一个具有两对平行边的四边形。

也就是说，它的对边是平行的。

平行四边形的特点是具有两对等长的边和两对对等的角。

性质平行四边形有以下几个重要的性质：1.对角线互相等分：平行四边形的两条对角线互相等分对方。

2.颜色相同：平行四边形的对边颜色相同，也就是说，两对平行边是相似的。

3.对边平行：平行四边形的两对边是平行的。

4.对角线交于一点：平行四边形的对角线交于一点，这个点叫做对角线的交点。

计算公式在计算平行四边形的面积和周长时，我们可以使用以下公式：1.面积：平行四边形的面积可以通过底边长和高的乘积来计算，即 $A = S\\times H$，其中A是面积，S是底边长，H是高。

2.周长：平行四边形的周长可以通过四条边长相加来计算，即C=a+b+c+d，其中C是周长，a、b、c、d是四条边的长度。

梯形定义梯形是一个具有两条平行边的四边形，其中两条平行边被称为底边和顶边，两个非平行的边被称为腰。

性质梯形有以下几个重要的性质：1.对角和相等：梯形的对角和相等，即两个对角角度之和等于180度。

2.颜色相同：梯形的上下底边颜色相同，也就是说，两条平行边是相似的。

3.腰的长度相等：梯形的两个腰的长度相等。

计算公式在计算梯形的面积和周长时，我们可以使用以下公式：1.面积：梯形的面积可以通过上底和下底的和与高的乘积的一半来计算，即$A = \\frac{(a + b) \\times h}{2}$，其中A是面积，a是上底，b是下底，ℎ是高。

2.周长：梯形的周长可以通过将上底、下底和两个腰的长度相加来计算，即C=a+b+s1+s2，其中C是周长，a是上底，b是下底，s1、s2是腰的长度。

总结平行四边形和梯形是常见的多边形，它们具有各自独特的定义和性质。