VAR模型、Johansen协整检验在eviews中的具体操作步骤及

VAR模型基本操作指引（Eviews）1、ADF检验双击序列——打开序列数据窗口——View——Unit Root Test——单位根检验对话框（1st difference，即检验△X；intercept：包含截距项；trend：包含趋势项）临界值判断：如果ADF检验值小于某一显著性水平下的临界值，则序列在此显著性水平下平稳。

2、根据SIC和AC值确定VAR的滞后期单位根检验操作的输出结果中3、建立VAR模型在workfile里——Quick——Estimate VAR…——对话窗缺省的是非约束VAR，另一选择是向量误差修正模型。

给出内生变量的滞后期间。

给出用于运算的样本范围。

Endogenous要求给出VAR模型中所包括的内生变量。

Exogenous要求给出外生变量（一般包含常数项）。

结果显示中，回归系数下第一个括号中的为标准差，第二个括号中的为t值。

4、脉冲响应分析/方差分解在进行脉冲响应函数诊断之前，需要先检验VAR模型的平稳性，用AR根图(Inverse Roots of AR Characteristic polunomial)进行检验。

AR根图中，如果点都落在单位圆里，才可以做脉冲分析。

如果模型不平稳，则要重新修改变量，去掉不显著变量。

VAR模型估计结果窗口中——View——impulse response——table5、协整关系检验前提条件：序列同阶单整打开序列组数据窗口——View——Cointegration Test…——6、误差修正模型Quick——Estimate VAR…——对话窗——选择VEC——相比较VAR的设置中要多填入误差修正项个数（Number of CE’s），且此时的外生变量设置中不需要再另外设置常数项。

—OK7、格兰杰因果检验前提条件：序列间存在协整关系Eviews可以直接给出两个变量间的双向格兰杰因果检验结果。

打开数据组窗口——View——Granger Causality…——选择最大滞后长度—OK8、建立协整回归方程建立回归模型后，如果模型存在自相关，则建立广义差分模型欢迎您的下载，资料仅供参考！致力为企业和个人提供合同协议，策划案计划书，学习资料等等打造全网一站式需求。

EViews统计分析基础教程
一、向量自回归（VAR）模型
3. VAR模型的建立
选择“Quick”|“Estimate VAR…”选项，将会弹出下图所示的 对话框。 该对话框包括三个选项卡，分别是“Basics”、 “Cointegration”和“VEC Restrictions”， 后两个选项卡在VEC模型操 作中使用。系统默认是“Basics” 选项卡。。
EViews统计分析基础教程
一、向量自回归（VAR）模型
3. VAR模型的建立
VAR模型的滞后结构检验 （4）滞后阶数标准
选择VAR对象工具栏中的“View”|“Lag Structure”|“Lag Length Criteria”选项，在弹出的对话框中输入最大滞后 阶数，然后单击“OK”按钮即可得到检验结果。
EViews统计分析基础教程
四、Johansen协整检验
1、Johansen协整理论
设变量y1t， y2t，…，ykt均是非平稳的一阶单整序列，即 yt~I(1)。xt是d维外生向量，代表趋势项、常数项等， yt=A1 yt-1 +A2 yt-2 +…+ Ap yt-p+B xt + μt 变量y1t， y2t，…，ykt的一阶单整过程I(1)经过差分后变 为零阶单整过程I(0)
EViews统计分析基础教程
四、 Johansen协整检验
EViews操作
在 EViews 软 件 操 作 中 ， 选 择 VAR01 对 象 工 具 栏 中 的 “View”|“Cointegration Test…”选项，打开下图所示的协整检 验设定对话框。
EViews统计分析基础教程
-1.0
-0.5

Eviews基本把持指引：之巴公井开创作1、ADF检验双击序列——翻开序列数据窗口——View——Unit Root Test ——单元根检验对话框（1 st difference ,即检验△X ； intercept：包括截距项； trend：包括趋势项）临界值判断：如果ADF检验值小于某一显著性水平下的临界值,则序列在此显著性水平下平稳.2、根据SIC和AC值确定VAR的滞后期单元根检验把持的输出结果中3、建立VAR模型在workfile里——Quick——Estimate VAR…——对话窗缺省的是非约束VAR,另一选择是向量误差修正模型.给出内生变量的滞后期间.给出用于运算的样本范围.Endogenous要求给出VAR模型中所包括的内生变量.Exogenous要求给出外生变量（一般包括常数项）.结果显示中,回归系数下第一个括号中的为标准差,第二个括号中的为t值.4、脉冲响应分析（Response of * to * Innovations）/ 方差分解（Variance Decornposition）在进行脉冲响应函数诊断之前,需要先检验VAR模型的平稳性,用AR根图(Inverse Roots of AR Characteristic polunomial)进行检验.AR根图中,如果点都落在单元圆里,才可以做脉冲分析～如果模型不服稳,则要重新修改变量,去失落不显著变量.VAR模型估计结果窗口中——View——impulse response——table5、协整关系检验前提条件：序列同阶单整翻开序列组数据窗口——View——Cointegration Test…——6、误差修正模型Quick——Estimate VAR…——对话窗——选择VEC——相比力VAR的设置中要多填入误差修正项个数（Number of CE’s）,且此时的外生变量设置中不需要再另外设置常数项.——OK7、格兰杰因果检验前提条件：序列间存在协整关系Eviews可以直接给出两个变量间的双向格兰杰因果检验结果.翻开数据组窗口——View——Granger Causality…——选择最年夜滞后长度——OK8、建立协整回归方程建立回归模型后,如果模型存在自相关,则建立广义差分模型。

Eviews基本操作指引：1、ADF检验双击序列——打开序列数据窗口——View——Unit Root Test ——单位根检验对话框（1 st difference ，即检验△X ； intercept：包含截距项； trend：包含趋势项）临界值判断：如果ADF检验值小于某一显著性水平下的临界值，则序列在此显著性水平下平稳。

2、根据SIC和AC值确定VAR的滞后期单位根检验操作的输出结果中3、建立VAR模型在workfile里——Quick——Estimate VAR…——对话窗缺省的是非约束VAR，另一选择是向量误差修正模型。

给出内生变量的滞后期间。

给出用于运算的样本范围。

Endogenous要求给出VAR模型中所包括的内生变量。

Exogenous要求给出外生变量（一般包含常数项）。

结果显示中，回归系数下第一个括号中的为标准差，第二个括号中的为t值。

4、脉冲响应分析（Response of * to * Innovations）/ 方差分解（Variance Decornposition）在进行脉冲响应函数诊断之前，需要先检验VAR模型的平稳性，用AR根图(Inverse Roots of AR Characteristic polunomial)进行检验。

AR根图中，如果点都落在单位圆里，才可以做脉冲分析～如果模型不平稳，则要重新修改变量，去掉不显著变量。

VAR模型估计结果窗口中——View——impulse response——table5、协整关系检验前提条件：序列同阶单整打开序列组数据窗口——View——Cointegration Test…——6、误差修正模型Quick——Estimate VAR…——对话窗——选择VEC——相比较VAR的设置中要多填入误差修正项个数（Number of CE’s），且此时的外生变量设置中不需要再另外设置常数项。

——OK7、格兰杰因果检验前提条件：序列间存在协整关系Eviews可以直接给出两个变量间的双向格兰杰因果检验结果。

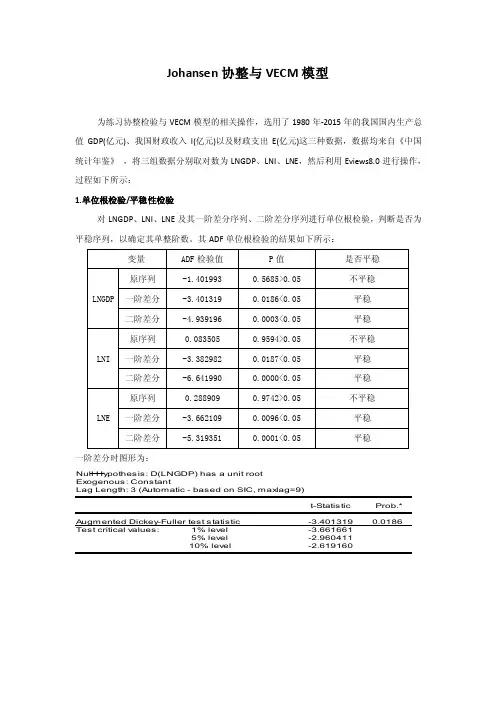
Johansen协整与VECM模型为练习协整检验与VECM模型的相关操作，选用了1980年-2015年的我国国内生产总值GDP(亿元)、我国财政收入I(亿元)以及财政支出E(亿元)这三种数据，数据均来自《中国统计年鉴》，将三组数据分别取对数为LNGDP、LNI、LNE，然后利用Eviews8.0进行操作，过程如下所示：1.单位根检验/平稳性检验对LNGDP、LNI、LNE及其一阶差分序列、二阶差分序列进行单位根检验，判断是否为平稳序列，以确定其单整阶数。

其ADF单位根检验的结果如下所示：一阶差分时图形为：从上述的检验结果中可以看出，原水平序列LNGDP 、LNI 和LNE的ADF 检验的P值都大于0.05，表现出非平稳特征。

而LNGDP 、LNI 和LNE一阶差分以及二阶差分的ADF检验的P值均小于0.05，表现出平稳特征，说明LNGDP 、LNI 和LNE的一阶差分就都已经是平稳序列，即LNGDP、LNI、LNE序列是一阶单整的，LNGDP~I(1)，LNI~I(1)，LNE~I(1)。

所以LNGDP序列、LNI序列和LNE序列是同阶单整的，因此具备了进行协整检验的条件。

2.Johansen协整（检验是否存在协整）（1）选择最优滞后期，则做VAR模型，而因为是年度数据，以3位最大滞后期数，进行实验，结果图如下：从上表打“*”处可知最优滞后期为3.（2）以最优滞后期3进行Johansen协整检验，结果如下由于当无协整时，p值为0.0004，小于0.05，拒绝原假设，所以看下一个；当有一个协整的时候，p值为0.0743，大于0.05，则接受原假设，所以存在一个协整关系。

3.VECM模型结果图如下：则最终结果为：(1)D(LNGDP t )=0.053123e t-1+1.050628DLNGDP t-1-0.373339DLNGDP t-2-0.527039DLNI t-1-0.378157DLNI t-2+ 0.457048DLNE t-1+0.372008DLNE t-2+ε1t(2)D(LNI t )=0.079927e t-1+0.260644DLNGDP t-1-0.386477DLNGDP t-2-0.064574DLNI t-1-0.566409DLNI t-2+ 0.812482DLNE t-1+0.373086DLNE t-2+ε2t(3)D(LNE t )=0.123095e t-1+0.158764DLNGDP t-1-0.422963DLNGDP t-2-0.129041DLNI t-1-0.410100DLNI t-2+ 0.872030DLNE t-1+0.100550DLNE t-2+ε3t4.补充内容VAR 模型的脉冲响应函数图Response of LNGDP to LNGDPResponse of LNGDP to LNIResponse of LNGDP to LNEResponse of LNI to LNGDPResponse of LNI to LNIResponse of LNI to LNEResponse of LNE to LNGDPResponse of LNE to LNIResponse of LNE to LNEResponse to Cholesky One S.D. Innovations ?2 S.E.以第一行第三图举例说明：Response of LNGDP to LNE 指来自于财政支出E 的一个标准差的冲击对国内生产总值的影响。

Eviews基本操作指引：1、ADF检验双击序列——打开序列数据窗口——View——Unit Root Test ——单位根检验对话框（1 st difference ，即检验△X ； intercept：包含截距项； trend：包含趋势项）临界值判断：如果ADF检验值小于某一显著性水平下的临界值，则序列在此显著性水平下平稳。

2、根据SIC和AC值确定VAR的滞后期单位根检验操作的输出结果中3、建立VAR模型在workfile里——Quick——Estimate VAR…——对话窗缺省的是非约束VAR，另一选择是向量误差修正模型。

给出内生变量的滞后期间。

给出用于运算的样本范围。

Endogenous要求给出VAR模型中所包括的内生变量。

Exogenous要求给出外生变量（一般包含常数项）。

结果显示中，回归系数下第一个括号中的为标准差，第二个括号中的为t值。

4、脉冲响应分析（Response of * to * Innovations）/ 方差分解（Variance Decornposition）在进行脉冲响应函数诊断之前，需要先检验VAR模型的平稳性，用AR根图(Inverse Roots of AR Characteristic polunomial)进行检验。

AR根图中，如果点都落在单位圆里，才可以做脉冲分析～如果模型不平稳，则要重新修改变量，去掉不显著变量。

VAR模型估计结果窗口中——View——impulse response——table5、协整关系检验前提条件：序列同阶单整打开序列组数据窗口——View——Cointegration Test…——6、误差修正模型Quick——Estimate VAR…——对话窗——选择VEC——相比较VAR的设置中要多填入误差修正项个数（Number of CE’s），且此时的外生变量设置中不需要再另外设置常数项。

——OK7、格兰杰因果检验前提条件：序列间存在协整关系Eviews可以直接给出两个变量间的双向格兰杰因果检验结果。

在EViews中进行协整检验和估计协整方程可以按照以下步骤进行：1. 导入数据：-打开EViews软件，选择"File" -> "Open"，导入需要进行协整检验的时间序列数据。

2. 创建VAR（向量自回归）模型：-选择"Quick/Estimation"或"Object/New Object"，然后选择"VAR"，创建一个新的VAR对象。

-在VAR对话框中，选择要包含在模型中的所有变量，并指定滞后阶数(lags)和其他选项。

-点击"OK"以创建VAR模型。

3. 进行协整检验：-在VAR对象上右键单击，选择"View/Residual Diagnostics"，打开模型诊断窗口。

-在模型诊断窗口中，选择"Tests"选项卡，在下拉菜单中选择"Engle-Granger Cointegration Test"。

-确定要检验的变量组合，点击"OK"进行协整检验。

结果将显示在输出窗口中。

4. 估计协整方程：-如果协整检验结果表明存在协整关系，可以进行协整向量估计。

-在VAR对象上右键单击，选择"View/Cointegrating Vectors"，打开协整向量窗口。

-在协整向量窗口中，选择所需的变量组合，并点击"OK"进行估计。

结果将显示在输出窗口中。

需要注意的是，以上步骤仅为一般性指导，具体操作可能因数据和研究目的而有所调整。

在使用EViews进行协整检验和估计协整方程时，建议参考EViews用户手册或相关教程以获取更详细的操作指导。

-4.3194
-5.4324 -5.7557
5% 临界值
-2.9202 -2.9202 -2.9202
模型形式 （C t p）
(c 0 3) (c 0 0) (c 0 0)
DW值
1.6551 1.9493 1.8996
结论
LGDPt ～I(1) LCt ～I( 1)
LIt～I(1)
注 C为位移项， t为趋势，p为滞后阶数。
yNt
的最大p阶滞后变量为解释变量的方程组模型，方程组模 型中共有N个方程。显然，VAR模型是由单变量AR模型推广到 多变量组成的“向量”自回归模型。
对于两个变量（N=2），Yt ( yt xt )T 时，VAR(2)模型为
2
Yt iYti Ut 1Yt1 2Yt2 Ut i 1
6
用矩阵表示：
xt
121 yt1
122xt1
221yt2
222xt2
u2t
显然，方程组左侧是两个第t期内生变量；右侧分 别是两个1阶和两个2阶滞后应变量做为解释变量，且 各方程最大滞后阶数相同,都是2。这些滞后变量与随 机误差项不相关（假设要求）。
7
由于仅有内生变量的滞后变量出现在等式的 右侧，故不存在同期相关问题，用“LS”法估计 参数，估计量具有一致和有效性。而随机扰动列 向量的自相关问题可由增加作为解释应变量的滞 后阶数来解决。
3
政策分析。但实际中，这种模型的效果并不令人满 意。
联立方程组模型的主要问题：
（1）这种模型是在经济理论指导下建立起来的结构模型 。遗憾的是经济理论并不未明确的给出变量之间的动态关 系。
（2）内生、外生变量的划分问题较为复杂； （3）模型的识别问题，当模型不可识别时,为达到可识别 的目的，常要将不同的工具变量加到各方程中，通常这种 工具变量的解释能力很弱； （4）若变量是非平稳的（通常如此），则会违反假设， 带来更严重的伪回归问题。

Eviews基本操作指引：1、ADF检验双击序列——打开序列数据窗口——View——Unit Root Test ——单位根检验对话框（1 st difference ，即检验△X ； intercept：包含截距项； trend：包含趋势项）临界值判断：如果ADF检验值小于某一显著性水平下的临界值，则序列在此显著性水平下平稳。

2、根据SIC和AC值确定VAR的滞后期单位根检验操作的输出结果中3、建立VAR模型在workfile里——Quick——Estimate VAR…——对话窗缺省的是非约束VAR，另一选择是向量误差修正模型。

给出内生变量的滞后期间。

给出用于运算的样本范围。

Endogenous要求给出VAR模型中所包括的内生变量。

Exogenous要求给出外生变量（一般包含常数项）。

结果显示中，回归系数下第一个括号中的为标准差，第二个括号中的为t值。

4、脉冲响应分析（Response of * to * Innovations）/ 方差分解（Variance Decornposition）在进行脉冲响应函数诊断之前，需要先检验VAR模型的平稳性，用AR根图(Inverse Roots of AR Characteristic polunomial)进行检验。

AR根图中，如果点都落在单位圆里，才可以做脉冲分析～如果模型不平稳，则要重新修改变量，去掉不显著变量。

VAR模型估计结果窗口中——View——impulse response——table5、协整关系检验前提条件：序列同阶单整打开序列组数据窗口——View——Cointegration Test…——6、误差修正模型Quick——Estimate VAR…——对话窗——选择VEC——相比较VAR的设置中要多填入误差修正项个数（Number of CE’s），且此时的外生变量设置中不需要再另外设置常数项。

——OK7、格兰杰因果检验前提条件：序列间存在协整关系Eviews可以直接给出两个变量间的双向格兰杰因果检验结果。

Eviews基本操作指引：1、ADF检验双击序列——打开序列数据窗口——View——Unit Root Test ——单位根检验对话框（1 st difference ，即检验△X ； intercept：包含截距项； trend：包含趋势项）临界值判断：如果ADF检验值小于某一显着性水平下的临界值，则序列在此显着性水平下平稳。

2、根据SIC和AC值确定VAR的滞后期单位根检验操作的输出结果中3、建立VAR模型在workfile里——Quick——Estimate VAR…——对话窗缺省的是非约束VAR，另一选择是向量误差修正模型。

给出内生变量的滞后期间。

给出用于运算的样本范围。

Endogenous要求给出VAR模型中所包括的内生变量。

Exogenous要求给出外生变量（一般包含常数项）。

结果显示中，回归系数下第一个括号中的为标准差，第二个括号中的为t值。

4、脉冲响应分析（Response of * to * Innovations）/ 方差分解（Variance Decornposition）在进行脉冲响应函数诊断之前，需要先检验VAR模型的平稳性，用AR根图(Inverse Roots of AR Characteristic polunomial)进行检验。

AR根图中，如果点都落在单位圆里，才可以做脉冲分析～如果模型不平稳，则要重新修改变量，去掉不显着变量。

VAR模型估计结果窗口中——View——impulse response——table5、协整关系检验前提条件：序列同阶单整打开序列组数据窗口——View——Cointegration Test…——6、误差修正模型Quick——Estimate VAR…——对话窗——选择VEC——相比较VAR的设置中要多填入误差修正项个数（Number of CE’s），且此时的外生变量设置中不需要再另外设置常数项。

——OK7、格兰杰因果检验前提条件：序列间存在协整关系Eviews可以直接给出两个变量间的双向格兰杰因果检验结果。

Eviews基本操作指引：1、ADF检验双击序列——打开序列数据窗口——View——Unit Root Test ——单位根检验对话框（1 st difference ，即检验△X ； intercept：包含截距项； trend：包含趋势项）临界值判断：如果ADF检验值小于某一显著性水平下的临界值，则序列在此显著性水平下平稳。

2、根据SIC和AC值确定VAR的滞后期单位根检验操作的输出结果中3、建立VAR模型在workfile里——Quick——Estimate VAR…——对话窗缺省的是非约束VAR，另一选择是向量误差修正模型。

给出内生变量的滞后期间。

给出用于运算的样本范围。

Endogenous要求给出VAR模型中所包括的内生变量。

Exogenous要求给出外生变量（一般包含常数项）。

结果显示中，回归系数下第一个括号中的为标准差，第二个括号中的为t值。

4、脉冲响应分析（Response of * to * Innovations）/ 方差分解（Variance Decornposition）在进行脉冲响应函数诊断之前，需要先检验VAR模型的平稳性，用AR根图(Inverse Roots of AR Characteristic polunomial)进行检验。

AR根图中，如果点都落在单位圆里，才可以做脉冲分析～如果模型不平稳，则要重新修改变量，去掉不显著变量。

VAR模型估计结果窗口中——View——impulse response——table5、协整关系检验前提条件：序列同阶单整打开序列组数据窗口——View——Cointegration Test…——6、误差修正模型Quick——Estimate VAR…——对话窗——选择VEC——相比较VAR的设置中要多填入误差修正项个数（Number of CE’s），且此时的外生变量设置中不需要再另外设置常数项。

——OK7、格兰杰因果检验前提条件：序列间存在协整关系Eviews可以直接给出两个变量间的双向格兰杰因果检验结果。

利用eviews实现时间序列的平稳性检验与协整检验在对时间序列Y、X1进行回归分析时需要考虑Y与X1之间是否存在某种切实的关系，所以需要进行协整检验。

1.1利用eviews创建时间序列Y、X1 ：打开eviews软件点击file-new-workfile，见对话框又三块空白处workfile structure type处又三项选择，分别是非时间序列unstructured/undate，时间序列dated-regular frequency，和不明英语balance panel。

选择时间序列dated-regular frequency。

在date specification中选择年度，半年度或者季度等，和起始时间。

右下角为工作间取名字和页数。

点击ok。

在所创建的workfile中点击object-new object，选择series，以及填写名字如Y，点击OK。

将数据填写入内。

1.2对序列Y进行平稳性检验：此时应对序列数据取对数，取对数的好处在于可将间距很大的数据转换为间距较小的数据。

具体做法是在workfile y的窗口中点击Genr，输入logy=log(y),则生成y的对数序列logy。

再对logy序列进行平稳性检验。

点击view-United root test，test type选择ADF检验，滞后阶数中lag length选择SIC 检验，点击ok得结果如下：Null Hypothesis: LOGY has a unit rootExogenous: ConstantLag Length: 0 (Automatic based on SIC, MAXLAG=1)t-Statistic Prob.*Augmented Dickey-Fuller teststatistic -2.75094601716637 0.0995139988900359Test critical values: 1% level -4.297072756022265% level -3.2126963902622510% level -2.74767611540013当检验值Augmented Dickey-Fuller test statistic的绝对值大于临界值绝对值时，序列为平稳序列。

Eviews 操作步骤：一、数据下载（百度国泰安）1、关于指数下载步骤:数据中心→单表查询→股票市场→指数信息2、字段选择指数代码如下：000001 上证指数000002 上证A股指数000003 上证B股指数399001 深成指数399106 深圳综合指数3991007 深圳综合A指数3、时间选择：2010．1.1~2017.9.204、条件筛选：指数代码→选条件→条件值→添加5、预览数据6、下载数据下载格式：.xsl下载详情→下载二、货币量下载1、数据中心→单表查询→经济研究系列→宏观经济→金融业2、字段：M0、M1、M23、时间：2010.1.1-2017.9.204、下载详情→下载5、居民消费指数和国内贷款总量的下载步骤：经济研究系列→宏观经济→固定资产投资三、EVIEWS数据导入File→Open→Foreign data as workfile→rename→File→Save as四、单位根检验Quick→Series Statistics→Unit root test→Seires name(输入如m等)→ok→选择level（1st different、2st different）分别检验，看显著性水平和p值五、VAR 模型Quick→Estimate VAR→Endogenous→输入shz、M0、M1、M2、LOAN→lag Internval →填两个数12或14等（确认找AIC最小的数）→确立六、脉冲影应函数在上面输出结果工具栏：Impulse（或view→impulse response）→display format（选如：mutiple sraphs）→选择冲击变量如：M0→在response中选入shz→ok七、方差分解：在六的结果中→View→variance→decomposition of：shz、m0、m1、m2、loan→ok八、协整检验：1、五、六、七中任选一结果→VIEW→cointegratiom→display format（选table）→decomposition of:shz、m0、m1、m2、loan→ok2、两个变量（两步法）：Quick→Estimation Equation→Equationg specification shz、m0等→ok3、Pro→make residual series（保存残差）→name for residual series（命名）→ok→view→unit root test→ok九、格兰杰因果检验：Quick→group statistics→granger causality test→series list（输变量，可以多个变量）十、保存输出结果→freez（然后编辑）→保存。

式中，lnl(p)和 lnl(p+i)分别为VAR(p)和
VAR(p+i)模型的对数似然函数值；f为自由度。 用对数似然比统计量LR确定P的方法用案例说
明。
13
案例1 我国1953年～2004年支出法国内生产总
值（GDP）、最终消费（Ct）和固定资本形成总额（It） 的时序数据列于D8.1中。数据来源于《中国统计年鉴》 各期。
9
（2）VAR模型对参数不施加零约束 （如t检 验）；
（3）VAR模型的解释变量中不含t期变量，所 有与联立方程组模型有关的问题均不存在；
（4）VAR模型需估计的参数较多。如VAR模型 含3个变量（N=3），最大滞后期为p=2，则有 PN2=2×32=18个参数需要估计；
（5）当样本容量较小时，多数参数估计的精 度较差，故需大样本，一般n>50。
f=VAR(3) 估计参数个数-VAR(1)估计参数 个数 332 132 18 。
20
利用Genr命令可算得用于检验原假设是否 成立的伴随概率 P：
p=1-@cchisq(42.4250,18) =0.000964
故 P=0.000964< =0.05，应拒绝原假设
，建立VAR(3)模型。
3
政策分析。但实际中，这种模型的效果并不令人满 意。
联立方程组模型的主要问题：
（1）这种模型是在经济理论指导下建立起来的结构模型 。遗憾的是经济理论并不未明确的给出变量之间的动态关 系。
（2）内生、外生变量的划分问题较为复杂； （3）模型的识别问题，当模型不可识别时,为达到可识别 的目的，常要将不同的工具变量加到各方程中，通常这种 工具变量的解释能力很弱； （4）若变量是非平稳的（通常如此），则会违反假设， 带来更严重的伪回归问题。

VAR模型和VEC模型Johansen协整 检验
一、向量自回归（VAR）模型
4. VAR模型的检验 VAR模型的滞后结构检验 （1）AR根的图与表 如果VAR模型所有根模的倒数都小于1，即都在单位圆内， 则该模型是稳定的；如果VAR模型所有根模的倒数都大于1， 即都在单位圆外，则该模型是不稳定的。如果被估计的VAR 模型不稳定，则得到的结果有些是无效的。
一、向量自回归（VAR）模型
3. VAR模型的建立
VAR模型的滞后结构检验 （3）滞后排除检验 滞后排除检验（Lag Exclusion Tests） 是对VAR模型中的每一阶数的 滞后进行排除检验。如右图所示。 第一列是滞后阶数， 第二列和第三列是方程的χ2统计 量， 最后一列是联合的χ2统计量。
四、 Johansen协整检验
EViews操作 在 EViews 软 件 操 作 中 ， 选 择 VAR01 对 象 工 具 栏 中 的 “View”|“Cointegration Test…”选项，打开下图所示的协整检 验设定对话框。
检验
一、向量自回归（VAR）模型
3. VAR模型的建立
选择“Quick”|“Estimate VAR…”选项，将会弹出下图所示的 对话框。 该对话框包括三个选项卡，分别是“Basics”、 “Cointegration”和“VEC Restrictions”， 后两个选项卡在VEC模型操 作中使用。系统默认是“Basics” 选项卡。。
VAR模型和VEC模型Johansen协整 检验
四、Johansen协整检验
2、Johansen协整检验 （1）特征根迹（Trace）检验 （2）最大特征值检验
VAR模型和VEC模型Johansen协整 检验
四、Johansen协整检验

在Eviews中验证VAR模型的方法稻草人颖一、平稳性检验（一）背景知识数据变量的平稳性是传统的计量经济分析的基本要求之一。

只有模型中的变量满足平稳性要求时，传统的计量经济分析方法才是有效的。

而在模型中含有非平稳时间序列式，基于传统的计量经济分析方法的估计和检验统计计量将失去通常的性质，从而推断得出的结论可能是错误的。

因此，在建立模型之前有必要检验数据的平稳性。

这就是平稳性检验。

常见的数据类型•时间序列数据（time-series data)；•截面数据(cross-sectional data)；•平行/面板数据（panel data/time-series cross-section data)；经典回归分析暗含着一个重要假设：数据是平稳的；数据非平稳，往往导致出现“虚假回归”。

故：时间序列首先遇到的问题就是平稳性的问题。

（二）操作步骤注：进行操作的数首先需要进行取对数的处理。

(1)File——New——Workfile。

(2)选择Ustructured/Undated，在Observations里输入数据量数——OK。

(3)Quick——Empty Group——复制并粘贴数据——关闭。

Test——Augmented Dickey-Fuller——OK。

(5)查看结果。

如果Prob的值大于0.05（或者0.1），或者1%、5%、10%水平下的临界值小于假设的Augmented Dickey-Fuller的值，则说明不能拒绝原假设，说明不平稳。

反之，则拒绝原假设，说明平稳。

为了得到的平稳的结果，如果第一次检验不平稳，可以尝试使用一阶差分，如若再不平稳，使用二阶差分，以此类推，直到得到平稳的结果为止。

二、协整性检验（一）背景知识协整即存在共同的随机性趋势。

协整检验的目的是决定一组非平稳序列的线性组合是否具有稳定的均衡关系，伪回归的一种特殊情况即是两个时间序列的趋势成分相同，此时可能利用这种共同趋势修正回归使之可靠。