小学数学格点与割补课件(四年级)奥数
- 格式:pptx
- 大小:10.74 MB
- 文档页数:132

正方形格点阵中多边形面积的计算公式,出现在各种形状的格点阵中的直线形的面积问题,以及借助构造格点阵求解的几何问题.通过恰当地分割与拼补进行计算的面积问题.1.如图6-1,每一个小方格的面积都是l平方厘米,那么用粗线围成的图形的面积是多少平方厘米【分析与解】方法一:正方形格点阵中多边形面积公式:(N+L2-1)×单位正方形面积,其中N为图形内格点数,L为图形周界上格点数.有N=4,L=7,则用粗线围成图形的面积为:(4+72-1)×1=(平方厘米)方法二:如下图,先求出粗实线外格点内的图形的面积,有①=3÷2=,②=2÷2=1,③=2÷2=1,④=2÷2=1,⑤=2÷2=l,⑥=2÷2=1,还有三个小正方形,所以粗实线外格点内的图形面积为+l+1+1+1+1+3=,而整个格点阵所围成的图形的面积为16,所以粗线围成的图形的面积为:=平方厘米.2.如图6-2,如果每一个小三角形的面积是1平方厘米,那么四边形ABCD的面积是多少平方厘米【分析与解】方法一:正三角形方形格点阵中多边形面积公式:(2N+L-2)x单位正三角形面积,其中N为图形内格点数,L为图形周界上格点数.有N=9,L=4,所以用粗线围成的图形的面积为:(9×2+4-2)×1=20(平方厘米).方法二:如下图,我们先数出粗实线内完整的小正三角形有10个,而将不完整的小正三角形分成4部分计算,其中①部分对应的平行四边形面积为4,所以①部分的面积为2,②、③、④部分对应的平行四边形面积分别为2,8,6,所以②、③、④部分的面积分别为1,4,3.所以粗实线内图形的面积为lO+2+1+4+3=20(平方厘米).3.如果图6-3是常见的一副七巧板的图,图6-4是用这副七巧板的7块板拼成的小房子图,那么,第2块板的面积等于整幅图的面积的几分之几第4块板与第7块板面积的和等于整幅图的面积的几分之几【分析与解】 如下图,我们在图6-3中标出图6-4中各块图形的位置.设整个七巧板组成的正方形的边长为1,显然整幅图形的面积为1,且有第2块的面积为12×12×12=18.有3S =4S ,2S =5S =7S =23S ,有2、3、4、5、7五块图形的面积之和为12,所以4S =IGFB S 长方形,7S =18.所以第2块板的面积等于整幅图面积的18,第4块板与第7块板面积和为整幅图面积的116+18=316.4.把正三角形每边三等分,将各边的中间段取来向外面作小正三角形,得到一个六角形.再将这个六角形的各个“角”(即小正三角形)的两边三等分,又以它们的中间段向外作更小的正三角形,这样就得到图6-5所示的图形.如果这个图形面积是1,那么原来的正三角形面积是多少【分析与解】方法一:如右图,我们将图6-5分成若干个大小、形状完全相同的小正三角形,由40块小正三角形组成图6-5,而由27块小正三角形组成了图中最大的正三角形.120块小正三角形的面积为1,所以每块为1120,那么原来的正三角形由81块小正三角形组成,其面积显然为27 40.方法二:如下图,我们把图6-5中的三角形分成A、B、C三种,设A形正三角形面积为“1”,则B、C两种正三角形的面积依次为“19”、“181”.在图6-5中,A种、B种、C种正三角形的个数依次为1,3,12,所以图6-5中图形的面积为1+3×19+12×181=4027.所以有“1”对应2740,而原来的正三角形即为三角形A,所以原来的正三角形的面积为27 40.5.如图6-6,正六边形ABCDEF的面积是6平方厘米,M是AB中点,N是CD中点,P是EF中点.问:三角形MNP的面积是多少平方厘米【分析与解】如下图,我们将图6-6分成大小、形状相同的三角形,有正六边形ABCDEF 包含有24个小正三角形,而阴影部分MNP包含有9个小正三角形.正六边形ABCDEF的面积为6,所以每个小正三角形的面积为6÷24=14,所以三角形MNP的面积为9×14=(平方厘米).6.把同一个三角形的三条边分别五等分、七等分,适当连接这些分点,便得到了若干个面积相等的小三角形.已知图6-7中阴影部分的面积是294平方分米,那么图6-8中的阴影部分的面积是多少平方分米【分析与解】在图6-7中,原正三角形被分成25个小正三角形,而阴影部分含有12个小正三角形,所以每个小正三角形的面积为294÷12=,所以原正三角形的面积为×25=(平方分米).而在图6-8中,原正三角形被分成49块,而阴影部分含有16块,所以阴影部分的面积为÷49×16=200(平方分米).7.图6-9是5×5的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点.请你在图上选7个格点,要求选出的点中任意3点都不在同一条直线上,并且使这7个点用直线连接后所围成的面积尽可能大.那么所围图形的面积是多少平方厘米【分析与解】我们知道满足题意的7个点可以组成一个七边形,适当的切去正方形的一个角可以得到一个五边形,切出2个角可以得到一个六边形,切去3个角可以得到七边形.为了使最后留下的七边形的面积尽可能大,那么切去的3个角面积应尽可能的小.如下切法得到的七边形的面积最大,为25-3×=(平方厘米).8.在图6-10中,三角形ABC和DEF是两个完全相同的等腰直角三角形,其中DF长9厘米,CF长3厘米,那么阴影部分的面积是多少平方厘米【分析与解】 方法一:如图(a),将原题中图形分为12个完全一样的小等腰三角形.△ABC 占有9个小等腰三角形,其中阴影部分占有6个小等腰三角形,SABC=9×9÷2=(平方厘米),所以阴影部分的面积为÷9×6=27(平方厘米).方法二:如图(b),连接IG ,有四边形ADGI 为正方形,易知FG=FC=3(厘米),所以DG=DF-FG=9-3=6(厘米),于是SHIG =14×AIGD S 正方形=14×26=9. 而四边形IGFB 为长方形,有BF=AD=DG=6(厘米),GF=3(厘米),所以IGFB S 长方形=6×3=18.阴影部分面积为A HIG 与长方形IGFB 的面积和,即为9+18=27(平方厘米).方法三:如图(C),为了方便叙述,将图6-10中某些交点标上字母. 易知三角形BIE 、CGF 、AIH 、DGH 均为等腰直角三角形.先求出等腰直角三角形AHI 、CGF 的面积,再用已知的等腰三角形ABC 的面积与其作差,即为需求阴影部分的面积.有S ABC =DEF S=12×EF ×DF=812,CGF S =12×CF×FG=92.因为CF=FG=3,所以DG=DF-FG=6.如图(d),可以将4个三角形DGH 拼成一个边长为DG 的正方形.所以,ACD S DGHS=14×DG×DG=9,而AIHS =DGHS=9,所以BFGHI S 阴影=SABC -CGF S-AIH S=812 -92-9=27(平方厘米).即阴影部分的面积为27平方厘米.9.如图6-11,在长方形ABCD 中,O 是长方形的中心,BC 长20厘米,AB 长12厘米,DE=4AE ,CF=3DF ,那么阴影部分的面积是多少平方厘米【分析与解】 我们只用先求出四边形ADFO 的面积,再将其减去两个三角形AEO 、EFD 的面积和,即为所求阴影部分的面积.而四边形ADFO 的面积等于两个三角形AOD 、ODF 的面积和.由题意知AE=4,ED=16,DF=3,FC=9. 有AOD S =14ABCD S 矩形=14×20×12=60,ODF S=12×DF×(14AD)= 12×3×12×20=15.AEO S=12×AE×(12AB)= 12×4×12×12=12,EFD S=12×ED×DF=12×16×3=24.有S 阴影=(AODS +ODFS)-AEOS-EFDS=60+15-12-24=39(平方厘米).即阴影部分的面积为39平方厘米.10.如图6-12,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米【分析与解】 如下图,我们将大正方形中的所有图形分成A 、B 两种三角形.其中含有A 形三角形8个,B 形三角形16个,其中阴影部分含有A 形三角形4个,B 形三角形8个.所以,阴影部分面积恰好为大正方形面积的12,即为12×10×10=50(平方厘米).11.如图6-13,ABCD 是边长为8厘米的正方形,梯形AEBD 的对角线相交于0,三角形AOE 的面积比三角形BOD 的面积小16平方厘米,则梯形AEBD 的面积是多少平方厘米【分析与解】如下图,将梯形AEBD 内4个三角形的面积分别记为①、②、③、④.在梯形AEBD 中,有△EBD、△ABD 同底等高,所以有EBDS =ABDS,即③+②=①+②.显然有①=③.由题意知BODS-AOES=16,即②-④=16,于是有(①+②)-(③+④)=16.已知①+②=ABD S=12×8×8=32,所以③+④=(①+②)-16=16.所以有AEBD S 梯形=(①+②)+(③+④)=32+16=48(平方厘米).评注:在任意梯形ABCD 中,两条对角线将其分成四个部分,记它们的面积为“上”、“下”、“左”、“右”,有:左=右;左×右=上×下;上:下=A 2D :B 2C .12.如图6-14,ABCD 是长方形,长AD 等于厘米,宽AB 等于5厘米,CDEF 是平行四边形.如果BH 的长是3厘米,那么图中阴影部分的面积是多少平方厘米【分析与解】 CDEF S 平行四边形=DC ×BC=5×=36,HC=BC-BH==,所以CDH S=12×CD×HC=12×5×=.S 阴影=CDEF S 平行四边形-CDHS==(平方厘米).13.如图6-15,已知一个四边形的两条边的长度和三个角,那么这个四边形的面积是多少【分析与解】 将AD 、BC 延长交于E ,有∠EDC=45°,∠ECD=90°,所以△CDE 为等腰直角三角形,有EC=DC .而∠ECD =45°,∠EAB=90°,所以△ABE 也是等腰直角三角形,有EA=AB . 有ABE S =12×AB×EA =492,EDC S =12×EC×DC=92.有ABCD S 四边形=ABE S-EDC S=492-92=20.14.图6-16是边长为1的正方形和一个梯形拼成的“火炬”.梯形的上底长1.5米,A 为上底的中点,B 为下底的中点,线段AB 恰好是梯形的高,长为0.5米,CD 长为丢米.那么图中阴影部分的面积是多少平方米【分析与解】 方法一:为了方便叙述.将下图中一些点标上字母.延长AB 交正方形边EF 于H 点,我们先求出梯形JICK 与正方形IFEC 的面积和,再求出三角形AFH 与梯形AHED 的面积和,将前者与后者做差所得到的值即为所求阴影部分的面积.JICK S 梯形=12×+1)×=, IFEC S 正方形=1×1=1.AFH S=12×AH ×FH=12×(AB+BH )×(12FE)= 12×+1)-(12×1)=,AHED S 梯形=12×(AH+DE)×HE=12×(AB+BH+CE -CD)×(12FE)=12×+1+1-13)×(12×1)=1324.有S 阴影=JICK S 梯形+IFEC S 正方形-AFH S -AHED S 梯形=+1324=1724(平方米).即阴影部分的面积为1724平方米.方法二:如下图,连接AI 、AC ,将阴影部分分成四个部分.△AJI 可以看作以AJ 为底,AB 的长为高的三角形;△AKC 可以看作以AK 为底,AB 的长为高的三角形;△AJF 可以看作以IF 为底,IB 的长为高的三角形;△ACD 可以看作CD 为底.CB 的长为高的三角形.阴影部分面积为AJIS+AKCS+AIFS+ACDS=×÷2+×÷2+l×÷2+13×÷2=+++112=1724(平方米)15.从一块正方形木板锯下宽为12米的一个木条以后,剩下的面积是6518平方米.问锯下的木条面积是多少平方米【分析与解】我们画出示意图(a),则剩下的木块为图(b),将4块剩下的木块如下拼成一个正方形得到图(c).我们称AB为长,AD为宽,有长与宽的差为12,所以图(c)中心的小正方形边长为12,于是大正方形AEHK的面积为6518×4+12×12=52936=236×236,所以AK长为236.即,长+宽=236,已知:长-宽=12,得长=136,于是锯去部分的木条的面积为136×1 2=1312=112(平方米).。

格点与面积知识要点:毕克定理:格点多边形面积=图内格点个数+周界格点数÷2-1(1)正方形格点问题就是它的格点都是由两组互相垂直相交的平行线的交点构成的.每一个小方格都是一个小正方形.正方形格点问题:多边形面积=边÷2+内-1(2)所谓三角形格点多边形是指:每相邻三点成“∵”或“∴”,所形成的三角形都是等边三角形.规定它的面积为1,以这样的点为顶点画出的多边形为三角形格点多边形.三角形格点问题:多边形面积=(边÷2+内-1)×2三角形格点问题所谓三角形格点多边形是指:每相邻三点成“∵”或“∴”,所形成的三角形都是等边三角形.规定它的面积为1,以这样的点为顶点画出的多边形为三角形格点多边形.关于三角形格点多边形的面积同样有它的计算公式:如果用S表示面积,N表示图形内包含的格点数,L表示图形周界上的格点数,那么有22S N L=⨯+-,就是格点多边形面积等于图形内部所包含格点数的2倍与周界上格点数的和减去2.例1:计算下列各图的面积。
总结:面积=(注:内部点,外部点关系)(毕克定理)例2:判断下列图形哪些是格点多边形?⑴⑵⑶例3:如图,计算各个格点多边形的面积.例4:求下列各个格点多边形的面积.例5:我们开始提到的“乡村小屋”的面积是多少?例6:右图是一个812 面积单位的图形.求矩形内的箭形ABCDEFGH 的面积.⑵⑴⑷⑶H GFED C BA例7:右图中每个小正方形的面积都是1,那么图中这只“狗”所占的面积是多少?例8:求下列格点多边形的面积(每相邻三个点“∵”或“∴”成面积为1的等边三角形).⑴⑵⑶⑷例9:右图中有21个点,其中每相邻的三点“∴”或“∵”所形成的三角形都是面积为1的等边三角形, 的面积.试计算ABC例10:右图中有21个点,其中每相邻的三点“∴”或“∵”所形成的三角形都是面积为1的等边三角形,试计算四边形DEFG的面积.例11:.把等边三角形ABC每边六等分,组成如右图的三角形网.若图中每个小三角形的面积均为cm,试求图中三角形DEF的面积.12例12:图中正六边形ABCDEF 的面积是54,AP=2PF,CQ=2BQ,求阴影四边形CEPQ 的面积。

正方形格点阵中多边形面积的计算公式,出现在各种形状的格点阵中的直线形的面积问题,以及借助构造格点阵求解的几何问题.通过恰当地分割与拼补进行计算的面积问题.1.如图6-1,每一个小方格的面积都是l平方厘米,那么用粗线围成的图形的面积是多少平方厘米?【分析与解】方法一:正方形格点阵中多边形面积公式:(N+L2-1)×单位正方形面积,其中N为图形内格点数,L为图形周界上格点数.有N=4,L=7,则用粗线围成图形的面积为:(4+72-1)×1=6.5(平方厘米)方法二:如下图,先求出粗实线外格点内的图形的面积,有①=3÷2=1.5,②=2÷2=1,③=2÷2=1,④=2÷2=1,⑤=2÷2=l,⑥=2÷2=1,还有三个小正方形,所以粗实线外格点内的图形面积为1.5+l+1+1+1+1+3=9.5,而整个格点阵所围成的图形的面积为16,所以粗线围成的图形的面积为:16-9.5=6.5平方厘米.2.如图6-2,如果每一个小三角形的面积是1平方厘米,那么四边形ABCD的面积是多少平方厘米?【分析与解】方法一:正三角形方形格点阵中多边形面积公式:(2N+L-2)x单位正三角形面积,其中N为图形内格点数,L为图形周界上格点数.有N=9,L=4,所以用粗线围成的图形的面积为:(9×2+4-2)×1=20(平方厘米).方法二:如下图,我们先数出粗实线内完整的小正三角形有10个,而将不完整的小正三角形分成4部分计算,其中①部分对应的平行四边形面积为4,所以①部分的面积为2,②、③、④部分对应的平行四边形面积分别为2,8,6,所以②、③、④部分的面积分别为1,4,3.所以粗实线内图形的面积为lO+2+1+4+3=20(平方厘米).3.如果图6-3是常见的一副七巧板的图,图6-4是用这副七巧板的7块板拼成的小房子图,那么,第2块板的面积等于整幅图的面积的几分之几?第4块板与第7块板面积的和等于整幅图的面积的几分之几?【分析与解】如下图,我们在图6-3中标出图6-4中各块图形的位置.设整个七巧板组成的正方形的边长为1,显然整幅图形的面积为1,且有第2块的面积为1 2×12×12=18.有3S =4S ,2S =5S =7S =23S ,有2、3、4、5、7五块图形的面积之和为12,所以4S =IGFB S 长方形,7S =18.所以第2块板的面积等于整幅图面积的18,第4块板与第7块板面积和为整幅图面积的116+18=316.4.把正三角形每边三等分,将各边的中间段取来向外面作小正三角形,得到一个六角形.再将这个六角形的各个“角”(即小正三角形)的两边三等分,又以它们的中间段向外作更小的正三角形,这样就得到图6-5所示的图形.如果这个图形面积是1,那么原来的正三角形面积是多少?【分析与解】 方法一:如右图,我们将图6-5分成若干个大小、形状完全相同的小正三角形,由40块小正三角形组成图6-5,而由27块小正三角形组成了图中最大的正三角形.120块小正三角形的面积为1,所以每块为1120,那么原来的正三角形由81块小正三角形组成,其面积显然为2740.方法二:如下图,我们把图6-5中的三角形分成A 、B 、C 三种,设A 形正三角形面积为“1”,则B 、C 两种正三角形的面积依次为“19”、“181”.在图6-5中,A 种、B 种、C 种正三角形的个数依次为1,3,12,所以图6-5中图形的面积为1+3×19+12×181=4027.所以有“1”对应2740,而原来的正三角形即为三角形A,所以原来的正三角形的面积为27 40.5.如图6-6,正六边形ABCDEF的面积是6平方厘米,M是AB中点,N是CD中点,P是EF中点.问:三角形MNP的面积是多少平方厘米?【分析与解】如下图,我们将图6-6分成大小、形状相同的三角形,有正六边形ABCDEF包含有24个小正三角形,而阴影部分MNP包含有9个小正三角形.正六边形ABCDEF的面积为6,所以每个小正三角形的面积为6÷24=14,所以三角形MNP的面积为9×14=2.25(平方厘米).6.把同一个三角形的三条边分别五等分、七等分,适当连接这些分点,便得到了若干个面积相等的小三角形.已知图6-7中阴影部分的面积是294平方分米,那么图6-8中的阴影部分的面积是多少平方分米?【分析与解】在图6-7中,原正三角形被分成25个小正三角形,而阴影部分含有12个小正三角形,所以每个小正三角形的面积为294÷12=24.5,所以原正三角形的面积为24.5×25=612.5(平方分米).而在图6-8中,原正三角形被分成49块,而阴影部分含有16块,所以阴影部分的面积为612.5÷49×16=200(平方分米).7.图6-9是5×5的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点.请你在图上选7个格点,要求选出的点中任意3点都不在同一条直线上,并且使这7个点用直线连接后所围成的面积尽可能大.那么所围图形的面积是多少平方厘米?【分析与解】我们知道满足题意的7个点可以组成一个七边形,适当的切去正方形的一个角可以得到一个五边形,切出2个角可以得到一个六边形,切去3个角可以得到七边形.为了使最后留下的七边形的面积尽可能大,那么切去的3个角面积应尽可能的小.如下切法得到的七边形的面积最大,为25-3×0.5=23.5(平方厘米).8.在图6-10中,三角形ABC和DEF是两个完全相同的等腰直角三角形,其中DF长9厘米,CF长3厘米,那么阴影部分的面积是多少平方厘米?【分析与解】方法一:如图(a),将原题中图形分为12个完全一样的小等腰三角形.△ABC占有9个小等腰三角形,其中阴影部分占有6个小等腰三角形,S=9×9÷2=40.5(平方厘ABC米),所以阴影部分的面积为40.5÷9×6=27(平方厘米).方法二:如图(b),连接IG ,有四边形ADGI 为正方形,易知FG=FC=3(厘米),所以DG=DF-FG=9-3=6(厘米),于是SHIG =14×AIGD S 正方形=14×26=9. 而四边形IGFB 为长方形,有BF=AD=DG=6(厘米),GF=3(厘米),所以IGFB S 长方形=6×3=18.阴影部分面积为A HIG 与长方形IGFB 的面积和,即为9+18=27(平方厘米).方法三:如图(C),为了方便叙述,将图6-10中某些交点标上字母. 易知三角形BIE 、CGF 、AIH 、DGH 均为等腰直角三角形.先求出等腰直角三角形AHI 、CGF 的面积,再用已知的等腰三角形ABC 的面积与其作差,即为需求阴影部分的面积.有SABC =DEF S=12×EF ×DF=812,CGF S =12×CF×FG=92.因为CF=FG=3,所以DG=DF-FG=6.如图(d),可以将4个三角形DGH 拼成一个边长为DG 的正方形.所以,ACDS DGH S=14×DG×DG=9,而AIH S =DGH S =9,所以BFGHI S 阴影= S ABC -CGF S -AIH S=812-92-9=27(平方厘米).即阴影部分的面积为27平方厘米.9.如图6-11,在长方形ABCD 中,O 是长方形的中心,BC 长20厘米,AB 长12厘米,DE=4AE ,CF=3DF ,那么阴影部分的面积是多少平方厘米?【分析与解】 我们只用先求出四边形ADFO 的面积,再将其减去两个三角形AEO 、EFD 的面积和,即为所求阴影部分的面积.而四边形ADFO 的面积等于两个三角形AOD 、ODF 的面积和.由题意知AE=4,ED=16,DF=3,FC=9.有AOD S =14ABCD S 矩形=14×20×12=60,ODF S=12×DF×(14AD)= 12×3×12×20=15.AEO S=12×AE×(12AB)= 12×4×12×12=12,EFD S=12×ED×DF=12×16×3=24.有S 阴影=(AOD S+ODFS)-AEO S-EFD S=60+15-12-24=39(平方厘米).即阴影部分的面积为39平方厘米.10.如图6-12,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?【分析与解】 如下图,我们将大正方形中的所有图形分成A 、B 两种三角形.其中含有A 形三角形8个,B 形三角形16个,其中阴影部分含有A 形三角形4个,B 形三角形8个.所以,阴影部分面积恰好为大正方形面积的12,即为12×10×10=50(平方厘米).11.如图6-13,ABCD 是边长为8厘米的正方形,梯形AEBD 的对角线相交于0,三角形AOE 的面积比三角形BOD 的面积小16平方厘米,则梯形AEBD 的面积是多少平方厘米?【分析与解】如下图,将梯形AEBD 内4个三角形的面积分别记为①、②、③、④.在梯形AEBD 中,有△EBD、△ABD 同底等高,所以有EBDS=ABDS,即③+②=①+②.显然有①=③.由题意知B O DS -AOES=16,即②-④=16,于是有(①+②)-(③+④)=16.已知①+②=ABD S=12×8×8=32,所以③+④=(①+②)-16=16.所以有AEBD S 梯形=(①+②)+(③+④)=32+16=48(平方厘米).评注:在任意梯形ABCD 中,两条对角线将其分成四个部分,记它们的面积为“上”、“下”、“左”、“右”,有: 左=右;左×右=上×下;上:下=A 2D :B 2C .12.如图6-14,ABCD 是长方形,长AD 等于7.2厘米,宽AB 等于5厘米,CDEF 是平行四边形.如果BH 的长是3厘米,那么图中阴影部分的面积是多少平方厘米?【分析与解】 CDEF S 平行四边形=DC×BC=5×7.2=36,HC=BC-BH=7.2-3=4.2,所以CDH S=12×CD×HC=12×5×4.2=10.5.S 阴影=CDEF S 平行四边形-CDHS=36-10.5=25.5(平方厘米).13.如图6-15,已知一个四边形的两条边的长度和三个角,那么这个四边形的面积是多少?【分析与解】 将AD 、BC 延长交于E ,有∠EDC=45°,∠ECD=90°,所以△CDE 为等腰直角三角形,有EC=DC .而∠ECD =45°,∠EAB=90°,所以△ABE 也是等腰直角三角形,有EA=AB .有ABE S =12×AB×EA =492,EDC S =12×EC×DC=92.有ABCD S 四边形=ABE S-EDC S=492-92=20.14.图6-16是边长为1的正方形和一个梯形拼成的“火炬”.梯形的上底长1.5米,A 为上底的中点,B 为下底的中点,线段AB 恰好是梯形的高,长为0.5米,CD 长为丢米.那么图中阴影部分的面积是多少平方米?【分析与解】 方法一:为了方便叙述.将下图中一些点标上字母.延长AB 交正方形边EF 于H 点,我们先求出梯形JICK 与正方形IFEC 的面积和,再求出三角形AFH 与梯形AHED的面积和,将前者与后者做差所得到的值即为所求阴影部分的面积.JICK S 梯形=12×(1.5+1)×0.5=0.625, IFEC S 正方形=1×1=1. AFH S=12×AH ×FH=12×(AB+BH )×(12FE)= 12×(0.5+1)-(12×1)=0.375,AHED S 梯形=12×(AH+DE)×HE=12×(AB+BH+CE -CD)×(12FE)=12×(0.5+1+1-13)×(12×1)=1324.有S 阴影=JICK S 梯形+IFEC S 正方形-AFH S -AHED S 梯形=0.625+l-0.375-1324=1724(平方米).即阴影部分的面积为1724平方米.方法二:如下图,连接AI 、AC ,将阴影部分分成四个部分.△AJI 可以看作以AJ 为底,AB 的长为高的三角形;△AKC 可以看作以AK 为底,AB 的长为高的三角形;△AJF 可以看作以IF 为底,IB 的长为高的三角形;△ACD 可以看作CD 为底.CB 的长为高的三角形.阴影部分面积为AJIS+AKCS+AIFS+ACDS=0.75×0.5÷2+O .75×O .5÷2+l×O .5÷2+13×0.5÷2 =0.1875+O.1875+0.25+112=1724(平方米)Powered by Powered by 15.从一块正方形木板锯下宽为12米的一个木条以后,剩下的面积是6518平方米.问锯下的木条面积是多少平方米?【分析与解】 我们画出示意图(a),则剩下的木块为图(b),将4块剩下的木块如下拼成一个正方形得到图(c).我们称AB 为长,AD 为宽,有长与宽的差为12,所以图(c)中心的小正方形边长为12,于是大正方形AEHK 的面积为6518×4+12×12=52936=236×236,所以AK 长为236.即,长+宽=236,已知:长-宽=12,得长=136,于是锯去部分的木条的面积为136×12=1312=112(平方米).。


格点和面积这一讲我们主要介绍利用格点求几何图形的面积,先来介绍什么叫“格点”。
见右图:这是一张由水平线和垂直线组成的方格纸,我们把水平线和垂直线相交的点称为“格点”,水平线和垂直线围成的每个小正方形称为“面积单位”。
借助小格点,我们可以很快地比较和计算图形的面积大小。
利用格点求图形的面积有两种思路,一是直接将图形分成若干个面积单位,然后通过计算有多少个面积单位来求图形的面积;二是将某些图形转化成长方形的面积来求。
当然还可以将这两种方法结合起来,求出某些较复杂图形的面积。
格点面积公式=中间格点数+图形一周的格点数÷2﹢1【典型例题】例1:计算下列各图的面积。
分析:先仔细观察图中的每个图形,选择方法,显然第一、三、五图可以直接数出包含多少个面积单位,而二、四、六显然不适合用数单位面积的方法来求面积,可以采用虚线把这些图形扩展或割补成长方形,通过求长方形的面积来求这些图形的面积。
解:(1)图中长方形的面积包括了3×2=6(个)面积单位,所以它的面积为6个面积单位。
(2)将图中的平行四边形割补成一个长方形,长方形的面积为3×2=6,而平行四边形的面积等于长方形的面积,所以平行四边形的面积是3×2=6(个)面积单位。
(3)将图中三角形用虚线分成3块,它包含1个单位面积和2个单位面积的一半,合起来有2个面积单位,所以它的面积是2个面积单位。
(4)图中三角形扩展成一个长方形,长方形的面积为3×2=6,而三角形面积为长方形面积的一半,则三角形面积为3个面积单位。
(5)将图中梯形用虚线分成3块,它包含了有5个单位面积和2个单位面积的一半。
合起来有6个面积单位。
所以它的面积为6个面积单位。
(6)将图中梯形互相平行的一组对边延长,补出一个与原来梯形方向颠倒,但面积一样的梯形,形成一个大的长方形。
长方形面积为(2+4)×3=18,而梯形的面积为长方形面积的一半,所以梯形的面积是(2+4)×3÷2=9(个)面积单位。

知识点回顾一,格点图形的计算:•1,分割法与添补法计算格点图形的面积•2,在最小的正方形面积为1的图形中正方形格点多边形面积=边界格点数÷2+内部格点数-1 •3,在最小正三角形面积为1的图形中三角形格点多边形面积=边界格点数+内部格点数×2-2知识点回顾二,割补法巧算面积:•1、用割补法把不规则图形变成规则图形计算面积。
•2、正方形、等腰直角三角形、等边三角形、正六边形等已知图形分割成小块,与所求图形面积相联系。
【1】下图中相邻格点围成的最小正方形或正三角形的面积均为l 平方厘米.这三个多边形的面积分别是多少平方厘米?【2】(1)下图中每个小正方形的面积是2平方厘米.阴影部分面积是多少平方厘米?(2)下图中每个小正三角形的面积是4平方厘米.阴影部分面积是多少平方厘米?【3】图中每个小正方形的边长为1厘米.阴影部分的面积是多少平方厘米?【4】如下左图和右图,把两个相同的正三角形的各边分别五等分和七等分,并连接这些分点.已知左图中阴影部分的面积是294平方分米.请问:右图中的阴影部分的面积是多少平方分米?【5】如下图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A的面积是36平方厘米,那么正方形B的面积是多少平方厘米?【6】如下图所示,正六边形ABCDEF的面积是6平方厘米,M 是AB中点,N是CD中点,P是EF中点.请问:三角形MNP的面积是多少平方厘米?【7】在下图中,五个小正方形的边长都是2厘米,求三角形ABC的面积.【8】下图中小正方形和大正方形的边长分别是4厘米和6厘米.阴影部分的面积是多少平方厘米?【9】如下图所示,四边形ABCD是长方形,长AD等于7厘米,宽AB等于5厘米,四边形CDEF是平行四边形.如果BH的长是3厘米,那么图中阴影部分面积是多少平方厘米?【10】下图中,三角形ABC和DEF是两个完全相同的等腰直角三角形,其中DF长9厘米,CF长3厘米,求阴影部分的面积.【11】下图是一个边长为l米的正方形和一个等腰梯形拼成的“火炬”.梯形的上底长1.5米,A为上底的中点,B为下底的中点,线段AB恰好是梯形的高,长为0.5米,CD长为0.3米.图中阴影部分的面积是多少平方米?【12】在下图中,每一个小正方形的面积都是1平方厘米.用粗线围成的图形面积是多少平方厘米?【13】如下图,正方形网格的总面积等于96平方厘米,求阴影图形的面积.【14】如图19-24,每个小等边三角形的面积都是1平方厘米.阴影部分的面积是多少平方厘米?下节课见!。


一、 掌握格点多边形面积的计算方法,以及这些方法的推广和拓展.二、 分割法,正所谓“大事化小”,把不规则的大图形化为规则的小图形,来进行计算. 三、 添补法,则正好相反,是“以小见大”,把不规则图形周围添上规则的小图形,使总面积便于计算.四、 遇在图形中进行适当的分割拼补,把不规则的形状拼成规则形状,也是常见的方法. 五、 公式法:在最小的正方形面积为1的图形中:21=÷+−正方形格点多边形面积边界格点数内部格点数. 在最小正三角形面积为1的图形中:22=+×−三角形格点多边形面积边界格点数内部格点数.六、 对于很多非格点图形的面积计算,分割和添补的方法依然适用.知识精讲第三讲格点与割补【例1】 图17-27中每个小正方形的边长为1厘米,阴影部分的面积是多少平方厘米?【例2】 如图17-28,平面上有16个点,相邻两点间隔为1厘米,在每个点都钉上钉子,形成4行4列的正方形钉阵.现在有许多皮筋,请问:可以套出多少种不同面积的三角形?(面积相同但形状不同的三角形算一种)图17‐28图17‐27例题解析【例3】 已知大的正六边形面积是72平方厘米,按图17-29中不同方式切割(切割点均为等分点),形成的阴影部分面积各是多少平方厘米?【例4】 图17-30为一个边长为2厘米的正方形,分别连接顶点与对应边中点.围成的阴影部分的面积为多少平方厘米?【例5】如图17-31所示,已知一个四边形的两条边的长度和三个角的度数,这个四边形的面积是多少平方厘米?(单位:厘米)图17‐3111图17‐3011图17‐29【例6】如图17-32所示,这个多边形六条边的长度分别是1,2,3,4,5,7.问:这个图形的面积最大可能是多少?【例7】如图17-33,有一个80100×的长方形网格,它的四个顶点分别为A,B,C,D.已知图中每一个小方格的面积都是1,请选出一个合适的格点P,使得三角形P AC的面积尽可能小(不能等于0),那么这个最小的面积是多少?【例8】正12边形的边长为1厘米,阴影部分都是正三角形(边长也为1厘米),如图17-34.那么空白部分面积等于多少平方厘米?图17‐34A BCD图17‐33图17‐32。


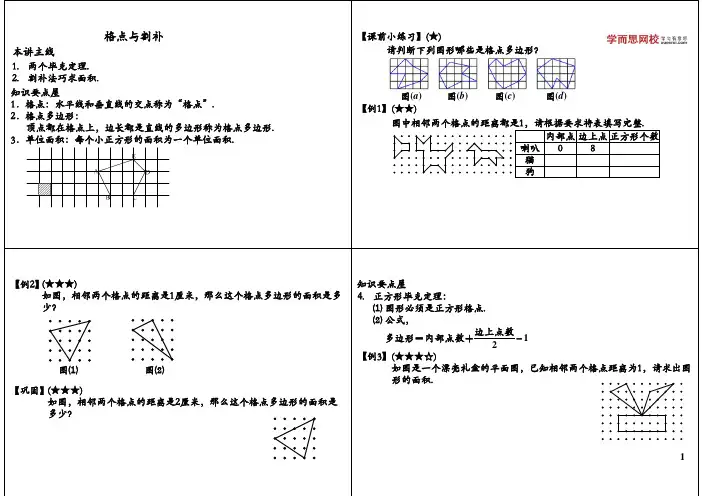
格点与面积知识要点:毕克定理:格点多边形面积=图内格点个数+周界格点数÷2-1(1)正方形格点问题就是它的格点都是由两组互相垂直相交的平行线的交点构成的.每一个小方格都是一个小正方形.正方形格点问题:多边形面积=边÷2+内-1(2)所谓三角形格点多边形是指:每相邻三点成“∵”或“∴”,所形成的三角形都是等边三角形.规定它的面积为1,以这样的点为顶点画出的多边形为三角形格点多边形.三角形格点问题:多边形面积=(边÷2+内-1)×2三角形格点问题所谓三角形格点多边形是指:每相邻三点成“∵”或“∴”,所形成的三角形都是等边三角形.规定它的面积为1,以这样的点为顶点画出的多边形为三角形格点多边形.关于三角形格点多边形的面积同样有它的计算公式:如果用S表示面积,N表示图形内包含的格点数,L表示图形周界上的格点数,那么有22S N L=⨯+-,就是格点多边形面积等于图形内部所包含格点数的2倍与周界上格点数的和减去2.例1:计算下列各图的面积。
总结:面积=(注:内部点,外部点关系)(毕克定理)例2:判断下列图形哪些是格点多边形?⑴⑵⑶例3:如图,计算各个格点多边形的面积.例4:求下列各个格点多边形的面积.例5:我们开始提到的“乡村小屋”的面积是多少?例6:右图是一个812 面积单位的图形.求矩形内的箭形ABCDEFGH 的面积.⑵⑴⑷⑶H GFED C BA例7:右图中每个小正方形的面积都是1,那么图中这只“狗”所占的面积是多少?例8:求下列格点多边形的面积(每相邻三个点“∵”或“∴”成面积为1的等边三角形).例9:右图中有21个点,其中每相邻的三点“∴”或“∵”所形成的三角形都是面积为1的等边三角形,试计算ABC的面积.例10:右图中有21个点,其中每相邻的三点“∴”或“∵”所形成的三角形都是面积为1的等边三角形,试计算四边形DEFG的面积.⑴⑵⑶⑷例11:.把等边三角形ABC每边六等分,组成如右图的三角形网.若图中每个小三角形的面积均为12cm,试求图中三角形DEF的面积.例12:图中正六边形ABCDEF 的面积是54,AP=2PF,CQ=2BQ,求阴影四边形CEPQ 的面积。