对勾函数图象性质

对勾函数的性质及运用一、对勾函数by ax x =+)0,0(>>b a 的图像与性质：1. 界说域：),0()0,(+∞⋃-∞2. 值域：),2[]2,(+∞⋃--∞ab ab3.奇偶性：奇函数,函数图像整体呈两个“对勾”的外形,且函数图像关于原点呈中间对称,即0)()(=-+x f x f4. 图像在一.三象限, 当0x >时,b y ax x =+≥ab 2（当且仅当bx a =取等号）,即)(x f 在x=ab时,取最小值ab 2由奇函数性质知：当x<0时,)(x f 在x=ab -时,取最大值ab 2-5.单调性：增区间为（∞+,ab）,（ab -∞-,）,减区间是（0,ab ）,（ab -,0）二、对勾函数的变形情势类型一：函数by ax x =+)0,0(<<b a 的图像与性质1.界说域：),0()0,(+∞⋃-∞2.值域：),2[]2,(+∞⋃--∞ab ab3.奇偶性：奇函数,函数图像整体呈两个“对勾”的外形.4.图像在二.四象限, 当x<0时,)(x f 在x=ab 时,取最小值ab 2;当0x >时,)(x f 在x=ab -时,取最大值ab 2-5.单调性：增区间为（0,ab ）,（ab -,0）减区间是（∞+,a b）,（a b -∞-,）,类型二：斜勾函数by ax x =+)0(<ab①0,0<>b a 作图如下1.界说域：),0()0,(+∞⋃-∞2.值域：R3.奇偶性：奇函数4.图像在二.四象限,无最大值也无最小值.5.单调性：增区间为（-∞,0）,（0,+∞）. ②0,0><b a 作图如下：1.界说域：),0()0,(+∞⋃-∞2.值域：R3.奇偶性：奇函数4.图像在二.四象限,无最大值也无最小值.5.单调性：减区间为（-∞,0）,（0,+∞）. 类型三：函数)0()(2>++=ac x c bx ax x f .此类函数可变形为bx c ax x f ++=)(,可由对勾函数x c ax y +=高低平移得到演习1.函数x x x x f 1)(2++=的对称中间为类型四：函数)0,0()(≠>++=k a k x ax x f此类函数可变形为kk x ak x x f -+++=)()(,则)(x f 可由对勾函数x a x y +=阁下平移,高低平移得到演习 1.作函数21)(-+=x x x f 与xx x x f +++=23)(的草图2.求函数421)(-+=x x x f 在),2(+∞上的最低点坐标3. 求函数1)(-+=x xx x f 的单调区间及对称中间类型五：函数)0,0()(2>≠+=b a bx axx f .此类函数界说域为R ,且可变形为x b x axbx a x f +=+=2)( a.若0>a ,图像如下：1．界说域：),(+∞-∞ 2. 值域：]21,21[b a ba ⋅⋅-3. 奇偶性：奇函数.4. 图像在一.三象限.当0x >时,)(x f 在b x =时,取最大值ba2,当x<0时,)(x f 在x=b -时,取最小值b a 2-5. 单调性：减区间为（∞+,b ）,（b -∞-,）;增区间是],[b b -演习1.函数1)(2+=x xx f 的在区间[)2,+∞上的值域为b. 若0<a ,作出函数图像：1．界说域：),(+∞-∞ 2. 值域：]21,21[ba ba ⋅⋅- 3. 奇偶性：奇函数.4. 图像在一.三象限.当0x >时,)(x f 在b x =时,取最小值ba 2-,当x<0时,)(x f 在x=b -时,取最大值b a 25. 单调性：增区间为（∞+,b ）,（b -∞-,）;减区间是],[b b -演习1.如2214xa x +=-+()1,2x ∈-,则的取值规模是类型六：函数)0()(2≠+++=a mx c bx ax x f .可变形为)0()()()()(2>++++=+++++=at s m x t m x a m x t m x s m x a x f ,则)(x f 可由对勾函数x tax y +=阁下平移,高低平移得到演习 1.函数11)(2+++=x x x x f 由对勾函数x x y 1+=向（填“左”.“右”）平移单位,向（填“上”.“下”）平移单位. 2.已知1->x ,求函数1107)(2+++=x x x x f 的最小值;3.已知1<x ,求函数199)(2--+=x x x x f 的最大值 类型七：函数)0()(2≠+++=a c bx ax mx x f演习1.求函数21)(2++-=x x x x f 在区间),1(+∞上的最大值;若区间改为),4[+∞则)(x f 的最大值为 2.求函数232)(22++++=x x x x x f 在区间),0[+∞上的最大值类型八：函数ax b x x f ++=)(.此类函数可变形为尺度情势：)0()(>-+-++=+-++=a b ax a b a x ax ab a x x f演习1.求函数13)(-+=x x x f 的最小值;2．求函数15)(++=x x x f 的值域;3.求函数32)(++=x x x f 的值域 类型九：函数)0()(22>++=a ax b x x f .此类函数可变形为尺度情势：)()()(22222o a b ax a b a x ax ab a x x f >-+-++=+-++=演习 1.求函数45)(22++=x x x f 的最小值;2. 求函数171)(22++=x x x f 的值域。

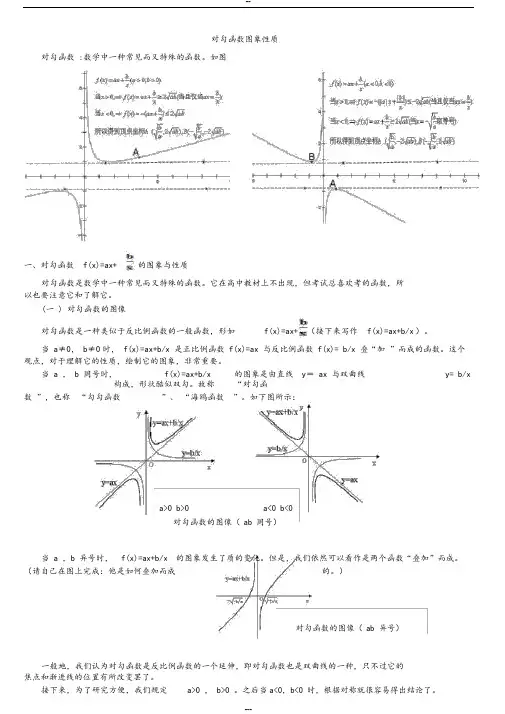
对勾函数图象性质对勾函数 :数学中一种常见而又特殊的函数。

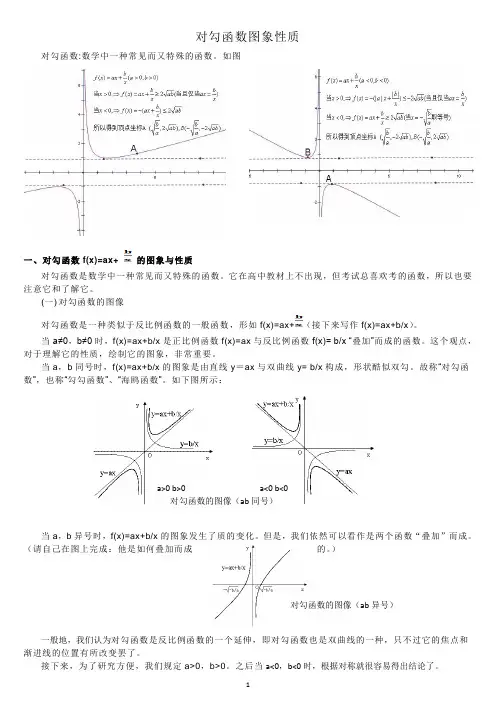
如图一、对勾函数f(x)=ax+ 的图象与性质对勾函数是数学中一种常见而又特殊的函数。

它在高中教材上不出现，但考试总喜欢考的函数，所以也要注意它和了解它。

(一 ) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数，形如f(x)=ax+ （接下来写作f(x)=ax+b/x ）。

当 a≠0， b≠0时， f(x)=ax+b/x 是正比例函数 f(x)=ax 与反比例函数 f(x)= b/x 叠“加”而成的函数。

这个观点，对于理解它的性质，绘制它的图象，非常重要。

当 a ， b 同号时，f(x)=ax+b/x 的图象是由直线y＝ ax 与双曲线y= b/x 构成，形状酷似双勾。

故称“对勾函数”，也称“勾勾函数”、“海鸥函数”。

如下图所示：a>0 b>0 a<0 b<0对勾函数的图像（ ab 同号）当 a ，b 异号时， f(x)=ax+b/x 的图象发生了质的变化。

但是，我们依然可以看作是两个函数“叠加”而成。

（请自己在图上完成：他是如何叠加而成的。

）对勾函数的图像（ab 异号）一般地，我们认为对勾函数是反比例函数的一个延伸，即对勾函数也是双曲线的一种，只不过它的焦点和渐进线的位置有所改变罢了。

接下来，为了研究方便，我们规定a>0 ， b>0 。

之后当a<0，b<0 时，根据对称就很容易得出结论了。

1(二 ) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。

利用均值不等式可以得到：当 x>0 时，。

当 x<0 时，。

即对勾函数的定点坐标：(三 ) 对勾函数的定义域、值域由（二）得到了对勾函数的顶点坐标，从而我们也就确定了对勾函数的定义域、值域等性质。

(四 ) 对勾函数的单调性y(五 ) 对勾函数的渐进线O Xy=ax由图像我们不难得到：(六 ) 对勾函数的奇偶性：对勾函数在定义域内是奇函数，二、类耐克函数性质探讨函数y ax b，在 a0或b0时为简单的单调函数，不予讨论。

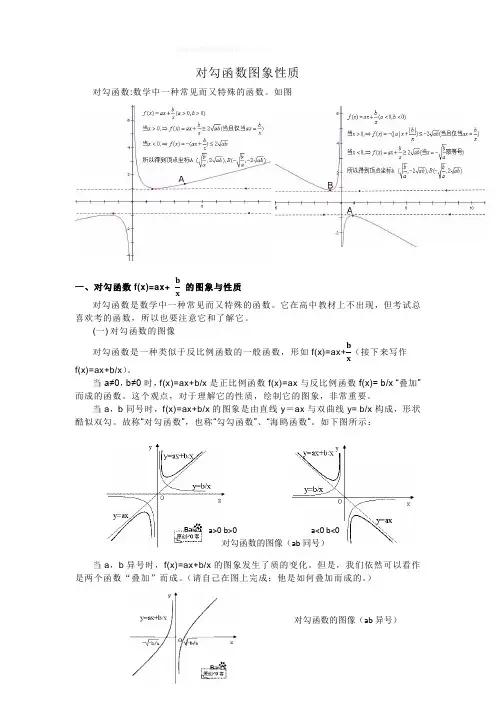
对勾函数图象性质对勾函数:数学中一种常见而又特殊的函数。

如图一、对勾函数f(x)=ax+bx 的图象与性质对勾函数是数学中一种常见而又特殊的函数。

它在高中教材上不出现，但考试总喜欢考的函数，所以也要注意它和了解它。

(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数，形如f(x)=ax+bx （接下来写作f(x)=ax+b/x ）。

当a≠0，b≠0时，f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。

这个观点，对于理解它的性质，绘制它的图象，非常重要。

当a ，b 同号时，f(x)=ax+b/x 的图象是由直线y ＝ax 与双曲线y= b/x 构成，形状酷似双勾。

故称“对勾函数”，也称“勾勾函数”、“海鸥函数”。

如下图所示：当a ，b 异号时，f(x)=ax+b/x 的图象发生了质的变化。

但是，我们依然可以看作是两个函数“叠加”而成。

（请自己在图上完成：他是如何叠加而成的。

）a>0 b>0 a<0 b<0 对勾函数的图像（ab 同号） 对勾函数的图像（ab 异号）一般地，我们认为对勾函数是反比例函数的一个延伸，即对勾函数也是双曲线的一种，只不过它的焦点和渐进线的位置有所改变罢了。

接下来，为了研究方便，我们规定a>0，b>0。

之后当a<0，b<0时，根据对称就很容易得出结论了。

(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。

利用均值不等式可以得到：当x>0时，f (x )=ax +bx ≥2√ab (当且尽当ax =bx 时取等号)，此时x =√ba 。

当x<0时，f (x )=ax +bx ≤−2√ab (当且尽当ax =bx 时取等号)，此时x =−√ba 。

(三) 对勾函数的定义域、值域由（二）得到了对勾函数的顶点坐标，从而我们也就确定了对勾函数的定义域、值域等性质。

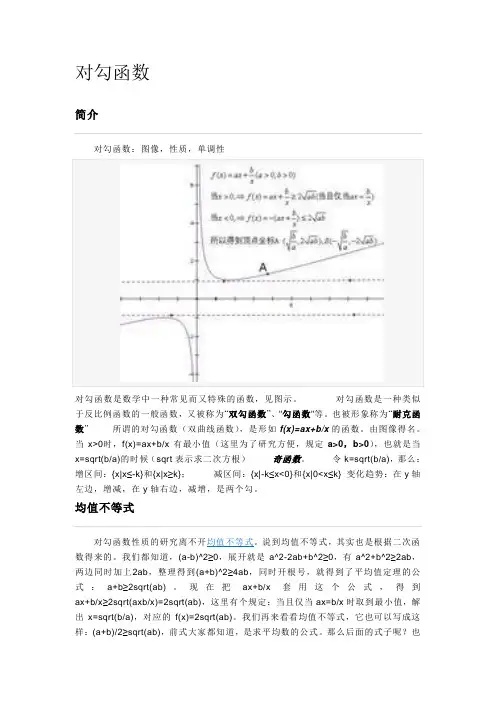
对勾函数简介对勾函数：图像，性质，单调性对勾函数是数学中一种常见而又特殊的函数，见图示。

对勾函数是一种类似于反比例函数的一般函数，又被称为“双勾函数”、"勾函数"等。

也被形象称为“耐克函数”所谓的对勾函数（双曲线函数），是形如f(x)=ax+b/x的函数。

由图像得名。

当x>0时，f(x)=ax+b/x有最小值（这里为了研究方便，规定a>0，b>0），也就是当x=sqrt(b/a)的时候（sqrt表示求二次方根）奇函数。

令k=sqrt(b/a)，那么：增区间：{x|x≤-k}和{x|x≥k}；减区间：{x|-k≤x<0}和{x|0<x≤k} 变化趋势：在y轴左边，增减，在y轴右边，减增，是两个勾。

均值不等式对勾函数性质的研究离不开均值不等式。

说到均值不等式，其实也是根据二次函数得来的。

我们都知道，(a-b)^2≥0，展开就是a^2-2ab+b^2≥0，有a^2+b^2≥2ab，两边同时加上2ab，整理得到(a+b)^2≥4ab，同时开根号，就得到了平均值定理的公式：a+b≥2sqrt(ab)。

现在把ax+b/x套用这个公式，得到ax+b/x≥2sqrt(axb/x)=2sqrt(ab)，这里有个规定：当且仅当ax=b/x时取到最小值，解出x=sqrt(b/a)，对应的f(x)=2sqrt(ab)。

我们再来看看均值不等式，它也可以写成这样：(a+b)/2≥sqrt(ab)，前式大家都知道，是求平均数的公式。

那么后面的式子呢？也是平均数的公式，但不同的是，前面的称为算术平均数，而后面的则称为几何平均数，总结一下就是算术平均数绝对不会小于几何平均数。

这些知识点也是非常重要的。

导数求解其实用导数也可以研究对勾函数的性质。

不过首先要会负指数幂的换算，这也很简单，但要熟练掌握。

举几个例子：1/x=x^-1，4/x^2=4x^-2。

明白了吧，x为分母的时候可以转化成负指数幂。

对勾函数一、定义对勾函数是由两个幂函数相加得到的，对勾函数是一种类似于反比例函数的一般双曲函数，其标准形式为f(x)=ax+（其中ab>0）。

由于函数图像形似两个中心对称的对勾，因此得名“对勾函数”，又被称为“双勾函数”、“勾函数”、“对号函数”、“双飞燕函数”等。

在许多情况下，为了简化分析，常取a=b=1，即函数形式为f(x)=x+。

研究初等函数的一般路径，背景—概念—图象—性质—应用二、图象及性质图像特征：1、对勾函数的图像是分别以y 轴和直线y=ax 为渐近线的两支曲线。

2、图像上任意一点到两条渐近线的距离之积恰为渐近线夹角（0-180°）的正弦值与|b|的乘积。

3、函数图像整体呈两个“对勾”的形状，且关于原点呈中心对称。

定义域：，即除了x=0外，所有实数都是其定义域内的元素。

值域：。

单调性：函数在(−∞,−1)∪(1,+∞)上单调递增，在(1,0)∪(0,1)上单调递减。

奇偶性：对勾函数是奇函数，即满足f(−x)=−f(x)。

x 122严禁复制三、题型1、基础计算题给定对勾函数表达式，求函数在特定点的值或特定区间的最值。

2.、图像结合题根据对勾函数的图像，判断函数在哪些区间内满足特定条件（如大于某值、小于某值）。

利用图像分析函数与直线、其他曲线的交点情况。

3.、综合应用题求最值问题：利用对勾函数的性质，可以快速求解形如ax+（ab>0）的函数的最值问题。

不等式证明：在不等式证明中，对勾函数的性质也常被用来进行放缩或构造反例。

实际问题建模：在某些经济学问题中，如成本分析、收益最大化等，也可能涉及到对勾函数的应用。

4、参数变化分析：探讨参数a 和b 变化时，对勾函数图像和性质的变化规律。

5、复杂函数组合将对勾函数与其他函数（如二次函数、指数函数等）组合，分析新函数的性质和应用。

四、解题步骤1、对勾函数求最值问题的解题步骤（1）理解函数形式确认函数f(x)=ax+的形式，注意a 和b 都是正数且不相等。

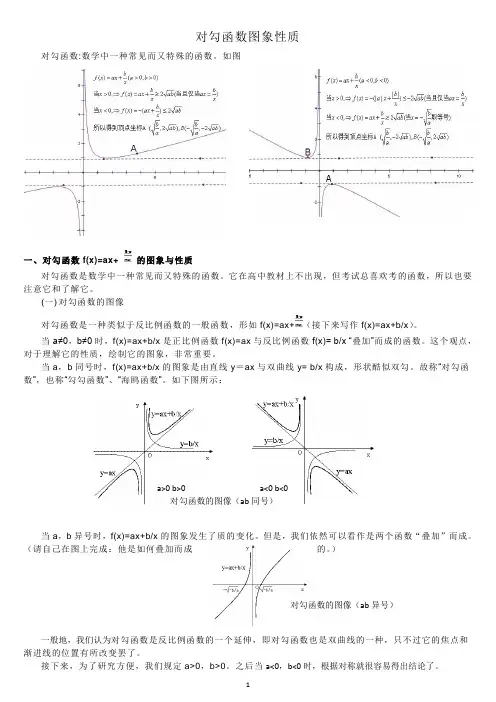
对勾函数图象性质对勾函数:数学中一种常见而又特殊的函数。

如图一、对勾函数f(x)=ax+ 的图象与性质对勾函数是数学中一种常见而又特殊的函数。

它在高中教材上不出现，但考试总喜欢考的函数，所以也要注意它和了解它。

(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数，形如f(x)=ax+（接下来写作f(x)=ax+b/x）。

当a≠0，b≠0时，f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)= b/x “叠加”而成的函数。

这个观点，对于理解它的性质，绘制它的图象，非常重要。

当a，b同号时，f(x)=ax+b/x的图象是由直线y＝ax与双曲线y= b/x构成，形状酷似双勾。

故称“对勾函数”，也称“勾勾函数”、“海鸥函数”。

如下图所示：a>0 b>0 a<0 b<0对勾函数的图像（ab同号）当a，b异号时，f(x)=ax+b/x的图象发生了质的变化。

但是，我们依然可以看作是两个函数“叠加”而成。

（请自己在图上完成：他是如何叠加而成的。

）对勾函数的图像（ab异号）一般地，我们认为对勾函数是反比例函数的一个延伸，即对勾函数也是双曲线的一种，只不过它的焦点和渐进线的位置有所改变罢了。

接下来，为了研究方便，我们规定a>0，b>0。

之后当a<0，b<0时，根据对称就很容易得出结论了。

(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。

利用均值不等式可以得到： 当x>0时，。

当x<0时，。

即对勾函数的定点坐标：(三) 对勾函数的定义域、值域由（二）得到了对勾函数的顶点坐标，从而我们也就确定了对勾函数的定义域、值域等性质。

(四) 对勾函数的单调性(五) 对勾函数的渐进线由图像我们不难得到：(六) 对勾函数的奇偶性 ：对勾函数在定义域内是奇函数， 二、类耐克函数性质探讨 函数xbax y +=，在时或00==b a 为简单的单调函数，不予讨论。

对勾函数的性质及应用一、对勾函数b y ax x =+)0,0(>>b a 的图像与性质：1. 定义域：),0()0,(+∞⋃-∞2. 值域：),2[]2,(+∞⋃--∞ab ab3. 奇偶性：奇函数，函数图像整体呈两个“对勾”的形状，且函数图像关于原点呈中心对称，即0)()(=-+x f x f 4. 图像在一、三象限, 当0x >时，by ax x=+≥ab 2（当且仅当b x a ，即)(x f 在x=a b 时，取最小值ab 2由奇函数性质知：当x<0时，)(x f 在x=ab -时，取最大值ab 2-5. 单调性：增区间为（∞+,a b ），（a b -∞-,）,减区间是（0，a b ），（ab -,0）二、对勾函数的变形形式 类型一：函数by ax x=+)0,0(<<b a 的图像与性质 1.定义域：),0()0,(+∞⋃-∞ 2.值域：),2[]2,(+∞⋃--∞ab ab3.奇偶性：奇函数，函数图像整体呈两个“对勾”的形状.4.图像在二、四象限, 当x<0时，)(x f 在x=ab 时，取最小值ab 2；当0x >时，)(x f 在x=ab -时，取最大值ab 2-5.单调性：增区间为（0，ab ），（a b -,0）减区间是（∞+,a b ），（ab -∞-,）,类型二：斜勾函数by ax x=+)0(<ab ①0,0<>b a 作图如下1.定义域：),0()0,(+∞⋃-∞2.值域：R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值.5.单调性：增区间为（-∞，0），（0，+∞）.②0,0><b a 作图如下：1.定义域：),0()0,(+∞⋃-∞2.值域：R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值.5.单调性：减区间为（-∞，0），（0，+∞）.类型三：函数)0()(2>++=ac xcbx ax x f 。

对勾函数的性质及应用 一、对勾函数b y ax x =+)0,0(>>b a 的图像与性质： 1. 定义域：),0()0,(+∞⋃-∞2. 值域：),2[]2,(+∞⋃--∞ab ab3. 奇偶性：奇函数，函数图像整体呈两个“对勾”的形状，且函数图像关于原点呈中心对称，即0)()(=-+x f x f4. 图像在一、三象限, 当0x >时，b y ax x=+≥ab 2（当且仅当b x a=取等号），即)(x f 在x=a b 时，取最小值ab 2由奇函数性质知：当x<0时，)(x f 在x=ab -时，取最大值ab 2- 5. 单调性：增区间为（∞+,ab ），（a b -∞-,）,减区间是（0，a b ），（a b -,0）二、对勾函数的变形形式类型一：函数b y ax x=+)0,0(<<b a 的图像与性质 1.定义域：),0()0,(+∞⋃-∞2.值域：),2[]2,(+∞⋃--∞ab ab3.奇偶性：奇函数，函数图像整体呈两个“对勾”的形状.4.图像在二、四象限, 当x<0时，)(x f 在x=ab 时，取最小值ab 2；当0x >时，)(x f 在x=ab -时，取最大值ab 2- 5.单调性：增区间为（0，a b ），（a b -,0）减区间是（∞+,ab ），（a b -∞-,）,类型二：斜勾函数b y ax x=+)0(<ab ①0,0<>b a 作图如下1.定义域：),0()0,(+∞⋃-∞2.值域：R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值.5.单调性：增区间为（-∞，0），（0，+∞）.②0,0><b a 作图如下：1.定义域：),0()0,(+∞⋃-∞2.值域：R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值.5.单调性：减区间为（-∞，0），（0，+∞）.类型三：函数)0()(2>++=ac x c bx ax x f 。