浙江省临海市新概念教育咨询有限公司八年级数学竞赛讲座第五讲 有条件的分式的化简与求值

初二数学分式的通分与化简的技巧一、通分的技巧1、整体通分例1、计算：-x2-x-1分析：将整式-(x2+x+1)视为分母为1的分式，进行整体通分解：原式= -(x2+x+1)2、局部通分：例2、化简：分析：将分式的分子，分母分别整体通分，就很容易了。

解：原式= ÷= ×=3、分部通分例3、化简分析：将前两项通分化简，与恰好是用分母的分式然后再加减解：原式= +4、逐步通分例4、化简：- - -分析：因为分式的分母依次呈平方差型，(x-1)(x+1)=x2-1(x2+1)(x2-1)=x4-1，所以可采取逐步通分进行化简解：原式= - - = - =5、一次通分例5、化简：+ +解：原式=6、先约分，后通分。

例6、化简- -分析：将分式中的分子，分母先因式分解，进行约分后再通分。

解：原式= - -= - -= - -7、先变换条件，后通分。

例7、当a=-2,b=3,c= 时，求代数式+ + 的值。

分析；因为abc=(-2）×3×( )=1,利用代换法将各分式化为同分母的分式相加减。

解：∵a=-2,b=3,c= ∴abc=1原式= + += + += + += + + = =18、先变号，后通分。

例8、计算+ +解：先变号===后通分：原式=9、先分离，后通分。

例9、化简：+ -分析：如果先通分后计算，显然很复杂，借用除法将各个分式化成整式部分与分式部分的和，这样计算可以化繁为简。

解：由多项式的除法，得(x3+5x2+8x+4)÷(x2+5x+6)=x+2(2x3+13x2+27x+18)÷(x2+5x+6)=2x+3(3x3+26x2+71x+59)÷(x2+7x+12)=(3x+5)-∴原式=(x+2)+(2x+3)-[(3x+5)- ]=10、先换元，后通分。

例10、计算[ - ]÷（- ）解：换元，设=x =y则=x2=y2原式=(x2-y2)÷(x-y)=x+y= + =例11、化简÷分析：利用换元法可简化运算，将互为倒数的两个分式分别换成x,y并巧妙地利用倒数关系为简化运算创造了条件。

八年级数学分式与分式方程分式与分式方程学习资料。

一、分式的概念。

1. 定义。

- 一般地，如果A、B（B≠0）表示两个整式，且B中含有字母，那么式子(A)/(B)就叫做分式。

例如(1)/(x)，(x + 1)/(x - 1)等都是分式，而(2)/(3)不是分式，因为分母是常数3，不含有字母。

2. 分式有意义的条件。

- 分式(A)/(B)有意义的条件是B≠0。

例如，对于分式(1)/(x - 2)，当x - 2≠0，即x≠2时，这个分式有意义。

3. 分式值为零的条件。

- 分式(A)/(B)的值为零的条件是A = 0且B≠0。

例如，对于分式(x)/(x+1)，当x = 0且x+1≠0（即x≠ - 1）时，分式的值为0。

二、分式的基本性质。

1. 性质内容。

- 分式的分子与分母同乘（或除以）一个不等于0的整式，分式的值不变。

用式子表示为(A)/(B)=(A× C)/(B× C)，(A)/(B)=(A÷ C)/(B÷ C)（C≠0）。

2. 约分。

- 定义：根据分式的基本性质，把一个分式的分子与分母的公因式约去，叫做分式的约分。

- 例如，对于分式(6x^2y)/(8xy^2)，分子分母的公因式是2xy，约分后得到(3x)/(4y)。

3. 通分。

- 定义：根据分式的基本性质，把几个异分母的分式分别化成与原来的分式相等的同分母的分式，叫做分式的通分。

- 例如，将(1)/(x)和(1)/(x + 1)通分，先找最简公分母为x(x + 1)，则(1)/(x)=(x +1)/(x(x + 1))，(1)/(x+1)=(x)/(x(x + 1))。

三、分式的运算。

1. 分式的乘除法。

- 分式乘分式，用分子的积做积的分子，分母的积做积的分母，即(A)/(B)·(C)/(D)=(A· C)/(B· D)。

例如(2)/(3x)·(6x)/(4)=(2×6x)/(3x×4)= 1。

八年级下册数学的分式知识点整理八年级下册数学的分式知识点整理在平时的学习中，大家最不陌生的就是知识点吧！知识点就是“让别人看完能理解”或者“通过练习我能掌握”的内容。

为了帮助大家掌握重要知识点，下面是店铺精心整理的八年级下册数学的分式知识点整理，欢迎大家分享。

1.分式的定义：如果A、B表示两个整式，并且B中含有字母，那么式子叫做分式。

2.分式有意义、无意义的条件：分式有意义的条件：分式的分母不等于0;分式无意义的条件：分式的分母等于0。

3.分式值为零的`条件：分式AB =0的条件是A=0，且B≠0.(首先求出使分子为0的字母的值，再检验这个字母的值是否使分母的值为0.当分母的值不为0时，就是所要求的字母的值。

)4.分式的基本性质：分式的分子与分母同乘(或除以)一个不等于0的整式，分式的值不变。

用式子表示为 (其中A、B、C是整式 )，5.分式的通分：和分数类似，利用分式的基本性质，使分子和分母同乘适当的整式，不改变分式的值，把几个异分母分式化成相同分母的分式，这样的分式变形叫做分式的通分。

通分的关键是确定几个式子的最简公分母。

几个分式通分时，通常取各分母所有因式的最高次幂的积作为公分母，这样的分母就叫做最简公分母。

求最简公分母时应注意以下几点：(1)“各分母所有因式的最高次幂”是指凡出现的字母(或含字母的式子)为底数的幂选取指数最大的;(2)如果各分母的系数都是整数时，取它们系数的最小公倍数作为最简公分母的系数;(3)如果分母是多项式，一般应先分解因式。

6.分式的约分：和分数一样，根据分式的基本性质，约去分式的分子和分母中的公因式，不改变分式的值，这样的分式变形叫做分式的约分。

约分后分式的分子、分母中不再含有公因式，这样的分式叫最简公因式。

约分的关键是找出分式中分子和分母的公因式。

(1)约分时注意分式的分子、分母都是乘积形式才能进行约分;分子、分母是多项式时，通常将分子、分母分解因式，然后再约分;(2)找公因式的方法：① 当分子、分母都是单项式时，先找分子、分母系数的最大公约数，再找相同字母的最低次幂，它们的积就是公因式;②当分子、分母都是多项式时，先把多项式因式分解。

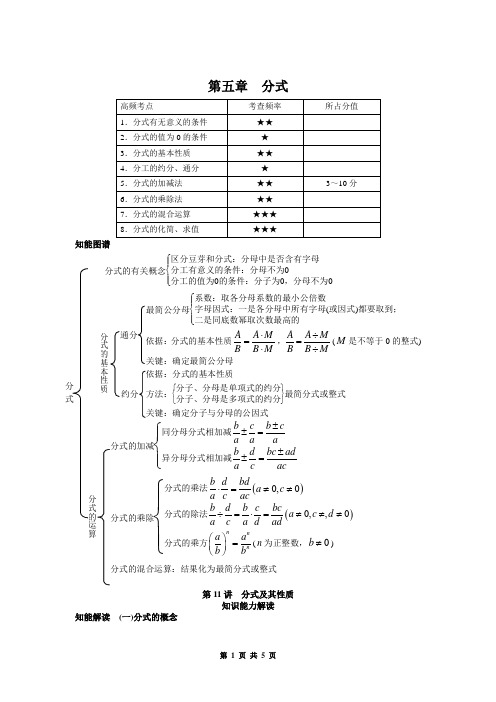
第五章 分式知能图谱分式的有关概念⎩⎪⎨⎪⎧区分豆芽和分式：分母中是否含有字母分工有意义的条件：分母不为0分工的值为0的条件：分子为0，分母不为0最简公分母⎩⎪⎨⎪⎧系数：取各分母系数的最小公倍数字母因式：一是各分母中所有字母(或因式)都要取到；二是同底数幂取次数最高的依据：分式的基本性质A A MB B M ⋅=⋅，A A M B B M÷=÷(M 是不等于0的整式) 关键：确定最简公分母 依据：分式的基本性质方法：⎩⎨⎧⎭⎬⎫分子、分母是单项式的约分分子、分母是多项式的约分最简分式或整式 关键：确定分子与分母的公因式分式的加减⎩⎪⎨⎪⎧同分母分式相加减b c b ca a a±±=异分母分式相加减b d bc ada c ac±±=分式的乘除⎩⎪⎨⎪⎧分式的乘法()0,0b d bda c a c ac⋅=≠≠分式的除法()0,,0b d b c bca c d a c a d ad÷=⋅=≠≠≠分式的乘方nnn a a b b⎛⎫= ⎪⎝⎭(n 为正整数，0b ≠)分式的混合运算：结果化为最简分式或整式第11讲 分式及其性质知识能力解读知能解读 (一)分式的概念分式通分约分 分式的基本性质分式的运算一般地，如果A ，B 表示两个整式，并且B 中含有字母，那么式子AB叫作分式．分式会AB中A 叫作分子，B 叫作分母． 注意：(1)判断一个式子是否为分式，关键是看分母中是否有字母．(2)分式与整式的根本区别：分式的分母中含有字母，如12，2x 是整式，而2x是分式． (3)分式有无意义的条件：①若0B ≠，则分式A B 有意义；②若0B =，则分式AB无意义．(4)分式的值为零的条件：若{0A B =≠，则分式A B的值为零，反之也成立． (二)分式的基本性质分式的基本性质：分式的分子与分母同乘(或除以)同一个不等于0的整式，分式的值不变．用式子表示是：A A MB B M ⋅=⋅，()0A A M M B B M÷=≠÷，其中A ，B ，M 是整式． 注意：(1)分式的基本性质可类比分数的基本性质去理解记忆．利用分式的基本性质，可以在不改变分式的值的条件下，对分式作一系列的变形．(2)当分式的分子(或分母)是多项式，运用分式的基本性质时，要先把分式的分子(或分母)用括号括上．再将分子与分母同乘(或除以)相同的整式． (三)约分、最简分式及通分的概念(1)约分：根据分式的基本性质，把一个分式的分子与分母的公因式约去，叫作分式的约分．说明：约分的关键是准确找出分子与分母的公因式，找公因式的方法：(1)当分子和分母都是单项式时，先找出它们系数的最大公约数，再确定相同字母的最低次幂，它们的乘积就是分子与分母的公因式．(2)当分子、分母是多项式时，先将分子、分母因式分解，把分子、分母化为几个因式的积后，再找出分子、分母的公因式．约分应注意一定要把公因式约尽，还应注意分子、分母的整体都要除以同一个公因式．当分子或分母是多项式时，要用分子、分母的公因式去除整个多项式，不能只除某一项，更不能减去某一项．例如2233a x ab x b+=+是错误的．(2)最简分式：分子与分母没有公因式的分式叫作最简分式．判断一个分式是否为最简分式，关键是确定其分子与分母是否有公因式(1除外)．分式的约分，一般要约去分子和分母的所有公因式，使所得结果成为最简分式或整式． 注意：(1)最简分式与小学学过的最简分数类似．(2)最简分式是对一个独立的分式而言的，最大的特点是只有一条分数线．形如322x y++，233ax y ++的分式都不是最简分式． (3)通分：根据分式的基本性质，把几个异分母的分式分别化成与原来的分式相等的同分母的分式，叫作分式的通分．通分的关键是确定几个分式的最简公分母．(4)最简公分母：各分母所有因式的最高次幂的积，叫作最简公分母． 注意：确定最简公分母的一般方法：(1)如果各分母都是单项式，确定最简公分母的方法是：①取各分母系数的最小公倍数；②凡单独出现的字母，连同它的指数作为最简公分母的一个因式；③同底数幂取次数最高的．这样得到的积就是最简公分母．(2)如果各分母都是多项式，就要把它们分解因式，再按照分母是单项式求最简公分母的方法，从系数、相同因式、不同因式三个方面去求．方法技巧归纳方法技巧 (一)应用分式概念解题的规律1．分式的判别方法根据定义判定式子AB是否为分式要注意两点：一是A ，B 都是整式，二是B 中含字母且0B ≠．判断一个代数式是否为分式，还应注意不能把原式变形(如约分等)，而只能根据它的最初形式进行判断．如根据()()()()22222a b a b a b a b a b a b +---==++，判定()222a b a b -+不是分式，这是错误的．2．对分式有无意义或值为0的条件判断 (二)分式基本性质的应用分式的基本性质是分式恒等变形和分式运算的理论依据，正确理解和熟练掌握这一性质是学好分式的关键．利用分式的基本性质可将分式恒等变形，化简分式，简化计算等．1．约分 2．通分(三)分式值的特殊情况(拓展)1．分式的值为1或1-的讨论若分成()10AB B=≠，则A B =，反之也成立；若分式()10A B B =-≠，则A 与B 互为相反数，反之也成立．2．分式的值为正数的讨论 分式的值为正数时，分式的分子与分母同号，利用这一关系构造不等式组可求出待定字母的取值范围．3．分式的值为负数的讨论 分式的值为负数时，分式的分子与分母异号，利用这一关系构造不等式组可求出待定字母的取值范范围．4．分式的值为整数的讨论若分式的值为整数，则分母必为分子的约数，利用这一关系可对分母进行讨论．易混易错辨析易混易错知识1．误认为只要分子等于0，就能使分式的值为0．2．利用分式基本性质把分子、分母都乘(或除以)非零整式M 时，只乘(或除以)其中某些项，有漏乘(或漏除)的项．3．分式变号时极易出错，易误只将分子或分母的第一项改变符号． 易混易错 (一)分式基本性质的误用 (二)忽视分式值为0的前提条件 (三)约分时易出现符号错误 (四)确定最简公分母出错中考试题研究中考命题规律本讲考点是考查分式有无意义、分式的值为零条件的判断，以及用分式基本性质进行变形；以填空题、选择题及简单的解答题的形式出现． 中考试题 (一)对分式概念的理解 (二)分式基本性质的应用 (三)确定最简公分母第12讲 分式的运算知识能力解读知能解读 (一)分式的乘除法分式的乘除法与分数的乘除法类似，法则如下：(1)乘法法则：分式乘分式，用分子的积作为积的分子，分母的积作为积的分母，用式子表示是：a c a cb d b d⋅⋅=⋅．(2)除法法则：分式除以分式，把除式的分子、分母颠倒位置后，与被除式相乘，用式子表示是：a c a d a db d bc b c⋅÷=⋅=⋅．(3)分式的乘方：分式乘方要把分子、分母分别乘方，用式子表示是：n nna ab b⎛⎫=⎪⎝⎭(n是正整数)．注意：(1)法则中的字母a，b，c，d所代表的可以是单项式，也可以是多项式．(2)运算的结果必须是最简分式或整式．(二)分式的加减法1．同分母分式加减法的法则与同分母的分数加减法类似，同分母分式相加减，分母不变，把分子相加减．用式子表示是：a b a bc c c±±=．注意：(1)“同分母分式相加减”是把各个分式的“分子的整体”相加减，即当分子是多项式时，应将各分子加括号，括号不能省略，(2)运算结果必须化为最简分式或整式．2．异分母分式加减法的法则与异分母的分数加减法类似，异分母分式相加减，先通分，变为同分母的分式，再加减．用式子表示是：a c ad bc ad bcb d bd bd bd±±=±=．(三)分式的混合运算分式的混合运算的顺序是：先乘方，再乘除，最后算加减；遇到括号，先算括号内的；在同级运算中，从左向右依次进行．注意：(1)实数的运算律对分式同样适用，注意灵活运用，提高解题的质量和速度．(2)结果必须化为最简分式或整式．(3)分子或分母的系数是负数时，要把“－”提到分数线的前边．(4)对于分式的乘除混合运算，应先将除法运算转化为乘法运算，分子、分母是多项式时，可先将分子、分母分解因式，再相乘．方法技巧归纳方法技巧(一)分式的乘除法及乘方运算的解题技巧1．分式的乘除法分式的乘除运算可以统一成乘法运算，分式的乘法一般情况下是先约分再相乘，这样做省时简单易行，又不易出错；当除式(或被除式)是整式时，可以看作分母是1的式子，然后再按分式的乘除法则计算．2．分式的乘方做分式乘方时，一是注意养成先确定结果的符号，再做其他运算的良好习惯；二是注意运算顺序，先乘方，再乘除，最后加减．(二)分式加减运算的解题技巧分式的加减法与分数的加减法的运算法则实质是相同的，分为同分母加减法和异分母加减法，所不同的是分式的加减运算比分数的加减运算要复杂得多，它是整式运算、因式分解和分式运算的综合运用．分式加减运算需要运用较多的基础知识，运算步骤增多，符号变换复杂，解题方法灵活多样．(三)分式化简、求值的解题技巧分式的化简、求值问题，一是化简要求值的分式，只要能化简就考虑化简；二是化简已知条件，化到最简后，再考虑代入求值．(四)分式混合运算的解题技巧分式的混合运算，除了掌握运算顺序外，在运算过程中，可灵活运用交换律、结合律、分配律使运算简化，值得提醒的是最后结果必须是最简分式或整式． (五)分式通分的解题技巧分式的加减运算，分同分母分式相加减和异分母分式相加减，对于异分母分式的加减法，有时直接通分会很繁琐，我们可以根据式子的特点，灵活的采用不同的方法通分，从而起到事半功倍的效果．1．分组通分 2．逐项通分3．公式()11111n n n n =-++的运用 易混易错辨析易混易错知识在分式的乘除运算或混合运算中，运算顺序易出错．在分式的混合运算中，若有括号，先算括号里面的，同级运算应按从左到右的顺序依次进行．易混易错 (一)运算顺序有误 (二)分子符号出错(三)运算结果不是最简分式 (四)错用运算律中考试题研究中考命题规律本讲考查的知识面广，综合性强．中考热点是分式的运算及分式的化简、求值，常与二次根式、三角函数等知识结合起来命题，题型以解答题为主，也出现填空题．近几年又出现了开放式的新题型，应给予关注． 中考试题 (一)分式的加减 (二)分式的乘除 (三)分式的混合运算 (四)分式的化简求值。

八年级分式知识点总结分式知识是比较容易拿分的题目，那么相关的分式知识点我们又要掌握什么呢?以下是小编为大家精心整理的八年级分式知识点总结，欢迎大家阅读。

八年级分式知识点总结1.分式的定义：如果A、B表示两个整式，并且B中含有字母，那么式子叫做分式。

2.分式有意义、无意义的条件：分式有意义的条件：分式的分母不等于0;分式无意义的条件：分式的分母等于0。

3.分式值为零的条件：分式AB =0的条件是A=0，且B≠0.(首先求出使分子为0的字母的值，再检验这个字母的值是否使分母的值为0.当分母的值不为0时，就是所要求的字母的值。

)4.分式的基本性质：分式的分子与分母同乘(或除以)一个不等于0的整式，分式的值不变。

用式子表示为 (其中A、B、C是整式 )，5.分式的通分：和分数类似，利用分式的基本性质，使分子和分母同乘适当的整式，不改变分式的值，把几个异分母分式化成相同分母的分式，这样的分式变形叫做分式的通分。

通分的关键是确定几个式子的最简公分母。

几个分式通分时，通常取各分母所有因式的最高次幂的积作为公分母，这样的分母就叫做最简公分母。

求最简公分母时应注意以下几点：(1)“各分母所有因式的最高次幂”是指凡出现的字母(或含字母的式子)为底数的幂选取指数最大的;(2)如果各分母的系数都是整数时，取它们系数的最小公倍数作为最简公分母的系数;(3)如果分母是多项式，一般应先分解因式。

6.分式的约分：和分数一样，根据分式的基本性质，约去分式的分子和分母中的公因式，不改变分式的值，这样的分式变形叫做分式的约分。

约分后分式的分子、分母中不再含有公因式，这样的分式叫最简公因式。

约分的关键是找出分式中分子和分母的公因式。

(1)约分时注意分式的分子、分母都是乘积形式才能进行约分;分子、分母是多项式时，通常将分子、分母分解因式，然后再约分;(2)找公因式的方法：① 当分子、分母都是单项式时，先找分子、分母系数的最大公约数，再找相同字母的最低次幂，它们的积就是公因式;②当分子、分母都是多项式时，先把多项式因式分解。

八年级数学《分式方程》知识点一、理解定义1、分式方程：含分式，并且分母中含未知数的方程——分式方程。

2、解分式方程的思路是：（1） 在方程的两边都乘以最简公分母，约去分母，化成整式方程。

（2） 解这个整式方程。

（3） 把整式方程的根带入最简公分母，看结果是不是为零，使最简公分母为零的根是原方程的增根，必须舍去。

（4） 写出原方程的根。

“一化二解三检验四总结”3、 增根：分式方程的增根必须满足两个条件：（1）增根是最简公分母为0；（2）增根是分式方程化成的整式方程的根。

4、分式方程的解法：(1)能化简的先化简(2)方程两边同乘以最简公分母，化为整式方程；(3)解整式方程； (4)验根．注：解分式方程时，方程两边同乘以最简公分母时，最简公分母有可能为０，这样就产生了增根，因此分式方程一定要验根。

分式方程检验方法：将整式方程的解带入最简公分母，如果最简公分母的值不为0，则整式方程的解是原分式方程的解；否则，这个解不是原分式方程的解。

5、分式方程解实际问题（1）步骤：审题—设未知数—列方程—解方程—检验—写出答案，检验时要注意从方程本身和实际问题两个方面进行检验。

（2）应用题基本类型；二、例题讲析例1：解方程214111x x x +-=-- （1） 增根是使最简公分母值为零的未知数的值。

（2） 增根是整式方程的根但不是原分式方程的，所以解分式方程一定要验根。

例2：解关于x 的方程223242ax x x x +=--+有增根，则常数a 的值。

解：化整式方程的(1)10a x -=-由题意知增根2,x =或2x =-是整式方程的根，把2,x =代入得2210a -=-,解得4a =-,把2x =-代入得-2a+2=-10，解得6a = 所以4a =-或6a =时，原方程产生增根。

方法总结：1.化为整式方程。

2.把增根代入整式方程求出字母的值。

例3：解关于x 的方程223242ax x x x +=--+无解，则常数a 的值。