2016中考选择题专项训练 含答案(共三十五套)
- 格式:doc
- 大小:2.01 MB
- 文档页数:45

中考2016数学试题及答案第一部分选择题1. 当x=3时,下列各式中必然成立的是()A. 2x + 1 = 8B. x - 5 = 2xC. 3x + 2 = 2x + 3D. 4x - 3 = 3 - x答案: B2. 下列各点坐标中,纵坐标是负数的点是()A. (3, 4)B. (-2, -5)C. (-1, 3)D. (0, 1)答案: B3. 如果a:b = 4:5, b:c = 3:2,那么a:c的值为()A. 12:10B. 20:27C. 8:15D. 16:9答案: C4. 在矩形ABCD中,AB = 3cm, BC = 4cm,如图所示。
若点A沿着矩形与圆心重合的圆弧BC移动,点A所走过的弧长为()(图略)A. 4π cmB. 6π cmC. 8π cmD. 12π cm答案: C5. 若图中所示的“AxB”表示包含x个正方形的正方形,那么当x=3时,共有的小正方形数量是()A. 64B. 63C. 57D. 56答案: C第二部分解答题1. 完整准确地用两个自然数的乘法结果表示小写字母“a”的值。
答案: "a"的值为ab或ba,其中a, b为两个自然数。
2. 设数a, b满足2a + b = 10,a - 2b = 1,求a和b的值。
答案: 将第一个等式的a用第二个等式表示出来,得到a = 2b + 1;将该式代入第一个等式,得到2(2b + 1) + b = 10,解得b = 2,代入第二个等式得到a = 5。
因此,a = 5,b = 2。
3. 在数轴上,点A表示数a, B表示数b,若a < b,则点A与B的位置关系是()A. A在B的左边B. A在B的右边C. A、B在同一点上D. 无法确定答案: A4. 如图,正方形ABCD的边长为6cm,点P, Q分别在AB, CD边上,且AP : PB = DQ : QC = 1:3,那么线段PQ的长度是多少?(图略)答案: 可以设AP的长度为x,因此PB的长度为6 - x。
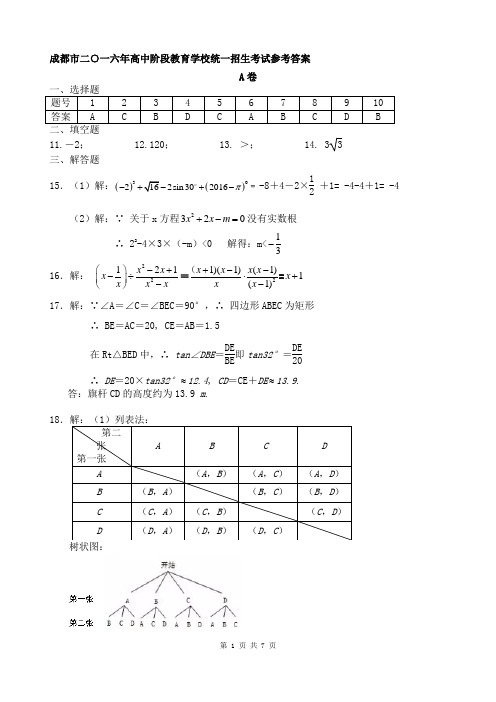
成都市二○一六年高中阶段教育学校统一招生考试参考答案A 卷11.-2; 12.120; 13. >; 14. 3 3 三、解答题15.(1)解:()()3022sin 302016π-+-o ﹦-8+4-2×12 +1= -4-4+1= -4(2)解:∵ 关于x 方程2320x x m +-=没有实数根∴ 22-4×3×(-m )<0解得:m<13-16.解:22121x x xx x x -+⎛⎫-÷ ⎪-⎝⎭=21)(1)(1)(1)x x x x x x +--⋅-(=1x + 17.解:∵∠A =∠C =∠BEC =90°,∴ 四边形ABEC 为矩形 ∴ BE =AC =20, CE =AB =1.5 在Rt △BED 中,∴ tan ∠DBE =DE BE 即tan32°=DE 20∴ DE =20×tan32°≈12.4, CD =CE +DE ≈13.9.答:旗杆CD 的高度约为13.9 m .18由列表或树状图可知,两次抽取卡片的所有可能出现的结果有12种,分别为(A ,B ),(A ,C ),(A ,D ),(B ,A ),(B ,C ),(B ,D ),(C ,A ),(C ,B ),(C ,D ),(D ,A ),(D ,B ),(D ,C ).(2)由(1)知:所有可能出现的结果共有12种,其中抽到的两张卡片上的数都是勾股数的有(B ,C ),(B ,D ),(C ,B ),(C ,D ),(D ,B ),(D ,C )共6种. ∴ P (抽到的两张卡片上的数都是勾股数)=612=12.19.解:(1) ∵ 正比例函数y kx =的图象与反比例函数直线my x=的图象都经过点A(2,-2)., ∴ 2222k m =-⎧⎪⎨=-⎪⎩解得:14k m =-⎧⎨=-⎩∴ y =-x , y=- 4x(2) ∵ 直线BC 由直线OA 向上平移3个单位所得 ∴ B (0,3),k bc = k oa =-1 ∴ 设直线BC 的表达式为 y =-x +3由 43y x y x ⎧=-⎪⎨⎪=-+⎩解得1141x y =⎧⎨=-⎩,2214x y =-⎧⎨=⎩ ∵ 因为点C 在第四象限 ∴ 点C 的坐标为(4,-1)解法一:如图1,过A 作AD ⊥y 轴于D ,过C 作CE ⊥y 轴于E.∴ S △ABC =S △BEC +S 梯形ADEC -S △ADB =12×4×4+12(2+4) ×1-12×2×5=8+3-5=6解法二:如图2,连接OC.∵ OA ∥BC ,∴S △ABC =S △BOC =12⋅OB ⋅x c =12×3×4=620.(1) 证明:∵ DE 为⊙C 的直径 ∴∠DBE =90°又∵ ∠ABC =90°, ∴ ∠DBE +∠DBC =90°,∠CBE +∠DBC =90° ∴ ∠ABD =∠CBE又∵ CB =CE ∴ ∠CBE =∠E, ∴ ∠ABD =∠E. 又∵∠BAD =∠EAB, ∴△ABD ∽△AEB.(2)由(1)知,△ABD ∽△AEB ,∴BD BE =AB AE∵AB BC =43, ∴ 设 AB =4x ,则CE =CB =3x 在R t △ABC 中,AB =5x ,∴ AE =AC +CE =5x +3x =8 x ,BD BE =AB AE =4x 8x =12 .在R t △DBE 中,∴ tanE =BD BE =12. (3) 解法一:在R t △ABC 中,12AC ⋅BG =12AB ⋅BG 即12⋅5x ⋅BG =12⋅4x ⋅3x ,解得BG =125x .∵ AF 是∠BAC 的平分线,∴BF FE =AB AE =4x 8x =12如图1,过B 作BG ⊥AE 于G ,FH ⊥AE 于H ,∴ FH ∥BG ,∴ FH BG =EF BE =23∴ FH =23 BG =23×125x =85x又∵ tanE =12,∴ EH =2FH =165x ,AM =AE -EM =245x在R t △AHF 中,∴ AH 2+HF 2=AF 2即222248)()255x x +=(,解得x =108 ∴ ⊙C 的半径是3x =3108. 解法二:如图2过点A 作EB 延长线的垂线,垂足为点G.∵ AF 平分∠BAC ∴ ∠1=∠2 又∵ CB =CE ∴∠3=∠E 在△BAE 中,有∠1+∠2+∠3+∠E =180°-90°=90° ∴∠4=∠2+∠E =45° ∴ △GAF 为等腰直角三角形 由(2)可知,AE=8 x ,tanE =12∴AG =55AE =855 x∴AF =2AG =855 x=2 ∴x=108∴ ⊙C 的半径是3x =3108.解法三:如图3,作BH ⊥AE 于点H ,NG ⊥AE 于点G ,FM ⊥AE 于点M ,设BN =a ,∵ AF 是∠BAC 的平分线,∴NG =BN =a ∴CG =34a ,NC =54a ,∴BC =94a ,∴BH =95a∴ AB =3a ,AC =154a ,∴ AG =3a ∴ tan ∠NAC =NG AG =13,∴ sin ∠NAC =1010∴ 在Rt △AFM 中,FM =AF ·sin ∠NAC =2×1010=105,AM =3105∴ 在Rt △EFM 中,EM =FM tan E=2105∴AE =10 在Rt △DBE 中,∵BH =95a ,∴EH =185a ,DH =910a ,∴DE =92a ∴DC =94a ,∴AD =32a ,又∵AE +DE =AE ,∴32a +92a =10,∴a =106 ∴DC =94a =3108B 卷一、填空题21.解:“非常清楚”的居民占该辖区的百分比为:1-(30%+15%+90360×100%)=30% ∴ 可以估计其中慈善法“非常清楚”的居民约为:9000×30%=2700(人). 22.解:由题知: 323(1)327(2)a b b a -=⋅⋅⋅⋅⋅⋅⋅⋅⎧⎨-=-⋅⋅⋅⋅⋅⋅⎩由(1)+(2)得:a +b =-4,由(1)-(2)得:a -b =2,∴ ()()a b a b +-=-8.23.解:连结AO 并延长交⊙O 于E ,连结CE. ∵ AE 为⊙O 的直径,∴∠ACD=90°.又∵ AH ⊥BC ,∴∠AHB=90°.又∵ ∠B =∠D ,∴ sinB =sinD ,∴ AH AB =ACAD即 18AB =2426 ,解得:AB =39224.解:∵2AM BM AB =⋅,2BN AN AB =⋅∴ M 、N 为线段AB 的两个黄金分割点∴ 11()122AM AB b a ==-=33)322AN AB b a ==-=∴ 1)(34m n MN AM AN -==-=-=25. 解:如图③,由题意可知,∠MPN =90°,剪裁可知,MP =NP 所以△MPN 是等腰直角三角形 ∴ 欲求MN 最小,即是求PM 最小 ∴ 在图②中,AE 最小时,MN 最小易知AE 垂直于BD 最小,∴ AE 最小值易求得为655 , ∴ MN 的最小值为6105二、解答题26.解:(1)6005y x =-;(2) 设果园多种x 棵橙子树时,橙子的总产量为z 个.由题知: Z =(100+x )y =(100+x )(600-5x )=-5(x -10)2+60500 ∵ a =-5<0 ∴ 当x =10时,Z 最大=60500.∴ 果园多种10棵橙子树时,可以使橙子的总产量最大,最大为60500个.27.(1)证明:在Rt △AHB 中,∵∠ABC=45°,∴AH=BH又∵∠BHD =∠AHC =90°,DH =CH ,∴△BHD ≌△AHC (SAS ) ∴ BD =AC.(2) ( i) 在Rt △AHC 中,∵tanC =3,∴AHHC=3, 设CH =x ,则BH =AH=3x ,∵BC=4, ∴ 3x +x =4, ∴ x =1.AH =3, CH =1. 由旋转知:∠EHF =∠BHD =∠AHC =90°,EH =AH =3,CH =DH =FH.∴∠EHA =∠FHC ,EH AH =FHHC=1,∴△EHA ∽△FHC ,∴∠EAH =∠C ,∴tan ∠EAH =tanC=3如图②,过点H 作HP ⊥AE 于P ,则HP =3AP ,AE =2AP. 在Rt △AHP 中,AP 2+HP 2= AH 2, ∴AP 2+(3AP)2= 9,解得:AP =31010,AE =3105. ⅱ)由题意及已证可知,△AEH 和△FHC 均为等腰三角形 ∴∠GAH =∠HCG =30°,∴△AGQ ∽△CHQ , ∴AQ CQ =GQ HQ , ∴AQ GQ =CQHQ又∵∠AQC =∠GQE ∴△AQC ∽△GQH ∴EF HG =AC GH =AQ GQ =sin30°=1228.解:(1)∵ 抛物线()213y a x =+-与与y 轴交于点C (0,-83).∴ a -3=-83,解得:a =13,∴y =13(x +1)2-3当y =0时,有13(x +1)2-3=0,∴ X 1=2,X 2=-4 ∴A(-4,0),B(2,0).(2)∵ A(-4,0),B(2,0),C (0,-83),D(-1,-3)∴ S 四边形ABCD =S △AHD +S 梯形OCDH +S △BOC = 12×3×3+12(83 + 3) ×1+12×2×83=10.从面积分析知,直线l 只能与边AD 或BC 相交,所以有两种情况:① 当直线l 边AD 相交与点M 1时,则S △AHM1=310×10=3,∴12×3×(-y M1)=3∴ y M1=-2,点M 1(-2,-2),过点H (-1,0)和M 1(-2,-2)的直线l 的解析式为y =2x +2. ②当直线l 边BC 相交与点M 2时,同理可得点M 2(12,-2),过点H (-1,0)和M 2(12,-2)的直线l 的解析式为y =-43x -43.综上:直线l 的函数表达式为y =2x +2或y =-43x -43.(3)设P (x 1,y 1)、Q (x 2,y 2)且过点H (-1,0)的直线PQ 的解析式为y =k x +b,∴ -k +b =0,∴y =k x +k.由⎪⎩⎪⎨⎧-+=+=3832312x x y kkx y , ∴ 038)32(312=---+k x k x∴ x 1+x 2=-2+3k,y 1+y 2=kx 1+k+kx 2+k =3k 2, ∵点M 是线段PQ 的中点,∴由中点坐标公式的点M (32k -1,32k 2).假设存在这样的N 点如下图,直线DN ∥PQ ,设直线DN 的解析式为y =k x +k-3由⎪⎩⎪⎨⎧-+=-+=38323132x x y k kx y ,解得:x 1=-1, x 2=3k -1, ∴N (3k -1,3k 2-3) ∵ 四边形DMPN 是菱形,∴ DN =DM ,∴ 222222)323()23()3()3(++=+k k k k 整理得:3k 4-k 2-4=0,0)43)(1(22=-+k k ,∵ k 2+1>0,∴3k 2-4=0, 解得332±=k ,∵ k <0,∴332-=k , ∴P (-133-,6),M (-13-,2),N (-132-, 1)∴PM =DN =27,∴四边形DMPN 为菱形 ∴以DP 为对角线的四边形DMPN 能成为菱形,此时点N 的坐标为(-132-, 1).。

2016年全国各地中考数学试题分类解析汇编(第一辑)第12章全等三角形一.选择题(共13小题)1.(2016•新疆)如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是()A.∠A=∠D B.BC=EF C.∠ACB=∠F D.AC=DF2.(2016•永州)如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD()A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD3.(2016•金华)如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD 的是()A.AC=BD B.∠CAB=∠DBA C.∠C=∠D D.BC=AD4.(2016•怀化)如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是()A.PC=PD B.∠CPD=∠DOP C.∠CPO=∠DPO D.OC=OD5.(2016•莆田)如图,OP是∠AOB的平分线,点C,D分别在角的两边OA,OB 上,添加下列条件,不能判定△POC≌△POD的选项是()A.PC⊥OA,PD⊥OB B.OC=OD C.∠OPC=∠OPD D.PC=PD6.(2016•淮安)如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD 的面积是()A.15 B.30 C.45 D.607.(2016•湖州)如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是()A.8 B.6 C.4 D.28.(2015•莆田)如图,AE∥DF,AE=DF,要使△EAC≌△FDB,需要添加下列选项中的()A.AB=CD B.EC=BF C.∠A=∠D D.AB=BC9.(2015•宜昌)如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有()A.1个B.2个C.3个D.4个10.(2015•海南)如图,下列条件中,不能证明△ABC≌△DCB的是()A.AB=DC,AC=DB B.AB=DC,∠ABC=∠DCBC.BO=CO,∠A=∠D D.AB=DC,∠DBC=∠ACB11.(2015•六盘水)如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB 的是()A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD12.(2015•贵阳)如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是()A.∠A=∠C B.∠D=∠B C.AD∥BC D.DF∥BE13.(2015•宜昌)两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=AC;③△ABD≌△CBD,其中正确的结论有()A.0个B.1个C.2个D.3个2016年全国各地中考数学试题分类解析汇编(第一辑)第12章全等三角形参考答案与试题解析一.选择题(共13小题)1.(2016•新疆)如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是()A.∠A=∠D B.BC=EF C.∠ACB=∠F D.AC=DF【分析】根据全等三角形的判定,利用ASA、SAS、AAS即可得答案.【解答】解:∵∠B=∠DEF,AB=DE,∴添加∠A=∠D,利用ASA可得△ABC≌△DEF;∴添加BC=EF,利用SAS可得△ABC≌△DEF;∴添加∠ACB=∠F,利用AAS可得△ABC≌△DEF;故选D.【点评】本题考查了全等三角形的判定,掌握全等三角形的判定方法:SSS、ASA、SAS、AAS和HL是解题的关键.2.(2016•永州)如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD()A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD【分析】欲使△ABE≌△ACD,已知AB=AC,可根据全等三角形判定定理AAS、SAS、ASA添加条件,逐一证明即可.【解答】解:∵AB=AC,∠A为公共角,A、如添加∠B=∠C,利用ASA即可证明△ABE≌△ACD;B、如添AD=AE,利用SAS即可证明△ABE≌△ACD;C、如添BD=CE,等量关系可得AD=AE,利用SAS即可证明△ABE≌△ACD;D、如添BE=CD,因为SSA,不能证明△ABE≌△ACD,所以此选项不能作为添加的条件.故选:D.【点评】此题主要考查学生对全等三角形判定定理的理解和掌握,此类添加条件题,要求学生应熟练掌握全等三角形的判定定理.3.(2016•金华)如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD 的是()A.AC=BD B.∠CAB=∠DBA C.∠C=∠D D.BC=AD【分析】根据全等三角形的判定:SAS,AAS,ASA,可得答案.【解答】解:由题意,得∠ABC=∠BAD,AB=BA,A、∠ABC=∠BAD,AB=BA,AC=BD,(SSA)三角形不全等,故A错误;B、在△ABC与△BAD中,,△ABC≌△BAD(ASA),故B正确;C、在△ABC与△BAD中,,△ABC≌△BAD(AAS),故C正确;D、在△ABC与△BAD中,,△ABC≌△BAD(SAS),故D正确;故选:A.【点评】本题考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.4.(2016•怀化)如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是()A.PC=PD B.∠CPD=∠DOP C.∠CPO=∠DPO D.OC=OD【分析】先根据角平分线的性质得出PC=PD,再利用HL证明△OCP≌△ODP,根据全等三角形的性质得出∠CPO=∠DPO,OC=OD.【解答】解:∵OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,∴PC=PD,故A正确;在Rt△OCP与Rt△ODP中,,∴△OCP≌△ODP,∴∠CPO=∠DPO,OC=OD,故C、D正确.不能得出∠CPD=∠DOP,故B错误.故选B.【点评】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.也考查了全等三角形的判定与性质,得出PC=PD是解题的关键.5.(2016•莆田)如图,OP是∠AOB的平分线,点C,D分别在角的两边OA,OB 上,添加下列条件,不能判定△POC≌△POD的选项是()A.PC⊥OA,PD⊥OB B.OC=OD C.∠OPC=∠OPD D.PC=PD【分析】要得到△POC≌△POD,现有的条件为有一对角相等,一条公共边,缺少角,或着是边,根据全等三角形的判定定理即可得到结论.于是答案可得.【解答】解:∵OP是∠AOB的平分线,∴∠AOP=∠BOP,∵OP=OP,∴根据‘HL’需添加PC⊥OA,PD⊥OB,根据‘SAS’需添加OC=OD,根据‘AAS’需添加∠OPC=∠OPD,故选D.【点评】本题考查了角平分线的定义,全等三角形的判定,熟记全等三角形的判定定理是解题的关键.6.(2016•淮安)如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是()A.15 B.30 C.45 D.60【分析】判断出AP是∠BAC的平分线,过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得DE=CD,然后根据三角形的面积公式列式计算即可得解.【解答】解:由题意得AP是∠BAC的平分线,过点D作DE⊥AB于E,又∵∠C=90°,∴DE=CD,∴△ABD的面积=AB•DE=×15×4=30.故选B.【点评】本题考查了角平分线上的点到角的两边距离相等的性质以及角平分线的画法,熟记性质是解题的关键.7.(2016•湖州)如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是()A.8 B.6 C.4 D.2【分析】过点P作PE⊥BC于E,根据角平分线上的点到角的两边的距离相等可得PA=PE,PD=PE,那么PE=PA=PD,又AD=8,进而求出PE=4.【解答】解:过点P作PE⊥BC于E,∵AB∥CD,PA⊥AB,∴PD⊥CD,∵BP和CP分别平分∠ABC和∠DCB,∴PA=PE,PD=PE,∴PE=PA=PD,∵PA+PD=AD=8,∴PA=PD=4,∴PE=4.故选C.【点评】本题考查了角平分线上的点到角的两边的距离相等的性质,熟记性质并作辅助线是解题的关键.8.(2015•莆田)如图,AE∥DF,AE=DF,要使△E AC≌△FDB,需要添加下列选项中的()A.AB=CD B.EC=BF C.∠A=∠D D.AB=BC【分析】添加条件AB=CD可证明AC=BD,然后再根据AE∥FD,可得∠A=∠D,再利用SAS定理证明△EAC≌△FDB即可.【解答】解:∵AE∥FD,∴∠A=∠D,∵AB=CD,∴AC=BD,在△AEC和△DFB中,,∴△EAC≌△FDB(SAS),故选:A.【点评】此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.9.(2015•宜昌)如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有()A.1个B.2个C.3个D.4个【分析】根据全等三角形的判定得出点P的位置即可.【解答】解:要使△ABP与△ABC全等,点P到AB的距离应该等于点C到A B的距离,即3个单位长度,故点P的位置可以是P1,P3,P4三个,故选C【点评】此题考查全等三角形的判定,关键是利用全等三角形的判定进行判定点P 的位置.10.(2015•海南)如图,下列条件中,不能证明△ABC≌△DCB的是()A.AB=DC,AC=DB B.AB=DC,∠ABC=∠DCBC.BO=CO,∠A=∠D D.AB=DC,∠DBC=∠AC B【分析】本题要判定△ABC≌△DCB,已知BC是公共边,具备了一组边对应相等.所以由全等三角形的判定定理作出正确的判断即可.【解答】解:根据题意知,BC边为公共边.A、由“SSS”可以判定△ABC≌△DCB,故本选项错误;B、由“SAS”可以判定△ABC≌△DCB,故本选项错误;C、由BO=CO可以推知∠ACB=∠DBC,则由“AAS”可以判定△ABC≌△DCB,故本选项错误;D、由“SSA”不能判定△ABC≌△DCB,故本选项正确.故选:D.【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.11.(2015•六盘水)如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB 的是()A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD【分析】本题要判定△ABC≌△DCB,已知∠ABC=∠DCB,BC是公共边,具备了一组边对应相等,一组角对应相等,故添加AB=CD、∠ACB=∠DBC、∠A=∠D后可分别根据SAS、ASA、AAS能判定△ABC≌△DCB,而添加AC=BD后则不能.【解答】解:A、可利用AAS定理判定△ABC≌△DC B,故此选项不合题意;B、可利用SAS定理判定△ABC≌△DCB,故此选项不合题意;C、利用ASA判定△ABC≌△DCB,故此选项不符合题意;D、SSA不能判定△ABC≌△DCB,故此选项符合题意;故选:D.【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.12.(2015•贵阳)如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是()A.∠A=∠C B.∠D=∠B C.AD∥BC D.DF∥BE【分析】利用全等三角形的判定与性质进而得出当∠D=∠B时,△ADF≌△CBE.【解答】解:当∠D=∠B时,在△ADF和△CBE中∵,∴△ADF≌△CBE(SAS),故选:B.【点评】此题主要考查了全等三角形的判定与性质,正确掌握全等三角形的判定方法是解题关键.13.(2015•宜昌)两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,詹姆斯在探究筝形的性质时,得到如下结论:①AC⊥BD;②AO=CO=AC;③△ABD≌△CBD,其中正确的结论有()A.0个B.1个C.2个D.3个【分析】先证明△ABD与△CBD全等,再证明△AOD与△COD全等即可判断.【解答】解:在△ABD与△CBD中,,∴△ABD≌△CBD(SSS),故③正确;∴∠ADB=∠CDB,在△AOD与△COD中,,∴△AOD≌△COD(SAS),∴∠AOD=∠COD=90°,AO=OC,∴AC⊥DB,故①②正确;故选D【点评】此题考查全等三角形的判定和性质,关键是根据SSS证明△ABD与△CBD 全等和利用SAS证明△AOD与△COD全等.智汇文库专业文档。

山东中考数学试卷一.选择题(本大题共20小题,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,选错,不选或选出的答案超过一个,均记零分)题号 1 2 3 4 5 6 7 8 9 10 答案 题号 11 12 13 14 45 16 17 18 19 20 答案一、选择题:(本大题共20题,每小题3分,共60分.在每小题给出的代号为ABCD 四个选项中,只有一项是符合题目要求的) 1.3--的值为 A. 3B. -3C.31D. -31 2.下列各图是选自历届世博会徽中的图案,其中是中心对称图形的是AB CD3.在电子显微镜下测得一个圆球体细胞的直径是5×105-cm ,3102⨯个这样的细胞排成的细胞链的长是A .cm 210- B .cm 110- C .cm 310-D .cm 410-4.将右图所示的直角梯形绕直线l 旋转一周,得到的立体图形是A B C D5.自上海世博会开幕以来,中国馆以其独特的造型吸引了世人的目光.据预测,在会展期间,参观中国馆的人次数估计可达到14 900 000,此数用科学记数法表示是 A.61049.1⨯ B.810149.0⨯ C.7109.14⨯D.71049.1⨯6.下列运算正确的是 A .22a a a =⋅B .33)(ab ab =C .632)(a a = D .5210a a a=÷7.如图,将一副三角板按图中的方式叠放,则角α等于 A .75B .60C .45D .30 8.如果33-=-b a ,那么代数式b a 35+-的值是 A .0 B .2 C .5 D .89.计算2(3)-的结果是 A .3 B .3- C .3± D .910.右图是由五个完全相同的小正方体组合成的一个立体图形,则它的俯视图...是11.不等式组32>2(4)x xx +⎧⎨--⎩≥1 的解集在数轴上表示正确的是12.方程(5)x x x -=的解是 A .0x =B .0x =或5x =C .6x =D .0x =或6x = 13.如图,正六边形螺帽的边长是2cm ,这个扳手的 开口a 的值应是A .23 cmB .3cmC .23cm D .1cmA .92B .94 C .95 D .32 15.已知反比例函数y =x2,则下列点中在这个反比例函数图象的上的是A .(-2,1)B .(1,-2)C .(-2,-2)D .(1,2)16.如图,四边形ABCD 的对角线互相平分,要使它成为矩形,那么需要添加的条件是A .AB CD = B .AD BC = C .AB BC =D .AC BD =17.在一次信息技术考试中,某兴趣小组8名同学的成绩(单位:分)分别是:7,10,9,8,7,9,9,8,则这组数据的众数是A .7B .8C .9D .1018.手工制作课上,小红利用一些花布的边角料,剪裁后装裱手工画.下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边,其中,每个图案花边的宽度都相同,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是A B C D 19.右图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么关于 该班40名同学一周参加体育锻炼时间 的说法错误..的是 A .极差是3 B .中位数为8 C .众数是8D .锻炼时间超过8小时的有21人20.如右图是夜晚小亮从点A 经过路灯C 的正下方沿直线走到点B ,他的影长y 随他与点A 之间的距 离x 的变化而变化,那么表示y 与x 之间的函数关 系的图像大致为二、填空题(每小题3分,满分12分请将答案直接填在题中横线上)21.已知抛物线2y x bx c=++的对称轴为2x=,点A,B均在抛物线上,且AB与x轴平行,其中点A的坐标为(0,3),则点B的坐标为.22.如图,AB切⊙O于点A,BO交⊙O于点C,点D是CmA异于点C、A的一点,若∠ABO=°32,则∠ADC的度数是.23.如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD = 2,将腰CD以D为中心逆时针旋转90°至DE,连接AE、CE,△ADE的面积为3,则BC的长为.24.端午节时,王老师用72元钱买了荷包和五彩绳共20个.其中荷包每个4元,五彩绳每个3元,设王老师购买荷包x个,五彩绳y个,根据题意,可列出的方程组应为.三、解答题(本大题共5个小题)25.(本题满分8分)进入防汛期后,某地对河堤进行了加固.该地驻军在河堤加固的工程中出色完成了任务.这是记者与驻军工程指挥官的一段对话:你们是用9天完成4800米长的大坝加固任务的?我们加固600米后,采用新的加固模式,这样每天加固长度是原来的2倍.26.(本题满分10分)如图,在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.(1)求证:△BDF≌△CDE;(2)当△ABC满足什么条件时,四边形BFCE是菱形?27.(本题满分10分)某学校组织八年级学生参加社会实践活动,若单独租用35座客车若干辆,则刚好坐满;若单独租用55座客车,则可以少租一辆,且余45个空座位.(1)求该校八年级学生参加社会实践活动的人数;(2)已知35座客车的租金为每辆320元,55座客车的租金为每辆400元.根据租车资金不超过1500元的预算,学校决定同时租用这两种客车共4辆(可以坐不满).请你计算本次社会实践活动所需车辆的租金.28.(本题满分10分)如图1,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D在边AB上运动,DE平分∠CDB交边BC于点E,EM⊥BD垂足为M,EN⊥CD垂足为N.(1)当AD=CD时,求证DE∥AC;(2)探究:AD为何值时,以B,M,E为顶点的三角形与以C,E,N为顶点的三角形相似?29.(本题满分10分)我市是世界有机蔬菜基地,数10种蔬菜在国际市场上颇具竞争力.某种有机蔬菜上市时,某经销商按市场价格10元/千克在我市收购了2000千克某种蔬菜存放入冷库中.据预测,该种蔬菜的市场价格每天每千克将上涨0.5元,但冷库存放这批蔬菜时每天需要支出各种费用合计340元,而且这种蔬菜在冷库中最多保存110天,同时,平均每天将会有6千克的蔬菜损坏不能出售.(1)若存放x天后,将这批蔬菜一次性出售,设这批蔬菜的销售总金额为y元,试写出y与x之间的函数关系式.(2)经销商想获得利润22500元,需将这批蔬菜存放多少天后出售?(利润=销售总金额-收购成本-各种费用)(3)经销商将这批蔬菜存放多少天后出售可获得最大利润?最大利润是多少?参考答案一、选择题:1-5BCBCD6-10CADAD11-15BDABD16-20DCDBA二、填空题:21.(4,3)22.°2923.524.20, 4372 x yx y+=⎧⎨+=⎩三、解答题926004800600=-+xx ……………………………………………………4分 去分母,得 1200+4200=18x (或18x =5400)解得 300x =检验:当300x =时,20x ≠(或分母不等于0).∴300x =是原方程的解.答:该地驻军原来每天加固300米.………………………………………8分 26.解:(1)证明:∵D 是BC 的中点,∴BD =CD∵CE ∥BF ,∴∠DBF =∠DCE又∵∠BDF =∠CDE ,∴△BDF ≌△CDE ………………………………3分(2)当△ABC 是等腰三角形,即AB =AC 时,四边形BFCE 是菱形………4分证明:∵△CDE ≌△BDF ,∴DE =D F∵BD =CD ,∴四边形BFCE 是平行四边形…………………………………7分 在△ABC 中,∵AB =AC ,BD =CD ,∴AD ⊥BC ,即EF ⊥BC ∴四边形BFCE 是菱形……………………………………………………10分27.解:(1)设单独租用35座客车需x 辆,由题意得:3555(1)45x x =--解得:5x =∴35355175x =⨯=(人)答:该校八年级参加社会实践活动的人数为175人.………4分 (2)设租35座客车y 辆,则租55座客车(4y -)辆,由题意得:3555(4)175,320400(4)1500y y y y +-⎧⎨+-⎩≥≤………………………………………7分 解这个不等式组,得11144y ≤≤2.∵y 取正整数,∴y = 2. ∴4-y = 4-2 = 2.∴320×2+400×2 = 1440(元).所以本次社会实践活动所需车辆的租金为1440元.………………10分28.(1)证明:∵AD =CD ∴∠DAC =∠DCA∴∠BDC =2∠DAC又∵DE 是∠BDC 的平分线 ∴∠DAC =∠BDE∴DE ∥AC ………………………………………………………………3分(2)解:分两种情况:①若△BME ∽△CNE ,必有∠MBE =∠NCE 此时BD =DC ∵DE 平分∠BDC ∴DE ⊥BC ,BE =EC 又∠ACB =90° ∴DE ∥AC ∴BE BD BC AB =即2211522BD AB AC BC =+=∴AD=5…………………………………………………………………7分②若△BME ∽△ENC ,必有∠EBM =∠CEN 此时NE ∥MC∴8cos 6 4.810BC AD AC A AC AB =⋅=⋅=⨯= ∴当AD =5或AD =4.8时,以B ,M ,E 为顶点的三角形与以C ,E ,N 为顶点的三角形相似…………………………………………………………………………10分 29.解:(1)由题意得y 与x 之间的函数关系式为y =()()100.520006x x +-=2394020000x x -++(1≤x ≤110)……………………………………3分(2)由题意得:2394020000x x -++-10×2000-340x =22500解方程得:1x =50;2x =150(不合题意,舍去)经销商想获得利润2250元需将这批蔬菜存放50天后出售. ………………6分 (3)设最大利润为W ,由题意得W =2394020000x x -++-10 ×2000-340x23(100)30000x =--+∴当100x =时,30000W 最大=100天<110天∴存放100天后出售这批香菇可获得最大利润30000元.………………10分。

保密 ★ 启用前2016年中考真题数学试卷一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一个是符合题目要求的,把正确答案的标号填在答题卡内相应的位置上) 1、计算2(1)⨯-的结果是( ) A 、12-B 、2-C 、1D 、22、若∠α的余角是30°,则cos α的值是( )A 、12B 、 32C 、22D 、 333、下列运算正确的是( )A 、21a a -=B 、22a a a +=C 、2a a a ⋅=D 、22()a a -=-4、下列图形是轴对称图形,又是中心对称图形的有( )A 、4个B 、3个C 、2个D 、1个5、如图,在平行四边形ABCD 中,∠B=80°,AE 平分∠BAD 交BC 于点E ,CF ∥AE 交AE 于点F ,则∠1=( ) A 、40° B 、50° C 、60° D 、80°6、已知二次函数2y ax =的图象开口向上,则直线1y ax =-经过的象限是( )A 、第一、二、三象限B 、第二、三、四象限C 、第一、二、四象限D 、第一、三、四象限 7、如图,你能看出这个倒立的水杯的俯视图是( )8、如图,是我市5月份某一周的最高气温统计图,则这组数据(最高气温)的众数与中位数分别是( ) A 、28℃,29℃ B 、28℃,℃ C 、28℃,30℃ D 、29℃,29℃ 9、已知拋物线2123y x =-+,当15x ≤≤时,y 的最大值是A B C D( ) A 、2B 、23C 、 53D 、7310、小英家的圆形镜子被打碎了,她拿了如图(网格中的每个小正方形边长为1)的一块碎片到玻璃店,配制成形状、大小与原来一致的镜面,则这个镜面的半径是( ) A 、2 B 、5 C 、22D 、3 11、如图,是反比例函数1k y x=和2ky x =(12k k <)在第一象限的图象,直线AB ∥x 轴,并分别交两条曲线于A 、B 两点,若2AOB S ∆=,则21k k -的值是( ) A 、1B 、2C 、4D 、812、一个容器装有1升水,按照如下要求把水倒出:第1次倒出12升水,第2次倒出的水量是12升的13,第3次倒出的水量是13升的14,第4次倒出的水量是14升的15,…按照这种倒水的方法,倒了10次后容器内剩余的水量是( ) A 、1011升 B 、19升C 、110升 D 、111升二、填空题(本大题共6小题,每小题3分,共18分.把答案填在答题卡中的横线上) 13、2011-的相反数是__________ 14、近似数有__________个有效数字. 15、分解因式:39a a -= __________16、如图,是某校三个年级学生人数分布扇形统计图,则九年级学生人数所占扇形的圆心角的度数为__________17、如图,等边△ABC 绕点B 逆时针旋转30°时,点C 转到C ′的位置,且BC ′与AC 交于点D ,则'C DCD的值为__________18、如图,AB 是半圆O 的直径,以0A 为直径的半圆O ′与弦AC 交于点D ,O ′E ∥AC ,并交OC 于点E .则下列四个结论:16题图 17题图 18题图①点D 为AC 的中点;②'12O OE AOC S S ∆∆=;③2AC AD = ;④四边形O'DEO 是菱形.其中正确的结论是 __________.(把所有正确的结论的序号都填上)三、解答题(本大题共8小题,满分共66分,解答过程写在答题卡上,解答应写出文字说明,证明过程或演算步骤).19、计算:101()(5)342π-----+20、已知:12x x 、是一元二次方程2410x x -+=的两个实数根. 求:2121211()()x x x x +÷+的值.21、假日,小强在广场放风筝.如图,小强为了计算风筝离地面的高度,他测得风筝的仰角为60°,已知风筝线BC 的长为10米,小强的身高AB 为米,请你帮小强画出测量示意图,并计算出风筝离地面的高度.(结果精确到1米,参考数据23≈ )22、如图,△OAB 的底边经过⊙O 上的点C ,且OA=OB ,CA=CB ,⊙O 与OA 、OB 分别交于D 、E 两点. (1)求证:AB 是⊙O 的切线;(2)若D 为OA 33π,求⊙O 的半径r .23、一个不透明的纸盒中装有大小相同的黑、白两种颜色的围棋,其中白色棋子3个(分别用白A 、白B 、白C 表示),若从中任意摸出一个棋子,是白色棋子的概率为34. (1)求纸盒中黑色棋子的个数;(2)第一次任意摸出一个棋子(不放回),第二次再摸出一个棋子,请用树状图或列表的方法,求两次摸到相同颜色棋子的概率.24、上个月某超市购进了两批相同品种的水果,第一批用了2000元,第二批用了5500元,第二批购进水果的重量是第一批的倍,且进价比第一批每千克多1元. (1)求两批水果共购进了多少千克?(2)在这两批水果总重量正常损耗10%,其余全部售完的情况下,如果这两批水果的售价相同,且总利润率不低于26%,那么售价至少定为每千克多少元? (利润率=100%⨯利润进价)25、如图,点G 是正方形ABCD 对角线CA 的延长线上任意一点,以线段AG 为边作一个正方形AEFG ,线段EB 和GD 相交于点H . (1)求证:EB=GD ;(2)判断EB 与GD 的位置关系,并说明理由; (3)若AB=2,2,求EB 的长.26、已知抛物线223 (0)y ax ax a a =--<与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,点D 为抛物线的顶点. (1)求A 、B 的坐标;(2)过点D 作DH 丄y 轴于点H ,若DH=HC ,求a 的值和直线CD 的解析式;(3)在第(2)小题的条件下,直线CD 与x 轴交于点E ,过线段OB 的中点N 作NF 丄x 轴,并交直线CD 于点F ,则直线NF 上是否存在点M ,使得点M 到直线CD 的距离等于点M 到原点O 的距离?若存在,求出点M 的坐标;若不存在,请说明理由.中考数学试题答案一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B A C C B D B A C B C D二、填空题 13. 201114. 315. (3)(3)a a a +- 16. 144°17. 23- 18. ①③④三、解答题19. 解:原式=2-1-3+2, =0.故答案为:0.20. 解:∵一元二次方程x 2-4x+1=0的两个实数根是x 1、x 2, ∴x 1+x 2=4,x 1•x 2=1, ∴(x 1+x 2)2÷( )=42÷=42÷4 =4.21. 解:在Rt △CEB 中, sin60°=,∴CE=BC•sin60°=10×≈,∴CD=CE+ED=+=≈10m ,答:风筝离地面的高度为10m .22. (1)证明:连OC ,如图, ∵OA=OB ,CA=CB , ∴OC ⊥AB ,∴AB 是⊙O 的切线;(2)解:∵D 为OA 的中点,OD=OC=r , ∴OA=2OC=2r , ∴∠A=30°,∠AOC=60°,AC= r , ∴∠AOB=120°,AB=2 r , ∴S 阴影部分=S △OAB -S 扇形ODE = •OC•AB - =- ,∴ •r•2r- r 2=- ,∴r=1,即⊙O 的半径r 为1. 23. 解:(1)3÷ -3=1. 答:黑色棋子有1个;(2)共12种情况,有6种情况两次摸到相同颜色棋子,所以概率为.24. 解:(1)设第一批购进水果x千克,则第二批购进水果千克,依据题意得:,解得x=200,经检验x=200是原方程的解,∴x+=700,答:这两批水果功够进700千克;(2)设售价为每千克a元,则:,630a≥7500×,∴,∴a≥15,答:售价至少为每千克15元.25. (1)证明:在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,∴∠GAD=∠EAB,又∵AG=AE,AB=AD,∴△GAD≌△EAB,∴EB=GD;(2)EB⊥GD,理由如下:连接BD,由(1)得:∠ADG=∠ABE,则在△BDH中,∠DHB=180°-(∠HDB+∠HBD)=180°-90°=90°,∴EB⊥GD;(3)设BD与AC交于点O,∵AB=AD=2在Rt△ABD中,DB= ,∴EB=GD= .26. 解:(1)由y=0得,ax2-2ax-3a=0,∵a≠0,∴x2-2x-3=0,解得x1=-1,x2=3,∴点A的坐标(-1,0),点B的坐标(3,0);(2)由y=ax2-2ax-3a,令x=0,得y=-3a,∴C(0,-3a),又∵y=ax2-2ax-3a=a(x-1)2-4a,得D(1,-4a),∴DH=1,CH=-4a-(-3a)=-a,∴-a=1,∴a=-1,∴C(0,3),D(1,4),设直线CD的解析式为y=kx+b,把C、D两点的坐标代入得,,解得,∴直线CD的解析式为y=x+3;(3)存在.由(2)得,E(-3,0),N(- ,0)∴F(,),EN= ,作MQ⊥CD于Q,设存在满足条件的点M(,m),则FM= -m,EF= = ,MQ=OM=由题意得:Rt△FQM∽Rt△FNE,∴= ,整理得4m2+36m-63=0,∴m2+9m= ,m2+9m+ = +(m+ )2=m+ =±∴m1= ,m2=- ,∴点M的坐标为M1(,),M2(,- ).。

16年中考试卷和答案****一、选择题(每题2分,共20分)1. 下列哪个选项是正确的?A. 地球是宇宙的中心B. 太阳是太阳系的中心C. 月球是地球的卫星D. 火星是太阳系的行星答案:B2. 以下哪个选项是化学元素?A. 氢B. 氧气C. 氮气D. 二氧化碳答案:A3. 以下哪个选项是正确的?A. 光年是时间单位B. 光年是长度单位C. 光年是速度单位D. 光年是质量单位答案:B4. 以下哪个选项是正确的?A. 牛顿是力的单位B. 牛顿是质量的单位C. 牛顿是时间的单位D. 牛顿是速度的单位答案:A5. 以下哪个选项是正确的?A. 光速是最快的速度B. 光速是最快的速度,但可以被超越C. 光速是最快的速度,但不是极限速度D. 光速是最快的速度,但不是绝对速度答案:A6. 以下哪个选项是正确的?A. 植物通过光合作用产生氧气B. 植物通过光合作用产生二氧化碳C. 植物通过光合作用产生水D. 植物通过光合作用产生葡萄糖答案:A7. 以下哪个选项是正确的?A. 细胞是所有生物的基本单位B. 细胞是所有生物的基本单位,除了病毒C. 病毒是所有生物的基本单位D. 病毒不是生物的基本单位答案:B8. 以下哪个选项是正确的?A. 遗传信息存储在DNA中B. 遗传信息存储在RNA中C. 遗传信息存储在蛋白质中D. 遗传信息存储在脂肪中答案:A9. 以下哪个选项是正确的?A. 酸雨是由于大气中的二氧化碳过多造成的B. 酸雨是由于大气中的二氧化硫过多造成的C. 酸雨是由于大气中的氮氧化物过多造成的D. 酸雨是由于大气中的臭氧过多造成的答案:B10. 以下哪个选项是正确的?A. 温室效应是由于大气中的二氧化碳过多造成的B. 温室效应是由于大气中的甲烷过多造成的C. 温室效应是由于大气中的臭氧过多造成的D. 温室效应是由于大气中的水蒸气过多造成的答案:A二、填空题(每题2分,共20分)1. 地球的自转周期是________小时。
2016年北京市高级中等学校招生考试物理试卷答案二、多项选择题三、实验与探究题20.3921.422.7223.5024.OA25.OD26. 20 1 变速直线27. 2 0.5 428.示例:体表温度降低与皮肤表面上水的蒸发快慢有关吗?29.示例:手握金属棒产生的电流的方向是否与金属棒的材质有关30.0.8t+4℃31.(1)D(2)铜棒32.BD33.示例:猜想:电流表无法检测该实验产生的微小电流。
检验方法:将电流表更换为灵敏电流计,闭合开关后,左右快速移动金属棒,观察灵敏电流计指针是否发生偏转。
34.(1)没有改变自变量“物体的高度”,改变了控制变量“物距”。
(2)步骤④改为:将发光物体B放在光具座上距凸透镜30cm处,移动光屏,在光屏上得到发光物体B清晰的像,用刻度尺分别测量发光物体B及其像的高度,并记录在表格中。
35.(1)0.16(2)0.8×10336.示例:实验步骤:实验者持手机在屋外,观察到手机有信号;然后,实验者持手机在屋内关门后,观察手机是否有信号。
判断方法:如果屋内手机无信号,说明电磁屏蔽玻璃有屏蔽作用;如果屋内手机有信号,说明电磁屏蔽玻璃没有屏蔽作用。
37.示例:实验步骤:①将微小压强计的探头放入烧杯的水中,用刻度尺分别测量探头到烧杯底的距离L1,探头到水面的距离H,读出压强计U形管两侧的液面高度差h1,将以上数据记录在表格中。
②向烧杯中倒入适量的水,调整探头所在的位置,使探头到水面的距离仍为H,用刻度尺测量探头到烧杯底部的距离L2,读出压强计U形管两侧的液面高度差h2,将以上数据记录在表格中。
实验现象:通过数据可发现L1≠ L2,h1=h2。
由此证明液体内部任意一点的压强跟该点到容器底的距离L无关,所以小亮的观点是错误的。
38. 示例:(1)电路图如图1所示(2)实验步骤:①按照电路图连接电路。
②闭合开关,调节滑动变阻器滑片P到适当位置,观察电流表A1、A2的示数,分别用I A和I B表示,并将I A和I B的数据记录在表格中。
2016年数学中考试题及答案【篇一:2016年全国中考数学模拟卷及答案】=txt>数学试卷一、选择题下面各题均有四个选项,其中只有一个是符合题意的。
..1.截止到2016年6月1日,北京市已建成39个地下调蓄设施,蓄水能力达到2 40 000立方平米。
将1240 000用科学记数法表示应为2.实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最大的是a.a b.bc.cd.d3.一个不透明的盒子中装有3个红球,2个黄球和1个绿球,这些球除了颜色外无其他差别,从中随机摸出一个小球,恰好是黄球的概率为 a. b. c. d.4.剪纸是我国传统的民间艺术,下列剪纸作品中,是轴对称图形的为6.如图,公路ac,bc互相垂直,公路ab的中点m与点c被湖隔开,若测得am的长为1.2km,则m,c两点间的距离为a.0.5km b.0.6km c.0.9km d.1.2km7.某市6月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是 a.21,21 b.21,21.5 c.21,22 d.22,228.右图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图。
若这个坐标系分别以正东、正北方向为x轴、y轴的正方向。
表示太和门的点坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是a.景仁宫(4,2)b.养心殿(-2,3) c.保和殿(1,0) d.武英殿(-3.5,-4)9.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:a.购买a类会员年卡b.购买b类会员年卡 c.购买c类会员年卡d.不购买会员年卡10.一个寻宝游戏的寻宝通道如图1所示,通道由在同一平面内的ab,bc,ca,oa,ob,oc组成。
为记录寻宝者的进行路线,在bc的中点m处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图2所示,则寻宝者的行进路线可能为a.a→o→bb.b→a→cc.b→o→c d.c→b→o 二、填空题11.分解因式:5x2-10x2=5x=_________.12.右图是由射线ab,bc,cd,de,组成的平面图形,则∠1+∠2+∠3+∠4+∠5=_____.13.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架。
16年山东中考试题及答案一、语文选择题1. 题目:下列短文中划线词的读音全都是正确的一组是:A. 少少燕燕身身人人B. 八百无形细细易易C. 讲求纵横正直甘甘D. 拮据积极面面堂堂答案:B2. 题目:下面各句中,加点的成语使用恰当的一项是:A. 把话说开了,不要拖来拖去。
B. 这次考试是关键,同学们要以更加饱满的热情投入到学习中。
C. 她总是故作神秘,不肯告诉我们事情的真相。
D. 他的乐观向上的态度使他的心情慢慢地舒畅了起来。
答案:D3. 题目:下面各句中的错别字是:A. 阻碍B. 难熬C. 吐露D. 副的答案:D4. 题目:以下读音错误的一项是:A. 滕回(huit)B. 进言(dian)C. 白榆(baiyu)D. 棕榈(zong)答案:D5. 题目:小红在课上要阅读《红楼梦》的某一段文字。
下列对小红要阅读的文字描述不准确的一项是:A. 这个段落主要描写了黛玉对贾母的痛恨与不满。
B. 这个段落中运用了大量的形象术和比喻手法。
C. 在这个段落中,作者运用了夸张的修辞手法,增强了情感的表达力。
D. 在这个段落中,贾母的人物形象得到进一步的丰满和细腻描绘。
答案:A二、数学填空题1. 题目:x+y+z=1,分别填入下列方程后的两个等式是_______。
A. x+y=1 x+z=1B. y+z=1 x+z=1C. x+y=1 y+z=1D. x+z=1 y+z=1答案:A2. 题目:大雁南飞,每小时飞行200千米。
下面的表格中,关于30分钟飞行距离的选择是_______。
A. 10千米B. 100千米C. 150千米D. 300千米答案:C3. 题目:小明和小红比赛用200元钱买果子。
如果小明用100元钱买了苹果,那么用100元钱买了多少个橙子?答案:5个4. 题目:已知直角三角形的一条直角边长为9cm,斜边长为15cm,则另一条直角边长为_______。
答案:12cm5. 题目:设正方形ABCD的边长为a,则其对角线的长度是_______。
2016年中考数学选择题专项训练(共三十五套)本试题是选择题专项训练的训练载体,按照中考要求设计,覆盖中考数学选择题所有题型及考点,难度较中考略难。
试题最后配备参考答案。
1.建议重在对选择题进行中考适应性训练,熟悉中考选择题题型结构,掌握选择题答题的一整套标准动作,确保在中考中飞速拿到满分,顺利找到做题节奏,调整考试状态。
2.套题不一定要全部做完,关键是每做一套都按训练要求做,并能认真总结考点,分析存在的问题,积极解决。
建议:分别标记,采取策略:(1)自己不会的题,特别是超过3分钟无思路的题型,务必查找资源查漏补缺;(2)对自己会做、却屡次出错的题型务必借助资源找到根本原因,对症解决。
(课本、老师、同学都是可以利用的资源)3.当考试一样,限时做题,模拟考试场景,提升实战能力。
建议限时15分钟完成,刚开始训练时可以放宽至20分钟。
中考数学选择题专项训练课堂配套试题(一)一、选择题(每小题3分,共24分) 1. 下列各组数中,互为相反数的是【 】A .2和-2B .-2和12 C .-2和12- D .12和22. 初步核算,去年全年国内生产总值519 322亿元.请你以亿元为单位用科学记数法表示去年我国的国内生产总值为【 】A .0.519 322×106B .5.2×1013C .5.1×105D .5.19 3222×1053. 下列说法:①一组数据不可能有两个众数;②将一组数据中的每一个数据都加上(或都减去)同一个常数后,方差恒不变;③随意翻到一本书的某页,这页的数码是奇数,这个事件是必然发生的;④要反映郑州市某一天内气温的变化情况,宜采用折线统计图.其中正确的是【 】A .①和③B .②和④C .①和②D .③和④4. 把抛物线y =x 2+bx +c 的图象向左平移3个单位,再向下平移2个单位,所得图象的关系式为y =x 2-3x +5,则有【 】A .b =3,c =7B .b =-9,c =25C .b =3,c =3D .b =-9,c =215. 函数y =1kx-的图象与直线y =x 没有交点,那么k 的取值范围是【 】 A .k >1 B.k <1 C .k >-1 D .k <-16.如图是一个正六棱柱的主视图和左视图,则图中的a =【 】左视图主视图A .32B .3C .2D .17. 如图,AD 是△ABC 的角平分线,DF ⊥AB ,垂足为F ,DE =DG ,△ADG和△AED 的面积分别为50和39,则△EDF 的面积为【 】A .11B .5.5C .7D .3.5GF EDC BA第7题图 第8题图8. 如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm 2,则该半圆的半径为【 】A .(4+B .9cmC .D .cm中考数学选择题专项训练课堂配套试题(二)一、选择题(每小题3分,共24分)1.的结果是【】A.±B.C.3 D2.如图,a∥b,∠1=65°,∠2=140°,则∠3=【】A.100°B.105°C.110°D.115°3.下列各式运算正确的是【】A.2a2·3a2=5a2 B.(-a2)3=a6 C.+=D.2210(0.1)1--⨯=4.有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了【】个人A.12 B.11 C.10 D.95.某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是610x=甲千克,608x=乙千克,亩产量的方差分别是229.6S=甲,2 2.7S=乙,则关于两种小麦推广种植的合理决策是【】A.甲的平均亩产量较高,应推广甲B.甲、乙的平均亩产量相差不多,均可推广C.甲的平均亩产量较高,且亩产量比较稳定,应推广甲D.甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙1)表示方格纸上A点的位置,(1,2)表示B点的位置,那么点P的位置为【】A.(5,2) B.(2,5) C.(2,1) D.(1,2)8.如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自A点出发沿折线AD-DC-CB以每秒3cm的速度运动,到达B点时运动同时停止,设△AMN的面积为y(cm2).运动时间为x(秒),则下列图象中能大致反映y与x 之间函数关系的是【】MND CBAFEDCBAA .B .C .D .中考数学选择题专项训练课堂配套试题(三)一、选择题(每小题3分,共24分) 1. 3×(-4)的值是【 】A .-12B .-7C .-1D .122. 若一个所有棱长都相等的三棱柱,它的主视图和俯视图分别是正方形和正三角形,则左视图是【 】A .矩形B .正方形C .菱形D .正三角形3. 某种鲸的体重约为1.36×105kg ,关于这个近似数,下列说法正确的是【 】A .精确到百分位,有3个有效数字B .精确到个位,有6个有效数字C .精确到千位,有6个有效数字D .精确到千位,有3个有效数字 4. 如图,在四边形ABCD 中,AD ∥BC ,对角线AC ,BD 相交于点O ,下列结论不一定正确.....的是【 】 A .AC =BD B .∠OBC =∠OCBC .S △AOB =S △COD D .∠BCD =∠BDC 5. 某校九年级有17名同学参加百米竞赛,预赛成绩各不相同,要取前9名参加决赛,小梅已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这17名同学成绩的【 】A .中位数B .众数C .平均数D .极差6. 如图,O 为原点,点A 的坐标为(3,0),点B 的坐标为(0,4),⊙D 过A ,B ,O 三点,点C 为弧ABO 上的一点(不与O ,A 两点重合),则cos ∠C 的值是【 】A .34B .35C .43D .457. 如图,D 是△ABC 内一点,BD ⊥CD ,AD =6,BD =4,CD =3,E ,F ,G ,H 分别是AB ,AC ,CD ,BD 的中点,则四边形EFGH 的周长是【 】 A .7 B .9 C .10 D .118. 如图,在△ABC 中,∠ACB =90º,AC >BC ,分别以AB ,BC ,CA 为一边向△ABC 外作正方形ABDE ,BCMN ,CAFG ,连接EF ,GM ,ND ,设△AEF ,△CGM ,△BND 的面积分别为S 1,S 2,S 3,则下列结论正确的是【 】 A .S 1=S 2=S 3 B .S 1=S 2<S 3 C .S 1=S 3<S 2 D .S 2=S 3<S 1OBCDAH GFE CD ABS 3S 2S 1MNB A DC EF G中考数学选择题专项训练课堂配套试题(四)一、选择题(每小题3分,共24分) 1. 计算(-1)2+(-1)3的值为【 】A .-2B .-1C .0D .22. 如图所示是一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方体块数最多是【 】俯视图主视图A .8B .10C .12D .153. 某中学九年级一班准备组织参加旅游,班长把全班48名同学对旅游地点的意向绘制成了扇形统计图,其中“想去海洋馆的学生数”的扇形圆心角为60°,则下列说法中正确的是【 】 A .想去海洋馆的学生占全班学生的60% B .想去海洋馆的学生有12人 C .想去海洋馆的学生肯定最多 D .想去海洋馆的学生占全班学生的164. 某游泳池的横截面如图所示,用一水管向池内持续注水,若单位时间内注入的水量保持不变,则在注水过程中,下列图象能反映深水区水深h 与注水时间t 之间关系的是【 】深水区浅水区D .C .B .A .5. 如图,直线l 和双曲线0ky k x=>()交于A ,B 两点,P 是线段AB 上的点(不与A ,B 重合).过点A ,B ,P 分别向x 轴作垂线,垂足分别为C ,D ,E ,连接OA ,OB ,OP .设△AOC 的面积为1S ,△BOD 的面积为2S ,△POE 的面积为3S ,则【 】A .123S S S <<B .123S S S >>C .123S S S =>D .123S S S =<第5题图第6题图6.如图,在平面直角坐标系中,线段AB的端点坐标为A(-2,4),B(4,2),直线y=kx-2与线段AB 有交点,则k的值不可能是【】A.-5 B.-2 C.2 D.57.如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=,CD P在四边形ABCD的边上,若P到BD的距离为32,则点P的个数为【】A.1 B.2 C.3 D.4DC第7题图第8题图8.在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点,且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点,…,则边长为8的正方形内部的整点的个数为【】A.64B.49C.36D.251.】A .3B .3± CD.2. 下列命题中,真命题是【 】A .对角线互相垂直且相等的四边形是正方形B .B .等腰梯形既是轴对称图形又是中心对称图形C .C .圆的切线垂直于经过切点的半径D .D .垂直于同一直线的两条直线互相垂直3. 将一张平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积.则这样的折纸方法共有【 】 A .1种B .2种C .4种D .无数种4. 某公司共有51名员工(包括经理),经理的工资高于其他员工的工资.今年经理的工资从去年的200 000元增加到225 000元,而其他员工的工资同去年一样,这样,这家公司所有员工今年工资的平均数和中位数与去年相比将会【 】 A .平均数和中位数都不变 B .平均数增加,中位数不变 C .平均数不变,中位数增加D .平均数和中位数都增加5. 关于x 的方程12mx x -=的解为正实数,则m 的取值范围是【 】A .m ≥2B .m ≤2C .m >2D .m <26. 若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为【 】A .75°或15°B .36°或60°C .75°D .30°7. 如图,△ABC 中,A ,B 两个顶点在x 轴的上方,点C 的坐标是(-1,0).以点C 为位似中心,在x轴的下方作△ABC 的位似图形△A ′B ′C ,并把△ABC 的边长放大到原来的2倍.设点B 的对应点B ′的横坐标是a ,则点B 的横坐标是【 】A .12a -B .1(1)2a -+ C .1(1)2a -- D .1(3)2a -+8. 已知二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,有下列结论:①abc >0;②2a +b <0;③a +b <m (am +b )(m ≠1);④(a +c )2<b 2;⑤a >1.其中正确的是【 】A .①⑤B .①②⑤C .②⑤D .①③④1. 计算:-1-2=【 】A .-1B .1C .-3D .32. 如图,把一个长方形纸片沿EF 折叠后,点D ,C 分别落在D′,C ′的位置,若∠EFB =65°,则∠AED ′等于【 】 A .50° B .55°C .60°D .65°3. 已知一组数据:2,1,x ,7,3,5,3,2的众数是2,则这组数据的中位数是【 】 A .2B .2.5C .3D .54. 下列计算正确的是【 】AB0 CD=-35. 一个几何体的三视图如下图所示,其中主视图和左视图都是腰长为4,底边为2的等腰三角形,则这个几何体侧面展开图的面积为【 】 A .2πB .12π C .4πD .8π6. 直线l 1:y =k 1x +b 与直线l 2:y =k 2x +c 在同一平面直角坐标系中的图象如图所示,则关于x 的不等式k 1x +b <k 2x +c 的解集为【 】 A .x >1 B .x <1 C .x >-2 D .x <-2B .7. 如图,在平面直角坐标系中,正方形ABCO 的顶点A ,C 分别在y 轴,x 轴上,以AB 为弦的⊙M 与x 轴相切.若点A 的坐标为(0,8),则圆心M 的坐标为【 】 A .(-4,5) B .(-5,4) C .(5,-4)D .(4,-5)8. 已知二次函数y =ax 2+bx +c 同时满足下列条件:对称轴是直线x =1;最值是15;二次函数的图象与x轴有两个交点,其横坐标的平方和为15-a .则b 的值是【】 A .-2B .-2或15C .4D .4或-3065°D'C'F EDCBAb2424主视图 左视图 俯视图1. 一个实数a 的相反数是5,则a 等于【 】A .15B .5C .15-D .-53. 在平面直角坐标系中,若点P (m -3,m +1)在第二象限,则m 的取值范围为【 】A .-1<m <3B .m >3C .m <-1D .m >-14. 如图,△ABC 是等腰三角形,点D 是底边BC 上异于BC 中点的一个点,∠ADE =∠DAC ,DE =AC .运用这个图(不添加辅助线)可以说明下列哪一个命题是假命题?【 】 A .一组对边平行,另一组对边相等的四边形是平行四边形 B .有一组对边平行的四边形是梯形C .一组对边相等,一组对角相等的四边形是平行四边形D .对角线相等的四边形是矩形ED BA第4题图 第5题图5. 如图,该图形绕点O 按下列角度旋转后,不能与其自身重合的是【 】A .72°B .108°C .144°D .216°6. 如图,函数y =-x 2+bx +c 的部分图象与x 轴、y 轴的交点分别为A (1,0),B (0,3),对称轴是直线x =-1,则下列结论中错误的是【 】 A .顶点坐标为(-1,4) B .函数的解析式为y =-x 2-2x +3 C .当x <0时,y 随x 的增大而增大 D .抛物线与x 轴的另一个交点是(-3,0)·O7. 如图,在△ABC 中,∠C =90°,将△ABC 沿直线MN 翻折后,顶点C 恰好落在AB 边上的点D 处,已知MN ∥AB ,MC =6,NC=MABN 的面积是【 】8. 如图,O 是正方形ABCD 的对角线BD 上一点,⊙O 与边AB ,BC 都相切,点E ,F 分别在AD ,DC 上,现将△DEF 沿着EF 对折,折痕EF 与⊙O 相切,此时点D 恰好落在圆心O 处.若DE =2,则正方形ABCD 的边长是【 】 A .3B .4C .2D .BDAN MCFOCBDE A中考数学选择题专项训练(九)一、选择题(每小题3分,共24分)1. 16的平方根是【 】A .8B .4C .±4D .±22. 有四包真空小包装火腿,每包以标准克数(450克)为基准,超过的克数记作正数,不足的克数记作负数,以下数据是记录结果,其中表示实际克数最接近标准克数的是【 】 A .+2B .-3C .+3D .+43. 如图是某几何体的三视图及相关数据,则判断正确的是【 】俯视图左视图主视图A .a >cB .b >cC .4a 2+b 2=c 2D .a 2+b 2=c 2则这次测试成绩的中位数m 满足【 】 A .40<m ≤50B .50<m ≤60C .60<m ≤70D .m >705.如图,一次函数y 1=kx +n (k ≠0)与二次函数y 2=ax 2+bx +c (a ≠0)的图象相交于A (-1,5),B (9,2)两点,则关于x 的不等式kx +n ≥ax 2+bx +c 的解集为【】 A .-1≤x ≤9 B .-1≤x <9C .-1<x ≤9D .x ≤-1或x ≥96. 如图,Rt △ABC 中,∠ACB =90º,AC =BC =Rt △ABC 绕边AB 所在的直线旋转一周,则所得几何体的表面积为【 】B .C .8πD .GEFDBCA第7题图7. 如图,在平行四边形ABCD 中,E 为AB 的中点,F 为AD 上一点,EF 交AC 于G ,AF =2cm ,DF =4cm ,AG =3cm ,则AC 的长为【 】A .9cmB .14cmC .15cmD .18cmA .(0,4) B .(0,3) C .(0,3) D .(0,4)A中考数学选择题专项训练(十)一、选择题(每小题3分,共24分)1. 如图所示,将数轴上-2和-1之间的部分用小隔线分成八等份,则图中A 点表示的数是【 】A .54-B .74-C .94-D .114- 2. 若点A (n ,2)与B (-3,m )关于原点对称,则n -m 等于【 】A .-1B .-5C .1D .53. 如图,将正方体的相邻两个面各划分成九个全等的小正方形,并分别标上“○”、“×”两符号.若下列有一图形为此正方体的展开图,则此图为【 】DCB AA .B .C .D .4. 如图所示,直线l 表示地图上的一条直线型公路,其中A ,B 两点分别表示公路上第140公里处及第157公里处.若将直尺放在此地图上,使得刻度15,18的位置分别对准A ,B 两点,则此时刻度0的位置对准地图上公路的第几公里处【 】A .17B .55C .72D .855. 如图所示,将正五边形ABCDE 的C 点固定,并按顺时针方向旋转,则旋转多少度,可使得新五边形A ′B ′CD ′E ′的顶点D ′落在直线BC 上【 】lB A 第157公里第140公里6.如图,直线y=kx+b交坐标轴于A(-3,0),B(0,5)两点,则不等式-kx-b<0的解集为【】A.x>-3 B.x<-3 Array C.x>3 D.x<37.如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,8.如图所示,△ABC中,∠B=90°,AB=21,BC=20.若有一半径为10的圆分别与AB,BC相切,则下列何种方法可找到此圆的圆心【】A.∠B的角平分线与AC的交点AB.AB的中垂线与BC中垂线的交点C.∠B的角平分线与AB中垂线的交点D.∠B的角平分线与BC中垂线的交点21BC1. A 为数轴上表示-1的点,将A 点沿数轴向左移动2个单位长度到B 点,则B 点所表示的数为【 】A .-3B .3C .1D .1或-32. 有一个铁制零件(正方体中间挖去一个圆柱形孔)如图放置,它的左视图是【 】A .B .C .D .A .123B .213C .312D .1326. 已知整数x 满足-5≤x ≤5,y 1=x +1,y 2=-2x +4,对任意一个x ,m 都取y 1,y 2中的较小值,则m 的最大值是【 】 A .1B .2C .24D .-97. 如图,在四边形ABCD 中,AB ∥DC ,∠D =90°,AD =DC =4,AB =1,F 为AD 的中点,则点F 到BC 的距离是【 】 A .2 B .4C .8D .18. 如图,⊙P 内含于⊙O ,⊙O 的弦AB 切⊙P 于点C ,且AB ∥OP ,若阴影部分的面积为9π,则弦AB 的长为【 】A .3B .4C .6D .94.一次函数14y x=+的图象如图所示,则一次函数2y x b=-+的图象与14y x=+的图象的交点不.可能..在【】A.第一象限B.第二象限C.第三象限D.第四象限第4题图第5题图5.如图,点A,B,C的坐标分别为(0,-1),(0,2),(3,0).从下面四个点M(3,3),N(3,-3),P(-3,0),Q(-3,1)中选择一个点,使得以A,B,C与该点为顶点的四边形不是中心对称图形,则该点是【】A.M B.N C.P D.Q7. 如图,在直角梯形ABCD 中,AD ∥BC ,∠C =90°,AD =5,BC =9,以A 为中心将腰AB 顺时针旋转90°至AE ,连接DE ,则△ADE 的面积等于【 】 A . 10B .11C .12D . 13EDA BCB AE DCHMF第7题图 第8题图8. 如图,在菱形ABCD 中,AB =BD ,点E ,F 分别在BC ,CD 上,且BE =CF ,连接BF ,DE 交于点M ,延长ED 到H 使DH =BM ,连接AM ,AH .则以下四个结论:①△BDF ≌△DCE ;②∠BMD =120°;③△AMH 是等边三角形;④S 四边形ABCD=4AM 2.其中正确的有【 】 A .1个B .2个C .3个D . 4个图1 图21. 4的平方根是【 】A .±16B .16C .±2D .2B .2. 如图,图1是一个底面为正方形的直棱柱,现将图1切割成图2的几何体,则图2的俯视图是【 】A .B .C .D .3. 目前,全球淡水资源日益减少,提倡全社会节约用水.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x 分钟后,水龙头滴出y 毫升的水,则y 与x 之间的函数关系式是【 】 A .y =0.05xB .y =5xC .y =100xD .y =0.05x +1004. 如图,平行四边形ABCD 中,过点B 的直线与对角线AC ,边AD 分别交于点E 和点F .过点E 作EG ∥BC ,交AB 于G ,则图中相似三角形有【 】 A .4对 B .5对 C .6对D .7对5. 如图所示,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD +PE 的和最小,则这个最小值为【 】 A. B.C .3DAB CDEPA B CDEFG6. 如图,直线y =x +2与双曲线y =xm 3-在第二象限内有两个交点,那么m 的取值范围在数轴上表示为【 】A .B .C .D .7. 在圆柱形油槽内装有一些油.截面如图,油面宽AB 为6分米,如果再注入一些油后,油面AB 上升1分米,油面宽变为8分米,那么圆柱形油槽的直径MN 为【 】 A .6分米 B .8分米C .10分米D .12分米8. 如图,在正方形纸片ABCD 中,E ,F 分别是AD ,BC 的中点,沿过点B 的直线折叠,使点C 落在EF 上,落点为N ,折痕交CD 边于点M ,BM 与EF 交于点P .再展开,则下列结论中:①CM =DM ;②∠ABN =30°;③AB 2=3CM 2;④△PMN 是等边三角形.正确的有【 】 A .1个 B .2个 C .3个D .4个NM FNMABCE D P中考数学选择题专项训练(十六)一、选择题(每小题3分,共24分)1.(-2+5)的相反数是【】A.3 B.-3 C.-7 D.72.用科学记数法表示的如下事实:地球绕太阳公转的速度是1.1×105千米/时;1纳米=1×10-9米;一天有8.64×104秒;一个氢原子的质量是1.67×10-27千克.仅从数的大小来说,其中最大的一个数是A.1.1×105B.1×10-9C.8.64×104D.1.67×10-273.下列图形中能够说明∠1>∠2的是【】A.B.C.D.4.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为【】A.16 B.17 C.18 D.19S2S1第4题图第5题图5.已知函数))((bxaxy--=(其中a b>)的图象如图所示,则函数baxy+=的图象可能正确的是【】A.B.C.D.6.如图,在矩形ABCD中,AB=4cm,BC=3cm,点P是AB上除A,B外任一点,对角线AC,BD相交于点O,DP,CP分别交AC,BD于点E,F.若△ADE和△BCF的面积之和为4cm2,则四边形PEOF的面积为【】A.1cm2B.1.5cm2 C.2cm2D.2.5cm2OPE FD CBA第6题图第7题图7.如图,直线y=+x轴、y轴分别相交于A,B两点,⊙P与y轴相切于点O,且圆心P 的坐标为(1,0).若将⊙P沿x轴向左移动,当⊙P与该直线相交时,横坐标为整数的点P的个数是【】A.2 B.3 C.4 D.58.如图,四边形ABCD是边长为9的正方形纸片,将其沿MN折叠,使点B落在CD边上的B′处,点A的对应点为A′,且B′C=3,则AM的长为【】A.1.5 B.2 C.2.25 D.2.5B'A'NMCDBA11221221中考数学选择题专项训练(十七)一、选择题(每小题3分,共24分) 1. 下列实数中,是无理数的为【 】A .3.14B .13CD2. 小颖家离学校1 200米,其中有一段为上坡路,另一段为下坡路.她去学校共用了16分钟.假设小颖上坡路的平均速度是3千米/时,下坡路的平均速度是5千米/时.若设小颖上坡用了x 分钟,下坡用了y 分钟,根据题意可列方程组为【 】A .35120016x y x y +=⎧⎨+=⎩ B .35 1.2606016x y x y ⎧+=⎪⎨⎪+=⎩ C .35 1.216x y x y +=⎧⎨+=⎩ D .351200606016x y x y ⎧+=⎪⎨⎪+=⎩ 3. 如图,AB 是⊙O 的直径,C ,D ,E 都是⊙O 上的点,则∠ACE +∠BDE =【 】A .60°B .75°C .90°D .120°第3题图 第4题图5. 为了了解某地区17 200名学生参加初中升学考试数学成绩情况,教育局从中抽取了291名考生的数学试卷进行成绩统计,在这个问题中,下列说法:①这17 200名考生的初中升学考试数学成绩的全体是总体;②每个考生是个体;③291名考生是总体的一个样本;④样本容量是291.其中正确的有【 】 A .4个 B .3个 C .2个 D .1个 6. 已知抛物线C :y =x 2+3x -10,将抛物线C 平移到C ′.若两条抛物线C ,C ′关于直线x =1对称,则下列平移方法中正确的是【 】A .将抛物线C 向右平移52个单位 B .将抛物线C 向右平移3个单位C .将抛物线C 向右平移5个单位D .将抛物线C 向右平移6个单位7. 甲、乙两人准备在一段长为1 200米的笔直公路上进行跑步,甲、乙跑步的速度分别为4m/s 和6m/s ,起跑前乙在起点,甲在乙前面100米处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两人之间的距离y (m )与时间t (s )的函数图象是【 】A .B .C .D .8. 正方形ABCD ,正方形BEFG 和正方形RKPF 的位置如图所示,点G 在线段DK 上,且G 为BC 的三等分点,R 为EF 的中点,正方形BEFG 的边长为4,则△DEK 的面积为【 】 A .10 B .12C .14D .16中考数学选择题专项训练(十八)一、选择题(每小题3分,共24分) 1. 计算:(a 2)3=【 】A .a 5B .a 6C .a 8D .3a 22. 长城是古代中国在不同时期为抵御塞北游牧部落联盟侵袭而修筑的规模浩大的军事工程的统称.据2012年国家文物局发布数据,历代长城总长为21 196.18千米.把21 196.18用科学记数法(保留三个有效数字)表示为【 】 A .321.210⨯B .42.1110⨯C .42.1210⨯D .52.1210⨯3. 如图是由5个底面直径与高度相等的大小相同的圆柱搭成的几何体,其左视图是【 】A .B .C .D .4. 如图所示,将△ABC 的三边分别扩大一倍得到△A 1B 1C 1(顶点均在格点上),它们是以P 点为位似中心的位似图形,则P 点的坐标是【 】 A .(-4,-3) B .(-3,-3) C .(-4,-4) D .(-3,-4)5. 如图,将△ADE 绕正方形ABCD 的顶点A 顺时针旋转90°,得△ABF ,连接EF 交AB 于H ,则下列结论错误的是【 】 A .AE ⊥AF B .EF :AF 1C .AF 2=FH ·FED .FB :FC =HB :EC6. 二次函数y =-x 2+bx +c 的图象如图所示,下列几个结论:①对称轴为直线x =2;②当y ≤0时,x <0或x >4;③函数解析式为y =-x 2+4x ;④当x ≤0时,y 随x 的增大而增大.其中正确的结论有【 】 A .①②③④ B .①②③ C .①③④ D .②③④7. 如图,在平面直角坐标系中,过格点A ,B ,C 作一圆弧,点B 与下列格点的连线中,能够与该圆弧相切的是【 】A .122k b ==,B .419k b ==, C .33k b ==,D .4193k b ==,H D ECBFA yxC 1B 1A 1O (C )BA3. 已知点M (1-2m ,m -1)关于x 轴的对称点在第一象限,则m 的取值范围在数轴上表示正确的是【】A .B .C .D .4. 如图,在矩形ABCD 中,AB =2,BC =4,对角线AC 的垂直平分线分别交AD ,AC 于点E ,O ,连接CE ,则CE 的长为【 】 A .3B .3.5C .2.5D .2.85. 某篮球队队员共16人,每人投篮6次,下表为其投进球数的次数分配表.若此队投进球数的中位数是2.5,则众数为【 】 A .2B .3C .4D .66. 如图,两个反比例函数1y x=和2y x =-的图象分别是l 1和l 2.设点P 在l 1上,PC ⊥x 轴,垂足为C ,交l 2于点A ,PD ⊥y 轴,垂足为D ,交l 2于点B,则△PAB 的面积为【 】 A .3B .4C .92D .5第6题图 第7题图7. 如图,在Rt △ABC 中,∠ACB =90°,∠BAC =60°.把△ABC 绕点A 按顺时针方向旋转60°后得到△AB'C',若AB =4,则线段BC 在上述旋转过程中所扫过部分(阴影部分)的面积是【 】 A .23π B .53π C .2π D .4π8. 大于1的正整数m 的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…,若m 3分裂后,其中有一个奇数是2014,则m 的值是【 】 A .43B .44C .45D .46OEDCBA1. |-5|的倒数是【 】A .15 B .15- C .5 D .-5 2. 如图,直线BD ∥EF ,AE 与BD 交于点C ,若∠ABC =30°,∠BAC =75°,则∠CEF的大小为【 】A .60°B .75°C .90°D .105° 3. 下面的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有【 】A .4个B .3个C .2个D .1个 4. 下表为72人参加某商店举办的单手抓糖果活动的统计结果.若抓到糖果数的中位数为a ,众数为b ,则a +b 为【 】A .(7,5)B .(4,6)C .(3,4)D .(-2,1)7. 已知矩形ABCD 中,AB =1,在BC 上取一点E ,沿AE 将△ABE 向上折叠,使B 点落在AD 上的F8. 如图是跷跷板示意图,横板AB 绕中点O 上下转动,立柱OC 与地面垂直,设B 点的最大高度为h 1.若将横板AB 换成横板A′B′,且A′B ′=2AB ,O 仍为A′B′的中点,设B′点的最大高度为h 2,则下列结论正确的是【 】A .h 2=2h 1B .h 2=32h 1 C .h 2=h 1 D .h 2=12h 1 FD CB A中考数学选择题专项训练(二十一)一、选择题(每小题3分,共24分)1.一个数的绝对值等于3,这个数是【】A.3 B.-3 C.±3 D.1 32.经专家估算,整个南海属我国传统海疆线的油气资源约合15 000亿美元,开采前景甚至要超过英国的北海油田,用科学记数法表示15000亿美元是【】美元.A.1.5×104B.1.5×105 C.1.5×1012 D.1.5×10133.某物体的侧面展开图如图所示,则它的左视图为【】A.B.C.D.4.如图,将△A BC绕着点C顺时针旋转50°后得到△A′B′C.若∠A=40°,∠B′=110°,则∠BCA′的度数是【】A.110°B.80°C.40°D.30°5.某校每位学生上、下学期各选择一个社团,下表为该校学生上、下学期各社团的人数比例.若该校上、下学期的学生人数不变,相较于上学期,下学期各社团的学生人数变化,下列叙述正确的是【】A.舞蹈社不变,溜冰社减少B.舞蹈社不变,溜冰社不变C.舞蹈社增加,溜冰社减少D.舞蹈社增加,溜冰社不变6.如图所示,已知A(12,y1),B(2,y2)为反比例函数1yx=图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是【】A.(12,0) B.(1,0) C.(32,0) D.(52,0)第6题图第7题图第8题图7.如图,等腰梯形ABCD中,AD∥BC,以点C为圆心,CD为半径的弧与BC交于点E.若四边形ABED是平行四边形,AB=3,则扇形CDE(阴影部分)的面积是【】A.32πB.2πC.πD.3π8.如图,点D是△ABC的边AB的延长线上一点,点F是边BC上的一个动点(不与点B重合).以BD,BF为邻边作平行四边形BDEF,又AP//BE,且AP=BE(点P,E在直线AB的同侧),如果14BD AB=,那么△PBC的面积与△ABC的面积之比为【】A.14B.35C.15D.34GPFEDBA中考数学选择题专项训练(二十二)一、选择题(每小题3分,共24分)1. 计算:-1-(-1)0=【 】A .0B .1C .2D .-22. 如图,是由8个相同的小立方块搭成的几何体,它的三个视图都是2×2的正方形.若拿掉若干个小立方块后(几何体不倒掉),其三个视图仍都为2×2的正方形,则最多能拿掉小立方块的个数为【 】A .1B .2C .3D .4 3. 有13位同学参加学校组织的才艺表演比赛,已知他们所得的分数互不相同,共设7个获奖名额.某同学知道自己的比赛分数后,要判断自己能否获奖,在下列13名同学成绩的统计量中只需知道一个量,它是【 】A .众数B .方差C .中位数D .平均数4. 小明原有30元,下表记录了他今天的所有支出,其中饼干支出的金额被涂黑.若每包饼干的售价为3元,则小明可能剩下【 】元.A .4B .5C .6D .75. 在平面直角坐标系中,已知点O (0,0),A (0,2),B (1,0),点P 是反比例函数1y x=-图象上的一个动点,过点P 作PQ ⊥x 轴,垂足为Q .若以点O ,P ,Q 为顶点的三角形与△OAB 相似,则相应的点P 共有【 】中考数学选择题专项训练(二十三)一、 选择题(每小题3分,共24分)2. 下列事件中是必然事件的是【 】A .一个直角三角形的两锐角分别是47°和53°B .抛掷一枚硬币,落地后正面朝上C .当x 是实数时,x 2≥0D .长为5cm ,5cm ,11cm 的三条线段能围成一个三角形3. 如图所示,∠E =∠F =90°,∠B =∠C ,AE =AF ,有以下结论:①EM =FN ;②CD =DN ;③∠F AN =∠EAM ;④△ACN ≌△ABM .其中正确结论的个数为【 】 A .1个 B .2个 C .3个 D .4个4. 若正比例函数y =(1-2m )x 的图象经过点A (x 1,y 1)和点B (x 2,y 2),当x 1<x 2时,y 1>y 2,则m 的取值范围是【 】A .2B .3C .4D .6第6题图 第7题图7. 如图所示,在完全重合放置的两张矩形纸片ABCD 中,AB =4,BC =8,将上面的矩形纸片折叠,使点C 与点A 重合,折痕为EF ,点D 的对应点为点G ,连接DG ,则图中阴影部分的面积为【 】 A B .6 C .185 D .3658. 已知y =x 2+(1-a )x +1是关于x 的二次函数,当x 的取值范围是1≤x ≤3时,y 在x =1时取得最大值,则实数a 的取值范围是【 】A .a ≤-5B .a ≥5C .a =3D .a ≥3ACB D EF MN中考数学选择题专项训练(二十四)一、选择题(每小题3分,共24分) 3. 如图,∠BDC =98°,∠C =38°,∠B =23°,∠A 的度数是【 】A .61°B .60°C .37°D .39°4. 一个铝质三角形框架三条边长分别为24cm 、30cm 、36cm ,要做一个与它相似的铝质三角形框架,现有长为27cm 、45cm 的两根铝材,要求以其中的一根为一边,从另一根上截下两段(允许有余料)作为另外两边.截法有【】 A .0种B .1种C .2种D .3种5. 如图,边长为1的正方形ABCD 绕点A 逆时针旋转30°到正方形AB ′C ′D ′,则它们的公共部分的面积等于【 】 A .1B.1 C .12DA .2B .C .D .7第6题图 第7题图7. 如图,已知在直角梯形AOBC 中,AC ∥OB ,CB ⊥OB ,OB =18,BC =12,AC =9,对角线OC ,AB交于点D ,点E ,F ,G 分别是CD ,BD ,BC 的中点,以O 为原点,直线OB 为x 轴建立平面直角坐标系,则G ,E ,D ,F 四个点中与点A 在同一反比例函数图象上的是【 】 A .点GB .点EC .点DD .点F8. 如图,四边形ABCD 中,∠BAD =∠ACB =90°,AB =AD ,AC =4BC ,设CD的长为x ,四边形ABCD 的面积为y ,则y 与x 之间的函数关系式是【 】A .2225y x =B .2425y x =C .225y x =D .245y x =AD BD'C'B'D C BA DA。