时变电磁场
- 格式:doc
- 大小:214.00 KB
- 文档页数:6






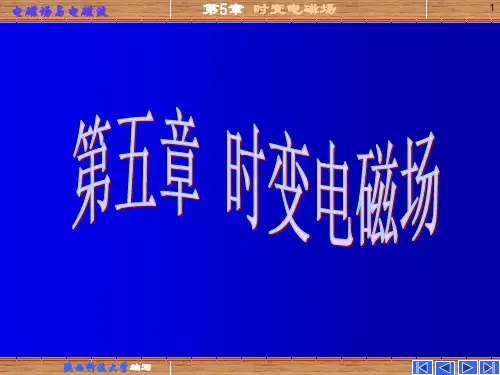




时变电磁场功率密度计算公式功率密度(W/m²)= (信号强度(V/m))²/ 377。
什么是时变电磁场:时变电磁场亦称交变电磁场。
当电场和磁场都随时间变化时,由变化着的电场激发的磁场和由变化的磁场激发的电场的总称。
时变电磁场遵守麦克斯韦方程。
时变电磁场的边界条件,(基础电子)1、在任何边界上电场强度的切向分量是连续的(条件:磁感应强度的变化率有限)。
2、在任何边界上,磁感应强度的法向分量是连续的。
3、电通密度的法向分量边界条件与媒质特性有关。
两种理想介质形成的边界上,电通密度的法向分量是连续的。
4、磁场强度的切线分量边界条件也与媒质特性有关。
在一般边界上,磁场强度的切向分量是连续的(条件:电通密度的时间变化率有限)。
但在理想导电体表面上可以形成表面电流,此时磁场强度的切向分量是不连续的。
5、理想导体内部不可能存在电场,否则将会导致无限大的电流;理想导体内部也不可能存在时变磁场,否则这种时变磁场在理想导体内部会产生时变电场。
在理想导体内部也不可能存在时变的传导电流,否则这种时变的传导电流在理想导体内部会产生时变磁场。
所以,在理想导电体内部不可能存在时变电磁场及时变的传导电流,它们只可能分布在理想导电体的表面。
6、在任何边界上,电场强度的切向分量及磁感应强度的法向分量是连续的,因此理想导体表面上不可能存在电场切向分量及磁场法向分量,只可能存在法向电场及切向磁场,也就是说,时变电场必须垂直于理想导电体的表面,而时变磁场必须与其表面相切。
7、无源区中的正弦电磁场被其边界上的电场切向分量或磁场切向分量唯一地确定时变电磁场的两种形态的发生:伴随时变电磁场有电磁波的传播。
根据场随时间变化的频率不同,时变电磁场又可分为似稳电磁场和迅变电磁场两种,前者场变化的频率较小,可以忽略场似辐射效应和推迟效应,可以用处理稳恒电磁场的方法近似处理;后者由于场变化频率较大,不可忽略辐射效应和推迟效应。
时变电磁场和各个参数的关系电磁场的能量线性媒质中电场能量密度we与磁场能量密度wm分别为式中D为电位移矢量;E为电场强度;B为磁感应强度;H为磁场强度。
第五章 时变电磁场1 什么是时变电磁场:场源(电荷、电流或时变场量)和场量(电场、磁场)随时间变化的电磁场。
由于时变的电场和磁场相互转换,也可以说时变电磁场就是电磁波。
2 时变电磁场的特点:1)电场和磁场互为对方的涡旋(旋度)源。
2)电场和磁场共存,不可分割。
3)电力线和磁力线相互垂直环绕。
3 本教科书自第五章以后内容全是关于电磁波的,第五章主要是基础,引入波动方程去掉电场与磁场的耦合,引入复矢量,简化时间变量的分析。
第六章以平面波为例,首先研究无限大区域内的电磁波的传播特点,引入用于描述电磁波特性的参量。
然后介绍半无限大区域内的电磁波的传播特点-电磁波的反射和折射。
第七章首先介绍一个坐标方向无限、其余坐标方向有限的区域内的电磁波传播特性—导行电磁波特性,然后介绍了有限区域内的电磁波谐振特性。
第八章介绍了电磁波的产生-天线。
4 本章内容线索:1)理论方面:基本场方程,位函数(引入矢量位),边界条件,波动方程。
2)基本方法:复矢量§5.1时变电磁场方程及边界条件1 1)因为t∂∂不为零,电场和磁场相互耦合,不能分开研究。
其基本方程就是Maxwell 方程。
微分形式:⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧∂∂-=⋅∇=⋅∇=⋅∇∂∂-=⨯∇∂∂+=⨯∇t J B D t BE t DJ H ρρ0 积分形式⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧∂∂-=⋅=⋅=⋅⋅∂∂-=⋅⋅∂∂+=⋅⎰⎰⎰⎰⎰⎰⎰⎰⎰s V s s V c s c s dV t s d J s d B dV s d D s d t B l d E s d t D J l d H ρρ 0)(2)物质(本构)方程:在线性、各向同性媒质中HB E D με== 其它媒质有:非线性,各向异性,双各向异性,负相对电导率、负相对磁导率媒质等人工媒质。
这些媒质在微波、光学、隐身、伪装方面有很多应用。
3)上面的电流J 包括传导电流E J c σ=和运移电流v J vρ=2 边界条件:§5.2 时变电磁场的唯一性定理1 如果1)一个区域内0=t 时,每一点的电场强度和磁场强度的初始值已知,2)区域边界面上电场强度的切向分量或磁场强度的切向分量已知,则该区域内每一点0>t 时Maxwell 方程组有唯一的确定解。
§5.3 时变电磁场的位函数 1 关于电场的波动方程:由t B E ∂∂-=⨯∇ 得tBE ∂∂⨯-∇=⨯∇⨯∇左边由矢量恒等变换得(考试点) E E E E 22)()(∇-∇=∇-⋅∇∇=⨯∇⨯∇ερ右边 22)()()(t E t J t D J t H t B t t B ∂∂+∂∂=∂∂+∂∂=⨯∇∂∂=⨯∇∂∂=∂∂⨯∇ μεμμμ 故得关于电场的波动方程:ερμμε∇+∂∂=∂∂-∇t J t E E 2222用类似的方法可以得到关于磁场的波动方程(补充作业)J t H H ⨯-∇=∂∂-∇222με3 既然Maxwell 方程已经囊括所有宏观电磁现象,为什么还要波动方程:答案是求解的需要。
Maxwell 方程里电场和磁场耦合在一起,而波动方程里电场和磁场是独立出现的,它们有各自的波动方程。
后者有时便于求解,但方程的阶数是二阶,比Maxwell 方程高一阶。
所以也有不用波动方程,直接用Maxwell 方程求解。
现在流行的FDTD 方法就是直接求解Maxwell 方程。
用于电磁场模拟仿真软件CST 就是基于FDTD 方法。
4 时变电磁场的位函数1) 矢量磁位的定义(同静磁场定义):A B⨯∇=2) 标量电位的定义(不同于静电场):由于电场的旋度不等于零,不能直接定义。
但有t AA t tB E ∂∂⨯-∇=⨯∇∂∂-=∂∂-=⨯∇)(可得 0)(=∂∂+⨯∇t AE 我们可以令 ϕ-∇=∂∂+)(tAE 上面就是标量电位的定义。
由上式可得tA E ∂∂--∇=ϕ这样我们就实现了用位函数表示电磁场量的目的。
5 位函数的波动方程: 1)矢量位的波动方程22tA t J t A t J t E JB A ∂∂-∂∂∇-=⎪⎪⎭⎫ ⎝⎛∂∂-∇-∂∂+=∂∂+=⨯∇=⨯∇⨯∇ μεϕμεμϕμεμμεμ 根据恒等式 A A A 2)(∇-⋅∇∇=⨯∇⨯∇上式可写成:)(222t A J tA A ∂∂+⋅∇∇+-=∂∂-∇ϕμεμμε 由于矢量位A的散度尚待规定,从简化角度,我们可以令:0=∂∂+⋅∇tA ϕμε这就是洛仑兹规范(请与库仑规范比较)。
由此可得矢量位的波动方程J tA A μμε-=∂∂-∇2222) 标量位的波动方程:)())(()()(22222tA t t A t A E ∂∂-∇-=⋅∇∂∂+∇-=∂∂⋅∇+∇-=∂∂+∇⋅-∇=⋅∇ϕμεϕϕϕϕ同时ερ-=⋅∇E故得标量位的波动方程 ερϕμεϕ-=∂∂-∇222t6 Helmholtz 方程:在无源区域,ρ与J均为零,上述场量和位函数的波动方程变为齐次波动方程,即Helmholtz方程:0222=∂∂-∇t E E με0222=∂∂-∇t HH με 0222=∂∂-∇tAA με0222=∂∂-∇tϕμεϕ若静态场,0→∂∂t,上述波动方程退化为相应的泊松方程和拉普拉斯方程。
§5 4 正弦电磁场1 与电路和信号分析类似,为了便于分析,我们可以把一般随时间变化的时变电磁场,用傅立叶变换分解为许多不同时间频率的正弦电磁场(简谐场,也称时谐电磁场)的叠加。
2 时谐电磁场中场量的瞬时表示式:以余弦函数为基准(工程界惯例。
少数也有用正弦函数的),以电场强度矢量为例)cos(),,()cos(),,()cos(),,(),,,(z z z y y y x x x t z y x E a t z y x E a t z y x E a t z y x E ϕωϕωϕω+++++= 注意场量与时间变量t 的关系非常简单和确定,这是引入复矢量的前提。
3时谐电磁场中场量的复数表示式 上式可以也表示为]),,(Re[])),,(),,(),,(Re[(),,(Re ),,(Re ),,(Re ]),,(Re[]),,(Re[]),,(Re[),,,()()()(t j tj zz y y x x t j z z t j y y t j x x t j z z t j y y t j x x e z y x E e z y x E a z y x E a z y x E a ez y x E a e z y x E a e z y x E a e z y x E a e z y x E a e z y x E a t z y x E z y x ωωωωωϕωϕωϕω =++=++=++=+++),,(z y x E称为电场强度的复矢量。
同样时谐电磁场的其它场量也可以有类似的表示式,如 ]),,(Re[),,,(t j e z y x J t z y x J ω=上面的表示式建立了时谐电磁场场量的瞬时表示式与复数表示式之间的联系。
4 Maxwell 方程的复数形式以电场旋度方程tBE ∂∂-=⨯∇ 为例,代入相应场量的复数表示式,可得)][Re()][Re(t j t j e B te E ωω∂∂-=⨯∇∇、t∂∂可与Re 交换次序,得)](Re[)](Re[t j t j e B te E ωω∂∂-=⨯∇复数相等与其实部及虚部分别相等是等效的,故可以去掉上式两边的Re ,接着可以消去t j e ω,得到B j E ω-=⨯∇上面的方程里已经没有时间变量了,因此方程得到了简化。
从形式上讲,只有把微分算子t∂∂用ωj 代替,就可以把时谐电磁场场量之间的线性关系,转换为等效的复矢量关系。
如复数形式的Maxwell 方程微分形式⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-=⋅∇=⋅∇=⋅∇-=⨯∇+=⨯∇ρωρωω j J B D B j E D j J H 0 积分形式⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧-=⋅=⋅=⋅⋅-=⋅⋅+=⋅⎰⎰⎰⎰⎰⎰⎰⎰⎰s V s s V c s cs dV j s d J s d B dV s d D s d B j l d E s d D j J l d H ρωρωω 0)( 线性、各向同性媒质中,有vJ E J HB E Dρσμε==== 5 边界条件的复数形式:边界条件由于不含有时间导数,故复矢量形式的边界条件与瞬时表示式形式的边界条件在形式上完全一样。
6 波动方程的复矢量形式:因为ωj t→∂∂,故222ω-→∂∂t 因此矢量位复数形式的波动方程是J A A μμεω-=-∇22令μεω22=k 波动方程可写成J A k A μ-=-∇227 复数介电常数,复数磁导率:1)E j j E j E D j J H )(ωσεωωεσω-=+=+=⨯∇令ωσεεj -= 为导电媒质的等效复介电常数,则上式可写成 E j H εω=⨯∇ 用途:把导电媒质也视为一种等效的电介质,从而可以统一采用电介质的分析方法。
另外,即使介质不导电,也会有能量损耗,且与频率有关。
这时同样可以用复介电常数表示这种介质损耗,即εεε''-'=j 虚部表示有能量损耗,从能量损耗的角度,ε''与ωσ作用一样。
考虑上述两种能量损耗,总的复介电常数是)(ωσεεε+''-'=j c 2 )同样在磁介质有损耗的情况下,也可以采用复数磁导率,μμμ''-'=j c3) 损耗角正切:表示介质损耗的相对大小。
介电质损耗角正切:εεδε'''=tan 磁介质损耗角正切:μμδμ'''=tan 8 复数坡印亭矢量,复数坡印亭定理。
1)即使是时谐电磁场,由于坡印亭矢量是电场与磁场的矢量乘法,其瞬时表示式与其复数表示式的关系不再是简单的取实部的关系。
经推导可得(参考教科书145-146页)坡印亭矢量S的瞬时表示式与电场强度和磁场强度复数表示式之间的关系][21]Re[212*t j e H E H E S ω⨯+⨯=由上式可计算出S在一个时间周期内的平均值 ]21Re[*H E S av ⨯=于是可以定义复数坡印亭矢量*21H E S ⨯=,因此有]Re[S S =。
2) 复数坡印亭定理:经推导可得(参考教科书146-147页)复数坡印亭定理dV D E H B j dV J E s d H E V V s )2121(21)21(****⋅-⋅+⋅=⋅⨯-⎰⎰⎰ω 如果考虑传导电流的焦耳热损耗,有E J σ=;极化电流的介电损耗,有εεε''-'=j ;磁损耗,有μμμ''-'=j 上式可写成 ⎰⎰⎰⎰⎰-+++='-'+''+''+=⋅-Veav mav Vm e T V V s dVj dV P P P dV E H j dV H E E s d S )(2)()4141(2)212121(22222ωωωεμωμωεωσ物理意义:上式右边是体积内的有功功率和无功功率,所以上式左边的面积分是穿过闭合面的复功率,其实部是有功功率,即功率的平均值。