下载文档原格式
7.3补充练习题及参考答案7.3.1单项选择题1.对于一棵具有n 个结点、度为4的树来说,_____________.A.树的高度最多是n-3B.树的高度最多是是n-4C.第i 层上最多有4(i-1)个结点D.至少在某一层上正好有4个结点答:这样的树中至少有一个结点的度为4,也就是说,至少有一层中有4个或以上的结点,因此树的高度最多是n-3。
本题的答案为A 。
2.度为4、高度为h 的树_____________.A.至少有h+3个结点B.最多有4h -1个结点C.最多有4h 个结点D.至少有h+4个结点答:与上小题分析相同,本题的答案为A 。
3.对于一棵具有n 个结点、度为4的树来说,树的高度至少是_____________.A.)]2([log 4nB.)]13([log 4-nC.)]13([log 4+nD.)]12([log 4+n答:由树的性质4可知,具有n 个结点的m 次树的最小高度为)]1)1(([log +-m n m 。
这里m=4,因此最小高度为)]13([log 4+n 。
本题的答案为C 。
4.在一棵3次树中度为3的结点数为两个,度为2的结点数为一个,度为1的结点数为两个,则度为0的结点数为_____________个。
A.4B.5C.6D.7答：3n =2，2n =1，1n =2，001235n n n n n n +=+++=，n=度之和+1=33n +22n +1n +1=11， 所以65110=-=n 。
本题的答案为C 。
5.若一棵有n 个结点的树,其中所有分支结点的度均为k,该树中的叶子结点个数 是_____________。
A.n(k 一1)/kB.n-kC.(n+1)/kD.(nk 一n+1)/k答:m=k,有k n n n +=0,度之和=n-1=k kn ,k n n k /)1(-=,所以0n =n-k n =n-(n-1)/k=(nk-n+1)/k.本题的答案为D 。
简答一.1、已知模式串pat=’ADABBADADA’,写出该模式串的next函数值和nextval值；2、模式匹配算法是在主串中快速寻找模式的一种有效的方法，如果设主串的长度为m，模式的长度为n，则在主串中寻找模式的KMP算法的时间复杂性是多少？如果，某一模式 P=’abcaacabaca’，请给出它的NEXT函数值及NEXT函数的修正值NEXTVAL之值。
3、已知模式串pat=“abaabc”,写出该模式串的next函数值和nextval值；4、给出字符串‘abacabaaad’在KMP算法中的next和nextval数组。
二、（意思对即可，不一定是这种写法）1、数据结构按照逻辑结构分为哪四种结构，说出元素之间的关系？集合：无关系线性结构：一对一树形结构：一对多图形结构：多对多2、图形结构有几种存储结构？分别是什么存储结构？4种。
邻接矩阵，邻接表，十字链表，邻接多重表3、度数为2的树和二叉树有何区别？（1）度为2的树中至少有一个结点的度为2，而二叉树中没有这种要求。
（2）度为2的树不区分左右子树，而二叉树严格区分左右子树。
4、简述栈和队列的特点。
栈：是一种只能在一端进行插入或删除操作的线性表。
“后进先出”队列：是一种仅允许在表的一端进行插入操作，而在表的另一端进行删除操作的受限的线性表“先进先出”三（只是最终的结果，有的题可能需要中间步骤，自己完善一下）1、已知某有向图的顶点集合为{A，B，C，D，E，F}，边集合为{〈A，B〉，〈A，C〉，〈A，E〉，〈C，F〉，〈E，D〉}，画出该图的邻接表,以它为基写出深度优先、广度优先遍历序列（深度、广度遍历要求从结点A开始）。
深度：A B C F E D广度：A B C E F D2、设无向图G（如右图所示），给出该图的最小生成树上边的集合并计算最小生成树各边上的权值之和。
3、对下图所示的无向图，从顶点1开始，写出该图的深度优先遍历和广度优先遍历。
第5章树和二叉树一、填空题1、指向结点前驱和后继的指针称为线索。
二、判断题1、二叉树是树的特殊形式。
（）2、完全二叉树中，若一个结点没有左孩子，则它必是叶子。
（）3、对于有N个结点的二叉树，其高度为。
（）4、满二叉树一定是完全二叉树，反之未必。
（）5、完全二叉树可采用顺序存储结构实现存储，非完全二叉树则不能。
（）6、若一个结点是某二叉树子树的中序遍历序列中的第一个结点，则它必是该子树的后序遍历序列中的第一个结点。
（）7、不使用递归也可实现二叉树的先序、中序和后序遍历。
（）8、先序遍历二叉树的序列中，任何结点的子树的所有结点不一定跟在该结点之后。
（）9、赫夫曼树是带权路径长度最短的树，路径上权值较大的结点离根较近。
（）110、在赫夫曼编码中，出现频率相同的字符编码长度也一定相同。
（）三、单项选择题1、把一棵树转换为二叉树后，这棵二叉树的形态是（A）。
A．唯一的Ｂ．有多种C．有多种，但根结点都没有左孩子Ｄ．有多种，但根结点都没有右孩子解释：因为二叉树有左孩子、右孩子之分，故一棵树转换为二叉树后，这棵二叉树的形态是唯一的。
2、由3个结点可以构造出多少种不同的二叉树？（D）A．2 B．3 C．4 D．5解释：五种情况如下：3、一棵完全二叉树上有1001个结点，其中叶子结点的个数是（D）。
A．250 B． 500 C．254 D．501解释：设度为0结点（叶子结点）个数为A，度为1的结点个数为B，度为2的结点个数为C，有A=C+1，A+B+C=1001，可得2C+B=1000，由完全二叉树的性质可得B=0或1，又因为C为整数，所以B=0，C=500，A=501，即有501个叶子结点。
4、一个具有1025个结点的二叉树的高h为（C）。
A．11 B．10 C．11至1025之间 D．10至1024之间解释：若每层仅有一个结点，则树高h为1025；且其最小树高为⎣log21025⎦ + 1=11，即h在11至1025之间。
计算机专业基础综合考试模拟试卷（一）一、单项选择题：第1～40小题，每小题2分，共80分。
下列每题给出的四个选项中，只有一个选项最符合试题要求。
1．已知一个栈的进栈序列是1、2、3、…、n，其输出序列为p1、p2、p3、…、p n，若p1=3，则p2为（）。
A．2或4、5、…、n都有可能B．可能是1C．一定是2 D．只可能是2或4 2．利用栈求表达式的值时，设立运算数栈OPEN。
假设OPEN只有两个存储单元，则在下列表达式中，不会发生溢出的是（）。
A．A−B*(C−D) B．(A−B)*C−D C．(A−B*C)−DD．(A−B)*(C−D)3．已知A[1…N]是一棵顺序存储的完全二叉树，9号结点和11号结点共同的祖先是（）。
A．4 B．6 C．2D．84．在常用的描述二叉排序树的存储结构中，关键字值最大的结点是（）。
A．左指针一定为空B．右指针一定为空C．左、右指针均为空D．左、右指针均不为空5．分别以下列序列构造二叉排序树，与用其他三个序列所构造的结果不同的是（）。
A．（100,80, 90,60,120,110,130）B．（100,120,110,130,80,60,90）C．（100,60,80,90,120,110,130）D．（100,80, 60,90,120,130,110）6．设无向图G=(V,E)和G′=(V′,E′)，如果G′是G的生成树，则下面说法错误的是（）。
A．G′是G的子图B．G′是G的连通分量C．G′是G的极小连通子图且V=V′D．G′是G的一个无环子图7．若G是一个具有36条边的非连通无向简单图，则图G的结点数至少是（）。
A．11 B．10 C．9D．88．在有向图G的拓扑序列中，若顶点V i在顶点V j之前，则下列情形不可能出现的是（）。
A．G中有弧<V i，V j> B．G中有一条从V i到V j的路径C．G中没有弧< V i，V j> D．G中有一条从V j到V i的路径9．具有12个关键字的有序表中，对每个关键字的查找概率相同，折半查找查找成功和查找失败的平均查找长度依次为（）。
数据结构期末考试试题（含答案）2005年－2006学年第⼆学期“数据结构”考试试题（A）姓名学号(序号)_答案隐藏班号要求：所有的题⽬的解答均写在答题纸上（每张答题纸上要写清楚姓名、班号和学号），需写清楚题⽬的序号。
每张答题纸都要写上姓名和序号。
⼀、单项选择题（每⼩题2分，共20分）1．数据的运算a 。
A.效率与采⽤何种存储结构有关B.是根据存储结构来定义的C.有算术运算和关系运算两⼤类D.必须⽤程序设计语⾔来描述答：A。
2.链表不具备的特点是 a 。
A.可随机访问任⼀结点B.插⼊删除不需要移动元素C.不必事先估计存储空间D.所需空间与其长度成正⽐答：参见本节要点3。
本题答案为：A。
3.在顺序表中删除⼀个元素的时间复杂度为 c 。
A.O(1)B.O(log2n)C.O(n)D.O(n2)答：C。
4．以下线性表的存储结构中具有随机存取功能的是d 。
A.不带头结点的单链表B.带头结点的单链表C.循环双链表D.顺序表解D。
5.⼀个栈的进栈序列是a，b，c，d，e，则栈的不可能的输出序列是c 。
A.edcba B.decbaC.dceabD.abcde答：C。
6.循环队列qu的队空条件是 d 。
A. (qu.rear+1)%MaxSize==(qu.front+1)%MaxSizeB. (qu.rear+1)%MaxSize==qu.front+1C.(qu.rear+1)%MaxSize==qu.frontD.qu.rear==qu.front答：D。
7.两个串相等必有串长度相等且 b 。
A.串的各位置字符任意B.串中各位置字符均对应相等C.两个串含有相同的字符D.两个所含字符任意答：B。
8.⽤直接插⼊排序对下⾯四个序列进⾏递增排序，元素⽐较次数最少的是c 。
A.94,32,40,90,80,46,21,69B.32,40,21,46,69,94,90,80C.21,32,46,40,80,69,90,94D.90,69,80,46,21,32,94,40答：C。
一、算法设计题1. 设二叉树bt采用二叉链表结构存储。
试设计一个算法输出二叉树中所有非叶子结点，并求出非叶子结点的个数。
【答案】int count=0;void algo2(BTNode *bt){if (bt){if(bt->lchild || bt->rchild){printf(bt->data);count++;}algo2(bt->lchild);algo2(bt->rchild);}}2. 阅读下列函数arrange()int arrange(int a[],int 1,int h,int x){//1和h分别为数据区的下界和上界int i,j,t；i=1；j=h；while(i<j){while(i<j && a[j]>=x)j--；while(i<j && a[j]>=x)i++；if(i<j){ t=a[j]；a[j]=a[i]；a[i]=t；}}if(a[i]<x) return i；else return i－1；}（1）写出该函数的功能；（2）写一个调用上述函数实现下列功能的算法：对一整型数组b[n]中的元素进行重新排列，将所有负数均调整到数组的低下标端，将所有正数均调整到数组的高下标端，若有零值，则置于两者之间，并返回数组中零元素的个数。
【答案】（1）该函数的功能是：调整整数数组a[]中的元素并返回分界值i，使所有＜x的元素均落在a[1..i]上，使所有≥x的元素均落在a[i＋1..h]上。
（2）int f(int b[],int n) 或 int f(int b[],int n){ {int p,q； int p,q；p=arrange(b,0,n－1,0)； p=arrange(b,0,n－1,1)；q= arrange(b,p+1,n－1,1)； q= arrange(b,0,p,0)；return q－p； return p－q；} }3. 假设线性表以带表头结点的循环单链表表示。
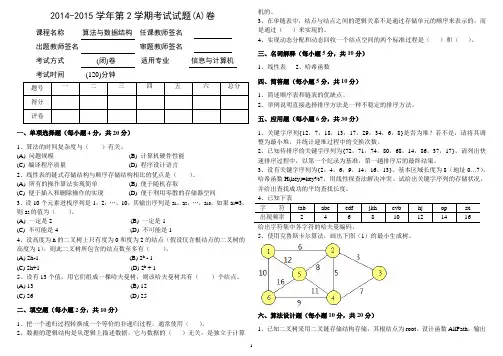
2014-2015学年第2学期考试试题(A)卷课程名称算法与数据结构任课教师签名出题教师签名审题教师签名考试方式(闭)卷适用专业信息与计算机考试时间(120)分钟一、单项选择题（每小题4分，共20分）1、算法的时间复杂度与（）有关。
(A) 问题规模(B) 计算机硬件性能(C) 编译程序质量(D) 程序设计语言2、线性表的链式存储结构与顺序存储结构相比的优点是（）。
(A) 所有的操作算法实现简单(B) 便于随机存取(C) 便于插入和删除操作的实现(D) 便于利用零散的存储器空间3、设10个元素进栈序列是1，2，…，10，其输出序列是a1，a2，…，a10，如果a1=3，则a2的值为（）。
(A) 一定是2 (B) 一定是1(C) 不可能是4 (D) 不可能是14、设高度为h的二叉树上只有度为0和度为2的结点（假设仅含根结点的二叉树的高度为1），则此二叉树所包含的结点数至多有（）。
(A) 2h-1 (B) 2h - 1(C) 2h+1 (D) 2h + 15、设有13个值，用它们组成一棵哈夫曼树，则该哈夫曼树共有（）个结点。
(A) 13 (B) 12(C) 26 (D) 25二、填空题（每小题2分，共10分）1、把一个递归过程转换成一个等价的非递归过程，通常使用（）。
2、数据的逻辑结构是从逻辑上描述数据，它与数据的（）无关，是独立于计算机的。
3、在单链表中，结点与结点之间的逻辑关系不是通过存储单元的顺序来表示的，而是通过（）来实现的。
4、实现动态分配和动态回收一个结点空间的两个标准过程是（）和（）。
三、名词解释（每小题5分，共10分）1、线性表2、哈希函数四、简答题（每小题5分，共10分）1、简述顺序表和链表的优缺点。
2、举例说明直接选择排序方法是一种不稳定的排序方法。
五、应用题（每小题6分，共30分）1、关键字序列{12，7，18，13，17，29，34，6，8}是否为堆？若不是，请将其调整为最小堆，并统计建堆过程中的交换次数。
福师《数据结构概论》在线作业二-0002试卷总分：100得分：100一、单选题（共25道试题,共50分）1.设森林F对应的二叉树为B，它有m个结点，B的根为p,p的右子树结点个数为 n,森林F中第一棵树的结点个数是（）A.m-nB.m-n-1C.n+1D.条件不足，无法确定答案:A2.若二叉树采用二叉链表存储结构，要交换其所有分支结点左、右子树的位置，利用（）遍历方法最合适。
A.前序B.中序C.后序D.按层次答案:C3.一个算法应该是（）。
A.程序B.问题求解步骤的描述C.要满足五个基本特性D.A 和 C.答案:B4.栈和队列的共同点是（）。
A.都是先进先出8.都是先进后出C.只允许在端点处插入和删除元素D.没有共同点E.限制存取点的线性结构F.限制存取点的非线性结构答案:C5.下面的程序段中，对x的赋值语句的频度为（）FOR i:=1 TO n DOFOR j:=1 TO n DO x:=x+1;A.O（2n）B.O（n）C.O（n"2）D.O（log2n）答案:C6.算法的计算量的大小称为计算的（）A.效率B.复杂性C.现实性D.难度答案:B7.对于栈操作数据的原则是（）A.先进先出8.后进先出C.后进后出D.不分顺序答案:B8.下列表达式中结果不是日期型的是？A.CT0D（"2000/10/01"）B.「99/10/01}+365C.VAL（"2000/10/01"）D.DATE（）答案:C9.关键路径是事件结点网络中（）A.从源点到汇点的最长路径B.从源点到汇点的最短路径C.最长回路D.最短回路答案:A10.就平均性能而言，目前最好的内排序方法是（）排序法。
A.冒泡B.希尔插入C.交换D.快速答案:D11.栈和队都是（）A.顺序存储的B.线性结构C.链式存储的D.非线性结构答案:B12.关系数据库中，实现实体之间的联系是通过表与表之间的?A.公共索引B.公共存储C.公共元组D.公共属性答案:D13.下列关于候选键的说法中错误的是？A.键是惟一标识实体的属性集B.候选键能惟一决定一个元组C.能惟一决定一个元组的属性集是候选键D.候选键中的属性均为主属性答案:C14.假设以行序为主序存储二维数组A=array[1..100，1..100]，设每个数据元素占2个存储单元，基地址为10，则LOC[5，5]=（）A.808B.818C.1010D.1020答案:B15.链表不具有的特点是（）儿插入、删除不需要移动元素B.可随机访问任一元素C.不必事先估计存储空间D.所需空间与线性长度成正比答案:B16.若要求尽可能快地对序列进行稳定的排序，则应选（A.快速排序B.归并排序C.冒泡排序D.堆答案:B17.下面关于关系数据模型的说法，正确的是哪一项？A.只能表示实体间的1：1联系B.只能表示实体间的l：n联系C.只能表示实体间的m：n联系D.可以表示实体间的上述三种联系答案:D18.若长度为n的线性表采用顺序存储结构，在其第i个位置插入一个新元素的算法的时间复杂度为（）（1<=i<=n+1）。
假设二叉树采用二叉链存储结构存储，分别实现以下算法，并在程序中完成测试：（1）计算二叉树节点个数；（2）输出所有叶子节点；（3）求二叉树b的叶子节点个数；（4）求二叉树b的宽度#include<>#include<>#define MaxSize 100typedef char ElemType;typedef struct node{ElemType data; //数据元素struct node *lchild; //指向左孩子struct node *rchild; //指向右孩子} BTNode;void CreateBTNode(BTNode *&b,char *str); //由str串创建二叉链BTNode *FindNode(BTNode *b,ElemType x); //返回data域为x的节点指针BTNode *LchildNode(BTNode *p); //返回*p节点的左孩子节点指针BTNode *RchildNode(BTNode *p); //返回*p节点的右孩子节点指针int BTNodeDepth(BTNode *b); //求二叉树b的深度void DispBTNode(BTNode *b); //以括号表示法输出二叉树void DestroyBTNode(BTNode *&b); //销毁二叉树void LevelOrder(BTNode *b){BTNode *p;BTNode *qu[MaxSize]; //定义环形队列,存放节点指针int front,rear; //定义队头和队尾指针front=rear=-1; //置队列为空队列rear++;qu[rear]=b; //根节点指针进入队列while (front!=rear) //队列不为空{front=(front+1)%MaxSize;p=qu[front]; //队头出队列printf("%c ",p->data); //访问节点if (p->lchild!=NULL) //有左孩子时将其进队{rear=(rear+1)%MaxSize;qu[rear]=p->lchild;}if (p->rchild!=NULL) //有右孩子时将其进队{rear=(rear+1)%MaxSize;qu[rear]=p->rchild;}}}void CreateBTNode(BTNode *&b,char *str) //由str串创建二叉链{BTNode *St[MaxSize],*p=NULL;int top=-1,k,j=0;char ch;b=NULL; //建立的二叉树初始时为空ch=str[j];while (ch!='\0') //str未扫描完时循环{switch(ch){case'(':top++;St[top]=p;k=1;break; //为左节点case')':top--;break;case',':k=2;break; //为右节点default:p=(BTNode *)malloc(sizeof(BTNode));p->data=ch;p->lchild=p->rchild=NULL;if (b==NULL) //p指向二叉树的根节点b=p;else//已建立二叉树根节点 {switch(k){case 1:St[top]->lchild=p;break;case 2:St[top]->rchild=p;break;}}}j++;ch=str[j];}}BTNode *FindNode(BTNode *b,ElemType x) //返回data域为x的节点指针{BTNode *p;if (b==NULL)return NULL;else if (b->data==x)return b;else{p=FindNode(b->lchild,x);if (p!=NULL)return p;elsereturn FindNode(b->rchild,x);}}BTNode *LchildNode(BTNode *p) //返回*p节点的左孩子节点指针{return p->lchild;}BTNode *RchildNode(BTNode *p) //返回*p节点的右孩子节点指针{return p->rchild;}int BTNodeDepth(BTNode *b) //求二叉树b的深度{int lchilddep,rchilddep;if (b==NULL)return(0); //空树的高度为0 else{lchilddep=BTNodeDepth(b->lchild); //求左子树的高度为lchilddep rchilddep=BTNodeDepth(b->rchild); //求右子树的高度为rchilddepreturn (lchilddep>rchilddep)? (lchilddep+1):(rchilddep+1); }}void DispBTNode(BTNode *b) //以括号表示法输出二叉树{if (b!=NULL){printf("%c",b->data);if (b->lchild!=NULL || b->rchild!=NULL){printf("(");DispBTNode(b->lchild);if (b->rchild!=NULL) printf(",");DispBTNode(b->rchild);printf(")");}}}void DestroyBTNode(BTNode *&b) //销毁二叉树{if (b!=NULL){DestroyBTNode(b->lchild);DestroyBTNode(b->rchild);free(b);}}void PreOrder1(BTNode *b){BTNode *St[MaxSize],*p;int top=-1;if (b!=NULL){top++; //根节点入栈St[top]=b;while (top>-1) //栈不为空时循环{p=St[top]; //退栈并访问该节点top--;printf("%c ",p->data);if (p->rchild!=NULL) //右孩子入栈{top++;St[top]=p->rchild;}if (p->lchild!=NULL) //左孩子入栈{top++;St[top]=p->lchild;}}printf("\n");}}void InOrder1(BTNode *b){BTNode *St[MaxSize],*p;int top=-1;if (b!=NULL){p=b;while (top>-1 || p!=NULL){while (p!=NULL){top++;St[top]=p;p=p->lchild;}if (top>-1){p=St[top];top--;printf("%c ",p->data);p=p->rchild;}}printf("\n");}}void PostOrder1(BTNode *b){BTNode *St[MaxSize];BTNode *p;int flag,top=-1; //栈指针置初值if (b!=NULL){do{while (b!=NULL) //将t的所有左节点入栈{top++;St[top]=b;b=b->lchild;}p=NULL; //p指向当前节点的前一个已访问的节点 flag=1;while (top!=-1 && flag){b=St[top]; //取出当前的栈顶元素if (b->rchild==p) //右子树不存在或已被访问,访问之{printf("%c ",b->data); //访问*b节点top--;p=b; //p指向则被访问的节点}else{b=b->rchild; //t指向右子树flag=0;}}}while (top!=-1);printf("\n");}}int main(){BTNode *b;CreateBTNode(b,"A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))");printf("二叉树b: ");DispBTNode(b);printf("\n");printf("先序遍历序列:\n");PreOrder1(b);printf("中序遍历序列:\n");InOrder1(b);printf("后序遍历序列:\n"); PostOrder1(b);DestroyBTNode(b);getchar();}。
