2017清华大学自主招生暨领军计划数学试题[精校版,带解析]_历年自主招生考试数学试题大全,推荐文档

自主招生数学试题及答案一、选择题（每题5分，共20分）1. 若函数f(x) = x^2 - 4x + 3，求f(2)的值。

A. 1B. 3C. 5D. 7答案：B2. 已知等差数列{a_n}的首项a_1 = 3，公差d = 2，求a_5的值。

A. 13B. 15C. 17D. 19答案：A3. 计算定积分∫(0到1) x^2 dx的值。

A. 1/3B. 1/2C. 2/3D. 1答案：B4. 设A = {1, 2, 3}，B = {3, 4, 5}，求A∩B的值。

A. {1, 2}B. {3}C. {4, 5}D. 空集答案：B二、填空题（每题5分，共20分）5. 已知函数f(x) = 2x - 1，求f(-1)的值。

答案：-36. 计算等比数列1, 2, 4, ...的第5项。

答案：167. 已知圆的半径为5，求圆的面积。

答案：25π8. 已知向量a = (3, 4)，向量b = (-4, 3)，求向量a与向量b的点积。

答案：-7三、解答题（共60分）9. 已知函数f(x) = x^3 - 6x^2 + 11x - 6，求f(x)的导数。

答案：f'(x) = 3x^2 - 12x + 1110. 已知直线l1: y = 2x + 1和直线l2: y = -x + 3，求两直线的交点坐标。

答案：交点坐标为(1, 3)11. 已知圆心在原点，半径为5的圆，求圆的方程。

答案：x^2 + y^2 = 2512. 已知函数f(x) = x^2 - 6x + 8，求函数的最小值。

答案：函数的最小值为2，当x = 3时取得。

2017自主招生必刷真题200道数学篇前言自2003年22所高校首批启动自主选拔录取改革试点以来，截至2017年，试点高校达到90所（其中77所高校面向全国招生，13所高校在本省内招生），通过教育部“阳光高考”平台累计公示自主选拔录取资格考生以逾25万人，实际录取超过14万人。

目前，自主招生已经成为一个稳定的招生渠道，受到越来越多优秀考生的青睐，对于促进科学选拔人才起到了积极作用。

爱尖子作为学科竞赛和自主招生培训的专业品牌，在国际数学奥赛金牌和物理奥赛金牌选手的领衔下，长期致力于竞赛和自主招生培训的研发工作。

2016年，爱尖子学员在竞赛上取得了惊人的成绩，北京地区53名学员获得高中数学联赛一等奖（共62人），数学IMO国家队6名成员均曾参与爱尖子培训，1人进入物理IPhO国家队，1人进入APhO国家队。

2015年，爱尖子成立自主招生研究中心，经过对近年来清华北大自主招生及博雅领军计划真题的分析与整理，甄选数学和物理学科核心考点下的经典真题，按照专题分类后，编写了这份《2017自主招生必刷真题200道》。

帮助今年备战以清华北大等国内顶级高校为目标的同学节省备考时间，精准高效的突破笔试。

为保证同学们在使用本题集时获得更好的体验，爱尖子特为本题集搭配详细解析，希望同学们经过200题的“洗刷”后，能在自主招生笔试上取得长足的进步。

目录（一）代数式变形 (4)（二）复数、平面向量 (9)（三）函数与方程 (12)（四）三角函数 (21)（五）概率 (25)（六）平面几何与立体几何 (26)（七）解析几何 (36)（八）数列 (41)（九）数论 (45)（十）排列、组合与二项式定理 (48)（一） 代数式变形001（2016年清华大学领军计划）2221,,,1a b c a b c R a b c ⎧++=∈⎨++=⎩那么 A.max 23a =B.max ()0abc =C.min13a =- D.max 4()27abc =- 002（2016年清华大学领军计划）,,x y z 均为非负实数，满足2221327()(1)()224x y z +++++=，则x y z ++的最大值为_________________最小值为__________________.003（2016年清华大学领军计划）实数22322()4xy x y +=，则22x y +的最大值为_____________.004（2015年北京大学博雅计划）已知226450x y x y -+++=，则22x y +的最小值是________．005（2016年清华大学领军计划）已知,,x y z 满足x y z ≥≥，且22211x y z x y z ++=⎧⎨++=⎩，则（ ） A ．max()0xyz = B.min 4()27xyz =-C.min 13Z =- 006（2016年清华大学领军计划）22120()(1sin )n n x x dx ππ--+=⎰___________.007（2016年北京大学自主招生）已知11112016,2016x y z x y z ++=++=，则(2016)(2016)(2016)x y z ---=______ 008（2016年北京大学博雅计划）已知ABC ∆的三边长分别为,,a b c ，有以下4个命题:① ②以222,,a b c 为边长的三角形一定存在； ③以,,222a b b c a c+++为边长的三角形一定存在； ④以||1,||1,||1a b b c c a -+-+-+为边长的三角形一定存在； 其中正确命题的个数为（ ）.A.2B.3C.3D.前三个答案都不对009（2016年北京大学博雅计划）三个不同的实数,,x y z 满足323232333x x y y z z -=-=-，则x y z ++等于（ ）. A.-1 B.0 C.1 D.前三个答案都不对010（2016年北京大学博雅计划）已知1a b c ++= ）. A.[10,11) B.[11,12) C.[12,13) D.前三个答案都不对011(2015年北京大学自主招生)设实数x ，y 满足221x y +≤，则222x xy y +-的最大值为(A)3(C)2012(2015年北京大学自主招生)设集合(){},,lg A x xy xy =与集合{}0,,B x y =相等，则x y +的值是 (A)2(B)2-(C)1(D)以上均不对013(2015年北京大学自主招生)已知1x >，1y >，且()()112x y --=，则2x y +具有 (A)最大值4(B)最小值4(C)最大值7(D)最小值7014（2015年北京大学自主招生）设关于x 的不等式()2414k x k +≤+的解集为A ，则对任意的实数k ，一定成立的是 (A)2,0A A ∈∈(B)2,0A A ∉∉(C)2,0A A ∈∉(D)2,0A A ∉∈015（2015年北京大学自主招生）设,,a b c 为两两不等的有理数，()()()222N a b b c c a ---=-+-+- (A)整数(B)有理数(C)无理数(D)前述三种关系均有可能016（2015年北京大学自主招生）已知实数,,a b c 满足0a b c ++>，0ab bc ac ++>，0abc >，则对,,a b c 来说，下面成立的是 (A)全是正数(B)至多有两个正数(C)至多有一个正数(D)全是负数017(2015年北京大学博雅计划)已知a 、b 、c 、d [2,4]∈，则22222()()()ab cd a d b c +++的最大值与最小值之和是_________．018(2015年北京大学博雅计划)已知22x px q ++≤，[1,5]x ∀∈________．019(2015年北京大学博雅计划)设2222b c a x bc +-=，2222c a b y ca+-=，2222a b c z ab +-=，且1x yz ，则201520152015x y z ++的值是________．020（2014年北大全国优秀中学生体验营）设a 、b 、c 满足3330a b c a b c ++=++=，n 为任意自然数。

一、选择题1.设复数z=cos 23π+isin 23π，则2111-1z z +-=（ ） (A)0 (B)1 (C)12 (D)322.设数列{}n a 为等差数列，p,q,k,l 为正整数，则“p+q>k+l ”是“p q k l a a a a +>+”的( )条件(A)充分不必要 (B)必要不充分 (C)充要 (D)既不充分也不必要 3.设A 、B 是抛物线y=2x 上两点，O 是坐标原点，若OA ⊥OB,则( )(A)|OA|·|OB|≥2 (B)|OA|+|OB|≥(C)直线AB 过抛物线y=2x 的焦点 (D)O 到直线AB 的距离小于等于14.设函数()f x 的定义域为(-1,1)，且满足：①()f x >0,x ∈(-1,0)；②()f x +()f y =()1x yf xy++，x 、y ∈(-1,1)，则()f x 为(A)奇函数 (B)偶函数 (C)减函数 (D)有界函数5.如图，已知直线y=kx+m 与曲线y=f (x)相切于两点，则F(x)=f (x)−kx 有（ ）(A)2个极大值点 (B)3个极大值点 (C)2个极小值点 (D)3个极小值点 6.△ABC 的三边分别为a 、b 、c ．若c=2，∠C=3π，且sinC+sin(B −A)−2sin2A=0,则有（ ）(A)b=2a (B)△ABC 的周长为△ABC 的面积为3(D)△ABC 的外接圆半径为7.设函数2()(3)x f x x e =-，则（ ）(A)()f x 有极小值，但无最小值 (B) ()f x 有极大值，但无最大值 (C)若方程()f x =b 恰有一个实根，则b>36e (D)若方程()f x =b 恰有三个不同实根，则0<b<36e 8.已知A={(x,y)∣222x y r +=}，B={(x,y)∣222()()x a y b r -+-=，已知A∩B={(11,x y ),(22,x y )}，则（ ）(A)0<22a b +<22r (B)1212()(y )0a x x b y -+-= (C)12x x +=a ，12y y +=b (D)22a b +=1122ax by +9.已知非负实数x,y,z 满足22244x y z +++2z=3，则5x+4y+3z 的最小值为（ ） (A)1 (B)2 (C)3 (D)410.设数列{n a }的前n 项和为n S ，若对任意正整数n ，总存在正整数m ，使得n S =m a ，则（ ）（A ）{n a }可能为等差数列 （B ）{n a }可能为等比数列（C ）{n a }的任意一项均可写成{n a }的两项之差(D)对任意正整数n ，总存在正整数m ，使得n a =m S11.运动会上，有6名选手参加100米比赛，观众甲猜测：4道或5道的选手得第一名；观众乙猜测：3道的选手不可能得第一名；观众丙猜测：1,2,6道选手中的一位获得第一名；观众丁猜测：4,5,6道的选手都不可能获得第一名．比赛后发现没有并列名次，且甲、乙、丙、丁中只有1人猜对比赛结果，此人是（ ） (A)甲 (B)乙 (C)丙 (D)丁12.长方体ABCD −1111A B C D 中，AB=2，AD=A 1A =1，则A 到平面1A BD 的距离为（ ）(A)13 (B)23 (C)2(D)313.设不等式组||||22(1)x y y k x +≤⎧⎨+≤+⎩所表示的区域为D ，其面积为S ，则（ ）(A)若S=4，则k 的值唯一 (B)若S=12，则k 的值有2个(C)若D 为三角形，则0<k ≤23(D)若D 为五边形，则k>4 14.△ABC 的三边长是2,3,4，其外心为O ，则O A A B O B B C O C C A ⋅+⋅+⋅=（ ）(A)0 (B)−15 (C)−212(D)−29215.设随机事件A 与B 互相独立，且P(B)=0.5，P(A −B)=0.2，则（ ）(A)P(A)=0.4 (B)P(B −A)=0.3 (C)P(AB)=0.2 (D)P(A+B)=0.916.过△ABC 的重心作直线将△ABC 分成两部分，则这两部分的面积之比的（ ） (A)最小值为34 (B)最小值为45 (C)最大值为43 (D 最大值为5417.从正15边形的顶点中选出3个构成钝角三角形，则不同的选法有（ ）(A)105种 (B)225种 (C)315种 (D)420种18.已知存在实数r ，使得圆周222x y r +=上恰好有n 个整点，则n 可以等于（ ） (A)4 (B)6 (C)8 (D)12 19.设复数z 满足2|z|≤|z −1|，则（ ） (A)|z|的最大值为1 (B)|z|的最小值为13 (C)z 的虚部的最大值为23(D)z 的实部的最大值为1320.设m,n 是大于零的实数，a =(mcos α,msin α)，b =(ncos β,nsin β)，其中α,β∈[0,2π)α,β∈[0,2π)．定义向量12a =(2α2α),12b 2β2β)，记θ=α−β，则（ ）(A)12a ·12a =a (B)1122a b ⋅=2θ(C)112222||44a b mn θ-≥(D)112222||44a b mn θ+≥21.设数列{n a }满足：1a =6，13n n n a a n++=，则（ ） (A)∀n ∈N ∗,n a <3(1)n + (B)∀n ∈N ∗,n a ≠2015 (C)∃n ∈N ∗,n a 为完全平方数 (D)∃n ∈N ∗, n a 为完全立方数 22.在极坐标系中，下列方程表示的图形是椭圆的有（ ） （A ）ρ=1cos sin θθ+ （B ）ρ=12sin θ+ （C ）ρ=12cos θ- （D ）ρ=112sin θ+23.设函数2sin ()1xf x x x π=-+，则（ ）（A ）()f x ≤43(B)|()f x |≤5|x| (C)曲线y=()f x 存在对称轴 (D)曲线y=()f x 存在对称中心24.△ABC 的三边分别为a ,b,c ，若△ABC 为锐角三角形，则（ ） (A)sinA>cosB (B)tanA>cotB (C)222a b c +> (D)333a b c +>25.设函数()f x 的定义域是(−1,1)，若(0)f =(0)f '=1，则存在实数δ∈(0,1)，使得（ ） (A)()f x >0，x ∈(−δ,δ) (B)()f x 在(−δ,δ)上单调递增 (C)()f x >1，x ∈(0,δ) (D)()f x >1，x ∈(−δ,0)26.在直角坐标系中，已知A(−1,0)，B(1,0)．若对于y 轴上的任意n 个不同的点k P (k=1,2,…,n)，总存在两个不同的点i P ,j P ，使得|sin ∠A i P B −sin ∠A j P B|≤13，则n 的最小值为（ ）(A)3 (B)4 (C)5 (D)627.设非负实数x,y 满足2x+y=1，则的（ ）(A)最小值为45 (B)最小值为25 (C)最大值为1 (D)最大值为13+ 28.对于50个黑球和49个白球的任意排列（从左到右排成一行），则（ ）(A)存在一个黑球，它右侧的白球和黑球一样多 (B)存在一个白球，它右侧的白球和黑球一样多(C)存在一个黑球，它右侧的白球比黑球少一个 (D)存在一个白球，它右侧的白球比黑球少一个29.从1,2,3,4,5中挑出三个不同数字组成五位数，其中有两个数字各用两次，例如12231，则能得到的不同的五位数有（ ） (A)300个 (B)450个 (C)900个 (D)1800个30.设曲线L 的方程为42242(22)(2)y x y x x +++-=0，则（ ） (A)L 是轴对称图形 (B)L 是中心对称图形 (C)L ⊂{(x,y)∣22x y +≤1} (D)L ⊂{(x,y)∣−12≤y ≤12} ##Answer## 1.【解析】2111-1z z +-=211-zz z zz z +-=11-z z z z+-=22cos sin 1332221-cos sin 2sin 333i i i πππππ-+--=212sin 2sincos333i πππ-⋅-22cos()sin()33sin )22i i ππππ-+-+ =cos0sin 02sin [cos()sin()]366i i πππ+-+-77)sin()]66i ππ-+-1sin )662i i ππ+-=1，选B2.【简解】 ()p q k l a a a a +-+=[(p+q)-(k+l)]d ，与公差d 的符号有关，选D3.【解析】设A(211,x x ),B(222,x x ),OA OB ⋅=1212(1)x x x x +=0⇒211x x =-答案(A),||||OA OB ⋅=2，正确；答案(B),|OA|+|OB|≥2≥2,正确；答案(C),直线AB 的斜率为222121x x x x --=21x x +=111x x - 方程为y-21x =(111x x -)(x-1x ),焦点(0,14)不满足方程，错误；答案(D)，原点到直线AB ：(111x x -)x-y+1=0的距离≤1，正确。

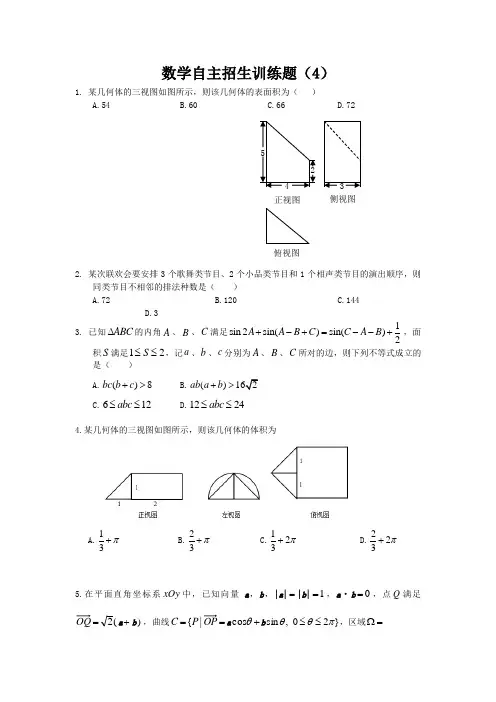
数学自主招生训练题（4）1. 某几何体的三视图如图所示，则该几何体的表面积为（ ）A.54B.60C.66D.722. 某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序，则同类节目不相邻的排法种数是（ ）A.72B.120C.144D.3 3. 已知ABC ∆的内角A 、B 、C 满足1sin 2sin()sin()2A ABC C A B +-+=--+，面积S 满足12S ≤≤，记a 、b 、c 分别为A 、B 、C 所对的边，则下列不等式成立的是（ ） A.()8bc b c +>B.()ab a b +>C.612abc ≤≤D.1224abc ≤≤4.某几何体的三视图如图所示，则该几何体的体积为A.π+31 B.π+32 C.π231+ D.π232+5.在平面直角坐标系xOy 中，已知向量a ，b ，|a |=|b |1=，a ·b 0=，点Q 满足(2=a +b )，曲线==P C |{a +θcos b }20,sin πθθ≤≤，区域=Ω正视图 侧视图 俯视图},0|{R r R r P <≤≤<，若Ω C 为两段分离的曲线，则（A ）31<<<R r （B ）R r ≤<<31（C ） 31<<≤R r （D ）R r <<<316.若定义在R 上的函数f （x ）满足f （0）=﹣1，其导函数f ′（x ）满足f ′（x ）＞k ＞1，则下．8.已知，若P 点是△ABC 所在平面内一点，且，则的最大值等于（ ）9.在614x x ⎛⎫- ⎪⎝⎭ 的展开式中，2x 的系数为 .10.在ABC ∆ 中，内角,,A B C 所对的边分别为,,a b c ，已知ABC ∆的面积为，12,cos ,4b c A -==- 则a 的值为 .11.在等腰梯形ABCD 中,已知//,2,1,60AB DC AB BC ABC ==∠= ,动点E 和F 分别在线段BC 和DC 上, 且1,9BE BC DF DC λλ==，则A E A F 的最小值为 .12.平面直角坐标系xOy 中，双曲线C 1：﹣=1（a ＞0，b ＞0）的渐近线与抛物线C 2：x 2=2py （p ＞0）交于点O ，A ，B ，若△OAB 的垂心为C 2的焦点，则C 1的离心率为 ．13．如图，在三棱台DEF ﹣ABC 中，AB=2DE ，G ，H 分别为AC ，BC 的中点． （Ⅰ）求证：BD∥平面FGH ； （Ⅱ）若CF⊥平面ABC ，AB⊥BC，CF=DE ，∠BAC=45°，求平面FGH 与平面ACFD 所成的角（锐角）的大小．14．设数列{a n}的前n项和为S n，已知2S n=3n+3．（Ⅰ）求{a n}的通项公式；（Ⅱ）若数列{b n}，满足a n b n=log3a n，求{b n}的前n项和T n．15.若n是一个三位正整数，且n的个位数字大于十位数字，十位数字大于百位数字，则称n为“三位递增数”（如137，359，567等）．在某次数学趣味活动中，每位参加者需从所有的“三位递增数”中随机抽取1个数，且只能抽取一次，得分规则如下：若抽取的“三位递增数”的三个数字之积不能被5整除，参加者得0分，若能被5整除，但不能被10整除，得﹣1分，若能被10整除，得1分．（Ⅰ）写出所有个位数字是5的“三位递增数”；（Ⅱ）若甲参加活动，求甲得分X的分布列和数学期望EX．16．平面直角坐标系xOy中，已知椭圆C：+=1（a＞b＞0）的离心率为，左、右焦点分别是F1，F2，以F1为圆心以3为半径的圆与以F2为圆心以1为半径的圆相交，且交点在椭圆C上．（Ⅰ）求椭圆C的方程；（Ⅱ）设椭圆E：+=1，P为椭圆C上任意一点，过点P的直线y=kx+m交椭圆E于A，B两点，射线PO交椭圆E于点Q．（i）求||的值；（ii）求△ABQ面积的最大值．17．设函数f（x）=ln（x+1）+a（x2﹣x），其中a∈R，（Ⅰ）讨论函数f（x）极值点的个数，并说明理由；（Ⅱ）若∀x＞0，f（x）≥0成立，求a的取值范围．18.已知函数()n ,nf x x x x R =-∈，其中*n ,n 2N ∈≥.(I)讨论()f x 的单调性；(II)设曲线()y f x =与x 轴正半轴的交点为P ，曲线在点P 处的切线方程为()y g x =,求证：对于任意的正实数x ，都有()()f x g x ≤；(III)若关于x 的方程()=a(a )f x 为实数有两个正实根12x x ，，求证：21|-|21ax x n<+-.数学自主招生训练题（4）答案1-8.BBAAACDA 9.1516 10.8 11. 2918 12.为平面，则：，则：；=|cos；14.===+++﹣=﹣（Ⅱ）由题意知，全部“三位递增数”的个数为个进行组合，即进行组合，即进行组合，即=，=，=0 ﹣1 1EX=0×）×+1×．=的方程为+y的方程为+=1，由于+y，即（|=2﹣，所以，|m|•|x|=|m|•，设在（，6．时，△≤0，时，1+x2=，0≤a时，函数）当＜a≤1＞＞18 （I ）解：由()f x =n nx x -，可得'()f x =1n n nx --=()11n n x --，其中n N *∈，且2n ≥. 下面分两种情况讨论： （1）当n 为奇数时.令'()f x =0，解得1x =，或1x =-.当x 变化时，'()f x ，()f x 的变化情况如下表：所以，()f x 在(),1-∞-，()1,+∞上单调递减，在()1,1-内单调递增。

2017清华自主招生笔试真题
清华大学也有自主招生，那么清华自主招生真题都有哪些呢?下面YJBYS小编为大家整理了2017清华自主招生笔试真题，欢迎阅读参考!
备注：2015-2017年清华大学自主招生、筑梦、领军计划笔试共用一套试卷。

一、考试模式
考试模式：机考系统分发和回收考卷。

考生更加安全高效，阅卷也更为及时准确，还可大大降低作弊的可能性。

考试科目：
文科——数学、语文
理科——数学、物理
试卷结构：试题不仅引入多选题，而且采用单选题、多选题混合编排的方式，用以区分不同水平的学生，也增加了能力考查的力度。

多选题学生全部选对得满分，选对但不全得部分分，有选错的得0分。

科目分数：每科100分
考试内容：语文——30题，数学——40题，物理——30题，数学和物理都难度大于高考
考试时间：三个小时8:30-11:30
考察方向
数学与逻辑和物理探究着重考查学生较高层次的思维能力以及综合运用所学知识分析和解决问题的能力。

阅读与表达重点考查学生的文学文化水平和各类文章的阅读水平等能力，在考查学生语言运用能力的同时也考查了学生的写作能力。

二、数学真题。

数学试卷一、选择题（每小题3分，共24分）1．如下面的四幅简笔画是从杭州的文化活动中抽象出来的，其中是轴对称图形的是2．如图，图中的五角星是用螺栓将两端打有孔的5根长度相等木条连接而构成的，它的形状不稳定．如果用在图中木条交叉点打孔加装螺栓的办法来达到使其形状稳定的目的，且所加螺栓尽可能少，那么需要要添加螺栓A 、 1个B 、 2个C 、3个D 、4个3．已知((10120162x -⎛⎛⎫=⨯----- ⎪ ⎝⎭⎝⎭，则有 A 、45x << B 、56x << C 、78x << D 、89x <<4．如图，在△ABC 中，D 、E 分别是AB 、AC 的中点，过点E 作EF ∥AB ，交BC 于点F ．当四边形DBFE 是菱形时，则△ABC 满足的条件是A 、等腰三角形B 、AC=BC C 、AB=ACD 、AB=BC第2题图 第4题图 第7题图5．若反比例函数20167a y x-=的图象与正比例函数9(2016)y a x =+的图象没有公共点，则化简20162016y a a =-++的结果为A 、2016B 、4032C 、 2aD 、-40326．已知1x ，2x 是方程220160x x --=的两实数根，则代数式31220172016x x +-的值为A 、2017B 、2016C 、 2015D 、10087．二次函数()20y ax bx c a =++≠的图象如图所示，给出下列五个结论： ①20c b ->； ②42a c b +<； ③320b c +<； ④30a c +<⑤()m am b b a ++> (1)m ≠-，其中正确结论的是A 、③④⑤B ．①③④C 、①②③④D 、①③④⑤8．如图，弦CD 在一个以AB 为直径的半圆上滑动，E 是CD 的中点，CP ⊥AB ，垂足为点P ，若AB=4.则sin CPE ∠值．A 、3B 、8C 、4D 、无法确定 二、填空题（共6小题，24分）9.用 “＜”连接6的立方根和平方根. ▲ 第8题图10.如图，点P 为正六边形ABCDEF 內部一点，若△PBC 、△PEF 的面积分別为3.5与14.5，则正六边形ABCDEF 的面积是 ▲ 。

一、 选择题1.设复数z=cos23π+isin 23π，则2111-1z z +-=（） (A)0(B)1(C)12(D)322.设数列{}n a 为等差数列，p,q,k,l 为正整数，则“p+q>k+l ”是“p q k l a a a a +>+”的()条件 (A)充分不必要(B)必要不充分(C)充要(D)既不充分也不必要3.设A 、B 是抛物线y=2x 上两点，O 是坐标原点，若OA ⊥OB,则()(A)|OA|·|OB|≥2(B)|OA|+|OB|≥22(C)直线AB 过抛物线y=2x 的焦点(D)O 到直线AB 的距离小于等于14.设函数()f x 的定义域为(-1,1)，且满足：①()f x >0,x ∈(-1,0)；②()f x +()f y =()1x yf xy++，x 、y ∈(-1,1)，则()f x 为(A)奇函数(B)偶函数(C)减函数(D)有界函数5.如图，已知直线y=kx+m 与曲线y=f (x)相切于两点，则F(x)=f (x)?kx 有（）(A)2个极大值点(B)3个极大值点(C)2个极小值点(D)3个极小值点 6.△ABC 的三边分别为a 、b 、c ．若c=2，∠C=3π，且sinC+sin(B?A)?2sin2A=0,则有（??） (A)b=2a (B)△ABC 的周长为3(C)△ABC 的面积为33(D)△ABC 的外接圆半径为337.设函数2()(3)xf x x e =-，则（）(A)()f x 有极小值，但无最小值(B)()f x 有极大值，但无最大值 (C)若方程()f x =b 恰有一个实根，则b>36e (D)若方程()f x =b 恰有三个不同实根，则0<b<36e 8.已知A={(x,y)∣222x y r +=}，B={(x,y)∣222()()x a y b r -+-=，已知A∩B={(11,x y ),(22,x y )}，则（）(A)0<22a b +<22r (B)1212()(y )0a x x b y -+-= (C)12x x +=a ，12y y +=b(D)22a b +=1122ax by +9.已知非负实数x,y,z 满足22244x y z +++2z=3，则5x+4y+3z 的最小值为（） (A)1(B)2 (C)3(D)410.设数列{n a }的前n 项和为n S ，若对任意正整数n ，总存在正整数m ，使得n S =m a ，则（） （A ）{n a }可能为等差数列（B ）{n a }可能为等比数列（C ）{n a }的任意一项均可写成{n a }的两项之差(D)对任意正整数n ，总存在正整数m ，使得n a =m S 11.运动会上，有6名选手参加100米比赛，观众甲猜测：4道或5道的选手得第一名；观众乙猜测：3道的选手不可能得第一名；观众丙猜测：1,2,6道选手中的一位获得第一名；观众丁猜测：4,5,6道的选手都不可能获得第一名．比赛后发现没有并列名次，且甲、乙、丙、丁中只有1人猜对比赛结果，此人是（）(A)甲(B)乙(C)丙(D)丁12.长方体ABCD?1111A B C D 中，AB=2，AD=A 1A =1，则A 到平面1A BD 的距离为（??）(A)13(B)23(C)2(D)313.设不等式组||||22(1)x y y k x +≤⎧⎨+≤+⎩所表示的区域为D ，其面积为S ，则（）(A)若S=4，则k 的值唯一(B)若S=12，则k 的值有2个 (C)若D 为三角形，则0<k ≤23(D)若D 为五边形，则k>4 14.△ABC 的三边长是2,3,4，其外心为O ，则OA AB OB BC OC CA ⋅+⋅+⋅=（） (A)0(B)?15 (C)?212(D)?29215.设随机事件A 与B 互相独立，且P(B)=0.5，P(A?B)=0.2，则（）(A)P(A)=0.4(B)P(B?A)=0.3 (C)P(AB)=0.2(D)P(A+B)=0.916.过△ABC 的重心作直线将△ABC 分成两部分，则这两部分的面积之比的（） (A)最小值为34(B)最小值为45(C)最大值为43(D 最大值为5417.从正15边形的顶点中选出3个构成钝角三角形，则不同的选法有（） (A)105种(B)225种(C)315种(D)420种18.已知存在实数r ，使得圆周222x y r +=上恰好有n 个整点，则n 可以等于（） (A)4(B)6 (C)8(D)1219.设复数z 满足2|z|≤|z?1|，则（） (A)|z|的最大值为1(B)|z|的最小值为13(C)z 的虚部的最大值为23(D)z 的实部的最大值为1320.设m,n 是大于零的实数，a =(mcosα,msinα)，b =(ncosβ,nsinβ)，其中α,β∈[0,2π)α,β∈[0,2π)．定义向量12a =(2α,2α),12b =(2β2β)，记θ=α?β，则（）(A)12a ·12a =a (B)1122ab ⋅=2θ(C)112222||44a b mn θ-≥(D)112222||44a b mn θ+≥21.设数列{n a }满足：1a =6，13n n n a a n++=，则（） (A)?n ∈N?,n a <3(1)n +(B)?n ∈N?,n a ≠2015(C)?n ∈N?,n a 为完全平方数(D)?n ∈N?,n a 为完全立方数 22.在极坐标系中，下列方程表示的图形是椭圆的有（）（A ）ρ=1cos sin θθ+（B ）ρ=12sin θ+（C ）ρ=12cos θ-（D ）ρ=112sin θ+23.设函数2sin ()1xf x x x π=-+，则（）（A ）()f x ≤43(B)|()f x |≤5|x|(C)曲线y=()f x 存在对称轴(D)曲线y=()f x 存在对称中心24.△ABC 的三边分别为a ,b,c ，若△ABC 为锐角三角形，则（）(A)sinA>cosB(B)tanA>cotB(C)222a b c +>(D)333a b c +>25.设函数()f x 的定义域是(?1,1)，若(0)f =(0)f '=1，则存在实数δ∈(0,1)，使得（?）(A)()f x >0，x ∈(?δ,δ)(B)()f x 在(?δ,δ)上单调递增 (C)()f x >1，x ∈(0,δ)(D)()f x >1，x ∈(?δ,0)26.在直角坐标系中，已知A(?1,0)，B(1,0)．若对于y 轴上的任意n 个不同的点k P (k=1,2,…,n)，总存在两个不同的点i P ,j P ，使得|sin ∠A i P B?sin ∠A j P B|≤13，则n 的最小值为（?） (A)3(B)4 (C)5(D)627.设非负实数x,y 满足2x+y=1，则的（??）(A)最小值为45(B)最小值为25(C)最大值为1(D)最大值为13+28.对于50个黑球和49个白球的任意排列（从左到右排成一行），则（）(A)存在一个黑球，它右侧的白球和黑球一样多(B)存在一个白球，它右侧的白球和黑球一样多 (C)存在一个黑球，它右侧的白球比黑球少一个(D)存在一个白球，它右侧的白球比黑球少一个 29.从1,2,3,4,5中挑出三个不同数字组成五位数，其中有两个数字各用两次，例如12231，则能得到的不同的五位数有（）(A)300个(B)450个(C)900个(D)1800个30.设曲线L 的方程为42242(22)(2)y x y x x +++-=0，则（） (A)L 是轴对称图形(B)L 是中心对称图形 (C)L?{(x,y)∣22x y +≤1}(D)L?{(x,y)∣?12≤y ≤12} ##Answer##1.【解析】2111-1z z +-=211-zz z zz z +-=11-z z z z +-=22cos sin 1332221-cos sin 2sin 333i i i πππππ-+-- =212sin 2sincos333i πππ-⋅-22cos()sin()33sin )22i i ππππ-+-+ =cos 0sin 02sin [cos()sin()]366i i πππ+-+-77)sin()]66i ππ-+-1sin )662i i ππ+-=1，选B2.【简解】()p q k l a a a a +-+=[(p+q)-(k+l)]d ，与公差d 的符号有关，选D3.【解析】设A(211,x x ),B(222,x x ),OA OB ⋅=1212(1)x x x x +=0⇒211x x =-答案(A),||||OA OB ⋅==2，正确；答案(B),|OA|+|OB|≥2≥2,正确；答案(C),直线AB 的斜率为222121x x x x --=21x x +=111x x -方程为y-21x =(111x x -)(x-1x ),焦点(0,14)不满足方程，错误；答案(D)，原点到直线AB ：(111x x -)x-y+1=0的距离≤1，正确。

XXX2017年自主招生考试数学试题 Word版含答案1.XXX2017年面向全省自主招生考试《科学素养》测试数学试卷一、选择题（本大题共8小题，每小题5分，共40分）1.已知$a=\frac{5+35-3}{5-35+3}$，$b=$，则二次根式$a^3b+ab^3+19$的值是（）A、6.B、7.C、8.D、92.有9张卡片，分别写有1～9这九个数字，将它们背面朝上洗匀后，任意抽取一张，记卡片上的数字为a，则使关于x的不等式组有解的概率为（）begin{cases}4x\geq3(x+1)\\2x-<a\end{cases}$A、$\frac{3}{452}$B、$\frac{1}{993}$C、$\frac{1}{452}$ D、$\frac{1}{165}$3.已知一次函数$y=kx+b$的图像经过点（3,0），且与坐标轴围成的三角形的面积为6，满足条件的函数有（）A、2个B、3个C、4个D、5个4.若实数$a\neq b$，且a、b满足$a^2-8a+5=0$，$b^2-8b+5=.$则A、-20.B、2.C、2或20.D、2或205.对于每个非零自然数n，抛物线$y=x-\frac{b-1}{a-1}$的值为$\frac{2n+1}{n(n+1)}$，其中$x+$与x轴交于A$_n$、B$_n$以及A$_{2017}$、B$_{2017}$的值是（）表示这两点间的距离，则A、$\frac{2017}{2016}+\frac{2018}{2017}$B、$\frac{2016}{2017}+\frac{2018}{2017}$ C、$\frac{2016}{2017}+\frac{2017}{2016}$ D、$\frac{2017}{2016}+\frac{2017}{2016}$6.已知$a,b,c$是$\triangle ABC$的三边，则下列式子一定正确的是（）A、$a^2+b^2+c^2>ab+bc+ac$B、$\frac{a+bc}{a+b+1c+1}c$ D、$a^3+b^3>c^3$7.如图，从$\triangle ABC$各顶点作平行线$AD\parallel EB\parallel FC$，各与其对边或其延长线相交于D，E，F.若$\triangle ABC$的面积为1，则$\triangle DEF$的面积为（）A、3.B、3C、D、28.半径为2.5的圆$\odot O$中，直径AB的不同侧有定点C和动点P，已知$A、$\frac{169}{25}$B、$\frac{32}{43}$C、$\frac{3}{4}$ D、$\frac{5}{6}$二、填空题（本大题共7小题，每小题5分，共35分）9.若分式方程$\frac{x-a}{x+1}=a$无解，则$a$的值为_________满足$a<1$，则方程$\frac{x-a}{x+1}=a$的解为$x=\frac{a}{1-a}$，当$a\geq1$时，分母$x+1$始终大于分子$x-a$，方程无解。

数学自主招生训练题（3）1.有语文、数学两学科，成绩评定为“优秀”“合格”“不合格”三种.若A 同学每科成绩不 低于B 同学，且至少有一科成绩比B 高，则称“A 同学比B 同学成绩好.”现有若干同学，他们之间没有一个人比另一个成绩好，且没有任意两个人语文成绩一样，数学成绩也一样 的.问满足条件的最多有多少学生（ ）（A ）2 （B ）3 （C ）4 （D ）52、已知双曲线C ：2222-1(00)x y a b a b=>>，的离心率为5e 4=，且其右焦点为F 2（5，0），则双曲线的方程为A 、22-143x y = B 、22-1169x y = C 、22-1916x y = D 、22-134x y = 3、若空间中n 个不同的点两两距离都相等，则正整数n 的取值A 、大于5B 、等于5C 、至多等于4D 、至多等于34.若空间中四条两两不同的直线1234,,,l l l l ，满足122334,,l l l l l l ⊥⊥⊥，则下列结论一定正确的是A.14l l ⊥B.14//l lC.14,l l 既不垂直也不平行D.14,l l 的位置关系不确定 5.设集合(){}12345=,,,,{1,0,1},1,2,3,4,5iA x x x x x x i ∈-=，那么集合A 中满足条件“1234513x x x x x ≤++++≤”的元素个数为A.60B.90C. 120D.130 6.一个四面体的三视图如图所示，则该四面体的表面积是（ ）+2（A）321+（B ）318+（C ）21（D ）18正（主）视图侧（左）视图8.若函数a x x x f +++=21)(的最小值为3，则实数a 的值为（A ）5或8 （B ）1-或5 （C ）1-或4- （D ）4-或89.若46b ax x ⎛⎫+ ⎪⎝⎭的展开式中3x 项的系数为20，则22a b +的最小值为 。

10.在ABC D 中，内角,,A B C 所对的边分别是,,a b c .已知14b c a -=，2sin 3sin B C =，则cos A 的值为_______.11.在以O 为极点的极坐标系中，圆4sin r q =和直线sin a r q =相交于,A B 两点.若AOB D 是等边三角形，则a 的值为___________.12.已知函数()23f x x x =+，x R Î.若方程()10f x a x --=恰有4个互异的实数根，则实数a 的取值范围为__________.13.如图，在四棱锥P ABCD -中，PA ^底面ABCD ，AD AB ^，//AB DC ，2AD DC AP ===，1AB =，点E 为棱PC 的中点.（Ⅰ）证明 BE DC ^；（Ⅱ）求直线BE 与平面PBD 所成角的正弦值； （Ⅲ）若F 为棱PC 上一点，满足BF AC ^， 求二面角F AB P --的余弦值.14.设椭圆22221x y a b+=（0a b >>）的左、右焦点为12,F F ，右顶点为A ，上顶点为B .已知12AB F =. （Ⅰ）求椭圆的离心率；（Ⅱ）设P 为椭圆上异于其顶点的一点，以线段PB 为直径的圆经过点1F ，经过原点的直线l 与该圆相切. 求直线的斜率.15.已知q 和n 均为给定的大于1的自然数.设集合{}0,1,2,1,q M =-，集合{}112,,1,2,,n n i A x x x x q x q x M in -+?==++.（Ⅰ）当2q =，3n =时，用列举法表示集合A ； （Ⅱ）设,s t A Î，112n n s a a q a q -=+++，112n n t b b q b q -=+++，其中,i i a b M Î，1,2,,i n =. 证明：若n n a b <，则s t <.16.已知椭圆2222+=1(0)x y a b a b >>的左焦点为F -c （,0）,M 在椭圆上且位于第一象限，直线FM 被圆422+4b x y =截得的线段的长为c ，|FM|=3.(I)求直线FM 的斜率； (II)求椭圆的方程；(III)设动点P 在椭圆上，若直线FP OP （O 为原点）的斜率的取值范围.17.已知函数()xf x x ae=-()a R Î，x R Î.已知函数()y f x =有两个零点12,x x ，且12x x <.（Ⅰ）求a 的取值范围； （Ⅱ）证明21x x 随着a 的减小而增大； （Ⅲ）证明 12x x +随着a 的减小而增大.18.已知函数22()2()ln 22f x x a x x ax a a =-++--+，其中0a >， （I ）设()g x 是()f x 的导函数，讨论函数()g x 的单调性（II ）证明：存在(0,1)a ∈使得()0f x ≥在区间(1,)+∞内恒成立，且()0f x =在区间(1,)+∞内有唯一解数学自主招生训练题（3）答案1-8.BBCDDBAD 9. 2 10.14-11.3 12. 01a <<或9a > 13. 解：依题意，以点A 为原点建立空间直角坐标系（如图），可得()1,0,0B ，()2,2,0C ，()0,2,0D ，()0,0,2P .由E 为棱PC 的中点，得()1,1,1E .（Ⅰ）证明：向量()0,1,1BE =，()2,0,0DC =，故0BE DC ?. 所以，BE DC ^.（Ⅱ）解：向量()1,2,0BD =-，()1,0,2PB =-.设(),,n x y z =为平面PBD 的法向量，则0,0,n BD n PBìï?ïíï?ïî即20,20.x y x z ì-+=ïïíï-=ïî不妨令1y =，可得()2,1,1n =为平面PBD 的一个法向量.于是有Ccos ,36n BE n BE n BE×===× 所以，直线BE 与平面PBD 所成角的正弦值为3. （Ⅲ）解：向量()1,2,0BC =，()2,2,2CP =--，()2,2,0AC =，()1,0,0AB =. 由点F 在棱PC 上，设CF CP l =，01l＃.故()12,22,2BF BC CF BC CP l l l l =+=+=--. 由BF AC ^，得0BF AC?，因此，()()2122220l l -+-=，解得34l =.即113,,222BF 骣÷ç=-÷ç÷ç桫. 设()1,,n x y z =为平面FAB 的法向量，则110,0,n AB n BFìï?ïíï?ïî即0,1130.222x x y z ì=ïïïíï-++=ïïî 不妨令1z =，可得()10,3,1n =-为平面FAB 的一个法向量. 取平面ABP 的法向量()20,1,0n=，则121211cos ,1010nn n n n n ×===-×. 易知，二面角F AB P --是锐角，所以其余弦值为10. （方法二）（Ⅰ）证明：如图，取PD 中点M ，连接EM ，AM . 由于,E M 分别为,PC PD 的中点， 故//EM DC ，且12EM DC =，又由已知，可得//EM AB 且EM AB =，故四边形ABEM 为平行四边形，所以//BE AM .因为PA ^底面ABCD ，故PA CD ^，而CD DA ^，从而CD ^平面PAD ，因为AM Ì平面PAD ，于是CD AM ^，又//BE AM ，所以BE CD ^.（Ⅱ）解：连接BM ，由（Ⅰ）有CD ^平面PAD ，得CD PD ^，而//EM CD ，故PD EM ^.又因为AD AP =，M 为PD 的中点，故PD AM ^，可得PD BE ^，所以PD ^平面BEM ，故平面BEM ^平面PBD .所以直线BE 在平面PBD 内的射影为直线BM ，而BE EM ^，可得EBM Ð为锐角，故EBM Ð为直线BE 与平面PBD 所成的角.依题意，有PD =，而M 为PD 中点，可得AM =BE =故在直角三角形BEM 中，tanEM AB EBMBE BE ?==，因此in s EMB ?.所以，直线BE 与平面PBD（Ⅲ）解：如图，在PAC D 中，过点F 作//FH PA 交AC 于点H .因为PA ^底面ABCD ，故FH ^底面ABCD ，从而FH AC ^.又BF AC ^，得AC ^平面FHB ，因此AC BH ^.在底面ABCD 内，可得3CH HA =，从而3CF FP =.在平面PDC 内，作//FG DC 交PD 于点G ，于是3DG GP =.由于//DC AB ，故//GF AB ，所以,,,A B F G 四点共面. 由AB PA ^，AB AD ^，得AB ^平面PAD ，故AB AG ^. 所以PAG Ð为二面角F AB P --的平面角.在PAG D 中，2PA =，142PG PD ==，45APG ?，由余弦定理可得AG =，os c PAG ?.所以，二面角F AB P --.14. （Ⅰ）解：设椭圆的右焦点2F 的坐标为(),0c .由12AB F =，可得2223a b c +=，又222b ac =-，则2212c a =.所以，椭圆的离心率2e =. ，所以22223a c c -=，解得a =，2e =. （Ⅱ）解：由（Ⅰ）知222a c =，22b c =.故椭圆方程为222212x y c c+=.设()00,P x y .由()1,0F c -，()0,B c ，有()100,F P x c y =+，()1,F B c c =. 由已知，有110FP FB ?，即()000x c c y c ++=.又0c ¹，故有000x y c ++=. ①又因为点P 在椭圆上，故22002212x y c c+=. ② 由①和②可得200340x cx +=.而点P 不是椭圆的顶点，故043c x =-，代入①得03cy =，即点P 的坐标为4,33c c 骣÷ç-÷ç÷ç桫. 设圆的圆心为()11,T x y ，则1402323c x c -+==-，12323ccy c +==，进而圆的半径r =. 设直线l 的斜率为k ，依题意，直线l 的方程为y kx =.由l r ==， 整理得2810kk -+=，解得4k =?所以，直线l的斜率为4+或4-15. （Ⅰ）解：当2q =，3n =时，{}0,1M =，{}12324,,1,2,3i A x x x x x M x i==+?+.可得，{}0,1,2,3,4,5,6,7A =.（Ⅱ）证明：由,s t A Î，112n n s a a q a q -=+++，112n n t b b q b q -=+++，,i i a b M Î，1,2,,i n =及n n a b <，可得()()()()11222111n n n n n n a b q a b q s t a b a b q -----=-+-++-+-()()()21111n n qq q q q q --?+-++--()()11111n n q q q q----=--10=-<. 所以，s t <.16.（I ）解：由已知有2213c a =，又由222+a b c =，可得22223,2a c b c ==.设直线FM 的斜率为(0)k k，则直线FM 的方程为()y k x c =+.由已知，有2⎛⎫+2222c b ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，解得k =. （II ）解：由（I ）得椭圆方程为2222132x y c c +=，直线FM的方程为)y x c =+，两个方程联立，消去y ，整理得223250x cx c +-=，解得53x c =-，或x c =.因为点M 在第一象限，可得M的坐标为,3c c ⎛⎫ ⎪ ⎪⎝⎭.有FM ==，解得1c =，所以椭圆的方程为22132x y +=.（III ）解：设点P 的坐标为(),x y ，直线FP 的斜率为t ，得1yt x =+，即()1y t x =+()1x ≠-，与椭圆方程联立22(1),1,32y t x x y =+⎧⎪⎨+=⎪⎩消去y ，整理得22223(1)6x t x ++=.又由已知，得2t =，解得312x --，或10x -.设直线OP 的斜率为m ，得ym x=，即(0)y mx x =≠，与椭圆方程联立，整理可得22223m x =-. ①当3,12x ⎛⎫∈-- ⎪⎝⎭时，有(1)0y t x =+，因此0m ，于是m =，得3m ⎛∈ ⎝⎭.②当()1,0x ∈-时，有(1)0y t x =+，因此0m ，于是m=，得,m ⎛∈-∞ ⎝⎭. 综上，直线OP 的斜率的取值范围是,3⎛-∞-⎝⎭,33⎛ ⎝⎭. 17（Ⅰ）解：由()xf x x ae =-，可得()1x f x ae ¢=-.下面分两种情况讨论： （1）0a £时()0f x ¢>在R 上恒成立，可得()f x 在R 上单调递增，不合题意. （2）0a >时，由()0f x ¢=，得ln x a =-.当x 变化时，()f x ¢，()f x 的变化情况如下表：这时，()f x 的单调递增区间是(),ln a -?；单调递减区间是()ln ,a -+¥.于是，“函数()y f x =有两个零点”等价于如下条件同时成立： 1°()ln 0f a ->；2°存在()1,ln a s ??，满足()10f s <；3°存在()2ln ,a s ?+?，满足()20f s <.由()ln 0f a ->，即ln 10a -->，解得10a e -<<，而此时，取10s =，满足()1,ln a s ??，且()10f s a =-<；取222ln s a a=+，满足()2ln ,a s ?+?，且()22222ln 0a a f s e e a a骣骣鼢珑鼢=-+-<珑鼢珑鼢珑桫桫. 所以，a 的取值范围是()10,e-.（Ⅱ）证明：由()0xf x x ae =-=，有x x a e=. 设()x x g x e =，由()1xxg x e -¢=，知()g x 在(),1-¥上单调递增，在()1,+¥上单调递减.并且，当(],0x ??时，()0g x £；当()0,x ??时，()0g x >.由已知，12,x x 满足()1a g x =，()2a g x =. 由()10,a e -Î，及()g x 的单调性，可得()10,1x Î，()21,x ??.对于任意的()1120,,a a e -Î，设12a a >，()()121g g a x x ==，其中1201x x <<<；()()122g g a h h ==，其中1201h h <<<.因为()g x 在()0,1上单调递增，故由12a a >，即()()11g g x h >，可得11x h >；类似可得22x h <.又由11,0x h >，得222111x h h x x h <<. 所以，21x x 随着a 的减小而增大. （Ⅲ）证明：由11x x ae =，22x x ae =，可得11ln ln x a x =+，22ln ln x a x =+.故221211ln ln lnx x x x x x -=-=. 设21x t x =，则1t >，且2121,ln ,x tx x x t ì=ïïíï-=ïî解得1ln 1t x t =-，2ln 1t t x t =-.所以， ()121ln 1t tx x t ++=-. ①令()()1ln 1x xh x x +=-，()1,x ??，则()()212ln 1x x x h x x -+-¢=-.令()12ln u x x x x=-+-，得()21x u x x 骣-÷ç¢=÷ç÷ç桫. 当()1,x ??时，()0u x ¢>.因此，()u x 在()1,+¥上单调递增，故对于任意的()1,x ??，()()10u x u >=，由此可得()0h x ¢>，故()h x 在()1,+¥上单调递增.因此，由①可得12x x +随着t 的增大而增大.而由（Ⅱ），t 随着a 的减小而增大，所以12x x +随着a 的减小而增大. 18解：（1）()()222ln 22=-++--+f x x a x x ax a a()()()2'2ln 2220,0∴==---+->>ag x f x x x a a x x()()()222222'20,0-+-∴=++=>>x x a ag x a x x x x令()'0≥g x ，即()200-+≥>x x a x ，讨论此不等式的解，可得：① 当140∆=-≤a 时，即14≥a 时，不等式恒成立。

数学自主招生训练题（1）1．已知函数f(x ）=ax 3﹣3x 2+1,若f （x)存在唯一的零点x 0，且x 0＞0，则a 的取值范围是（ ） A ． （2，+∞） B ． (1，+∞） C ． (﹣∞，﹣2） D ． （﹣∞，﹣1） 2.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中，最长的棱的长度为（ )A ． 6B ． 6C ． 4D ． 43.设函数()3x f x mπ=。

若存在()f x 的极值点0x 满足()22200x f x m +<⎡⎤⎣⎦，则m的取值范围是（ ）A 。

()(),66,-∞-⋃∞ B. ()(),44,-∞-⋃∞ C. ()(),22,-∞-⋃∞ D.()(),14,-∞-⋃∞4。

记,max{,},x x y x y y x y≥⎧=⎨<⎩,y,min{,}x,x y x y x y≥⎧=⎨<⎩，设,a b 为平面向量,则（ ) A ．min{||,||}min{||,||}a b a b a b +-≤B 。

min{||,||}min{||,||}a b a b a b +-≥C 。

2222max{||,||}||||a b a b a b +-≤+ D 。

2222max{||,||}||||a b a b a b +-≥+5. 已知甲盒中仅有1个球且为红球，乙盒中有m 个红球和n 个篮球(3,3)m n ≥≥，从乙盒中随机抽取(1,2)i i =个球放入甲盒中.（a ）放入i 个球后，甲盒中含有红球的个数记为(1,2)ii ξ=;（b ）放入i 个球后，从甲盒中取1个球是红球的概率记为(1,2)ip i =. 则 （ ）A 。

1212,()()p p E E ξξ>< B. 1212,()()p p E E ξξ<> C. 1212,()()p p E E ξξ>> D. 1212,()()pp E E ξξ<<6 设函数21()f x x =，22()2()f x x x =-，31()|sin 2|3f x x π=，99iai=，,2,1,0=i 99,，记1219998|()()||()()||()()|kkkkkkkI f a f a f a f a f a f a=-+-++-，1,2,3k = 则 （ ）A 。

、选择题2( )(A)充分不必要(B)必要不充分(C)充要(D)3.设A、B是抛物线y=x2上两点，0是坐标原点，若OAL 0B,则()(A)|OA| •|OB| > 2 (B)|OA|+|OB| (C)直线AB过抛物线y=x2的焦点(D)O至煩线AB的距离小于等于X yf (x) >0,x € (-1,0)；② f (X) + f (y) = f ( ) , X、y €1 xy(-1,1)，则f (x)为(A)奇函数(B)偶函数(C)减函数(D)有界函数5. 如图，已知直线y=kx+m与曲线y=f(x)相切于两点，则F(x)= f (x) - kx有(/ C=—，且sinC+sin(B - A) -2sin2A=0,则有(3(A)b=2 a (B) △ ABC的周长为2+2-. 3 (C) △ ABC的面积为一空(D) △ ABC的外接圆半径为37.设函数f(x) (x23)e x，则( )(A) f (x)有极小值，但无最小值(B) f (x)有极大值，但无最大值(C)若方程f (x) =b恰有一个实根，则b>-6| (D)若方程f (x) =b恰有三个不同实根，则0<b<£e e1.设复数z=cos -3+isin (A)0 (B)1 (C) 2 冲13 ，则仁(D)3211 z22.设数列｛aj为等差数列, p,q,k, l为正整数，则p+q>k+l ”是“ a p aqa k a l ”的()条件既不充分也不必要4.设函数f(x)的定义域为(-1,1)，且满足：①个极小值点(D)3个极小值点8.已知 A={(x,y) 1 x 22 2y r },B={(x,y)1 (x2 2 2a) (y b) r ,已知 A n B={(x 1,yJ ,( X 2,y 2)},则()(A)0< a 2 b 2 <2r 2(B)aXX 2) b(y1 y 2) 0(C)X 1 X 2 = a , y 1y 2=b (D)2a b 2 = 2ax 1 2by 19.已知非负实数x,y,z满足4x 24y 22z +2z=3, 则5x+4y+3z 的最小值为()(A)1 (B)2 (C)3 (D)410.设数列｛ a n ｝的前n 项和为S n ，若对任意正整数n ,总存在正整数 m,使得S n =a m ，则( )(A )｛ a n ｝可能为等差数列(B )｛ a n ｝可能为等比数列(c )｛a n ｝的任意一项均可写成｛a n ｝的两项之差(D)对任意正整数n ，总存在正整数 m 使得a n = S m 11.运动会上，有6名选手参加100米比赛，观众甲猜测：4道或5道的选手得第一名；观众乙猜测： 3道的选手不可能得第一名；观众丙猜测：1,2,6道选手中的一位获得第一名；观众丁猜测：4,5,6道的选手都不可能获得第一名•比赛后发现没有并列名次，且甲、乙、丙、丁中只有 1人猜对比赛结果，此人是( )(A)甲(B)乙(C)丙(D) 丁1(A)若S=4,则k 的值唯一(B) 若S=^，贝U k 的值有2个22(C)若D 为三角形，则0<k <(D)若D 为五边形，则312.长方体 ABCDAEGD 中,AB=2, AD=A A 1=1，贝U A 到平面 A BD 的距离为((A) - (B)3(D)13.设不等式组|x| |y| 2 y 2 k(x 1)所表示的区域为 D,其面积为S,U(k>414. △ ABC 勺三边长是 2,3,4，其外心为 0,则 uuu uuu OA AB uuu uuu uuur uuu OB BC 0C CA =((A)0 (B)-15 (C) -21(D)229 215. 设随机事件 A 与B 互相独立，且 P(B)=0.5(A)P(A)=0.4 (B)P(B -A)=0.3 (C)P(AB)=0.2 (D)P(A+B)=0.916. 过厶ABC 的重心作直线将厶 3(A)最小值为一(B)最小值为417. 从正15边形的顶点中选出,P(A- B)=0.2，则(ABC 分成两部分，则这两部分的面积之比的(4 4(C)最大值为一533个构成钝角三角形，5(D 最大值为一4则不同的选法有((A)105 种(B)225 种(C)315 种(D)420 种18. 已知存在实数r，使得圆周x2y2 r2上恰好有n个整点，则n可以等于(22.在极坐标系中，下列方程表示的图形是椭圆的有(4 2 1 V2(A)最小值为一(B)最小值为一 (C)最大值为1 (D)最大值为--------------------5 5 3(A)4 (B)6 (C)8 (D)1219. 设复数z 满足2|z| w |z-1|，则(1(A)|z|的最大值为1 (B)|z| 的最小值为—(C)z321的虚部的最大值为2(D)z 的实部的最大值为13320.设 m,n 是大于零的实数， a =(mcos a ,msin a ),b =(ncos 3 ,nsin 3 )，其中 a , B€ [0,2 n ) a , B€r 1, _[0,2 n ) •定义向量 a 2 =( 、、. m cos — ,、. m sin 一 ), b 2=(、. n 2cos — 2 ，、齐 sin —)，记 9 = a - 3,贝U2r [ r 1 r r 1 r 1 ___ (A) a 2 • a 2 = a (B) a 2 b 2=、.mn cos — (C) 2r] r] … |a 2 b 2|4、一 mn sin 2 —4r 1 r] 2 _ 2 (D) |a 2 b 2 |24, mncos 2 —421.设数列｛ a n ｝满足：a 1=6, an 1，则((A) ? n € N?, a n <(n 1)3 (B) ? n € N?, a n 丰 2015 (C) ? n € N?, a n 为完全平方数(D)? n € N?, a n 为完全立方数1 (A )p=cos sin23. 设函数 f(x)s in x，则( x x 14(A ) f(x) w (B)| f (x) | w 5|x| (C)曲线 y= f (x)存在对称轴324. △ ABC 的三边分别为a ,b,c ，若△ ABC 为锐角三角形，则((B )p=—1(C ) 2 sin1p= —2 cos(D )(D) 1 1 2si n曲线y= f (x)存在对称中心(A)si nA>cosB (B)ta nA>cotB (C) a 2 b 2 c 2 (D) a 3 b 3 c 325.设函数f (x)的定义域是(-1,1), 若f(0) = f (0) =1,则存在实数 s€ (0,1)，使得()(A) f (x) >0, x € (- S , S) (B)f (x)在(-S , S )上单调递增 (C) f (x) >1, x € (0, S) (D)f (x)>1 , x € (- S ,0)26.在直角坐标系中，已知A(-1,0),B(1,0) •若对于y 轴上的任意n 个不同的点 P k (k=1,2，…,n)，总存在两个不同的点R ,P j ,1使得 |sin / A P j B-sin / A P j B| w —,贝V n 的最小值为( 3(A)3 (B)4(C)5 (D)627.设非负实数x,y 满足2x+y=1，则 x+ x 2 y 2 的()128.对于50个黑球和49个白球的任意排列(从左到右排成一行)，则((A)存在一个黑球，它右侧的白球和黑球一样多(B)存在一个白球，它右侧的白球和黑球一样多(C)存在一个黑球，它右侧的白球比黑球少一个 (D)存在一个白球，它右侧的白球比黑球少一个 29.从1,2,3,4,5 中挑出三个不同数字组成五位数, 同的五位数有( (A)300 个(B)450其中有两个数字各用两次，例如 12231,则能得到的不 30.设曲线L 的方程为 (A)L 是轴对称图形 (C)L ? {(x,y) I ##A nswer##1.【解析】 丄1-z) 个(C)900 y 4 (2x 2(B)L 个(D)1800 个 2 4 2 2)y (x 2x ) =0,则(是中心对称图形 1 (D)L ? {(x,y)zz 1 zz_______ 1 - 2. 21-cos i sin332 cos 3..2 i sin ___ 3 2 2i sin32sin 2 i 2sin cos —3 3 3 cos0 isinO 2sin — [cos( —) i sin(-)i sin(3、、3(cos —2-洽 2os(cos( i sin ) 27) i sin(67)]丄(cos — isi n —.3 6 6△ )=1,选 B22.【简解】 a p (a k Q )=[(p+q)-(k+l)]d ，与公差 d 的符号有关，选 3.【解析】设A( 2X 1,X 1 ),B( 2 uuu uuu X 2,X 2 ), OA OB =X 1X 2(1 X 1X 2) =0 X 2 X1 答案(A), |0A| l OBI ^x^(1 好)4(1 —1^) = j1 X2 1 2 X 11 > /2 2|X 1 | 丄=2,正确; |X 1 | 答案(B),|OA|+|OB| > 2..|OA 「|OB| > 2 .2,正确；答案(C),直线 AB 的斜率为 2 22^=X 2 x 2 x 1X1程为 y- xj =( x 1 1)(x-x 1),焦点(0, 1)不满足方程，错误；答案(D)，原点到直线AB ：(4X11)x-y+ 仁X 1的距离d=w 1,正确。