双星及三星模型教学内容

高中双星问题教案一、教学目标1. 知识目标：了解高中双星问题的概念与基本性质，掌握相关计算方法。

2. 技能目标：能够运用所学知识解决实际问题。

3. 情感目标：培养学生对数学的兴趣和探究精神。

二、教学重点与难点1. 教学重点：高中双星问题的概念、基本性质及计算方法。

2. 教学难点：如何应用所学知识解决实际问题。

三、教学过程步骤一：引入1. 引入活动：通过展示两颗星星的图片，让学生猜测这两颗星星是否会相撞，并引出“双星问题”。

2. 引入概念：介绍“双星问题”的概念，即两个质量很大的天体相互绕转的运动状态。

步骤二：理论探究1. 讲解基本性质：（1）双星系统的重心是不动点；（2）重心到两个天体的距离之比等于它们的质量之比；（3）两个天体围绕重心做圆周运动，圆周半径之比等于它们的质量之比。

2. 讲解计算方法：（1）计算重心坐标；（2）计算重心到两个天体的距离之比；（3）计算圆周半径之比。

步骤三：实例演练1. 案例分析：通过一些实际案例，让学生掌握如何应用所学知识解决问题。

2. 练习题：布置一些练习题，让学生巩固所学知识。

步骤四：拓展应用1. 实际应用：介绍双星问题在现代科技领域中的应用，如卫星轨道设计、恒星运动规律研究等。

2. 探究任务：布置一些探究任务，让学生自主探究双星问题在其他领域中的应用。

四、教学方式1. 讲授法：通过讲解基本概念和性质，引导学生理论探究。

2. 案例分析法：通过实际案例分析，帮助学生理解和应用所学知识。

3. 课堂练习法：通过课堂练习巩固所学知识，并培养自主思考能力。

4. 探究式学习法：通过探究任务，培养学生探究精神和创新能力。

五、教学评价1. 课堂表现：评价学生在课堂上的听讲、思考和回答问题的表现。

2. 作业完成情况：评价学生完成作业的质量和数量。

3. 考试成绩：通过考试成绩评价学生对所学知识的掌握情况。

六、教学资源1. 图片资料：两颗星星的图片等。

2. 教材资料：高中数学教材相关章节。

双星模型、三星模型、四星模型一、双星问题1.模型构建：在天体运动中，将两颗彼此相距较近，且在相互之间万有引力作用下绕两者连线上的某点做角速度、周期相同的匀速圆周运动的恒星称为双星。

2．模型条件： (1)两颗星彼此相距较近。

(2)两颗星靠相互之间的万有引力提供向心力做匀速圆周运动。

(3)两颗星绕同一圆心做圆周运动。

3．模型特点: (1)“向心力等大反向”——两颗星做匀速圆周运动的向心力由它们之间的万有引力提供。

(2)“周期、角速度相同”——两颗恒星做匀速圆周运动的周期、角速度相等。

(3)三个反比关系：m1r1＝m2r2；m1v1＝m2v2；m1a1＝m2a2推导：根据两球的向心力大小相等可得，m1ω2r1＝m2ω2r2，即m1r1＝m2r2；等式m1r1＝m2r2两边同乘以角速度ω，得m1r1ω＝m2r2ω，即m1v1＝m2v2；由m1ω2r1＝m2ω2r2直接可得，m1a1＝m2a2。

(4)巧妙求质量和：Gm1m2L2＝m1ω2r1①Gm1m2L2＝m2ω2r2②由①＋②得：G m1＋m2L2＝ω2L ∴m1＋m2＝ω2L3G4. 解答双星问题应注意“两等”“两不等”(1)“两等”: ①它们的角速度相等。

②双星做匀速圆周运动向心力由它们之间的万有引力提供，即它们受到的向心力大小总是相等。

(2)“两不等”:①双星做匀速圆周运动的圆心是它们连线上的一点，所以双星做匀速圆周运动的半径与双星间的距离是不相等的，它们的轨道半径之和才等于它们间的距离。

②由m1ω2r1＝m2ω2r2知由于m1与m2一般不相等，故r1与r2一般也不相等。

二、多星模型(1)定义：所研究星体的万有引力的合力提供做圆周运动的向心力，除中央星体外，各星体的角速度或周期相同．(2)三星模型：①三颗星位于同一直线上，两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图甲所示)．②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示)．(3)四星模型：①其中一种是四颗质量相等的恒星位于正方形的四个顶点上，沿着外接于正方形的圆形轨道做匀速圆周运动(如图丙)．②另一种是三颗恒星始终位于正三角形的三个顶点上，另一颗位于中心O，外围三颗星绕O做匀速圆周运动(如图丁所示)．三、卫星的追及相遇问题1、某星体的两颗卫星从相距最近到再次相距最近遵从的规律：内轨道卫星所转过的圆心角与外轨道卫星所转过的圆心角之差为2π的整数倍。

双星三星四星问题双星模型、三星模型、四星模型一、双星问题1.模型构建：在天体运动中，将两颗彼此相距较近，且在相互之间万有引力作用下绕两者连线上的某点做角速度、周期相同的匀速圆周运动的恒星称为双星。

2．模型条件： (1)两颗星彼此相距较近。

(2)两颗星靠相互之间的万有引力提供向心力做匀速圆周运动。

(3)两颗星绕同一圆心做圆周运动。

3．模型特点: (1)“向心力等大反向”——两颗星做匀速圆周运动的向心力由它们之间的万有引力提供。

(2)“周期、角速度相同”——两颗恒星做匀速圆周运动的周期、角速度相等。

(3)三个反比关系：m1r1＝m2r2；m1v1＝m2v2；m1a1＝m2a2推导：根据两球的向心力大小相等可得，m1ω2r1＝m2ω2r2，即m1r1＝m2r2；等式m1r1＝m2r2两边同乘以角速度ω，得m1r1ω＝m2r2ω，即m1v1＝m2v2；由m1ω2r1＝m2ω2r2直接可得，m1a1＝m2a2。

(4)巧妙求质量和：Gm1m2L2＝m1ω2r1①Gm1m2L2＝m2ω2r2②由①＋②得：G m1＋m2L2＝ω2L ∴m1＋m2＝ω2L3G4. 解答双星问题应注意“两等”“两不等”(1)“两等”: ①它们的角速度相等。

②双星做匀速圆周运动向心力由它们之间的万有引力提供，即它们受到的向心力大小总是相等。

(2)“两不等”:①双星做匀速圆周运动的圆心是它们连线上的一点，所以双星做匀速圆周运动的半径与双星间的距离是不相等的，它们的轨道半径之和才等于它们间的距离。

②由m1ω2r1＝m2ω2r2知由于m1与m2一般不相等，故r1与r2一般也不相等。

二、多星模型(1)定义：所研究星体的万有引力的合力提供做圆周运动的向心力，除中央星体外，各星体的角速度或周期相同．(2)三星模型：①三颗星位于同一直线上，两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图甲所示)．②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示)．(3)四星模型：①其中一种是四颗质量相等的恒星位于正方形的四个顶点上，沿着外接于正方形的圆形轨道做匀速圆周运动(如图丙)．②另一种是三颗恒星始终位于正三角形的三个顶点上，另一颗位于中心O，外围三颗星绕O做匀速圆周运动(如图丁所示)．三、卫星的追及相遇问题1、某星体的两颗卫星从相距最近到再次相距最近遵从的规律：内轨道卫星所转过的圆心角与外轨道卫星所转过的圆心角之差为2π的整数倍。

《双星及三星模型》导学提纲设计人： 审核人：高三物理备课组班级： 组名： 姓名：【学习目标】1. 理解双星模型特点2. 掌握双星及三星运动的向心力来源 【导读流程】一．双星模型条件及特点 ：例1 双星系统由两颗恒星组成，两恒星在相互引力的作用下，分别围绕其连线上的某一点做周期相同的匀速圆周运动．研究发现，双星系统演化过程中，两星的总质量、距离和周期均可能发生变化．若某双星系统中两星做圆周运动的周期为T ，经过一段时间演化后，两星总质量变为原来的k 倍，两星之间的距离变为原来的n 倍，则此时圆周运动的周期为（ ）A.T k n 23B.T k n 3C.T kn 2D.T k n例2（2015•天门模拟）经长期观测人们在宇宙中已经发现了“双星系统”．“双星系统”由两颗相距较近的恒星组成，每个恒星的线度远小于两个星体之间的距离，而且双星系统一般远离其他天体．如图所示，两颗星球组成的双星，在相互之间的万有引力作用下，绕连线上的O 点做周期相同的匀速圆周运动．现测得两颗星之间的距离为L ，质量之比为m 1：m 2=3：2．则可知（ ）A. m 1、m 2做圆周运动的线速度之比为3：2B. m 1、m 2做圆周运动的角速度之比为3：2C. m 1做圆周运动的半径为 2/5LD. m 2做圆周运动的半径为 2/5L二． 三星模型的向心力来源 ：例3. （2015安微理综）由三颗星体构成的系统，忽略其它星体对它们的作用，存在着一种运动形式：三颗星体在相互之间的万有引力作用下，分别位于等边三角形的三个顶点上，绕某一共同的圆心O 在三角形所在的平面内做相同角速度的圆周运动（图示为A 、B 、C 三颗星体质量不相同时的一般情况）。

若A 星体质量为2m ，B 、C 两星体的质量均为m ，三角形的边长为a ，求：（1）A 星体所受合力大小F A ； （2）B 星体所受合力大小F B ； （3）C 星体的轨道半径R C ； （4）三星体做圆周运动的周期T 。

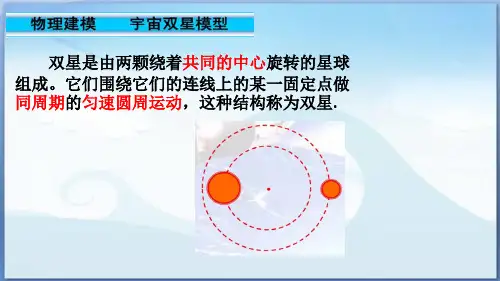
“双星”及“三星”问题宇宙中，因天体间的相互作用而呈现出诸如双星、三星及多星系统组成的自然天文现象，天体之间相互作用遵循万有引力的规律，他们的运动规律也同样遵循开普勒行星运动的三条基本规律。

现代实验观测表明，在天体运动中，将两颗彼此距离较近而绕同一点做圆周运动的行星称为双星模型。

而三星等多星模型则是指彼此相互依存和相互作用且围绕某一点作圆周运动的行星。

多星系统问题的求解方法仍然是建立万有引力方程和牛顿第二定律方程。

由于多星间的引力和运动情况特殊性，从而产生了很多有趣的天文现象。

一、“双星”问题：两颗质量可以相比的恒星相互绕着旋转的现象，叫双星。

双星问题是万有引力定律在天文学上的应用的一个重要内容，现就这类问题的处理作简要分析。

1.要明确双星中两颗子星做匀速圆周运动的向心力来源双星中两颗子星相互绕着旋转可看作匀速圆周运动，其向心力由两恒星间的万有引力提供。

由于力的作用是相互的，所以两子星做圆周运动的向心力大小是相等的，利用万有引力定律可以求得其大小。

2.要明确双星中两颗子星匀速圆周运动的运动参量的关系两子星绕着连线上的一点做圆周运动，所以它们的运动周期是相等的，角速度也是相等的，所以线速度与两子星的轨道半径成正比。

3.要明确两子星圆周运动的动力学关系。

设双星的两子星的质量分别为M1和M2，相距L，M1和M2的线速度分别为v1和v2，角速度分别为ω1和ω2，由万有引力定律和牛顿第二定律得：在这里要特别注意的是在求两子星间的万有引力时两子星间的距离不能代成了两子星做圆周运动的轨道半径。

4.“双星”问题的分析思路质量m1，m2；球心间距离L；轨道半径 r1 ，r2；周期T1，T2 ；角速度ω1，ω2 线速度V1 V2；周期相同：（参考同轴转动问题） T1=T2角速度相同：（参考同轴转动问题）ω1 =ω2向心力相同：Fn1=Fn2（由于在双星运动问题中，忽略其他星体引力的情况下向心力由双星彼此间万有引力提供，可理解为一对作用力与反作用力）轨道半径之比与双星质量之比相反：（由向心力相同推导）r1：r2=m2：m1m1ω2r1=m2ω2r2m1r1=m2r2 r1:r2=m2:m1线速度之比与质量比相反：（由半径之比推导） V1:V2=m2:m1V1=ωr1 V2=ωr2双星系统由两颗恒星组成，两恒星在相互引力的作用下，分别围绕其连线上的某一点做周期相同的匀速圆周运动.研究发现，双星系统演化过程中，两星的总质量、距离和周期均可能发生变化.若某双星系统中两星做圆周运动的周期为，经过一段时间演化后，两星总质量变为原来的倍，两星之间的距离变为原来的倍，则此时圆周运动的周期为（）A. B.C. D.设两颗恒星的质量分别为和，两颗恒星的运行半径分别为和，两恒星之间的距离，两恒星运动时都是由它们之间的万有引力提供向心力，即，，联立得两恒星的质量和，故，当质量和变为原来的k倍，距离变为原来倍时，两恒星做圆周运动的周期，B项正确.二、“三星”问题有两种情况：第一种三颗星连在同一直线上，两颗星围绕中央的星（静止不动）在同一半径为R的圆轨道上运行，周期相同；第二种三颗星位于等边三角形的三个顶点上，并沿外接于等边三角形的外接圆轨道运行，三星运行周期相同。

双星模型问题的教案教案标题：探索双星模型问题教案目标：1. 理解双星模型问题的概念和应用。

2. 学会使用数学方法解决双星模型问题。

3. 培养学生的逻辑思维和问题解决能力。

教学步骤：引入活动：1. 向学生介绍双星模型问题的概念，并提供一个简单的例子来引发学生的兴趣和好奇心。

2. 引导学生思考：在实际生活中，我们是否遇到过类似的问题？这些问题对我们有什么影响？知识讲解：3. 解释双星模型问题的定义和特点。

强调问题中的两个变量之间的关系以及如何使用数学方法解决问题。

4. 介绍常见的双星模型问题类型，如速度、时间、距离等问题，并提供相应的解题方法和技巧。

示范与练习：5. 列举一些具体的双星模型问题，并与学生一起解决这些问题。

在解题过程中，引导学生分析问题、建立方程、运用数学知识解决问题。

6. 分组活动：将学生分成小组，让每个小组设计一个双星模型问题，并向其他小组提出挑战。

鼓励学生在解答问题的同时，思考不同的解题方法和策略。

拓展活动：7. 鼓励学生应用所学知识解决实际生活中的问题，如交通流量、物体运动等。

让学生意识到数学在解决实际问题中的重要性和应用价值。

8. 提供一些拓展资源，如相关的练习题、在线模拟实验等，供学生进一步巩固和拓展所学内容。

总结与评价：9. 总结本节课所学的内容，并与学生一起回顾解题过程中的关键步骤和技巧。

10. 鼓励学生提出问题和反思，评价本节课的有效性和自己的学习收获。

教学资源：- PowerPoint演示文稿或白板- 教材或教辅资料- 练习题和答案- 小组活动材料- 拓展资源链接教学评估：- 观察学生在课堂上的参与程度和问题解决能力。

- 检查学生在小组活动中设计和解答问题的能力。

- 收集学生的作业和练习题，检查他们对所学内容的理解和掌握程度。

教学延伸：- 将双星模型问题与其他数学概念和应用进行关联，如图形、函数等。

- 引导学生进行更复杂的双星模型问题的研究和探索。

- 鼓励学生参加数学竞赛或挑战，提高他们的问题解决能力和数学思维水平。

第26讲 双星、多星模型1．（重庆高考）冥王星与其附近的另一星体卡戎可视为双星系统．质量比约为7：1，同时绕它们连线上某点O 做匀速圆周运动．由此可知，冥王星绕O 点运动的（ ）A ．轨道半径约为卡戎的17B ．角速度大小约为卡戎的17 C ．线速度大小约为卡戎的7倍D ．向心力大小约为卡戎的7倍一.知识回顾1．双星模型 (1)两颗星体绕公共圆心转动，如图1所示。

(2)特点①各自所需的向心力由彼此间的万有引力相互提供，即Gm 1m 2L2＝m 1ω21r 1， Gm 1m 2L2＝m 2ω22r 2。

②两颗星的周期及角速度都相同，即T 1＝T 2，ω1＝ω2。

③两颗星的轨道半径与它们之间的距离关系为：r 1＋r 2＝L 。

④两颗星到轨道圆心的距离r 1、r 2与星体质量成反比，即m 1m 2＝r 2r 1。

⑤双星的运动周期T ＝2πL 3Gm 1＋m 2。

⑥双星的总质量m 1＋m 2＝4π2L 3T 2G。

2．三星模型(1)三星系统绕共同圆心在同一平面内做圆周运动时比较稳定，三颗星的质量一般不同，其轨道如图2所示。

每颗星体做匀速圆周运动所需的向心力由其他星体对该星体的万有引力的合力提供。

(2)特点：对于这种稳定的轨道，除中央星体外(如果有)，每颗星体转动的方向相同，运行的角速度、周期相同。

(3)理想情况下，它们的位置具有对称性，下面介绍两种特殊的对称轨道。

①三颗星位于同一直线上，两颗质量均为m 的环绕星围绕中央星在同一半径为R 的圆形轨道上运行(如图3甲所示)。

②三颗质量均为m 的星体位于等边三角形的三个顶点上(如图3乙所示)。

3.四星模型：(1)如图所示，四颗质量相等的行星位于正方形的四个顶点上，沿外接于正方形的圆轨道做匀速圆周运动。

Gm 2L 2×2×cos 45°＋Gm 22L 2＝ma ，其中r ＝22 L 。

四颗行星转动的方向相同，周期、角速度、线速度的大小相等。

双星、三星问题探究史亚东教学分析:天体物理中的双星，三星，四星，多星系统是自然的天文现象，天体之间的相互作用遵循万有引力的规律,他们的运动规律也同样遵循开普勒行星运动的三条基本规律。

双星、三星系统的等效质量的计算，运行周期的计算等都是以万有引力提供向心力为出发点的。

双星系统的引力作用遵循牛顿第三定律：F F ='，作用力的方向在双星间的连线上，角速度相等,ωωω==21。

三维目标：知识与技能1、了解双星、三星模型.2、理解双星、三星模型的特点及其运动规律。

3、会用万有引力定律及相关公式解决简单问题。

过程与方法1、 通过双星、三星动画模型的演示，让学生对双星、三星模型有直观的认识。

2、 通过对双星三星问题的处理，加强学生运用万有引力定律处理天体运动问题的思路和方法。

情感态度与价值观通过双星、三星问题的学习活动，体会科学方法对人类认识自然的重要作用，体会万有引力定律对人类探索和认识未知世界的作用。

教学重点：1、 双星、三星模型的基本特点。

2、 双星、三星模型的分析与求解。

教学难点：双星、三星模型的分析与求解.教学方法:引导、讨论、归纳教学过程：复习导入：请同学们回顾处理天体问题的两天思路。

第一条：忽略天体自转的前提下，在天体表面附近的物体受到的重力近似等于万有引力. 第二条:环绕天体或者卫星绕中心天体公转的向心力来源于中心天体对环绕天体的万有引力.宇宙中有这样质量相当的两个恒星,地位相同，两颗恒星相互绕着两者连线上某固定点旋转的现象，叫双星。

推进新课：展示双星模型让学生观察，并思考以下问题： (1）两恒星的角速度、周期有什么关系？（2)两恒星圆周运动的向心力由谁提供？二者有什么关系？（3）两恒星间的距离和二者的轨道半径是否相同?尝试找出对应的轨道半径与两者间距离的关系？ 讨论回答：（1）两星具有相同的旋转周期T , 相同的角速度w ；（2）靠它们间的相互吸引力作为向心力，所以它们做圆周运动的向心力相等; (3)两星轨道半径之和等于两星间的距离；r 1＋r 2＝L 。

物理建模系列(八) 天体运行中的“两种常见模型”1．双星模型 (1)模型构建在天体运动中，将两颗彼此相距较近，且在相互之间万有引力作用下绕两者连线上的某点做周期相同的匀速圆周运动的行星称为双星．(2)模型条件①两颗星彼此相距较近．②两颗星靠相互之间的万有引力做匀速圆周运动． ③两颗星绕同一圆心做圆周运动． (3)模型特点①“向心力等大反向”——两颗星做匀速圆周运动的向心力由它们之间的万有引力提供，故F 1＝F 2，且方向相反，分别作用在两颗行星上，是一对作用力和反作用力．②“周期、角速度相同”——两颗行星做匀速圆周运动的周期、角速度相等． ③“半径反比”——圆心在两颗行星的连线上，且r 1＋r 2＝L ，两颗行星做匀速圆周运动的半径与行星的质量成反比．2．三星模型 系统三星系统(正三角形排列)三星系统(直线等间距排列)图示向心力的来源另外两星球对其万有引力的合力另外两星球对其万有引力的合力例 (2018·河北定州中学摸底)双星系统中两个星球A 、B 的质量都是m ，相距L ，它们正围绕两者连线上某一点做匀速圆周运动．实际观测该系统的周期T 要小于按照力学理论计算出的周期理论值T 0，且TT 0＝k (k <1)，于是有人猜测这可能是受到了一颗未发现的星球C的影响，并认为C 位于A 、B 的连线正中间，相对A 、B 静止，则A 、B 组成的双星系统周期理论值T 0及C 的质量分别为( )A ．2π L 22Gm ，1＋k 24k m B ．2π L 32Gm ，1－k 24k m C ．2π2Gm L 3，1＋k 24km D ．2πL 32Gm ，1－k 24k2m 【解析】 由题意知，A 、B 的运动周期相同，设轨道半径分别为r 1、r 2，对A 有，Gm 2L2＝m ⎝⎛⎭⎫2πT 02r 1，对B 有，Gm 2L2＝m ⎝⎛⎭⎫2πT 02r 2，且r 1＋r 2＝L ，解得T 0＝2π L 32Gm；有C 存在时，设C 的质量为M ，A 、B 与C 之间的距离r ′1＝r ′2＝L 2，则Gm 2L 2＋GMm r ′21＝m ⎝⎛⎭⎫2πT 2r 1，Gm 2L 2＋GMm r ′22＝m ⎝⎛⎭⎫2πT 2r 2，解得T ＝2π L 32G (m ＋4M )，TT 0＝mm ＋4M＝k 得M ＝1－k 24k 2m .【答案】 D解答双星问题应注意“两等”“两不等”(1)“两等”①它们的角速度相等．②双星做匀速圆周运动的向心力由它们之间的万有引力提供，即它们受到的向心力大小总是相等的．(2)“两不等”①双星做匀速圆周运动的圆心是它们连线上的一点，所以双星做匀速圆周运动的半径与双星间的距离是不相等的，它们的轨道半径之和才等于它们间的距离．②由m 1ω2r 1＝m 2ω2r 2知由于m 1与m 2一般不相等，故r 1与r 2一般也不相等.[高考真题]1．(2016·课标卷Ⅲ，14)关于行星运动的规律，下列说法符合史实的是( ) A ．开普勒在牛顿定律的基础上，导出了行星运动的规律 B ．开普勒在天文观测数据的基础上，总结出了行星运动的规律C ．开普勒总结出了行星运动的规律，找出了行星按照这些规律运动的原因D ．开普勒总结出了行星运动的规律，发现了万有引力定律【解析】 开普勒在天文观测数据的基础上，总结出了开普勒天体运动三定律，找出了行星运动的规律，而牛顿发现了万有引力定律，A 、C 、D 错误，B 正确．【答案】 B2．(2014·课标卷Ⅱ，18)假设地球可视为质量均匀分布的球体．已知地球表面重力加速度在两极的大小为g 0；在赤道的大小为g ；地球自转的周期为T ；引力常量为G .地球的密度为( )A.3πGT 2g 0－gg 0 B ．3πGT 2g 0g 0－gC.3πGT2 D ．3πGT 2g 0g【解析】 由万有引力定律可知：在两极处G Mm R 2＝mg 0，在赤道上：G Mm R 2＝mg ＋m (2πT )2R ，地球的质量：M ＝43πR 3ρ，联立三式可得：ρ＝3πGT 2g 0g 0－g，选项B 正确．【答案】 B3．(2015·课标卷Ⅱ，16)由于卫星的发射场不在赤道上，同步卫星发射后需要从转移轨道经过调整再进入地球同步轨道．当卫星在转移轨道上飞经赤道上空时，发动机点火，给卫星一附加速度，使卫星沿同步轨道运行．已知同步卫星的环绕速度约为3.1×103 m/s ，某次发射卫星飞经赤道上空时的速度为1.55×103 m/s ，此时卫星的高度与同步轨道的高度相同，转移轨道和同步轨道的夹角为30°，如图所示，发动机给卫星的附加速度的方向和大小约为( )A ．西偏北方向，1.9×103 m/sB ．东偏南方向，1.9×103 m/sC ．西偏北方向，2.7×103 m/sD ．东偏南方向，2.7×103 m/s【解析】 附加速度Δv 与卫星飞经赤道上空时速度v 2及同步卫星的环绕速度v 1的矢量关系如图所示．由余弦定理可知，Δv ＝v 21＋v 22－2v 1v 2cos 30°≈1.9×103 m/s ，方向东偏南方向，故B 正确，A 、C 、D 错误．【答案】 B[名校模拟]4．(2018·山东临沂高三上学期期中)据报道，2020年前我国将发射8颗海洋系列卫星，包括2颗海洋动力环境卫星和2颗海陆雷达卫星(这4颗卫星均绕地球做匀速圆周运动)，以加强对黄岩岛、钓鱼岛及西沙群岛全部岛屿附近海域的监测．设海陆雷达卫星的轨道半径是海洋动力环境卫星的n 倍，下列说法正确的是( )A ．在相同时间内，海陆雷达卫星到地心的连线扫过的面积与海洋动力环境卫星到地心的连线扫过的面积相等B ．海陆雷达卫星做匀速圆周运动的半径的三次方与周期的平方之比等于海洋动力环境卫星做匀速圆周运动的半径的三次方与周期的平方之比C ．海陆雷达卫星与海洋动力环境卫星角速度之比为n 32∶1D ．海陆雷达卫星与海洋动力环境卫星周期之比为1∶n 32【解析】 由于轨道半径不同，相同时间内扫过的面积不相等，A 错；由开普勒第三定律r 3T2＝k 可知，B 项正确；由ω＝GM r 3∝r －32得，ω1∶ω2＝n －32∶1，由T ＝2πr 3GM得，T 1∶T 2＝1∶n －32，C 、D 均错．【答案】 B5．(2018·山东济南一中上学期期中)在未来的“星际穿越”中，某航天员降落在一颗不知名的行星表面上．该航天员从高h ＝L 处以初速度v 0水平抛出一个小球，小球落到星球表面时，与抛出点的距离是5L ，已知该星球的半径为R ，引力常量为G ，则下列说法正确的是( )A ．该星球的质量M ＝v 20R22GLB ．该星球的质量M ＝2v 20R25GLC ．该星球的第一宇宙速度v ＝v 0 R 2LD ．该星球的第一宇宙速度v ＝v 0R L【解析】 在该星球表面处：mg ＝GMm R 2，g ＝GM R 2，x ＝v 0t ，y ＝12gt 2＝L ，t ＝2Lg，由5L ＝x 2＋y 2，得g ＝v 202L ，M ＝v 20R 22GL，该星球的第一宇宙速度v ＝gR ＝v 0R2L，故A 、C 正确．【答案】 AC 6.(2018·山东潍坊高三上学期期中)2017年8月16日凌晨，中国量子卫星“墨子”在酒泉卫星发射中心成功发射，目前“墨子”已进入离地面高度为h 的极地预定轨道(轨道可视为圆轨道)，如图所示．若“墨子”从北纬30°的正上方按图示方向第一次运行至南纬60°正上方，所用时间为t ，已知地球半径为R ，地球表面的重力加速度为g ，引力常量为G ，忽略地球自转，由以上条件可知( )A ．地球的质量为gRGB ．卫星运行的角速度为π2tC ．卫星运行的线速度为πR2tD ．卫星运行的线速度为π(R ＋h )2t【解析】 在地球表面Mg ＝GMm R 2，M ＝gR 2G ，A 错；第一次运行至南纬60°历时t ＝T4，而T ＝2πω，所以ω＝π2t ，B 对；v ＝ω(R ＋h )＝π(R ＋h )2t，C 错，D 对．【答案】 BD课时作业(十三) [基础小题练]1．(2018·华中师大第一附中高三上学期期中)已知甲、乙两行星的半径之比为2∶1，环绕甲、乙两行星表面运行的两卫星周期之比为4∶1，则下列结论中正确的是( )A ．甲、乙两行星表面卫星的动能之比为1∶4B ．甲、乙两行星表面卫星的角速度之比为1∶4C ．甲、乙两行星的质量之比为1∶2D ．甲、乙两行星的第一宇宙速度之比为2∶1 【解析】 由GMm r 2＝mrω2＝m v 2r 得ω＝GMr 3，v ＝ GM r ，E k ＝12m v 2， T ＝2πω＝2πr 3GM，代入数据得M 甲∶M 乙＝1∶2，ω甲∶ω乙＝1∶4，v 甲∶v 乙＝1∶2，卫星质量关系不知，不能比较动能大小．【答案】 BC2．天文学家新发现了太阳系外的一颗行星，这颗行星的体积是地球的a 倍，质量是地球的b 倍．已知某一近地卫星绕地球运动的周期约为T ，引力常量为G ，则该行星的平均密度为( )A.4πGb 2T 2a 2 B ．4πa GT 2bC.3πb GT 2aD ．4πbGT 2a【解析】 对于近地卫星，设其质量为m ，地球的质量为M ，半径为R ，则根据万有引力提供向心力有，G Mm R 2＝m ⎝⎛⎭⎫2πT 2R ，得地球的质量M ＝4π2R 3GT 2，地球的密度为ρ＝M 43πR 3＝3πGT2；已知行星的体积是地球的a 倍，质量是地球的b 倍，结合密度公式ρ＝mV ，得该行星的平均密度是地球的b a 倍，所以该行星的平均密度为3πbGT 2a，故C 正确．【答案】 C3．双星运动是产生引力波的来源之一，假设宇宙中有一双星系统由a 、b 两颗星体组成，这两颗星体绕它们连线的某一点在万有引力作用下做匀速圆周运动，测得两星体的轨道半径之和为l 1，轨道半径之差为l 2，a 星体轨道半径大于b 星体轨道半径，a 星体的质量为m 1，引力常量为G ，则b 星体的周期为( )A.2π2l 21(l 1－l 2)Gm 1B ．2π2l 21(l 1＋l 2)Gm 1C.2π2l 21(l 1－l 2)Gm 1(l 1＋l 2)D ．2π2l 21(l 1＋l 2)Gm 1(l 1－l 2)【解析】 设a 星体运动的轨道半径为r 1，b 星体运动的轨道半径为r 2，则r 1＋r 2＝l 1，r 1－r 2＝l 2，解得r 1＝l 1＋l 22，r 2＝l 1－l 22，双星系统根据Gm 1m 2l 21＝m 1⎝⎛⎭⎫2πT 2r 1，Gm 1m 2l 21＝m 2⎝⎛⎭⎫2πT 2r 2，得m 1m 2＝r 2r 1，即双星系统中星体质量与轨道半径成反比，得b 星体的质量m 2＝r 1m 1r 2＝(l 1＋l 2)m 1l 1－l 2，a 、b 两星体运动周期相同，对a 星体有Gm 1m 2l 21＝m 1⎝⎛⎭⎫2πT 2r 1，解得T ＝2π2l 21(l 1－l 2)Gm 1，A 选项正确．【答案】 A4．(2018·江苏泰州高三上学期期中)2016年10月19日3时31分，神舟十一号载人飞船与天宫二号空间实验室成功实现自动交会对接，此时天宫二号绕地飞行一圈时间为92.5 min ，而地球同步卫星绕地球一圈时间为24 h ，根据此两组数据我们能求出的是( )A ．天宫二号与地球同步卫星受到的地球引力之比B ．天宫二号与地球同步卫星的离地高度之比C ．天宫二号与地球同步卫星的线速度之比D ．天宫二号与地球同步卫星的加速度之比【解析】 由F ＝GMm r 2及GMm r 2＝mrω2＝m v 2r ＝ma 可知，ω＝GMr 3，T ＝2π r 3GM，a ＝GMr2，v ＝GMr，已知周期关系可确定半径关系，进而确定线速度关系，加速度关系，但由于不知天宫二号和同步卫星的质量关系，故所受地球引力关系不确定，地球半径未知，所以离地高度关系不确定，C 、D 正确．【答案】 CD5．(2018·安徽师大附中高三上学期期中)登上火星是人类的梦想，“嫦娥之父”欧阳自远透露：中国计划于2020年登陆火星．地球和火星的公转视为匀速圆周运动．忽略行星自转影响，火星和地球相比( )行星 半径/m 质量/kg 公转轨道半径/m地球 6.4×106 6.0×1024 1.5×1011 火星3.4×1066.4×10232.3×1011A.火星的“第一宇宙速度”约为地球的第一宇宙速度的0.45倍 B ．火星的“第一宇宙速度”约为地球的第一宇宙速度的1.4倍 C ．火星公转的向心加速度约为地球公转的向心加速度的0.43倍 D ．火星公转的向心加速度约为地球公转的向心加速度的0.28倍 【解析】 根据第一宇宙速度公式v ＝ GMR (M 指中心天体太阳的质量)，v 火v 地＝R 地R 火＝6.4×1063.4×106＝1.4 ，故A 错误，B 正确．根据向心加速度公式a ＝GMr 2(M 指中心天体太阳的质量)，a 火a 地＝r 2地r 2火＝(1.5×10112.3×1011)2＝0.43，故C 正确，D 错误．【答案】 BC6.(2018·山东泰安高三上学期期中)发射地球同步卫星时，先将卫星发射至近地圆轨道1，然后经点火，使其沿椭圆轨道2运行，最后再次点火，将卫星送入同步椭圆轨道3.轨道1、2相切于Q 点，轨道2、3相切于P 点．轨道3到地面的高度为h ，地球的半径为R ，地球表面的重力加速度为g .以下说法正确的是( )A ．卫星在轨道3上的机械能大于在轨道1上的机械能B ．卫星在轨道3上的周期小于在轨道2上的周期C ．卫星在轨道2上经过Q 点时的速度小于它在轨道3上经过P 时的速度D ．卫星在轨道3上的线速度为v ＝Rg R ＋h【解析】 卫星经历两次点火加速才转移至同步轨道3，在轨道3上的机械能肯定大于轨道1上的机械能，A 对；由T ＝2πr 3GM可知，B 错；由于v ＝GMr，所以v 1>v 3，又轨道2上Q 点离心运动，由v Q >v 1可知v Q >v 3，所以v Q >v P ，C 错；将r ＝R ＋h ，GM ＝gR 2，代入v ＝GMr得v ＝R gR ＋h，D 对． 【答案】 AD[创新导向练]7．巧思妙想——以“苹果”为话题考查天体运行规律已知地球的半径为6.4×106 m ，地球自转的角速度为7.27×10－5rad/s ，地球表面的重力加速度为9.8 m/s 2，在地球表面发射卫星的第一宇宙速度为7.9×103 m/s ，第三宇宙速度为16.7×103 m/s ，月地中心间距离为3.84×108 m ．假设地球上有一颗苹果树长到月球那么高，则当苹果脱离苹果树后，请根据此时苹果线速度的计算，判断苹果将不会( )A ．落回地面B ．成为地球的“苹果月亮”C ．成为地球的同步“苹果卫星”D ．飞向茫茫宇宙【解析】 地球自转的角速度为7.27×10－5rad/s ，月球到地球中心的距离为3.84×108 m ，地球上有一棵苹果树长到了接近月球那么高，根据v ＝rω得：苹果的线速度为v ＝2.8×104 m/s ，第三宇宙速度为16.7×103 m/s ，由于苹果的线速度大于第三宇宙速度，所以苹果脱离苹果树后，将脱离太阳系的束缚，飞向茫茫宇宙，故A 、B 、C 正确．【答案】 ABC8．科学探索——以“一箭20星”为背景考查卫星运行参数月球和地球的质量之比为a ∶1，半径之比为b ∶1，将一单摆由地球带到月球，将摆球从与地球表面相同高度处由静止释放(释放点高度低于悬点高度)，释放时摆线与竖直方向的夹角相同，当摆球运动到最低点时，在月球上和地球上摆线对摆球的拉力之比为( )A.b 2a B ．a b 2C.a 2bD ．b a2【解析】 设重力加速度大小为g ，摆球释放的高度为h ，摆球运动到最低点有mgh ＝12m v 2，摆球在最低点有F －mg ＝m v 2l ，得F ＝mg ＋2mghl，F 与g 成正比．在星球表面上有GMm R 2＝mg ，得g ＝GM R 2，故摆球在月球和地球上受到的拉力之比为ab 2，B 选项正确． 【答案】 B9．军事科技——以导弹拦截为背景考查万有引力定律知识2016年1月27日，我国在境内再次成功地进行了陆基中段反导拦截技术试验，中段是指弹道导弹在大气层外空间依靠惯性飞行的一段．如图所示，一枚蓝军弹道导弹从地面上A 点发射升空，目标是攻击红军基地B 点，导弹升空后，红军反导预警系统立刻发现目标，从C 点发射拦截导弹，并在弹道导弹飞行中段的最高点D 将其击毁．下列说法中正确的是( )A ．图中E 到D 过程，弹道导弹机械能不断增大B ．图中E 到D 过程，弹道导弹的加速度不断减小C ．弹道导弹在大气层外运动轨迹是以地心为焦点的椭圆D ．弹道导弹飞行至D 点时速度大于7.9 km/s【解析】 图中E 到D 过程， 导弹在大气层外空间依靠惯性飞行，没有空气阻力，机械能不变，远离地球，轨道变大，速度减小，万有引力减小，所以加速度减小，在万有引力作用下，运动轨迹是以地心为焦点的椭圆，A 错误，B 、C 正确；第一宇宙速度是近地卫星的环绕速度，而D 点在大气层外部，所以轨道要大于近地卫星轨道，运行速度要小于第一宇宙速度，D 错误；故选B 、C.【答案】 BC10．探测火星——以火星探测为背景考查星体运行规律随着人类航天事业的进步，太空探测越来越向深空发展，火星正在成为全球航天界的“宠儿”．我国计划于2020年发射火星探测器，一步实现绕、落、巡工程目标．假设某宇航员登上了火星，在其表面以初速度v 竖直上抛一小球(小球仅受火星的引力作用)，小球上升的最大高度为h ，火星的直径为d ，引力常量为G ，则( )A ．火星的第一宇宙速度为v d hB ．火星的密度为3v 24πGhdC ．火星的质量为v 2d 22GhD ．火星的“近火卫星”运行周期为2πvd h【解析】 在火星表面竖直上抛的小球做匀减速直线运动，设火星表面的重力加速度为g ，第一宇宙速度为v 0，火星的自转周期为T ，则2gh ＝v 2，得g ＝v 22h，在火星表面的物体的重力等于万有引力，也是在火星表面附近做圆周运动的向心力，mg ＝G Mm r 2＝m (2πT )2r ，又r＝d 2，M ＝43πr 3·ρ，得：v 0＝v d 4h ，M ＝v 2d 28Gh ，ρ＝3v 24πGhd，T ＝2πv dh2，故选B. 【答案】 B[综合提升练]11.(2018·山东淄博一中高三上学期期中)如图所示，火箭载着宇宙探测器飞向某行星，火箭内平台上还放有测试仪器．火箭从地面起飞时，以加速度g 02竖直向上做匀加速直线运动(g 0为地面附近的重力加速度)，已知地球半径为R 0.(1)到某一高度时，测试仪器对平台的压力是起飞前的1718，求此时火箭离地面的高度h ；(2)探测器与箭体分离后，进入行星表面附近的预定轨道，进行一系列科学实验和测量，若测得探测器环绕该行星运动的周期为T 0，试问：该行星的平均密度为多少？(假定行星为球体，且已知万有引力恒量为G )【解析】 (1)火箭起飞前有：N 1＝mg 0 火箭起飞后有：N 2－mg ＝mg 02 且有N 1N 2＝1718GMmR 2＝mg 0 GMm(R ＋h )2＝mg联立以上各式解得h ＝R2.(2)设行星半径为r ，质量为M ，密度为ρ，则 GM 1m r 2＝mr ⎝⎛⎭⎫2πT 02由ρ＝M 1V ，V ＝43πr 3得ρ＝3πGT 20. 【答案】 (1)R 2 (2)3πGT 2012．中国计划在2017年实现返回式月球软着陆器对月球进行科学探测，宇航员在月球上着陆后，自高h 处以初速度v 0水平抛出一小球，测出水平射程为L (这时月球表面可以看成是平坦的)，已知月球半径为R ，万有引力常量为G .求：(1)月球表面处的重力加速度及月球的质量M 月；(2)如果要在月球上发射一颗绕月球运行的卫星，所需的最小发射速度为多大？(3)当着陆器绕距月球表面高H 的轨道上运动时，着陆器环绕月球运动的周期是多少？【解析】 (1)设月球表面的重力加速度为g ，由平抛运动规律有h ＝12gt 2① L ＝v 0·t ②得g ＝2h v 20L 2③ 着陆器在月球表面所受的万有引力等于重力，GM 月m R 2＝mg ④得M 月＝2h v 20R 2GL 2⑤ (2)卫星绕月球表面运行，有GM 月m ′R 2＝m ′v 2R ⑥联立⑤⑥得v ＝v 0L2hR ⑦ (3)由牛顿第二定律有G M 月m (R ＋H )2＝m (R ＋H )4π2T 2⑧联立⑤⑧得T ＝2π2L 2(R ＋H )3hR 2v 20. 【答案】 (1)2h v 20L 2 2h v 20R 2GL 2 (2)v 0L 2hR (3)2π2L 2(R ＋H )3hR 2v 20。