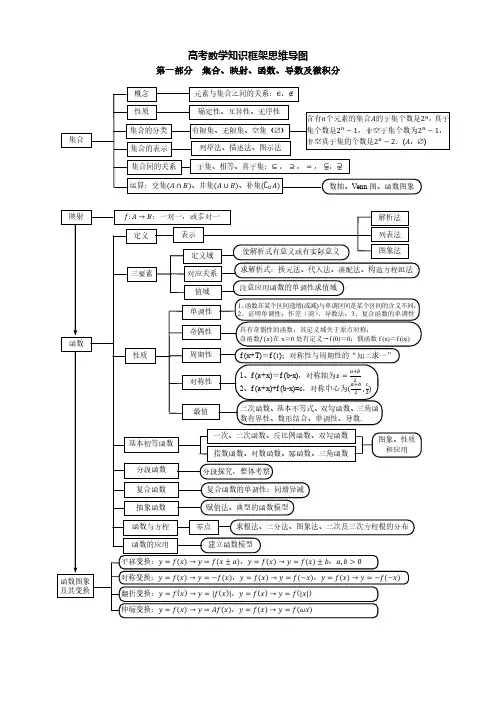
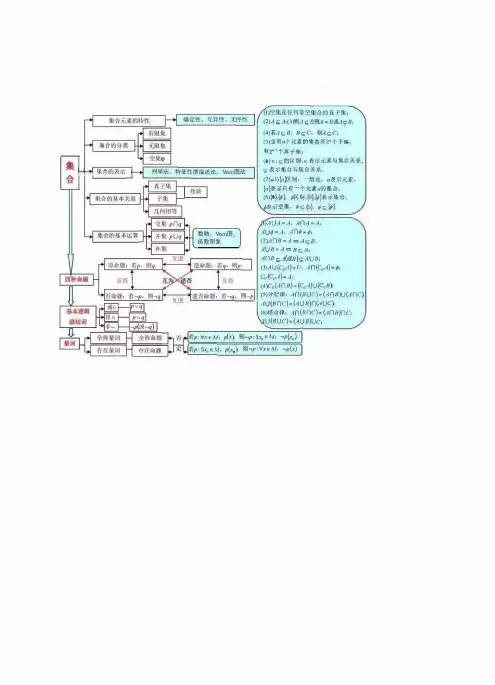
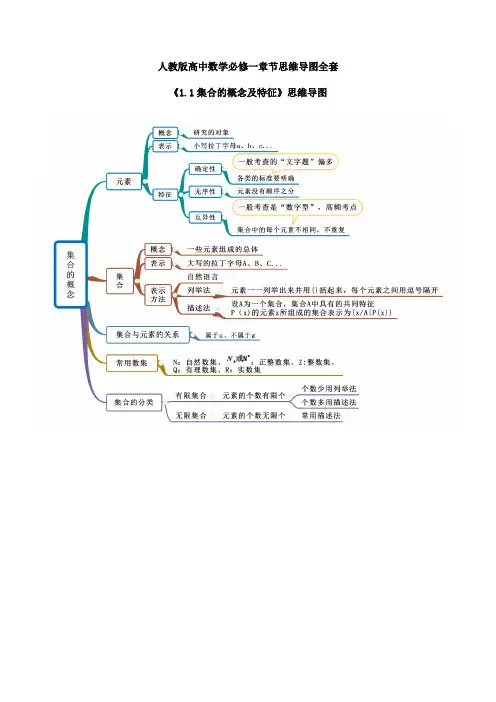
最新人教版(含苏教版)高中数学考试重点整理(全套思维导图)

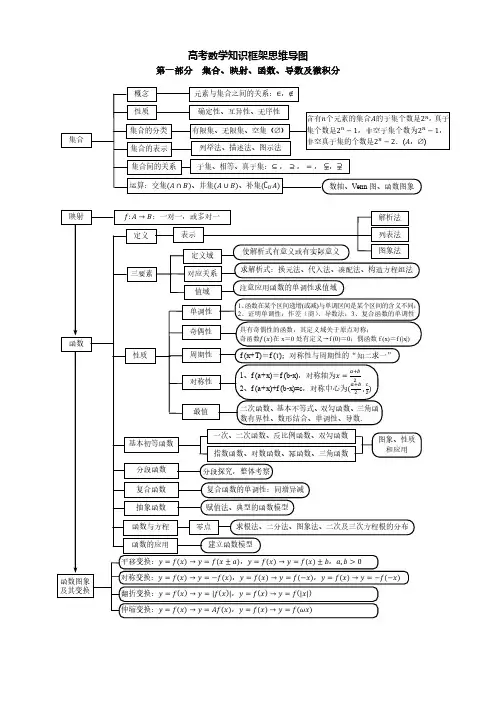
高三数学新教材知识点归纳总结一、函数与方程1. 函数的基本概念函数是一个或多个自变量和因变量之间的对应关系，通常表示为y=f(x)。

函数的定义域、值域和图像为常见的函数性质。

2. 基本初等函数包括常数函数、幂函数、指数函数、对数函数、三角函数等。

学习基本初等函数的性质和图像，掌握其函数图像的平移、翻折、伸缩等变换规律。

3. 方程与不等式解方程和不等式的基本方法，包括二次方程、一次方程、分式方程等。

通过应用数学工具解决实际问题。

二、数列与数学归纳法1. 数列的概念与表示数列是按照一定规律排列的一组数字。

常见的数列有等差数列和等比数列。

2. 数列的通项与前n项和掌握求等差数列和等比数列的通项公式和前n项和公式。

3. 数学归纳法数学归纳法是证明数学命题的常用方法，通过证明基准情形成立和归纳假设成立，推导出待证情形成立。

三、三角函数与解三角形1. 三角函数的基本概念与性质掌握正弦函数、余弦函数、正切函数等的定义和基本性质，能够利用三角函数解决实际问题。

2. 特殊角与通角熟练掌握特殊角的计算和通角的概念，能够灵活运用它们解决问题。

3. 解三角形熟练掌握利用三角函数解三角形的基本思路和方法，包括解任意三角形和解直角三角形。

四、立体几何1. 空间直角坐标系与向量了解空间直角坐标系的定义和性质，熟悉坐标表示点、直线和平面的方法。

掌握向量的定义、加法和数量积的运算。

2. 空间几何体的表示能够根据给定条件，利用空间直角坐标系表示球、圆锥、椭球等几何体。

3. 空间几何体的性质与计算熟悉立体几何体的性质和计算方法，如计算体积、表面积等。

五、导数与微分应用1. 导数的概念与计算掌握导数的定义和基本性质，能够利用求导法则计算导数。

2. 函数的求导与应用了解函数的增减性、极值和曲线的凹凸性等，能够利用导数求解函数相关问题。

3. 微分与线性近似掌握微分的概念与计算方法，能够利用微分求解近似问题，如线性近似、最优化问题等。

六、概率与统计1. 随机事件与概率了解随机事件、样本空间和事件概率的基本概念，掌握概率的计算方法。

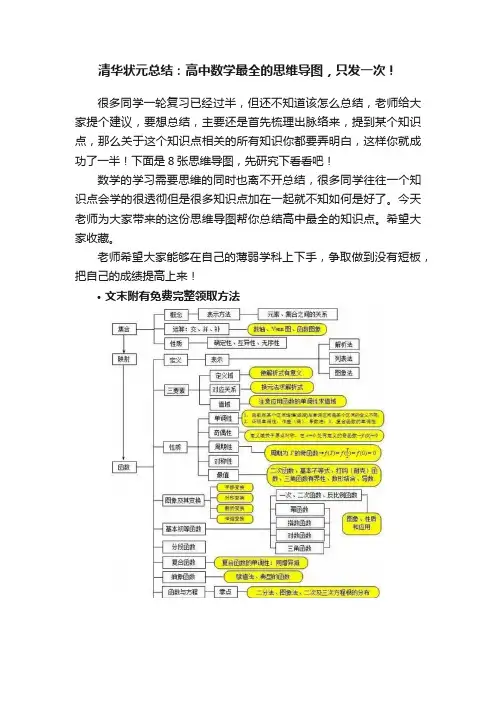
清华状元总结：高中数学最全的思维导图，只发一次！
很多同学一轮复习已经过半，但还不知道该怎么总结，老师给大家提个建议，要想总结，主要还是首先梳理出脉络来，提到某个知识点，那么关于这个知识点相关的所有知识你都要弄明白，这样你就成功了一半！下面是8张思维导图，先研究下看看吧！
数学的学习需要思维的同时也离不开总结，很多同学往往一个知识点会学的很透彻但是很多知识点加在一起就不知如何是好了。

今天老师为大家带来的这份思维导图帮你总结高中最全的知识点。

希望大家收藏。

老师希望大家能够在自己的薄弱学科上下手，争取做到没有短板，把自己的成绩提高上来！
•文末附有免费完整领取方法。

高中数学知识点全总结苏教一、代数表达式与方程1. 代数基础代数表达式是由数字、字母和运算符组成的式子。

例如：3x^2 + 2x - 1。

字母代表变量，数字称为系数。

2. 单项式与多项式单项式是只有一个乘法运算的代数式，如：5x^3。

多项式是由若干个单项式相加或相减组成的代数式，如：2x^2 + 3x - 5。

3. 同类项与合并同类项同类项是指变量的指数相同的项，如：3x^2 和 -2x^2。

合并同类项即将同类项的系数相加。

4. 一元一次方程一元一次方程是只含有一个变量，且变量的最高次数为1的方程，如：3x + 2 = 0。

5. 二元一次方程组二元一次方程组是由两个含有两个变量的一次方程组成的方程组，如：x + y = 3 和 2x - y = 1。

6. 一元二次方程一元二次方程是只含有一个变量，且变量的最高次数为2的方程，标准形式为：ax^2 + bx + c = 0。

二、函数1. 函数的概念函数是将一个集合中的每个数（自变量）映射到另一个集合中的一个唯一确定的数（因变量）的关系。

2. 函数的表示方法函数通常用f(x)表示，其中x是自变量，f(x)是因变量。

3. 函数的性质函数具有单调性、奇偶性、周期性等基本性质。

4. 基本初等函数包括幂函数、指数函数、对数函数、三角函数等。

5. 函数的图像函数的图像是函数关系的几何表示，通过坐标系可以直观地展示函数的性质。

6. 函数的应用函数在实际问题中有着广泛的应用，如物理中的运动规律、经济学中的成本收益分析等。

三、立体几何1. 空间几何体包括点、线、面、体等基本元素，以及由这些元素构成的多面体、旋转体等。

2. 空间直线与平面空间直线是一维的无限延伸，平面是二维的无限延展。

直线与平面的位置关系有平行和相交两种。

3. 立体图形的性质包括体积、表面积的计算，以及棱柱、棱锥、圆柱、圆锥、球等常见几何体的性质。

4. 空间向量空间向量是具有大小和方向的量，可以用来表示空间中的位置关系和直线与平面的方程。

一般地我们把研究对象统称为元素,把一些元素组成的总体叫同向可加性我们把只含有一个未知数，并且未知求出相应的一元二次方程的根利用二次函数的图像与X轴的交点确定一元二次不等式的解集如果积xy等于定值P，那么当x=y时，和x+y有最小值如果积xy等于定值S，那么当x=y时，积xy有最大值积定和最小，和定积最大设A、B是非空的实数集，如果按照某个确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数y和它对应，那么就称f：A→B为从集合A到集合B的一个函数,是幂函数的底数，幂函数的系数是1， 比如2不是幂函数一次函数：二次函数：反比例函数：第五章 三角函数角的定义平面内一条射线绕着它的端点旋转所成的图形叫做角角的分类按照旋转方向正角负角零角按照终边位置第一象限角第二象限角第三象限角第四象限角度量角的两种制度角度制弧度制诱导公式公式一：设α为任意角，终边相同的角的同一三角函数的值相等sin（2kπ+α）=sinα k∈zcos（2kπ+α）=cosα k∈ztan（2kπ+α）=tanα k∈z 公式二:设α为任意角，π+α的三角函数值与α的三角函数值之间的关系sin（π+α）=－sinα k∈zcos（π+α）=－cosα k∈ztan（π+α）=tanα k∈z 公式三：任意角α与 -α的三角函数值之间的关系sin（－α）=－sinαcos（－α）=cosαtan（－α）=－tanα弧长与角的换算1°=π/180°，1rad=180°/π弧长公式L=n× π× r/180，L=α× r扇形面积公式S=LR/2三角函数的定义域、值域y＝sinαy＝cosαy＝tanα三角函数的单调性正弦函数余弦函数一周是360度，也是2π弧度，即360°=2π.（n是圆心角度数，r是半径，L是圆心角弧长，α是圆心角度数）（R是扇形半径，L是扇形对应的弧长）定义域是R，值域[-1,1]定义域是R，值域[-1,1]定义域是α≠kπ+π/2区间是(kπ-π/2,kπ+π/2)值域是Ry=sinx在[2kπ-π/2，2kπ+π/2]，k∈Z，上是增函数；在[2kπ+π/2，2kπ+3π/2]，k∈Z，上是减函数；三角函数y=sin x，它的定义域为全体实数，值域为[-1,1]y=cosx在[2kπ，2kπ+π]，k∈Z，上是减函数；在[2kπ+π，2kπ+2π]，k∈Z，上是增函数；余弦函数的定义域是整个实数集，值域是[-1,1]；余弦函数是周期函数，其最小正周期为2π。

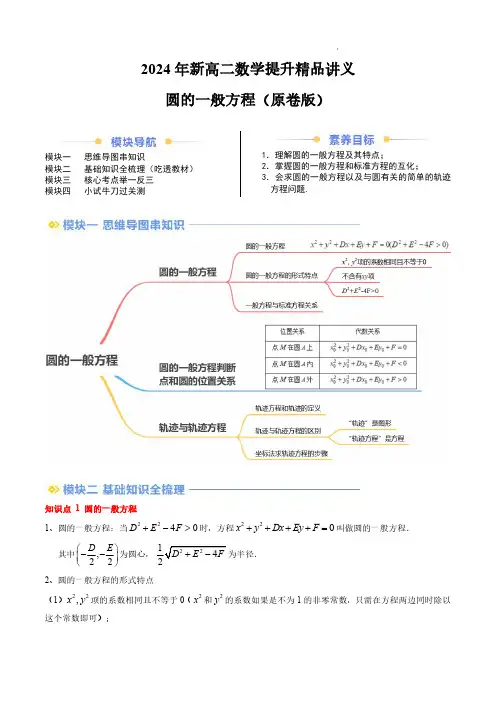
2024年新高二数学提升精品讲义圆的一般方程（原卷版）模块一思维导图串知识模块二基础知识全梳理（吃透教材）模块三核心考点举一反三模块四小试牛刀过关测1．理解圆的一般方程及其特点；2．掌握圆的一般方程和标准方程的互化；3．会求圆的一般方程以及与圆有关的简单的轨迹方程问题.知识点1圆的一般方程1、圆的一般方程：当2240D E F +->时，方程220x y Dx Ey F ++++=叫做圆的一般方程．其中,22D E ⎛⎫-- ⎪⎝⎭为圆心，为半径．2、圆的一般方程的形式特点（1）22,x y 项的系数相同且不等于0（2x 和2y 的系数如果是不为1的非零常数，只需在方程两边同时除以这个常数即可）；（2）不含xy 项；（3）2240D E F +->．3、一般方程与标准方程关系：对方程220x y Dx Ey F ++++=的左边配方，并将常数移项到右边，得22224224D E D E F x y +-⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭，根据圆的标准方程可知：（1）当2240D E F +-=时，方程只有实数解,22D E x y =-=-.它表示一个点,22D E ⎛⎫-- ⎪⎝⎭．（2）当2240D E F +-<时，方程没有实数解，因而它不表示任何图形．（3）当2240D E F +->时，可以看出方程表示以,22D E ⎛⎫-- ⎪⎝⎭为圆心，知识点2圆的一般方程判断点和圆的位置关系已知点()00,M x y ，和圆的一般方程220x y Dx Ey F ++++=（2240D E F +->）则知识点3轨迹与轨迹方程1、轨迹方程和轨迹的定义已知平面上一动点(,)M x y ，点M 的轨迹方程是指点M 的坐标(,)x y 满足的关系式。

轨迹是指点在运动变化过程中形成的图形，在解析几何中，我们常常把图形看作点的轨迹（集合）.2、“轨迹”与“轨迹方程”有区别：（1）“轨迹”是图形，要指出形状、位置、大小（范围）等特征；（2）“轨迹方程”是方程，不仅要给出方程，还要指出变量的取值范围．3、坐标法求轨迹方程的步骤（1）建系：建立适当的平面直角坐标系；（2）设点：用(,)x y 表示轨迹（曲线）上任意一点的M 的坐标；（3）列式：列出关于.x y 的方程；（4）化简：把方程化为最简形式；（5）证明：证明以化简后的方程的解为坐标的点都是曲线上的点．考点一：二元二次方程与圆例1．（23-24高二上·山西吕梁·期末）已知圆22:4650O x y x y +-++=，则圆心O 和半径r 分别为（）A ．()2,3,O r -=B ．()2,3,O r -=C ．()2,3,O r -=D ．()2,3,O r -=【变式1-1】（23-24高二上·福建厦门·期中）若32,1,0,,14a ⎧⎫∈--⎨⎬⎩⎭，则方程2222210x y ax ay a a +++++-=表示的圆的个数为（）A ．1B ．2C ．3D ．4【变式1-2】（23-24高二上·广东江门·期末）方程22210x y x m ++--=表示一个圆，则实数m 的取值范围是（）A ．(),1-∞-B ．()1,-+∞C ．(),2-∞-D ．()2,-+∞【变式1-3】（23-24高二上·安徽马鞍山·月考）（多选）已知方程()()2224232141690x y m x m y m +-++-++=表示一个圆，则实数m 可能的取值为（）A ．－1B ．0C ．12D ．1考点二：求圆的一般方程例2.（23-24高二上·内蒙古·期末）已知圆C 经过点()1,1-和点()1,3B ，且圆心在y 轴上，则圆C的方程为（）A ．()2222x y ++=B ．()22210x y -+=C ．()2222x y +-=D ．()22210x y ++=【变式2-1】（23-24高二上·江苏·假期作业）过坐标原点，且在x 轴和y 轴上的截距分别为2和3的圆的方程为（）A ．22230x y x y +--=B ．22230x y x y ++-=C ．22230x y x y +-+=D ．22230x y x y +++=【变式2-2】（23-24高二下·重庆铜梁·开学考试）已知(2,0)A ，(4,2)B ，O 为原点，则AOB 的外接圆方程为.【变式2-3】（23-24高二上·安徽·月考）已知在ABC 中，AB 边所在直线的方程为360x y --=，AC 边所在直线的方程为20x y --=，AC 边上的中线所在直线的方程为20x y +-=．(1)求C 点的坐标；(2)求ABC 的外接圆方程．考点三：点与圆的位置关系例3.（22-23高二上·天津和平·月考）已知圆C ：22220x y x y +--=，则点(3,1)P 在（）A ．圆外B ．圆上C ．圆内D ．以上情况均有可能【变式3-1】（23-24高二上·内蒙古·期中）若点()2,1在圆220x y x y a +-++=的外部，则a 的取值范围是（）A ．(4,)-+∞B ．1,2⎛⎫-∞ ⎝C ．14,2⎛⎫- ⎪⎝⎭D ．1(,4),2⎛⎫-∞-+∞ ⎪⎝⎭【变式3-2】（23-24高二上·湖北荆门·期末）已知圆C 的方程为222245330x y mx my m m +-++-+=，若点(1,2)m -在圆外，则m 的取值范围是（）A ．(,1)(4,)-∞+∞B ．(1,)+∞C ．(1,4)D ．(4,)+∞【变式3-3】（23-24高二上·全国·课后作业）若点()1,1a a +-在圆22240x y ay +--=的内部，则a 的取值范围是（）.A ．1a >B ．01a <<C ．115a -<<D ．1a <考点四：与圆有关的轨迹问题例4.（23-24高二上·北京·期末）已知点(2,0)B 和点(2,4)C ，直角ABC 以BC 为斜边，求直角顶点A 的轨迹方程.【变式4-1】（23-24高二上·上海青浦·月考）已知两点(5,0)A -，(5,0)B ，动点P 到点A 的距离是它到点B 的距离的3倍，则点P 的轨迹方程是．【变式4-2】（23-24高二上·山东威海·期末）（多选）已知A ，B 是平面内两个定点，且||6AB =，则满足下列条件的动点P 的轨迹为圆的是（）A ．||||6PA PB +=B ．1PA PB ⋅=-C ．||2||PA PB =D ．22||||18PA PB +=【变式4-3】（22-23高二上·云南昆明·期中）已知点(6,0)A ，O 为坐标原点，若动点(,)P x y 满足2OP PA =．(1)试求动点P 的轨迹方程；(2)过点P 作y 轴的垂线，垂足为Q ，试求线段PQ 的中点M 的轨迹方程．考点五：圆过定点问题例5.（23-24高二上·湖北荆州·期末）圆:²²250C x y ax ay ++--=恒过的定点为（）A ．()()2,1,2,1--B ．()()1,2,2,1--C ．()()1,2,1,2--D ．()()2,1,2,1--【变式5-1】（23-24高二上·全国·专题练习）点(),P x y 是直线250x y +-=上任意一点，O 是坐标原点，则以OP 为直径的圆经过定点（A ．()0,0和()1,1B ．()0,0和()2,2C ．()0,0和()1,2D ．()0,0和()2,1【变式5-2】（23-24高二上·全国·专题练习）对任意实数m ，圆2236920x y mx my m +--+-=恒过定点，则定点坐标为．【变式5-3】（23-24高二上·河南信阳·期中）圆2220x y mx y m ++--=恒过的定点是.考点六：与圆有关的实际问题例6.（23-24高二上·河南洛阳·期中）如图，一座圆拱桥，当拱顶离水面2米时，水面宽12米，则当水面下降1米后，水面宽为（）A B C ．米D ．【变式6-1】（23-24高二上·广东佛山·期中）如图是某圆拱形桥一孔圆拱的示意图．圆拱跨度20AB =米，拱高4OP =米，建适时每间隔4米需要用一根支柱支撑，则支柱22A P 的高度为米．（精确到0.01米，参考数据：33 5.744≈）【变式6-2】（23-24高二上·北京丰台·期中）赵州桥，又名安济桥，位于河北省石家庄市赵县的洨河上，距今已有1400多年的历史，是保存最完整的古代单孔敞肩石拱桥，其高超的技术水平和不朽的艺术价值，彰显了中国劳动人民的智慧和力量．2023年以来，中国文旅市场迎来强劲复苏，某地一旅游景点为吸引游客，参照赵州桥的样式在景区兴建圆拱桥，该圆拱桥的圆拱跨度为16m ，拱高为4m ，在该圆拱桥的示意图中建立如图所示的平面直角坐标系．(1)求这座圆拱桥的拱圆的方程；(2)若该景区游船宽10m ，水面以上高3m ，试判断该景区游船能否从桥下通过，并说明理由.(3 1.732)≈一、单选题1．（23-24高二上·陕西汉中·期末）圆222440x y x y +-+-=的圆心和半径分别为（）A ．()1,2,3B ．()1,2,3-C ．()1,2,2-D ．()1,2,3-2．（23-24高二上·四川成都·月考）过三点()()()4,2,1,1,14A B C --,的圆的一般方程为（）A ．227320x y x y ++-+=B ．227320x y x y ++++=C ．227320x y x y +-++=D ．227320x y x y +--+=3．（2024·河北沧州·二模）若点()2,1A 在圆222250x y mx y +--+=（m 为常数）外，则实数m 的取值范围为（）A ．(),2-∞B ．()2,+∞C ．(),2-∞-D ．()2,-+∞4．（23-24高二上·湖北武汉·期中）“4k >”是“方程22(2)50x y kx k y +++-+=表示圆的方程”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5．（23-24高二上·辽宁抚顺·期中）已知圆22224590x y ax ay a +-++-=上所有点都在第二象限，则a 的取值范围（）A ．(),3-∞-B ．(],3-∞-C ．33,2⎡⎤--⎢⎥⎣⎦D ．33,2⎛⎫-- ⎪⎝⎭6．（23-24高二上·四川绵阳·期中）阿波罗尼斯（公元前262年~公元前190年），古希腊人，与阿基米德、欧几里得一起被誉为古希腊三大数学家．阿波罗尼斯研究了众多平面轨迹问题，其中阿波罗尼斯圆是他的论著中的一个著名问题：已知平面上两点A ，B ，则所有满足PA PBλ=（0λ>，且1λ≠）的点P 的轨迹是一个圆．已知平面内的两个相异定点(1,0)P ，(1,0)Q -，动点M 满足MP =，记M 的轨迹为C ，则轨迹C 围成图形的面积是（）A ．2πB ．4πC ．8πD ．16π二、多选题7．（23-24高二上·重庆万州·期中）若()2,1，()4,2，()3,4，()1,m 四点共圆，则m 的值为（）A ．2B C ．12+D ．38．（23-24高二上·河北邢台·222:240C ax ay x a y +-+=，下列结论正确的是（）A ．当0a =时，曲线C 是一条直线B ．当0a ≠时，曲线C 是一个圆C ．当曲线C 是圆时，它的面积的最小值为2πD ．当曲线C 是面积为5π的圆时，1=a 三、填空题9．（23-24高二上·广东茂名·期末）已知圆2264120x y x y +-++=与圆22142140x y x y +--+=，则两圆心之间的距离为.10．（23-24高二上·四川泸州·期末）若圆22:220C x y mx y ++-=被直线210x y ++=平分，则圆C 的半径为．11．（23-24高二上·安徽合肥·期中）已知点()0,5A ，()1,2B -，()3,4C --，()2,D a 四点共圆，则=a .四、解答题12．（23-24高二上·全国·专题练习）已知曲线C ：()()2211480a x a y x ay +++-+=．(1)当a 取何值时，方程表示圆？(2)求证：不论a 为何值，曲线C 必过两定点．13．（23-24高二上·江苏徐州·期末）已知直线12:20,:0l x y l x y ++=+=，直线l 过点()10,4-且与1l 垂直.(1)求直线l 的方程；(2)设l 分别与12,l l 交于点A ，B ，O 为坐标原点，求过三点A ，B ，O 的圆的方程.。

2024年新高二数学提升精品讲义圆的标准方程（原卷版）模块一思维导图串知识模块二基础知识全梳理（吃透教材）模块三核心考点举一反三模块四小试牛刀过关测1．会用定义推导圆的标准方程，并掌握圆的标准方程的特征；2．能根据所给条件求圆的标准方程；3．掌握点与圆的位置关系并能解决相关问题.知识点1圆的定义平面内到定点的距离等于定长的点的集合叫做圆．如图，在平面直角坐标系中，⊙A 的圆心A 的坐标为(,)a b ，半径为r ，(,)M x y 为圆上任意一点，⊙A 就是集合{}P M MA r ==．定义中，定点指的是圆心，定长指的是圆的半径．知识点2圆的标准方程1、圆的标准方程：我们把()()222-+-=x a y b r 称为圆心为(),A a b ，半径长为r 的圆的标准方程．【注意】（1）所谓标准方程，是指方程的形式．圆的标准方程体现了圆的集合性质，突出了圆的几何意义：圆心位置和半径．（2）圆的标准方程的右端20r >，当方程右端小于或等于0时，对应方程不是圆的标准方程．2、圆的标准方程的推导过程（1）建系设点：建立坐标系时，原点在圆心是特殊情况，就一般情况来说，因为A 是定点，设(),A a b ，半径为r ，且设圆上任意一点M 的坐标为(,)x y ．（2）写点集：根据定义，圆就是集合{}P M MA r ==．（3r =．（4）化简方程：将上式两边平方得222()()x a y b r -+-=．3、几种特殊位置的圆的标准方程知识点3点与圆的位置关系1、几何法：点()00,M x y ，圆心(),A a b ，圆的半径r ，设M 与点A 间的距离MA d =，d r >⇔点M 在圆A 外；d r <⇔点M 在圆A 内；d r =⇔点M 在圆A 上．2、代数法：将点()00,M x y 直接代入圆的标准方程()()222-+-=x a y b r 进行判断，即若点()00,M x y 在圆外，则()()22200->+-x a y b r ；若点()00,M x y 在圆内，则()()22200x a y b r +-<-；若点()00,M x y 在圆上，则()()22200x a y b r +-=-．知识点4圆上的点到定点的最大、最小距离设圆心A 到定点C 的距离为d ，圆的半径为r ，圆上的动点为点P ．（1）若点C 在圆外时，max PC d r =+，min PC d r =-；（2）若点C 在圆上时，max 2PC r =，min 0PC =；（2）若点C 在圆内时，max PC d r =+，min PC r d =-．综上：max PC d r =+，min PC d r =-．考点一：求圆的标准方程例1．（23-24高二上·安徽马鞍山·月考）已知圆的圆心在(3,4)-，半径为5，则它的方程为（）A ．()()22345x y -+-=B ．()()223425x y +++=C ．22(3)(4)25x y ++-=D ．()()22345x y ++-=【变式1-1】（23-24高二上·山西太原·期末）已知圆C 的一条直径的两个端点坐标分别为()4,1-，()2,3，则圆C 的方程是.【变式1-2】（22-23高二上·广东东莞·期中）求经过点(2,0),(2,2)--且圆心在直线:0l x y +=上的圆的标准方程为.【变式1-3】（23-24高二下·云南玉溪·期中）过三点()()()120,01,33,1O M M ---､､的圆的标准方程是.考点二：点与圆的位置关系例2.（23-24高二上·安徽亳州·月考）（多选）已知()14,9P ，()26,3P 两点，以线段12PP为直径的圆为圆P ，则（）A ．()6,9M 在圆P 上B ．()3,3N 在圆P 内C ．()5,3Q 在圆P 内D ．()2,7R 在圆P 外【变式2-1】（23-24高二上·江苏·专题练习）已知点(,10)P a ，圆的标准方程为()()221112x y -+-=，则点P （）A ．在圆内B ．在圆上C ．在圆外D ．与a 的取值有关【变式2-2】（23-24高二上·重庆·期中）若点(),3A a 在圆()22:15C x y +-=外，则实数a 的取值范围是（）A ．(),1-∞-B ．(),1-∞C ．()(),11,-∞-⋃+∞D ．()1,1-【变式2-3】（23-24高二上·广西·期末）已知两直线2y x k =+与y x =-的交点在圆228x y +=的内部，则实数k 的取值范围是（）A ．11k -<<B ．2<<2k -C ．33k -<<D ．k <考点三：与圆有关的最值问题例3.（23-24高二上·湖北·期中）已知半径为2的圆经过点()3,4，则其圆心到原点的距离的最大值为（）A ．4B ．5C ．6D ．7【变式3-1】（23-24高二上·浙江湖州·月考）若实数x y ，满足221x y +=，则()()2234x y -+-的最大值是（）A ．5B ．6C ．25D ．36【变式3-2】（23-24高二上·上海·期末）已知P 为圆22(3)(4)4x y -+-=上一点，Q 为圆221x y +=上一点，则点Q 到点P 的距离的最大值为.【变式3-3】（23-24高二上·天津武清·月考）已知圆C :()()22124x y ++-=，点()2,0A -，()2,0B .设P 是圆C 上的动点，令22d PA PB =+，则d 的最小值为．考点四：与圆有关的对称问题例4.（23-24高二上·河南周口·期末）若曲线()()22124x y -+-=上相异两点P 、Q 关于直线20kx y --=对称，则k 的值为（）A ．1B ．2C ．3D ．4【变式4-1】（23-24高二上·云南昆明·月考）已知圆()()22124x y +++=关于直线10ax by ++=（0a >，0b >）对称，则12a b+的最小值为（）A ．52B ．9C ．4D ．8【变式4-2】（23-24高二上·河北·期中）已知圆M ：()2211x y ++=与圆N ：()()22231x y -+-=关于直线l 对称，则l 的方程为（）A ．210x y --=B ．210x y -+=C ．230x y +-=D ．230x y +-=【变式4-3】（23-24高二上·四川成都·期末）圆()()22:112C x y -+-=关于直线:1l y x =-对称后的方程为（）A ．()2222x y -+=B ．()2222x y ++=C ．()2222x y +-=D ．()2212x y ++=一、单选题1．（23-24高二上·广东湛江·期中）在平面直角坐标系中，圆心为()1,0，半径为2的圆的方程是（）A ．()2212x y -+=B ．()2212x y ++=C ．()2214x y -+=D ．()2214x y ++=2．（23-24高二上·河南开封·期末）已知圆M 经过点()()0,20,4,，且圆心M 在直线210x y --=上，则圆M 的面积为（）A ．2πB 5πC ．4πD ．5π3．（23-24高二上·安徽黄山·期末）圆22:(2)(1)1M x y -+-=与圆N 关于直线0x y -=对称，则圆N 的方程为（）A ．22(1)(2)1x y +++=B ．22(2)(1)1x y -++=C ．22(2)(1)1x y +++=D ．22(1)(2)1x y -+-=4．（23-24高二上·广东惠州·期中）点(,3)P m 与圆()()22212x y -+-=的位置关系为（）A ．点在圆外B ．点在圆内C ．点在圆上D ．与m 的值无关5．（2023高二上·全国·专题练习）点(1,1)--在圆22()()4x a y a ++-=的内部，则a 的取值范围是（）A ．11a -<<B ．01a <<C ．1a <-或1a >D ．1a =±6．（23-24高二上·浙江温州·期中）已知半径为2的圆经过点()3,4，则其圆心到原点的距离最小值为（）A ．1B ．2C ．3D ．4二、多选题7．（23-24高二上·四川宜宾·期末）已知圆C 经过点()0,0A 、()2,0B ，ABC 为直角三角形，则圆C 的方程为（）A ．()()22114x y -+-=B ．()()22112x y -++=C ．()()22112x y -+-=D ．()()22125x y -+-=8．（23-24高二上·重庆九龙坡·月考）若有一组圆k C ：()()()224R x k y k k -+-=∈，下列命题正确的是（）A ．所有圆k C 的半径均为2B ．所有的圆kC 的圆心恒在直线y x =上C ．当2k =时，点()3,0在圆k C 上D ．经过点()2,2的圆k C 有且只有一个三、填空题9．（23-24高二上·贵州毕节·期末）与圆222430x y x y +-++=有相同圆心，且过点()4,2-的圆的标准方程是.10．（22-23高二下·四川凉山·月考）若圆221:(1)9C x y -+=和圆222:(3)(2)9C x y +++=关于直线l 对称，则直线l 的方程是11．（23-24高二上·全国·专题练习）已知,x y 满足22(1)(2)16x y -+-=，则22x y +的取值范围是.四、解答题12．（23-24高二上·福建福州·期末）已知A 关于直线y x =对称，点()0,0O ，()4,0N 都在A 上.(1)求线段ON 垂直平分线的方程；(2)求A 的标准方程13．（23-24高二上·山东济南·期末）已知圆心为C 的圆经过()0,0O ，(0,A 两点，且圆心C 在直线:l y =上．(1)求圆C 的标准方程；(2)点P 在圆C 上运动，求22PO PA +的取值范围．。

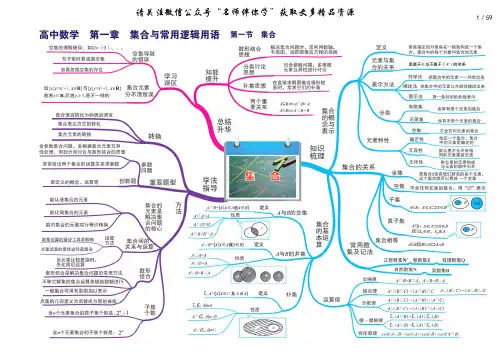
2024年新高二数学提升精品讲义直线的交点坐标与距离公式（原卷版）模块一思维导图串知识模块二基础知识全梳理（吃透教材）模块三核心考点举一反三模块四小试牛刀过关测1．会用解方程组的方法求两条相交直线的交点坐标；2．会根据方程解的个数判定两条直线的位置关系；3．会求两点间的距离、点到直线的距离、两条平行直线间的距离.知识点1两条直线的交点坐标1、点与坐标的一一对应关系几何元素及关系代数表示点P (,)P a b 直线l:0l Ax By C ++=点P 在直线l 上Aa Bb C ++=直线1l 与2l 的交点是P方程组11122200A xB yC A x B y C ++=⎧⎨++=⎩的解是x ay b =⎧⎨=⎩2、直线的交点与方程的解求两直线1111110(0)++=≠A x B y C A B C 与2222220(0)++=≠A x B y C A B C 的交点坐标，只需求两直线方程联立所得方程组1112220++=⎧⎨++=⎩A x B y C A x B y C 的解即可．若有111222==A B C A B C ，则方程组有无穷多个解，此时两直线重合；若有111222=≠A B C A B C ，则方程组无解，此时两直线平行；若有1122≠A B A B ，则方程组由唯一解，此时两直线相交，此解即两直线的交点坐标．3、判断两直线的位置关系关键是看两直线的方程组成的方程组的解的情况．（1）解方程组的重要思想就是消元，先消去一个变量，代入另外一个方程能解出另一个变量的值．（2）解题过程中注意对其中参数进行分类讨论．（3）最后把方程组解的情况还原为直线的位置关系．4、过两条直线交点的直线系方程一般地，具有某种共同属性的一类直线的集合称为直线系，它的方程叫做直线系方程，直线系方程中除含有,x y 以外，还有根据具体条件取不同值的变量，称为参变量，简称参数．由于参数取法不同，从而得到不同的直线系．经过两直线1111:0++=l A x B y C ，2222:0++=l A x B y C 交点的直线方程为111222()0+++++=A x B y C A x B y C λ，其中λ是待定系数．在这个方程中，无论λ取什么实数，都得不到2220++=A x B y C ，因此它不能表示直线2l ．知识点2两点间的距离1、距离公式：平面内两点()111,P x y ，()222,P x y 间的距离公式为：12=PP 【注意】公式中1P 和2P位置没有先后之分，也可以表示为：12=PP 2、三种特殊距离：（1）原点O 到任意一点(),P x y 的距离为=OP ；（2）当12PP 平行于x 轴时，1221=-PPx x ；（3）当12PP 平行于y 轴时，1221=-PP y y ．3、坐标法解题的基本步骤（1）建立适当的坐标系，用坐标表示有关的量；（2）进行有关代数运算；（3）把代数运算的结果“翻译”成几何关系．知识点3点到直线的距离1、定义：过一点向直线作垂线，则该点与垂足之间的距离，就是该点到直线的距离，即垂线段的长度．2、距离公式：点()00,P x y 到直线:0++=l Ax By C 的距离=d ．【注意】（1）直线方程应用一般式，若给出其他形式，应先化成一般式再用公式．（2）点到直线的距离是直线上的点与直线外一点的最短距离．（3）点到直线的距离公式适用任何情况，当点P 在直线l 上时，它到直线的距离为0．3、点到几种特殊直线的距离（1）点()00,P x y 到x 轴的距离0d y =；（2）点()00,P x y 到y 轴的距离0d x =；（3）点()00,P x y 到直线y a =的距离0d y a =-；（4）点()00,P x y 到直线x b =的距离0d x b =-．知识点4两条平行线间的距离1、定义：两条平行线间的距离是指夹在这两条平行线间的公垂线段的长．2、距离公式：两条平行直线11:0++=l Ax By C ，()2212:0++=≠l Ax By C C C ，它们之间的距离为：=d 【注意】在使用公式时，两直线方程为一般式，且x 和y 的系数对应相等．3、两平行线间的距离另外一种解法：转化为点到直线的距离，在任一条直线上任取一点（一般取直线上的特殊点），此点到另一条直线的距离即为两直线之间的距离．考点一：两条直线的交点问题例1．（23-24高二上·内蒙古呼伦贝尔·月考）直线1:3450l x y -+=与21:4303l x y --=的交点坐标为（）A ．(2,3)B ．7,33⎛⎫ ⎪⎝⎭C ．73,3⎛⎫ ⎪⎝⎭D ．3,37⎛⎫ ⎪⎝⎭【变式1-1】（23-24高二上·重庆长寿·期末）直线260x y -+=与直线3x y +=的交点坐标是（）A ．(30)，B ．(1,4)-C ．(3,6)-D ．(4,)1-【变式1-2】（23-24高二上·江苏·单元测试）已知直线250x y ++=与直线20kx y +=互相垂直，则它们的交点坐标为（）A ．()1,3--B ．()2,1--C ．1,12⎛⎫-- ⎪⎝⎭D ．()1,2--【变式1-3】（2023高二上·江苏·专题练习）分别判断下列直线l 1与l 2的位置关系，若相交，求出它们的交点坐标.(1)12:230,:210l x y l x y ++=--=；(2)12:310,:2620l x y l x y +-=+-=；(3)12:6230,:320l x y l x y -+=-+=.考点二：根据两直线交点求参数例2.（23-24高二上·北京·期中）已知直线420mx y +-=与250x y n -+=互相垂直，垂足为()1,P p ，则m n p -+的值是（）A ．24B ．0C ．20D ．4-【变式2-1】（23-24高二上·福建莆田·月考）若直线1:40l ax y +-=与直线22:0x y l --=的交点位于第一象限，则实数a 的取值范围是（）A ．()1,2-B ．()1,-+∞C ．(),2-∞D ．()(),12,-∞-+∞ 【变式2-2】（2023·海南海口·二模）若直线24y x =-+与直线y kx =的交点在直线2y x =+上，则实数k =（）A ．4B ．2C ．12D ．14【变式2-3】（23-24高二上·全国·课后作业）直线210x my ++=与直线1y x =+相交，则m 的取值范围为．考点三：三条直线的相交问题例3.（23-24高二上·安徽·月考）已知三条直线240,30,20x y kx y x y +-=-+=--=交于一点，则实数k =（）A ．1-B ．1C ．32-D ．14【变式3-1】（22-23高二上·山东聊城·月考）若三条直线370x y ++=，10x y --=，20x ny n ++=能围成一个三角形，则n 的值可能是（）A ．32B ．1C ．13-D ．12-【变式3-2】（23-24高二下·上海·期中）直线123:7210,:0,:10l x y l mx y l x my ++=+=+-=，若三条直线无法构成三角形，则实数m ）A ．3B ．4C ．5D ．6【变式3-3】（23-24高二上·湖南·期末）若三条不同的直线1:20l ax y ++=，2:10l x y +-=，3:30l x y -+=不能围成一个三角形，则a 的取值集合为（）A ．{1,1}-B ．{4,1}C ．1,12⎧⎫-⎨⎬⎩⎭D ．{4,1,1}-考点四：过两直线交点的直线方程例4.（23-24高二上·湖北武汉·月考）过两直线2023202210x y --=和2022202310x y ++=的交点且过原点的直线方程为．【变式4-1】（23-24高二上·全国·课后作业）经过点(1,0)P 和两直线1:220l x y +-=；2:3220l x y -+=交点的直线方程为.【变式4-2】（23-24高二上·安徽马鞍山·期中）平面直角坐标系xOy 中，过直线1:7310l x y -+=与2:430l x y +-=的交点，且在y 轴上截距为1的直线l 的方程为．（写成一般式）【变式4-3】（23-24高二·全国·假期作业）求过直线220x y -+=和10x y ++=的交点，且斜率为3的直线方程．考点五：两点间的距离公式例5.（23-24高二上·内蒙古呼伦贝尔·月考）已知()()3,6,2,4A B ，则A ，B 两点间的距离为（）A ．5B C ．3D【变式5-1】（23-24高二上·江苏徐州·期中）已知过(,2),(,1)A m B m m --两点的直线的倾斜角是45 ，则,A B 两点间的距离为（）A ．2B C ．D ．【变式5-2】（23-24高二上·天津·期末）三角形的三个顶点为()()()3,2,3,4,5,4A B C --，D 为AC 中点，则BD 的长为（）A ．3B ．5C ．9D ．25【变式5-3】（23-24高二上·海南·期中）在平面直角坐标系xOy 中，原点O 到直线1l ：240x y -+=与2l ：390x y +-=的交点的距离为（A B ．C D考点六：点到直线的距离公式例6.（23-24高二下·浙江·开学考试）已知点()0,3A 及直线:10l x y +-=上一点B ，则AB 的值不可能是（）A ．1B ．2C ．3D ．4【变式6-1】（23-24高二上·安徽马鞍山·月考）已知()3,4A --，()6,3B 两点到直线:10l ax y ++=的距离相等，求a 的值（）A ．13B ．97-C ．13-或79-D ．13或79-【变式6-2】（22-23高二上·云南临沧·月考）若点()3,1P 到直线:340(0)l x y a a ++=>的距离为4，则=a （）A ．2B ．3C ．5D ．7【变式6-3】（23-24高二上·广西南宁·月考）已知(4,0)A 到直线430x y a -+=的距离等于3，则a 的值为.考点七：平行线间的距离公式例7.（23-24高二上·河北石家庄·月考）两平行直线1:10l x y +-=和2:30l x y +-=之间的距离为（）A ．2B ．2C ．22D ．3【变式7-1】（23-24高二上·湖北孝感·期末）两条平行直线3420x y --=与6810x y -+=间的距离为（）A ．35B ．1C ．310D ．12【变式7-2】（23-24高二上·贵州铜仁·月考）（多选）已知两条平行直线m ，n ，直线:3420m x y ++=，直线:680n x y a ++=，直线m ，n 之间的距离为1，则a 的值可以是（）A ．8-B ．6-C ．12D ．14【变式7-3】（23-24高二上·广东茂名·期末）（多选）已知两条平行直线,m n ，直线:10m x y +-=，直线:220n x y a ++=，直线,m n 之间的距离为2，则a 的值可以是（）A ．-8B ．-6C ．2D ．4考点八：点与直线的对称问题例8.（22-23高二·全国·课堂例题）已知不同的两点(),P a b -与()1,1Q b a +-关于点()3,4对称，则ab =（）A ．5-B ．14C ．14-D ．5【变式8-1】（23-24高二上·安徽怀宁·月考）直线2360x y +-=关于点(1,1)对称的直线方程为（）A ．3220x y -+=B ．2370x y ++=C ．32120x y --=D ．2340x y +-=【变式8-2】（23-24高二下·四川雅安·开学考试）点()3,0关于直线30x y -+=对称的点的坐标为（）A ．()3,6B ．()6,3-C ．()6,3-D ．()3,6-【变式8-3】（23-24高二上·河北石家庄·月考）直线1y x =+关于直线2y x =对称的直线方程为（）A ．310x y --=B ．420x y --=C ．530x y --=D ．750x y --=一、单选题1．（23-24高二上·新疆喀什·期中）已知(6,0),(2,0)A B -，则||AB =（）A ．3B ．4C ．6D ．82．（23-24高二上·安徽马鞍山·月考）原点到直线912100x y +-=间的距离是（）A ．23B ．13C ．1D ．253．（23-24高二上·福建三明·期末）两条平行线1:220l x y +-=，2:690l ax y +-=间的距离等于（）ABCD4．（23-24高二上·浙江杭州·期中）已知1212//,:240,:620l l l x y l x ay ++=++=,则它们的距离为（）A．15BCD．35．（23-24高二上·四川绵阳·期末）已知()2,0A -，()4,B m 两点到直线l ：10x y -+=的距离相等，则m =（）A ．2-B ．6C ．2-或4D ．4或66．（23-24高二上·湖南·期中）已知()111,P x y ，()222,P x y 是直线2023y kx =+（k 为常数）上两个不同的点，则关于x 和y 的方程组112211x x y y x x y y +=⎧⎨+=⎩的解的情况，下列说法正确的是（）A ．无论k ，1P ，2P 如何，总是无解B ．无论k ，1P ，2P 如何，总有唯一解C ．存在k ，1P ，2P ，使12x y =⎧⎨=⎩是方程组的一组解D ．存在k ，1P ，2P ，使之有无穷多解二、多选题7．（22-23高二上·全国·期中）若直线1:32l y kx k =+-与直线2:30l x y +-=的交点在第四象限，则实数k 的取值可以是（）A ．0B ．13C ．12-D ．1-8．（23-24高二上·河南商丘·月考）（多选）平面上有三条直线250,10,0x y x y x ky -+=++=-=，将平面划分为六个部分，则实数k 的所有可能取值为（）A ．12B ．1-C ．2-D ．1三、填空题9．（22-23高二上·云南昆明·期中）在△ABC 中，点(1,1)A ，(4,2)B ，(4,1)C -，则ABC 的面积为．10．（2023高二上·全国·专题练习）直线230x y -=与321x y -=上任意两点最小距离为.11．（23-24高二下·上海黄浦·期中）已知直线1:40l x y +=，2:1l mx y +=，3:234l x my -=，若它们不能围成三角形，则实数m 的取值所构成的集合为．四、解答题12．（23-24高二上·山西大同·月考）已知直线:2310l x y -+=，点()1,2--A ．求：(1)点A 关于直线l 的对称点A '的坐标；(2)直线:3260m x y --=关于直线l 的对称直线m '的方程；(3)直线l 关于点()1,2--A 对称的直线l '的方程．13．（22-23高二上·云南临沧·月考）已知直线12:340,:3220l x y l x y --=-+=，设直线12,l l 的交点为P .(1)求点P 的坐标；(2)若直线l 过点P 且在两坐标轴上的截距相等，求直线l 的方程.。

基本不等式实际是对勾函数的特例，可以考虑利用对勾实际应用题考虑解析式有意义且考虑实际问题有意义
解析式表示的斜率、截距、距离等几何意义一般适用含有绝对值的函数
6种基本函数及其加减形式
形如f[g(x)]
确定函数的定义域．
将复合函数分解成基本初等函数y ＝f(u)，u ＝g(x)．分别确定这两个函数的单调区间．如果一个函数的图像沿一个点旋转180度，所得的图像能与原函数图像完全重合，则称该函数具备对称性中的中心对称，对称轴是两个横坐标的中点
对称中心为函数对称两点的中点，可以利用中点坐标
如果一个奇函数f(x)在原点处有定义，即f(0)有意义，那么一定有奇偶性的判断利用奇偶性求解析式公
众
么
难。