连续时间系统卷积的计算

第二章连续信号的时域分析所谓信号的时域分析，指的是整个分析过程都在时间域内进行，分析过程中所有的信号都用以时间t为自变量的时间函数表达式或时间波形图表示。

本章首先介绍几个典型的连续时间信号，以及对这些信号的基本运算。

此外，连续信号的卷积积分也是信号与系统时域分析中的基本运算，本章将详细介绍卷积积分的定义及其运算方法。

2.1 基本要求1．基本要求♦了解基本的连续信号及其相关参数和描述；♦了解信号的基本运算；♦掌握阶跃信号和冲激信号的定义、性质及作用；♦掌握卷积积分的定义、性质及计算。

2．重点和难点♦冲激信号的定义及性质♦含有阶跃和冲激函数的信号的求导和求积分运算♦卷积积分的计算2.2 知识要点1．基本的连续信号了解正弦信号、实指数信号、复简谐信号、门信号及抽样函数信号的函数表达式、时间波形及其相关参数。

2．信号的基本运算从数学意义上看，系统对信号的处理和变换就是对信号进行一系列的运算。

一个复杂的运算可以分解为一些基本运算的组合。

本章主要了解信号的加减乘除运算、翻转平移和尺度变换、微积分等几种基本的运算。

所有运算既可以利用信号的时间函数表达式进行，也可以在时间波形图上进行运算。

注意与数学上相关运算的区别。

这里强调，作为信号基本运算之一的积分运算，运算结果得到的是一个新的以t 为自变量的函数，具体表示符号和定义为⎰∞--=tf t fττd )()()1( （2-1）3．阶跃信号和冲激信号阶跃信号和冲激信号是对实际系统中的某类信号进行理想近似后得到的两个特殊信号，这两种信号用于描述一类特殊的物理现象，对于信号特性和系统性能的分析，起着十分重要的作用。

阶跃信号和冲激信号的时间波形如图2-1所示。

在信号与系统的分析过程中，经常利用阶跃函数将分段信号的时间函数表达式统一为一个解析表达式，以简化信号的运算。

利用阶跃函数还可以方便地表示因果、非因果信号等。

由于阶跃函数和冲激函数是两个特殊的函数，因此在进行求导和求积分等运算时，必须根据其定义和性质对函数表达式进行分析，以便化为普通函数的运算。

信号与系统-公式总结信号与系统是电子信息类专业中的一门核心课程，主要研究信号的产生、变换、传输和处理过程，以及系统对信号的响应和处理。

信号与系统的学习需要掌握大量的数学知识和公式，下面就是信号与系统中一些重要的公式总结。

1. 信号的分类和表示：- 狄拉克脉冲函数：δ(t)- 单位阶跃函数：u(t)- 奇函数和偶函数性质：x(t) = x(-t) 和 x(t) = -x(-t)- 周期信号的频率和周期关系：f = 1/T2. 傅里叶变换：- 连续时间傅里叶变换（CTFT）：X(jω)= ∫[−∞,∞]x(t)e^(-jωt)dt- 傅里叶反变换：x(t) = (1/2π) ∫[−∞,∞]X(jω)e^(jωt)dω- 周期信号的傅里叶级数展开：x(t) = ∑[k=−∞,∞]c(k)e^(jωk0t) - 频谱为实数的信号的性质：X(jω) = X*(−jω)3. 拉普拉斯变换：- 连续时间拉普拉斯变换（CTLT）：X(s) = ∫[−∞,∞]x(t)e^(-st)dt- 拉普拉斯反变换：x(t) = (1 / 2πj) ∫[σ-j∞,σ+j∞]X(s)e^(st)ds- 零极点的性质：如果x(t)的拉普拉斯变换X(s)的极点位于左半平面，那么系统是稳定的。

4. Z变换：- 离散时间Z变换（DTZT）：X(z) = ∑[n=−∞,∞]x(n)z^(-n) - Z反变换：x(n) = (1 / 2πj) ∮ X(z)z^(n-1)dz- 零极点的性质：如果X(z)的极点的模都小于1，则系统是稳定的。

5. 系统函数和频率响应：- 系统函数：H(s) = Y(s) / X(s) = L{h(t)}- 系统函数的零极点分解：H(s) = (s-z1)(s-z2)...(s-zn) / (s-p1)(s-p2)...(s-pm)- 频率响应：H(jω) = |H(jω)|e^(jφ(ω))6. 系统的时域响应和频域响应：- 系统的单位冲激响应：h(t) = L^{-1}{H(s)} 或 h(n) = Z^{-1}{H(z)}- 系统的频域响应：H(s) = ∫[−∞,∞]h(t)e^(-st)dt 或 H(z) =∑[n=−∞,∞]h(n)z^(-n)7. 信号的卷积运算：- 连续时间信号的卷积：y(t) = x(t) * h(t) = ∫[−∞,∞]x(t-τ)h(τ)dτ - 离散时间信号的卷积：y(n) = x(n) * h(n) = ∑[k=-∞,∞]x(k)h(n-k)8. 频域中的乘法和卷积：- 频域乘法：y(t) = x(t)h(t) = x(t) ⊗ h(t)- 频域卷积：y(t) = x(t) * h(t) = X(jω)H(jω)9. 系统的稳定性：- 连续时间系统的稳定性：系统零极点的实部都小于0时，系统是稳定的。

《信号与系统》课程实验报告《信号与系统》课程实验报告一图1-1 向量表示法仿真图形2．符号运算表示法若一个连续时间信号可用一个符号表达式来表示，则可用ezplot命令来画出该信号的时域波形。

上例可用下面的命令来实现（在命令窗口中输入，每行结束按回车键）。

t=-10:0.5:10;f=sym('sin((pi/4)*t)');ezplot(f,[-16,16]);仿真图形如下：图1-2 符号运算表示法仿真图形三、实验内容利用MATLAB实现信号的时域表示。

三、实验步骤该仿真提供了7种典型连续时间信号。

用鼠标点击图0-3目录界面中的“仿真一”按钮，进入图1-3。

图1-3 “信号的时域表示”仿真界面图1-3所示的是“信号的时域表示”仿真界面。

界面的主体分为两部分：1) 两个轴组成的坐标平面（横轴是时间，纵轴是信号值）；2) 界面右侧的控制框。

控制框里主要有波形选择按钮和“返回目录”按钮，点击各波形选择按钮可选择波形，点击“返回目录”按钮可直接回到目录界面。

图1-4 峰值为8V，频率为0.5Hz，相位为180°的正弦信号图1-4所示的是正弦波的参数设置及显示界面。

在这个界面内提供了三个滑动条，改变滑块的位置，滑块上方实时显示滑块位置代表的数值，对应正弦波的三个参数：幅度、频率、相位；坐标平面内实时地显示随参数变化后的波形。

在七种信号中，除抽样函数信号外，对其它六种波形均提供了参数设置。

矩形波信号、指数函数信号、斜坡信号、阶跃信号、锯齿波信号和抽样函数信号的波形分别如图1-5～图1-10所示。

图1-5 峰值为8V，频率为1Hz，占空比为50%的矩形波信号图1-6 衰减指数为2的指数函数信号图1-7 斜率=1的斜坡信号图1-8 幅度为5V，滞后时间为5秒的阶跃信号图1-9 峰值为8V，频率为0.5Hz的锯齿波信号图1-10 抽样函数信号仿真途中，通过对滑动块的控制修改信号的幅度、频率、相位，观察波形的变化。

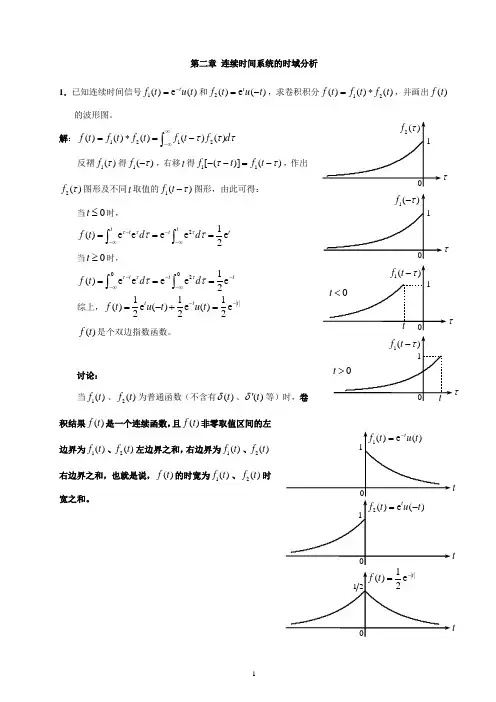
第二章 连续时间系统的时域分析1．已知连续时间信号1()e ()t f t u t -=和2()e ()t f t u t =-，求卷积积分12()()()f t f t f t =*，并画出()f t 的波形图。

解：1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰反褶1()f τ得1()f τ-，右移t 得11[()]()f t f t ττ--=-，作出2()f τ图形及不同t 取值的1()f t τ-图形，由此可得：当0t ≤时，21()e e ee e 2ttt tt f t d d τττττ---∞-∞===⎰⎰当0t ≥时，0021()e e e e e 2t t t f t d d τττττ----∞-∞===⎰⎰综上，||111()e ()e ()e 222t t t f t u t u t --=-+=()f t 是个双边指数函数。

讨论：当1()f t 、2()f t 为普通函数（不含有()t δ、()t δ'等）时，卷积结果()f t 是一个连续函数，且()f t 非零取值区间的左边界为1()f t 、2()f t 左边界之和，右边界为1()f t 、2()f t 右边界之和，也就是说，()f t 的时宽为1()f t 、2()f t 时宽之和。

τttt2．计算题图2（a ）所示函数)(1t f 和)(2t f 的卷积积分)()()(21t f t f t f *=，并画出)(t f 的图形。

解法一：图解法1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰其中1()f t τ-的波形见题图2(b)，由此可得： 当10t +≤，即1t ≤-时，()0f t = 当011t ≤+≤，即10t -≤≤时，120()2(1)t f t d t ττ+==+⎰当11t +≥但10t -≤，即01t ≤≤时，1()21f t d ττ==⎰当011t ≤-≤，即12t ≤≤时，121()21(1)t f t d t ττ-==--⎰当11t -≥，即2t ≥时，()0f t =综上，220,1,2(1),10()1,011(1),12t t t t f t t t t ≤-≥⎧⎪+-≤≤⎪=⎨≤≤⎪⎪--≤≤⎩ ()f t 波形见题图2(c)。

信号与系统第一章1。

1 连续时间与离散时间信号确知信号可以表示成一个或几个自变量的函数连续时间信号在［t1，t2］区间的能量定义为：连续时间信号在［t1,t2］区间的平均功率定义为：离散时间信号在［n1,n2］区间的能量定义为离散时间信号在[n1，n2]区间的平均功率为在无限区间上也可以定义信号的总能量：连续时间情况下:离散时间情况下:在无限区间内的平均功率可定义为： 21lim 2()TTT P dtTx t ∞-→∞=⎰能量信号——信号具有有限的总能量，即：功率信号—-信号有无限的总能量,但平均功率有限。

即：信号的总能量和平均功率都是无限的。

即:如果信号是周期信号，则或这种信号也称为功率信号，通常用它的平均功率来表征或或如果信号是非周期的，且能量有限则称为能量信号。

1.2 自变量的变换1.时移变换当时，信号向右平移时，信号向左平移当时，信号向右平移 时，信号向左平移,0E P ∞∞<∞=,E P ∞∞=∞=∞2。

反转变换信号以t=0为轴呈镜像对称。

与连续时间的情况相同。

3. 尺度变换时，是将在时间上压缩a倍,时,是将在时间上扩展1/a倍。

由于离散时间信号的自变量只能取整数值，因而尺度变换只对连续时间信号而言。

周期信号与非周期信号：周期信号：满足此关系的正实数（正整数)中最小的一个，称为信号的基波周期（）。

可视为周期信号，但它的基波周期没有确定的定义。

可以视为周期信号,其基波周期。

奇信号与偶信号：对实信号而言：如果有和则称该信号是偶信号。

（镜像偶对称）如果有和则称该信号为奇信号。

(镜像奇对称）对复信号而言：如果有和则称该信号为共轭偶信号.如果有和则称为共轭奇信号。

任何信号都能分解成一个偶信号与一个奇信号之和。

对实信号有：其中其中对复信号有：其中：其中：1。

3 复指数信号与正弦信号一. 连续时间复指数信号与正弦信号其中C, a 为复数1. 实指数信号：C,a 为实数呈单调指数上升呈单调指数下降。

信号与系统概念，公式集：第一章：概论1.信号：信号是消息的表现形式。

（消息是信号的具体内容）2.系统：由若干相互作用和相互依赖的事物组合而成的具有特定功能的整体。

第二章：信号的复数表示：1.复数的两种表示方法：设C 为复数，a 、b 为实数。

常数形式的复数C=a+jb a 为实部，b 为虚部；或C=|C|e j φ，其中，22||b a C +=为复数的模，tan φ=b/a ，φ为复数的辐角。

（复平面）2.欧拉公式：wt j wt e jwtsin cos +=（前加-，后变减） 第三章：正交函数集及信号在其上的分解1.正交函数集的定义：设函数集合)}(),(),({21t f t f t f Fn =如果满足：ni K dt t f j i dt t f t f iT T i T T j i 2,1)(0)()(21212==≠=⎰⎰则称集合F 为正交函数集 如果n i K i,2,11==，则称F 为标准正交函数集。

如果F 中的函数为复数函数条件变为：ni K dt t f t f j i dt t f t f iT T i i T T j i 2,1)()(0)()(2121**==⋅≠=⋅⎰⎰其中)(*t f i 为)(t f i 的复共轭。

2.正交函数集的物理意义：一个正交函数集可以类比成一个坐标系统；正交函数集中的每个函数均类比成该坐标系统中的一个轴； 在该坐标系统中，一个函数可以类比成一个点；点向这个坐标系统的投影（体现为该函数与构成坐标系的函数间的点积）就是该函数在这个坐标系统中的坐标。

3.正交函数集完备的概念和物理意义：如果值空间中的任一元素均可以由某正交集中的元素准确的线性表出，我们就称该正交集是完备的，否则称该正交集是不完备的。

如果在正交函数集()()()()t g n ,t g ,t g ,t g 321之外，不存在函数x （t ）()∞<<⎰2120t t dt t x ，满足等式：()()⎰=210t t i dt t g t x ，则此函数集称为完备正交函数集。

信号与系统常用公式信号与系统是现代电子信息工程学科中的重要基础课程，它涉及到了信号的产生、传输和处理等方面的知识。

在学习和应用信号与系统的过程中，我们经常会使用到一些公式和定理。

本文将为大家介绍一些信号与系统中常用的公式和定理，希望能对大家的学习和工作有所帮助。

一、信号的基本性质：1.基本信号及其性质：矩形信号：rect(t/T) =1，-T/2≤t≤T/20，其他三角信号：tri(t/T) =1-，t/T，-T≤t≤T0，其他正弦信号：sin(ωt) = （e^jωt - e^(-jωt))/(2j)余弦信号：cos(ωt) = （e^jωt + e^(-jωt))/22.对称性：奇对称信号：如果s(t)=-s(-t)，则s(t)是奇对称信号。

偶对称信号：如果s(t)=s(-t)，则s(t)是偶对称信号。

3.平均功率：平均功率：P = lim(T→∞)1/T ∫_(T/2)^(T/2) ，s(t)，^2 dt4.交流分量：交流分量：s_AC=1/2*[s(t)-s_DC]二、线性时不变系统的基本性质：1.线性时不变系统的定义：线性性：s_1(t)+s_2(t)—>LTI—>s_1(t)+s_2(t)时不变性：s(t-t_0)—>LTI—>s(t-t_0)2.系统的冲激响应：系统的冲激响应：h(t) = d(s(t))/dt，其中d是微分算子。

3.系统的单位阶跃响应：系统的单位阶跃响应：H(t)=∫_(-∞)^th(τ)dτ4.线性卷积定理：线性卷积定理：s_1(t)*s_2(t)—>LTI—>S_1(ω)*S_2(ω)三、频域分析：1.傅里叶级数：傅里叶级数：s(t)=∑_(n=-∞)^∞C_n*e^(jω_nt)，其中C_n是频谱系数，ω_n是频率。

2.傅里叶变换：傅里叶变换：S(ω) = ∫_(-∞)^∞ s(t) * e^(-jωt) dt3.周期信号的频谱：周期性信号的频谱：S(ω)=∑_(k=-∞)^∞(1/T)*S(kω_0)*δ(ω-kω_0)，其中S(kω_0)是周期频谱系数。

离散卷积：1. 找出以下离散时间系统的脉冲响应： )[]0.2[1][][1]a y n y n x n x n +-=-- )[] 1.2[1]2[1]b y n y n x n +-=-)[]0.24([][1][2][3])c y n x n x n x n x n =+-+-+- )[][]0.5[1][2]d y n x n x n x n =+-+-2. 计算以下卷积，x[n]*v[n])[][][4],[]0.5[]n a x n u n u n v n u n =--=)[][1482],[][01234](n )b x n v n ==顺序均从=0开始)[][],[]2(0.8)[]n c x n u n v n u n == )[][1],[]2(0.5)[]n d x n u n v n u n =-=1. )[]0.2[1][][1]a y n y n x n x n +-=--[]0.2[1][][1]h n h n n n δδ+-=--1[0]0.2[1][0][1]1[1]0.2[0][1][0] 1.2[2]0.2[1][2][1]0.24[3]0.2[2][3][2]0.048[](0.2)( 1.2)n h h h h h h h h h n δδδδδδδδ-=--+--==-+-=-=-+-==-+-=-=--≥当n 1)[] 1.2[1]2[b y n y n x n +-=-[] 1.2[1]2[1]h n h n n δ+-=-21[0] 1.2[1]2[1]0[1] 1.2[0]2[0]2[2] 1.2[1]2[1] 1.2(2)[3] 1.2[2]2[2]( 1.2)(2)[]( 1.2)(2)n 1n h h h h h h h h h n δδδδ-=--+-==-+==-+=-=-+=-=-≥当时)[]0.24([][1][2][c y n x n x n x n x n =+-+-+-[]0.24([][1][2][3])0.24030h n n n n n n δδδδ=+-+-+-≤≤⎧=⎨⎩其它)[][]0.5[1][d y n x n x n x n =+-+-[][]0.5[1][2]100.51[]120h n n n n n n h n n n δδδ=+-+-=⎧⎪=⎪=⎨=⎪⎪⎩为其它值2.5450)[][][4],[]0.5[]012040.50.50.50.512n n knn n k a x n u n u n v n u n n --==--=-≤≤===-+-∑[]*[][][]([][4])0.5[]k n kk x n u n x k v n ku ku k u n k +∞=-∞+∞-=-∞=-=---∑∑如果04n ≤≤ 10120.50.5(0.52)12n nn knn k +-=-===---∑如果n>4 5450120.50.50.50.512n knn n k --=-===-+-∑)[][1482],[][01234](n )b x n v n ==顺序均从=0开始[]148200000[]0123400000123416328048122460816402[][0161934443880]x n v n y n === )[][],[]2(0.8)[]n c x n u n v n u n ==01n[]*[][]2(0.8)[]2(0.8)2(0.8)(0.8)1 1.2521 1.258[0.8 1.25],08(0.8)10,n kk nnn knkk k n n n x n v n u k u n k n n +∞-=-∞--==+=-==-=-=--≥=-+≥∑∑∑（0.8）)[][1],[]2(0.5)[]n d x n u n v n u n =-=110112[]*[][1]2(0.5)[]2(0.5)2(0.5)22(0.5)(21)122(0.5)[1]122(0.5)(22)(0.5)4,1nk nn kk nnkk nn k k n nn n n x n v n u k u n k n +∞=-∞-===++-=--===--=--=-+=-+≥∑∑∑∑连续时间卷积：1．求出以下卷积()()*()y t x t h t =，其中()()(4);()()x t u t u t h t r t =--= 2．计算以下卷积：3. 如果()sin(2)()h t t u t =，计算系统对输入()2(10)x t u t =-的响应。

连续时间信号的卷积与相关计算连续时间信号的卷积和相关计算是信号处理中常见的操作。

卷积是通过将两个信号进行叠加积分来获得新的信号。

给定两个连续时间信号f(t)和g(t)，它们的卷积表示为(f * g)(t)，计算公式如下：
(f * g)(t) = ∫[f(τ)g(t-τ)]dτ
其中，τ是积分变量。

卷积的结果是一个新的信号h(t)，它包含着两个信号f(t)和g(t)间的相互影响。

相关计算用于衡量两个信号之间的相似性。

给定两个连续时间信号f(t)和g(t)，它们的相关函数表示为R(t)，计算公式如下：
R(t) = ∫[f(τ)g(t+τ)]dτ
相关计算中，τ也是积分变量。

通过计算相关函数的值，可以了解信号f(t)和g(t)的相似程度。

卷积和相关计算在信号处理中具有广泛的应用。

它们可以用于滤波、系统建模、特征提取等任务，有助于理解和处理连续时间信号的特性。

信号与系统常用公式汇总_1.傅里叶级数公式：信号x(t)的周期为T时，它的傅里叶级数展开式为：x(t) = a0 + Σ(an*cos(nω0t) + bn*sin(nω0t))，其中n为整数，ω0 = 2π/T，an和bn为傅里叶系数。

2.傅里叶变换公式：连续时间信号x(t)的傅里叶变换为：X(ω) = ∫( -∞到+∞ ) x(t)*e^(-jωt)dt。

3.逆傅里叶变换公式：连续频率信号X(ω)的逆傅里叶变换为：x(t)=(1/2π)*∫(-∞到+∞)X(ω)*e^(jωt)dω。

4.傅里叶变换对称性：X(-ω)=X(ω)*，即傅里叶变换对称于原点。

5.卷积定理：连续时间卷积的傅里叶变换等于信号的傅里叶变换之积，即：x(t)*h(t)的傅里叶变换为X(ω)*H(ω)。

6.系统频率响应：系统的频率响应H(ω)是指系统对频率为ω的输入信号的增益和相位的影响。

7.系统单位冲激响应：系统对单位冲激信号δ(t)的响应称为系统的单位冲激响应h(t)。

8.系统的冲激响应和频率响应的关系：系统的冲激响应h(t)和频率响应H(ω)满足傅里叶变换的关系：H(ω) = ∫( -∞到+∞ ) h(t)*e^(-jωt)dt。

9.系统的传递函数：系统的传递函数H(ω)是频率响应H(ω)的傅里叶变换。

10.系统的单位阶跃响应：系统对单位阶跃信号u(t)的响应称为系统的单位阶跃响应s(t)。

11.傅里叶变换的线性性质：对于信号x(t)和y(t)和常数a和b，有以下性质：a*x(t)+b*y(t)的傅里叶变换为a*X(ω)+b*Y(ω)。

12.傅里叶变换的时移性质：对于信号x(t)，有以下性质：x(t-t0)的傅里叶变换为e^(-jωt0)*X(ω)。

13.周期信号的傅里叶变换：周期信号x(t)的傅里叶变换可以通过傅里叶级数的频谱乘以δ函数的序列得到。

14.采样定理：若连续时间信号x(t)的带宽为BHz，则它的采样频率应大于2BHz，以避免采样失真。

《信号与信息系统》专业课程考试大纲
第一部分通信原理
考试题型：选择题、概念问答题、计算题
总分：60分
一、基本概念
通信系统的基本构成单元；模拟与数字系统、模拟信号与数字信号基本概念；如何客观评价一个通信系统，通信系统性能与资源、复杂度等之间的折中。

二、随机过程
随机信号基本概念；随机信号统计特性；随机信号通过线性系统；高斯白噪声，窄带高斯白噪声。

三、连续波模拟调制
信号与系统基础知识；连续波幅度调制的四种方式（DSB-LC, DSB-SC, SSB, VSB）的调制解调原理，抗噪声性能；FM、PM的调制解调原理，抗噪声性能。

四、脉冲调制
抽样定理；均匀量化与非均匀量化；PCM与DM。

五、数字传输
数字传输的基本原理；数字基带传输与数字频带传输概念；
奈奎斯特第一准则；传输带宽与码速率、比特速率之间关系；
二进制数字调制解调原理；M-ASK, M-PSK, M-QAM调制解调原理；
数字频带信号的等效基带表示，信号空间与星座点；
最佳接收机，匹配滤波器与相关接收机形式，误码率计算；
信道容量概念及其与功率、带宽之间的关系。

第二部分数字信号处理
考试题型：选择题、计算题
总分：50分
一、离散时间信号及系统:
DSP系统的构成；采样与量化；序列及运算；线性移不变系统；常系数线性差分方程
二、z变换
Z变换；Z变换收敛域，稳定性(证明)；Z反变换；Z变换性质。